ISCMF: Integrated similarity-constrained matrix factorization for drug–drug interaction prediction

Abstract

Drug–drug interaction (DDI) prediction prepares substantial information for drug discovery. As the exact prediction of DDIs can reduce human health risk, the development of an accurate method to solve this problem is quite significant. Despite numerous studies in the field, a considerable number of DDIs are not yet identified. In the current study, we used Integrated Similarity-constrained matrix factorization (ISCMF) to predict DDIs. Eight similarities were calculated based on the drug substructure, targets, side effects, off-label side effects, pathways, transporters, enzymes, and indication data as well as Gaussian interaction profile for the drug pairs. Subsequently, a non-linear similarity fusion method was used to integrate multiple similarities and make them more informative. Finally, we employed ISCMF, which projects drugs in the interaction space into a low-rank space to obtain new insights into DDIs. However, all parts of ISCMF have been proposed in previous studies, but our novelty is applying them in DDI prediction context and combining them. We compared ISCMF with several state-of-the-art methods. The results show that It achieved more appropriate results in five-fold cross-validation. It improves AUPR, and F-measure to 10% and 18%, respectively. For further validation, we performed case studies on numerous interactions predicted by ISCMF with high probability, most of which were validated by reliable databases. Our results provide support for the notion that ISCMF might be used unequivocally as a powerful method for predicting the unknown DDIs. The data and implementation of ISCMF are available at https://github.com/nrohani/ISCMF.

1 Introduction

Predicting drug–drug interactions (DDIs) as one of the most vital issues in drug discovery has attracted huge attention (Magnus et al. 2002; Bjornsson et al. 2003; Percha and Altman 2013). Interaction between drugs can cause unpredictable side effects that, in some cases are severe and harmful for patients (Lazarou et al. 1998; Prueksaritanont et al. 2013; Kusuhara 2014). In recent years, a specific trend in mathematics has been developed for the prediction of DDIs using computations (Magnus et al. 2002; Bjornsson et al. 2003; Percha and Altman 2013; Rohani and Eslahchi 2019). Assessment of any hypothesis, even on a small set of unknown DDIs, requires time-consuming, expensive experiments (Hanton 2007), but an accurate machine learning techniques can be helpful and reduce the costs.

DDI inference is performed based on various types of information that are available such as similarity matrices. Vilar et al. (2012) have devised a neighbor recommender algorithm that exploits the substructure similarity of drugs. Afterward, Zhang et al. have proposed an integrative label propagation method via a random walk on the labeled weighted similarity network Zhang et al. (2015). These methods are hampered by exploiting only one or a few types of drug information. Each type of drug data might be useful to disclose the patterns of interactions. Accordingly, Zhang et al. (2017) have proposed an ensemble method, which uses a mixture of basic biological and network-based similarities. It applies the neighbor recommender, label propagation, and matrix perturbation methods. At last, two ensemble rules for integrating methods are adopted to aggregate these models. While ensemble methods present excellent performance, acquiring higher prediction accuracy is still hugely required.

In the current work, we propose “ISCMF”, an integrated similarity-constrained matrix factorization, for DDI prediction. Recently, matrix factorization provides a simple but powerful mathematical basis for modeling various systems in real-life situations (Koren et al. 2009), and also in bioinformatics problems (Stražar et al. 2016; Zhang et al. 2017). Matrix factorization can learn latent features from the topological structure of a graph. These latent features have been shown to result in better performance, especially when we combine these latent features with explicit features for nodes or edges (Menon and Elkan 2011). Our study was inspired by a similarity constrained matrix factorization for drug-disease interaction prediction proposed by Zhang et al. (2018). This model combines three types of data, including latent features, explicit features for drugs, and DDI data. These three types of data provide a valuable source of inference. Furthermore, for the explicit features of drugs, we use various explicit features for drugs and compute various drug–drug similarities to have a more informative perspective. ISCMF uses several types of drug similarities and integrates them by Similarity network fusion (SNF) method Wang et al. (2014). ISCMF finds latent features based on integrated similarity and known DDIs.

The evaluations done by cross-validation and case-studies fully demonstrate the ISCMF efficiency in biomedical researches. Our findings suggest that integrating different features can provide a more comprehensive view to predict unknown DDIs, and hence, more satisfactory results will be achieved.

2 Materials and method

2.1 Databases

Various databases exist which supply some information about drugs such as:

• TWOSIDES (Tatonetti et al. 2012): contains DDIs from unsafe co-prescriptions.

• KEGG (Kanehisa et al. 2009): provides the protein pathways of the drug targets.

• SIDER (Kuhn et al. 2010): includes information about side effects, adverse drug reactions and the indication of drugs.

• OFFSIDES (Tatonetti et al. 2012): contains the side effect information about the drugs which are not still accepted (off-label side effects).

• PubChem (Wang et al. 2009; Li et al. 2010): provides chemical information about drug structures.

• DrugBank (Wishart et al. 2006; Knox et al. 2010; Law et al. 2013; Wishart et al. 2007): includes comprehensive information about drug enzymes, drug transporters, and drug targets.

To evaluate the robustness of ISCMF, we adopted the benchmark of Zhang et al. (2017), which includes 584 drugs and 48,584 DDIs (about 0.14 % of pairs). Thus, a large ratio of drug pairs is unlabeled. Besides DDI data, eight types of drug similarities were obtained from benchmark are calculated based on different drug features, including drug substructure, targets, side effects, off-label side effects, pathways, transporters, enzymes, and indication data from mentioned databases. More information about drug features and similarities is available in Supplementary File 1.

2.1.1 Gaussian interaction profile

In addition to eight similarities based on various drug data types, Gaussian interaction profile (GIP) of drug pairs was also regarded as an additional similarity, defined by van Laarhoven et al. (2011). Let $D_{n\times n} =[d_{ij}]$ be the interaction matrix of drugs based on known DDIs; that $d_{ij} =1$ indicates interaction between drugs i and j, while $d_{ij} =0$ denotes unknown interaction. GIP, for drugs i and j is :

$$\begin{aligned} \mathrm{GIP}_{d}(I,j)= \mathrm{exp} (-\gamma _d (d_{i}-d_{j})^2), \end{aligned}$$

(1)

where $d_{i}$ is the ith row of D and $\gamma _d$ controls the bandwidth. We set

$$\begin{aligned} \gamma _d=\tilde{\gamma _d}/\left( \frac{1}{n}\sum _{i=1}^{n}|d_{i}|^2\right) \end{aligned}$$

(2)

To make GIP values independent of the size of the dataset, we normalized them via dividing to the average number of interactions per drug. Here, we set $\tilde{\gamma _d}=1$ according to Olayan et al. (2017).

2.2 Method overview

• 1. Calculating drug similarities and GIP for each drug pair.

• 2. Selecting the most informative and less redundant subset of similarities.

• 3. Integrating the selected similarities and obtaining an integrated similarity that represents all information in one matrix.

• 4. Applying matrix factorization on DDI matrix and estimating the latent matrices constrained by integrated similarities

• 5. Predicting DDI probabilities by multiplying the latent matrices

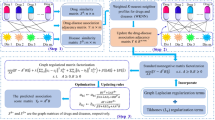
These steps are depicted in Fig. 1.

Fig. 1

The scheme of ISCMF work-flow. a: Selecting the k best subset of m similarity matrices and applying SNF, a fusion method, to integrate all selected similarities in one matrix. b: Matrix factorization is applied to decompose the known DDI matrix into the latent matrices constrained to integrated similarities. c: New interaction probabilities are obtained by multiplying latent matrices

2.3 Similarity selection

In ISCMF, eight similarity matrices for drugs based on various data types, as well as GIP similarity matrix is considered. Hence, integrating these similarities and constructing a single integrated similarity matrix is substantial. Because these various types of similarities contain different types of data, noise, and random data, as well as some overlap and redundancy between different similarity matrices, before integrating the matrices, a similarity selection step must be done. Due to the mentioned reasons, an appropriate selection procedure must be done before integration.

Olayan et al. (2017) introduced an efficient heuristic similarity selection method that selects the most informative and less redundant subset of similarity matrices. In ISCMF, we utilize this approach which contains the following steps:

• 1. Calculating entropy of each matrix.

• 2. Calculating the pairwise distance measure between matrices.

• 3. Final selection based on low entropy and redundancy.

2.3.1 Calculating entropy

The carried information by each matrix can be measured by entropy. The entropy of each matrix is defined as the average entropy of its rows. Assuming $M=[m_{ij}]$ is a similarity matrix, $E_i(M)$ is the entropy of ith row of the matrix which is computed as follows:

$$\begin{aligned} E_i(M)=-\sum _j p_{ij}\log p_{ij}, \end{aligned}$$

(3)

where

$$\begin{aligned} p_{ij}=\frac{m_{ij}}{\sum _{j}m_{ij}}. \end{aligned}$$

(4)

Then, the similarity matrices with entropy greater than $c_1$ are eliminated. We have tested numerous values for $c_1$ in (0, 1) and the performance of model suggests that $c_1=0.6$ is more suitable. After applying this step, all similarity matrices were selected except the substructure-based similarity, because its entropy is higher than 0.6.

2.3.2 Calculating the pairwise distance

To remove redundancy, we need to compute the similarity of two matrices M and K which is calculated by

$$\begin{aligned} \mathrm{Sim} (M,K)=\frac{1}{1+D (M,K)}, \end{aligned}$$

(5)

where D(M, N) is the Euclidean distance between M and K matrices. Let $m_{ij}$ and $k_{ij}$ be the entries of M and K matrices, respectively. Accordingly, D(M, K) is measured by:

$$\begin{aligned} D (M, N)=\sqrt{\sum _{i}\sum _{j}\left( m_{ij}-k_{ij}\right) ^2} \end{aligned}$$

(6)

2.3.3 Final selection

Suppose there exist n similarity matrices $M_1 , \ M_2, \ \cdots , \ M_n$. First, matrices are sorted ascending based on their entropies. Subsequently, the selected subset of the matrices is obtained by an iterative procedure that selects the first matrix in the sorted list in each iteration and eliminating all other matrices that their similarity with the selected matrix is higher that $c_2$, before moving to the next iteration. This procedure iterates until the sorted list becomes empty. The value of threshold $c_2$ is considered in (0, 1) and the performance of model has been evaluated. The best results were obtained when $c_2=0.6$.

Ultimately, a subset of similarity matrices with high information and low redundancy can be obtained by this procedure. After applying this step, all the remained similarity matrices were selected.

2.4 Similarity fusion

Wang et al. (2014) proposed the similarity network fusion method to integrate multiple matrices, using an iterative non-linear network-based approach and KNN.

After selecting a reasonable subset of similarity matrices, SNF method is applied to integrate the selected matrices into a single fused similarity that carries an appropriate representation of all information.

2.5 ISCMF

Zhang et al. (2018) have proposed a similarity constrained matrix factorization method. We make use of this method on the integrated similarity of drugs that calculated by SNF. Let $D_{n\times n} =[d_{ij}]$ be the interaction matrix of drugs based on known DDIs; which $d_{ij} =1$ the known interaction between drugs i and j and $d_{ij} =0$ denotes unknown interaction; therefore, we use matrix factorization method and decompose matrix $D_{n\times n}$ into matrices $A_{n\times l}$ and $B_{l\times n}$. This can be viewed as mapping data from a high dimensional space to a lower space. Recent studies indicate that mapping data to a lower space with suitable constraints can maintain their topological data and yield better features. Here, we aim to map D into latent space by decomposing it into A and B, such that their elements are not very large and their multiplication is almost equal to the original matrix. In other words, we can formulate our loss function as:

$$\begin{aligned}&L_{A,B}=\frac{1}{2}||D-AB||^2_F+\frac{\lambda }{2} (||A||_{F}^{2}+||B||_{F}^{2})\nonumber \\&\quad =\frac{1}{2}\Sigma _{ij}(d_{ij}-a_ib_j)^2+\frac{\lambda }{2}(\Sigma _i||a_i||_{2}^{2}+\Sigma _j||b-j||_{2}^{2}), \end{aligned}$$

(7)

where $||.||_{F}$ is the Frobenius norm, $\lambda \ge 0$ is the regularization coefficient, $a_i$ is the ith row of A and $b_j$ is the jth column of B. Therewith, the goal is to find A and B such that the loss function is minimized. It should be noted that $||A||_{F}^{2}$ and $||B||_{F}^{2}$ terms are added as the regularization terms to the loss function that prevents A and B elements from growing exceptionally. In this way, it controls model variance and avoids over-fitting. Thus, one can project the drug space into a latent space that is expected to provide insights into DDIs. Hence, it is required that the similarity of drugs in the latent space to be the representative of their similarities in the original space. Formally, the aim is to minimize two subsequent following similarity losses:

$$\begin{aligned} L_A=\frac{1}{2}\Sigma _{ij}s_{ij } ||a_i-a_j||^{2}_{2} , \ \ \ L_B=\frac{1}{2}\Sigma _{ij}s_{ij } ||b_i-b_j||^{2}_{2}, \end{aligned}$$

(8)

where $s_{ij}$ is the integrated similarity of drugs. Particularly, $L_A$ and $L_B$ impose $s_{ij }$ penalty; so that the values of $a_i$ , $a_j$ must be selected close to each other for the drug pairs with high similarity. Similarly, the values of $b_i$ and $b_j$ should have low difference for similar drugs. These constraints guarantee the mapping conserve the topological distance between samples. Taking all these costs into consideration, the overall loss function is

$$\begin{aligned} L= & {} \frac{1}{2}\Sigma _{ij}(d_{ij}-a_ib_j)^2+\frac{\lambda }{2}\left( \Sigma _i||a_i||_{2}^{2}+\Sigma _j||b-j||_{2}^{2}\right) \nonumber \\&+\frac{\mu }{2}\left( \Sigma _{ij}s_{ij} ||a_i-a_j||^{2}_{2} +\Sigma _{ij}s_{ij} ||b_i-b_j||^{2}_{2}\right) , \end{aligned}$$

(9)

where $\mu \ge 0$ is the similarity coefficient. In this way, we can map D into A and B with lower dimensions. After training the model, each row of A and each column of B can be considered as features of drugs in new latent space. These features are extracted from a combination of known drug interactions and similarities. Thus, they can get us better insights about unknown DDIs.

2.6 Training the model

Newton’s method can be adopted for optimizing the latent matrices A and B. The Newton’s method is an iterative optimization method that updates the parameter estimation in each turn until the convergence. It first initializes the parameters randomly and then obeys the following updating rules to optimize the parameter estimation.

$$\begin{aligned} a_i \leftarrow a_i -\nabla _{a_i} L(\nabla ^2_{a_i}L )^{-1}\end{aligned}$$

(10)

$$\begin{aligned} b_j \leftarrow b_j -\nabla _{b_j} L(\nabla ^2_{b_j}L )^{-1} \end{aligned}$$

(11)

To manipulate Newton’s method, the first and second derivatives of loss function must be computed. The first derivatives of loss function in formula 9 with respect to $a_i$ and $b_i$ are

$$\begin{aligned}&\nabla _{a_i} L = \Sigma _j (a_ib_j-d_{ij})b_{j}+\lambda a_i \nonumber \\& \quad +\mu \{\Sigma _js_{ij} (a_i-a_j)-\Sigma _j s_{ji}(a_j-a_i)\} \end{aligned}$$

(12)

$$\begin{aligned}&\nabla _{b_j} L = \Sigma _i (b_ja_i^{T}-d_{ij})b_{j}+\lambda b_j \nonumber \\ & \quad +\mu \{\Sigma _is_{ji} (b_j-b_i)-\Sigma _i s_{ij}(b_i-b_j)\} \end{aligned}$$

(13)

In addition, the second derivatives of loss function with respect to $a_i$ and $b_i$ are

$$\begin{aligned} \nabla _{a_i}^{2} L= \, & {} \Sigma _j b_jb_j+\lambda I +\mu \{\Sigma _j s_{ij}-\Sigma _j s_{ji}\}\nonumber \\= & {} B^TB+\lambda I+\mu \{\Sigma _j s_{ij}-\Sigma _j s_{ji}\} \end{aligned}$$

(14)

$$\begin{aligned} \nabla _{b_j}^{2} L= \, & {} \Sigma _i a_j^{T}a_j+\lambda I +\mu \{\Sigma _i s_{ji}-\Sigma _i s_{ij}\}\nonumber \\= & {} A^TA+\lambda I+\mu \{\Sigma _j s_{ji}-\Sigma _i s_{ij}\} \end{aligned}$$

(15)

Substituting Eqs. 12, 13, 14, 15 into Eqs. 10, 11, the updating rules of Newton’s method can be rewritten as follows.

$$\begin{aligned}&a_i \leftarrow \{\Sigma _jd_{ij}b_j+\mu \Sigma _j (s_{ij}+s_{ji})a_j\} \{B^{T}B+\lambda I\nonumber \\&\quad +\mu \{\Sigma _j s_{ij}-\Sigma _j s_{ji}\}I\}^{-1}\end{aligned}$$

(16)

$$\begin{aligned}&b_j \leftarrow \{\Sigma _id_{ij}a_i+\mu \Sigma _i (s_{ji}+s_{ij})b_i\} \{A^{T}A+\lambda I \nonumber \\&\quad +\mu \{\Sigma _i s_{ji}-\Sigma _i s_{ij}\}I\}^{-1} \end{aligned}$$

(17)

Notably, the second derivatives are positive definite; thus, the convergence of Newton’s method is guaranteed because the loss function will be decreased after each iteration.

When the learning phase accomplished, the estimated matrices A and B can be used to predict DDIs according to the following equation.

$$\begin{aligned} D_\mathrm{new}=AB \end{aligned}$$

(18)

It is evident that the elements of $D_\mathrm{new}$ is the probability of interaction of drug pairs. It should be noted that the multiplication of A and B do not yield the original matrix D, since the loss function has multiple regularization and similarity constraint terms. Thus, it can be conceived that the new interactions are somehow the combination of known interactions and similarity matrices.

3 Results

In this study, we classified drug pairs into two classes, namely interacting and non-interacting pairs. Therefore, we exploited commonly used metrics in classification, including precision, recall, F-measure, AUPR, and AUC. Precision and recall have a trade-off; thus, increasing one may lead to a reduction in the other. Therefore, utilizing F-measure, the geometric mean of them is more reasonable.

Since the values of precision, recall, and F-measure are dependent on the value of the threshold, we also evaluated methods via AUC, which is the area under ROC curve, and AUPR, which is the area under the precision-recall curve. These criteria are independent of the threshold value. In cases that the negative and positive samples are imbalanced, AUPR is the fairer criterion for evaluation.

We considered all combinations of $\lambda \in \{1, 2,\ldots , 9\}$, $\mu \in \{1, 2,\ldots , 9\}$, $k\in \{0.2,\ 0.3,\ \ldots$, $0.8\}$ and $k \in \{20\%,30\%,40\%,50\%,60\%,70\%,80\%\ \mathrm{of \ original \ dimension}\}$ and evaluated them by fivefold-cross-validation. The best results were obtained when $\mu =1, \lambda =1$, and $k=60\%$. The following assessments of method performances were conducted by 20 runs of five-fold cross-validation on known DDI to ensure low-variance and unbiased evaluations.

3.1 Performance of ISCMF on different similarity types

ISCMF utilizes an integrated similarity matrix, while the similarity matrix of the learning phase can be substituted by any similarity matrices. Consequently, the beneficial role of similarity selection and integration procedures in ISCMF performance can be evaluated by using various types of data in ISCMF.

As shown in Table 1, using integrated data yielded greater AUPR and F-measure, indicating that the similarity selection and fusion make a great impact on improving performance.

Table 1 Performance of ISCMF on different similarity types

3.2 Comparison with the state-of-the-art methods

To date, numerous computational methods have been proposed for unknown DDI prediction, such as neighbor recommender, label propagation, matrix perturbation, etc. Table 2 represents the evaluated criteria of these methods. One can realize the ISCMF’s superiority due to its high AUPR and F-measure that are almost unbiased criteria. Noteworthy, the higher AUC and accuracy of other methods stem from high true negatives. Moreover, a huge number of samples are negative. Therefore, a simple method yielding negative output in all cases can obtain high accuracy and AUC. Thus, AUC and accuracy are not fair metrics, and their high values are not statistically significant. However, ISCMF can obtain satisfactory AUC and accuracy. Furthermore, it is usually difficult to obtain high values of precision and recall simultaneously. It is highly surprising that ISCMF can do that. In line with this, our results provide support for the efficiency and performance of ISCMF.

Table 2 Comparison with the state-of-the-art methods

The drugs can induce or inhibit cytochrome P450 enzymes, which may lead to the interaction of drugs with adverse reactions and dangerous issues such as failure in medication CYP2C9 and CYP2D6 (2007). To investigate the role of CYP P450 enzymes in drug–drug interaction, we analyzed the performance of ISCMF on another benchmark containing both CYP (the Cytochrome P450 involved DDIs) and NCYP (the DDIs without involving cytochrome P450) interactions Gottlieb et al. (2012). A report of ISCMF results for each of these interactions is presented in Supplementary File 2.

3.3 Effect of using integration on the performance of methods

To demonstrate the importance of integration procedure in improving methods, we executed the methods mentioned above once with each similarity matrices and once with the integrated matrix. Figure 2 depicts the obtained AUPR values. Accordingly, AUPR of label propagation method significantly improves when utilizing integrated similarities. Furthermore, the integrated similarity-based enhance AUPR of neighbor recommender method in comparison to five models. On the other hand, the performance of neighbor recommender does not improve compared to the substructure, side effect, and off-side effect models. This may be due to the fact that neighbor recommender applies a simple linear method, and when using an integrated similarity matrix, the nonlinearity of feature may not be helpful.

Fig. 2

Comparison between the AUPR values of methods in case of using a single type of similarity and using integrated similarity

3.4 Case studies

To further investigate ISCMF efficiency, we inquired into our top false positives (FPs) with the highest interaction probabilities into DrugBank and other reliable sources and literature. DrugBank is one of the most authentic databases for drug interactions. As both a bioinformatics and a cheminformatics resource, DrugBank collects different types of information about drugs. Because of its broad scope and comprehensive referencing, DrugBank is more akin to a drug encyclopedia than a drug database (Knox et al. 2010). Amazingly, inspecting the top 50 FPs in DrugBank confirmed the efficiency of ISCMF. There are great pieces of evidence to confirm the newly predicted DDIs, some of which are listed in Supplementary File 3. The top ten predicted DDIs are presented in Table 3, from which seven interactions now exist in the DrugBank database, but they were labeled zero in our training samples.

Table 3 Top ten predicted interactions (confirmed interactions by DrugBank database is shown in bold)

4 Conclusion

In the current study, we proposed ISCMF, Integrated Similarity-Constrained Matrix Factorization, the method to predict unknown DDIs. To validate the robustness of ISCMF, we compared it to several state-of-the-art methods with five-fold cross-validation. Our results suggest the superiority of ISCMF over previous methods. The better performance is due to several reasons. First, ISCMF considers an integrated similarity matrix which carries more informative features. Second, it makes use of the matrix factorization method, which is very applicable to bioinformatics problems. Moreover, the appropriate regularization and similarity constraints assist in providing great insights into DDIs. Case studies provided more pieces of evidence to validate our model. Interestingly, a great number of predicted DDIs were validated by DrugBank database. Many more false positives are expected to be verified by reliable resources in the near future. Consequently, the proposed method is promising for DDI prediction and biomedical researches.

We aim to do some works in the future. First, we intend to take advantage of network-based similarities together with biological similarities. It may change the results significantly. Furthermore, we want to investigate the rule of using various similarity integration approaches to the performance of DDI prediction methods.