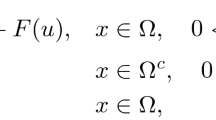Global solutions of nonlinear fractional diffusion equations with time-singular sources and perturbed orders

Abstract

In a Hilbert space, we consider a class of nonlinear fractional equations having the Caputo fractional derivative of the time variable t and the space fractional function of the self-adjoint positive unbounded operator. We consider various cases of global Lipschitz and local Lipschitz source with time-singular coefficient. These sources are generalized of the well–known fractional equations such as the fractional Cahn–Allen equation, the fractional Burger equation, the fractional Cahn–Hilliard equation, the fractional Kuramoto–Sivashinsky equation, etc. Under suitable assumptions, we investigate the existence, uniqueness of maximal solution, and stability of solution of the problems with respect to perturbed fractional orders. We also establish some global existence and prove that the global solution can be approximated by known asymptotic functions as $t\rightarrow \infty$.

1 Introduction

1.1 Statement of the problem

Let H be a Hilbert space, $A : D(A) \subset H \rightarrow H$ be a self-adjoint positive definite unbounded operator, and $f: [0, +\infty ) \times D(A^s) \rightarrow H$ with $s\ge 0$. For $\alpha \in (0, 1]$, $\beta >0$, we consider the problem to find a function $u: [0,T]\rightarrow H$ satisfying

$$\begin{aligned} D_t^\alpha u + A^\beta u = f(t, u(t)), \ \, t > 0, \end{aligned}$$

(1.1)

where $D_t^\alpha$ is the Caputo fractional derivative

$$\begin{aligned} D_t^\alpha u (t) = \left\{ \begin{array}{lll} &{} \frac{1}{\varGamma (1-\alpha )} \int _0^t (t-s)^{-\alpha }u'(s) \mathrm {d}s, &{} \ \text {if} \ \, \alpha \in (0, 1),\\ &{} \ u'(t), &{} \text {if} \ \, \alpha =1, \end{array} \right. \end{aligned}$$

and the fractional power of the operator $A^\beta$ will be defined later. The equation (1.1) is a general form of a lot of well-known equations such as the Ginzburg–Landau equation ($\alpha =1, A=-\varDelta , f(t,u)=au-bu^3$), Burger equation ($\alpha =1, A=-\varDelta , f(t,u)=u u_x$), and Kuramoto–Sivashinsky equation ($\alpha =1, A=\varDelta ^2, f(t,u)=\nabla ^2 u + (1/2)\Vert \nabla u \Vert ^2)$). In the present paper, we will investigate the stability of solution of the initial value and the final value problems for (1.1).

The equation (1.1) subject to the initial data

$$\begin{aligned} u(0)=\zeta \end{aligned}$$

(1.2)

is called the fractional initial value (or the Cauchy, the forward) problem (FIVP).

By the definition of the spectral resolution of the operator A and the Laplace transform, we can rewrite the FIVP as

$$\begin{aligned} \mathbf{Problem}~P_{{\zeta ,\alpha ,\beta }}:~~~~u(t) = E_\alpha \big (- t^\alpha A^\beta \big ) \zeta + \int _0^t { E}_{\alpha , \beta }(A, t, \tau ) f(\tau , u(\tau )) \mathrm {d}\tau ,\qquad \end{aligned}$$

(1.3)

where ${ E}_{\alpha , \beta }(z, t, \tau ) = (t-\tau )^{\alpha -1} E_{\alpha , \alpha }(-z^\beta (t-\tau )^\alpha )$ is expressed by the Mittag-Leffler function, and the operators $E_\alpha \big (- t^\alpha A^\beta \big ), { E}_{\alpha , \beta }(A, t, \tau )$ will be defined in Sect. 2.

A function u that satisfies Eq. (1.3) is called a mild solution of the FIVP and denote by $u=u_{\zeta ,\alpha ,\beta }$.

1.2 History and motivation

The abstract parabolic equation $u_t+Au=f$ was considered for the last thirty years in many works on this area. The readers can see the classical book by Cazenave and Haraux [5] and references therein. The FIVP was also studied by lot of researchers. Xing et al. [24] discussed the existence, uniqueness, analyticity and the long-time asymptotic behavior of solutions of space-time fractional reaction–diffusion equations in $\mathbb {R}^n$

$$\begin{aligned} D_t^\alpha u +(- \varDelta )^\beta u =p(x) u, \end{aligned}$$

subject to the initial condition $u(x, 0) =a(x)$. Existence and uniqueness of the maximal solutions of some linear and nonlinear fractional problems were investigated in [2, 6, 10, 12, 21]. The blow–up and global solution of time–fractional nonlinear diffusion–reaction equations were studied recently with some kind of nonlinear sources as $f(t,u)=au+u^p$ (see Cao et al. [4]), $f(t,u)=|u|^{p-1}u$ (see [27]), $f(t,u)=|u|^p$ (Zhang [26]), Asogwa et al. [3] studied finite time blow up results for a version of equation (1.1).

The first motivation of our paper is to study the existence and uniqueness of maximal solution of the initial value problem with respect to a singular source. In many practical situation, the source is often assumed to satisfy ${\left| \!\left| f(t,u)-f(t,v)\right| \!\right| } \le K(t, M)\Vert u-v\Vert \ \mathrm{for \ } \Vert u\Vert ,\Vert v\Vert \le M,$ where $K: (0,\infty )\times (0,\infty )\rightarrow \mathbb {R}$ is the Lipschitz coefficient. If K(t, M) is dependent (independent) on t, we say that the coefficient is t-dependent (t-independent). Generally, in a lot of papers, the coefficient is assumed to be t-independent. A time-dependent coefficient which can be unbounded in a time interval (0, T), i.e. $\sup _{0<t<T}K(t,M)=\infty$, is rarely studied. In the present paper, we consider a generalized form of singular source

$$\begin{aligned} {\left| \!\left| f(t,u)-f(t,v)\right| \!\right| }_H \le K(t,M)\Vert u-v\Vert _{D(A^s)} \ \ \mathrm{for \ } \Vert u\Vert _H ,\Vert v\Vert _H \le M, \end{aligned}$$

with $K(t,M)=\kappa _0(t)L(M)$ for $\lim _{t\rightarrow 0^+}\kappa _0(t)=\infty$. In the special case $\kappa _0(t)=t^{-\nu }\kappa (t)$, the condition of K(t, M) is similar to the generalized Nagumo condition (see, e.g., [13], Ch. 7 or [11]). In particular, the time-dependent source promises to bring many interesting global properties to the solution of the problem.

The second motivation of our paper is of studying the continuity of solution with respect to the fractional orders $\alpha , \beta$ and the initial data $\zeta$. In the papers mentioned above, the parameters $\alpha ,\beta$ are assumed to be perfectly known. But in the real word of applications, the fractional orders can only be approximated from the mathematical model or statistical methods. In [1, 7], the Caputo derivatives can be identified approximately from observation data $u(x_0,t)$ with $t>0$, or u(x, T) with $x\in \Omega \subset \mathbb {R}^n$. Besides, Kateregga [15] used statistical methods as the quantiles, logarithmic moments method, maximum likelihood, and the empirical characteristic function method to identify the parameters of the Lévy process. In these examples, the fractional orders are obtained only as approximate values. Hence, a natural question is that whether the solutions of fractional equations is continuous with respect to the perturbed orders. The papers devoted to these questions are still rare. We can list here some papers. Li and Yamamoto [16] investigated the solution $u_{\gamma , D}$ of the problem

$$\begin{aligned} D_t^\gamma u = \frac{\partial }{ \partial x} \left( D(x)\frac{\partial u}{\partial x} \right) , \ \ (x, t) \in (0, 1) \times (0, T), \end{aligned}$$

subject to the Neumann condition $u_x(0, t) =u_x(1, t)=0$ and the initial condition $u(x, 0)=f(x)$. They proved that

$$\begin{aligned} \Vert u_{\gamma _1, D_1}(0, \cdot ) - u_{\gamma _2, D_2}(0, \cdot )\Vert _{L^2(0, T)} \le C(|\gamma _1 -\gamma _2| + \Vert D_1 - D_2\Vert _{C[0,1]}). \end{aligned}$$

Dang et al. [8] studied the continuity of solutions of some linear fractional PDEs with perturbed orders. In the references [9, 19, 22], the authors considered the stability of solution of some class of nonlinear space–fractional diffusion problems taking into account the disturbance of parameters. To the best of our knowledge, until now, there is very few papers devoted to the stability of solutions of time-fractional problems with respect to the fractional time and space derivative parameters: $\alpha , \beta$. In [20, 23], the stability was considered for the global Lipschitz source. The problem with the local time-singular Lipschitz source is still a topic of investigation. This stability result will serve as the foundation for numerical computation schemes for equations with imprecise fractional derivative parameters.

1.3 Outline of the paper

Summarizing the discussion of the FIVP, in the present paper, we will:

• Investigate the existence and uniqueness of the maximal solution of the nonlinear FIVP with respect to the singular nonlinear source on the maximal interval $[0,T_{\zeta ,\alpha ,\beta })$. To solve the problem, we have to establish an appropriate Gronwall-type inequality which also has a specific merit in investigating other fractional problems.

• Study the stability of the nonlinear FIVP with respect to the perturbed orders $\alpha ,\beta$. In fact, we establish

  $$\begin{aligned} u_{\zeta ',\alpha ',\beta '}\rightarrow u_{\zeta ,\alpha ,\beta }~~\ \text {as}\ ~~ (\zeta ',\alpha ',\beta ')\rightarrow (\zeta ,\alpha ,\beta ) \end{aligned}$$

  in an appropriate norm. Especially, for $\alpha \rightarrow 1^-$, we will prove that the solution of the nonlinear FIVP tends to that of classical nonlinear initial value parabolic problem.

• Study the existence of global solution on $[0,\infty )$ and prove decay estimates for the global solution. To illustrate for our results, we present an asymptotic result. Under some conditions, we will prove that

  $$\begin{aligned} \lim _{t\rightarrow \infty } (1+t)^{\alpha }\Vert u_{\zeta ,\alpha ,\beta }(t)\Vert _s=\frac{1}{\varGamma (1-\alpha )}\Vert \zeta \Vert _{s-\beta } \end{aligned}$$

  for every $\zeta \in D(A^s), \zeta \not =0$. The result shows that the decay of the FIVP is of polynomial order.

The rest of the paper is organized as follows. Section 2 gives the main results of our paper without proofs. In Sect. 3 the proofs of these results are presented.

2 Main results

2.1 Notations

To state our problem precisely, we will give some definitions. Firstly, in the paper, we always denote by $C,C'$ generic constants which could be different from line to line. We denote the inner product in Hilbert space H by $\langle .,.\rangle$ and the associated norm by $\Vert .\Vert$.

We recall (see, e.g., [17, page 61, Ch.4]) that a resolution of the identity on a Hilbert space H is a one-parameter family {$S_\lambda : \lambda \in R$} of orthogonal projections on H such that

• (i) $S_\lambda \le S_{\lambda '}$ if $\lambda \le \lambda '$ (monotonicity),

• (ii) $\lim _{\lambda '\rightarrow \lambda ^+}S_{\lambda '}\zeta = S_\lambda \zeta$ for $\zeta \in H$ (strong right continuity),

• (iii) $\lim _{\lambda \rightarrow -\infty }S_\lambda \zeta = 0$ and $\lim _{\lambda \rightarrow +\infty }S_\lambda \zeta = \zeta$ for $\zeta \in H$.

Assume that $\theta >0$ is the lower bound of the spectrum of the operator A. Let us denote by $\{{S_\lambda }\}$ the spectral resolution of the identity associated to operator A such that $A=\int _\theta ^\infty \lambda dS_\lambda$. We follow [25, page 29] (see also [17, page 92]) to define the power of the self-adjoint positive definite unbounded operator as

$$\begin{aligned} A^\beta u = \int _\theta ^{+\infty } \lambda ^\beta \mathrm {d}{S_\lambda }u, \ \ \beta \in \mathbb {R}. \end{aligned}$$

Generally, for a continuous function $h: \mathbb {R} \rightarrow \mathbb {R}$, we denote the domain of h(A) to be

$$\begin{aligned} D(h(A)) := \left\{ w\in H: \ \int _\theta ^{+\infty } |h(\lambda )|^2 \mathrm {d} {\left| \!\left| {S_\lambda }w\right| \!\right| }^2<+\infty \right\} . \end{aligned}$$

(2.1)

If $w \in D(h(A))$, we define the linear operator

$$\begin{aligned} h(A) w =\int _\theta ^{+\infty } h(\lambda ) \mathrm {d}{S_\lambda }w. \end{aligned}$$

Particularly, if $h(z)=z^s$ for $z \ge 0, s\in \mathbb {R}$, we have the Hilbert space $D(A^s)$ with the norm ${\left| \!\left| w\right| \!\right| }_s = \left( \int _\theta ^{+\infty } \lambda ^{2 s} \mathrm {d} {\left| \!\left| {S_\lambda }w\right| \!\right| }^2 \right) ^{1/2}$. For $v\in C([0,T]; D(A^s))$ we denote $|v|_{s,t}=\sup _{0 \le \tau \le t} \Vert v(\tau )\Vert _s$. Let $0 \le s_* \le s^*$ and $s_1, s_2 \in [s_*, s^*]$, $s_2\le s_1$. It is easy to see that

$$\begin{aligned} D(A^{s_1}) \subset D(A^{s_2}) \subset D(A^0) = H \, \, \text {and} \,\, {\left| \!\left| w\right| \!\right| }_{s_2} \le \theta ^{s_2-s_1} {\left| \!\left| w\right| \!\right| }_{s_1}. \end{aligned}$$

For ${ M}, s>0$, we put

$$\begin{aligned} B_s({ M})= & {} \{ w\in D(A^s ): \Vert w\Vert _s\le { M}\}, \\ B_{s,T}({ M})= & {} \left\{ v\in C([0,T];D(A^s )) : | v |_{s,T} \le { M}\right\} . \end{aligned}$$

In this section, we also remind the Mittag–Leffler function and its properties which play important roles in the proof of main results of current paper. We recall also the Gamma and Beta functions,

$$\begin{aligned} \varGamma (z) = \int _0^\infty t^{z-1}e^{-t}dt, \ \ B(p,r) = \int _0^1t^{p-1}(1-t)^{r-1}dt \ \ \text {for}\ \ \text {Re}(z), p, r>0. \end{aligned}$$

The Mittag–Leffler function with two parameters is defined as

$$\begin{aligned} E_{p, r} (z) = \sum _{k=0}^{+\infty } \frac{z^k}{\varGamma (k p+r)}, \ \ E_{p} (z):=E_{p, 1} (z), \,\, z \in \mathbb {C} \ \ \text {for}\ \ p, r >0. \end{aligned}$$

Definition 1

A function $u\in C([0,T);D(A^s)$ is a maximal solution of Problem $P_{\zeta ,\alpha ,\beta }$ if u satisfies $P_{\zeta ,\alpha ,\beta }$ on the interval [0, T) such that $T=\infty$ or that $T<\infty$, $\limsup _{t\rightarrow T^-}\Vert u(t)\Vert _s=\infty$. In the case $T=\infty$, we say that u is aglobal solution of $P_{\zeta ,\alpha ,\beta }$. The global solution u is said to have

• the sub-polynomial decay rate if there are $\rho$, $C>0$ such that

  $$\begin{aligned} \Vert u(t)\Vert _s\le C(1+t)^{-\rho }~~\text {for every}~t>0. \end{aligned}$$

• the asymptotically polynomial decay if there is $\rho , C_\rho >0$ such that

  $$\begin{aligned} \lim _{t\rightarrow \infty }(1+t)^{\rho } \Vert u(t)\Vert _s=C_\rho . \end{aligned}$$

2.2 The global Lipschitz source

Using the notations defined, we can state precisely the assumption for the singular source. In fact, we consider the source function of the problem satisfying the following assumptions.

Assumption F1($\alpha$) Let $T>0$, $\alpha \in (0,1]$ and $f\in C( (0,\infty ) \times D(A^s); H)$. We assume that

$$\begin{aligned} m_{T,\alpha }:= \sup _{0 \le t \le T} \int _0^t (t-\tau )^{\alpha -1}E_{\alpha ,\alpha }(-\theta ^\beta (t-\tau )^\alpha ) \Vert f(\tau ,0)\Vert ^2 \mathrm {d}\tau <\infty . \end{aligned}$$

Assumption G1 Let $T>0$, $s >0$, $\nu \le \alpha /2$ and $f\in C( (0,\infty ) \times D(A^s); H)$, $\kappa \in C([0,\infty );[0,\infty ))$. We assume that

$$\begin{aligned} {\left| \!\left| f(t,w_1)-f(t,w_2)\right| \!\right| } \le t^{-\nu }\kappa (t) {\left| \!\left| w_1-w_2 \right| \!\right| }_s~~~\mathrm{for\ all\ } \ \ w_1,w_2\in D(A^s). \end{aligned}$$

(2.2)

Remark 1

Assumption F1($\alpha$) holds in many cases. For example, as shown in Lemma 2 (see the part of proofs), if $\Vert f(t,0)\Vert \le t^{-\nu _f}\kappa _f(t)$ for $2\nu _f<\alpha , \kappa _f\in C([0,\infty );\mathbb {R})$, then Assumption F1($\alpha$) holds.

Using the assumptions, we can obtain the following existence result.

Theorem 1

Let $\alpha \in (0,1), \beta >0$, $s \in [0, \beta /2]$, $\zeta \in D(A^s)$ and let $f\in C( (0,\infty )\times D(A^s); H)$. Assume that Assumption F1($\alpha$) and Assumption G1 hold. For $\nu <\alpha /2$, the equation (1.3) has a unique solution $u=u_{\zeta ,\alpha ,\beta }\in C([0,\infty );D(A^s))$. Moreover, for a $T>0$, if we put

$$\begin{aligned} \kappa _{T,s}=\max _{0\le t\le T}\kappa (t),~~ g(t) = E_\alpha \big (- t^\alpha A^\beta \big ) \zeta + \int _0^t { E}_{\alpha , \beta }(A, t, \tau ) f(\tau , 0) \mathrm {d}\tau , \end{aligned}$$

then $g \in C\left( [0, T], D(A^s)\right)$ and there is a constant C independent of t such that

$$\begin{aligned} \Vert u(t) \Vert _s^2 \le 2 C \varGamma (1-2\nu ) | g|_{s, t}^2 E_{\alpha -2\nu ,1-2\nu } \left( 2 \theta ^{2s-\beta }\kappa _{T,s}^2 t^{\alpha -2\nu }\right) \ \ \text {for any} \ \ t\in [0,T], \end{aligned}$$

(2.3)

where we recall $|g|_{s,t}=\sup _{0\le \tau \le t}\Vert g(\tau )\Vert _s$.

For $\nu = \alpha /2$,  $\kappa _{T,s} < \theta ^{\beta /2-s} \left( \varGamma (1-\alpha )\right) ^{-1/2}$, the equation (1.3) has a unique solution $u\in C([0,T];D(A^s))$.

Remark 2

We can use the Edelstein fixed point theorem (see, e.g., [13], Ch. 7) to obtain the desired result for the case $\nu =\alpha /2, \kappa _{T,s}=\theta ^{\beta /2-s} \left( \varGamma (1-\alpha )\right) ^{-1/2}$. We note that if we put $u_{n+1}=\mathcal {F}(u_n)$, where $\mathcal {F}(u)$ is the right hand side of equation (1.3), then the sequence $(u_n)$ converges to the solution u in C([0, T],  $D(A^s))$.

From the existence result stated, we can obtain an interesting global existence result. Moreover, we also give an asymptotically polynomial result for decay estimates.

Theorem 2

Let $\alpha \in (0,1), \beta >0$, $s \in [0, \beta /2]$, $\zeta \in D(A^s)$, $\nu ,\nu _f>0$, $\nu <\alpha /2$, $\nu _f<\alpha /2$ and let $f\in C( (0,\infty )\times D(A^s); H)$. Assume : 

• Assumption G1 holds and there are $\kappa _1>0$, $\ell \in \mathbb {R}$ such that

  $$\begin{aligned} 0\le \kappa (t)\le \kappa _1 (1+t)^{\ell }, \end{aligned}$$

• There exist $\kappa _f>0,\nu _f>0$, $\ell _f\in \mathbb {R}$ such that

  $$\begin{aligned} \Vert f(t,0)\Vert _s\le \kappa _f t^{-\nu _f}(1+t)^{\ell _f}. \end{aligned}$$

With these assumptions, we have the following two results : 

• 1. If $\ell ,\ell _f<\nu$, $\alpha >\frac{1}{2}-\nu$, then, for every $\zeta \in D(A^s)$, the problem $P_{\zeta ,\alpha ,\beta }$ has a unique global solution $u_{\zeta ,\alpha ,\beta }\in C([0,\infty );D(A^s))$ which has the sub-polynomial decay rate. More explicitly, for every $\omega$ satisfying $0<\omega <\min \left\{ \frac{1}{2},\frac{1}{2}-\ell ,\frac{1}{2}-\ell _f\right\}$, we can find $C_\omega >0$ such that

  $$\begin{aligned} \Vert u_{\zeta ,\alpha ,\beta }(t)\Vert _s\le C(1+t)^{-\min \{\alpha ,\omega \}}~~~\text {for}\, ~t>0. \end{aligned}$$

• 2. If $\ell ,\ell _f< \frac{1}{2}-\alpha$, $0<\alpha <1/2$ then, for every $\zeta \in D(A^s)$, the problem $P_{\zeta ,\alpha ,\beta }$ has a unique global solution $u_{\zeta ,\alpha ,\beta }\in C([0,\infty );D(A^s))$ which has the sub-polynomial decay rate. More explicitly, for every $\alpha<\omega <\min \left\{ \frac{1}{2}, \frac{1}{2}-\ell ,\frac{1}{2}-\ell _f\right\}$ we can find $C_{\alpha ,\omega }>0$ such that

  $$\begin{aligned} \Vert u_{\zeta ,\alpha ,\beta }(t)-E_{\alpha }(-t^\alpha A^\beta )\zeta \Vert _s\le C_{\alpha ,\omega }\Vert \zeta \Vert _s(1+t)^{-\omega }. \end{aligned}$$

  In addition, the solution $u_{\zeta ,\alpha ,\beta }$ has the asymptotically polynomial decay rate

  $$\begin{aligned} \lim _{t\rightarrow \infty } (1+t)^{\alpha }\Vert u_{\zeta ,\alpha ,\beta }(t)\Vert _s=\frac{1}{\varGamma (1-\alpha )}\Vert \zeta \Vert _{s-\beta }. \end{aligned}$$

Remark 3

As mentioned, the set $D(A^s)$ is dense in H. Hence the polynomial decay rate of the solution holds for almost every $\zeta \in H$.

In the next two theorems, we state some results on stability of solution of the initial problem with respect to the initial data and the fractional orders. In the following stability results, we recall that $u_{\zeta , \alpha ,\beta }$ is the solution of Problem $P_{\zeta ,\alpha ,\beta }$ in (1.3) corresponding to the initial data $\zeta$ and the orders $\alpha ,\beta$. We first have the classical stability with respect to the fixed orders $\alpha ,\beta$. More precisely, for $\alpha _*,\alpha ^*,\beta _*,\beta ^*$ satisfying $0<\alpha _*<\alpha ^*<2\alpha _*\le 2$, and $0<\beta _*<\beta ^*$, we consider

$$\begin{aligned} (\alpha ,\beta ) \in \varDelta :=[\alpha _* , \alpha ^*] \times [\beta _*,\beta ^*] . \end{aligned}$$

(2.4)

Theorem 3

Let $\zeta , \xi \in D(A^s)$ be two initial data with $s \in [0, \beta /2]$, and let $T>0$, $({\alpha }, {\beta })\in \varDelta$ be as in (2.4). Let the source function f satisfy Assumption F1($\alpha$) and Assumption G1. Then the problems $P_{\xi ,\alpha ,\beta }, P_{\zeta ,\alpha ,\beta }$ have the unique solutions $u_{\xi , {\alpha }, {\beta }}, u_{\zeta , {\alpha }, {\beta }} \in C([0,T],D(A^s))$, respectively. Moreover, there exists a positive constant $P_1$ independent of $\zeta ,\xi$ such that

$$\begin{aligned} |u_{\xi , {\alpha }, {\beta }} - u_{\zeta , {\alpha }, {\beta }} |_{s,T} \le P_1 {\left| \!\left| \zeta - \xi \right| \!\right| }_s. \end{aligned}$$

Hence, letting $\zeta ,\zeta _k\in D(A^s)$, $\zeta _k\rightarrow \zeta$ in $D(A^s)$, we obtain

$$\begin{aligned} \lim _{k\rightarrow \infty }| u_{\zeta _k,\alpha ,\beta }-u_{\zeta ,\alpha ,\beta }|_{s,T}=0. \end{aligned}$$

Moreover, we also have the stability results with respect to the perturbed orders $\alpha ,\beta$. To investigate the stability of the solution of the problem (FIVP), we will restrict the value $(\alpha , \beta )$ in the bounded domain.

Theorem 4

Let $(\alpha , \beta ), (\alpha _k, \beta _k)\in \varDelta$ (defined in (2.4)) such that $(\alpha _k, \beta _k) \rightarrow (\alpha , \beta )$, and let $\zeta , \, \zeta _k \in D(A^{s})$ such that $\zeta _k \rightarrow \zeta$ in $D(A^{s})$ as $k\rightarrow \infty$. Let the source function f satisfy Assumption F1($\alpha _*$) and Assumption G1. Then the problems $P_{\zeta ,\alpha ,\beta }, P_{\zeta _k,\alpha _k,\beta _k}$ have the unique solutions

$$\begin{aligned} u_{\zeta , \alpha , \beta }\in C([0,T], D(A^s)), \ \, u_{\zeta _k, \alpha _k, \beta _k}\in C([0,T], D(A^{\min \{s,\beta _k/2\}})), \end{aligned}$$

respectively. In addition, the following results hold : 

• (i) If $s \in [0, \beta /2)$, then

  $$\begin{aligned} \lim _{k\rightarrow \infty } |u_{\zeta _k, \alpha _k, \beta _k} - u_{\zeta , \alpha , \beta }|_{s, T} = 0. \end{aligned}$$

  (2.5)

• (ii) If $s = \beta /2$ and $\beta _k\ge \beta$ for $k\rightarrow \infty$, then

  $$\begin{aligned} \lim _{k\rightarrow \infty } |u_{\zeta _k, \alpha _k, \beta _k} - u_{\zeta , \alpha , \beta }|_{s, T} = 0. \end{aligned}$$

  (2.6)

• (iii) If $\beta _k \le \beta$ as $k \rightarrow \infty$, then

  $$\begin{aligned} \lim _{k\rightarrow \infty } |u_{\zeta _k, \alpha _k, \beta _k} - u_{\zeta , \alpha , \beta }|_{\beta _k/2, T} = 0. \end{aligned}$$

  (2.7)

• (iv) If we suppose further that $\zeta _k, \zeta \in D\left( A^{\beta ^*/2+r_1}\right)$ such that $\zeta _k \rightarrow \zeta$ in $D\left( A^{\beta ^*/2+r_1}\right)$ for some $r_1>0$. We also suppose that $s \!\in \! \left[ \frac{\beta _*}{2}, \frac{\beta }{2}\right)$, $f(., u_{\zeta ,\alpha ,\beta }(.))$ $\in C([0, T], D\left( A^{r_2}\right) )$ for some $r_2>0$. Then, there exists constants $L_0, L_1$ independent of $\zeta , \zeta _k$ such that

  $$\begin{aligned} {\left| u_{\zeta _k, \alpha _k, \beta _k} - u_{\zeta , \alpha , \beta }\right| }_{s, T} \le L_0\Vert \zeta - \zeta _k\Vert _s + L_1 (|\alpha - \alpha _k| +|\beta - \beta _k|) ^{\frac{\gamma _2}{2(\gamma _1+\gamma _2+2)}}, \end{aligned}$$

  (2.8)

  where $L_0, L_1$ is depended on $(\alpha _*,\alpha ^*, \beta _*, \beta ^*, T)$, $\gamma _1 = 2\beta ^*$, and $\gamma _2=\min \{\beta ^*+2(r_1-s), 2r_2\}$.

Remark 4

Theorem 4 shows that if $\alpha \rightarrow 1^-, \beta \rightarrow 1$, then the solutions of the fractional equation (1.1)–(1.2) tend to the solution of the classical equation

$$\begin{aligned} u_t = A u + f(t, u(t)) . \end{aligned}$$

2.3 The local Lipschitz source

Assumption G2 Let $s \in [0, \beta /2]$, $\nu \le \alpha /2$, $\kappa \in C([0,\infty );\mathbb {R})$, $\kappa (t)\ge 0$ for $t\ge 0$, and $f\in C( (0,\infty ) \times D(A^s); H)$. For every $T, { M}>0$, we assume that there is an $L_T({ M})$ such that

$$\begin{aligned} \begin{aligned} {\left| \!\left| f(t,w_1)-f(t,w_2)\right| \!\right| }&\le t^{-\nu }\kappa (t) L_T({ M}) {\left| \!\left| w_1-w_2 \right| \!\right| }_s\\&~~~~~\mathrm{for~ all~}\ t\in [0,T],\, w_1,w_2\in D(A^s), \Vert w_1\Vert _s, \Vert w_2\Vert _s\le { M}. \end{aligned} \end{aligned}$$

Put $\Xi =(0, 1)$, $H=L^2(\Xi )$, we can directly check that some common sources of the following equations satisfy: the Ginzburg Landau equation and the Burger equation for $\nu =0, s=1$, the Cahn–Hilliard and Kuramoto–Sivashinsky equations for $\nu =0, s=2$.

In this section, we investigate the existence and uniqueness of the solution of the problem with local source defined in (2.2). In addition, we study the dependence of the solution with respect to the fractional order $\alpha , \beta$ and the initial data $\zeta$. To emphasize the dependence of the solution u on these given data, let us write it by $u_{\zeta , \alpha , \beta }$. We have the following theorem.

Theorem 5

Let $\alpha \in (0, 1)$, $\beta \in (0, +\infty )$, $s\in [0, \beta /2]$, $\nu <\alpha /2$, and let $\zeta$ be the initial data defined in (1.2) such that $\zeta \in D(A^{\beta /2})$. Let the source function f satisfy Assumption F1($\alpha$) and Assumption G2.

Then, for any ${ M}> 2 {\left| \!\left| \zeta \right| \!\right| }_{\beta /2}$, we have : 

• (i) (Local existence) There exists a $T_{ M}>0$ such that the FIVP has a unique mild solution $u_{\zeta , \alpha , \beta }$ which belongs to $C([0, T_{ M}]; D(A^s))$.

• (ii) (Uniqueness) If $V,W\in C([0,T];D(A^s))$ are solutions of (1.3) on [0, T], then $V=W$.

• (iii) (Maximal existence) Let

  $$\begin{aligned} T_{\zeta , \alpha , \beta }=\sup \{T>0:\ 1.3 \quad \text {has a unique solution on}\ [0,T]\}. \end{aligned}$$

  Then the equation (1.3) has a unique solution $u_{\zeta ,\alpha ,\beta }\in C([0,T_{\zeta ,\alpha ,\beta });D(A^s))$. Moreover, we have either $T_{\zeta , \alpha , \beta } = +\infty$ or $T_{\zeta , \alpha , \beta }<+\infty$ and $\Vert u_{\zeta , \alpha , \beta }(t)\Vert _s \rightarrow \infty$ as $t \rightarrow T_{\zeta , \alpha , \beta }^-$. Besides, if $u_{\zeta , \alpha , \beta } \in B_{s, T}({ M})$ then

  $$\begin{aligned} \Vert u_{\zeta , \alpha , \beta }(t) \Vert _s^2 \le 2 \varGamma (1-2\nu ) | g|_{s, t}^2 E_{\alpha -2\nu ,1-2\nu } \left( 2\theta ^{2s-\beta } L_T^2({ M}) t^{\alpha -2\nu }\right) , \end{aligned}$$

  for any $t\in [0,T]$.

• (iv) Let $\zeta ,\zeta _k\in D(A^s), \alpha ,\alpha _k\in [\alpha _*,\alpha ^*], \beta ,\beta _k\in [\beta _*,\beta ^*]$ satisfy

  $$\begin{aligned} \zeta _k\rightarrow \zeta ~\, \mathrm{in}\, ~D(A^s),~~\alpha _k\rightarrow \alpha ,~~\beta _k\rightarrow \beta ~~~~{as} \ ~k\rightarrow \infty . \end{aligned}$$

Assume in addition that Assumption F1($\alpha _*$) hold and $s=\beta /2$, $\beta _k\ge \beta$ as $k\rightarrow \infty$ or $0\le s<\beta /2$. Then for every $T\in (0,T_{\zeta ,\alpha ,\beta })$ we can find a $k_0>0$ such that $T_{\zeta _k,\alpha _k,\beta _k}>T$ for every $k>k_0$ and

$$\begin{aligned} \lim _{k\rightarrow \infty }|u_{\zeta _k,\alpha _k,\beta _k}-u_{\zeta ,\alpha ,\beta }|_{T,s}=0. \end{aligned}$$

Moreover, we have

$$\begin{aligned} \liminf _{k\rightarrow \infty }T_{\zeta _k,\alpha _k,\beta _k}\ge T_{\zeta ,\alpha ,\beta }. \end{aligned}$$

If $T_{\zeta ,\alpha ,\beta }=\infty$ then $\lim _{k\rightarrow \infty }T_{\zeta _k,\alpha _k,\beta _k}=\infty$.

Using Theorem 5, we can obtain global existence and polynomial decay results. To state precisely the theorem, we state the following

Assumption G3  For $\nu >0$, $f: C((0,\infty ) \times D(A^s) ; H)$, $\kappa \in C([0,\infty );[0,\infty ))$ we assume that there is an $L_\infty ({ M})>0$ for every ${ M}>0$ such that

$$\begin{aligned}\begin{aligned} {\left| \!\left| f(t,w_1)-f(t,w_2)\right| \!\right| }&\le t^{-\nu }\kappa (t) L_\infty ({ M}) {\left| \!\left| w_1-w_2 \right| \!\right| }_s\\&~~~~~\mathrm{for~ all~}\ t\in [0,\infty ), w_1,w_2\in D(A^s), \Vert w_1\Vert _s, \Vert w_2\Vert _s\le { M}\end{aligned} \end{aligned}$$

and there are constants $\kappa _1,\eta >0,\ell \in \mathbb {R}$ such that

$$\begin{aligned} \Vert f(t,v)-f(t,0)\Vert \le \kappa _1 t^{-\nu }(1+t)^\ell \Vert v\Vert ^{1+\eta }_s~~\mathrm{for\ every\ } t>0, v\in D(A^s). \end{aligned}$$

Theorem 6

Let $(\alpha ,\beta )\in \varDelta$ be as in (2.4), let $0\le 2\nu \le \alpha <1$, $\eta ,\omega >0$, $s \in [0, \beta /2]$, $\ell \in \mathbb {R}$ and suppose that Assumption G3 hold. Assume that

• (i) $\eta >\max \left\{ 2(\ell -\nu ),0\right\}$ and $\max \left\{ \frac{\ell -\nu }{\eta },0\right\}<\omega <1/2,$

• (ii) $m^2_{\infty ,\alpha ,\omega }:= \sup _{t \ge 0}(1+t)^{2\omega } \int _0^t (t-\tau )^{\alpha -1}E_{\alpha ,\alpha }(-\theta ^\beta (t-\tau )^\alpha ) \Vert f(\tau ,0)\Vert ^2 \mathrm {d}\tau$ $<\infty .$

Then there exists $\delta _0>0$ such that Problem $P_{\zeta ,\alpha ,\beta }$ has a unique solution $u_{\zeta ,\alpha ,\beta }\in C([0,\infty );D(A^s))$ which has the optimal decay rate for

$$\begin{aligned} \Vert \zeta \Vert ^2_s+m^2_{\infty ,\alpha ,\omega }\le \delta ^2_0. \end{aligned}$$

Moreover, if $\frac{\ell -\nu }{\eta }<\alpha <1/2$, then

$$\begin{aligned} \lim _{t\rightarrow \infty }(1+t)^{\alpha }\Vert u_{\zeta ,\alpha ,\beta }(t)\Vert _s= \frac{1}{\varGamma (1-\alpha )}\Vert \zeta \Vert _{s-\beta }. \end{aligned}$$

Remark 5

From the condition (i), the global result holds for $\nu<\ell <1/2$. In this case the Lipschitz coefficient can be unbounded as $t\rightarrow \infty$ since $\lim _{t\rightarrow \infty }\kappa _1 t^{-\nu }(1+t)^\ell =\infty$.

3 Proofs

3.1 Preliminary lemmas

Lemma 1

[see [18]] Letting $\lambda>0, p>0$ and $k\in \mathbb {N}$, we have

$$\begin{aligned} \frac{\mathrm {d}^k}{\mathrm {d}t^k} E_{p}(-\lambda t^p) = - \lambda t^{p - k } E_{p, p-k+1}(-\lambda t^p), \ \, t\ge 0. \end{aligned}$$

Lemma 2

Let $0<p_*<p^*<2$ such that $p^*<2p_*$, and $r_*>0$. Then for any $p, p_0 \in [p_*, p^*]$, and $r, r_0 \ge r_*$, and $\lambda \ge 0$, we have : 

• (a) There exists a constant $C=C(p_*, p^*, r_*)>0$ such that

  $$\begin{aligned} {\left| E_{p, r}(-\lambda )\right| } + {\left| \frac{\partial E_{p, r}}{\partial p}(-\lambda )\right| } + {\left| \frac{\partial E_{p, r}}{\partial r}(-\lambda )\right| } \le \frac{C}{1+\lambda }. \end{aligned}$$

  We also have

  $$\begin{aligned} 0\le E_\alpha (-z)\le 1,\ \ 0\le E_{\alpha ,\alpha }(-z)\le \frac{1}{\varGamma (\alpha )}\ \ \ \text {for}\ \ z\ge 0. \end{aligned}$$

  (3.1)

• (b) Let $0<p_*<p^*<1$. There exist two constants $C_1, C_2$ which depend only on $p_*, p^*$ such that

  $$\begin{aligned} \frac{1}{\varGamma (1-p)} \frac{C_1}{1+\lambda } \le E_{p}(- \lambda ) \le \frac{1}{\varGamma (1-p)} \frac{C_2}{1+\lambda } . \end{aligned}$$

  Moreover, we have $\lim _{\lambda \rightarrow +\infty }\lambda E_p(-\lambda )=\frac{1}{\varGamma (1-p)}$.

• (c) There exists a constant $C=C(p_*, p^*)$ such that

  $$\begin{aligned} \left| E_{p}(-\lambda ^r t^p) - E_{p_0}(-\lambda ^{r_0} t^{p_0}) \right| \le C \lambda ^{r^*} (1+\ln \lambda ) \left( |p - p_0| +|r - r_0 | \right) , \, \, \forall \, \lambda \ge 1. \end{aligned}$$

• (d) We denote

  $$\begin{aligned} { E}_{a, b}(\lambda , t, \tau ) = (t-\tau )^{a-1} E_{a, a}(-\lambda ^b (t-\tau )^a). \end{aligned}$$

  Then, there exists a constant $C=C(p_*, p^*, r_*)$ such that

  $$\begin{aligned} \int _0^t \left| { E}_{p, r}(\lambda , t, \tau ) - { E}_{p_0, r_0}(\lambda , t, \tau ) \right| \mathrm {d}\tau \le C \left( (1+\lambda ^r)|p- p_0| +|\lambda ^r - \lambda ^{r_0} | \right) . \end{aligned}$$

• (e) Put

  $$\begin{aligned} I_{\alpha ,\nu ,\omega }(t)=\int _{0}^{t} (t - \tau )^{\alpha - 1}E_{\alpha ,\alpha }(-\theta ^\beta (t-\tau )^\alpha ) \frac{\tau ^{-2\nu }}{(1+\tau )^{2\omega }} \mathrm {d}\tau . \end{aligned}$$

  For $t\ge 1$, $\nu +\omega '<1/2$, $0<\omega '\le \omega$, there is a constant $D_{\omega ,\omega '}>0$ such that

  $$\begin{aligned} 0\le I_{\alpha ,\nu ,\omega }(t)\le D_{\omega ,\omega '}t^{-2\nu -2\omega '}. \end{aligned}$$

Proof

We only prove (3.1) and (b), (e). The readers can see the proof of other cases in [8]. From the complete monotonicity of the Mittag-Leffler function $E_{\alpha }(-z)$ for $z\ge 0$ (see [14], Ch. 3) we have $(-1)^n\frac{d^n}{dz^n}E_\alpha (-z)\ge 0$ for $z\ge 0$. Hence we have $E_\alpha (-z), E_{\alpha ,\alpha }(-z)$ is decreasing which give $0\le E_{\alpha }(-z)\le 1$, $0\le E_{\alpha ,\alpha }(-z)\le \frac{1}{\varGamma (\alpha )}$ for $z\ge 0$.

We prove (b). Using the asymptotic expansion in [14, page 19, Ch. 3] we have $\lambda E_p(-\lambda )=\frac{1}{\varGamma (1-p)}+O(\lambda ^{-1})$. Hence $\lim _{\lambda \rightarrow +\infty }\lambda E_p(-\lambda )=\frac{1}{\varGamma (1-p)}$.

We prove (e) next. In fact, noting that $\sup _{\tau \ge 0}\frac{\tau ^{2\omega '}}{(1+\tau )^{2\omega }}\le 1$, we have

$$\begin{aligned} I_{\alpha ,\nu ,\omega }= & {} \int _{0}^{t} (t - \tau )^{\alpha - 1}E_{\alpha ,\alpha }(-\theta ^\beta (t-\tau )^\alpha ) \frac{\tau ^{-2\nu -2\omega '}\tau ^{2\omega '}}{(1+\tau )^{2\omega }} \mathrm {d}\tau \\\le & {} \int _{0}^{t} (t - \tau )^{\alpha - 1}E_{\alpha ,\alpha }(-\theta ^\beta (t-\tau )^\alpha ) \tau ^{-2\nu -2\omega '} \mathrm {d}\tau \\= & {} t^{\alpha -2\nu -2\omega '}(J_1+J_2), \end{aligned}$$

where

$$\begin{aligned} J_1&=\int _{0}^{1/2} (1 - s )^{\alpha - 1}E_{\alpha ,\alpha }(-\theta ^\beta t^\alpha (1-s)^\alpha ) s^{-2\nu -2\omega '}\mathrm {d}s,\\ J_2&=\int _{1/2}^{1} (1 - s )^{\alpha - 1}E_{\alpha ,\alpha }(-\theta ^\beta t^\alpha (1-s)^\alpha ) s^{-2\nu -2\omega '}\mathrm {d}s. \end{aligned}$$

Using Lemma 2 (a) and estimating directly $J_1$ gives

$$\begin{aligned} J_1\le & {} \frac{2^{1-\alpha }E_{\alpha ,\alpha }(-\theta ^\beta t^\alpha 2^{-\alpha })}{(1-2\nu -2\omega ')2^{1-2\nu -2\omega '}}\\\le & {} \frac{2^{1-\alpha }C}{(1+\theta ^\beta t^\alpha 2^{-\alpha })(1-2\nu -2\omega ')2^{1-2\nu -2\omega '}} \le \frac{C'}{t^\alpha }. \end{aligned}$$

Similarly, by Lemma 1, we have

$$\begin{aligned} J_2\le & {} 2^{2\nu +2\omega '}\int _{1/2}^{1} (1 - s )^{\alpha - 1}E_{\alpha ,\alpha }(-\theta ^\beta t^\alpha (1-s)^\alpha ) \mathrm {d}s\\= & {} \frac{2^{2\nu +2\omega '}}{\theta ^\beta \alpha t^\alpha }\int _{1/2}^{1} \frac{\mathrm {d}}{\mathrm {d}s} E_{\alpha }(-\theta ^\beta t^\alpha (1-s)^\alpha ) \mathrm {d}s\\= & {} \frac{2^{2\nu +2\omega '}}{\theta ^\beta \alpha t^\alpha }(1- E_{\alpha }(-\theta ^\beta t^\alpha 2^{-\alpha })) \le \frac{2^{2\nu +2\omega '}}{\theta ^\beta \alpha t^\alpha }. \end{aligned}$$

From the estimation of $J_1, J_2$ we complete the proof of Part (e). $\square$

In this paper, we also need the following useful inequality.

Lemma 3

Let $\alpha , q\in \mathbb {R}$, $0<\alpha \le 1$, $q<\alpha$, and let $v, g\in C[0, T]$. Then the equation

$$\begin{aligned} u(t) = v(t) + g(t) \int _0^t (t - \tau )^{\alpha -1} \tau ^{-q} u(\tau ) \mathrm {d}\tau \end{aligned}$$

has a unique solution $u\in C[0,T]$ which satisfies

$$\begin{aligned} |u(t)| \le \varGamma (1-q) \Vert v\Vert _{C[0,t]} E_{\alpha -q, 1-q} \left( \Vert g\Vert _{C[0,t]}\varGamma (\alpha ) t^{\alpha -q}\right) \end{aligned}$$

(3.2)

for $t \in [0,T]$. As a consequence, if $w\in C[0,T]$ satisfies

$$\begin{aligned} 0 \le w(t) \le v(t)+g(t)\int _0^t (t-\tau )^{\alpha -1}\tau ^{-q}w(\tau )d\tau \ \ \ \text {for}\ \ t\in [0,T], \end{aligned}$$

and if $g(t)\ge 0$ for $t\in [0,T]$, then

$$\begin{aligned} w(t) \le C \varGamma (1-q) \Vert v\Vert _{C[0,t]} E_{\alpha -q, 1-q} \left( \Vert g\Vert _{C[0,t]}\varGamma (\alpha ) t^{\alpha -q}\right) \ \ \ \text {for}\ \ t\in [0,T] , \end{aligned}$$

where $C=\max _{k \ge 1} d_k$ with $d_1=\varGamma ((\alpha -q)+1-q)/\varGamma (\alpha +1-q)$ and $d_k=\varGamma (k(\alpha -q)+1-q)/\varGamma (k(\alpha -q)+1)$.

Remark 6

We note that $\varGamma (a) \le \varGamma (b)$ for any $2 \le a \le b$, therefore, $\varGamma (k(\alpha -q)+1-q)/\varGamma (k(\alpha -q)+1) \le 1$ for k large enough or $d_{k+1} \le d_k$. This implies that $C=\max _{k \ge 1} d_k<+\infty$.

Proof of Lemma 3

Put

$$\begin{aligned} Su(t)=v(t) + g(t) \int _0^t (t - \tau )^{\alpha -1} \tau ^{-q} u(\tau ) \mathrm {d}\tau . \end{aligned}$$

Using the similar technique as in Theorem 1, we can prove that there exists $k_0 \in \mathbb {N}$ such that $S^{k_0}$ is contraction in C[0, T]. Consequently, there exists a unique $u \in C[0, T]$ such that $u=Su$.

We put $u_0=0, u_{n+1}=Su_{n}$. The function can be represented by the series $u=\sum _{n=0}^\infty (u_{n+1}-u_{n})$ . The Weierstrass theorem shows that the series converges in C[0, T] and

$$\begin{aligned} | u(t)|\le & {} \Vert u_1-u_0\Vert _{C[0,t]} \sum _{k=0}^\infty \frac{ \varGamma (1-q)(\Vert g\Vert _{C[0,t]}\varGamma (\alpha ))^k t^{k(\alpha -q)} }{ \varGamma (k(\alpha -q)-q+1) }\\= & {} C \varGamma (1-q) \Vert v\Vert _{C[0,t]} E_{\alpha -q, 1-q} \left( \Vert g\Vert _{C[0,t]}\varGamma (\alpha ) t^{\alpha -q}\right) . \end{aligned}$$

Now, we prove the final inequality. Put $w_0=Sw$, $w_{n+1}=Sw_n$. Since $g(t)\ge 0$ for $t\in [0,T]$, we have $Sw_1(t)\le Sw_2(t)$ for $w_1(t)\le w_2(t)$, $t\in [0,T]$. We note that $w\le w_0$, hence, by induction we obtain $w_{n}\le w_{n+1}$. Using the contraction principle we obtain $\lim _{n\rightarrow \infty }\Vert w_{n}-u\Vert _{C[0,T]}=0$. Since $w_n\le w_{n+1}$ for every $n=0,1,\ldots$, we obtain $w(t)\le w_0(t)\le u(t)$ for $t\in [0,T]$. From (3.2) we obtain the desired inequality. $\square$

We also need the following results.

Lemma 4

Let $T, \theta>0, \alpha \in (0, 1], \beta >0$, $s \in [0, \beta /2]$, $r \ge 0$, $t\in (0,T]$, $w\in C([0,T]; D(A^r))$.

(i) For $\zeta \in D(A^{s+r})$, we have $E_\alpha (-t^\alpha A^\beta )\zeta \in D(A^{s+r})$ and $\Vert E_\alpha (-t^\alpha A^\beta )\zeta \Vert _{s+r}$ $\le \Vert \zeta \Vert _{s+r}$, and

$$\begin{aligned} \lim _{t\rightarrow \infty }(1+t)^{\alpha } \Vert E_\alpha (-t^\alpha A^\beta )\zeta \Vert _s=\frac{1}{\varGamma (1-\alpha )}\Vert \zeta \Vert _{s-\beta }. \end{aligned}$$

(3.3)

For every $0\le \omega \le \alpha /2$, we also have

$$\begin{aligned} \varLambda ^2_\omega := \sup _{\xi }\sup _{t>0} (1+t)^{2\omega } \Vert E_\alpha \big (- t^\alpha A^\beta \big ) \xi \Vert ^2_s <\infty ~~\mathrm{for~}\xi \in D(A^s), \Vert \xi \Vert _s=1 \end{aligned}$$

(3.4)

and

$$\begin{aligned} \sup _{t>0} (1+t)^{2\omega } \Vert E_\alpha \big (- t^\alpha A^\beta \big ) \zeta \Vert ^2_s\le \varLambda ^2_\omega \Vert \zeta \Vert _s^2. \end{aligned}$$

(3.5)

(ii) Put

$$\begin{aligned} Q_{ \alpha , \beta , A}(w)(t)= & {} \int _{0}^{t} { E}_{\alpha , \beta }(A, t, \tau ) w(\tau ) \mathrm {d}\tau , \end{aligned}$$

(3.6)

where

$$\begin{aligned} { E}_{\alpha , \beta }(\lambda , t, \tau ) = (t-\tau )^{\alpha -1} E_{\alpha , \alpha }(-\lambda ^\beta (t-\tau )^\alpha ) = \frac{1}{\lambda ^\beta }\frac{d}{d\tau }E_\alpha (-\lambda ^\beta (t-\tau )^\alpha ). \end{aligned}$$

If $w\not \equiv 0$ on [0, t], then

$$\begin{aligned} {\left| \!\left| Q_{ \alpha , \beta , A}(w)( t )\right| \!\right| }_{s+r}^2 \! < \! \sup _{\lambda \ge \theta } \lambda ^{2s-\beta }H_0(\lambda ,t)\! \int _{0}^{t} \! (t - \tau )^{\alpha - 1}E_{\alpha ,\alpha }(-\theta ^\beta (t \!-\! \tau )^\alpha ) {\left| \!\left| w(\tau ) \right| \!\right| }_r^2 \mathrm {d}\tau , \end{aligned}$$

(3.7)

where

$$\begin{aligned} H_0(\lambda ,t) := 1- E_{\alpha }\big (- \lambda ^\beta t^\alpha \big ). \end{aligned}$$

Proof

We first prove (i). One has

$$\begin{aligned} {\left| \!\left| E_\alpha (-t^\alpha A^\beta )\zeta \right| \!\right| }^2_{s+r}= & {} \int _\theta ^\infty \lambda ^{2(s+r)} E_\alpha (-t^\alpha \lambda ^\beta ) \mathrm {d} {\left| \!\left| S_\lambda \zeta \right| \!\right| }^2\\\le & {} \int _\theta ^\infty \lambda ^{2(s+r)} \mathrm {d} {\left| \!\left| S_\lambda \zeta \right| \!\right| }^2 = \Vert \zeta \Vert ^2_{s+r}. \end{aligned}$$

We next prove (3.3). In fact, we have

$$\begin{aligned} (1+t)^{2\alpha } {\left| \!\left| E_\alpha (-t^\alpha A^\beta )\xi \right| \!\right| }^2_{s}&= (1+t)^{2\alpha } \int _\theta ^\infty \lambda ^{2s} E^2_\alpha (-t^\alpha \lambda ^\beta ) \mathrm {d} {\left| \!\left| S_\lambda \xi \right| \!\right| }^2. \end{aligned}$$

Using Lemma 2 we have $\lim _{t\rightarrow \infty } (1+t)^{\alpha }E_\alpha (-t^\alpha \lambda ^\beta ) =\frac{1}{\lambda ^\beta \varGamma (1-\alpha )}$ and

$$\begin{aligned} \sup _{t\ge 0}|(1+t)^{\alpha }E_\alpha (-t^\alpha \lambda ^\beta )|< \infty . \end{aligned}$$

Hence, applying the Lebesgue dominated convergence theorem yields

$$\begin{aligned} \begin{aligned} \lim _{t\rightarrow \infty } (1+t)^{2\alpha } \int _\theta ^\infty \lambda ^{2s} E^2_\alpha (-t^\alpha \lambda ^\beta ) \mathrm {d} {\left| \!\left| S_\lambda \xi \right| \!\right| }^2&= \frac{1}{\varGamma ^2(1-\alpha )}\int _\theta ^\infty \lambda ^{2s-2\beta }\mathrm {d} {\left| \!\left| S_\lambda \xi \right| \!\right| }^2\\&= \frac{1}{\varGamma ^2(1-\alpha )}\Vert \xi \Vert ^2_{s-\beta }. \end{aligned} \end{aligned}$$

From (3.3), we deduce (3.4). Put $\xi =\zeta /\Vert \zeta \Vert _s$ we obtain (3.5).

Now, we consider Part (ii). We have $E_{\alpha ,\alpha }(z)\ge 0$ (see [14], Ch. 3). Hence, Lemma 1 yields

$$\begin{aligned} \int _{0}^{t} |{ E}_{\alpha , \beta }(\lambda , t, \tau )| \mathrm {d}\tau = \int _{0}^{t} { E}_{\alpha , \beta }(\lambda , t, \tau ) \mathrm {d}\tau = \frac{1}{\lambda ^\beta } H_0(\lambda ,t). \end{aligned}$$

(3.8)

By the Hölder inequality, Lemma 2 and (2.1), we obtain for $t\in (0,T]$

$$\begin{aligned} {\left| \!\left| Q_{ \alpha , \beta , A}(w)( t )\right| \!\right| }_{s+r}^2= & {} {\left| \!\left| \int _{0}^{t} |{ E}_{\alpha , \beta }(A, t, \tau )| w(\tau ) \mathrm {d}\tau \right| \!\right| }_{s+r}^2 \\\le & {} \int _\theta ^{+\infty } \lambda ^{2(s+r)} \int _{0}^{t} |{ E}_{\alpha , \beta }(\lambda , t, \tau )| \mathrm {d}\tau \times \int _{0}^{t} |{ E}_{\alpha , \beta }(\lambda , t, \tau )| \mathrm {d} {\left| \!\left| {S_\lambda }w(\tau )\right| \!\right| }^2 \mathrm {d}\tau \\\le & {} \int _{0}^{t} \int _\theta ^{+\infty } \frac{\lambda ^{2s}}{\lambda ^\beta } H_0(\lambda ,t) |{ E}_{\alpha , \beta }(\lambda , t, \tau )| \lambda ^{2r} \mathrm {d} {\left| \!\left| {S_\lambda }w(\tau )\right| \!\right| }^2 \mathrm {d}\tau . \end{aligned}$$

Noting that $E_{\alpha ,\alpha }(-\lambda ^\beta (t-\tau )^\alpha )\le E_{\alpha ,\alpha }(-\theta ^\beta (t-\tau )^\alpha )$ for $\lambda \ge \theta$, we obtain

$$\begin{aligned}&{\left| \!\left| Q_{ \alpha , \beta , A}(w)( t )\right| \!\right| }_{s+r}^2\\&\quad < \frac{1}{\varGamma (\alpha )} \sup _{\lambda \ge \theta } \lambda ^{2s-\beta } H_0(\lambda ,t) \int _{0}^{t} (t -\tau )^{\alpha -1} E_{\alpha ,\alpha }(-\theta ^\beta (t-\tau )^\alpha ) {\left| \!\left| w(\tau )\right| \!\right| }_r^2 \mathrm {d}\tau . \end{aligned}$$

$\square$

3.2 Proof of Theorem 1

For $w\in C([0,T],D(A^s))$, we put

$$\begin{aligned} { F}(w)(t) = E_\alpha \big (- t^\alpha A^\beta \big ) \zeta + \int _0^t { E}_{\alpha , \beta }(A, t, \tau ) f(\tau , w(\tau )) \mathrm {d}\tau . \end{aligned}$$

Choosing $r=0$ in Lemma 4 (ii) gives $\sup _{\lambda \ge \theta }\lambda ^{2s-\beta }H_0(\lambda ,t_1,t_2)\le \theta ^{2s-\beta }$ and

$$\begin{aligned}&{\left| \!\left| { F}(w_1)(t)-{ F}(w_2)(t)\right| \!\right| }^2_s \end{aligned}$$

(3.9)

$$\begin{aligned}\le & {} \frac{1}{\varGamma (\alpha )} \theta ^{2s-\beta } \int _0^t (t -\tau )^{\alpha -1} {\left| \!\left| f(\tau , w_1(\tau ))-f(\tau , w_2(\tau )\right| \!\right| }^2 \mathrm {d}\tau \nonumber \\\le & {} \frac{1}{\varGamma (\alpha )} \theta ^{2s-\beta } \kappa _{T,s}^2\int _0^t (t -\tau )^{\alpha -1} \tau ^{-2\nu } {\left| \!\left| w_1(\tau )-w_2(\tau )\right| \!\right| }_s^2 \mathrm {d}\tau . \end{aligned}$$

(3.10)

So we have

$$\begin{aligned} {\left| \!\left| { F}(w_1)(t)-{ F}(w_2)(t)\right| \!\right| }^2_s\le & {} \frac{1}{\varGamma (\alpha )} \theta ^{2s-\beta } \kappa _{T,s}^2 |w_1-w_2|_{s,T}^2 \int _0^t(t-\tau )^{\alpha -1}\tau ^{-2\nu }d\tau \\= & {} \frac{1}{\varGamma (\alpha )} B(\alpha ,1-2\nu ) \theta ^{2s-\beta } \kappa _{T,s}^2 |w_1-w_2|_{s,T}^2 t^{\alpha -2\nu }\\= & {} d_1\frac{\varGamma {(1-2\nu )}}{\varGamma (\alpha +1-2\nu )} \theta ^{2s-\beta }\kappa _{T,s}^2|w_1-w_2|_{s,T}^2 t^{\alpha -2\nu }, \end{aligned}$$

where $d_1=\varGamma ((\alpha -2\nu )+1-2\nu )/\varGamma (\alpha +1-2\nu )$. We consider the case $\nu <\alpha /2$. For $w_1,w_2\in C([0,T],D(A^s))$, using the similar technique as in [8], we can prove by induction that

$$\begin{aligned} {\left| \!\left| { F}^k(w_1)(t)-{ F}^k(w_2)(t)\right| \!\right| }^2_s\le & {} d_k \frac{ \varGamma (1-2\nu ) \left( \theta ^{2s-\beta } \kappa _{T,s}^2\right) ^k t^{k(\alpha -2\nu )} }{ \varGamma (k(\alpha -2\nu )-2\nu +1) } |w_1-w_2|^2_{s,T}\\\le & {} C \frac{ \varGamma (1-2\nu ) \left( \theta ^{2s-\beta } \kappa _{T,s}^2\right) ^k t^{k(\alpha -2\nu )} }{ \varGamma (k(\alpha -2\nu )-2\nu +1) } |w_1-w_2|^2_{s,T} , \end{aligned}$$

where $d_k=\varGamma (k(\alpha -2\nu )+1-2\nu )/\varGamma (k(\alpha -2\nu )+1) d_{k-1}$ with $k \ge 2$ and $C=\max _{k \ge 1} d_k$. This gives

$$\begin{aligned} \lim _{k\rightarrow \infty } C \frac{ \varGamma (1-2\nu ) \left( \theta ^{2s-\beta } \kappa _{T,s}^2\right) ^k T^{k(\alpha -2\nu )} }{ \varGamma \left( k(\alpha -2\nu )-2\nu +1\right) } =0. \end{aligned}$$

Hence there is a $k_0\in \mathbb {N}$ such that

$$\begin{aligned} C \frac{ \varGamma (1-2\nu ) \left( \theta ^{2s-\beta } \kappa _{T,s}^2\right) ^{k_0} T^{k_0(\alpha -2\nu )} }{ \varGamma \left( k_0(\alpha -2\nu )-2\nu +1\right) } \le \frac{1}{2} \end{aligned}$$

which gives

$$\begin{aligned} \begin{aligned} | { F}^{k_0}(w_1)-{ F}^{k_0}(w_2)|^2_{s,T}&\le C \frac{ \varGamma (1-2\nu ) \left( \theta ^{2s-\beta } \kappa _{T,s}^2\right) ^{k_0} T^{k_0(\alpha -2\nu )} }{ \varGamma \left( k_0(\alpha -2\nu )-2\nu +1\right) } |w_1-w_2|^2_{s,T}\\&\le \frac{1}{2} |w_1-w_2|^2_{s,T}, \end{aligned} \end{aligned}$$

i.e., ${ F}^{k_0}$ is a contraction in $C([0,T],D(A^s))$. Hence, the exists a unique fixed point $u\in C([0,T],D(A^s))$ satisfying $u={ F}^{k_0}(u)$. We deduce that ${ F}u={ F}^{k_0}({ F}u)$, i.e., ${ F}u$ is also a fixed point of the operator ${ F}^{k_0}$. Hence $u={ F}u$.

We give the estimate of u. In fact, from (3.10) we obtain

$$\begin{aligned} \begin{aligned} \Vert u(t)-g \Vert ^2_s&= {\left| \!\left| \mathcal {F}u(t)-\mathcal {F}(0)(t)\right| \!\right| }^2_s\\&\le \frac{1}{\varGamma (\alpha )} \theta ^{2s-\beta }\kappa _{T,s}^2 \int _0^t (t -\tau )^{\alpha -1} \tau ^{-2\nu } {\left| \!\left| u(\tau )-0\right| \!\right| }_s^2 \mathrm {d}\tau . \end{aligned} \end{aligned}$$

(3.11)

Hence

$$\begin{aligned} \begin{aligned} \Vert u(t) \Vert _s^2&\le 2\Vert g(t) \Vert _s^2+2\Vert u(t)-g\Vert ^2_s\\&\le 2\Vert g(t)\Vert ^2_s+\frac{2}{\varGamma (\alpha )}\theta ^{2s-\beta }\kappa _{T,s}^2 \int _0^t (t -\tau )^{\alpha -1} \tau ^{-2 \nu } {\left| \!\left| u(\tau )\right| \!\right| }_s^2 \mathrm {d}\tau . \end{aligned} \end{aligned}$$

(3.12)

Using (3.2) of Lemma 3, we obtain the inequality of the theorem.

Finally, we consider the case $\nu =\alpha /2$. We can find a $\xi \in (0,T]$ such that ${\left| \!\left| { F}(w_1)(\xi )-{ F}(w_2)(\xi )\right| \!\right| }^2_s=\sup _{0\le t\le T} {\left| \!\left| { F}(w_1)(t)-{ F}(w_2)(t)\right| \!\right| }^2_s$. Lemma 4 gives

$$\begin{aligned} {\left| \!\left| { F}(w_1)(\xi )\!-\!{ F}(w_2)(\xi )\right| \!\right| }^2_s&< \frac{1}{\varGamma (\alpha )}\theta ^{2s-\beta }\! \int _0^\xi (\xi \!-\!\tau )^{\alpha -1} {\left| \!\left| f(\tau , w_1(\tau ))\!-\! f(\tau , w_2(\tau )\right| \!\right| }^2 \mathrm {d}\tau \\&\le \frac{1}{\varGamma (\alpha )} \theta ^{2s-\beta } \kappa _{T,s}^2 \! \int _0^\xi (\xi \!-\!\tau )^{\alpha -1} \tau ^{-\alpha } {\left| \!\left| w_1(\tau )\!-\! w_2(\tau )\right| \!\right| }_s^2 \mathrm {d}\tau \\&\le \frac{1}{\varGamma (\alpha )} B(\alpha , 1-\alpha ) \theta ^{2s-\beta }\kappa _{T,s}^2 |w_1-w_2|_{s,T}^2\\&= \varGamma (1-\alpha ) \theta ^{2s-\beta }\kappa _{T,s}^2 |w_1-w_2|_{s,T}^2. \end{aligned}$$

If $\kappa _{T,s} < \theta ^{\beta /2-s} \left( \varGamma (1-\alpha )\right) ^{-1/2}$ then ${ F}$ is a contraction in $C([0,T],D(A^s))$. Consequently, the problem (1.3) has a unique solution in $C([0,T],D(A^s))$.

3.3 Proof of Theorem 2

In the proof we denote $u=u_{\zeta ,\alpha ,\beta }$ for short. We verify that $\sup _{t\ge 0}(1+t)^\omega \Vert u(t)\Vert _s<\infty$. Assume by contradiction that $\sup _{t\ge 0}(1+t)^\omega \Vert u(t)\Vert _s=\infty$. For every $\lambda >0$, we put

$$\begin{aligned} T_\lambda =\inf \{T>0:(1+t)^\omega \Vert u(t)\Vert _s\le \lambda ~\ \mathrm{for~every}\ ~t\in [0,T]\}. \end{aligned}$$

By the continuity of u, we have

$$\begin{aligned} (1+T_\lambda )^\omega \Vert u(T_\lambda )\Vert _s=\lambda , ~~\lim _{\lambda \rightarrow \infty }T_\lambda =\infty ,~~ (1+t)^\omega \Vert u(t)\Vert _s\le \lambda ,\, \forall t\in [0,T_\lambda ]. \end{aligned}$$

We note that

$$\begin{aligned} \Vert f(t,u(t))\Vert \le \Vert f(t,u(t))-f(t,0)\Vert +\Vert f(t,0)\Vert \le \kappa _1 t^{-\nu }(1+t)^{\ell }\Vert u(t)\Vert _s+\Vert f(t,0)\Vert . \end{aligned}$$

As in the proof of Theorem 1, choosing $r=0$ in Lemma 4 gives

$$\begin{aligned} \sup _{\lambda \ge \theta }\lambda ^{2s-\beta }H_0(\lambda ,t_1,t_2)\le \theta ^{2s-\beta } \end{aligned}$$

and we have

$$\begin{aligned}&{\left| \!\left| u(t)\right| \!\right| }^2_s\nonumber \\&\le 2\Vert E_\alpha \big (- t^\alpha A^\beta \big ) \zeta \Vert ^2_s \nonumber \\&\quad + 2 \theta ^{2s-\beta } \int _0^t (t -\tau )^{\alpha -1} E_{\alpha ,\alpha }(-\theta ^\beta (t-\tau )^\alpha ) {\left| \!\left| f(\tau , u(\tau ))\right| \!\right| }^2 \mathrm {d}\tau \nonumber \\&\le 2\Vert E_\alpha \big (- t^\alpha A^\beta \big ) \zeta \Vert ^2_s\nonumber \\&\quad +4 \theta ^{2s-\beta } \int _0^t (t -\tau )^{\alpha -1} \tau ^{-2\nu } \kappa _1^2(1+\tau )^{2\ell }E_{\alpha ,\alpha }(-\theta ^\beta (t-\tau )^\alpha ) {\left| \!\left| u(\tau )\right| \!\right| }_s^2 \mathrm {d}\tau \nonumber \\&\quad +4 \theta ^{2s-\beta } \int _0^t (t -\tau )^{\alpha -1} \tau ^{-2\nu }E_{\alpha ,\alpha }(-\theta ^\beta (t-\tau )^\alpha ) \Vert f(\tau ,0)\Vert ^2 \mathrm {d}\tau . \end{aligned}$$

(3.13)

For every $\lambda >0$, denoting $w(t)=(1+t)^\omega u(t)$ and using (3.13) yield

$$\begin{aligned} {\left| \!\left| w(t)\right| \!\right| }^2_s&\le 4\varLambda _\omega ^2\Vert \zeta \Vert _s^2+(1+t)^{2\omega }V_1^2+(1+t)^{2\omega }V_2^2, \end{aligned}$$

(3.14)

where $0<t\le T_\lambda$ and

$$\begin{aligned} V_1^2&=4 \theta ^{2s-\beta }\lambda ^2\int _0^t (t -\tau )^{\alpha -1} \tau ^{-2\nu } \kappa _1^2(1+\tau )^{2\ell -2\omega }E_{\alpha ,\alpha }(-\theta ^\beta (t-\tau )^\alpha ) \mathrm {d}\tau , \\ V_2^2&=4 \theta ^{2s-\beta } \int _0^t (t -\tau )^{\alpha -1}E_{\alpha ,\alpha }(-\theta ^\beta (t-\tau )^\alpha ) \kappa _f^2\tau ^{-2\nu _f} (1+\tau )^{2\ell _f} \mathrm {d}\tau . \end{aligned}$$

To prove the theorem, we will use two necessary inequalities. In fact, we can find two constants $\gamma _1,\gamma _2>0$ such that

$$\begin{aligned} (1+t)^{2\omega }V_1^2\le Ct^{-2\gamma _1},\ ~(1+t)^{2\omega }V_2\le Ct^{-2\gamma _2}. \end{aligned}$$

(3.15)

The proof of these inequalities will be postponed to the end of the proof of the theorem.

• (i) We first consider the case $\ell ,\ell _f<\nu$, $\alpha >\frac{1}{2}-\nu$. Using the inequalies (3.14), (3.15) yield

  $$\begin{aligned} \Vert w(t)\Vert _s^2&\le 4\varLambda _\omega ^2\Vert \zeta \Vert _s^2+ Ct^{-2\gamma _1}+Ct^{-2\gamma _2}. \end{aligned}$$

  Choosing $t=T_\lambda$, we obtain

  $$\begin{aligned} \lambda ^2&\le 4\varLambda _\omega ^2\Vert \zeta \Vert _s^2+C'\lambda ^2 T_\lambda ^{-2\gamma _1}+C' T_\lambda ^{-2\gamma _2} \end{aligned}$$

  which implies

  $$\begin{aligned} 4\lambda ^{-2} \varLambda _\omega ^2\Vert \zeta \Vert _s^2+C'T_\lambda ^{-2\gamma _1}+C' \lambda ^{-2}T_\lambda ^{-2\gamma _1}\ge 1. \end{aligned}$$

  (3.16)

  Noting that $\lim _{\lambda \rightarrow \infty }T_\lambda =\infty$, we obtain in view of (3.16) that $0\ge 1$ which is a contradiction.

• (ii) We consider the case $\ell ,\ell _f\le \frac{1}{2}-\alpha$. For the upper bound of $\Vert u(t)\Vert _s$ we can use the same argument as Part (i) with $\omega >\alpha$. We verify the asymptotic value for $(1+t)^{\alpha }\Vert u(t)\Vert _s$. Using Lemma 2 yields

  $$\begin{aligned} \lim _{t\rightarrow \infty }(1+t)^{2\alpha } {\left| \!\left| E_\alpha (-t^\alpha A^\beta )\zeta \right| \!\right| }^2_{s} =\frac{1}{\varGamma ^2(1-\alpha )}\Vert \zeta \Vert ^2_{s-\beta }. \end{aligned}$$

  Choose $\omega =\alpha$, denoting $w(t)=(1+t)^\omega u(t)$ and using (3.13) yield

  $$\begin{aligned}&{\left| \!\left| w(t)-(1+t)^\omega E_\alpha \big (- t^\alpha A^\beta \big ) \zeta \right| \!\right| }_s\\&\le \left( 4\theta ^{2s-\beta } \int _0^t (t -\tau )^{\alpha -1} \tau ^{-2\nu } \kappa _1^2(1+\tau )^{2\ell -2\omega }E_{\alpha ,\alpha }(-\theta ^\beta (t-\tau )^\alpha ) {\left| \!\left| w(\tau )\right| \!\right| }_s^2 \mathrm {d}\tau \right. \\&\left. \quad +4 \theta ^{2s-\beta }(1+t)^{2\omega } \int _0^t (t -\tau )^{\alpha -1} E_{\alpha ,\alpha }(-\theta ^\beta (t-\tau )^\alpha ) \Vert f(\tau ,0)\Vert ^2 \mathrm {d}\tau \right) ^{1/2} \\&\le \sqrt{(1+t)^{2\omega }V_1^2+(1+t)^{2\omega }V_2^2}. \end{aligned}$$

  Combining the latter inequality with (3.15) yields

  $$\begin{aligned} {\left| \!\left| w(t)-(1+t)^\omega E_\alpha \big (- t^\alpha A^\beta \big ) \zeta \right| \!\right| }_s\le \sqrt{Ct^{-2\gamma _1}+Ct^{-2\gamma _2}}. \end{aligned}$$

  Hence

  $$\begin{aligned} \lim _{t\rightarrow \infty }\Vert w(t)\Vert _s=\lim _{t\rightarrow \infty }\Vert (1+t)^\alpha E_\alpha \big (- t^\alpha A^\beta \big ) \zeta \Vert _s = \frac{1}{\varGamma (1-\alpha )}\Vert \zeta \Vert _{s-\beta }. \end{aligned}$$

  Finally, we prove (3.15). Since the proof for the case $\ell \le 0$ is different from the one of the case $\ell >0$, we divide the proof into two cases.

In the case $\ell \le 0$, since $0<\omega <1/2,\nu >0$ we obtain $\omega -\nu <\min \{1/2-\nu ,\omega -\ell \}.$ Hence we can choose $\omega '$ such that

$$ \omega -\nu<\omega '<\min \{1/2-\nu ,\omega -\ell \}$$

which gives $\omega '<\omega -\ell$, $\nu +\omega '<1/2$, $\gamma _1:=-\omega +\nu +\omega '>0$. We can use (3.14) to obtain

$$\begin{aligned} V_1^2&\le \theta ^{2s-\beta }\lambda ^2 \kappa _1^2 I_{\alpha ,\nu ,\omega -\ell }\le Ct^{-2\nu -2\omega '}, \end{aligned}$$

where $I_{\alpha ,\nu ,\omega }$ is defined in Lemma 2. Applying Lemma 2 (e) we can find a $C>0$ such that

$$\begin{aligned} (1+t)^{2\omega }V_1^2\le Ct^{-2\gamma _1}. \end{aligned}$$

Next, we consider the case $0\le \ell <\nu$ we have $\omega +\ell -\nu <1/2-\nu$ and $\omega +\ell -\nu <\omega$. Hence we can find $\omega '$ such that $\omega +\ell -\nu<\omega '<\min \{1/2-\nu ,\omega \}.$ It follows that $\omega '+\nu <1/2, \omega '\le \omega$ and $\gamma _2:=-\omega -\ell +\nu +\omega '>0$. Using Lemma (2) (e) gives

$$\begin{aligned} V_1^2&\le \theta ^{2s-\beta }\lambda ^2 \kappa _1^2(1+t)^{2\ell } I_{\alpha ,\nu ,\omega }\le Ct^{-2\gamma _1}. \end{aligned}$$

In the second case, if $0< \ell \le \frac{1}{2}-\alpha$, we can choose $\omega =\alpha$.

Similarly, we can prove that there is a $\gamma _2>0$ such that

$$\begin{aligned} (1+t)^\omega V_2^2\le Ct^{-2\gamma _2}. \end{aligned}$$

This completes the proof of the theorem.

3.4 Proof of Theorem 3

We denote

$$\begin{aligned} { F}_{\zeta , \alpha , \beta , A}(v)(t)= & {} E_\alpha \big (- t^\alpha A^\beta \big ) \zeta + \int _0^t { E}_{\alpha , \beta }(A, t, \tau ) f(\tau , v(\tau )) \mathrm {d}\tau , \end{aligned}$$

where ${ E}_{a, b}(., t, \tau )$ defined in Lemma 4. Using (3.7) and direct computations, one has

$$\begin{aligned}&{\left| \!\left| { F}_{\xi , \widetilde{\alpha }, \widetilde{\beta }, A}(w) (t) - { F}_{\zeta , \widetilde{\alpha }, \widetilde{\beta }, A}(v) (t) \right| \!\right| }^2_s \\&\le 2 {\left| \!\left| E_{\widetilde{\alpha }} \big (- A^{\widetilde{\beta }} t^{\widetilde{\alpha }} \big ) (\xi -\zeta ) \right| \!\right| }_s^2 + 2 {\left| \!\left| Q_{\widetilde{\alpha }, \widetilde{\beta }, A}(f(\cdot ,w))(0,t) - Q_{\widetilde{\alpha }, \widetilde{\beta }, A}(f(\cdot ,v))(0,t) \right| \!\right| }_s^2\\&\le 2 {\left| \!\left| \zeta - \xi \right| \!\right| }_s^2 + \frac{2}{\varGamma (\widetilde{\alpha })}\theta ^{2s-\widetilde{\beta }} \int _0^t (t-\tau )^{\widetilde{\alpha } - 1} {\left| \!\left| f( \tau , w) - f( \tau , v)\right| \!\right| }^2 \mathrm {d}\tau \\&\le 2 {\left| \!\left| \zeta - \xi \right| \!\right| }_s^2 + \frac{2}{\varGamma (\widetilde{\alpha })} \theta ^{2s-\widetilde{\beta }} \kappa _{T,s}^2 \int _0^t (t-\tau )^{\widetilde{\alpha } - 1} \tau ^{-2\nu } {\left| \!\left| w(\tau ) - v(\tau )\right| \!\right| }_s^2 \mathrm {d}\tau . \end{aligned}$$

Since $u_{\xi , \widetilde{\alpha }, \widetilde{\beta }}$ and $u_{\zeta , \widetilde{\alpha }, \widetilde{\beta }}$ are solution of equations ${ F}_{\xi , \widetilde{\alpha }, \widetilde{\beta }, A}(w) = w$ and ${ F}_{\xi , \widetilde{\alpha }, \widetilde{\beta }, A}(v)$ $= v$, respectively, by Lemma 3, we conclude that

$$\begin{aligned} {\left| \!\left| u_{\xi , \widetilde{\alpha }, \widetilde{\beta }}(t) - u_{\zeta , \widetilde{\alpha }, \widetilde{\beta }}(t) \right| \!\right| }_s^2 \le 2 \varGamma (1-2\nu ) E_{\widetilde{\alpha }-2\nu , 1-2\nu } \left( 2 \theta ^{2s-\widetilde{\beta }} \kappa _{T,s}^2 t^{\widetilde{\alpha }-2\nu }\right) {\left| \!\left| \zeta - \xi \right| \!\right| }_s^2. \end{aligned}$$

This leads to the result of Theorem 3.

3.5 Proof of Theorem 4

We first state the following lemma necessary to prove the theorem. The proof of this lemma is postponed to the next subsection.

Lemma 5

Let $T>0$, $\zeta \in D(A^{s})$, $\alpha , \, \widetilde{\alpha } \in [\alpha _*, \alpha ^*]$ , $\beta , \, \widetilde{\beta }\in [\beta _*, \, \beta ^*].$ Let the source function f satisfy Assumption F1($\alpha _*$) and Assumption G1. Then the initial problems have the unique solutions $u_{\zeta , \widetilde{\alpha }, \widetilde{\beta }} , u_{\zeta , \alpha , \beta } \in C([0,T], D(A^s))$ with $s\in [0, \min \{\beta /2, \widetilde{\beta }/2\}]$. Then, for any $\epsilon >0$, there exist two constants $P, \, P_\epsilon >0$ which are independent of $\alpha , \widetilde{\alpha }, \, \beta , \widetilde{\beta }$ and t such that

$$\begin{aligned} {\left| \!\left| u_{\zeta , \widetilde{\alpha }, \widetilde{\beta }}(t) - u_{\zeta , \alpha , \beta }(t) \right| \!\right| }_s \le P \left( \epsilon + P_\epsilon \left( |\alpha - \widetilde{\alpha }| + |\beta - \widetilde{\beta } |\right) \right) ^{1/2} \end{aligned}$$

for every $t\in [0, T]$. Suppose further that $\zeta \in D\left( A^{\beta ^*/2+r_1}\right)$ for some $r_1>0$ and $f(., u_{\zeta ,\alpha ,\beta }(.)) \in C([0, T], D\left( A^{r_2}\right) )$. Then, there exists a constant $Q_0>0$ which is independent of $\alpha , \widetilde{\alpha }, \, \beta , \widetilde{\beta }, \, N$ and t such that

$$\begin{aligned} {\left| \!\left| u_{\zeta , \widetilde{\alpha }, \widetilde{\beta }}(t) - u_{\zeta , \alpha , \beta }(t) \right| \!\right| }_s \le Q_0 \left( 2^{\gamma _1+2} +1\right) \left( |\alpha - \widetilde{\alpha }| + |\beta - \widetilde{\beta } | \right) ^{\frac{\gamma _2}{2(\gamma _1+\gamma _2+2)}} \end{aligned}$$

for every $t\in [0, T]$. Herein, $\gamma _1=2\beta ^*$, $\gamma _2=\min \{\beta ^*+2r_1-2s, 2r_2\}$.

Proof of Theorem 4

Using Theorem 3 and Lemma 5, we will prove the results of the theorem. Using the triangle inequality, we obtain

$$\begin{aligned}&{\left| \!\left| u_{\zeta _k, \alpha _k, \beta _k}(t) - u_{\zeta , \alpha , \beta }(t) \right| \!\right| }_{\min \{\beta _k/2, \, s\}} \\&\le {\left| \!\left| u_{\zeta _k, \alpha _k, \beta _k}(t) - u_{\zeta , \alpha _k, \beta _k}(t) \right| \!\right| }_{\min \{\beta _k/2, \, s\}} + {\left| \!\left| u_{\zeta , \alpha _k, \beta _k}(t) - u_{\zeta , \alpha , \beta }(t) \right| \!\right| }_{\min \{\beta _k/2, \, s\}}\\&\le P_1 {\left| \!\left| \zeta - \zeta _k\right| \!\right| }_{s} + P\left( \epsilon + P_\epsilon (|\alpha - \alpha _k| + | \beta - \beta _k|) \right) ^{1/2}, \end{aligned}$$

for any $t \in [0, T]$. In addition, we note that

$$\begin{aligned} {\left| \!\left| w\right| \!\right| }_p \le \theta ^{p-q} {\left| \!\left| w\right| \!\right| }_q \ \, \text {for any} \ \, 0 \le p \le q. \end{aligned}$$

(3.17)

From the latter result, we can verify directly the main results (2.5), (2.6), (2.7) and (2.8) of the theorem. In fact, if $s\in [0, \beta /2)$ then with k large enough, we have $\beta _k/2 \ge s$. Hence, we can combine Lemma 3, Lemma 5 with (3.17) to obtain (2.5). We also use Lemmas 3 and 5 to deduce (2.6)-(2.7). Finally, combining Lemmas 3 with 5 (ii), we obtain (2.8). This completes the core of the proof. $\square$

3.6 The proof of Lemma 5

By a direct computation, we have

$$\begin{aligned} {\left| \!\left| { F}_{\zeta , \widetilde{\alpha }, \widetilde{\beta }, A}(v)(t) - { F}_{\zeta , \alpha , \beta , A}(u)(t) \right| \!\right| }_s^2\le & {} 2 {\left| \!\left| \left( E_{\widetilde{\alpha }} \big (- A^{\widetilde{\beta }} t^{\widetilde{\alpha }} \big ) - E_\alpha \big (- A^\beta t^\alpha \big ) \right) \zeta \right| \!\right| }_s^2 \nonumber \\&\, + 2 {\left| \!\left| Q_{\widetilde{\alpha }, \widetilde{\beta }, A}(v)(t) - Q_{\alpha , \beta , A}(u)(t) \right| \!\right| }_s^2\nonumber \\\le & {} 2 I_1 + 4(I_2+I_3), \end{aligned}$$

(3.18)

where

$$\begin{aligned} I_1= & {} {\left| \!\left| \left( E_{\widetilde{\alpha }} \big (- A^{\widetilde{\beta }} t^{\widetilde{\alpha }} \big ) - E_\alpha \big (- A^\beta t^\alpha \big ) \right) \zeta \right| \!\right| }_s^2 ,\\ I_2= & {} {\left| \!\left| Q_{\widetilde{\alpha }, \widetilde{\beta }, A}(v)(t) - Q_{\widetilde{\alpha }, \widetilde{\beta }, A}(u)(t) \right| \!\right| }_s^2 ,\\ I_3= & {} {\left| \!\left| Q_{\widetilde{\alpha }, \widetilde{\beta }, A}(u)(t) - Q_{\alpha , \beta , A}(u)(t) \right| \!\right| }_s^2 , \end{aligned}$$

and the function Q is defined in (3.6). We will estimate $I_k (k=1, 2, 3)$ one by one.

Estimate for $I_1$. To give an estimation for $I_1$, we separate the sum $I_1$ into two sums as follows:

$$\begin{aligned} I_1 = I_{11}(N) + I_{12}(N), \end{aligned}$$

(3.19)

where

$$\begin{aligned} I_{11}( N)= & {} \int _\theta ^N \lambda ^{2s} \left| E_{\widetilde{\alpha }} \big (- \lambda ^{\widetilde{\beta }} t^{\widetilde{\alpha }} \big ) - E_\alpha \big (- \lambda ^\beta t^\alpha \big ) \right| ^2 \mathrm {d} {\left| \!\left| {S_\lambda }\zeta \right| \!\right| }^2,\\ I_{12}(N)= & {} \int _{\lambda >N} \lambda ^{2s} \left| E_{\widetilde{\alpha }} \big (- \lambda ^{\widetilde{\beta }} t^{\widetilde{\alpha }} \big ) - E_\alpha \big (- \lambda ^\beta t^\alpha \big ) \right| ^2 \mathrm {d} {\left| \!\left| {S_\lambda }\zeta \right| \!\right| }^2. \end{aligned}$$

For convenience in estimating for $I_{11}(N), I_{12}(N)$, let us assume $N> \max \{e, \theta \}$.

Estimate for $I_{11}(N)$. By Lemma 2, there exist two constants

$C=C(\alpha _*, \alpha ^*, \beta _*, \beta ^*, T)>0$ , $C_0=C_0(\alpha _*, \alpha ^*, \beta _*, \beta ^*, \theta , T)>0$ such that

$$\begin{aligned} I_{11}(N)\le & {} C \left( |\alpha - \widetilde{\alpha }| + |\beta - \widetilde{\beta }|\right) ^2 \left( \int _\theta ^N \lambda ^{2(\beta ^* + s)}(1+ |\ln \lambda |)^2 \mathrm {d} {\left| \!\left| {S_\lambda }\zeta \right| \!\right| }^2 \right) \nonumber \\\le & {} C_0 \left( |\alpha - \widetilde{\alpha }| + |\beta - \widetilde{\beta }|\right) ^2 N^{2\beta ^*} \ln ^2 N \int _\theta ^N \lambda ^{2s}\mathrm {d} {\left| \!\left| {S_\lambda }\zeta \right| \!\right| }^2 \nonumber \\\le & {} C_N \left( |\alpha - \widetilde{\alpha }| + |\beta - \widetilde{\beta }|\right) ^2, \end{aligned}$$

(3.20)

where $C_N=C_0 {\left| \!\left| \zeta \right| \!\right| }^2_s N^{2\beta ^*} \ln ^2 N$.

Estimate for $I_{12}(N)$. We note that $0\le E_\alpha (-x) \le 1$ for $x>0$. This gives

$$\begin{aligned} I_{12}(N) \le \int _{\lambda >N} \lambda ^{2s} \mathrm {d} {\left| \!\left| {S_\lambda }\zeta \right| \!\right| }^2. \end{aligned}$$

(3.21)

Substituting (3.20) and (3.21) into (3.19), we obtain

$$\begin{aligned} I_1 \le C_N (|\alpha - \widetilde{\alpha } | + | \beta - \widetilde{\beta } |)^2 + \int _{\lambda >N} \lambda ^{2s} \mathrm {d} {\left| \!\left| {S_\lambda }\zeta \right| \!\right| }^2, \end{aligned}$$

(3.22)

where $C_N$ is defined in (3.20).

Estimate for $I_2$. Similarly to the proof of Lemma 3, we get

$$\begin{aligned} I_2 \le \frac{1}{\varGamma (\widetilde{\alpha })}\theta ^{2s-\widetilde{\beta }} \kappa _{T,s}^2 \int _0^t (t - \tau )^{\widetilde{\alpha } - 1} \tau ^{-2\nu } {\left| \!\left| v(\tau ) - u(\tau )\right| \!\right| }_s^2 \mathrm {d}\tau . \end{aligned}$$

(3.23)

Estimate for $I_3$. Recall that Q is defined in (3.6) as follows:

$$\begin{aligned} Q_{\alpha , \beta , A}(f(\cdot ,u))(t) = \int _0^t { E}_{\alpha , \beta }(A, t, \tau ) f(\tau , u) \mathrm {d}\tau . \end{aligned}$$

By the Hölder inequality and direct computation, we have

$$\begin{aligned} I_3\le & {} \int _\theta ^{+\infty } \lambda ^{2s} \int _0^t \left| { E}_{\alpha , \beta }(\lambda , t, \tau ) - { E}_{\widetilde{\alpha }, \widetilde{\beta }}(\lambda , t, \tau ) \right| \mathrm {d}\tau \nonumber \\&\times \int _0^t \left| { E}_{\alpha , \beta }(\lambda , t, \tau ) - { E}_{\widetilde{\alpha }, \widetilde{\beta }}(\lambda , t, \tau ) \right| \mathrm {d} {\left| \!\left| {S_\lambda }f(\tau , u(\tau ))\right| \!\right| }^2 \mathrm {d}\tau \nonumber \\= & {} I_{31}(N)+I_{32}(N), \end{aligned}$$

(3.24)

where

$$\begin{aligned} I_{31}(N)= & {} \int _\theta ^N \lambda ^{2s} \int _0^t \left| { E}_{\alpha , \beta }(\lambda , t, \tau ) - { E}_{\widetilde{\alpha }, \widetilde{\beta }}(\lambda , t, \tau ) \right| \mathrm {d}\tau \nonumber \\&\times \int _0^t \left| { E}_{\alpha , \beta }(\lambda , t, \tau ) - { E}_{\widetilde{\alpha }, \widetilde{\beta }}(\lambda , t, \tau ) \right| \mathrm {d} {\left| \!\left| {S_\lambda }f(\tau , u(\tau ))\right| \!\right| }^2 \mathrm {d}\tau , \nonumber \\ I_{32}(N)= & {} \int _{\lambda > N} \lambda ^{2s} \int _0^t \left| { E}_{\alpha , \beta }(\lambda , t, \tau ) - { E}_{\widetilde{\alpha }, \widetilde{\beta }}(\lambda , t, \tau ) \right| \mathrm {d}\tau \nonumber \\&\times \int _0^t \left| { E}_{\alpha , \beta }(\lambda , t, \tau ) - { E}_{\widetilde{\alpha }, \widetilde{\beta }}(\lambda , t, \tau ) \right| \mathrm {d} {\left| \!\left| {S_\lambda }f(\tau , u(\tau ))\right| \!\right| }^2 \mathrm {d}\tau . \end{aligned}$$

(3.25)

We will estimate $I_{31}(N)$ and $I_{32}(N)$ one by one.

Estimate for $I_{31}(N)$. By Lemma 2, we have

$$\begin{aligned} \int _0^t \left| { E}_{\alpha , \beta }(\lambda , t, \tau ) - { E}_{\widetilde{\alpha }, \widetilde{\beta }}(\lambda , t, \tau ) \right| \mathrm {d}\tau \le C_1 \left( (1+\lambda ^\beta ) |\alpha - \widetilde{\alpha }| + |\lambda ^\beta - \lambda ^{\widetilde{\beta }} | \right) . \end{aligned}$$

By the mean value theorem, for $\lambda \le N$ with N large enough, we obtain

$$\begin{aligned}&\int _0^t \left| { E}_{\alpha , \beta }(\lambda , t, \tau ) - { E}_{\widetilde{\alpha }, \widetilde{\beta }}(\lambda , t, \tau ) \right| \mathrm {d}\tau \nonumber \\&\qquad \le C_2 \lambda ^{\beta ^*} |\ln \lambda | \left( |\alpha - \widetilde{\alpha }|+ |\beta -\widetilde{\beta }| \right) . \end{aligned}$$

(3.26)

On the other hand, there exists $C_3=C_3(\alpha _*, \alpha ^*, \beta _*)$ such that

$$\begin{aligned} \left| { E}_{\alpha , \beta }(\lambda , t, \tau ) - { E}_{\widetilde{\alpha }, \widetilde{\beta }}(\lambda , t, \tau ) \right|\le & {} C_3 \left( (t-\tau )^{\alpha -1}+(t-\tau )^{\widetilde{\alpha }-1}\right) \nonumber \\\le & {} 2 C_3 \left( (t-\tau )^{\alpha _*-1}+(t-\tau )^{\alpha ^*-1}\right) . \end{aligned}$$

(3.27)

Plugging (3.26) and (3.27) into (3.25), we obtain

$$\begin{aligned} I_{31}(N)\le & {} C_4 N^{\beta ^*+2s} \ln N \left( |\alpha - \widetilde{\alpha }|+ |\beta -\widetilde{\beta }| \right) \nonumber \\&\times \int _\theta ^N \! \int _0^t \! \left( (t-\tau )^{\alpha ^*-1} \!+\! (t-\tau )^{\alpha _*-1}\right) \mathrm {d} {\left| \!\left| {S_\lambda }f(\tau , u(\tau ))\right| \!\right| }^2 \mathrm {d}\tau \end{aligned}$$

(3.28)

for N large enough and $C_4=2C_2C_3$. Furthermore, thanks to the condition (2.2), we get that

$$\begin{aligned}&\int _\theta ^N \int _0^t \left( (t-\tau )^{\alpha ^*-1}+(t-\tau )^{\alpha _*-1}\right) \mathrm {d} {\left| \!\left| {S_\lambda }f(\tau , u(\tau ))\right| \!\right| }^2 \mathrm {d}\tau \nonumber \\&\quad \le \int _\theta ^{+\infty } \int _0^t \left( (t-\tau )^{\alpha ^*-1}+(t-\tau )^{\alpha _*-1}\right) \mathrm {d} {\left| \!\left| {S_\lambda }f(\tau , u(\tau ))\right| \!\right| }^2 \mathrm {d}\tau \nonumber \\&\quad \le \int _0^t \left( (t-\tau )^{\alpha ^*-1}+(t-\tau )^{\alpha _*-1}\right) \left( {\left| \!\left| f(\tau , 0)\right| \!\right| }^2 + \kappa _{T,s}^2 \tau ^{-2\nu }\Vert u(\tau )\Vert ^2_s \right) \mathrm {d}\tau \nonumber \\&\quad := C_5, \end{aligned}$$

(3.29)

where $C_5=C_5(\alpha _*, \alpha ^*, \beta _*, { M})$. Combining the inequality (3.28) with (3.29), we obtain

$$\begin{aligned} I_{31}(N) \le D_N \left( |\alpha - \widetilde{\alpha }| + |\beta - \widetilde{\beta }|\right) , \end{aligned}$$

(3.30)

where $D_N=C_4C_5 N^{\beta ^*+2s} \ln N$.

Estimate for $I_{32}(N)$. Thanks to (3.8), one has

$$\begin{aligned}&\int _0^t \left| { E}_{\alpha , \beta }(\lambda , t, \tau ) - { E}_{\widetilde{\alpha }, \widetilde{\beta }}(\lambda , t, \tau ) \right| \mathrm {d}\tau \\&\quad \le \int _0^t { E}_{\alpha , \beta }(\lambda , t, \tau ) \mathrm {d}\tau + \int _0^t { E}_{\widetilde{\alpha }, \widetilde{\beta }}(\lambda , t, \tau ) \mathrm {d}\tau \\&\quad \le \dfrac{1}{\lambda ^\beta } + \dfrac{1}{\lambda ^{\widetilde{\beta }}}. \end{aligned}$$

Consequently,

$$\begin{aligned} \lambda ^s \int _0^t \left| { E}_{\alpha , \beta }(\lambda , t, \tau ) - { E}_{\widetilde{\alpha }, \widetilde{\beta }}(\lambda , t, \tau ) \right| \le C_6, \end{aligned}$$

where $C_6=C_6(\beta _*, \beta ^*, \theta )$, and that

$$\begin{aligned} I_{32}(N)\le & {} C_6 \int _{\lambda >N} \int _0^t \left| { E}_{\alpha , \beta }(\lambda , t, \tau ) - { E}_{\widetilde{\alpha }, \widetilde{\beta }}(\lambda , t, \tau ) \right| \mathrm {d} {\left| \!\left| {S_\lambda }f(\tau , u(\tau ))\right| \!\right| }^2 \mathrm {d}\tau \nonumber \\\le & {} 2C_6C_3\int _0^t \left( (t-\tau )^{\alpha ^*-1}+(t-\tau )^{\alpha _*-1}\right) \nonumber \\&\times \int _N^{+\infty } \mathrm {d} {\left| \!\left| {S_\lambda }f(\tau , u(\tau ))\right| \!\right| }^2 \mathrm {d}\tau . \end{aligned}$$

(3.31)

From (3.22), (3.24), (3.30) and (3.31), for $|\alpha - \widetilde{\alpha } | + | \beta - \widetilde{\beta } |\le 1$, we obtain

$$\begin{aligned} I_1 + I_3\le & {} E_N \left( |\alpha - \widetilde{\alpha } | + | \beta - \widetilde{\beta } | \right) + 2 \int _{\lambda >N} \lambda ^{2s} \mathrm {d} {\left| \!\left| {S_\lambda }\zeta \right| \!\right| }^2 \nonumber \\&\quad + 4 C_6C_3\int _0^t \left( (t-\tau )^{\alpha ^*-1}+(t-\tau )^{\alpha _*-1}\right) \nonumber \\&\times \int _N^{+\infty } \mathrm {d} {\left| \!\left| {S_\lambda }f(\tau , u(\tau ))\right| \!\right| }^2 \mathrm {d}\tau , \end{aligned}$$

(3.32)

where $E_N=2C_N+6D_N$ with $C_N$ defined in (3.20) and $D_N$ defined in (3.30).

Let us mention (3.29) that

$$\begin{aligned}&\int _0^t \left( (t-\tau )^{\alpha ^*-1}+(t-\tau )^{\alpha _*-1}\right) \int _\theta ^{+\infty }\mathrm {d} {\left| \!\left| {S_\lambda }f(\tau , u(\tau ))\right| \!\right| }^2 \mathrm {d}\tau \\&\le \int _0^t \left( (t-\tau )^{\alpha ^*-1}+(t-\tau )^{\alpha _*-1}\right) \left( {\left| \!\left| f(\tau , 0)\right| \!\right| }^2 + \kappa _{T,s}^2 \tau ^{-2\nu }\Vert u(\tau )\Vert _s^2 \right) \mathrm {d}\tau = C_5 \end{aligned}$$

and $\zeta \in D(A^s)$. This leads to the fact that there exists $N=N(\epsilon )$ independent of $\alpha , \widetilde{\alpha }$ and $\beta , \widetilde{\beta }$ such that

$$\begin{aligned} \begin{aligned}&2 \int _{\lambda >N} \lambda ^{2s} \mathrm {d} {\left| \!\left| {S_\lambda }\zeta \right| \!\right| }^2\\&+ 4 C_6C_3\int _0^t \left( (t-\tau )^{\alpha ^*-1}+(t-\tau )^{\alpha _*-1}\right) \int _N^{+\infty } \mathrm {d} {\left| \!\left| {S_\lambda }f(\tau , u(\tau ))\right| \!\right| }^2 \mathrm {d}\tau \\&< \epsilon . \end{aligned} \end{aligned}$$

Combining (3.32) and the latter inequality, one gets

$$\begin{aligned} I_1+ I_3 \le \epsilon + P_\epsilon (|\alpha -\widetilde{\alpha }| + |\beta - \widetilde{\beta }|). \end{aligned}$$

(3.33)

Substituting (3.23) and (3.33) into (3.18), we obtain

$$\begin{aligned}&{\left| \!\left| { F}_{\zeta , \widetilde{\alpha }, \widetilde{\beta }, A}(v)(t) - { F}_{\zeta , \alpha , \beta , A}(u)(t) \right| \!\right| }_s^2 \\&\quad \le 4(\epsilon + P_\epsilon (|\alpha -\widetilde{\alpha }| \\&\qquad + |\beta - \widetilde{\beta }|)) + \frac{4}{\varGamma (\widetilde{\alpha })}\theta ^{2s-\widetilde{\beta }} \kappa _{T,s}^2 \int _0^t (t - \tau )^{\widetilde{\alpha } -1} \tau ^{-2\nu } {\left| \!\left| v(\tau )-u(\tau )\right| \!\right| }^2_s \mathrm {d}\tau . \end{aligned}$$

Since $u_{\zeta , \widetilde{\alpha }, \widetilde{\beta }}$ and $u_{\zeta , \alpha , \beta }$ are the solution of the equations ${ F}_{\zeta , \widetilde{\alpha }, \widetilde{\beta }, A}(v)=v$ and ${ F}_{\zeta , \alpha , \beta , A}(u)=u$, respectively. We conclude from Lemma 3 that

$$\begin{aligned}&{\left| \!\left| u_{\zeta , \widetilde{\alpha }, \widetilde{\beta }}(t) - u_{\zeta , \alpha , \beta }(t) \right| \!\right| }^2_s\\&\quad \le P_0 \left( \epsilon +P_\epsilon (|\alpha -\widetilde{\alpha }| + |\beta - \widetilde{\beta }|)\right) E_{\widetilde{\alpha }-2\nu , 1-2\nu } \left( 4\kappa _{T,s}^2 \theta ^{2s-\widetilde{\beta }} t^{\widetilde{\alpha }-2\nu }\right) , \end{aligned}$$

where $P_0=4 \varGamma (1-2\nu )$. This completes the proof of the first part of Theorem 5.

Now we consider the proof of the second part of the theorem. From (3.32) in the proof of Theorem 5, we obtain

$$\begin{aligned} I_1+I_3\le & {} CN^{2\beta ^*}\ln ^2 N \left( |\alpha - \widetilde{\alpha }| + |\beta - \widetilde{\beta } |\right) +J_1+J_2 , \end{aligned}$$

where

$$\begin{aligned} J_1= & {} 2\int _{\lambda >N} \lambda ^{2s} \mathrm {d} {\left| \!\left| {S_\lambda }\zeta \right| \!\right| }^2,\\ J_2= & {} 4 C_6C_3\int _0^t \left( (t-\tau )^{\alpha ^*-1}+(t-\tau )^{\alpha _*-1}\right) \int _N^{+\infty } \mathrm {d} {\left| \!\left| {S_\lambda }f(\tau , u(\tau ))\right| \!\right| }^2 \mathrm {d}\tau . \end{aligned}$$

In fact, using the assumption $\zeta \in D(A^{\beta ^*/2+r_1})$, $f(.,u(.))\in C([0,T],D(A^{r_2}))$ yields

$$\begin{aligned} J_1 \le 2N^{-(\beta ^*+2r_1-2s)}\int _{\lambda >N} \lambda ^{\beta ^*+2r_1} \mathrm {d} {\left| \!\left| {S_\lambda }\zeta \right| \!\right| }^2 \le 2N^{-(\beta ^*+2r_1-2s)}\Vert \zeta \Vert ^2_{\beta ^*/2+r_1} \end{aligned}$$

and $J_2 \le CN^{-2r_2}.$ Hence, putting $\gamma _1=2\beta ^*$, $\gamma _2=\min \{\beta ^*+2r_1-2s, 2r_2\}$, we get

$$\begin{aligned} I_1+I_3\le CN^{-\gamma _2}+CN^{2\gamma _1}\ln ^2 N \left( |\alpha - \widetilde{\alpha }| + |\beta - \widetilde{\beta } |\right) . \end{aligned}$$

Hence, we can use Lemma 3 to prove that

$$\begin{aligned} {\left| \!\left| u_{\zeta , \widetilde{\alpha }, \widetilde{\beta }}(t) - u_{\zeta , \alpha , \beta }(t) \right| \!\right| }_s \le Q_0 \left( N^{-\gamma _2} + N^{\gamma _1} \ln ^2 N \left( |\alpha - \widetilde{\alpha }| + |\beta - \widetilde{\beta } |\right) \right) ^{1/2}, \end{aligned}$$

where $Q_0$ is independent of $N, \, \alpha , \, \widetilde{\alpha }, \, \beta , \, \widetilde{\beta }$.

Since $\ln N<N$, we obtain

$$\begin{aligned} {\left| \!\left| u_{\zeta , \widetilde{\alpha }, \widetilde{\beta }}(t) - u_{\zeta , \alpha , \beta }(t) \right| \!\right| }_s \le Q_0 \left( N^{-\gamma _2} + N^{\gamma _1+2} \left( |\alpha - \widetilde{\alpha }| + |\beta - \widetilde{\beta } |\right) \right) ^{1/2}. \end{aligned}$$

(3.34)

Let us suppose that $|\alpha - \widetilde{\alpha }| + |\beta - \widetilde{\beta } | \le 1$, and we can choose

$$\begin{aligned} N = \left[ (|\alpha - \widetilde{\alpha }| + |\beta - \widetilde{\beta } |)^{- 1/(\gamma _1+\gamma _2+2)} \right] +1 . \end{aligned}$$

It is easy to see that

$$\begin{aligned} (|\alpha - \widetilde{\alpha }| + |\beta - \widetilde{\beta } |)^{- 1/(\gamma _1+\gamma _2+2)} < N \le 2 (|\alpha - \widetilde{\alpha }| + |\beta - \widetilde{\beta } |)^{-1/(\gamma _1+\gamma _2+2)} . \end{aligned}$$

Hence, by (3.34), we obtain

$$\begin{aligned} {\left| \!\left| u_{\zeta , \widetilde{\alpha }, \widetilde{\beta }}(t) - u_{\zeta , \alpha , \beta }(t) \right| \!\right| }_s \le Q_0 \left( 2^{\gamma _1+2} +1 \right) \left( |\alpha - \widetilde{\alpha }| + |\beta - \widetilde{\beta } | \right) ^{\gamma _2/\left( 2(\gamma _1+\gamma _2+2)\right) }. \end{aligned}$$

This completed the proof of Lemma 5.

3.7 Proof of Theorem 5

Proof

Before proving the theorem, we set up some notations. We will use Theorem 1 to prove Part (i). For $M>0$, we put

$$\begin{aligned} f_{M}(t,v) = f\left( t,\frac{M v}{\max \{M,\Vert v\Vert _s\}}\right) \ \, \text {for}\ \, v\in D(A^s). \end{aligned}$$

Verifying directly, we can prove that the function $f_M$ is global Lipschitz with respect to the variable v, i.e.,

$$\begin{aligned} {\left| \!\left| f_M(t,w_1)-f_M(t, w_2) \right| \!\right| } \le \kappa _M t^{-\nu } {\left| \!\left| w_1-w_2\right| \!\right| }_s \ \ \text {for all}\ \, w_1,w_2\in D(A^s), \end{aligned}$$

where $\kappa _M>0$ depends on M. We consider the problem of finding $U\in C([0,T],D(A^s))$ satisfying

$$\begin{aligned} U(t) = E_\alpha \big (- t^\alpha A^\beta \big ) \zeta + \int _0^t { E}_{\alpha , \beta }(A, t, \tau ) f_M(\tau , U(\tau )) \mathrm {d}\tau . \end{aligned}$$

(3.35)

From Theorem 1, for any $T>0$, the equation (3.35) has a unique solution

$$\begin{aligned} U_{M,T}\in C([0,T],D(A^s)). \end{aligned}$$

• (i) For any $m>0$, we put ${ M}= 2 \Vert \zeta \Vert + m$. Since $U_T(0)=\zeta$, we can use the continuity of $U_T$ to find a constant $T_{ M}\in (0,T]$ such that $\sup _{0\le t\le T_{ M}}\Vert U_{{ M},T}(t)\Vert _s\le { M}$. In this case $f_{ M}(t,U_{{ M},T}(t))=f(t,U_{{ M},T}(t))$ for all $t\in [0,T_{ M}]$ and $U_{{ M},T}(t)$ satisfies (1.3) for $t\in [0,T_{ M}]$.

• (ii) If $V,W\in C([0,T];D(A^s))$ are solutions of (1.3), we denote

  $$\begin{aligned} \mu =1+\max \left\{ \sup _{0\le t\le T}\Vert V(t)\Vert _s, \sup _{0\le t\le T}\Vert W(t)\Vert _s\right\} \end{aligned}$$

  and consider the equation

  $$\begin{aligned} U(t) = E_\alpha \big (- t^\alpha A^\beta \big ) \zeta + \int _0^t { E}_{\alpha , \beta }(A, t, \tau ) f_\mu (\tau , U(\tau )) \mathrm {d}\tau . \end{aligned}$$

  (3.36)

  From Theorem 1, the equation (3.36) has a unique solution

  $$\begin{aligned} U_{\mu ,T}\in C([0,T]; D(A^s)). \end{aligned}$$

  Since $\Vert V(t)\Vert _s,\Vert W(t)\Vert _s\le \mu$ for $t\in [0,T]$, we have

  $$\begin{aligned} f(t,V(t))=f_\mu (t,V(t)),\ f(t,W(t))=f_\mu (t,W(t)). \end{aligned}$$

  Hence, V, W satisfy (3.36). By Theorem 1, we have $V=U_{\mu ,T}=W$.

• (iii) For every $T\in (0,T_{\zeta ,\alpha ,\beta })$, the equation (1.3) has a unique solution $U_T\in C([0,T];D(A^s)$. From Part (ii), for $T_1,T_2\in (0,T_{\zeta ,\alpha ,\beta })$, $T_1<T_2$, we have $U_{T_1}(t)=U_{T_2}(t)$ for $t\in [0,T_1]$. Hence, we can put $u_{\zeta ,\alpha ,\beta }(t)=U_T(t)$ for all $t\in [0,T], T\in (0,T_{\zeta ,\alpha ,\beta })$. The function $u_{\zeta ,\alpha ,\beta }$ is the unique solution of (1.3) on $[0,T_{\zeta ,\alpha ,\beta })$. We prove the second result of Part (iii). Assume by contradiction that $T_{\zeta ,\alpha ,\beta }<\infty$ and $\Vert u_{\zeta ,\alpha ,\beta }(t)\Vert _s\le M$ for every $t\in [0,T_{\zeta ,\alpha ,\beta })$. We consider the equation

  $$\begin{aligned} U(t) = E_\alpha \big (- t^\alpha A^\beta \big ) \zeta + \int _0^t { E}_{\alpha , \beta }(A, t, \tau ) f_M(\tau , U(\tau )) \mathrm {d}\tau . \end{aligned}$$

  (3.37)

  From Theorem 1, the equation (3.37) has a unique solution $U_{M,\delta +T_{\zeta ,\alpha ,\beta }}$ with $\delta >0$. From Part (ii) we have $u_{\zeta ,\alpha ,\beta }(t)=U_{M,\delta +T_{\zeta ,\alpha ,\beta }}(t)$ for every $t\in [0,T_{\zeta ,\alpha ,\beta })$. Since $U_{M,\delta +T_{\zeta ,\alpha ,\beta }} \in C([0,\delta +T_{\zeta ,\alpha ,\beta }]; D(A^s))$, we can find a constant $\delta '\in (0,\delta )$ such that $\Vert U_{M,\delta +T_{\zeta ,\alpha ,\beta }}(t)\Vert _s\le M$ for $t\in [0,\delta '+T_{\zeta ,\alpha ,\beta }]$. Hence the equation (1.3) has a unique solution on $[0,T_{\zeta ,\alpha ,\beta }+\delta ']$. It follows that $T_{\zeta ,\alpha ,\beta }+\delta '\le T_{\zeta ,\alpha ,\beta }$, which is a contradiction. Finally, the proof of the last inequality of the theorem is similar to the inequality (2.3). Hence we omit it.

• (iv) Choose $T\in (0,T_{\zeta ,\alpha ,\beta })$ and $M=1+|u_{\zeta ,\alpha ,\beta }|_{s,T}$ and consider the problem (3.37) and

  $$\begin{aligned} U(t) = E_{\alpha _k} \big (- t^{\alpha _k} A^{\beta _k} \big ) \zeta _k + \int _0^t { E}_{\alpha _k, \beta _k}(A, t, \tau ) f_M(\tau , U(\tau )) \mathrm {d}\tau . \end{aligned}$$

  (3.38)

  Denote the solution of (3.37), (3.38) by $U_{\zeta ,\alpha ,\beta }$ and $U_{\zeta _k,\alpha _k,\beta _k}$ respectively. From the stability result, we obtain

  $$\begin{aligned} U_{\zeta _k,\alpha _k,\beta _k}\rightarrow U_{\zeta ,\alpha ,\beta }~\ \mathrm{in}\ ~C([0,T];D(A^s))~\ \mathrm{as}\ ~k\rightarrow \infty . \end{aligned}$$

  (3.39)

  Since $|u_{\zeta ,\alpha ,\beta }|_{s,T}<M$, we have $u_{\zeta ,\alpha ,\beta }=U_{\zeta ,\alpha ,\beta }$. From (3.39), there is a $k_0\in \mathbb {N}$ such that $| U_{\zeta _k,\alpha _k,\beta _k}|_{s,T}<M$ which gives $U_{\zeta _k,\alpha _k,\beta _k}=u_{\zeta _k,\alpha _k,\beta _k}$ is the solution of Problem $P_{\zeta _k,\alpha _k,\beta _k}$. It follows that $T<T_{\zeta _k,\alpha _k,\beta _k}$ for $k>k_0$ which implies $\liminf _{k\rightarrow \infty }T_{\zeta _k,\alpha _k,\beta _k}\ge T_{\zeta ,\alpha ,\beta }$. Using (3.39) yields

  $$\begin{aligned} \lim _{k\rightarrow \infty } |u_{\zeta _k,\alpha _k,\beta _k}-u_{\zeta ,\alpha ,\beta }|_{s,T}=0. \end{aligned}$$

  This completes the proof of the theorem.

$\square$

3.8 Proof of Theorem 6

Proof

$\omega '\le \omega (\eta +1)-\ell$, $\omega '<1/2-\nu$, $\omega -\nu -\omega '<0$. We have $\omega -\nu <\omega '\le \omega (\eta +1)-\ell$ which gives $-\nu <\omega \eta -\ell$ or $\omega >\frac{\ell -\nu }{\eta }$. We also need $\omega -\nu <1/2-\nu$ which gives $\omega <1/2$. Hence $\frac{\ell -\nu }{\eta }<1/2$ Since $\eta >\max \left\{ 2(\ell -\nu ),0\right\}$ we can choose $\omega$ such that

$$\begin{aligned} \max \left\{ \frac{\ell -\nu }{\eta },0\right\}<\omega <1/2 \end{aligned}$$

which gives

$$\begin{aligned} \max \{\omega -\nu ,0\}<\min \{\omega (\eta +1)-\ell ,1/2-\nu \}. \end{aligned}$$

Choosing $\omega '$ such that

$$\begin{aligned} \max \{\omega -\nu ,0\}<\omega '<\min \{\omega (\eta +1)-\ell ,1/2-\nu \} \end{aligned}$$

we obtain

$$\begin{aligned} \omega '<\min \{\omega (\eta +1)-\ell , 1/2-\nu \}, \omega -\nu -\omega '<0. \end{aligned}$$

(3.40)

The maximal solution $u=u_{\zeta ,\alpha ,\beta }\in C([0,T_{\zeta ,\alpha ,\beta }),D(A^s))$ satisfies

$$\begin{aligned} u(t) = E_\alpha \big (- t^\alpha A^\beta \big ) \zeta + \int _0^t { E}_{\alpha , \beta }(A, t, \tau ) f(\tau , u(\tau )) \mathrm {d}\tau ~~~\mathrm{for~ all}~~ t\in [0,T_{\zeta ,\alpha ,\beta }). \end{aligned}$$

We claim that $T_{\zeta ,\alpha ,\beta }=\infty$ and   $\sup _{t>0}(1+t)^\omega \Vert u(t)\Vert _s<\infty$. We note that

$$\begin{aligned} \begin{aligned} \Vert f(t,u(t))\Vert&\le \Vert f(t,u(t))-f(t,0)\Vert +\Vert f(t,0)\Vert \\&\le \kappa _1 t^{-\nu }(1+t)^{\ell }\Vert u(t)\Vert _s^{1+\eta }+\Vert f(t,0)\Vert . \end{aligned} \end{aligned}$$

As in the proof of Theorem 1, choosing $r=0$ in Lemma 4 gives

$$\begin{aligned} \sup _{\lambda \ge \theta }\lambda ^{2s-\beta }H_0(\lambda ,t_1,t_2)\le \theta ^{2s-\beta } \end{aligned}$$

and we have

$$\begin{aligned}&{\left| \!\left| u(t)\right| \!\right| }^2_s\nonumber \\&\le 2\Vert E_\alpha \big (- t^\alpha A^\beta \big ) \zeta \Vert ^2_s\nonumber \\&\quad + 2 \theta ^{2s-\beta } \int _0^t (t -\tau )^{\alpha -1} E_{\alpha ,\alpha }(-\theta ^\beta (t-\tau )^\alpha ) {\left| \!\left| f(\tau , u(\tau ))\right| \!\right| }^2 \mathrm {d}\tau \nonumber \\&\le 2\Vert E_\alpha \big (- t^\alpha A^\beta \big ) \zeta \Vert ^2_s\nonumber \\&\quad +4 \theta ^{2s-\beta } \int _0^t (t -\tau )^{\alpha -1} \tau ^{-2\nu } \kappa _1^2(1+\tau )^{2\ell }E_{\alpha ,\alpha }(-\theta ^\beta (t-\tau )^\alpha ) {\left| \!\left| u(\tau )\right| \!\right| }_{2}^{2(\eta +1)} \mathrm {d}\tau \nonumber \\&\quad +4 \theta ^{2s-\beta } \int _0^t (t -\tau )^{\alpha -1}E_{\alpha ,\alpha }(-\theta ^\beta (t-\tau )^\alpha ) \Vert f(\tau ,0)\Vert ^2 \mathrm {d}\tau . \end{aligned}$$

(3.41)

Putting $w(t)=(1+t)^\omega u(t)$ and, for $\varLambda >\Vert \zeta \Vert _s$, denoting

$$\begin{aligned} T_\mathrm{bound} = \sup \{T_0\in [0,T_{\zeta ,\alpha ,\beta }) :~ \Vert w(t)\Vert _s<\varLambda ~\mathrm{for~} 0 \le t\le T_0\}. \end{aligned}$$

We claim that there are $\varLambda>0, \delta _0>0$ such that $T_\mathrm{bound}=T_{\zeta ,\alpha ,\beta }$ for every $\Vert \zeta \Vert ^2_s+m^2_{\infty ,\alpha ,\omega }<\delta _0$. Assume by contradiction that $T_\mathrm{bound}<T_{\zeta ,\alpha ,\beta }$. Then, we obtain $\Vert w(T_\mathrm{bound})\Vert _s=\varLambda$. The inequality (3.41) yields

$$\begin{aligned} {\left| \!\left| w(t)\right| \!\right| }^2_s&\le K_1+K_2~~\mathrm{for~} 0 \le t<T_\mathrm{bound}, \end{aligned}$$

where

$$\begin{aligned} K_1&= 2(1+t)^{2\omega }\Vert E_\alpha \big (- t^\alpha A^\beta \big ) \zeta \Vert ^2_s+4 \theta ^{2s-\beta }m^2_{\infty ,\alpha ,\omega },\\ K_2&= 4\theta ^{2s-\beta }(1+t)^{2\omega } \kappa _1^2 \int _0^t (t-\tau )^{\alpha -1} \tau ^{-2\nu }E_{\alpha ,\alpha }(-\theta ^\beta (t-\tau )^\alpha )\\&\quad \times (1+\tau )^{2\ell -2\omega (\eta +1)} \Vert w(\tau )\Vert _s^{2(\eta +1)} d\tau . \end{aligned}$$

From (3.4) we obtain

$$\begin{aligned} K_1\le 2\varLambda _0\Vert \zeta \Vert ^2_s+4 \theta ^{2s-\beta }m^2_{\infty ,\alpha ,\omega }<\zeta _0^2. \end{aligned}$$

Next, we consider $K_2$. For $t\ge 1$, we obtain in view of Lemma 2 and (3.40) that

$$\begin{aligned} K_2&\le 4\varLambda ^{2(\eta +1)} \theta ^{2s-\beta } (1+t)^{2\omega } \kappa _1^2 I_{\alpha ,\nu ,\omega (\eta +1)-\ell }\\&\le 4C\varLambda ^{2(\eta +1)} \theta ^{2s-\beta } (1+t)^{2\omega } \kappa _1^2 t^{-2\nu -2\omega '}\le C"\varLambda ^{2(\eta +1)}, \end{aligned}$$

where $\omega '\le \omega (\eta +1)-\ell$, $\omega '<1/2-\nu$, $\omega -\nu -\omega '<0$. We estimate for the case $0<t<1$. We have

$$\begin{aligned} K_2&\le 4\varLambda ^{2(\eta +1)} \theta ^{2s-\beta } (1+t)^{2\omega }) \kappa _1^2 \int _0^t (t-\tau )^{\alpha -1} \tau ^{-2\nu }E_{\alpha ,\alpha }(-\theta ^\alpha (t-\tau )^\alpha )\\&\quad \times (1+\tau )^{2\ell -2\omega (\eta +1)} \mathrm {d}\tau \\&\le \frac{4\varLambda ^{2(\eta +1)}}{\varGamma (\alpha )} \theta ^{2s-\beta } 2^{2\omega } \kappa _1^2 \int _0^t (t-\tau )^{\alpha -1} \tau ^{-2\nu } \mathrm {d}\tau \\&\le \frac{4\varLambda ^{2(\eta +1)}}{\varGamma (\alpha )} \theta ^{2s-\beta } 2^{2\omega } \kappa _1^2 t^{\alpha -2\nu }B(\alpha , 1-2\nu )\\&\le \frac{4\varLambda ^{2(\eta +1)}}{\varGamma (\alpha )} \theta ^{2s-\beta } 2^{2\omega } \kappa _1^2 B(\alpha , 1-2\nu ). \end{aligned}$$

Combining the two cases gives

$$\begin{aligned} K_2\le C\varLambda ^{2(\eta +1)}. \end{aligned}$$

From the estimates for $K_1, K_2$ we obtain

$$\begin{aligned} \varLambda ^2 = \Vert w(T_\mathrm{bound})\Vert _s^2 = \sup _{0\le t<T_\mathrm{bound}}\Vert w(t)\Vert _s^2 \le \zeta _0^2 + C\varLambda ^{2(\eta +1)} . \end{aligned}$$

Since $2(\eta +1)>2$ we can choose $\varLambda , \zeta _0>0$ such that $1 > C\varLambda ^{2\eta }, \zeta ^2_0 < \varLambda ^2-C\varLambda ^{2(\eta +1)}$ and

$$\begin{aligned} \delta _0^2&= \zeta _0^2\left( 2\varLambda _\omega +\frac{4}{\varGamma (\alpha )} \theta ^{2s-\beta }\right) ^{-1}. \end{aligned}$$

In this case we get $\varLambda ^2 = \Vert w(T_\mathrm{bound})\Vert _s^2 \le \zeta _0^2 + C\varLambda ^{2(\eta +1)}<\varLambda ^2$ which is a contradiction. Hence, we have to obtain $T_\mathrm{bound}=T_{\zeta ,\alpha ,\beta }$. So we have

$$\begin{aligned} \Vert u(t)\Vert _s \le (1+t)^{-\omega }\varLambda ~~~~\mathrm{for~every} ~t \in [0, T_{\zeta ,\alpha ,\beta }). \end{aligned}$$

Using the continuation result in Theorem 5 leads to $T_{\zeta ,\alpha ,\beta }=\infty$. Finally, we consider the case $\frac{\ell -\nu }{\eta }<\alpha <1/2$. In this case, we can choose $\omega =\alpha$ and obtain the desired result by a similar argument as in Theorem 2. This completes the proof of the theorem. $\square$