1 Introduction

The Anti-de Sitter/conformal field theories correspondence (AdS/CFT) turned out to be a very useful tool to map the physics of a quantum field theory at strong coupling in \(D-1\) dimensions to a classical gravity theory in D dimensions whose spatial infinity is isometric to the AdS spacetime [1,2,3].

Much attention has been given to the extensions of such a correspondence regarding the study of condensed matter systems defined at the AdS boundary, such as superconductivity and superfluidity [4, 5], non-fermi liquids [6] and strange metals [7].

In order to study condensed matter systems described by non-relativistic theories, we need solutions to the gravity side which exhibit the so-called Lifshitz scaling [8,9,10]. Recently, a black hole solution with such a symmetry was found in the context of new massive gravity (NMG) in three dimensions [11]. Therefore, temperature can be added to the holographic description resulting in a non-relativistic field theory at finite temperature at the boundary.

Such a black hole solution is stable under scalar and spinor perturbations [12] and from the point of view of the AdS/CFT correspondence the IR limit is a dual description of an integrable model system given by the Korteweg-de Vries (KdV) equation [13].

This paper is organized as follows. In Section 2, a brief review of the Lifshitz black hole in three dimensions is presented. In Section 3, the equations of motion for the matter fields in the bulk are derived and analyzed in the probe limit. In Section 4, using a semi analytical analysis, we obtain the phase transition in the Lifshitz boundary and the critical electric field where it occurs. In Section 5, we numerically solve the equations of motion and derive the order parameters. Finally in Section 6, we conclude and discuss some open questions.

2 The Gravity Background and the Matter Fields

The NMG is a three-dimensional theory of a spin-2 field [14] equivalent to the unitary Pauli-Fierz theory [15] at the linearized level. Moreover, a version of NMG with a non-vanishing cosmological constant was considered in [11] and the corresponding action reads

$$\begin{aligned} S_{g}=\frac{1}{16\pi G}\int d^{3}x\sqrt{-g}\left( R-2\Lambda -K\right) , \end{aligned}$$
(1)

where R is the Ricci scalar, \(\Lambda\) is the three-dimensional cosmological constant and K encodes the higher curvature terms,

$$\begin{aligned} K=\frac{1}{\bar{m}^{2}}\left[ R_{\mu \nu }R^{\mu \nu }-\frac{3}{8}R^{2}\right] , \end{aligned}$$
(2)

with \(\bar{m}\) being the graviton mass in three dimensions. Looking for black hole solutions in the equations of motion of the action (1), is assumed a line element

$$\begin{aligned} ds^{2}=-\frac{r^{2z}}{l^{2z}}f(r)dt^{2}+\frac{l^2}{r^2f(r)}dr^{2}+r^{2}d\phi ^{2}\quad , \end{aligned}$$
(3)

where z is the dynamic exponent which determines two different black hole solutions.

The first one, when \(z=3\), is a black hole solution named the AGGH black hole. It exhibits the anisotropic scale invariance \(t\rightarrow \lambda ^{z}t\), \(\textbf{x}\rightarrow \lambda \textbf{x}\). The line element that describes the geometry for this black hole [11] is given by

$$\begin{aligned} ds^{2}=-\frac{r^6}{l^6}f(r)dt^{2}+\frac{l^2}{r^2f(r)}dr^{2}+r^{2}d\phi ^{2}\quad , \end{aligned}$$
(4)

where

$$\begin{aligned} f(r)=\left( 1-\frac{r_{+}^{2}}{r^{2}}\right) \quad , \end{aligned}$$
(5)

with \(r_{+}=l\sqrt{M}\) denoting the event horizon location, M is related to the black hole mass and \(l=\sqrt{-13/32\Lambda }\) is the AdS radius. The spacetime represented by such a solution has a light-like singularity at \(r=0\). The spatial infinity (\(r\rightarrow \infty\)) has some properties similar to the AdS spacetime [12].

The second solution, for \(z=1\), is the well-known BTZ (Bañados-Teitelboim-Zanelli) black hole solution [16]

$$\begin{aligned} ds^{2}=-\frac{r^2}{l^2}f(r)dt^{2}+\frac{l^2}{r^2f(r)}dr^{2}+r^{2}d\phi ^{2}\quad , \end{aligned}$$
(6)

where f(r) is given by (5), the event horizon is located at \(r_{+}=l\sqrt{M}\) covering the singularity at \(r=0\) and in the limit \(r\rightarrow \infty\) the solution is AdS-like. Thus, the NMG allows us to study the relativistic case \(z=1\) and the non-relativistic case \(z=3\) in the same setup. The theory provides a scenario to observe the role of Lifshitz symmetry in the formation of the holographic phase transitions in comparison to the relativistic case \(z=1\).

Thus, we take as a background, the geometry given by the three-dimensional black holes of NMG. These solutions have all the main features needed in order to apply the gauge/gravity holographic prescription for phase transitions: there is an AdS-like spatial infinity and a regular event horizon, whose presence is necessary for the condensation of a charged scalar field.

The action describing a charged scalar field \(\Psi\) coupled to gravity and to the electromagnetic field in three dimensions can be written as

$$\begin{aligned} S_{f}=\int d^{3}x\sqrt{-g}\left[ -\frac{1}{4}F_{\mu \nu }F^{\mu \nu }-|\nabla \Psi -iqA\Psi |^{2}-m^{2}|\Psi |^2\right] , \end{aligned}$$
(7)

where \(F_{\mu \nu }=\nabla _{\mu } A_{\nu }-\nabla _{\mu }A_{\nu }\), q is the scalar field charge and m its mass. Here, we consider the scalar and gauge fields in the probe limit. This means that the fields do not backreact on the geometry. Thus, in order to describe the phase transition, it is enough to consider the equations of motion for the matter fields evolving in the fixed background of the metrics (4) or (6). If we perform the field rescaling \(\Psi \rightarrow \Psi /q\), \(A_{\mu }\rightarrow A_{\mu }/q\), the probe limit can be understood as the limit \(q\rightarrow \infty\). Since in this limit, the action of matter fields behaves as \(q^{-2}\) they decouple from gravity, whose action behaves as \(q^{0}\).

Finally, an important question arises when we work in \((2+1)\)-dimensional gravity. Clement [17] pointed out that rotating charged three-dimensional black holes present a logarithmic divergence in the mass and angular momentum. In such a case, the author introduced a Chern-Simons term in the Einstein-Maxwell action in order to heal those divergencies. However, Bañados et al. [16] have shown that for static charged BTZ such a divergence in the mass can be handled. Thus, we expect that not to be a problem in our cases. In fact, in a quick inspection, we observe that the introduction of a Chern-Simons term in the action 7 modifies the coupling between Abelian and scalar fields. The effect of this term in the phase transition of the system described on the boundary will be addressed in future work.

3 Equations of Motion and Symmetries

In this section, we are going to present the equations of motion for the fields \(\Psi\) and \(A_{\mu }\) in the probe limit, showing the role of the scaling symmetries of these fields in the equations.

The equations of motion for \(\Psi\) and \(A_{\mu }\) are, respectively,

$$\begin{aligned} \nabla ^{\mu }\nabla _{\mu }\Psi &+2iqA_{\mu }g^{\mu \nu }\nabla _{\nu }\Psi +iq g^{\mu \nu }\Psi \nabla _{\nu }A_{\mu } \\&-q^{2}g^{\mu \nu }A_{\mu }A_{\nu }\Psi -m^{2}\Psi =0\quad ,\end{aligned}$$
(8)
$$\begin{aligned} \nabla ^{\mu }F_{\mu \nu }=2q^{2}A_{\nu }\Psi ^{2}\quad , \end{aligned}$$
(9)

where we have taken \(\Psi\) to be real, without loss of generality. For our purposes, it is enough to consider the fields depending only on the radial coordinate r as

$$\begin{aligned} \Psi =\Psi (r),\ A=\phi (r)dt . \end{aligned}$$
(10)

Then, Eqs. (8)–(9) reduce to

$$\begin{aligned} \Psi ^{\prime \prime }(u)&+\left[ \frac{f^\prime (u)}{f(u)}-\frac{z}{u}\right] \Psi ^\prime (u) \\&+ \left[ \frac{q^{2}l^{2(z+1)}u^{2(z-1)}}{f(u)^{2}r_{+}^{2z}}\phi (u)^{2}- \frac{\alpha ^{2}}{f(u)u^{2}}\right] \Psi (u)=0\quad ,\end{aligned}$$
(11)
$$\begin{aligned} \phi ^{\prime \prime }(u)+\frac{z}{u}\phi ^\prime (u)-\frac{2q^{2}l^{2}\Psi (u)^{2}}{f(u)u^{2}}\phi (u)=0\quad , \end{aligned}$$
(12)

where \(\alpha = m l\) and \(z=1\), \(z=3\) correspond to the dynamical exponents for BTZ and AGGH cases, respectively. The coordinate \(u=r_{+}/r\) is the new radial coordinate which maps the event horizon and the boundary to the interval [1, 0] and \({}^ \prime\) represents the derivative with respect to u coordinate.

The above system of differential equations exhibits a very useful scaling symmetry for the fields \(\Psi (u)\) and \(\phi (u)\). If we perform the redefinitions

$$\begin{aligned} \Psi (u)\rightarrow \frac{1}{ql}\hat{\Psi }(u), \ \phi (u)\rightarrow \frac{2\pi T_H}{q}\hat{\phi }(u), \end{aligned}$$
(13)

where \(T_H\) is the Hawking temperature,

$$\begin{aligned} T_H=\frac{1}{2\pi }\frac{r_{+}^{z}}{l^{z+1}}\quad , \end{aligned}$$
(14)

the equations of motion (11)–(12) can be cast in the dimensionless form

$$\begin{aligned} \hat{\phi }^{\prime \prime }(u)+\frac{z}{u}\hat{\phi }^\prime (u)-\frac{2\hat{\Psi }(u)^{2}}{f(u)u^{2}}\hat{\phi }=0\quad ,\end{aligned}$$
(15)
$$\begin{aligned} \hat{\Psi }^{\prime \prime }(u)+\left[ \frac{f^\prime (u)}{f(u)}-\frac{z}{u}\right] \hat{\Psi }^\prime (u)+ \left[ \frac{u^{2(z-1)}}{f(u)^{2}}\hat{\phi }^{2}(u)- \frac{\alpha ^{2}}{f(u)u^{2}}\right] \hat{\Psi }(u)=0\quad , \end{aligned}$$
(16)

without an explicit dependence on the black hole temperature. As we will see in detail in the next section, the phase transition will be governed by the value of the electric field due the scalar field condensate in the neighborhood of the event horizon.

Furthermore, it is worth mentioning that the equations of motion (15) (16) are invariant under the anisotropic scale invariance \(t\rightarrow \lambda ^{z}\), \(r\rightarrow \lambda ^{-1}r\) if

$$\begin{aligned} \phi \rightarrow \lambda ^{-z}\phi , \ \Psi \rightarrow \Psi \quad , \end{aligned}$$
(17)

and the Hawking temperature scales as

$$\begin{aligned} T_{H}\rightarrow \lambda ^{-z}T_{H}. \end{aligned}$$
(18)

Looking into the solutions (21), we see that

$$\begin{aligned} \rho \rightarrow \lambda ^{-z}\rho , \ \mu \rightarrow \lambda ^{-z}\mu \quad . \end{aligned}$$
(19)

Thus, comparing (19) and (18), we can build up the variable \(T_{H}/\mu\) as playing the role of our temperature parameter in order to eliminate the scale factor \(\lambda\) from the description. Therefore, we set

$$\begin{aligned} \hat{T}=\frac{T_{H}}{\mu }\quad , \end{aligned}$$
(20)

implying that the critical temperature \(T_{c}\propto \mu\).

4 The Phase Transition and the Critical Electric Field

In this section, we obtain an approximate expression for the dual operators \(\langle \mathcal {O}_{1}\rangle\) and \(\langle \mathcal {O}_{2}\rangle\) in terms of the asymptotic behavior of the solutions for the fields \(\Psi\) and \(\phi\) following the standard AdS/CFT correspondence [4, 18]. In summary, the process consists in finding the leading order solutions in the region near the black hole event horizon \(u=1\) and in the spatial infinity \(u=0\), then match the two sets of solutions at an intermediate radius \(u=u_{0}\) requiring continuity of the functions \(\Psi\) and \(\phi\). The validity of these approximations and matching conditions are discussed in [19].

The result is an approximate expression for the phase transition and consequently the critical value of the order parameter which controls the charged scalar field condensation. Therefore, we will be able to see explicitly the condensate dependence on the Lifshitz exponent z.

4.1 Solutions at Spatial Infinity \(u\rightarrow 0\)

The solutions for the fields \(\phi (u)\) and \(\Psi (u)\)Footnote 1 from the Eqs. (15) and (16) in the spatial infinity are given by

$$\begin{aligned} \phi (u) = \left\{ \begin{array}{rl} \rho + \mu \ln {u} &{} \ \text {if} \ (z = 1),\\ \\ \rho + \mu \frac{u^{1-z}}{1-z} &{} \ \text {if} \ (z \ne 1). \\ \end{array} \right. \end{aligned}$$
(21)
$$\begin{aligned} \Psi (u)=C_{1}u^{\Delta _{+}}+C_{2}u^{\Delta _{-}}, \end{aligned}$$
(22)

with

$$\begin{aligned} \Delta _{\pm }=\frac{(z+1)}{2}\pm \frac{1}{2}\sqrt{(1+z)^{2}+4\alpha ^{2}}\quad ,\ \text {and}\ \alpha =m l\quad , \end{aligned}$$
(23)

where \(\rho\) is identify as the charge density of the dual field theory living at \(u=0\) and \(\mu\) its chemical potential. The factors \(C_1\) and \(C_2\) will be identified as the expectation value \(\langle \mathcal {O}_{1}\rangle\) and \(\langle \mathcal {O}_{2}\rangle\) of the dual operators in the AdS-like border. As we see in the expression (21) the leading term is \(\ln (u)\) (for \(z=1\)), and \(u^{1-z}\) (for \(z\not =1\)), its coefficient is interpreted as a chemical potential and the subleading term as the charge density.

An interesting effect of the Lifshitz symmetry in the evolution of the scalar field can be observed by inspecting the conformal dimension of its dual operator in Eq. (23). Besides the evident fact that the Lifshitz exponent z increases the conformal dimension, when \(z\ne 0\) a new BF bound to the mass of the scalar field is obtained

$$\begin{aligned} \alpha _{BFL}^2=-\frac{(1+z)^{2}}{4}. \end{aligned}$$
(24)

For \(z=3\) the BF-Lifshitz bound \(\alpha _{BFL}^2=-4\) is smaller than the traditional BF bound \(\alpha _{BF}^2=-1\) for \((2+1)\) dimensions. Thus, the presence of the Lifshitz symmetry expands the range of mass of the scalar field affecting the conformal dimension of the operator living on the boundary.

It is important to stress that to obtain the asymptotic fields presented in Eqs. (21) and (22), we had to impose restrictions on the values of the scalar field mass. In order to obtain the asymptotic solution to \(\phi\), we had to impose that \(\Psi \rightarrow 0\) faster than u near to the boundary \((u\rightarrow 0)\) resulting in a condition that must be satisfied, that is, \(\Delta _{\pm } > 1\). Because of this restriction the permitted range of the mass of the scalar field changes.

Fig. 1
figure 1

Limits of mass for \(\Delta _{\pm }\) for BTZ case (left) and in AGGH (right)

Full size image

In Fig. 1, we show these ranges according to the conformal dimension \(\Delta\) for BTZ and AGGH black holes. For the BTZ black hole such a restriction excludes \(\Delta _{-}\) as a possible conformal dimension for all range of mass while for \(\Delta _+\) the permitted range will be \(-1\le \alpha ^2\le 0\). For the AGGH black hole, the conformal dimension \(\Delta _{-}\) will have the range restricted to \(-4\le \alpha ^2\le -3\) while for \(\Delta _{+}\) the range will be \(-4\le \alpha ^2\le 0\). This limit is consistent with [9]. We exclude positive values of \(\alpha ^2\) for both cases because \(\Delta _{-}<0\) and \(\Psi\) would diverge as u tends to 0.

4.2 Solutions at the Event Horizon \(u\rightarrow 1\)

In order to have a finite electric potential at the event horizon, we must impose

$$\begin{aligned} \phi (1)=0, \end{aligned}$$
(25)

and Eq. (16) implies

$$\begin{aligned} \Psi ^\prime (1)=-\frac{\alpha ^{2}}{2}\Psi (1). \end{aligned}$$
(26)

We expand the fields \(\Psi\) and \(\phi\) near the event horizon \(u=1\) as

$$\begin{aligned} \Psi (u)=\Psi (1)+(u-1)\Psi ^\prime (1)+\frac{1}{2}(u-1)^{2}\Psi ^{\prime \prime }(1)+\cdots ,\end{aligned}$$
(27)
$$\begin{aligned} \phi (u)=\phi (1)+(u-1)\phi ^\prime (1)+\frac{1}{2}(u-1)^{2}\phi ^{\prime \prime }(1)+\cdots . \end{aligned}$$
(28)

Expanding the equation of motion for \(\Psi\) (16) near \(u=1\) an substituting \(\Psi ^{\prime \prime }(1)\) in the expansion (27), we have

$$\begin{aligned} \Psi (u)=\Psi (1)&-\frac{1}{2}\alpha ^{2}(u-1)\Psi (1) \\&-\left[ \frac{1}{8}\alpha ^{2}(3-z)+ \frac{1}{16}\alpha ^{4}-\frac{1}{2}\phi ^\prime (1)^{2}\right]\\&\quad \ (u-1)^{2}\Psi (1)^{2}. \end{aligned}$$
(29)

The same procedure for the electric potential \(\phi\) leads to

$$\begin{aligned} \phi (u)=\left[ (u-1)-\frac{z+\Psi (1)^{2}}{2}(u-1)^{2}\right] \phi ^\prime (1), \end{aligned}$$
(30)

where in the above two expressions, we have imposed the regularity conditions at the event horizon (25) and (26).

4.3 Matching the Solutions at \(u=u_{0}\)

Having the solutions (21) and (22) at spatial infinity and (30) and (29) near the event horizon, we can connect these two sets of solutions smoothly at a radius \(u=u_{0}\), which can be arbitrary without changing the main features of the phase transition. We begin by the BTZ black hole \((z=1)\), whose connection relations at \(u=u_{0}\) are

$$\begin{aligned} \rho + \mu \ln {u_{0}}=\left[ (1-u_{0})+\frac{1}{2}\left( 1+a^{2}\right) (1-u_{0})^{2}\right] b\quad ,\end{aligned}$$
(31)
$$\begin{aligned} \frac{\mu }{u_{0}}=-\left[ 1+(1+a^{2})(1-u_{0})\right] b\quad ,\end{aligned}$$
(32)
$$\begin{aligned} C_{1}u_{0}^{\Delta _{+}}=\left\{ 1-\frac{\alpha ^{2}}{2}(u_{0}-1)+\frac{1}{2}(u_{0}-1)^{2}\left[ \frac{\alpha ^{2}}{2}+ \frac{\alpha ^{4}}{8}-\frac{b^{2}}{8}\right] \right\} a\quad , \end{aligned}$$
(33)
$$\begin{aligned} \Delta _{+}C_{1}u_{0}^{\Delta _{+}-1}=\left\{ -\frac{\alpha ^{2}}{2}+\left[ \frac{\alpha ^{2}}{2}+\frac{\alpha ^{4}}{8}- \frac{b^{2}}{8}\right] (u_{0}-1)\right\} a\quad , \end{aligned}$$
(34)

where we have defined \(a\equiv \Psi (1)\) and \(b\equiv -\phi ^\prime (1)\) and taken \(C_2=0\) in order to find \(C_1\). On the other hand, if we take \(C_1=0\), we get \(C_2\).

Solving Eq. (32) for \(a^{2}\),

$$\begin{aligned} a^{2}=-\frac{\mu }{b(1-u_{0})u_{0}}\left[ 1+\frac{\left( 2-u_{0}\right) u_{0}b}{\mu }\right] \quad . \end{aligned}$$
(35)

For the charged scalar field to condense near the event horizon, we see that \(b/\mu\) must be negative, since a is assumed to be real, therefore, \(a^2>0\).

From Eqs. (33) and (34), we find

$$\begin{aligned} C_{1}=\Gamma _{+}\left( \frac{b_{c}}{b}\right) ^{\frac{1}{2}}\left( 1-\frac{b}{b_{c}}\right) ^{\frac{1}{2}}, \end{aligned}$$
(36)

where the critical value for b, denoted by \(b_{c}\), is given by

$$\begin{aligned} b_{c}=\frac{|\mu |}{\left( 2-u_{0}\right) u_{0}}\quad , \end{aligned}$$
(37)

and

$$\begin{aligned} \Gamma _{+}=\frac{1}{2\ u_{0}^{\Delta _{+}-1}}\left[ \frac{4+\alpha ^{2}(1-u_{0})}{2u_{0}+\Delta _{+}(1-u_{0})}\right] \left[ \frac{2-u_{0}}{1-u_{0}}\right] ^{\frac{1}{2}}\quad . \end{aligned}$$
(38)

Using the AdS/CFT dictionary, Eq. (36) can be read off as the expectation value \(\langle \mathcal {O}_{1}\rangle\) of the operator dual to the charged scalar field \(\Psi\),

$$\begin{aligned} \langle \mathcal {O}_{1}\rangle ^{\frac{1}{\Delta _{+}}}=\Gamma _{+}^{\frac{1}{\Delta _{+}}} \left( \frac{b_{c}}{b}\right) ^{\frac{1}{2\Delta _{+}}}\left( 1-\frac{b}{b_{c}}\right) ^{\frac{1}{2\Delta _{+}}}\quad . \end{aligned}$$
(39)

As expected, \(\langle \mathcal {O}_{1}\rangle\) is zero at the critical value of the electric field \(b=b_c\), the charged scalar field condensates and, of course, the phase transition occurs for \(b<b_{c}\). The exponent 1/2 shows us the general behavior of mean-field theory for a second-order phase transition. For the AGGH black hole (\(z=3\)) the same qualitative behavior is observed and the structure of a mean-field theory is preserved at the boundary.

Now, considering \(C_1=0\) and following the same steps for \(C_2\), we find that the expectation value \(\langle \mathcal {O}_{2}\rangle\) for the BTZ black hole is given by

$$\begin{aligned} \langle \mathcal {O}_{2}\rangle ^{\frac{1}{\Delta _{-}}}=\Gamma _{-}^{\frac{1}{\Delta _{-}}} \left( \frac{b_{c}}{b}\right) ^{\frac{1}{2\Delta _{-}}} \left( 1-\frac{b}{b_{c}}\right) ^{\frac{1}{2\Delta _{-}}}. \end{aligned}$$
(40)

Thereafter, the same procedure was performed for the AGGH black hole \((z=3)\). We just list the results for the two operators,

$$\begin{aligned} \langle \mathcal {O}_{1}\rangle ^{\frac{1}{\Delta _{+}}}_{z> 1}=\Gamma _{+,z > 1}^{\frac{1}{\Delta _{+}}}\left( \frac{b_{c}}{b}\right) ^{\frac{1}{2\Delta _{+}}} \left( 1-\frac{b}{b_{c}}\right) ^{\frac{1}{2\Delta _{+}}}\quad ,\end{aligned}$$
(41)
$$\begin{aligned} \langle \mathcal {O}_{2}\rangle ^{\frac{1}{\Delta _{-}}}_{z> 1}=\Gamma _{-,z > 1}^{\frac{1}{\Delta _{-}}}\left( \frac{b_{c}}{b}\right) ^{\frac{1}{2\Delta _{-}}} \left( 1-\frac{b}{b_{c}}\right) ^{\frac{1}{2\Delta _{-}}}\quad , \end{aligned}$$
(42)

where

$$\begin{aligned} \Gamma _{+,z > 1}=\frac{1}{2\ u_{0}^{\Delta _{+}-1}}\left[ \frac{4+\alpha ^{2}(1-u_{0})}{2u_{0}+\Delta _{+} (1-u_{0})}\right] \left[ \frac{1+z(1-u_{0})}{1-u_{0}}\right] ^{1/2}\quad , \end{aligned}$$
(43)
$$\begin{aligned} \Gamma _{-,z> 1}=\Gamma _{+,z > 1}\quad , \end{aligned}$$
(44)

if we exchange \(\Delta _{+}\) for \(\Delta _{-}\). The critical value of the electric field is

$$\begin{aligned} b_{c}=\frac{|\mu |}{u_{0}^{z}\left[ 1+z(1-u_{0})\right] }\; , \ \mu <0\quad . \end{aligned}$$
(45)

5 Numerical Results for the Phase Transition

In this section, we numerically solve Eqs. (15) and (16). They form a system of coupled second-order ordinary differential equations, which can be solved using fourth-order Runge-Kutta method. We input the boundary conditions at the event horizon \(u=1\) (\(r=r_+\)) and find the values of \(\Psi (u)\) and \(\phi (u)\) on a grid \(u = 1 - i*\Delta u\) with \(i\in (0,1,\ldots ,N-1)\), \(\Delta u = 1.0/N\) and \(N=1000\).

Equations (25) and (26) fix two conditions, but at this point, we still do not have a condition for \(\Psi (1) = \Psi _+\) and \(\phi ^\prime (1) = E_+\). So, for each pair \((\Psi _+,E_+)\), we integrate Eqs. (15) and (16) to look for a convenient behavior. As \(u \rightarrow 0\) (\(r \rightarrow \infty\)), \(\Psi (u)\) behaves as Eq. (22) and \(\phi (u)\) behaves as Eq. (21) which are linear on the parameters, so we can use the least square method to calculate the asymptotic behavior. With this procedure, we have a map

$$\begin{aligned} (\Psi _+,E_+) \rightarrow (C_1,C_2, \rho , \mu ) \ . \end{aligned}$$
(46)

We are interested in the cases where \(C_2=0\), in which we define \(\langle O_1 \rangle =C_1\). Similarly, for \(C_1=0\), we define \(\langle O_2 \rangle =C_2\). Using the shooting method, we search for pairs of boundary values for \((\Psi _+,E_+)\) mapped to such conditions. We vary \(E_+\) from 0 to 15 in 1500 steps for \(z=1\) and from 0 to 35 in 3500 steps for \(z=3\).Footnote 2 For each \(E_+\), we vary \(\Psi _+\) from 0 to 10 in 10000 steps.Footnote 3

For \(z=1\), keeping \(E_+\) fixed, we assume that \(C_1\) and \(C_2\) are smooth functions of \(\Psi _+\) when using the map (46).

Thus, whenever \(C_2\) changes sign, we add a point to the graph of \(\langle O_1 \rangle\) as a function of \(E_+\) and, whenever \(C_1\) changes sign, we add a point to the graph of \(\langle O_2 \rangle\) as a function of \(E_+\).

We notice that for \(z=1\), if we plot all the data our algorithm generates, we see several scattered points and in the middle of these points, we can see smooth curves that go to zero as we raise \(E_+\). If the first occurrences of sign change are isolated as one vary \(\Psi _+\), the isolated points correspond to the smooth curves observed. These curves can also be labeled by the number of times \(\Psi (u)\) changes sign, allowing us to identify the curve labeled as 0 as the fundamental mode and the others as excited modes. In [20], the role of the excited modes in the phase transition is explained. We choose to plot the five first occurrences of sign change in Fig. 2. For \(z=3\), no scattered points appear in our data. Even so, we choose to plot the five first occurrences of sign change in Fig. 3. One interesting property is that for \(\langle O_1 \rangle\), none of the smooth curves crosses another, while for \(\langle O_2 \rangle\), each curve crosses every other.

Fig. 2
figure 2

First five curves for \(z=1\) and \(\alpha ^2 = -0.75\)

Full size image
Fig. 3
figure 3

First five curves for \(z=3\) and \(\alpha ^2 = -2.75\)

Full size image

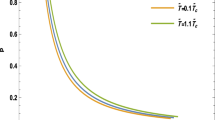
We can also see the dependence of \(\langle O_1 \rangle\) and \(\langle O_2 \rangle\) on the variable \(T = 1/(2\pi \mu )\) defined in Eq. (20) with the arbitrary choice \(r_+=l=1\). This dependence is plotted in Fig. 4 for \(z=1\) and Fig. 5 for \(z=3\). If the incoherent points not shown in Figs. 2 and 3 are plotted, one sees that they do not appear to be incoherent anymore, as they are now concentrated in a region of low temperatures. The curves shown behave as an order parameter of a phase transition.

Fig. 4
figure 4

First five curves for \(z=1\) and \(\alpha ^2 = -0.75\)

Full size image
Fig. 5
figure 5

First five curves for \(z=3\) and \(\alpha ^2 = -2.75\)

Full size image

The fundamental curve (labeled as 0) has the lowest critical electric field and highest critical temperature. We fit the behavior of the fundamental curves as \(y = a (b-x)^c\), where a is not important, b is the critical electrical field \(E_c\) in case of dependence on \(E_+\) or the critical temperature \(T_c\) in case of dependence on T, and c is the critical exponent. The order parameters are shown in Figs. 6, 7, 8, and 9 while the fitted parameters b and c are shown in Figs. 10, 11, 12, and 13.

Fig. 6
figure 6

Order parameters dependent on \(E_+\) for \(z=1\)

Full size image
Fig. 7
figure 7

Order parameters dependent on \(E_+\) for \(z=3\)  

Full size image
Fig. 8
figure 8

Order parameters dependent on T for \(z=1\)

Full size image
Fig. 9
figure 9

Order parameters dependent on T for \(z=3\)

Full size image
Fig. 10
figure 10

Critical electrical field for \(z=1\) (left) and \(z=3\) (right)

Full size image
Fig. 11
figure 11

Critical temperature for \(z=1\) (left) and \(z=3\) (right)

Full size image
Fig. 12
figure 12

Critical exponent dependent on \(E_+\) for \(z=1\) (left) and \(z=3\) (right)

Full size image
Fig. 13
figure 13

Critical exponent dependent on T for \(z=1\) (left) and \(z=3\) (right)

Full size image

We notice that for \(\langle O_2 \rangle\) and \(z=3\) the critical electrical field goes to zero as \(\alpha ^2\) reaches \(-3\). For \(-4<\alpha ^2<-3\), there are no fundamental curves, since the first occurrence of a sign change in \(C_1\) corresponds to boundary conditions for which \(\Psi (u)\) changes sign once. As seen in Fig. 1, this range of \(\alpha ^2\) should have been excluded, because it is assumed that \(\Psi (u)\) decays faster than u in order to obtain Eq. (21). However, we observe that this asymptotic expression fits the data derived by Runge–Kutta method, and all results for \(\langle O_2 \rangle\) are consistent with the results for \(\langle O_1 \rangle\), for which \(\Delta _+\) is always bigger than one. The same reasoning is valid for \(z=1\). All values of \(\alpha ^2\) should have been excluded for \(\langle O_2 \rangle\), but Eq. (21) fits the numerical data even in this case and all results are consistent with \(\langle O_1 \rangle\).

6 Discussions

The holographic description of a \((1+1)\) dimensional field theory with Lifshitz symmetry displaying a second-order phase transition is presented. This result might imply a contradiction with the Coleman-Mermin-Wagner theorem [21,22,23]. However, for a BTZ spacetime (namely our \(z=1\) case) it has been shown [24] that the theorem is evaded by means of a Berezinskii-Kosterlitz-Thouless phase transition [25, 26] as it has been usual in relativistic two-dimensional field theory with mass generation [27]. For \(z=3\) there is a further break of space-time symmetry and a possible prohibition of a phase transition is further removed. In this case, there is no ground for any version of the Coleman-Mermin-Wagner theorem. In fact, there is no global symmetry breaking. Thus, not even a Berezinskii-Kosterlitz-Thouless mechanism is envisaged, leaving the system free to have a phase transition of the kind found in the present paper.

Some similarities between both cases, \(z=1\) and 3 are pointed out. The fact that there is a phase transition in terms either of a critical electric field or a temperature is very much the same, even the dependence of the order parameters on the temperature is hardly seen to display any difference, thus indicating that the mechanism of obtaining the phase transition is very similar in both cases. This may sound a bit surprising, since in the real world superconductivity and other thermodynamical properties depend a lot on the details of the system, while here, we have a too robust result, always similar to the mean-field result, independent even on the dimensionality of the system.

The order parameters grow unbounded as T goes to zero. In [4], it is argued that this behavior indicates that we cannot assume no backreaction for small values of T. According to [28], our results also suggest strong pairing interactions. Indeed, the larger value of \(\langle O\rangle\) when \(T\rightarrow 0\) is expected for a strongly interacting field theory. Thus, being a strongly coupled system, backreaction must be considered, which does not mean that the order parameters do not diverge at small temperatures. This correction will be studied in future works.

For the conductivity, we tried to solve a differential equation for the field \(A_\phi\), which is coupled to Eqs. (15) and (16) and fitted an asymptotic behavior similar to Eq. (21) to find \(\langle J_\mu \rangle\) and \(A_\phi ^{(0)}\), which we used to find the conductivity \(\sigma (\omega )\). In the results, we found peaks consistent with resonances, but we could not explain what caused these resonances. If we smoothed the data with techniques such as plotting a Bezier curve from the data, we could get a behavior consistent with [4], but this approach seemed too artificial. Therefore, we decided to remove our conductivity analysis to focus on the phase transition.

A possible modification in these results could be obtained considering a Chern-Simons term in the action since that it introduces a new coupling between \(A_{t}\) and \(A_{\phi }\). In fact, in other works [17, 29] the presence of Chern-Simons term solves some problems in \((2+1)\) spacetimes. We will deal with this term in future work.