1 Introduction

Nanoscience and nanotechnology have played a vital role in energizing the conventional energy industries and stimulating the emerging renewable energy industries. All the forms of energy we are using today, out of which more than \(70\%\) are produced in or through the form of heat. In industry, heat must be passed either to inject energy into a system or to remove the produced energy from a system. That is why, the heat transfer process has become an important part in the era of nano-science and-technology. Nanotechnology was presented by Nobel laureate Feyman [1] during his well-known lecture “Plenty of Room at the Bottom.” Choi [2] gave the concept of “nanofluids” that are thinned suspensions of nanoparticles less than 100nm belonging to the new class of composite materials developed about last two decades ago by aiming the increase in thermal conductivity of heat transfer fluids.

The credit of enhancement in thermal conductivity completely goes to nanofluids which was initially reported since last decade, in spite of much controversial debates and discrepancies, though the deficiency to formulate the mechanism of nanofluids wedged their application [3]. The rapid progress on nanofluids tells us how these deficiencies have been cleared. Nanofluids can be encountered in nuclear reactors, automobile, cooling of electronic devices, micro and mini channels, and renewable energy systems to enhance the performance characteristics of engineering devices [4,5,6,7]. Later on, homogeneous models [8, 9], the dispersion model [10] and the Buongiorno model [11] have been proposed to enhance the thermal conductivity of fluids(or nanofluids) using with (or without) nanoparticles, respectively. The flow and heat transfer in a thin liquid film over a stretching surface has also many applications in thermal engineering, such as fiber glass production, polymeric sheets, lubricants performance, roofing shingles, paper production, insulating materials, and condensation process [11,12,13,14,15,16]. Khan et al. [17] investigated the effects of variable viscosity and thermal conductivity on the flow and heat transfer in a laminar liquid film over horizontal stretching sheet. Noghrehabadi et al. [18] studied the slip effects on the boundary layer flow and heat transfer over a stretching surface based on nanoparticle fractions. Moreover, the numerical and analytical studies upon nanofluids with slip conditions have been found in [19,20,21,22,23,24].

It should be noted that the convective heat transfer characteristic of nanofluids depends on the thermophysical properties of the flow pattern and flow structure of the base fluid, the volume fraction of suspended particles, the dimensions and the shape of nanoparticles. The thermophysical properties, shape factor, and viscosity coefficients of different nanoparticles with water as base fluid are given in Tables 1 and 2.

Table 1 Thermophysical properties of base fluid and nanoparticles [31]
Full size table
Table 2 Viscosity and shape factor value of nanoparticle [32]
Full size table

The thermal conductivity and viscosity models of metallic oxides nanofluids were presented by Alawi et al. [25]. Maiga et al. [26] observed heat transfer enhancement using nanofluids inforced convection flow. Tiwari and Das [27] proposed heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Dinarvand et al. [28] Buongiorno’s model for double-diffusive mixed convective stagnation-point flow of a nanofluid considering diffusio-phoresis effect of binary base fluid. Tzou [29] reported thermal instability of nanofluids in natural convection. Oztop and Abu-Nada [30] discussed numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids.

It has been seen clearly, from the cited literature, that the majority of the researchers analyze the thermal conductivity of different nanofluids over a stretching surface under various physical constraints. To the best of our knowledge, no study has been carried out for the development of thermal conductivity in thin film over a stretching surface along with convective conditions for different nanofluids.

The rest of article is organized as follows; the detailed description of the proposed model is discussed in Sect. 2. Dimensionless form of the model with physical quantities including similarity transformations are interpreted in Sect. 3 and its subsections, while the method of solution of the model with numerical technique Bvp4c is explained in Sect. 4. The pertinent features of the physical quantities are presented in Sect. 5 and its subsections. Finally, the concluding remarks are summarized in Sect. 6.

2 Mathematical Modeling of the Problem

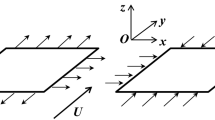
Consider a two-dimensional time dependent fluid flow and heat transfer in a thin film over a stretched surface attached with a slit. The rectangular coordinate system is chosen in such a way that \(x-\)axis and \(y-\)axis is taken along and normal to the surface, respectively. The assumed base nanofluid (water) with spherical shape nanoparticles, \(Cu,Ag,Al_{2}O_{3},SiO_{2},TiO_{2}\) is considered in thermal equilibrium, and moves with uniform velocity \(U_{w}=\frac{bx}{1-\alpha t}\) in x-direction due to stretching of surface. Film thickness is taken as h(t), while the temperature distribution at the wall is given by

$$\begin{aligned} T_{s}=T_{0}-T_{r}\left( \frac{bx^{2}}{2\nu _{f}}\right) (1-\alpha t)^{\frac{-3}{2}}, \end{aligned}$$

where

  • \(\alpha ,b=\) Dimensional constants,

  • \(T_{r}=\) Reference temperature,

  • \(T_{0}=\) Slit temperature,

  • \(\nu _{f}=\) Kinematic viscosity of base fluid.

The uniform magnetic field \(B(t)=\frac{B_{0}}{\sqrt{1-\alpha ~t}}\) is applied perpendicularly to the surface, as shown in Fig. 1.

Fig. 1
figure 1

Diagram of physical model with boundary conditions

Full size image

Assume coordinates axes are labeled with the respective velocity components, as \(u=u(x,y,t),~v=v(x,y,t)\), and temperature of the nanofluid is \(T=T(x,y,t)\). With all these suppositions, the equations of continuity, momentum, and energy are grabbed by following the Tiwari and Das model [27];

$$\begin{aligned} \frac{\partial u}{\partial x} +\frac{\partial v}{\partial y}= & {} 0, \end{aligned}$$
(1)
$$\begin{aligned} \frac{\partial u}{\partial t} +u\frac{\partial u}{\partial x} +v\frac{\partial u}{\partial y}= & {} \frac{\mu _{nf} }{\rho _{nf}} \frac{\partial ^{2}u }{\partial ^{2}y}-\frac{\sigma _{nf}}{\rho _{nf}}B(t)^{2}u, \end{aligned}$$
(2)
$$\begin{aligned} \frac{\partial T}{\partial t} +u\frac{\partial T}{\partial x} +v\frac{\partial T}{\partial y}= & {} \alpha _{nf} \frac{\partial ^{2}T}{\partial ^{2} y}+\frac{\mu _{nf}}{\rho _{nf}C_{p}}\left( \frac{\partial u}{\partial y}\right) ^{2}, \end{aligned}$$
(3)

subject to the boundary conditions

$$\begin{aligned} u=U_{w}+A\nu _{f}\frac{\partial u}{\partial y},~~v=0,~~-\kappa _{nf}\frac{\partial T}{\partial y}=h_{f}~(T_{0}-T)~~at~~y=0, \end{aligned}$$
(4)
$$\begin{aligned} \frac{\partial u}{\partial y}=0,~~\frac{\partial T}{\partial y}=0,~~v=\frac{dh}{dt}~~at~~y=h(t), \end{aligned}$$
(5)

where

\(A=\) Proportionality constant, \(h_{f}=\) Convective heat coefficient.

The thermophysical properties of the hybrid nanofluid defined in [33, 34] can be written as

$$\begin{aligned} \left. \begin{aligned} \alpha _{nf}=\frac{\kappa _{nf}}{(\rho C_{p})_{nf}}, \quad \rho _{nf}=(1-\phi )\rho _{f}+\phi \rho _{s}, \quad \mu _{nf}=\mu _{f}(1+A_{1}\phi +A_{2}\phi ^{2}),\\ \sigma _{nf}=\sigma _{f}(1-\phi )\sigma _{f}+\phi \sigma _{s}, \quad (\rho C_{p})_{nf}=(1-\phi )(\rho C_{p})_{f}+\phi (\rho C_{p})_{s}, \end{aligned}\right\} \end{aligned}$$
(6)

and

$$\begin{aligned} \frac{\kappa _{nf}}{\kappa _{f}}=\left[ \dfrac{\kappa _{s}+(m-1)\kappa _{f}+(m-1)(\kappa _{s}-\kappa _{f})\phi }{\kappa _{s}+(m-1)\kappa _{f}-(\kappa _{s}-\kappa _{f})\phi }\right] , \end{aligned}$$
(7)

where

  • \((\rho ~Cp)_{nf}\) = Heat capacity,

  • \(\phi\) = Volume fraction of nanofluid,

  • \(A_{1},A_{2}\) = Viscosity coefficients of enhancing heat capacitance.

Moreover, \(\kappa _{s}\) and m are the thermal conductivity and shape factor of the nanoparticle, and thermophysical properties of base fluid, nanofluid, and nanoparticles of solids are represented by f, nf and s.

3 Dimensionless Model

The non-dimensional form of the complete model with physical quantities have been presented in the following subsections.

3.1 Similarity Transformations

Introducing the transformations

$$\begin{aligned} \left. \begin{aligned} T=T_{0}-T_{r}\left( \frac{bx^{2}}{2\nu _{f}}\right) (1-\alpha t)^{\frac{-3}{2}} \theta (\eta ),\\ \eta =\left( \frac{b}{\nu _{f}(1-\alpha t)}\right) ^{\frac{1}{2}}y,\\ \psi =\left( \frac{b\nu _{f}}{1-\alpha t}\right) ^{\frac{1}{2}} x f(\eta ), \end{aligned}\right\} \end{aligned}$$
(8)

where the flow pattern is described by a stream function \(\psi\), defined as

$$\begin{aligned} u=\frac{\partial \psi }{\partial y},~~~v=-\frac{\partial \psi }{\partial x}, \end{aligned}$$

that trivially satisfy the continuity Eq. (1). The following coupled nonlinear system has been found by means of transformations (8) into (2–5), as

$$\begin{aligned} \epsilon _{1}f^{\prime \prime \prime }(\eta )-M\epsilon _{3}f^{\prime }(\eta )+\left[ f(\eta )f^{\prime \prime }(\eta )-f^{\prime 2}(\eta )-S\left( f^{\prime }(\eta )+\frac{\eta }{2}f^{\prime \prime }(\eta )\right) \right] =0, \end{aligned}$$
(9)
$$\begin{aligned} \frac{\epsilon _{2}}{Pr}\theta ^{\prime \prime }(\eta )+Ec\epsilon _{1}f^{\prime \prime 2}(\eta )+\left[ f(\eta )~\theta ^{\prime }(\eta )-2\theta (\eta )f^{\prime }(\eta )-\frac{S}{2}(3\theta (\eta )+\eta ~\theta ^{\prime }(\eta ))\right] =0, \end{aligned}$$
(10)

subject to convective boundary conditions

$$\begin{aligned} \left. \begin{aligned} f(0)=0, \quad f^{\prime }(0)=1+K f^{\prime \prime}(0),\quad \theta {^\prime }(0)=-\gamma ~\frac{\kappa _{f}}{\kappa _{nf}}(1-\theta (0)), \quad \mathrm {at}~\eta =0,\\ f(\beta )=\frac{S\beta }{2}, \quad f^{\prime \prime }(\beta )=0, \quad \theta {^\prime } (\beta )=0, \quad \mathrm {at}~\eta =\beta . \end{aligned}\right\} \end{aligned}$$
(11)

3.2 Physical Quantities

The dimensionless form of physical quantities, such as slip, magnetic, and unsteadiness parameters, and Eckert, Prandtl, and biot numbers, respectively, have been given here under:

$$\begin{aligned} K=A\sqrt{\frac{\nu _{f}U_{w}}{x}},~M=\frac{\beta ^{2}_{0}\sigma _{f}}{b\rho _{nf}},~S=\frac{\alpha }{b},~ \gamma =\frac{h_{f}}{\kappa _{f}}\left( \frac{x\nu _{f}}{U_{w}}\right) ^{\frac{1}{2}},~Ec=\frac{U_{w}^{2}}{C_p(T_{s}-T)}, ~Pr=\frac{(\rho C_{p})_{f}\nu _{f}}{\kappa _{f}}. \end{aligned}$$

The constants \(\epsilon _{i},~i=1,\dots ,3\) containing the solid volume fraction \(\phi\), defined as

$$\begin{aligned} \epsilon _{1}=\frac{1+A_{1}\phi +A_{2}\phi ^{2}}{1-\phi +\phi \left( \frac{\rho _{s}}{\rho _{f}}\right) },~~ \epsilon _{2}=\frac{\left( \frac{\kappa _{nf}}{\kappa _{f}}\right) }{1-\phi +\phi \frac{(\rho C_{p})_{s}}{(\rho C_{p})_{f}}},~~ \epsilon _{3}=\frac{1-\phi +\phi \left( \frac{\sigma _{s}}{\sigma _{f}}\right) }{1-\phi +\phi \left( \frac{\rho _{s}}{\rho _{f}}\right) }. \end{aligned}$$
(12)

In addition, the skin friction and Nusselt number can be written, instructively, as

$$\begin{aligned} C_{f}=\frac{\tau _{w}}{\rho _{f}~U_{w}^{2}}, \quad Nu=\frac{x~q_{w}}{\kappa _{f}~(T_{s}-T_{0})}, \end{aligned}$$
(13)

with

$$\begin{aligned} \tau _{w}=\mu _{nf}~\left[ \frac{\partial u}{\partial y}\right] _{y=0},\quad q_{w}=-\kappa _{nf}\left[ \frac{\partial T}{\partial y}\right] _{y=0}. \end{aligned}$$

The dimensionless form of (13) by means of transform variables is given by:

$$\begin{aligned} Re^{\frac{1}{2}}C_{f}=(1+A_{1}\phi +A_{2}\phi ^{2})~f^{\prime \prime }(0),\quad Re^{-\frac{1}{2}}Nu=-\frac{\kappa _{nf}}{\kappa _{f}}~\theta '(0). \end{aligned}$$
(14)

4 Solution Methodology

In order to solve the coupled nonlinear system (9–11) numerically, the set of first-order linear equations has been found by considering

$$\begin{aligned} f= & {} g_{0}, \end{aligned}$$
(15)
$$\begin{aligned} g_{0}^{\prime }= & {} g_{1}, \end{aligned}$$
(16)
$$\begin{aligned} g_{1}^{\prime }= & {} g_{2}, \end{aligned}$$
(17)
$$\begin{aligned} g_{2}^{\prime }= & {} \epsilon _{1}^{-1}\left[ S\left( g_{1}+\frac{\eta }{2}g_{2}\right) +g_{1}^{2}-g_{0}g_{2}+M\epsilon _{3}g_{1}\right] , \end{aligned}$$
(18)
$$\begin{aligned} \theta= & {} g_{3}, \end{aligned}$$
(19)
$$\begin{aligned} g_{3}^{\prime }= & {} g_{4}, \end{aligned}$$
(20)
$$\begin{aligned} g_{4}^{\prime }= & {} Pr\epsilon _{2}^{-1}\left[ \frac{S}{2}(3g_{3}+\eta g_{4})+2g_{1}g_{3}-g_{0}g_{4}-Ec\epsilon _{1}g_{2}^{2}\right] , \end{aligned}$$
(21)
$$\begin{aligned} g_{0}(0)= & {} 0,\quad g_{0}(\beta )=\frac{S\beta }{2},\quad g_{1}(0)=1+Kg_{2}(0),\quad g_{2}(\beta )=0, \end{aligned}$$
(22)
$$\begin{aligned} g_{4}(\beta )= & {} 0,\quad g_{4}(0)=-\gamma ~\frac{\kappa _{f}}{\kappa _{nf}}(1-g_{3}(0)), \end{aligned}$$
(23)

leads to a system of first-order equations subject to six boundary conditions. Initially, solve the Eqs. (16–18) and (22) with suitable guess of \(\beta\) which is given by the program Bvp4c in MATLAB, yields a relationship between S and \(\beta\) that reduces the number of boundary conditions. The \(\beta\) value is then chosen in such a way that satisfy the condition \(g_{0}(\beta )=\frac{S\beta }{2}\) which is done by hit and trail method. Finally, the above system of Eqs. (16–21) along with conditions (22) and (23) is then solved for known values of S and \(\beta\) using Bvp4c in MATLAB. More detail on Bvp4c with convergence and error analysis have been found in [35,36,37,38,39], and the references there in.

5 Results and Discussion

This section presents the analysis of thermal conductivity and effect of significant quantities in thin film of nanofluid by stretching a surface. The following subsections depicted results of velocity \(f^\prime (\eta )\) and temperature \(\theta (\eta )\) profiles, and interpreted using slip parameter K, unsteadiness parameter S, volume fraction \(\phi\), biot number \(\gamma\), Eckert number Ec, Prandtl number Pr.

5.1 Graphical Simulation

Comparison of velocity and temperature profiles of each nanosize particle are shown in Fig. 2(a) and (b) that inferred the velocity and temperature fields with film thickness \(\beta\) are getting rise by changing the nanoparticles continuously. It should also be noticed that both velocity and temperature fields with film thickness \(\beta\) are high for \(SiO_{2}\) nanoparticles of spherical-shape.

Fig. 2
figure 2

Comparisons of velocity and temperature profiles of different nanoparticles

Full size image

Figure 3(a–e) shows the comparison among different nanosize particles on temperature profile using different values of slip parameter K. It is shown in the graph that the rise in slip parameter K causes the curve to shift toward low-temperature profile for all nanoparticles and the thickness of boundary layer decreases as a consequence.

Fig. 3
figure 3

Temperature profiles for different values of slip parameter at \(S=0.4,M=1.0,\phi =0.02,\gamma =0.1,Pr=6.0,Ec=1.0\)

Full size image

Figure 4(a–e) represents the case of unsteadiness parameter S on temperature profile \(\theta (\eta )\) in the boundary layer. It can be observed that increase in unsteadiness parameter S declines the temperature profile. This implies that the enhancement in unsteadiness parameter reduces thermal boundary layer thickness which is due to variation in fluid viscosity decreasing the effect of buoyant forces of gravity. As a result, shear thinning is observed. In other words, the rise in unsteadiness parameter causes the reduction of heat transfer from the stretching sheet to the film in the boundary layer region.

Fig. 4
figure 4

Temperature profiles for different values of unsteadiness parameter at \(K=0.5,M= 1.0,\phi =0.02,\gamma =0.1,Pr=6.0,Ec=1.0\)

Full size image

The effect of volume fraction \(\phi\) on temperature profile is analyzed in Fig. 5(a-e) for different nanoparticles. It is evident from the graph that the temperature profile is the decreasing function of volume fraction regardless of the type of nanoparticles. This behavior points to decrease in thermal conductivity due to increase in \(\phi\). It should be mentioned here that the thermal conductivity is highly enhanced in the cases of \(SiO_{2}, Al_{2}O_{3}, TiO_{2}\) as compared to Cu and Ag. This indicates the effect of augumented heat transfer and specific heat. Also, \(SiO_{2}\) nanoparticles exhibit great efficiency in controlling the temperature variations for different practical situations.

Fig. 5
figure 5

Temperature profiles for different values of volume fraction at \(K=0.5,S=0.4,M=1.0,\gamma =0.1,Pr=6.0,Ec=1.0\)

Full size image

Figure 6(a–e) elucidates the influence of biot number \(\gamma\) on temperature profile. A stronger convection at high temperature and thermal boundary layer thickness is a result of increase in \(\gamma\). Physically, the relationship between the convection at the surface to the conduction within the surface is named as biot number. When the thermal gradient is applied to the stretching surface, then the ratio governing the temperature inside a surface varies significantly, while the surface heats or cools over time.

Fig. 6
figure 6

Temperature profiles for different values of biot number at \(K=0.5,S=0.4,M=1.0,\phi =0.02,Pr=6.0,Ec=1.0\)

Full size image

Figure 7(a-e) shows the increasing trend of Eckert number Ec on decreasing temperature profile \(\theta (\eta )\). Increase in Ec number enhances the heat dissipation potential but diminishes the temperature gradient between the sheet and the fluid film by the cause of frictional heating. Hence, heat transfer rate decreases with the increment of Ec number. Physically, much random motion of different nanosize particles are linked with higher values of Ec that results in enhancement of temperature. However, \(Ec=1\) points to reversion in the direction of heat transfer and change in temperature gradient sign.

Fig. 7
figure 7

Temperature profiles for different values of Eckert number at \(K=0.5,S=0.4,M=1.0,\phi =0.02,\gamma =0.1,Pr=6.0\)

Full size image

Figure 8(a-e) shows that by varying Prandtl number Pr, the temperature profile is successively getting increased from Cu to \(SiO_{2}\). It is worth mentioning that the temperature value is high for \(SiO_{2}\) nanosize particle. Physically, larger Prandtl fluids possess weaker thermal diffusivity as surrounding temperature becomes equal to the surface temperature and vice versa. So, a reduction in the temperature and thermal boundary layer thickness is due to the change in thermal diffusivity and it prevents spreading of heat in the fluid declining the heat transfer rate.

Fig. 8
figure 8

Temperature profiles for different values of Prandtl at \(K=0.5,S=0.4,M=1.0,\phi =0.02,\gamma =0.1,Ec=1.0\)

Full size image

5.2 Numerical Simulation

This section includes the numerical simulations of skin friction coefficient and Nusselt number along with comparison of present results with the existing ones from the literature.

Table 3 reveals the decreasing values of skin friction coefficient for different spherical-shaped nanosize particles against the rising value in slip parameter K and unsteadiness parameter S, while a reverse trend is seen for volume fraction parameter \(\phi\) and magnetic parameter M.

Table 3 Numerical results of skin friction coefficient of different nanoparticles
Full size table

In addition, the rate of heat transfer at the surface is given in Table 4. It is inferred that the Nusselt number is decreased for each spherical-shaped nanoparticle corresponding to Prandtl and Eckert numbers, as well. Particularly, the Nusselt number is grown up for both unsteadiness and biot number.

Table 4 Numerical results of Nusselt number of different nanoparticles
Full size table

Finally, the present results have been compared with Andersson et al. [40], Chen [41,42,43], Wang and Pop [44] and Li et al. [45] and are cited in Table 5.

Table 5 Comparison of present results when \(M=K=\phi =0\)
Full size table

6 Conclusion

The heat transfer development of nanofluids in a thin film over a stretching surface subject to convective boundary condition has been manipulated using \(Cu,Ag,Al_{2}O_{3},TiO_{2},SiO_{2}\) as nanoparticles of spherical-shape. The obtained results and their effects on both velocity and temperature fields have been elucidated through graphical simulations and tables. Moreover, the results have been verified by making a comparison with the existing ones that reveal the validity of the scheme. Thus, the main findings of the present work have been summarized, as under

  • The velocity and temperature fields of spherical shaped \(SiO_{2}\) nanoparticles are very high when compared to other types of nanoparticles with respect to the film thickness \(\beta\) while silver Ag nanoparticles was reported to have small velocity and temperature profiles.

  • Physical quantities, such as slip parameter K, unsteadiness parameter S, Eckert number Ec and volume fraction \(\phi\) showed decline in temperature profile for all nanoparticles when film thickness \(\beta\) was reduced.The \(SiO_{2}\) nanoparticles were found to have highest heat transfer rate when compared to other nanoparticles.

  • Decrease in heat transfer was observed for increasing volume fraction of nanoparticles, i.e., thermal conductivity was decreased with enhancement of particle concentration.

  • Rise in biot number \(\gamma\) augumented the temperature profile against for each increasing value of film thickness \(\beta\) and lead to strong convection.

  • The skin friction coefficient declines with slip boundary conditions and unsteadiness parameters, while augument for volume fraction parameter.

  • The Nusselt number increases for slip parameter, unsteadiness parameter, and biot number but decreases for Prandtl and Eckert number.