Amplitude Death, Bifurcations, and Basins of Attraction of a Planar Self-Sustained Oscillator with Delayed Feedback

Abstract

We investigate the nonlinear dynamics of a two-dimensional self-sustained oscillator subject to a delayed feedback by performing a phase reduction analysis and considering two cases of amplitude variations, which represent weakly and strongly nonlinear cases. We investigate the amplitude death phenomenon and show that the feedback phase takes a relevant role to the suppression of the oscillations when amplitude variations are taking into account. In particular, we show that amplitude death can only occur in certain ranges of the feedback phase, in which destructive interferences are more pronounced. We analytically compute codimension-one and codimension-two bifurcations of the steady states and show parameter space maps with the number of steady-state solutions. We pay an special attention to the feedback phase in antiphase configuration, in which a richer bifurcation scenario is observed. We also numerically compute basins of attraction for the investigated delayed-feedback models, which is a challenge task for time-delay systems, shedding some light to the domains of initial conditions leading to each stable phase-locked state. Finally, we briefly discuss the effects of the shear parameter, which describes the amplitude-phase coupling, in the models in which amplitude variations are taking into account.

1 Introduction

The effect of delayed feedback in oscillatory systems is a relevant area of study in several scientific contexts, including physics, chemistry, biology, engineering, among others [1, 2]. The delay or time lag arises due to the finite speed of signal propagation through the space, or the temporary storage of information [3, 4]. In many situations of practical interest, the delay cannot be neglected, playing an important role to describe the dynamical evolution of a variety of systems. Illustrative examples include single oscillators subject to some feedback mechanism [5,6,7,8,9,10,11,12] or mutually coupled oscillators, ranging from a few coupled units [13,14,15,16,17,18,19] to networks with a large number of coupled oscillators [20,21,22,23,24,25,26].

The presence of delay transforms a system in infinite dimensional. Therefore, the delay can easily induce dynamical instabilities, such as complex periodic oscillations, or chaotic and hyperchaotic dynamics [3]. On the other hand, the delay can also stabilize nonlinear systems, such as stabilizing an unstable fixed state or an unstable periodic orbit, making the delay an important element in the control of dynamical systems [27, 28]. In physics, the optics is a relevant area in which the delay can have major impacts, due to the fast time scales involved in these systems. A prominent example is the case of semiconductor lasers, where a small amount of light fed back to the laser cavity can induce dynamical instabilities, such as the so-called coherence collapse, or induce an improved laser stabilization, such as a linewidth reduction [29].

Over the past decades, a large number of theoretical and experimental investigations have been devoted to understand the dynamic effects of the delay in nonlinear systems. One of the main delay-induced effects is the appearance of multistability, since a large number of stationary states are usually created in time-delay systems [6, 13, 30]. Other dynamic phenomena include oscillation quenching [31], low-frequency fluctuations [32], anticipated synchronization [33], regular pulse packages [34], chimera states [35, 36], regenerative excitable pulses [37], explosive synchronization [38], temporal dissipative solitons [39, 40], equalization of pulse timings [41], just to name a few.

The phenomenon of oscillation quenching [42, 43] has received a considerable deal of attention in the study of time-delay systems [44,45,46,47,48,49,50,51,52], since it can serve as a control mechanism, leading to a stabilization of the systems. There are two types of oscillation quenching processes [43], amplitude death (AD) and oscillation death (OD). In AD the individual oscillators stop oscillating and converge to a common stable steady state, forming a homogeneous stable stationary state. In the case of OD, there may be different steady states, giving rise to stable non-homogeneous stationary states.

The aim of this article is to investigate the dynamics of a two-dimensional self-sustained oscillator with delayed feedback, paying an special attention to the amplitude death phenomenon in this simple configuration of a time-delay system. The phenomenon of amplitude death has been usually investigated as a collective phenomenon occurring in networks of two or more coupled oscillators in which the coupling can be with or without delay. In the case of coupled systems without an explicit delay time, the emergence of amplitude death has been shown to occur, e.g., in networks of coupled oscillators subject to mean field interaction [53] or time-varying interaction [54]. However, a single oscillator can also cease its oscillations due to some type of disturbance, such as a self-feedback mechanism. Although much less investigated, the cessation of oscillations has been shown to occur in single oscillators with delayed feedback, such as a Van der Pol oscillator [55] and a semiconductor laser [56], and also in single oscillators with delay-free feedback, such as a Stuart-Landau oscillator [57]. Since in a feedback oscillator there is just one oscillatory unit, OD cannot occur and the cessation of oscillations corresponds to AD. In laser dynamics, the AD regime is the off-state of the laser device, meaning that no light exists inside the optical cavity. The occurrence of the AD phenomenon in single oscillators is a relevant subject from theoretical and applied points of view, since an active oscillator can stop oscillating due to the presence of some disturbance. This fact can be positive, when oscillations are unwanted and a system stabilization is required. But also it can be negative, when oscillations are required and a signal fed back to the oscillator ceases its operation, such as, e.g., in a laser subject to an optical feedback. We mention that, instead of inducing the amplitude death phenomenon, a feedback mechanism can also be used to restore the oscillation in systems in which the oscillation has been suppressed, as discussed in recent works [54, 58].

Here we perform a systematic investigation starting from a phase model with delayed feedback and then including nonlinear amplitude oscillations, for both weak and strong nonlinearities. For the weakly nonlinear case, we investigate an oscillator operating close to a Hopf bifurcation, characterized by a cubic nonlinearity. For the strongly nonlinear case, we investigate a class-A laser model. The class-A laser model is a particular case of a planar nonlinear oscillator beyond the cubic case. Phase models, largely used to investigate the dynamics of delay systems, cannot exhibit amplitude death, since amplitude variations are neglected. Therefore, it is important to contrast the new ingredients added when amplitude variations are taking into account in the delayed feedback oscillator, such as the emergence of the AD phenomenon. For example, when a self-sustained oscillator is subject to an external periodic force, the forced oscillator can instantly touch the zero-amplitude state if the external force is enough strong. This situation represents a physical transition induced by a phase singularity [59]. In contrast, when a self-sustained oscillator is affected by a delayed feedback, the zero-amplitude state can be stabilized for enough strong feedback strength, as we show here.

Other contributions that we present in this work are as follows. We calculate the analytical bifurcations of the steady-state solutions as a function of the feedback parameters for the phase model and for the cases with amplitude variations. We compute basins of attraction for operation regimes containing several coexisting stable steady states. The computation of basins of attraction in time-delay systems is a challenging task because of the infinite dimensionality of these systems. Here we compute basins of attraction for the coexisting phase-locked states by using some particular choices of the initial history function of the time-delay models. Also, we briefly discuss the effects of the shear parameter, i.e., a parameter responsible for coupling the amplitude and phase variables. More complex dynamics is investigated through numerical analysis.

2 Model

A two-dimensional self-sustained oscillator, close to a Hopf bifurcation, under the influence of a delayed feedback is described by

$$\begin{aligned} \dot{A} = PA(1-|A|^2)(1+i \alpha ) + \eta e^{-i\theta } A'. \end{aligned}$$

(1)

Here, $A \equiv A(t)$ and $A'\equiv A(t-\tau )$ describe the normalized complex amplitude of the oscillator at the actual time and the delayed time, while $\tau$ and $\eta$ are the delay time and the feedback strength, respectively. $\alpha$ is the shear parameter, which introduces a coupling between the phase and amplitude of oscillations. $\theta$ is the feedback phase, sometimes called coupling phase, which is the phase shift during one roundtrip of the feedback signal returning to the oscillator. For a fixed speed and frequency of the feedback signal, $\theta$ and $\tau$ are not independent parameters. But, usually, tiny changes of $\tau$ (or the oscillator’s frequency) lead to substantial changes of $\theta$, as occurs, e.g., in optical systems. In these situations, $\theta$ and $\tau$ can be considered as independent parameters [60, 61]. Throughout this work, we consider $\theta$ and $\tau$ as independent parameters, since we are mostly interested in the qualitative changes induced by changing $\theta$. P is a gain parameter and describes a force moving the equilibrium state of the system without feedback to self-sustained oscillations. This parameter does not change the qualitative dynamics of the model given by Eq. (1), since it acts just as a scale factor. Therefore, P can be eliminated from Eq. (1) by rescaling $\hat{\eta }=\eta /P$, $\hat{\tau }=\tau P$, and $\hat{t}=t P$.

Without the feedback term, Eq. (1) arises in systems close to a Hopf bifurcation, when an equilibrium state is perturbated by some weak external force, giving rise to limit-cycle oscillations. Realistic situations modeled by this equation appear in a large variety of systems, including, e.g., electronic and optical oscillators. In the context of optics, Eq. (1) is usually referred as cubic laser model [59], where A describes the complex amplitude of the electric field, P is the pump, and $\alpha$ is the atomic detuning parameter. Throughout this work, we keep P in our analysis, since we compare the cubic model with the class-A laser model. In the class-A laser model, P can take a relevant role, due to the presence of higher-order nonlinearities, in contrast to the cubic model. The cubic model investigated here is a particular case of the Stuart-Landau oscillator which is a more general form of an oscillator close to a Hopf bifurcation, given by

$$\begin{aligned} {\dot{A} = \mu A -\nu A|A|^2 + \eta e^{-i\theta } A',} \end{aligned}$$

(2)

where $\mu =\mu _r+i\mu _i$ and $\nu =\nu _r+i\nu _i$ are complex parameters [62] and we have added a delayed-feedback interaction. In the case of $\mu =\nu$ the Stuart-Landau equation gets equal to the cubic model given by Eq. (1), in which $\mu _r=P$ and $\mu _i=P\alpha$ are the equivalence between the parameters. For strictly real $\mu$ and $\nu$ parameters in the Stuart-Landau equation, the phase and amplitude are decoupled. This case corresponds to the cubic model with $\alpha =0$ investigated here, where Eq. (2) is reduced to Eq. (1) in the case of $\mu _r=\nu _r=P$.

To numerically integrate the time-delay systems investigated here, we use the method described by Farmer [63], in which a delay differential equation is discretized in a finite map and integrated with a second order Euler method. Here, we use a map of dimension 600 and 1200 to discretize the phase model and the amplitude models, respectively.

3 Phase Model with Delayed Feedback

A physically relevant situation occurs when the feedback strength is weak, meaning that the amplitude of the oscillator remains almost unchanged in the presence of the delayed feedback, i.e., $|A|\approx 1$. Therefore, the phase is the relevant variable to describe the dynamics of the oscillator under the influence of the delayed feedback. By neglecting amplitude variations, the phase evolution is described by the following delay equation

$$\begin{aligned} \dot{\phi } = -\eta \sin (\theta + \phi - \phi '), \end{aligned}$$

(3)

where $\phi \equiv \phi (t)$ and $\phi '\equiv \phi (t-\tau )$ describe the phase of the oscillator at the actual time and the delayed time, respectively.

We now determine the steady-state solutions and the main bifurcations associated with Eq. (3).

3.1 Steady-State Solutions

Steady-state solutions of Eq. (1), often called continuous wave solutions, are periodic solutions in which the amplitude and frequency of oscillations are constant. The phase model given by Eq. (3) does not contain amplitude (since it is fixed at one when deriving the model) and we only look for the constant frequencies $\omega _s$. In these steady-state solutions, the phase changes linearly with time. Thus, the actual phase is $\phi =\omega _s t$ and the delayed phase is $\phi '=\omega _s t-\omega _s\tau$. By inserting these steady-state solutions in Eq. (3), we have

$$\begin{aligned} \omega _s&= - \eta \sin (\theta + \omega _s \tau ). \end{aligned}$$

(4)

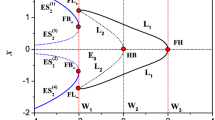
By numerically solving the transcendental equation above for $\omega _s$, we get the complete set of steady-state solutions of Eq. (3). In Fig. 1 we show the values of $\omega _s$ as a function of $\eta$ and the number of steady-state solutions in the parameter space $(\eta ,\tau )$, for three distinct values of $\theta$. As can be seen, the number of steady-state solutions increases as the feedback strength or the time delay increases, as it is well known from literature [29]. In the next section we compute analytically the bifurcations associated with the appearance of these solutions in the parameter space $(\eta ,\tau )$.

3.2 Analytical Determination of Bifurcations of the Steady States

The eigenvalues of the delay differential equation can be obtained using the characteristic equation

$$\begin{aligned} det[\lambda I - A - Be^{-\lambda \tau }]=0, \end{aligned}$$

(5)

where $\lambda$ are the eigenvalues, and A and B are the Jacobians with respect to the variables at time t and $\tau$, respectively, calculated for the steady state. The matrices A and B are

$$\begin{aligned} A&= \frac{d\dot{\phi }}{d\phi } \biggr |_{\omega _s} = -\eta \cos (\theta + \omega _s \tau ), \nonumber \\ B&= \left. \frac{d\dot{\phi }}{d\phi '}\right| _{\omega _s} e^{-\lambda \tau } = \eta \cos (\theta + \omega _s \tau )e^{-\lambda \tau }, \end{aligned}$$

(6)

and the characteristic equation is

$$\begin{aligned} \lambda - \eta \cos (\theta + \omega _s \tau ) (e^{-\lambda \tau }-1)&=0. \end{aligned}$$

(7)

By writing $\eta$ as a function of $\tau$, we obtain

$$\begin{aligned} \eta = \frac{\lambda }{\cos (\theta + \omega _s \tau ) (e^{-\lambda \tau }-1)}. \end{aligned}$$

(8)

Here, we analyze two particular solutions of Eq. (8): null and purely imaginary eigenvalues.

3.3 CASE I: Zero Eigenvalue

Assuming the condition $\lambda =0$ in Eq. (8), we get an indeterminacy of type zero divided by zero. We then use the L’Hôpital’s rule, such that

$$\begin{aligned} \eta&= \frac{1}{\cos (\theta + \omega _s \tau )}\lim _{\lambda \rightarrow 0}\frac{\frac{d\lambda }{d \lambda }}{\frac{d(e^{-\lambda \tau }-1)}{{d \lambda }}} , \nonumber \\&= \frac{1}{\cos (\theta + \omega _s \tau )} \lim _{\lambda \rightarrow 0} \frac{1}{- \tau e^{-\lambda \tau }}, \end{aligned}$$

(9)

giving us the following bifurcation curve

$$\begin{aligned} \eta&= -\frac{1}{\tau \cos (\theta + \omega _s \tau )}. \end{aligned}$$

(10)

3.4 CASE II: Purely Imaginary Eigenvalues

By considering $\lambda =\omega i$ in Eq. (8), we have

$$\begin{aligned} \eta = \frac{\omega i}{\cos (\theta + \omega _s \tau ) (e^{-\omega i \tau }-1)}. \end{aligned}$$

(11)

By using $e^{-\omega \tau i}=\cos (\omega \tau ) - i \sin (\omega \tau )$, follows that

$$\begin{aligned} \omega i - \eta \cos (\theta + \omega _s \tau ) [\cos (\omega \tau ) - i \sin (\omega \tau )-1]&= 0. \end{aligned}$$

(12)

Separating in real and imaginary parts, we have

$$\begin{aligned} \eta \cos (\theta + \omega _s \tau )&= \eta \cos (\theta + \omega _s \tau ) \cos (\omega \tau ), \nonumber \\ \omega&= -\eta \cos (\theta + \omega _s \tau ) \sin (\omega \tau ). \end{aligned}$$

(13)

Squaring and adding the two earlier equations, we have

$$\begin{aligned} \omega ^2 + \eta ^2 \cos (\theta + \omega _s \tau ) ^2= \eta ^2 \cos (\theta + \omega _s \tau ) ^2, \end{aligned}$$

(14)

which implies $\omega = 0$. Therefore, there is no Hopf bifurcation in the phase model with delayed feedback.

3.5 Bifurcation Diagrams

In Fig. 1(a)-(c) we show the $\omega _s$ solutions as a function of $\eta$. For the case $\theta =0$ (in-phase configuration), $\omega _s=0$ is always a stable solution. $\omega _s=0$ means that the oscillator disturbed by the delayed feedback oscillates with the same frequency of the free-running oscillator, i.e., the oscillator without delayed feedback. As $\eta$ increases, other values of constant frequencies are symmetrically created through saddle-node bifurcations, for both positive and negative $\omega _s$. For $\theta =180^{\circ }$ (antiphase configuration), the solution $\omega _s=0$ loses its stability through a pitchfork bifurcation, and two new stable frequencies $\pm \omega _s$ are symmetrically created, as shown in Fig. 1(b) by the dark red curve. Other $\omega _s$ solutions are symmetrically created through saddle-node bifurcations. For other values of $\theta$, the symmetry for positive and negative values of $\omega _s$ is broken, as illustrated in Fig. 1(c), for $\theta =150^{\circ }$ (out-of-phase configuration). In this case, the locations of the saddle-node bifurcations do not coincide anymore when looking at the positive and negative planes.

Fig. 1

Left column: Steady-state frequency solutions as a function of the feedback strength. Dark-gray lines denote the $\omega _s=0$ solution. Dark red lines denote the stable phase-locked states created by a pitchfork bifurcation. Other phase-locked solutions, created by saddle-node bifurcations are denoted by black lines. Solid and dashed lines correspond to stable and unstable phase-locked states, respectively. Right column: Parameter space containing the bifurcation curves of the steady-state solutions. The colors indicate the number of steady-state solutions, including stable and unstable solutions. The dark red and black lines denote pitchfork and saddle-node bifurcation curves, respectively. The parameter values used in the numerical simulations are $\tau =50$ and $\theta =0$ for (a) and (d), $\theta =180^{\circ }$ for (b) and (e), and $\theta =150^{\circ }$ for (c) and (f)

The analytical bifurcation curves obtained from Eq. (10) are plotted in the parameter space $\eta$ versus $\tau$, for fixed $\theta$, in Fig. 1(d)-(f). The regions with different number of steady states, including both stable and unstable $\omega _s$, are indicate by different colors in Fig. 1(d)-(f). In the dark gray region there is a single frequency solution, which is the stable solution $\omega _s=0$. In Fig. 1(d), the solution $\omega _s=0$ is stable in the whole parameter space. By changing the parameters $\eta$ or $\tau$, other $\omega _s$ solutions are born through saddle-node bifurcations (black lines). In Fig 1(e), the solution $\omega _s=0$ becomes unstable through a pitchfork bifurcation (dark red line). Other $\omega _s$ solutions are born through saddle-node bifurcations (black lines). For $\theta =150^{\circ }$, due to the symmetry breaking, the location of the saddle-node bifurcations for negative and positive frequencies do not coincide anymore and are slightly shifted, giving rise to the small stripes observed in Fig. 1(f).

Fig. 2

Steady-state frequencies ($\omega _s$) as a function of the feedback strength ($\eta$). Other parameters are $\tau =3$ and (a) $\theta =180^{\circ }$, (b) $\theta =179^{\circ }$, and (c) $\theta =181^{\circ }$. Stable and unstable steady states are denoted by solid and dashed lines, respectively. The gray line denotes the $\omega _s=0$ steady state, while the dark red line denotes the stable steady states created by the pitchfork bifurcation. Solid and dashed lines denote stable and unstable steady states, respectively

The scenario involving the symmetry breaking of the pitchfork bifurcation is highlighted in Fig. 2. The pitchfork bifurcation, responsible for the instability of the solution $\omega _s=0$ [Fig. 2(a)], is a special case that occurs only for $\theta =180^{\circ }$. If $\theta$ is slightly changed, the pitchfork bifurcation does not exist anymore. For example, if $\theta =179^{\circ }$, the continuation of the $\omega _s=0$ solution is shifted to negative values, while a new pair of positive stable and unstable frequencies is born through a saddle-bifurcation [Fig. 2(b)]. And if $\theta =181^{\circ }$, the continuation of the $\omega _s=0$ solution is shifted to positive values, while a new pair of negative stable and unstable frequencies is born through a saddle-bifurcation [Fig. 2(c)].

4 Cubic Model with Delayed Feedback

In this section, we consider the model given by Eq. (1), in which amplitude and phase variations are relevant to determine the dynamics of the oscillator under the presence of the delayed feedback. Written in terms of amplitude and phase coordinates of the complex variable $A=ae^{i\phi }$, Eq. (1) reads

$$\begin{aligned} \dot{a}&= Pa(1 - a^2) + \eta a'\cos (\theta + \phi - \phi '), \nonumber \\ \dot{\phi }&= -\eta \frac{a'}{a}\sin (\theta + \phi - \phi '), \end{aligned}$$

(15)

where we consider $\alpha = 0$. The influence of nonzero $\alpha$ is discussed in Sec. 7. In the above equations, the variables $a\equiv a(t)$ and $a'\equiv a(t-\tau )$ describe the amplitude of the oscillator at the actual time and the delayed time, respectively. The other variables and parameters are as described in Secs. 2 and 3.

4.1 Steady-State Solutions

Steady-state solutions of the cubic model are those solutions with constant amplitudes and constant frequencies, satisfying Eq. (1). As we have done in the analysis of the phase model, we use the continuous-wave solutions in Eq. (1). In the cubic model, the steady states are given by doing $a(t)=a(t-\tau )= a_s$, $\phi (t)=\omega _s t$, and $\phi (t-\tau )=\omega _s t -\omega _s\tau$. By inserting these solutions in Eq. (1), we have

$$\begin{aligned} a_{s0}&= 0, \nonumber \\ a_{s\pm }&= \pm \sqrt{ \frac{P + \eta \cos (\theta + \omega _s \tau )}{P} }, \nonumber \\ \omega _s&= -\eta \sin (\theta + \omega _s \tau ), \end{aligned}$$

(16)

where $a_{s0}$ and $a_{s+}$ are the physically relevant amplitude solutions.

4.2 Analytical Determination of Bifurcations for the Steady States

We follow the same prescription of Sec. 3.2 to compute the eigenvalues associated with the steady-state solutions of the cubic model. The matrices A e B for Eq. (1) are given by

$$\begin{aligned} A&= \left. \left( \begin{array}{cc} \dfrac{d\dot{a}}{da} &{} \dfrac{d\dot{a}}{d\phi } \\ \\ \dfrac{d\dot{\phi }}{da} &{} \dfrac{d\dot{\phi }}{d\phi } \\ \end{array} \right) \right| _{a_s, \omega _s} \end{aligned}$$

(17)

$$\begin{aligned}&=\left( \begin{array}{cc} P(1-3a_s^2) &{} -\eta a_s \sin (\theta + \omega _s \tau ) \\ \\ \frac{\eta }{a_s} \sin (\theta + \omega _s \tau ) &{} -\eta \cos (\theta + \omega _s \tau ) \\ \end{array} \right) , \end{aligned}$$

(18)

and

$$\begin{aligned} B&= \left. \left( \begin{array}{cc} \dfrac{d\dot{a}}{da'} &{} \dfrac{d\dot{a}}{d\phi '} \\ \\ \dfrac{d\dot{\phi }}{da'} &{} \dfrac{d\dot{\phi }}{d\phi '} \\ \end{array} \right) e^{-\lambda \tau } \right| _{a_s, \omega _s} \end{aligned}$$

(19)

$$\begin{aligned}&= \left( \begin{array}{cc} \eta \cos (\theta + \omega _s \tau ) &{} \eta a_s \sin (\theta + \omega _s \tau ) \\ -\frac{\eta }{a_s} \sin (\theta + \omega _s \tau ) &{} \eta \cos (\theta + \omega _s \tau ) \\ \end{array} \right) e^{-\lambda \tau }. \end{aligned}$$

(20)

The matrix $\Delta (\lambda )=\lambda I - A - Be^{-\lambda \tau }$ is

$$\begin{aligned} \Delta (\lambda )&= \begin{pmatrix} \lambda -P(1-3a_s^2) &{} -\eta a_s \sin (\theta + \omega _s \tau ) \\ -\eta \cos (\theta + \omega _s \tau ) e^{-\lambda \tau } &{} \times (e^{-\lambda \tau }-1) \\ \frac{\eta }{a_s} \sin (\theta + \omega _s \tau ) &{} \lambda -\eta \cos (\theta + \omega _s \tau ) \\ \times (e^{-\lambda \tau }-1) &{} \times (e^{-\lambda \tau }-1)\\ \end{pmatrix}, \end{aligned}$$

(21)

which give us the following characteristic equation

$$\begin{aligned}&[\lambda -P(1-3a_s ^2)-\eta \cos (\theta + \omega _s \tau ) e^{-\lambda \tau }] \times \nonumber \\&[\lambda -\eta \cos (\theta + \omega _s \tau )(e^{-\lambda \tau }-1)] + \nonumber \\&\eta ^2 \sin (\theta + \omega _s \tau ) ^2 (e^{-\lambda \tau }-1) ^2=0. \end{aligned}$$

(22)

Below we solve the characteristic equation for $\lambda =0$ and $\lambda =i\omega$, in order to look for bifurcations of steady states associated with these eigenvalues.

4.3 CASE I: Zero Eigenvalues

Dividing Eq. (22) by $(e^{-\lambda \tau }-1)$ we have

$$\begin{aligned} {\begin{matrix} &{}[\lambda -P(1-3a_s ^2)-\eta \cos (\theta + \omega _s \tau ) e^{-\lambda \tau }] \times \\ &{}\bigg [\frac{\lambda }{(e^{-\lambda \tau }-1)}-\eta \cos (\theta + \omega _s \tau ) \bigg ] + \\ &{}\eta ^2 \sin (\theta + \omega _s \tau ) ^2 (e^{-\lambda \tau }-1) =0. \end{matrix}} \end{aligned}$$

(23)

Assuming $\lambda =0$ in Eq. (23), we have an indeterminacy of type zero divided by zero in the term $\frac{\lambda }{(e^{-\lambda \tau }-1)}$. By using the L’Hôpital’s rule to avoid this, we have

$$\begin{aligned} {\begin{matrix} \lim _{\lambda \rightarrow 0} \\ &{}[\lambda -P(1-3a_s ^2)-\eta \cos (\theta + \omega _s \tau ) e^{-\lambda \tau }] \times \\ &{}\bigg [\frac{d\lambda /d\lambda }{d(e^{-\lambda \tau }-1)/d \lambda }-\eta \cos (\theta + \omega _s \tau ) \bigg ] + \\ &{}\eta ^2 \sin (\theta + \omega _s \tau ) ^2 (e^{-\lambda \tau }-1) =0. \end{matrix}} \end{aligned}$$

(24)

Therefore,

$$\begin{aligned} {\begin{matrix} &{} \;\;\;\;\; [-P(1-3a_s ^2)-\eta \cos (\theta + \omega _s \tau )] \\ &{} \times \bigg [\frac{1}{-\tau }-\eta \cos (\theta + \omega _s \tau ) \bigg ] =0. \end{matrix}} \end{aligned}$$

(25)

that is,

$$\begin{aligned} {\begin{matrix} &{} \;\;\;\; [P(1-3a_s ^2)+\eta \cos (\theta + \omega _s \tau )] \\ &{} \times [1+\eta \tau \cos (\theta + \omega _s \tau ) ] =0. \end{matrix}} \end{aligned}$$

(26)

From the first brackets, both for $a_{s0}$ and $a_{s+}$, we obtain

$$\begin{aligned} {\begin{matrix} \eta = -\frac{P}{\cos (\theta + \omega _s \tau )}. \end{matrix}} \end{aligned}$$

(27)

From the second brackets, we obtain

$$\begin{aligned} {\begin{matrix} \eta = -\frac{1}{\tau \cos (\theta + \omega _s \tau )}. \end{matrix}} \end{aligned}$$

(28)

4.4 CASE II: Purely Imaginary Eigenvalues

Assuming the condition $\lambda =\omega i$ and working only with the solution $\omega _s=0$ and $\theta =180^{\circ }$ in Eq. (22), we have

$$\begin{aligned}{}[\omega i -P+\eta e^{-\omega i \tau }][\omega i+\eta (e^{-\omega i \tau }-1)]&=0 \quad {(for\;a_{s0})}, \nonumber \\ [\omega i -\beta +\eta e^{-\omega i \tau }][\omega i+\eta (e^{-\omega i \tau }-1)]&=0 \quad {(for\;a_{s+})}, \end{aligned}$$

(29)

with $\beta = -2P+3\eta$. Since $e^{-\omega \tau i}=\cos (\omega \tau ) - i \sin (\omega \tau )$ follows that

$$\begin{aligned}&[\omega i -P+\eta (\cos (\omega \tau )-i\sin (\omega \tau ))] \times \nonumber \\&[\omega i+\eta (\cos (\omega \tau )-i\sin (\omega \tau )-1)]=0 \quad {(for\;a_{s0})}, \nonumber \\&[\omega i -\beta +\eta (\cos (\omega \tau )-i\sin (\omega \tau ))] \times \nonumber \\&[\omega i+\eta (\cos (\omega \tau )-i\sin (\omega \tau )-1)]=0 \quad {(for\;a_{s+})}. \end{aligned}$$

(30)

Separating in real and imaginary parts the second brackets of the two solutions of Eq. (30), give us

$$\begin{aligned} {\begin{matrix} \eta &{} = \eta \cos (\omega \tau ), \\ \omega &{}= \eta \sin (\omega \tau ). \end{matrix}} \end{aligned}$$

(31)

Squaring and adding the two earlier equations, we have

$$\begin{aligned} {\begin{matrix} \omega ^2 + \eta ^2&= \eta ^2, \end{matrix}} \end{aligned}$$

(32)

which give us, $\omega =0$.

Separating in real and imaginary parts the first brackets of the solution $a_{s0}$ of Eq. (30), we have

$$\begin{aligned} {\begin{matrix} P &{} = \eta \cos (\omega \tau ), \\ \omega &{}= \eta \sin (\omega \tau ). \end{matrix}} \end{aligned}$$

(33)

Squaring and adding the two earlier equations, we have

$$\begin{aligned} {\begin{matrix} \omega = \pm \sqrt{ \eta ^2 - P^2}. \end{matrix}} \end{aligned}$$

(34)

Replacing Eq. (34) in the first expression of Eq. (33), we obtain

$$\begin{aligned} {\begin{matrix} \tau&= \frac{ \arccos (\frac{P}{\eta } )}{\sqrt{ \eta ^2 - P^2}}. \end{matrix}} \end{aligned}$$

(35)

Analogously, for the solution $a_{s+}$ of Eq. (30), we find

$$\begin{aligned} {\begin{matrix} \tau&= \frac{ \arccos (\frac{\beta }{\eta })}{ \sqrt{\eta ^2 - \beta ^2}}. \end{matrix}} \end{aligned}$$

(36)

Equations (35) and (36) are the Hopf bifurcation curves for the cubic model.

4.5 Pitchfork-Hopf Bifurcation

When varying the feedback parameters for $\theta =180^{\circ }$ in the cubic model, there is not only a pitchfork bifurcation curve, as in the phase model, but also a Hopf bifurcation curve, as shown in the previous section. The point where the pitchfork and Hopf bifurcation curves intersect is a codimension-two bifurcation pitchfork-Hopf. To calculate this bifurcation point, we just combine the analytical expressions of the pitchfork and Hopf bifurcations. Therefore, replacing Eq. (28) for $\omega _s=0$ in Eqs. (35) and (36), we have

$$\begin{aligned} \tau&= \frac{ \arccos [\frac{P}{(1/\tau )}]}{ \sqrt{ (1/\tau ) ^2 - P^2}} \quad {(for\;a_{s0})}, \nonumber \\ \tau&= \frac{ \arccos [-2P/(1/\tau )+3]}{ \sqrt{(1/\tau ) ^2 - (-2P+3(1/\tau ))^2}} \quad {(for\;a_{s+})}, \end{aligned}$$

(37)

that is,

$$\begin{aligned} \tau&= \frac{ \arccos (\tau P)}{(\frac{1}{\tau }) \sqrt{1 - \tau ^2 P ^2}} \quad {(for\;a_{s0})}, \nonumber \\ \tau&= \frac{ \arccos (-2P\tau +3)}{ (\frac{1}{\tau }) \sqrt{1 - (-2P\tau +3)^2}} \quad {(for\;a_{s+})}. \end{aligned}$$

(38)

Therefore,

$$\begin{aligned} \sqrt{1-\tau ^2P^2}&= \arccos (\tau P) \quad {(for\;a_{s0})}, \nonumber \\ \sqrt{1 - (-2P\tau +3)^2}&= \arccos (-2P\tau +3) \quad {(for\;a_{s+})}, \end{aligned}$$

(39)

where $\tau =\frac{1}{P}$ satisfy both equations. Thus, the point where occur the intersection of the pitchfork and Hopf bifurcation curves is

$$\begin{aligned} \tau&= \frac{1}{P}, \nonumber \\ \eta&= P. \end{aligned}$$

(40)

4.6 Amplitude Death and Bifurcation Diagrams

In Fig. 3(a)-(c), we show the amplitude of the phase-locked states ($a_s$) as a function of the feedback strength ($\eta$), for three values of the feedback phase ($\theta$). As already seen in the analysis of the phase model, new branches of steady-state solutions are created as the feedback strength increases. The frequencies of these steady states are the same as those calculated using the phase model, as can be seen by the analytical solutions described by Eqs. (4) and (16). The steady-state frequencies are illustrated in Fig. 1(a)-(c). But, in contrast to the phase model, when amplitude variations are taken into account, the most of the higher frequency solutions are born unstable. As shown in Fig. 3(a)-(c), the saddle-node bifurcations responsible for creating the new branches of solutions (corresponding to steady states with higher frequencies) give rise to a pair of unstable steady states, except the first saddle-node bifurcation in Fig. 3(a), which create a stable steady state. The other higher frequency steady states become stable through Hopf bifurcations, as the feedback strength increases along each branch. Another feature that can be observed in Fig. 3(a)-(c) is that the higher frequency solutions contain a smaller amplitude, for the same level of feedback strength. Therefore, it is harder to stabilize higher frequency deviations from the free-running frequency, and when these frequencies are stabilized they exhibit smaller amplitudes.

Fig. 3

Left column: Stationary amplitudes ($a_s$) as a function of the feedback strength ($\eta$). Solid and dashed lines denote stable and unstable solutions, respectively. The parameter values are $P=0.3$, $\tau =50$, and (a) $\theta =0$, (b) $\theta =180^{\circ }$, (c) $\theta =150^{\circ }$. Right column: Analytical bifurcation curves plotted as a function of the feedback parameters. The colors correspond to the number of coexisting steady-state amplitudes ($a_s > 0$) as indicated by the colorbar. Dark red, black, and orange lines denote pitchfork, saddle-node, and Hopf bifurcations, respectively. Solid and dashed lines denote bifurcations associated with stable and unstable solutions, respectively. PH is the pitchfork-Hopf bifurcation. The parameter values are $P=0.3$ and (d) $\theta =0$, (e) $\theta =180^{\circ }$, (f) $\theta =150^{\circ }$

Fig. 4

(a) and (b) show a magnification of Fig. 3(a) and (b), respectively. Solid and dashed lines denote stable and unstable steady states. The black dot denotes a pitchfork bifurcation

The analytical bifurcations, described by Eqs. (27) and (28), are plotted in Fig. 3(d)-(f) and correspond to the parameters used in Fig. 3(a)-(c), respectively. As the feedback strength increases, new branches of steady-state solutions are created through saddle-node bifurcations, except for the case $\theta =180^{\circ }$, in which the first branch of solutions is created through a pitchfork bifurcation. This bifurcation corresponds to the instability of the $\omega _s=0$ solution. This is the same scenario observed in the analysis of the phase model. The difference when the amplitude is taking into account is that the most of new branches of solutions created by saddle-node bifurcations are unstable, as illustrated by the dashed black lines in Fig. 3(d)-(f). Also, additional pitchfork bifurcations appear connecting the unstable branches of the saddle-node bifurcations to the $a_s=0$ solution [as shown in Fig. 3(a)-3(c)]. These additional pitchfork bifurcations are shown by the dashed dark red lines in Fig. 3(d)-(f). Therefore, as the feedback strength increases, there is an alternation between saddle-node and pitchfork bifurcations when the amplitude variation is taking into account. Other main features induced by amplitude effects are as follows. A subcritical pitchfork bifurcation curve, given by $\eta =P$, appears associated with the solution $\omega _s=0$. This bifurcation curve is shown by the horizontal dark red line in Fig. 3(b). Also, a Hopf bifurcation associated with the solution $\omega _s=0$ appears, denoted by the orange line in Fig. 3(b). This Hopf bifurcation curve intersect the pitchfork bifurcation curve $\eta =P$, giving rise to the codimension-two point pitchfork-Hopf marked in Fig. 3(b). In addition to this Hopf bifurcation, other Hopf bifurcation curves for $\omega _s\ne 0$ exist, but are not shown in the parameter spaces of Fig. 3(d)-(f). These extra Hopf bifurcation curves are responsible for stabilizing the higher frequency steady states, as discussed in Fig. 3(a)-3(c).

A relevant consequence of the amplitude variations is the possibility to observe the amplitude death phenomenon. Amplitude death can only occur for the feedback phase in the range $90^{\circ }<\theta <270^{\circ }$ (for $\eta >0$). For example, for a short delay and $\theta =0$, the amplitude of the steady state increases as the feedback strength increases, as shown in Fig. 4(a). This is a consequence of a constructive interference between the oscillator and the feedback signal. In this case, no amplitude death is observed in the feedback parameter space. But for $\theta =180^{\circ }$, the amplitude of the steady state decreases as the feedback strength increases (before the occurrence of the pitchfork bifurcation), as shown in Fig. 4(b). This is a consequence of a destructive interference between the oscillator and the feedback signal. In this situation, the zero-amplitude solution can be stable over a portion of the parameter space, as shown by the black regions in Fig. 5(a) and (b) [which are magnified from Fig. 3(e) and (f)]. The bifurcations associated with the emergence of the amplitude death phenomenon, shown in Fig. 5(a) and (b), can be well understood by looking the one-parameter bifurcation diagrams shown in Fig. 5(c)-(f). Figure 5(c) and (d) show the amplitude and frequency of the steady state as a function of $\eta$, corresponding to a variation along a vertical line in Fig. 5(a), for $\tau =2.5$ and $\theta =180^{\circ }$. For small values $\eta$, the delayed-feedback oscillator oscillates with constant amplitude and $\omega _s=0$. As $\eta$ increases, the amplitude decreases until it becomes zero, as shown in Fig. 5(c). This transition to the amplitude death regime corresponds to the first pitchfork bifurcation along the line $\eta =0.3$ in Fig. 5(a). By keeping increasing $\eta$, there is another pitchfork bifurcation where the $\omega _s=0$ solution becomes unstable and two new $\omega _s\ne 0$ solutions are born, as shown in Fig. 5(d). However, when this bifurcation occurs, the amplitude is still zero, corresponding to the amplitude death regime, as shown in Fig. 5(c). This phenomenon, in which new frequency solutions are born having zero amplitude, is found in other delayed-feedback systems, such as semiconductor lasers with optical feedback [56]. As $\eta$ increases even more, the zero-amplitude solution becomes unstable through a Hopf bifurcation and the two new frequencies $\omega _s\ne 0$ start to be associated with a nonzero amplitude, as shown in Fig. 5(c) and (d). Figure 5(e) and (f) illustrate the amplitude and frequency of the steady state for $\tau =0.5$, corresponding to the case $\theta =150^{\circ }$ [shown in Fig. 5(b)]. As $\eta$ increases, the oscillator achieves the amplitude death regime through a pitchfork bifurcation [Fig. 5(e)]. The zero and nonzero amplitudes are associated with a branch $\omega _s\ne 0$ [Fig. 5(f)].

Fig. 5

(a) and (b) show a magnification of Fig. 3(e) and (f), respectively. The colors correspond to the number of steady-state amplitudes ($a_s > 0$). The black regions correspond to the amplitude death regime. (c) and (d) show the stationary frequencies and amplitudes, respectively, as a function of $\eta$, for $\tau =2.5$ and $\theta =180^{\circ }$. (e) and (f) show the same as (c) and (d), but for $\tau =0.5$ and $\theta =180^{\circ }$. Solid and dashed lines denote stable and unstable solutions, respectively

The minimum value of $\eta$ for which amplitude death emerges occurs for $\tau =0$. As we have previously commented, amplitude death can only occur for $90^{\circ }<\theta <270^{\circ }$. In Fig. 6, we show the emergence of amplitude death as a function of $\eta$, for three representative values of $\theta$ and $\tau =0.001$, i.e., very close to zero. For $\theta$ slightly above $90^{\circ }$, the amplitude death occurs only for very large values of $\eta$, as illustrated in Fig. 6(a). By increasing $\theta$, the minimum value of $\eta$ decreases, and the amplitude death can be more easily achieved, as illustrated in Fig. 6(b). For $\theta =180^{\circ }$ occurs the global minimum value of $\eta$ for which amplitude death emerges, as shown in Fig. 6(c). For this value of $\theta$, the minimum value of $\eta$ occurs along the line $\eta =P$, as shown in Fig. 5(a), spanning larger values of $\tau$. In this case, the amplitude death region is maximized in the feedback parameter space.

Fig. 6

The emergence of amplitude death as a function of $\eta$ for $\tau =0.001$ and (a) $\theta =93^{\circ }$, (b) $\theta =120^{\circ }$, and (c) $\theta =180^{\circ }$. The gain parameter is fixed at $P=0.3$

4.7 Numerical Results

For a better understanding of the bifurcation diagrams shown in the previous section, in this section we perform some numerical simulations of the cubic model with delayed feedback, for the case $\theta =180^{\circ }$.

In Fig. 7(a), we show the investigated bifurcation curves in the parameter space $(\eta ,\tau )$, while in Fig. 7(b), (c), and (d) we illustrate the real part of the complex amplitude $A=a_x+i a_y$, the modulus of the amplitude $a=(a_x^2+a_y^2)^{1/2}$, and the intensity $I=a^2$, respectively. In Fig. 7(a), the pitchfork bifurcation curve $\eta =\frac{1}{\tau }$ creates two stable steady-state solutions $(a_{s+}, \pm \omega _s)$ upwards, increasing the parameter $\eta$, while the bifurcation curve $\eta =P$ creates an unstable steady-state solution $(a_{s+}, \omega _s = 0)$ downwards, decreasing the parameter $\eta$ (the $a_{-}$ steady-state solutions, symmetrically created at the negative plane, have been omitted, since they are not of physical relevance) . The solution $(a_{s+}, \omega _s = 0)$, which is born unstable, stabilizes when passing through the pitchfork bifurcation curve $\eta =1/\tau$, being the only existing solution in the gray region. Thus, in the orange region, we have the coexistence between the steady-state solutions $(a_{s+}, \pm \omega _s)$ and $(a_{s+}, \omega _s = 0)$. Furthermore, at the Hopf bifurcation curve, an unstable periodic solution rises upwards, increasing the parameter $\eta$. Consequently, in the white region, we have the coexistence of steady-state solutions $(a_{s+}, \pm \omega _s)$ with an unstable periodic orbit created at the Hopf bifurcation curve.

Fig. 7

(a) Parameter space denoting regions of amplitude death (black color), phase-locked solution (gray color), coexistence between steady-state solutions (orange color), and coexistence between unstable continuous-wave and periodic solutions (white color). Solid and dashed dark red curves denotes supercritical and subcritical pitchfork bifurcation curves, respectively. Orange dashed curve denotes a subcritical Hopf bifurcation. Other panels show bifurcation diagrams of (b) the maxima and minima of the real part of the complex amplitude A, (c) the amplitude a, and (d) the intensity I, for $\tau = 30$. The vertical lines denote: supercritical Hopf bifurcation (solid orange line), subcritical Hopf bifurcation (dashed orange line), subcritical pitchfork bifurcation (dashed dark red line), supercritical pitchfork bifurcation (solid dark red line), supercritical transcritical bifurcation (solid blue line), and subcritical transcritical bifurcation (dashed blue line). The gain parameter is fixed at $P=0.3$

Throughout this work, we use Eq. (1) written in terms of amplitude and phase to compute the bifurcations of the steady states. Thus, the bifurcations characterized here as pitchfork and Hopf would be classified differently if we use Eq. (1) written in terms of the components of the complex amplitude ($A=a_x + i a_y$) or the intensity ($I=|A|^2$), instead of the amplitude ($a=|A|$), as shown in Fig. 7(b)-(d). In these figures, we present bifurcation diagrams for a line at $\tau =30$ in Fig. 7(a) by integrating Eq. (1) with real and imaginary components of the complex amplitude, amplitude and phase, and intensity and phase. For Eq. (1) written in terms of components of the complex amplitude, the bifurcations are super and subcritical Hopf bifurcations, and subcritical pitchfork bifurcation [Fig. 7(b)]. For Eq. (1) written in terms of amplitude and phase, we have super and subcritical pitchfork bifurcations, and a subcritical Hopf bifurcation [Fig. 7(c)]. And for Eq. 1 written in terms of intensity and phase, the bifurcations are super and subcritical transcritical bifurcations, and a subcritical Hopf bifurcation [Fig. 7(d)]. The time series of representative solutions for the gray, orange, and white regions of the parameter space described in Fig. 7(a) is shown in Fig. 8. In the gray region, there are infinite stationary solutions with the component equations [illustrated by the dark red area in Fig. 7(b)], corresponding to a single solution with the amplitude [Fig. 7(c)] or intensity [Fig. 7(d)] equations. Only one stationary solution of the component equations is shown in Fig. 8(a) and the correspondent amplitude solution is shown in Fig. 8(d). In the orange region, there is a coexistence of stationary and periodic solutions with the component equations, illustrated in Fig. 8(b), and two stationary solutions with the amplitude (or intensity) equations, illustrated in Fig. 8(e). And in the white region, there is a coexistence of two periodic solutions with the component equations, shown in Fig. 8(c), and a stationary and a periodic solution with the amplitude (or intensity) equations, illustrated in Fig. 8(f).

Fig. 8

Time series for $P=0.3$, $\tau = 30$, and $\eta = 0.015$ (upper row), $\eta = 0.1$ (middle row), $\eta = 0.2$ (bottom row). The dashed gray lines and the solid dark gray lines denote unstable solutions, while the other lines denote stable solutions

5 Class-A Laser Model with Delayed Feedback

In this section, in order to investigate the influence of higher-order nonlinear terms, we consider the particular case of a class-A laser model under the influence of a delayed feedback. By doing this, we can go beyond the cubic model, but still analyzing a planar oscillator model, as is our intention throughout this work. Moreover, we investigate an example of a physically relevant model, which has been little investigated in literature when considering the effects of a delayed feedback [64, 65]. The reason is because class-A lasers, which are described only by an electric field equation, are mostly gas lasers. These devices usually have a dynamics not so fast in order of having large impacts due to optical feedbacks. This is in sharp contrast, e.g., to the case of semiconductor lasers, which exhibit faster dynamics and are classified as class-B lasers. But certain types of semiconductor lasers, such as the quantum-dot semiconductor lasers, have fast relaxation times and are less sensitivities to optical feedback [66]. In a certain sense, the quantum-dot semiconductor lasers share some features resembling class-A devices. In this way, despite the fact that more complex models, including the carrier dynamics, is important to correctly describe quantum dot lasers [67], the class-A laser model can provide some first clues, sharing some similarities with quantum dot laser devices. In fact, we might say that quantum-dot semiconductor lasers have an intermediate dynamics in between class-A lasers and conventional semiconductor lasers. In this way, it is instructive to understand in some detail the dynamics of class-A lasers under the influence of a delayed feedback. Also, despite these specific physical considerations, it is also instructive to understand the effects of higher-order nonlinear terms beyond the cubic model from a more general perspective, since extra nonlinearities can usually impact the oscillator’s dynamics when the feedback strength increases.

The class-A laser under the effect of a delayed feedback is described by the equations

$$\begin{aligned} \dot{a}&= a\frac{(P - ca^2)}{1 + ca^2} + \eta a'\cos (\theta + \phi - \phi '), \nonumber \\ \dot{\phi }&= -\eta \frac{a'}{a}\sin (\theta + \phi - \phi '), \end{aligned}$$

(41)

where $c=\frac{P}{(P+1)}$ comes from the normalization done on the cubic model (see appendix for details). The variables and parameters are as described in the previous section.

The equilibrium solutions of Eqs. (41) are

$$\begin{aligned} a_s&= 0, \nonumber \\ a_s&= \pm \sqrt{ \frac{P + \eta \cos (\theta + \omega _s \tau )}{c[1-\eta \cos (\theta + \omega _s \tau )]} }, \nonumber \\ \omega _s&= -\eta \sin (\theta + \omega _s \tau ). \end{aligned}$$

(42)

By applying the same methodology used in the previous section to compute the bifurcations of the steady states, we find that the number of stationary solutions and the saddle-node and pitchfork bifurcation curves of Eq. (41) are the same as found in the cubic model. Therefore, we omit here these calculations. However, the amplitude of the steady states and the stability change when comparing both models. These results are illustrated in Fig. 9. In this figure, we can see that the number of solutions are the same in both models. Also, the parameter values in which the saddle-node and pitchfork bifurcations occur are exactly the same. In the vicinity of the saddle-node bifurcations, i.e., when new branch of solutions (or modes) are born, the amplitude of the steady states in both models is very close. As the feedback strength increases away from the saddle-node bifurcations, the amplitudes become more and more discrepant. Interestingly, the amplitudes of the steady-state solutions of the class-A laser model increase without any bound as the feedback strength increases away from the saddle-node bifurcations, as can be seen in Fig. 9(b). Therefore, one effect of the higher-order nonlinearities is to increase significantly the amplitude of the modes. On the other hand, the number of stable modes is decreased in the class-A laser model, as can be seen by comparing Fig. 9(a) and (b), meaning that instabilities are much more pronounced when the higher-order nonlinearities are present.

Fig. 9

Bifurcation diagrams showing the steady states $a_s$ for (a) the cubic model and (b) the class-A laser model. The parameters are $P=0.3$, $\tau =50$ and $\theta =180^{\circ }$. Solid and dashed lines denote stable and unstable solutions, respectively

6 Basins of Attraction

In this section, we compute domains of distinct initial conditions as a function of the feedback strength that leads to different steady-state solutions for the three investigated time-delay models, i.e., the phase model, the cubic model, and the class-A laser model. We vary the initial conditions using a specific initial function history and compute the asymptotic dynamics as we increase the feedback strength.

The results of the phase model are shown in Fig. 10. Since there is just one variable in the phase model, which is the phase of the oscillator, we need just one initial history function. Here we choose a straight line for the initial history function, given by $\phi (t_i)=\phi _0 \times i$, where $i=1,2,\dots ,600$. By starting with these 600 values of $\phi$ in the times $t_1,t_2,...t_{600}$, we can compute the phase evolution of the delay differential equation. In Fig. 10(a) and (b) we show the basins of attraction for the symmetric case $\theta =180^{\circ }$ and the asymmetric case $\theta =150^{\circ }$, respectively. The phase evolutions corresponding to the dots marked in these figures are shown in Fig. 10(c) and (d).

Fig. 10

Basins of attraction for the initial history function $\phi (i)=\phi _0 \times i$, for $i=1,2,...,N$, where $N=600$ is the map dimension. The parameter values are $\tau =50$, and (a) $\theta =180^{\circ }$ and (b) $\theta =150^{\circ }$. The white color represents the initial condition domain for the $\omega _s=0$ steady-state, while orange-red and green-blue shades represent positive and negative $\omega _s$, respectively. (c) and (d) show the phase-locked states for $\eta =0.01$, $\eta =0.2$, $\eta =0.32$, $\eta =0.4$, and $\eta =0.48$, corresponding to the points marked in (a) and (b), respectively

In Fig. 10(a), for very small $\eta$ denoted by the white area, there is not multistability, and the only possible solution is $\omega _s=0$, as shown by the horizontal black line in Fig. 10(c). As $\eta$ increases, the pitchfork bifurcation takes place, giving rise to new frequency solutions. Initial conditions in the light orange and light green areas in Fig. 10(a) correspond to the phase evolutions with positive and negative slopes, denoted by the light orange and light green lines in Fig. 10(c), respectively. As $\eta$ increases even more, new higher frequency solutions appear denoted by the darker areas in Fig. 10(a). The corresponding colors in Fig. 10(c) show the phase evolution as a function of time. The darker color lines exhibit higher slopes, corresponding to higher frequency deviations from the frequency of the free-running oscillator.

In Fig. 10(b), the basin of attraction is not symmetrical. For very small $\eta$, $\omega _s$ is very close to zero, as can be seen by the almost horizontal black line for the phase evolution in Fig. 10(d). As $\eta$ increases, the frequency varies continuously to negative values, without the occurrence of bifurcation, denoted by the light green area in Fig. 10(b). It is interesting to observe that there is a predominance to the attraction of negative frequencies. Even for a positive slope of the initial phase variation (as can be seen by the light green area above the light orange area) the solution is attracted to the negative frequency solution, as shown by the slope of the phase evolution denoted by light green line in Fig. 10(d). Other smaller frequencies solutions (higher slopes in the negative plane) appear in the darker color areas in Fig. 10(b), and the corresponding phase evolutions are shown in Fig. 10(d). The minimum value of $\eta$ for each distinct steady state in Fig. 10(a) and (b), which is the tip of each colored area, coincide with the saddle-node bifurcations that create the new frequency solutions. When the amplitude is taken into account, there are two variables in the equations and two initial history functions, for phase and amplitude are needed to integrate the models.

Fig. 11

Basins of attraction for the cubic model (left column) and the class-A laser model (right column). The colors correspond to the value of steady-state frequencies ($\omega _s$), where the white color represents the initial condition domain for the $\omega _s=0$ steady-state and orange-red (green-blue) shades represent positive (negative) $\omega _s$. The parameters are $P=0.3$, $\tau =50$, and $\theta =0^{\circ }$ (upper row), $\theta =180^{\circ }$ (middle row), and $\theta =150^{\circ }$ (bottom row). See text for details

We also compute basins of attraction for the cubic model and the class-A laser model. For both models, we use the same procedure used to compute the basins of attraction of the phase model, with the same initial history function for the phase. For the amplitude, We use a constant initial history function $a=1$, which is the amplitude value of the free-running oscillator (without feedback). The results, for $\theta =0$, $\theta =180^{\circ }$, and $\theta =150^{\circ }$ are shown in Fig. 11. As can be seen, for the cubic model (left panels in Fig. 11), the results are very similar to those found with the phase model, following the same kind of structure. For the class-A laser model (right panels in Fig. 11), there are fewer stable steady states, due to the stronger nonlinearity of this model, as discussed in Sec. 5. For larger values of $\eta$, instabilities are more pronounced, resulting in even fewer stable steady states and a decreasing in size of the stability domains of the higher frequency deviation solutions.

Moreover, we perform an analysis for basins of attractions varying both, amplitude and phase variables for the case of the cubic model. These results are shown in Fig. 12, for $\theta =0^{\circ }$, $\theta =180^{\circ }$, and $\theta =150^{\circ }$. We use the same initial history functions used in Fig. 12. But here, we use distinct constant values for the initial history functions for the amplitude. We compute the basins of attraction for the fixed value of the feedback strength $\eta =0.5$, to which a certain number of steady states coexist. In Fig. 12 we can see that there are not so big impacts when increasing the initial condition of the amplitude in the range between one and three for the cubic model.

Fig. 12

Basins of attraction for the cubic model varying both initial conditions, phase and amplitude. The colors correspond to the value of steady-state frequencies ($\omega _s$), where the white color represents the initial condition domain for the $\omega _s=0$ steady-state and orange-red (green-blue) shades represent positive (negative) $\omega _s$. The parameters are $P=0.3$, $\tau =50$, $\eta =0.5$, and (a) $\theta =0$, $\theta =180^{\circ }$, and (c) $\theta =150^{\circ }$. See text for details

7 Influence of the Shear Parameter

As a last analysis, in this section, we briefly discuss the effects of the shear parameter $\alpha$, which describes the coupling between phase and amplitude. In laser dynamics, this parameter is the atomic detuning parameter, which measures how much the electric field is off-resonance with respect to the atomic frequency [68]. The shear parameter is sometimes incorporated in oscillator models with cubic nonlinearity and class-A laser models [64, 69,70,71]. We observe that, in the case of semiconductor lasers, which are class-B lasers, the coupling between phase and amplitude is due to the so-called linewidth enhancement factor, also called Henry factor or $\alpha$ factor [29]. This parameter is crucial to describe the dynamics of semiconductor lasers and sometimes it appears in the modeling of other class-B lasers, such as solid-state lasers [72]. As it is well-known, the shear parameter $\alpha$ is responsible to introduce a number of dynamical instabilities in laser dynamics, usually leading to chaotic and complex dynamics [29, 69, 73].

We first show the influence of the shear parameter in the cubic oscillator. The case of null shear parameter ($\alpha =0$) has been investigated in Sec. 4. By including nonzero shear parameter ($\alpha \ne 0$), the amplitude and phase evolutions are given by the following equations

$$\begin{aligned} \dot{a}&= aP(1 - a^2) + \eta a'\cos (\theta + \phi - \phi '), \nonumber \\ \dot{\phi }&= -\eta \frac{a'}{a}\sin (\theta + \phi - \phi ')+\alpha P(1-a^2). \end{aligned}$$

(43)

Fig. 13

Upper row: Parameter space showing the number of steady-state amplitudes ($a_s>0$) for (a) $\alpha =1$ and (b) $\alpha =3$. The black color denotes the amplitude death region. Bottom row: Parameter space discriminating chaotic solutions (CH) in dark red color, stable steady states with nonzero amplitude (SS) in light gray color, amplitude death (AD) in black color, and periodic solutions in other colors. The numbers inside the colorbar indicate the amount of local maxima in one period of oscillation of the amplitude corresponding to the distinct colored areas in the parameter space. (c) $\alpha =1$ and (d) $\alpha =3$. Other parameters are $P=0.3$ and $\theta =180^{\circ }$

In Fig. 13, we show some numerical results obtained for the cubic model with nonzero shear parameter. Figure 13(a) and (b) show the number of amplitude solutions ($a_s>0$) of the steady states, computed through the Newton method, for $\alpha =1$ and $\alpha =3$, respectively. For $\alpha \ne 0$, the number of steady states increases greatly as the feedback parameters $\eta$ and $\tau$ increase. For this reason we limit the parameter space up to $\tau =20$, in contrast to the case $\alpha =0$ shown in Fig. 3, in which we have performed investigations up to $\tau =80$. As can be seen in Fig. 13(a) and (b), the regions of amplitude death (denoted by the black regions) continue to exist for the case $\alpha \ne 0$. Figure 13(c) and (d) show the number of local maxima of the amplitude computed through direct integration of Eq. 43, for $\alpha =1$ and $\alpha =3$, respectively. In the portion of the parameter space shown by Fig. 13(c), we mostly find a steady state, either $a_s>0$ in the gray area or $a_s=0$ in the black area. But for a larger value of $\alpha$, shown Fig. 13(d), more complex dynamics is found, including chaotic dynamics.

We briefly investigate the class-A laser model for $\alpha \ne 0$ (the case $\alpha =0$ has been investigated in Sec. 5), which is described by the following equations

$$\begin{aligned} \dot{a}&= a\frac{(P - ca^2)}{1 + ca^2} + \eta a'\cos (\theta + \phi - \phi '), \nonumber \\ \dot{\phi }&= -\eta \frac{a'}{a}\sin (\theta + \phi - \phi ') + \alpha \frac{(P - ca^2)}{1 + ca^2}. \end{aligned}$$

(44)

Fig. 14

Steady states (upper line), bifurcation diagrams (middle line), and Lyapunov exponents (bottom line) for the cubic model (left column) and the class-A laser model (right column). The parameters are $P=0.3$, $\tau =15$, $\alpha =3$, and $\theta =180^{\circ }$

In Fig. 14, we show a comparison between the cubic model (left column) and the class-A laser model (right column), under the influence of the delayed feedback, for $\alpha =3$. For the case $\alpha \ne 0$, the number of steady states for both models is the same, at the same way that we have found for the case $\alpha =0$. Again, the main difference is that the amplitudes for the class-A laser model are larger, as can be seen in Fig. 14(a) and (b). In these figures, the steady-state solutions are obtained by using the Newton method. For the case $\alpha \ne 0$, we do not perform the analytical calculations of the steady states and their bifurcations, since the coupling between phase and amplitude, introduced by the nonzero shear parameter, greatly increases the complexity of the system of Eq. (44). Therefore, information of the stability of the steady states is not provided in Fig. 14(a) and (b). Stable solutions obtained by direct integration for both models are shown in Fig. 14(c) and (d). Both models show regular solutions, such as steady states and periodic solutions, and irregular solutions, such as chaos and hyperchaos. The hyperchaotic behavior is confirmed in both models through the calculation of the Lyapunov exponents, shown in Fig. 14(e) and (f), which show that for enough large feedback strength both models exhibit more than one positive Lyapunov exponent.

8 Conclusion

We have theoretically investigated the nonlinear dynamics of a two-dimensional self-sustained oscillator under the effect of a delayed feedback. We have performed a phase reduction analysis and then we have considered two cases with amplitude variations: a cubic oscillator, representing a weakly nonlinear case, and a class-A laser model, representing a strongly nonlinear case.

We have investigated the emergence of the amplitude death phenomenon when amplitude variations are taken into account. The feedback phase takes a relevant role for the emergence of amplitude death in the cubic and class-A laser models. The amplitude death can only occur for the feedback phase in the range $90^{\circ }<\theta <270^{\circ }$. In this situation, a destructive interference caused by the feedback signal can decrease the steady-state amplitude of the delayed-feedback oscillator, and, for short delays and enough large feedback strength, the zero-amplitude state can be stabilized over a region of the parameter space. This amplitude death region is maximized for a feedback phase equals to $180^{\circ }$. In this antiphase scenario, the feedback strength required to achieve the amplitude death regime is a global minimum, and, for short delays, the amplitude death regime occurs when the feedback strength overcomes the gain parameter responsible for inducing the self-sustained oscillations. For the feedback phase in the range $0^{\circ }\le \theta \le 90^{\circ }$ or $270^{\circ }\le \theta \le 360^{\circ }$ the amplitude death regime never occurs, and the steady-state amplitudes always increase for any value of the delay and feedback strength, due to constructive interference caused by the feedback signal.

We have analytically calculated the main codimension-one and codimension-two bifurcations associated with the steady-state solutions for the phase model, cubic model, and the class-A laser model, for the cases in which the shear parameter is not taken into account. Also, an analytical expression to find the stability of the steady states has been calculated. We have analyzed three distinct regimes for the feedback phase, namely in-phase, out-of-phase, and antiphase configurations. For the antiphase configuration, the bifurcation structure of the steady states is richer. In this situation, a pitchfork bifurcation appears due to symmetry properties of the steady-state solutions, destabilizing the $\omega _s=0$ solution, which is the phase-locked solution with the same frequency of the free-running oscillator. Moreover, a pitchfork-Hopf codimension-two bifurcation has been found in the antiphase configuration. The pitchfork-Hopf bifurcation corresponds to the maximum delay value and the minimum feedback strength for which the amplitude death regime emerges.

We have shown that the number of steady states and the bifurcations associated with their appearance are the same for the cubic model and the class-A laser model. The main difference introduced by the higher-order nonlinearities beyond the cubic case is as follows. The stability of the steady states changes, the number of stable steady states is smaller, and the amplitude values of the steady states are larger in the class-A laser model. In particular, in the class-A laser model, steady-state amplitudes grow without limits when the feedback strength grows away from the bifurcations where they are born.

We have numerically computed basins of attraction for the three investigated models with delayed feedback. The basins of attraction have been computed for in-phase, out-of-phase, and antiphase configurations, for a particular choice of the initial history function of the investigated time-delay systems. The phase and cubic models show a good agreement in the structure of the basins, while in the class-A model, the attraction domains of the steady states are greatly reduced as the feedback strength increases.

Finally, we have briefly investigated the influence of the shear parameter when amplitude effects are taken into account. The number of steady states solutions increases considerably as the shear parameter increases. Also, the shear parameter greatly induces irregular dynamics, where transitions to chaos and hyperchaos have been observed in the cubic model and the class-A laser model with delayed feedback.

Appendix

A class-A laser [68] with delayed feedback is described by

$$\begin{aligned} \dot{\tilde{A}} = \tilde{A}\frac{(P - |\tilde{A}|^2)}{1+|\tilde{A}|^2}(1+i\alpha ) + \eta e^{-i\theta } \tilde{A}', \end{aligned}$$

(45)

where $\tilde{A}\equiv \tilde{A}(\tilde{t})$ and $\tilde{A}'\equiv \tilde{A}(\tilde{t}-\tilde{\tau })$ represent the value of the electric field at the actual time and the delayed time, respectively. $\tau$ is the delay time, $\eta$ is the feedback strength, P is the pump parameter, $\theta$ is the feedback phase, and $\alpha$ is the atomic detuning parameter. In the situation in which the electric field is not so large, we can approximate the first term of Eq. (45)

$$\begin{aligned} \frac{(P - |\tilde{A}|^2)}{1+|\tilde{A}|^2} = \frac{P - |\tilde{A}|^2 + 1 - 1}{1+|\tilde{A}|^2} =\frac{P +1}{1+|\tilde{A}|^2} - 1. \end{aligned}$$

(46)

By expanding the term below in a series Taylor, we have at first order

$$\begin{aligned} \frac{1}{1+|\tilde{A}|^2} \approx (1-|\tilde{A}|^2). \end{aligned}$$

(47)

By applying the earlier approximation in Eq. (46), we have

$$\begin{aligned} (P+1)(1-|\tilde{A}|^2) - 1=P\bigg [1-\frac{(P+1)}{P}|\tilde{A}|^2\bigg ]. \end{aligned}$$

(48)

Therefore,

$$\begin{aligned} \frac{P - |\tilde{A}|^2}{1+|\tilde{A}|^2}\approx P\bigg [1-\frac{(P+1)}{P}|\tilde{A}|^2\bigg ]. \end{aligned}$$

(49)

By using the earlier approximation in Eq. 45, we obtain

$$\begin{aligned} \dot{\tilde{A}}&= \tilde{A} P \bigg [1-\frac{(P+1)}{P}|\tilde{A}|^2 \bigg ](1+i\alpha ) + \eta e^{-i\theta } \tilde{A}'. \end{aligned}$$

(50)

By redefining the electric field as

$$\begin{aligned} \tilde{A}= \sqrt{\frac{P}{P+1}}{A}, \;\;\; \tilde{A}'= \sqrt{\frac{P}{P+1}}{A'}, \end{aligned}$$

(51)

we obtain a new system of equations known as the cubic laser model, which is known in literature as the simplest laser model [68]

$$\begin{aligned} \dot{A} = AP(1-|A|^2)(1+i\alpha ) + \eta e^{-i\theta } A'. \end{aligned}$$

(52)

Here, in the cubic laser model given by Eq. (52), we have included the atomic detuning parameter and the delayed feedback. Rewriting Eq. (52) in terms of amplitude and phase, we have

$$\begin{aligned} \dot{a}&= aP(1 - a^2) + \eta a'\cos (\theta + \phi - \phi '), \nonumber \\ \dot{\phi }&= \alpha (1 - a^2) - \eta \frac{a'}{a}\sin (\theta + \phi - \phi '), \end{aligned}$$

(53)

where the variables $a=a(t)$ and $a'\equiv a(t-\tau )$ represent the amplitude of the electric field at the actual time and the delayed time, and $\phi \equiv \phi (t)$ and $\phi '\equiv \phi (t-\tau )$ represent the phase of the electric field at the actual time and the delayed time, respectively. If the feedback strength is small, the amplitude of the electric field almost does not change. Therefore, by considering $a=1$ and neglecting amplitude variations, the laser dynamics is described by a single phase equation

$$\begin{aligned} \dot{\phi }&= -\eta \sin ( \theta + \phi - \phi '). \end{aligned}$$

(54)