1 Introduction

The deterministic approach to the spreading of a contagious disease consists of a description in terms of ordinary differential equations for the number of members in each class of individuals [1,2,3,4,5]. The main characteristics of the models for the spreading of disease that concern us here are (a) the presence of at least two classes of individuals, the infected and the susceptible, and (b) the catalytic infection of the susceptible. Examples are the susceptible–infected–susceptible (SIS) model and the susceptible–infected–removed (SIR) model [5].

The SIS model describes the spreading of an epidemic among a community of individuals of only two classes: the susceptible and the infected. A susceptible becomes infected in contact with an infected and an infected becomes susceptible spontaneously. If the infection rate is greater than a certain critical infection rate, the spreading sets in even if the number of infected is small. The number of infected individuals increases exponentially and reaches an asymptotic nonzero value in the long term. In other words, the SIS predicts a persistence of the disease.

In contrast to the SIS model, the SIR model predicts the extinction of the disease in the long term. The SIR model consists of three classes of individuals: the susceptible, the infected, and the removed, which are the individuals that have acquired permanent immunity. A susceptible becomes infected catalytically and an infected becomes recovered spontaneously. If the infection rate is greater than the critical rate, the disease sets in and the number of infected increases, reaches a maximum and then decreases and reaches the zero asymptotic value. In the long term, the disease disappears.

Here we are concerned with finding the conditions under which the spreading of epidemic can be controlled by immunization through vaccination. In the case of the SIS model, specifically, we wish to find the conditions under which the disease becomes extinct in the long term. The introduction of the process of immunization by vaccination in models for the spreading of a contagious disease has been considered in several studies. Usually it is introduced in a manner similar to that processes of the SIR model in which an infected individual becomes recovered [6,7,8,9,10,11,12,13,14,15,16], which is an internal process of immunization. Here, we propose a distinct approach to the process of vaccination, which is an external process of immunization.

In addition to the classes of individuals of a certain model, a new class of individuals is introduced which are composed by the individuals that have acquired permanent immunization by vaccination. The fraction of its members is denoted by v and we assume that v(t) is a known function of time and that in the long term it approaches a value k understood as the total fraction of individuals that have acquired immunization by vaccination. A possible dependence of v with time is the following function

$$\begin{aligned} v = k\left( 1-{\mathrm{{e}}}^{-\gamma t}\right), \end{aligned}$$
(1)

where \(\gamma\) is the rate in which the individuals acquire immunization by vaccination.

Our study of the SIS model with vaccination allows us to draw the following conclusion. If the fraction k of individuals that have been vaccinated is larger than a certain value that depends on the parameters of the original SIS model, the asymptotic value of infected individuals vanishes and the disease becomes extinct. Our results for the SIR model show that the vaccination flattens the epidemic curve. The flattening is greater the larger is the fraction k of individuals that have been vaccinated.

2 SIS Model with Vaccination

Let us denote by x and y the fraction of susceptible and infected individuals. The time evolution of these quantities in accordance with the SIS model is

$$\begin{aligned} \frac{\mathrm{{d}}x}{\mathrm{{d}}t}&= - bxy + c y ,\end{aligned}$$
(2)
$$\begin{aligned} \frac{\mathrm{{d}}y}{\mathrm{{d}}t}&= bxy - c y, \end{aligned}$$
(3)

where b is the infection rate and c is the recovery rate. If we sum these two equations, we find that \(x+y\) is constant in time which allows us to set \(x+y=1\). For long times, the fraction of susceptible and infected individuals approach the asymptotic values \(x^*\) and \(y^*\), which are the stationary solution of these equations and are given by

$$\begin{aligned} x^*=\frac{c}{b}, \qquad \qquad y^* = \frac{b-c}{b}, \end{aligned}$$
(4)

valid as long as \(b\ge c\). If \(b<c\), the solution is \(y=0\), and \(x=1\).

Let us consider as an initial condition that the overwhelming majority of individuals are susceptible, that is, at \(t=0\) \(y=y_0\) and \(x=1-y_0\) where \(y_0\) is very small. To determine the solution for the initial times, we take into account that y is small and neglect terms of second order in y in which case the equation for y becomes

$$\begin{aligned} \frac{\mathrm{{d}}y}{\mathrm{{d}}t} = (b-c)y, \end{aligned}$$
(5)

and y will increase exponentially with time if \(b>c\) and decrease to zero otherwise.

From the above results, we conclude that if \(b>c\), that is, if the infection rate is larger than its critical value c, the disease will spread, and for long times, there remains a fraction \(y*=(b-c)/c\) of infected individuals. In other words, the disease spreads and becomes persistent with a nonzero fraction \(y^*\) of infected individuals. If \(b<c\), the disease does not spread and the final value of infected individuals vanishes.

We modify this model so as to include vaccination and we focus on the case \(b>c\) and seek for the conditions for the extinction of the disease. That is, we wish to find the conditions leading to a vanishing of the asymptotic fractions of infected individuals. To this end, we add to the SIS model the class of individuals that have acquired permanent immunization through vaccination and denote the fraction of these individuals by v. We consider a process of vaccination in which in the long term only a certain fraction k of the individuals will acquire the permanent immunization. According to our assumptions, the variable v is considered to be a known function of time which approaches the value k for large values of t.

We consider that only the susceptible individuals are vaccinated leading to the modification of Eq. (2), which now reads

$$\begin{aligned} \frac{\mathrm{{d}}x}{\mathrm{{d}}t} = - bxy + c y - v'(t), \end{aligned}$$
(6)

where \(v'(t)=\mathrm{{d}}v/\mathrm{{d}}t\) and is understood as the rate in which the susceptible individuals are acquiring permanent immunization by vaccination. This equation together with Eq. (3) constitute the set of equation of the SIS model with vaccination, as v(t) is a known function of time.

Fig. 1
figure 1

Diagram showing the behavior of the SIS model with vaccination, where b/c is the ratio of the infection rate and the recovered rate and k is the fraction of individuals that have acquired permanent immunization by vaccination. In the region N, there is no spreading of the disease, whereas in P and E the disease spreads. In P, it becomes persistent, with a nonzero fraction of infected, and in E, it becomes extinct, with a zero fraction of infected

Full size image

If we sum Eqs. (3) and (6), we see that \((\mathrm{{d}}x/\mathrm{{d}}t)+(\mathrm{{d}}y/\mathrm{{d}}t)=-(\mathrm{{d}}v/\mathrm{{d}}t)\) from which follows that \(x+y+v\) is a constant which we choose to be equal to the unity. Replacing \(x=1-y-v\) into Eq. (3), we find

$$\begin{aligned} \frac{\mathrm{{d}}y}{\mathrm{{d}}t} = by(1-y-v) - c y, \end{aligned}$$
(7)

which gives the time evolution of y as long as v is given as a function of time.

Let us determine the solution of Eq. (7) for large times. In this regime, v approaches k and the fraction of infected individuals approaches an asymptotic value \(y^*\) which is the solution of

$$\begin{aligned} by(1-y-k) - c y = 0. \end{aligned}$$
(8)

Thus either \(y^*=0\) or

$$\begin{aligned} y^*=\frac{b(1-k)-c}{b} .\end{aligned}$$
(9)

This last solution occurs whenever \(b>b_o\), where \(b_o=c/(1-k)\); otherwise, the solution is \(y^*=0\). Therefore, the disease disappears if the infection rate b is below the value \(b_o\). Alternatively, it disappears if the fraction k of vaccinated is larger than the threshold value \(k_o=(b-c)/b\).

If initially all individuals are susceptible except for a small fraction \(y_0\) of infected individuals, then we may assume that y is small and Eq. (7) becomes

$$\begin{aligned} \frac{\mathrm{{d}}y}{\mathrm{{d}}t} = y(b - c -bv) \end{aligned}.$$
(10)

We suppose that the process of vaccination is continuous and begins at \(t=0\). That is, v is a continuous function of time and vanishes at \(t=0\). Therefore, we may set \(v=0\) in Eq. (10) and draw the following conclusion. If \(b>c,\) then the number of infected will increase exponentially and the epidemics sets in. Otherwise, there is no spreading of the disease, which is the same conclusions concerning the original SIS model.

Fig. 2
figure 2

Epidemic curve for the SIS model with vaccination, showing the fraction f of susceptible that are being converted into infected as a function of time t, for several values of the fraction k of vaccinated individuals, and \(b=2\), \(c=1\), \(\gamma =0.1\). If k is less than or equal to 0.5, f vanishes in the long term

Full size image

The results for the SIS with vaccination are summarized in the diagram of Fig. 1. If \(b\le c\), there is no spreading of the disease. If \(b>c\), then for larger values of the fraction k of the vaccinated individuals the disease disappears; otherwise, it becomes persistence.

We have solved numerically Eq. (7) by employing the specific time dependence of v given by Eq. (1) with \(\gamma =0.1\) and varying values of the fraction k of vaccinated individuals. We considered the case \(b=2\), \(c=1\), which corresponds to the spreading of the disease. Figure 2 shows the epidemic curve, which gives the fraction \(f=bxy\) of susceptible individuals that are being converted into infected as a function of time. In accordance with the above results, when k is above the threshold value \(k_o=(b-c)/b\), or \(k_o=0.5\), the asymptotic value of the fraction y of infected individuals as well as f vanishes, and the disease disappears.

3 SIR Model with Vaccination

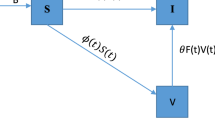
The SIR model has three classes of individuals. In addition to the susceptible and infected, there is another class of individuals which is the class of the recovered. A susceptible becomes infected by contact with an infected and an infected becomes recovered spontaneously. A recovered individual acquires permanent immunization and remains forever in this condition. Denoting by x, y, and z the fractions of susceptible, infected, and recovered, the equations of the SIR model with immunization are

$$\begin{aligned} \frac{\mathrm{{d}}x}{\mathrm{{d}}t}&= -bxy - v'(t), \end{aligned}$$
(11)
$$\begin{aligned} \frac{\mathrm{{d}}y}{\mathrm{{d}}t}&= bxy -cy, \end{aligned}$$
(12)
$$\begin{aligned} \frac{\mathrm{{d}}z}{\mathrm{{d}}t}&= cy, \end{aligned}$$
(13)

where b is the infection rate, c is the recovery rate, and v(t) is the fraction of vaccinated individuals. Again, the summation of these equations gives the constraint \(x+y+z+v\) equal to a constant, which we choose to be equal to the unity. Considering that \(v'(t)\) vanishes at \(t=0\), a linear stability analysis lead us to conclude that the state free from disease, defined by \(x=1\), \(y=0\), \(z=0\), is stable if \(b<c\). Therefore, the spreading of the epidemics occurs when \(b>c\).

For large times, v is assumed to approach k and \(v'(t)\) vanishes, and the asymptotic fraction of infected individuals vanishes. Thus, the SIR model predicts the disappearance of the disease with or without vaccination. The effect of vaccination in this model lies on the flattening of the epidemic curve as shown in Fig. 3. This result was obtained by solving numerically the set of Eqs. (12) and (13) replacing x by \(1-y-z-v\) and using the specific form of v(t) given by Eq. (1). We used \(\gamma =0.1\) and several values of k. The values of b and c were set equal to 2 and 1, which correspond to the spreading of the disease. The greater the value k of the fraction of vaccinated individuals, the larger the flattening of the epidemic curve and the smaller the integral of the epidemic curve, which is the total number of individuals that has got the disease.

Fig. 3
figure 3

Epidemic curve for the SIR model with vaccination, showing the fraction f of susceptible that are being converted into infected as a function of time t, for several values of the fraction k of vaccinated individuals, and \(b=2\), \(c=1\), and \(\gamma =0.1\)

Full size image

4 SIRS Model with Vaccination

The SIRS model is similar to the SIR model with three classes of individuals. A susceptible becomes infected by contact with an infected, and an infected becomes recovered spontaneously and acquires immunity. However, the immunization is only partial and the individual may become susceptible again. Denoting by x, y, and z the fractions of susceptible, infected, and recovered, the equations of the SIRS model with immunization is

$$\begin{aligned} \frac{\mathrm{{d}}x}{\mathrm{{d}}t}& = -bxy + az - v'(t), \end{aligned}$$
(14)
$$\begin{aligned} \frac{\mathrm{{d}}y}{\mathrm{{d}}t}& = bxy -cy, \end{aligned}$$
(15)
$$\begin{aligned} \frac{\mathrm{{d}}z}{\mathrm{{d}}t}& = cy - az, \end{aligned}$$
(16)

where b is the infection rate, c is the recovering rate, a is the rate of loss of immunization, and v(t) is the fraction of vaccinated individuals. Again, the summation of these equations gives the constraint \(x+y+z+v\) equal to constant, which we choose to be equal to the unity.

Replacing \(x=1-y-z-v\) in Eq. (15), it becomes

$$\begin{aligned} \frac{\mathrm{{d}}y}{\mathrm{{d}}t} = b(1-y-z-v)y -cy, \end{aligned}$$
(17)

which with Eq. (16) are to be solved for y and z. Considering that v(t) vanishes at \(t=0\), a linear stability analysis leads us to conclude that the state \(x=1\), \(y=0\), \(z=0\) is stable if \(b<c\). When \(b>c\), the spreading of the epidemics sets in.

For long times, v approaches k and the fractions of infected and recovered individuals approach the asymptotic values \(y^*\) and \(z^*\), solutions of

$$\begin{aligned} b(1-y-z-k)y -cy& = 0, \end{aligned}$$
(18)
$$\begin{aligned} cy - az& = 0. \end{aligned}$$
(19)

The nontrivial solution of these equations is

$$\begin{aligned} y^*& = \frac{a(b-c - bk)}{b(a+c)}, \end{aligned}$$
(20)
$$\begin{aligned} z^*& = \frac{c(b-c - bk)}{b(a+c)}, \end{aligned}$$
(21)

which give the following asymptotic value \(x^*\) for the fraction of the susceptible individuals, \(x^*=c/b\). These results are valid as long as \(b\ge b_o\) where \(b_o=c/(1-k)\). If \(b\le b_o\), the asymptotic value of the fraction of the infected vanish and the disease disappears.

The above results lead us to conclude that the effect of vaccination on the SIRS model is similar to that of the SIS model, and in fact, the diagram of possible states is identical to that of Fig. 1. If the fraction k of vaccinated individuals is larger than \(b_o=(b-c)/b,\) the infectious disease disappears in the long term.

5 Conclusion

We have analyzed the effect of vaccination on deterministic models for epidemic spreading. Our approach to the process of vaccination considers that the number of individuals that acquire immunization through vaccination is a given function of time, and in this sense, it differs from previous approach to the process of vaccination. For the SIS and SIRS models, which predict a persistence of the disease for long times, we have found that if the fraction of vaccinated individuals is large enough, the disease disappears. For the SIR model, which predicts the disappearance of the disease, we found that the epidemic curve becomes flattened. The larger the fraction of vaccinated individuals, the larger the flatness.

These main results were obtained by considering general properties of the function v(t) describing the fraction of vaccinated individuals. The general property of v(t) is that it vanishes at the initial time \(t=0\), increases monotonically and reaches the asymptotic value k, which is the total fraction of the vaccinated individuals. We remark that when we say a vaccinated individual we mean in fact an individual that has acquired permanent immunization by vaccination.