1 Introduction

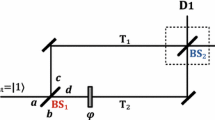
In 1928, Bohr proposed the principle of complementarity which played a key role in quantum mechanics. This complementarity states that quantum systems possess properties that are equally real but mutually exclusive [1] and has been continuously studied till our days [2]. A celebrated example is the illustration of wave-particle duality by considering single photons in a Mach–Zehnder interferometer (MZI) (Fig. 1). If the output beam splitter BS2 is removed, detecting the photon in one of the detectors D1 or D2 reveals unambiguously which path it has gone through so that no interference appears: the photon behaves like a classical particle. If BS2 is inserted, one observes interference fringes (dependence on the phase difference φ): photons behave as a classical wave which goes through both paths of the interferometer. When do photons decide to travel one way or two ways? This was answered by the Wheeler delayed choice (WDC) experiment [3] where one chooses to whether insert BS2 or not, when the photon has already entered the interferometer. Many WDC experiments have been realized [4,5,6,7]; they have all indicated that it does not matter whether the choice of arrangement is made before the photon reaches the first beam splitter BS1 or only after; the counting statistics are quite independent of this. This led Wheeler to his famous sentence: “No elementary quantum phenomenon is a phenomenon until it is a registered phenomenon.”

Fig. 1
figure 1

Mach–Zehnder interferometer

Full size image

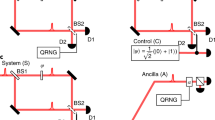
In the WDC, the choice of inserting or removing BS2 is classically controlled by a random number generator. Recently [8], a quantum delayed choice (QDC) experiment was proposed and realized [9,10,11,12,13,14]. In this experiment, the action of BS2 is controlled by an ancillary qubit: when the ancillary is in one basis state or the other, BS2 is removed or inserted and the photons show, correspondingly, a particle or a wave behavior. When the ancilla is in a superposition state, the wave- and particle-like behaviors of the photon can be jointly observed. An important feature of the QDC setup is that the quantum control allows to reverse the temporal order of the measurements: the photon can be detected before the ancilla, i.e., before choosing to remove BS2 or to insert it, this means the possibility to choose the particle- or wave-like behaviors of the photon after it has already been detected.

In the present article, we describe the QDC experiment as a generalized measurement characterized by a positive operator–valued measure (POVM). POVMs [15] are in fact the natural framework in which complementary observables (like interference and path) can be jointly measured.

The layout of this work is as follows. In Section 2, we recall briefly the essential features of the QDC experiment. Section 3 is devoted to a description of the QDC experiment as a joint generalized measurement of path and interference; duality relations are also deduced. Section 4 is devoted to a conclusion.

2 The Quantum Delayed Choice Experiment

Consider a Mach–Zehnder interferometer (Fig. 1). A photon is first split by a balanced beam splitter BS1, travels inside the interferometer with a tunable phase φ, and is finally recombined (or not) at the second beam splitter BS2 before detection at D1 or D2. In the QDC, BS2 is a quantum beam splitter which may be (as explained above) in a superposition of | −〉 (absent) and | +〉 (present) states:

$$ \left.| qBS\right\rangle =\cos \theta \left.|-\right\rangle +\sin \theta \left.|+\right\rangle, \kern0.5em 0\le \theta \le \frac{\pi }{2}. $$
(1)

Labelling by | 1〉 and | 2〉 the two input states of a photon impinging the interferometer, the action of the beam splitters BS1 and BS2 (when this latter is in the + state) is given by

$$ \left\{\begin{array}{c}\left.|1\right\rangle \to \frac{1}{\sqrt{2}}\left(\left.|1\right\rangle +\left.|2\right\rangle \right)\\ {}\left.|2\right\rangle \to \frac{1}{\sqrt{2}}\left(\left.|1\right\rangle -\left.|2\right\rangle \right)\end{array}\right.. $$
(2)

We consider that the input state of the photon, before BS1, is a general combination of the states | 1〉 and | 2〉 and so is the state | ψi〉 just after BS1:

$$ \left.|{\psi}_i\right\rangle =\left.\alpha |1\right\rangle +\left.\beta |2\right\rangle, \left({\left|\alpha \right|}^2+{\left|\beta \right|}^2=1\right). $$
(3)

The state of the photon and the quantum beam splitter just after BS1 is

$$ \left.|{\psi}_e\right\rangle =\left.|{\psi}_i\right\rangle \bigotimes \left.| qBS\right\rangle . $$
(4)

After evolution inside the interferometer and just before D1 and D2, the system’s state transforms to the entangled one:

$$ \left.|{\varPsi}_f\right\rangle =\left.\cos\ \theta |\mathrm{particle}\right\rangle \left.|-\right\rangle +\left.\sin\ \theta |\mathrm{wave}\right\rangle \left.|+\right\rangle, $$
(5)

where the wave functions

$$ \left.|\mathrm{particle}\right\rangle =\alpha \left.|1\right\rangle +{\beta e}^{i\varphi}\left.|2\right\rangle $$
(6)

and

$$ \left.|\mathrm{wave}\right\rangle =\left(\frac{1}{\sqrt{2}}\left(\alpha +\beta {e}^{i\varphi}\right)\left.|1\right\rangle +\frac{1}{\sqrt{2}}\left(\alpha -\beta {e}^{i\varphi}\right)\left.|2\right\rangle \right) $$
(7)

describe particle and wave behaviors, respectively.

Considering the simple case where \( \alpha =\beta =\frac{1}{\sqrt{2}} \) (corresponding to | 1〉 as an input state of the photon before BS1), Eqs. 6 and 7 become \( \left.|\mathrm{particle}\right\rangle =\frac{1}{\sqrt{2}}\left(\left.|1\right\rangle +{e}^{i\varphi}\left.|2\right\rangle \right) \) and \( \left.|\mathrm{wave}\right\rangle ={e}^{i\frac{\varphi }{2}}\left(\cos \frac{\varphi }{2}\left.|1\right\rangle -i\sin \left.\frac{\varphi }{2}|2\right\rangle \right) \), respectively. The probability to detect a photon in D1 is then P(D1) = Tr[ρe| 1〉〈1| ], where ρe is the photon’s reduced density matrix:

$$ {\rho}_e={Tr}_2\left.|{\varPsi}_f\right\rangle \left\langle {\varPsi}_f|\right.={\cos}^2\theta \left.|\mathrm{particle}\right\rangle \left\langle \mathrm{particle}|\right.+{\sin}^2\theta \left.|\mathrm{wave}\right\rangle \left\langle \mathrm{wave}|\right., $$
(8)
$$ P\left(\mathrm{D}1\right)=\frac{1}{2}{\cos}^2\theta +{\sin}^2\theta {\cos}^2\frac{\varphi }{2}. $$
(9)

Without correlating the photon data with the different states of the quantum beam splitter, an interference pattern with reduced visibility V = sin2θ (deduced from Eq. 9) is observed. The photon has a mixed behavior between a particle and a wave. On the other hand, if the photon is correlated with the measured state of the quantum beam splitter (see Eq. 5), the photons exhibit either a perfect wave-like behavior (BS2 in | +〉) or a particle-like one (BS2 in | −〉). The authors of [8] concluded that contrary to Bohr’s opinion, we do not have to change the experimental setup to measure complementary properties—we can measure both properties in a single experiment, provided that a component of the apparatus is a quantum object in a superposition state. Note that the photon can be detected before the measurement of the state of the quantum beam splitter, i.e., before choosing if the interferometer is open or closed. This implies that the behavior of the photon as a particle or as a wave can be chosen after it has already been detected.

3 Generalized (POVM) Measurement Description of the Quantum Delayed Choice Experiment

In quantum mechanics, physical quantities have been first represented by Hermitian operators. These operators have spectral representations consisting of projection operators Πm defined by

$$ {\Pi}_m\ge 0,{\Pi}_m^2={\Pi}_m,{\sum}_m{\Pi}_m=I\ \left(I\ \mathrm{the}\ \mathrm{identity}\ \mathrm{operator}\right). $$
(10)

The projection operators Πm are said to generate a projection-valued measure (PVM).

It is by now well known that this formalism is too restricted to encompass all possible experiments within the domain of application of quantum mechanics. Many experiments performed in actual practice are of the type of generalized measurements yielding probabilities determined by the expectation values of so-called positive operator–valued measures (POVM) [15] rather than projection-valued ones. A generalized observable (i.e., a generalized measurement) is represented by a POVM, generated by a set of non-negative operators Mm (called effects) that in general are not projection operators and obey to

$$ {M}_m\ge 0,{\sum}_m{M}_m=I. $$
(11)

When a quantum system is in the state | Ψ〉, measurement of {Mm} gives an outcome νm with probability

$$ {p}_m=\left\langle \varPsi |{M}_m|\varPsi \right\rangle . $$
(12)

PVMs are POVMs for which the effects are projection operators. A POVM for which the effects are all proportional to the identity operator provides no information on the measured quantum state. In this case, the probabilities for different outcomes do not, in fact, depend on the state.

Consider the quantum delayed choice experiment as recalled above. On the final state Eq. 5, the sharp output observable with projectors Πkl = | k〉〈k| ⨂| l〉〈l| (k = 1, 2; l = + , −) is measured. The probability to find the photon in detector Dk and BS2 in the state | l〉 is ⟨ψf| Πkl| ψf⟩. This defines a generalized measurement on the photon input state | ψi〉 = α| 1〉 + β| 2〉 characterized by the POVM \( \mathbbm{E}=\left\{{E}_{kl}\right\} \) whose effects Ekl(k = 1, 2; l = + , −) are defined by the relation [2, 17]

$$ \left\langle {\psi}_f|{\Pi}_{kl}|{\psi}_f\right\rangle =\left\langle {\psi}_i|{E}_{kl}|{\psi}_i\right\rangle . $$
(13)

Note that this definition assures that \( \mathbbm{E} \) is a POVM, and note also that no chronological order of the measurements of the photon and the quantum beam splitter is considered.

In Eq. 13, the left and right members constitute positive quadratic forms of α and β; the identification of their coefficients allows the calculation of the matrix elements of the operators Ekl:

$$ {\displaystyle \begin{array}{l}\left\langle {\varPsi}_f|{\Pi}_{1-}|{\varPsi}_f\right\rangle ={\cos}^2\theta {\left|\alpha \right|}^2=\left\langle {\psi}_i|{E}_{1-}|{\psi}_i\right\rangle, \\ {}\left\langle {\varPsi}_f|{\Pi}_{2-}|{\varPsi}_f\right\rangle ={\cos}^2\theta {\left|\beta \right|}^2=\left\langle {\psi}_i|{E}_{2-}|{\psi}_i\right\rangle, \\ {}\left\langle {\varPsi}_f|{\Pi}_{1+}|{\varPsi}_f\right\rangle =\frac{1}{2}{\sin}^2\theta {\left|\alpha +\beta {e}^{i\varphi}\right|}^2=\left\langle {\psi}_i|{E}_{1+}|{\psi}_i\right\rangle, \\ {}\left\langle {\varPsi}_f|{\Pi}_{2+}|{\varPsi}_f\right\rangle =\frac{1}{2}{\sin}^2\theta {\left|\alpha -\beta {e}^{i\varphi}\right|}^2=\left\langle {\psi}_i|{E}_{2+}|{\psi}_i\right\rangle .\end{array}} $$
(14)

Considering the two states | 1〉 and | 2〉 as eigenvectors of the Pauli matrix σz, one obtains

$$ {\displaystyle \begin{array}{l}{E}_{1-}=\frac{\cos^2\theta }{2}\left(I+{\sigma}_z\right),\\ {}{E}_{2-}=\frac{\cos^2\theta }{2}\left(I-{\sigma}_z\right),\\ {}{E}_{1+}=\frac{\sin^2\theta }{2}\left(I+\cos \varphi {\sigma}_x-\sin \varphi {\sigma}_y\right),\\ {}{E}_{2+}=\frac{\sin^2\theta }{2}\left(I-\cos \varphi {\sigma}_x+\sin \varphi {\sigma}_y\right),\end{array}} $$
(15)

Consider first the two limiting cases θ = 0 and \( \theta =\frac{\pi }{2} \). For θ = 0 (open interferometer) the measured observable is the PVM ℙ = {P+, P−},

$$ {\displaystyle \begin{array}{l}{P}_{+}=\frac{1}{2}\left(I+{\sigma}_z\right),\\ {}{P}_{-}=\frac{1}{2}\left(I-{\sigma}_z\right),\end{array}} $$
(16)

(E1+ and E2+ are both vanishing). P+ and P− are the projection operators corresponding, respectively, to the eigenvalues +1 and −1 of the Pauli matrix σz. We have σz = (+1)P+ + (−1)P−. This PVM represents, then, a sharp path measurement.

For \( \theta =\frac{\pi }{2} \) (closed interferometer), the measured observable is the PVM ℚ = {Q1, Q2},

$$ {\displaystyle \begin{array}{l}{Q}_1=\frac{1}{2}\left(I+\cos \varphi {\sigma}_x-\sin \varphi {\sigma}_y\right),\\ {}{Q}_2=\frac{1}{2}\left(I-\cos \varphi {\sigma}_x+\sin \varphi {\sigma}_y\right).\end{array}} $$
(17)

This is the observable \( {\sigma}_n=\overrightarrow{\sigma}.\overrightarrow{n} \), where \( \overrightarrow{n} \) is the unit vector \( \overrightarrow{n}=\cos \varphi {e}_x-\sin {\varphi e}_y \). This PVM represents a sharp interference measurement.

What kind of measurement is represented by the POVM \( \mathbbm{E} \) Eq. 14, for arbitrary?

3.1 The QDC as a Mixture of Sharp Path and Sharp Interference Measurements

On the one hand, consider the marginals \( \mathbbm{F}=\left\{{F}_1\right.,\left.{F}_2\right\} \) and \( \mathbbm{G}=\left\{{G}_1\right.,\left.{G}_2\right\} \) of the POVM \( \mathbbm{E} \) defined by

$$ \left\{\begin{array}{c}{F}_1={E}_{1-}+{E}_{2-}={\cos}^2\theta I\\ {}{F}_2={E}_{1+}+{E}_{2+}={\sin}^2\theta I\end{array}\right. $$
(18)

and

$$ \left\{\begin{array}{c}{G}_1={E}_{1-}+{E}_{1+}={\cos}^2\theta {P}_{+}+{\sin}^2\theta {Q}_1\\ {}{G}_2={E}_{2-}+{E}_{2+}={\cos}^2\theta {P}_{-}+{\sin}^2\theta {Q}_2\end{array}\right. $$
(19)

The first marginal is a trivial observable, not yielding any information on the state of the photon. The second marginal is a mixture of the PVMs ℙ and ℚ. In fact, Ludwig [16] (see also [17, 18]), by analogy with a non-ideal state preparation described by a convex combination of two density operators: ρ = p1ρ1 + p2ρ2 (p1 + p2 = 1), has proposed the following definition of a non-ideal measurement. A convex combination of two POVMs could represent a mixture of measurement procedures, in which the fluctuations of the measuring instrument induce a stochastic alternation of these two POVMs. Thus, given POVMs \( \left\{{M}_m^1\right\} \) and \( \left\{{M}_m^2\right\} \), according to this definition the POVM

$$ \left\{{s}_1{M}_m^1+{s}_2{M}_m^2\right\},{s}_1,{s}_2\ge 0,{s}_1+{s}_2=1 $$
(20)

represents a non-ideal measurement.

The POVM shown in Eq. 20 yields a correct representation of a measurement process if each individual measurement can be represented either by POVM \( \left\{{M}_m^1\right\} \) or by POVM \( \left\{{M}_m^2\right\} \). This can be the case if the duration of the measurement interaction is much shorter than the characteristic time of the fluctuations in the measuring instrument.

From Eq. 19, we see that the POVM \( \mathbbm{G} \) is a mixture of the PVMs ℙ and ℚ with s1 = cos2θ and s2 = sin2θ; it represents a joint non-ideal measurement of sharp path and sharp interference observables.

In the QDC experiment, the fluctuations in the measuring instrument are quantum mechanically controlled by the measurement of the state of the quantum beam splitter which can be done before as well as after the photon has arrived at the detectors. Each individual measurement is represented either by ℙ (BS2 in the state | −〉) or by ℚ (BS2 in the state | +〉). In this measurement, one can say that a fraction cos2θ of the photons impinging the interferometer really behave as particles and a fraction sin2θ really as a wave.

3.2 The QDC as a Joint Measurement of Unsharp Path and Interference Observables

On the other hand, from the original POVM, let’s define the following POVMs:

ℂ = {C1, C2, C3} and \( \mathbbm{I}=\left\{{I}_1\right.,\left.{I}_2,{I}_3\right\} \), where

$$ \left\{\begin{array}{c}{C}_1={E}_{1-}\\ {}{C}_2={E}_{2-}\\ {}{C}_3={E}_{1+}+{E}_{2+}\end{array}\right.\kern0.5em and\kern0.5em \left\{\begin{array}{c}{I}_1={E}_{1+}\\ {}{I}_2={E}_{2+}\\ {}{I}_3={E}_{1-}+{E}_{2-}\end{array}\right., $$
(21)

One can rewrite these formulae in the matrix form

$$ \left(\begin{array}{c}{C}_1\\ {}{C}_2\\ {}{C}_3\end{array}\right)=\left(\begin{array}{cc}{\cos}^2\theta & 0\\ {}0& {\cos}^2\theta \\ {}{\sin}^2\theta & {\sin}^2\theta \end{array}\right)\left(\begin{array}{c}{P}_{+}\\ {}{P}_{-}\end{array}\right) $$
(22)

and

$$ \left(\begin{array}{c}{I}_1\\ {}{I}_2\\ {}{I}_3\end{array}\right)=\left(\begin{array}{cc}{\sin}^2\theta & 0\\ {}0& {\sin}^2\theta \\ {}{\cos}^2\theta & {\cos}^2\theta \end{array}\right)\left(\begin{array}{c}{Q}_1\\ {}{Q}_2\end{array}\right). $$
(23)

An important feature of Eqs. 22 and 23 is that one POVM contains information only on the sharp path observable, whereas the other only refers to the sharp interference observable.

Equations 22 and 23 are applications of another general definition of a non-ideal measurement: a POVM {Mi} is said to represent a non-ideal measurement of a POVM {Nj}, if [17, 18]

$$ {M}_i=\sum \limits_j{\lambda}_{ij}{N}_j,{\lambda}_{ij}\ge 0,\sum \limits_j{\lambda}_{ij}=1. $$
(24)

This expression compares the measurement procedures of POVMs {Mi} and {Nj}. The first is interpreted as a non-ideal or an inaccurate version of the second, the non-ideality matrix λij representing the inaccuracy. A convenient measure of this non-ideality is the average row entropy of the non-ideality matrix [17],

$$ {J}_{\lambda }=-\frac{1}{N}\sum \limits_{ij}{\lambda}_{ij}\ln \frac{\lambda_{ij}}{\sum \limits_{j^{\prime }}{\lambda}_{i{j}^{\prime }}}, $$
(25)

where N is the number of effects of the POVM {Nj}.

Jλ is positive and is bounded from above by lnN: 0 ≤ Jλ ≤ ln N [17].

The POVMs ℂ and \( \mathbbm{I} \) are non-ideal measurements of the PVMs ℙ and ℚ, respectively. They represent non-ideal measurements of path and interference, respectively.

The POVMs ℂ and \( \mathbbm{I} \) are simultaneously determined by the original POVM \( \mathbbm{E} \); the quantum delayed choice experiment is, then, a non-ideal joint measurement of path and interference. Using the definition Eq. 25, the non-idealities of these measurements are given, respectively, by

$$ {J}_{\mathrm{C}}={\sin}^2\theta\ \ln 2\ \mathrm{and}\ {J}_{\mathrm{I}}={\cos}^2\theta\ \ln 2 $$
(26)

and satisfy the relation

$$ {J}_{\mathrm{C}}+{J}_{\mathrm{I}}=\ln 2. $$
(27)

Equation 27 is an instance of the so-called Martens inequalityFootnote 1 expressing the complementarity principle. In fact, from this equation, one has not simultaneously JC = 0 (sharp path measurement) and JI = 0 (sharp interference measurement), which means the impossibility of joint measurement of the incompatible sharp path and interference observables. This is the orthodox Bohr’s complementarity principle: the photon behaves as a particle or as a wave but not simultaneously as both. For \( 0<\theta <\frac{\pi }{2} \), Eq. 27 is a duality condition which is a less orthodox expression of the complementarity principle; wave and particle attributes coexist, but a stronger manifestation of the particle nature leads to a weaker manifestation of the wave nature and vice versa.

Note that Eq. 27, being independent of the initial vector state of the photon, refers to the measurement procedure alone and is understood as a consequence of the mutual exclusiveness of measurement arrangements for measuring incompatible standard (PVM) observables. We agree with the conclusion in [8] that the complementarity resides in the experimental data, rather than resulting from the experiment’s physical arrangement; but the experimental data is a consequence of the experiment’s arrangement which has, here, the particularity that it is quantum mechanically controlled.

4 Conclusion

In this paper, we have described the QDC experiment as a generalized measurement on the photon state and described by a POVM. This measurement may be seen as a mixture (Eq. 19) of path and interference measurements where a fraction of the photons behave as particles and a fraction as a wave. It may also be seen as a joint measurement of unsharp path and interference obeying a duality relation. This duality relation expresses the fact that wave and particle attributes coexist, but a stronger manifestation of the particle nature leads to a weaker manifestation of the wave nature and vice versa.