Qubit-Qutrit (2 ⊗ 3) Quantum Systems: an Investigation of Some Quantum Correlations Under Collective Dephasing

Abstract

We revisit qubit-qutrit quantum systems under collective dephasing and answer some of the questions which have not been asked and addressed so far in the literature. In particular, we examine the possibilities of non-trivial phenomena of time-invariant entanglement and freezing dynamics of entanglement for this dimension of Hilbert space. Interestingly, we find that for qubit-qutrit systems both of these peculiar features coexist, that is, we observe not only time-invariant entanglement for certain quantum states but we also find evidence that many quantum states freeze their entanglement after decaying for some time. To our knowledge, the existence of both these phenomena for a dimension of Hilbert space is not found so far. All previous studies suggest that if there is freezing dynamics of entanglement, then there is no time-invariant entanglement and vice versa. In addition, we study local quantum uncertainty and other correlations for certain families of states and discuss the interesting dynamics. Our study is an extension of similar studies for qubit-qubit, qubit-qutrit, and multipartite quantum systems.

1 Introduction

Quantum correlations have their role in potential applications in quantum information theory. This includes remote state preparation [1], entanglement distribution [2, 3], transmission of correlations [4], and quantum meteorology [5] to name a few. This utilization of quantum correlations is already enough motivation to study, characterize, and quantify them. There are classical correlations which have no quantum part in it. It is hard task to characterize and quantify quantum correlations. Entanglement, quantum discord, and local quantum uncertainty are three kinds of quantum correlations. Several authors have proposed different techniques to compute entanglement and quantum discord. The quantum correlations have attracted a lot of interest and considerable efforts have been devoted to develop a theoretical framework for it [6,7,8]. Meantime, the advancements in experimental setups have enabled us to work for realistic realizations of quantum devices utilizing quantum correlations. Due to unavoidable interactions of delicate quantum systems with their environment, it is essential to simulate the effects of noisy environments on quantum correlations. Such investigations are already an active area of research [9] and several authors have studied decoherence effects on quantum correlations for both bipartite and multipartite systems [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39].

There are several types of experimental setups to test the ideas of quantum information. One of the technological advanced setup is to trap the ions/atoms and perform quantum computations by logic gates, measurements, etc. In these experiments, the typical noise is caused by intensity fluctuations of electromagnetic fields which leads to collective dephasing process. This process degrades quantum correlations and there are several investigations on the effects of collective dephasing on entanglement for bipartite and multipartite quantum systems [40,41,42,43,44,45,46,47, 49,50,51,52,53]. It has been reported in these studies that collective dephasing process offers not only the expected exponential decay of entanglement but also the abrupt end of entanglement (sudden death of entanglement). In addition to these two dynamical behaviors, some of the recent studies demonstrated that there are two other types of non-trivial dynamics of entanglement present/observed under collective dephasing. First, there is so-called time-invariant entanglement [47, 49, 53]. Time-invariant entanglement does not necessarily mean that the quantum states live in decoherence-free subspaces (DFS). In fact, the quantum states may change at every instance whereas their entanglement remains constant throughout the dynamical process. This feature was first observed for qubit-qutrit systems [47] and then later on for qubit-qubit systems as well [49]. Recently, we have investigated time-invariant phenomenon for genuine entanglement of three and four qubits. We have found no evidence of time-invariant for three qubits, whereas for four qubits we have demonstrated its presence explicitly [53]. The second non-trivial feature of entanglement decay is the so-called freezing dynamics of entanglement [50,51,52]. It was shown that entanglement of a specific two-qubit state may first decay up to some numerical value before suddenly stopping decaying and maintaining this stationary entanglement [50, 51]. Recently, we have explored freezing dynamics for various genuine multipartite specific states of three and four qubits, including random states, and found evidence for it [52]. More recently, we have explored the possibility of either time-invariant entanglement or freezing dynamics for qutrit-qutrit (3 ⊗ 3) systems [54]. We found no evidence for time-invariant entanglement; however, we observed the exclusive evidence for freezing dynamics of entanglement [54]. We have noticed that in all previous studies on time-invariant entanglement and freezing dynamics for a given Hilbert space, there is either time-invariant entanglement or freezing dynamics behavior. We have not found so far these two features occurring together for one dimension of Hilbert space. Interestingly, for qubit-qutrit systems, we find both these features present. As we show below, there are certain states which exhibit either time-invariant entanglement or sudden death of entanglement but never freezing dynamics. On the other hand, some other quantum states exhibit either freezing dynamics or sudden death but never time-invariant dynamics. However, we get both peculiar features for Hilbert space of dimension 6.

The two other quantum correlations which we study in this work are quantum discord and local quantum uncertainty. Quantum discord may be defined as the difference between quantum mutual information and classical correlations [55,56,57,58,59,60]. Quantum discord may be nonzero even for separable states and have applications in quantum information. Due to the complicated minimization process, the computation of discord is not an easy task and analytical results are known only for some restricted families of states. For 2 ⊗ d quantum systems, analytical results for quantum discord are known for a specific family of states [61] and the general procedure to calculate discord is also worked out [62, 63]. The dynamics of quantum discord under decoherence has been studied [64,65,66] and is found to be more robust than quantum entanglement. In this work, we also study dynamics of quantum discord and classical correlation under collective dephasing for a specific family of states. The other quantum correlation which we study in this work is recently proposed, known as local quantum uncertainty [67]. This measure is based on the idea of skew information and it is discord-type correlation [68]. Recently, the effects of decoherence on discord-like measures including local quantum uncertainty have been studied [69,70,71,72]. Here, in this work, we study local quantum uncertainty for several families of quantum states under collective dephasing. We find that in situations where entanglement exhibits time-invariant feature, local quantum uncertainty first keeps on increasing to a specific value and then exhibits freezing dynamics after a long time. On the other hand, where there is entanglement sudden death, local quantum uncertainty first decays, then increases and finally tends to freeze for a long time. Whereas, in situations where entanglement exhibits freezing dynamics, local quantum uncertainty first decays very slowly to a value and then decays abruptly and finally tends to exhibit freezing dynamics as well. Finally, we examine the random pure states and calculate their entanglement at infinity. We find that around half of random states maintain their entanglement at infinity and hence all other correlations as well under collective dephasing.

This paper is organized as follows. In Section 2, we briefly discuss our model of interest and obtain the most general solution for an arbitrary initial density matrix. In Section 3, we review the idea of entanglement for qubit-qutrit systems and describe the method to compute negativity for an arbitrary initial quantum state. We also briefly examine the concept of quantum discord and how to compute it for an arbitrary bipartite state. We also briefly review local quantum uncertainty and how to compute it for any state for 2 ⊗ d quantum systems. In Section 4, we provide our main results for various initial states. Finally, we conclude our work in Section 5.

2 Collective Dephasing for Qubit-Qutrit Systems

Our physical model consists of a qubit and a qutrit (one two-level atom and one three-level atom for an example) A and B that are coupled to a noisy environment, collectively. The qutrit as an atom, can be realized in any configuration depending on experimental convenience. There are three well-known configurations for a three-level atom. In V -type energy level configuration, the transition among excited levels is forbidden. This means that the first excited state will decay to ground level only and similarly the second excited level will also decay to ground level. In Λ-type configuration, the excited level |2〉 can decay either to level |1〉 or directly to level |0〉. The transition from |1〉 to |0〉 is forbidden. The third type of configuration is called cascade configuration in which the energy level |2〉 first decays to |1〉 and then energy level |1〉 decays to ground level |0〉. For amplitude damping, it is very important to specify the configuration as the atomic transition operators for each configuration are different and hence the subsequent dynamics would be different. The atoms are sufficiently far apart and they do not interact with each other, so that we can treat them as independent. The collective dephasing refers to coupling of atoms to the same noisy environment, which can be stochastic magnetic fields B(t). There are at least two approaches to write a Hamiltonian for such physical situations. First, the Hamiltonian could be time independent, like in case of a qubit $H = \hbar \omega /2 \sigma _{z}$ with ω as energy splitting between excited states of atom. One can write a unitary propagator $U(t) = \exp (- i H t/\hbar )$. As there are fluctuations in magnetic field strength, the integration over it will induce a probability distribution p(w) of characteristic energy splitting. The time evolution of the atom can be written as an integral over p(ω) and unitary evolution, i.e., $\rho (t) = {\int \limits } p(\omega ) U(t) \rho (0) U(t)^{\dagger } d\omega$. The form of p(ω) will determine the nature of noise. Another approach, which we have taken in this work and most of the work in literature, is to take the Hamiltonian as time dependent and embed the fluctuations of magnetic field in stochastic function B(t), which already includes the information about characteristic function and so that the ensemble average over it introduces the decay parameter Γ. Both approaches are equivalent and generates the same dynamics. However, we point out, to our knowledge the present work and recent works are restricted to a very specific orientation of magnetic field and the theory of a general description of magnetic fields in any arbitrary directions is still not worked out. The Hamiltonian of the quantum system (with $\hbar = 1$) can be written as [47]:

$$ \begin{array}{@{}rcl@{}} H(t) = - \frac{\mu}{2} \left[ B(t) ({\sigma_{z}^{A}} + {\sigma_{z}^{B}}) \right] , \end{array} $$

(1)

where μ is gyro-magnetic ratio and ${\sigma _{z}^{A}}$ is standard Pauli matrix for qubit and ${\sigma _{z}^{B}}$ is the dephasing operator for qutrit B. The stochastic magnetic fields refer to statistically independent classical Markov processes satisfying the conditions:

$$ \begin{array}{@{}rcl@{}} \langle B(t) B(t^{\prime})\rangle &=& \frac{\Gamma}{\mu^{2}} \delta(t-t^{\prime}) , \\ \langle B(t)\rangle &=& 0 , \end{array} $$

(2)

with 〈⋯〉 as ensemble time average and Γ denoting the phase-damping rate for collective dephasing.

Let |2〉, |1〉, and |0〉 be the first excited state, second excited, and ground state of the qutrit, respectively. We choose the computational basis {|0,0〉, |0,1〉, |0,2〉|1,0〉, |1,1〉, and |1,2〉}, where we have dropped the subscripts A and B with the understanding that the first basis represents qubit A and second qutrit B. Also, the notation |0〉⊗|0〉 = |00〉 has been adopted for simplicity. The time-dependent density matrix for the system is obtained by taking ensemble average over the noisy field, i.e., ρ(t) = 〈ρ_st(t)〉, where ρ_st(t) = U(t)ρ(0)U^‡(t) and $U(t) = \exp [-\mathrm {i} {{\int \limits }_{0}^{t}} dt^{\prime } H(t^{\prime })]$. We assume that there are no initial correlations between the qubit-qutrit system and the stochastic field, that is, ρ(0) = ρ_S ⊗ ρ_R, where ρ_S is the density matrix for an arbitrary quantum state of qubit-qutrit system and ρ_R is the density matrix of environment. There are several ways to obtain the time-evolved density matrix of the qubit-qutrit system. We prefer to solve the system using the master equation approach.

According to the general reservoir theory [48], we consider a qubit-qutrit system (S) interacting with a reservoir (R). The combined density operator for system can be written as ρ_SR. The reduced density operator ρ_S for system (S) is calculated using the standard technique of taking partial trace over the reservoir degrees of freedom, that is, ρ_S = Tr_R(ρ_SR). In the interaction picture, the equation of motion can be written as:

$$ {\mathrm i} \dot{\rho}_{SR}(t) = \left[ H(t), \rho_{SR}(t) \right] . $$

(3)

We can simply integrate this equation to obtain:

$$ \rho_{SR}(t) = \rho_{SR}(t_{i}) - \mathrm{i} {\int}_{t_{i}}^{t} \left[ H(t^{\prime}), \rho_{SR}(t^{\prime}) \right] dt^{\prime} , $$

(4)

where t_i is starting time of interaction. Substituting (4) back into (3), we get equation of motion:

$$ \begin{array}{@{}rcl@{}} \dot{\rho}_{SR}(t) &=& - {\mathrm i} \left[ H(t), \rho_{SR}(t_{i}) \right] \\ &&- {\int}_{t_{i}}^{t} \left[ H(t) , \left[ H(t^{\prime}), \rho_{SR}(t^{\prime}) \right] \right] dt^{\prime} . \end{array} $$

(5)

As the interaction between the system and reservoir is weak, we look for a solution of (5) of the form:

$$ \rho_{SR}(t) = \rho_{S} (t) \otimes \rho_{R}(t_{i}) + \rho_{c}(t) , $$

(6)

where ρ_c(t) is of higher order in H(t). For consistency, we require that Tr_R(ρ_c(t)) = 0. Substituting (6) into (5) and after some simplifications, we get:

$$ \begin{array}{@{}rcl@{}} \dot{\rho}_{S}(t) &=& - {\mathrm i} {\mathrm Tr}_{R} \left[ H(t), \rho_{S}(t_{i}) \otimes \rho_{R}(t_{i}) \right]- {\mathrm Tr}_{R} \\ &&\times {\int}_{t_{i}}^{t} \left[ H(t) , \left[ H(t^{\prime}), \rho_{S}(t^{\prime}) \otimes \rho_{R}(t_{i}) \right] \right] dt^{\prime} . \end{array} $$

(7)

In this equation, the reduced density operator ρ_S(t) depends on past history from t = t_i to $t^{\prime }$. Typically, reservoir have many degrees of freedom, which leads to delta function $\delta (t - t^{\prime })$. Under Markovian assumption, the system density matrix $\rho _{S}(t^{\prime })$ can be replaced by ρ_S(t), which is quite reasonable since damping destroys memory of past. We can write (7):

$$ \begin{array}{@{}rcl@{}} \dot{\rho}_{S}(t) &=& - {\mathrm i} {\mathrm Tr}_{R} \left[ H(t), \rho_{S}(t_{i}) \otimes \rho_{R}(t_{i}) \right] - {\mathrm Tr}_{R} \\ &&\times {\int}_{t_{i}}^{t} \left[ H(t) , \left[ H(t^{\prime}), \rho_{S}(t) \otimes \rho_{R}(t_{i}) \right] \right] dt^{\prime} . \end{array} $$

(8)

This is a valid master equation for a system ρ_S interacting with a reservoir represented by ρ_R.

Substituting the Hamiltonian (1) in (8), using the relations in (2), and doing some algebra, we arrive at equation for system given as:

$$ \begin{array}{@{}rcl@{}} \dot{\rho}(t) &=& - \frac{\Gamma}{4} \left\{ {\sigma_{z}^{A}} {\sigma_{z}^{A}} \rho(t) - 2 {\sigma_{z}^{A}} \rho(t) {\sigma_{z}^{A}} + {\sigma_{z}^{B}} {\sigma_{z}^{A}} \rho(t)\right.\\ &&\left. - 2 {\sigma_{z}^{A}} \rho(t) {\sigma_{z}^{B}} + {\sigma_{z}^{A}} {\sigma_{z}^{B}} \rho(t) - 2 {\sigma_{z}^{B}} \rho(t) {\sigma_{z}^{A}}\right.\\ &&\left. + {\sigma_{z}^{B}} {\sigma_{z}^{B}} \rho(t) - 2 {\sigma_{z}^{B}} \rho(t) {\sigma_{z}^{B}} + \rho(t) {\sigma_{z}^{A}} {\sigma_{z}^{A}} \right.\\ &&\left.+ \rho(t) {\sigma_{z}^{A}} {\sigma_{z}^{B}} + \rho(t) {\sigma_{z}^{B}} {\sigma_{z}^{A}} + \rho(t) {\sigma_{z}^{B}} {\sigma_{z}^{B}} \right\} . \end{array} $$

(9)

We have dropped the subscript S for system as there is no chance of confusion now. This is a simple differential equation, which can be straightforwardly solved to give us the most general solution of the system as:

$$ \begin{array}{@{}rcl@{}} \rho(t) = \left( \begin{array}{llllll} \rho_{11} & \xi \rho_{12} & \xi^{4} \rho_{13} & \xi^{4} \rho_{14} & \xi^{9} \rho_{15} & \xi^{16} \rho_{16} \\ \xi \rho_{21} & \rho_{22} & \xi \rho_{23} & \xi \rho_{24} & \xi^{4} \rho_{25} & \xi^{9} \rho_{26} \\ \xi^{4} \rho_{31} & \xi \rho_{32} & \rho_{33} & \rho_{34} & \xi \rho_{35} & \xi^{4} \rho_{36} \\ \xi^{4} \rho_{41} & \xi \rho_{42} & \rho_{43} & \rho_{44} & \xi \rho_{45} & \xi^{4} \rho_{46} \\ \xi^{9} \rho_{51} & \xi^{4} \rho_{52} & \xi \rho_{53} & \xi \rho_{54} & \rho_{55} & \xi \rho_{56} \\ \xi^{16} \rho_{61} & \xi^{9} \rho_{62} & \xi^{4} \rho_{63} & \xi^{4} \rho_{64} & \xi \rho_{65} & \rho_{66} \end{array} \right),\\ \end{array} $$

(10)

where ξ = e^−Γt/4. We note that DFS [40,41,42] do appear in this system as a common characteristic of collective dephasing. Another interesting property of the dynamics is the fact that all initially zero matrix elements remain 0.

3 Entanglement, Quantum Discord, and Local Quantum Uncertainty for 2 ⊗ 3 Quantum Systems

In this section, we briefly review the correlations, which we study in this work for qubit-qutrit systems. In Section 3.1, we briefly review entanglement and a computable measures of entanglement. In Section 3.2, we review the quantum discord and how to compute it for any bipartite quantum state. In Section 3.3, we discuss local quantum uncertainty and how to compute it for a given state in 2 ⊗ d quantum systems.

3.1 Quantum Entanglement

The quantification of quantum entanglement for qubit-qubit (2 ⊗ 2) quantum systems and qubit-qutrit (2 ⊗ 3) quantum systems has been completely solved. It is well known that for bipartite quantum systems, if the partial transpose with respect of any one of the subsystem has at least one negative eigenvalue then the quantum state is entangled or NPT [73]. Whereas if the partial transposed matrix has all positive eigenvalues (PPT), then entanglement/separability depends upon the dimension of Hilbert space. The PPT states for 2 ⊗ 2 and 2 ⊗ 3 are separable (not entangled), whereas for larger dimensions of Hilbert space, there may exist PPT-entangled states (also called bound entangled states) [6]. There are many measures of entanglement defined in literature, like Entanglement of Formation [74], Concurrence [75, 76], Schmidt number [77], etc. The details of these and all other measures can be found in review article [6]. However, most of these measures have closed formulas only for qubit-qubit quantum system and in general it is not easy to calculate them for an arbitrary quantum mixed state of other dimension of Hilbert space. On the other hand, for a given density matrix of qubit-qutrit system, one can easily find the eigenvalues of partially transposed matrix (partial transpose can be taken with respect to any subsystem). It is not hard to look for possible negative eigenvalues. The sum of absolute values of all possible negative eigenvalues is defined as a legitimate measure of quantum entanglement, namely negativity [78]. Hence, negativity is defined as:

$$ N (\rho) = 2 \left( \sum\limits_{i} | \eta_{i}| \right) , $$

(11)

where η_i are possible negative eigenvalues and multiplication with 2 is for normalization so that for maximally entangled states, this measure should have the numerical value of 1. For specific quantum states, this definition is sufficient to compute and study the dynamics of negativity. For random states, it is more easy to use entanglement monotone, which is based on the PPT-mixtures idea [79,80,81] and very easy to compute numerical value of entanglement for any density matrix. The description of semi-definite programming (SDP) and genuine negativity is described in detail in Refs. [79,80,81]. We denote this measure by E(ρ) in this paper. For bipartite systems, this monotone is equivalent to negativity.

3.2 Quantum Discord

Quantum discord is one of the measure of quantum correlations which are captured using von Neumann entropy. This measure has been intensively investigated in the previous 18 years in various contexts and many studies focused on the quantification of this measure for various dimensions of Hilbert space. The literature on this measure is so extensive that it is not possible to cite each of them, so we only provide fundamental references. We discuss the main ideas very briefly to compute quantum discord for a given bipartite quantum state. Any bipartite state may have both quantum and classical correlations, which are jointly captured by quantum mutual information. In particular, if ρ^AB denotes the density operator of a composite bipartite system AB, and ρ^A (ρ^B) the density operator of part A (B), respectively, then the quantum mutual information is defined as [82]:

$$ \begin{array}{@{}rcl@{}} \mathcal{I} (\rho^{AB}) = S (\rho^{A}) + S (\rho^{B}) - S(\rho^{AB}) , \end{array} $$

(12)

where $S(\rho ) = - \text {tr} (\rho \log _{2} \rho )$ is the von Neumann entropy. We take all logarithms base 2 in this work. Quantum mutual information may be written as a sum of classical correlation $\mathcal {C}(\rho ^{AB})$ and quantum discord $\mathcal {Q} (\rho ^{AB})$, that is, $\mathcal {I} (\rho ^{AB}) = \mathcal {C} (\rho ^{AB}) + \mathcal {Q} (\rho ^{AB})$ [55,56,57,58,59,60]. Quantum discord can be positive in separable mixed states (that is, with no entanglement).

Quantum discord can be quantified [55] via von Neumann type measurements which consist of one-dimensional projectors that sum to the identity operator. Let the projection operators {A_k} describe a von Neumann measurement for subsystem A only, then the conditional density operator ρ_k associated with the measurement result k is:

$$ \begin{array}{@{}rcl@{}} \rho_{k} = \frac{1}{p_{k}} (A_{k} \otimes \mathbb{I}_{B}) \rho (A_{k} \otimes \mathbb{I}_{B}) , \end{array} $$

(13)

where the probability p_k equals $\text {tr} [(A_{k} \otimes \mathbb {I}_{B}) \rho (A_{k} \otimes \mathbb {I}_{B})]$. The quantum conditional entropy with respect to this measurement is given by [59, 60]:

$$ \begin{array}{@{}rcl@{}} S (\rho | \{A_{k}\}) := \sum\limits_{k} p_{k} S(\rho_{k}) , \end{array} $$

(14)

and the associated quantum mutual information of this measurement is defined as:

$$ \begin{array}{@{}rcl@{}} \mathcal{I} (\rho|\{A_{k}\}) := S (\rho^{B}) - S(\rho|\{A_{k}\}) . \end{array} $$

(15)

A measure of the resulting classical correlations is provided [55,56,57,58,59,60] by:

$$ \begin{array}{@{}rcl@{}} \mathcal{C}(\rho) := \sup_{\{A_{k}\}} \mathcal{I} (\rho|\{A_{k}\}) . \end{array} $$

(16)

The obstacle to computing quantum discord lies in this complicated maximization procedure for calculating the classical correlation because the maximization is to be done over all possible von Neumann measurements of A. Once $\mathcal {C}(\rho )$ is in hand, quantum discord is simply obtained by subtracting it from the quantum mutual information,

$$ \begin{array}{@{}rcl@{}} \mathcal{Q}(\rho) := \mathcal{I}(\rho) - \mathcal{C}(\rho) . \end{array} $$

(17)

This maximization process is not easy in general and analytical results for quantum discard are only known for very specific quantum states. In this work, we have been only able to calculate it for only one family of quantum states for 2 ⊗ 3 quantum system.

3.3 Local Quantum Uncertainty

First of all, we briefly review the concept of local quantum uncertainty (LQ). This is a measure of quantum correlations which has been defined for 2 ⊗ d quantum systems [67]. It is a quantum discord type measure and we will see in the results below that for certain quantum states, quantum discord, and local quantum uncertainty captures precisely same correlations and are equal to each other, whereas for some other states, they are different measures. It is defined as the minimum skew information which is obtained via local measurement on the qubit part only. This measure has the advantage that there is no need for complicated minimization over parameters related with measurement operations. This measure is defined as:

$$ LQ(\rho) \equiv \min\limits_{K_{A}} \mathcal{I} (\rho , K_{A} \otimes \mathbb{I}_{B}) , $$

(18)

where K_A is some local observable on subsystem A, and $\mathcal {I}$ is the skew information of the density operator ρ, defined as:

$$ \mathcal{I} (\rho , K_{A} \otimes \mathbb{I}_{B}) = - \frac{1}{2} \text{Tr} ( [ \sqrt{\rho}, K_{A} \otimes \mathbb{I}_{B} ]^{2} ) . $$

(19)

It has been shown [67] that for 2 ⊗ d quantum systems, the compact formula for local quantum uncertainty is given as:

$$ LQ(\rho) = 1 - \max \{ \lambda_{1} , \lambda_{2} , \lambda_{3} \} , $$

(20)

where λ_i are the eigenvalues of 3 × 3 matrix ${\mathscr{M}}$, whose matrix elements are calculated by the relationship:

$$ m_{ij} \equiv \text{Tr} \{ \sqrt{\rho} (\sigma_{i} \otimes \mathbb{I}_{B}) \sqrt{\rho} (\sigma_{j} \otimes \mathbb{I}_{B}) \} , $$

(21)

where i,j = 1,2,3 and σ_i are the standard Pauli matrices.

4 Main Results

In this section, we will present our main results for various families of quantum states.

4.1 Two-Parameter Class of States

The class of quantum states with two real parameters α and γ in a 2 ⊗ d quantum system [83] is given as:

$$ \begin{array}{@{}rcl@{}} \rho_{\alpha, \gamma} &=& \alpha \sum\nolimits_{i = 0}^{1} \sum\nolimits_{j = 2}^{d-1} | i j \rangle\langle i j| + \beta (| \phi^{+} \rangle\langle \phi^{+}| \\&&+ | \phi^{-} \rangle\langle \phi^{-}| + | \psi^{+} \rangle\langle \psi^{+}| ) + \gamma | \psi^{-} \rangle\langle \psi^{-}| , \end{array} $$

(22)

where {|ij〉 : i = 0,1,j = 0,1,…,d − 1} is an orthonormal basis for 2 ⊗ d quantum system and:

$$ \begin{array}{@{}rcl@{}} | \phi^{\pm} \rangle &=& \frac{1}{\sqrt{2}} ( |0 0\rangle \pm | 1 1 \rangle ) \end{array} $$

(23)

$$ \begin{array}{@{}rcl@{}} | \psi^{\pm} \rangle &=& \frac{1}{\sqrt{2}} ( |0 1 \rangle \pm |1 0 \rangle ) , \end{array} $$

(24)

and the parameter β is dependent on α and γ by the unit trace condition:

$$ \begin{array}{@{}rcl@{}} 2 (d - 2) \alpha + 3 \beta + \gamma = 1 . \end{array} $$

(25)

From (22), one can easily obtain the range of parameters as 0 ≤ α ≤ 1/(2(d − 2)) and 0 ≤ γ ≤ 1. We note that the states of the form ρ_0,γ are equivalent to Werner states [84] in 2 ⊗ 2 quantum systems. Moreover, the states ρ_α,γ have the property that their PPT (positive partial transpose) region is always separable [83]. It is also known that an arbitrary quantum state ρ in 2 ⊗ d can be transformed to ρ_α,γ with the help of local operations and classical communication (LOCC).

We have already calculated quantum discord, classical correlation, and entanglement for this family in an earlier work [61]. Here, we simply extend the previous results for collective dephasing (an additional parameter Γt). It turns out that classical correlations for this family of states do not depend on decay parameter and are constant in time. The expression for classical correlations is given as:

$$ \begin{array}{@{}rcl@{}} \mathcal{C}(\rho_{\alpha,\gamma}) &=& - (3 \beta + \gamma) \log(\frac{3 \beta + \gamma }{2}) + 2 \beta \log(2 \beta)\\ &&+ (\beta + \gamma) \log(\beta + \gamma) . \end{array} $$

(26)

The quantum discord is calculated using the standard procedure discussed in the previous section and is given as:

$$ \begin{array}{@{}rcl@{}} \mathcal{Q}(\rho_{\alpha,\gamma})(t) &=& 1 - 2 \alpha -2 \beta -(\beta + \gamma) \log(\beta + \gamma) \\&& + \frac{\beta + \gamma + \xi (\beta-\gamma)}{2} \\&& \times \log\left( \frac{\beta + \gamma + \xi (\beta - \gamma)}{2}\right) \\&& + \frac{\beta + \gamma - \xi (\beta - \gamma)}{2} \\&&\times\log\left( \frac{\beta + \gamma - \xi (\beta - \gamma)}{2}\right) . \end{array} $$

(27)

We can see that as $t \to \infty$, ξ → 0, and $\mathcal {Q}(\rho _{\alpha ,\gamma })(\infty ) = 1 - 2 \alpha - 3 \beta - \gamma = 0$ as expected.

The local quantum uncertainty for this family of state turns out to be:

$$ \begin{array}{@{}rcl@{}} LQ(\rho_{\alpha,\gamma})(t) &=& 1 - 2 \alpha - 2 \beta - \left[\sqrt{\beta (1 + \xi) + \gamma (1 - \xi)}\right.\\ &&\left. \sqrt{\beta (1 - \xi) + \gamma (1 + \xi)} \right] . \end{array} $$

(28)

We note the similarity between local uncertainty (28) and quantum discord (27). Indeed, it turns out that for t = 0, and for the initial states (i) α = β = 0 and γ = 1, (ii) α = γ = 0, and β = 1/3, (iii) γ = 0, and (iv) β = 0, local quantum uncertainty and quantum discord turn out to be exactly equal as can be checked easily. However, for more general cases with α,β,γ≠ 0, and under collective dephasing, both measures are different as will be shown below.

The negativity for this family of states is straightforward to calculate and is given as:

$$ N (\rho_{\alpha, \gamma})(t) = \max \left[ 0 , \xi (\gamma - \beta) - 2 \beta \right] . $$

(29)

It is easy to see that for β = 0, the states decay asymptotically and entanglement is lost only at infinity, whereas for β≠ 0, negativity is lost at:

$$ {\Gamma} t = 4 \log \frac{\gamma - \beta}{ 2 \beta} . $$

(30)

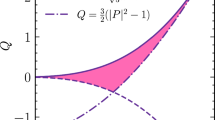
We plot entanglement, discord, classical correlation, and local quantum uncertainty for state ρ_α,γ(t) in Fig. 1. We have taken specific values of α = 0.1, β = 0.1, and γ = 0.5. Quantum discord $\mathcal {Q} (\rho _{\alpha , \gamma })(t)$ plotted as a solid line decays slowly as well as negativity (dashed line) and local quantum uncertainty (big dashed line). Classical correlation (dashed orange line) is constant in time with a fixed initial value. Negativity ends at Γt ≈ 2.77, whereas quantum discord becomes 0 at infinity. Local quantum uncertainty and quantum discord become 0 at the same time as expected.

Fig. 1

Entanglement (negativity) N(ρ_α,γ), classical correlation C(ρ_α,γ), quantum discord $\mathcal {Q}(\rho _{\alpha , \gamma })$, and local quantum uncertainty LQ(ρ_α,γ) are plotted against parameter Γt. It can be seen that all correlations maintain nonzero values for a long time due to the presence of decoherence-free subspace

Let us take another set of initial values with α = 0.12, β = 0.12, and γ = 0.4 for state ρ_α,γ(t). Figure 2 depicts entanglement (dashed line), classical correlation (thick dashed orange line), quantum discord (solid line), and local quantum uncertainty (big dashed line) for this set of values against decay parameter Γt. As we have reduced the fraction of maximally entangled state (γ) and increased the noisy components α and β slightly, nevertheless, the resulting dynamics is interesting and different from the earlier case. The numerical values of all correlations are lower than those of the earlier case. This fact is understandable as we have reduced the fraction of γ, so maximally entangled state feeds almost all correlations in ρ_α,γ. Entanglement vanishes at Γt ≈ 0.61, the so-called sudden death of entanglement. Classical correlation is constant as mentioned earlier. Quantum discord and local quantum uncertainty decay slowly as expected and both become 0 only at infinity.

Fig. 2

Entanglement (negativity) N(ρ_α,γ), classical correlation C(ρ_α,γ), quantum discord $\mathcal {Q}(\rho _{\alpha , \gamma })$, and local quantum uncertainty LQ(ρ_α,γ) are plotted against parameter Γt. It can be seen that all correlations except negativity maintain nonzero values for a long time

4.2 Search for Freezing Dynamics of Entanglement

It has already been shown explicitly [47] that certain qubit-qutrit entangled states exhibit time-invariant entanglement feature under collective dephasing. However, the question of freezing dynamics of entanglement has not been explored so far. Therefore, we look for such possibility encouraged by the existence of decoherence-free subspaces where entangled states can reside. Of course, the presence of such decoherence-free spaces alone does not guarantee that either time-invariant entanglement or freezing dynamics must occur. In fact, all previous studies suggest that for all other dimensions of Hilbert space studied so far, either time-invariant entanglement appears or freezing dynamics. To our knowledge, both of these possibilities have never been observed for any single dimension of Hilbert space. Interestingly, as we will demonstrate, qubit-qutrit systems offer all kind of dynamical features of entanglement, that is, entanglement sudden death, asymptotic decay of entanglement, time-invariant entanglement, and freezing dynamics of entanglement under collective dephasing.

Let us define a single-parameter class of states, which are a mixture of entangled states residing in decoherence-free subspace and states which decay. The states are defined as:

$$ \rho_{\alpha} = \alpha |\psi_{3} \rangle\langle \psi_{3}| + (1 - \alpha) |\psi_{2} \rangle\langle \psi_{2}| , $$

(31)

where 0 ≤ α ≤ 1, the maximally entangled state |ψ₂〉 is defined as:

$$ |\psi_{2} \rangle = \frac{1}{\sqrt{2}} (|0 1\rangle + |1 2 \rangle) , $$

(32)

and another maximally entangled state |ψ₃〉 is defined as:

$$ |\psi_{3} \rangle = \frac{1}{\sqrt{2}} (|0 2\rangle + |1 0 \rangle) . $$

(33)

In this mixture, |ψ₂〉 decays, whereas |ψ₃〉 lives in decoherence-free subspace. Therefore, the time evolution of this state can be written as:

$$ \rho_{\alpha} (t) = \alpha \rho_{3} + (1 - \alpha) \rho_{2} (t) . $$

(34)

There are only two possible negative eigenvalues for the partial transpose of this state, namely:

$$ \begin{array}{@{}rcl@{}} v_{1}(\alpha) = \frac{1}{4} \left[ (1-\alpha) - \sqrt{(1-\alpha)^{2} + 4 \alpha^{2}} \right] \\ v_{2} (\alpha, \xi) = \frac{1}{4} \left[ \alpha - \sqrt{\alpha^{2} + 4 \xi^{18} (1- \alpha)^{2}} \right] . \end{array} $$

(35)

Negativity for these states can be written as:

$$ N_{\alpha} = 2 \left[ \max (0, - v_{1}(\alpha) ) + \max (0, - v_{2}(\alpha)) \right] . $$

(36)

It is obvious that v₁(α) does not depend on decay parameter and this value is negative for any α > 0. The other eigenvalue v₂(α,ξ) is also negative for any α > 0 at the start (Γt = 0); however, as decoherence is turned on, this value quickly becomes positive. So, we can see very clearly that all states with 0 < α < 1 must exhibit freezing dynamics of entanglement.

Figure 3 shows negativity plotted against decay parameter Γt for various choices of parameter α. It is clear that all initial amounts of entanglement are determined by choice of α decay as evident from v₂(α) until it becomes 0, and hence, the residual entanglement in decoherence-free subspace becomes dominant as dictated by v₁(α). Hence, this family of states exhibits freezing dynamics of entanglement such that quantum states change with time but their entanglement is locked in time (stationary). It is interesting to note that for qubit-qutrit systems, time-invariant entanglement and freezing dynamics exist. We have not found this coincidence in any other dimension of Hilbert space so far.

Fig. 3

Negativity for an initial state ρ_α(t) is plotted against decay parameter Γt for various values of parameter α. It can be seen that initial entanglement decays to a specific value (depending on α) and then although quantum states keep changing with time, entanglement becomes stationary, hence exhibiting the so-called freezing dynamics of entanglement. See text for explanations

It is straightforward to calculate local quantum uncertainty for ρ_α which is given as:

$$ LQ_{\alpha} = 1 - \frac{1}{2} \sqrt{\alpha (1-\alpha)} . $$

(37)

This value is symmetric about α = 0.5 as expected because all correlations must be symmetric about this value. For time-evolved state, local quantum uncertainty is given as:

$$ LQ_{\alpha}(t) = 1 - \lambda_{\alpha}(t) , $$

(38)

where $\lambda _{\alpha }(t) = {\max \limits } [w_{11}(t), w_{33}(t)]$, and

$$ \begin{array}{@{}rcl@{}} w_{11}(t) &=& w_{22}(t)\\ &=& \frac{\sqrt{\alpha} \left[ \sqrt{(1 - \alpha)(1 - \xi^{9})} + \sqrt{(1 - \alpha)(1 + \xi^{9})} \right]}{2 \sqrt{2}} , \end{array} $$

(39)

and

$$ w_{33}(t) = (1-\alpha) \sqrt{1 - \xi^{18}} , $$

(40)

where w_ii(t) are the eigenvalues of the symmetric 3 × 3 matrix.

In Fig. 4, we plot the local quantum uncertainty against decay parameter Γt for the same values of parameter α as in Fig. 3. As can be seen just like entanglement freezing, the local quantum uncertainty initially decays to some value and then also tends to freezing dynamics of local uncertainty. At ${\Gamma } t = \infty$, the stationary value of local quantum uncertainty is given as:

$$ LQ_{\alpha} (\infty) = 1 - \max \left[ (1-\alpha), \sqrt{\alpha (1-\alpha)/2} \right] , $$

(41)

which is obviously a nonzero value.

Fig. 4

Local quantum uncertainty is plotted against parameter Γt for different values of parameter α. It can be seen that the first LQ_α decays but then tends to become stationary

4.3 A Review on Time-Invariant Entanglement for Qubit-Qutrit Systems

As we have noticed in all earlier reports of time-invariant entanglement, the quantum state exhibiting this interesting phenomenon must be a mixture of two entangled states and one of the state must reside in decoherence-free subspace. However, we have seen above that if we mix state |ψ₃〉 and |ψ₂〉, we do not observe any time-invariant entanglement but rather freezing dynamics of entanglement. So, this suggests that we must look for some other entangled state to be mixed with |ψ₃〉. One of such state is:

$$ |\psi_{1} \rangle = \frac{1}{\sqrt{2}} (|0 0\rangle + |1 2 \rangle) . $$

(42)

Actually, the first report of time-invariant entanglement for qubit-qutrit systems [47] took a state which was a mixture of these two types of states. To generalize this observation for more general states, first let us consider the states:

$$ \tilde{\rho}_{\alpha} = \alpha |\psi_{1} \rangle\langle \psi_{1}| + \frac{1 - \alpha}{6} \mathbb{I}_{6} , $$

(43)

where $\mathbb {I}_{6}$ is 6 × 6 identity matrix and 0 ≤ α ≤ 1. Such states are called isotropic states and they are NPT for 1/4 < α ≤ 1, and hence entangled. To avoid confusion, we differentiate these states by taking a tilde over ρ_α. This could have been avoided by calling the single parameter by a name other than α; however, we preferred to keep it like that. We can now define two-parameter family of states, which are a mixture of isotropic states and |ψ₃〉, given as:

$$ \rho_{\alpha,\beta} = \beta |\psi_{3}\rangle \langle \psi_{3} | + (1 - \beta) \tilde{\rho}_{\alpha} , $$

(44)

where 0 ≤ β ≤ 1. Entanglement properties for this family of states are quite interesting. The partial transpose with respect to subsystem A has a maximum of two possible negative eigenvalues and the rest of 4 eigenvalues are definitely positive for the given range of parameters α and β. The 2 possible negative eigenvalues are such that when one is positive, the other is negative, and vice versa. They are never negative at the same time. The time evolution of these states can be written as:

$$ \rho_{\alpha,\beta}(t) = \beta |\psi_{3}\rangle \langle \psi_{3} | + (1 - \beta) \tilde{\rho}_{\alpha}(t) . $$

(45)

Hence, $\tilde {\rho }_{\alpha }(t)$ decays, whereas |ψ₃〉 remains dynamically invariant as it lives in DFS. Now, there is an additional parameter Γt involved in the density matrix. The two possible negative eigenvalues of partially transposed matrix are given as:

$$ \begin{array}{@{}rcl@{}} x_{1} &=& \frac{1}{6} \left[ 1 + 2 \alpha (1-\beta) - 4 \beta \right] \\ x_{2} &=& \frac{1}{6} \left[ 1 + 2 \beta - \alpha (1-\beta)(1 + 3 \xi^{16} ) \right] . \end{array} $$

(46)

As we have mentioned earlier, these two eigenvalues can not be negative at the same time. We also observe that one of the eigenvalue x₁ does not depend upon ξ, so if this eigenvalue is negative, then as the other cannot be negative, this necessarily means time-invariant entanglement. On the other hand, if x₁ is positive then x₂ must be negative. However, x₂ depends on ξ and it is not difficult to see that x₂ can become positive in a finite time, leading to finite time end of entanglement. As long as β > 1/2, x₂ is positive for all ranges of α; hence, we can get time-invariant entanglement, whereas for other values we would get sudden death of entanglement. Negativity for these states is given as:

$$ N_{\alpha , \beta} = 2 \left[ \max \left( 0, - x_{1}(\alpha,\beta) \right) + \max \left( 0, - x_{2}(\alpha , \beta, \xi) \right) \right] . $$

(47)

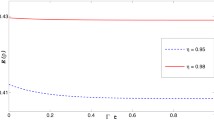
In Fig. 5, we plot negativity against parameter Γt for four different sets of values of α and β. We see that for β > 1/2, that is, for α = 0.4, β = 0.7 (red thick dashed line) and α = 0.5, β = 0.8 (blue thick dashed line), we get time-invariant entanglement on the one hand and for the other range, α = 0.9, β = 0.2 (solid line), and α = 0.8, β = 0.3 (thin dashed line), we see end of negativity at finite times.

Fig. 5

Negativity is plotted against parameter Γt for different sets of α and β. We observe time-invariant entanglement as well as finite time end of entanglement depending on the range of these two parameters

We have also calculated local quantum uncertainty for ρ_α,β(t). Following the procedure mentioned in the previous section, we get a diagonal matrix and hence the eigenvalues of the resulting 3 × 3 matrix. It is simple to pick the maximum eigenvalue for a given set of parameters. In Fig. 6, we plot LQ_α,β against parameter Γt for the same set of values for α and β as in Fig. 5. We observe quite interesting dynamics for local quantum uncertainty compared with earlier cases. First, we see that for two instances where we get time-invariant entanglement, the local quantum uncertainty first increases and then tends to freeze to a specific positive value. Intuitively, one can understand the freezing behavior of local quantum uncertainty as due to stationary correlations (not decaying due to decoherence subspace) in state |ψ₃〉. However, it is not intuitive why these correlations first increase before becoming stationary. For the other two instances, where we get sudden death of entanglement, that is, for (α = 0.8,β = 0.3) (thin dashed line), local quantum uncertainty first decays for a short time and then once again increases and then tends to freeze to a constant value. Whereas for (α = 0.9,β = 0.2) (solid line), local quantum uncertainty first decreases for a short time, then increases to a value and then once again decays to another value and then finally exhibits freezing dynamics. As we mentioned, the freezing part of correlations can be explained easily whereas other parts of dynamics are counterintuitive.

Fig. 6

Local quantum uncertainty is plotted against parameter Γt for four sets of values of α and β. It can be seen that in all cases, local quantum uncertainty tends to become stationary after exhibiting interesting dynamics at the start

4.4 Comparison with Dynamics of Random States

In order to compare the dynamics of quantum states with generic states, we have generated 100 random pure states. A state vector for qubit-qutrit systems, randomly distributed according to the Haar measure, can be generated in the following way [85]: First, we generate a vector such that both the real and the imaginary parts of the vector elements are Gaussian-distributed random numbers with a zero mean and unit variance. Second, we normalize the vector. It is easy to prove that the random vectors obtained this way are equally distributed on the unit sphere [85]. Note the random pure states, which we generate in the global Hilbert space of dimension 6, so the unit sphere is not the Bloch ball.

After generation of 100 random pure states, we find their time-evolved density matrices interacting with collective dephasing and compute negativity using PPT-mixture package [79,80,81], for each state against parameter Γt. From this data, we can also obtain an error estimate to indicate the reliability of the measure. This can, for instance, be defined as a confidence interval [28]:

$$ \begin{array}{@{}rcl@{}} CI = \mu \pm \sqrt{\delta} , \end{array} $$

(48)

where μ stands for mean value and δ for variance of quantity being measured. Note, however, that this is not a confidence interval in the mathematical sense.

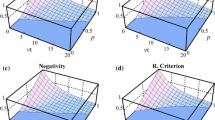
In Fig. 7, we plot entanglement monotone (negativity) E(ρ) for random pure states against parameter Γt. The thick dashed (blue) line presents the mean value of entanglement, whereas thick dashed-dotted (red) lines represent confidence interval CI with the top line as sum of mean value and variance, whereas below the thick dashed-dotted line are difference of mean value and variance. As we can see, many states tend to exhibit freezing dynamics of entanglement (about 50%), whereas many exhibit sudden death of entanglement (about 50%).

Fig. 7

Entanglement monotone (negativity) is plotted against parameter Γt for 100 initial random pure states. It can be seen that around half of states remain NPT and approach a fixed (freezing) value of entanglement after a sufficiently long time

Finally, we analyze the asymptotic states by taking ξ = 0 in time-evolved density matrices for random states. We then compute entanglement monotone (negativity) for these states and as mentioned earlier about 50% of them are found to be entangled. In Fig. 8, we show the bar graph for random states at infinity against number of random states. It is obvious that all entangled states will be having nonzero local quantum uncertainty as well.

Fig. 8

Entanglement monotone (negativity) is shown against number n for 100 initial random pure states. It can be seen that around half of all states remain NPT

5 Conclusions

We have studied the dynamics of quantum correlations of qubit-qutrit systems under Markovian collective dephasing. We have investigated some aspects of this simple system not studied before. In particular, we have studied two non-trivial features of entanglement dynamics, namely, time-invariant entanglement and freezing dynamics of entanglement. All previous studies on these two features of entanglement dynamics for bipartite as well as for multipartite quantum systems gave the impression that we could not have both features available for one specific quantum system under collective dephasing. The reason for this impression was the observation that for qubit-qubit systems we detected time-invariant entanglement whereas we did not find any freezing dynamics of entanglement under the same collective dephasing model [49]. We did find freezing dynamics for qubit-qubit systems however for more general directions of magnetic fields [50] instead of specific z-direction where we have only the time-invariant feature available. For three qubits, we found evidence for freezing dynamics of genuine entanglement whereas we found no evidence for time-invariant entanglement [53]. On the other hand, for four qubits, we found no evidence for freezing dynamics of entanglement but we do found time-invariant entanglement [53]. More recently, we examined qutrit-qutrit quantum systems where we found freezing dynamics of entanglement but no time-invariant entanglement [54]. There is no concrete mathematical arguments for mutual exclusiveness of these features for any specific Hilbert space. Contrary to earlier impression, for qubit-qutrit quantum systems, we found time-invariant entanglement as well as freezing dynamics entanglement. The future investigations might shed more light on relationship between these possibilities and dimensions of subsystems if there is any such relationship. In addition, we have studied dynamics of quantum discord for a specific family of quantum states and local quantum uncertainty for several families of states. We have seen that for some states quantum discord and local quantum uncertainty decay asymptotically and become zero only at infinity. For these states, only classical correlations remain constant and do not decay. For other states which exhibit freezing dynamics of entanglement, local quantum uncertainty also tends to exhibit freezing dynamics. For quantum states which exhibit time-invariant entanglement, local quantum uncertainty first increases to a specific value and then becomes stationary at nonzero values. For the same states which exhibit sudden death of entanglement, local quantum uncertainty first decays for a short time, then increases for some time and finally reaches a nonzero stationary value. Finally, we have compared the dynamics of specific states with generic states by generating random pure states. We have seen that most random pure states under collective dephasing exhibit freezing dynamics of entanglement and maintain this nonzero value even at infinity. Some random pure states do become separable at finite time. Another future avenue would be to explore more general d ⊗ N quantum systems for d≠N to find more examples.