1 Introduction

About three decades ago, Paul Benioff [1, 2] and Richard Feynman [3, 4] envisaged a computer whose basic constituents could be in a complex quantum superposition state. In the last few years, we have been witnessing astonishing theoretical and experimental developments in quantum computing and quantum simulation [5–7], and also in others sub-areas of quantum information science [8–11], with experimental implementations already going beyond the best present classical capabilities [12]. These are the first sights of what will turn out to be a revolution in our science and technology [13, 14].

Nevertheless, before that can in fact become a reality, we still have much to understand concerning quantum systems with many degrees of freedom. One important tool for accomplishing this task is the generation and analysis of RQS [15–31], which will have an analogous role to that that random numbers have in classical stochastic theories [32–35]. The parametrization of quantum states [15, 36, 37] is the initial step towards generating them numerically and is one of the main topics of this survey, which is organized in the following manner. In Section 2, we consider the generation of random pure states, for which the availability of unbiased random discrete probability distributions is indispensable and is hence also recapitulated. The remainder of the article is dedicated to the creation of general random density matrices. In Section 3, the standard method is described together with the Hurwitz parametrization for unitary matrices, which used in its implementation. Subsequently, in Section 4, the Bloch vector parametrization, though impractical for random quantum states (RQS) generation, is regarded for completeness. The last part of the article, the Section 5, is dedicated to present and investigate some issues regarding the overparametrized and related methods. In Section 5.1, we discuss unwanted physical consequences of the ranges usually used in the literature for the real and imaginary parts of the elements of the general complex matrices involved in this method and present a simple solution for the problem. In Section 5.2, we report an important possible drawback of the OPM regarding its use for random sampling in the quantum state space: its too fast concentration of measure. We discuss the Ginibre and Bures methods in Section 5.3. A brief summary of the article is presented in Section 6.

2 Pure States

When there is no classical uncertainty about the state of a quantum system, it is represented by a vector in a Hilbert space \(\mathcal {H}\). For discrete systems, \(\mathcal {H}\) is simply \(\mathbb {C}_{d}\) with the inner product between any two of its vectors defined as \(\langle \psi | \phi \rangle :=| \psi \rangle ^{\dagger } |\phi \rangle ={\sum }_{j=1}^{d}\psi _{j}^{*}\phi _{j}\), where z ∗ is the complex conjugate of z and d is the system dimension. Here, we use the standard notation of Dirac for vectors and, for a generic matrix A, we denote A † as its adjoint (conjugate transpose). Any state \(|\psi \rangle \in \mathcal {H}\) can be written as a linear combination of the vectors of any basis. One base of special interest is the computational or standard basis: |c 1〉 = [10 ⋯ 0]T, |c 2〉 = [01 ⋯ 0]T, ⋯ , |c d 〉 = [00 ⋯ 1]T, in terms of which

$$ |\psi\rangle =\textstyle{{\sum}_{j=1}^{d}}\psi_{j}|c_{j}\rangle, $$
(1)

with ψ j = 〈c j |ψ〉. Above, X T denotes the transpose of the matrix X.

The Born’s probabilistic interpretation of the state vector |ψ〉 requires its normalization:

$$ ||\vec{\psi}||:=\sqrt{\langle\psi | \psi\rangle}=\sqrt{\textstyle{{\sum}_{j=1}^{d}}|\psi_{j}|^{2}}=1. $$
(2)

Thus, as the numbers |ψ j |2 are non-negative and sum up to one, they form a probability distribution p j := |ψ j |2. Using ψ j = |ψ j |exp(i θ j ) one can write

$$ |\psi\rangle = \textstyle{{\sum}_{j=1}^{d}} \sqrt{p_{j}}\exp(i\theta_{j})|c_{j}\rangle, $$
(3)

with the phases θ j ∈ [0, 2π].

Now, we recall that if we have access to a random number generator yielding random numbers with uniform distribution in [0,1], an unbiased random discrete probability distribution (RDPD) [37, 38] can be generated as follows [39]. First, we create a biased RDPD generating q 1 in the interval [0, 1] and q j in \([0,1-{\sum }_{k=1}^{j-1}p_{k}]\) for j = 2, ⋯ , d. Then we use a random permutation of {1, ⋯ , d}, let us call it {k 1, ⋯ , k d }, and define the unbiased RDPD as

$$ \{p_{1},\cdots,p_{d}\}:=\{q_{k_{1}},\cdots,q_{k_{d}}\}. $$
(4)

The unbiased RDPD generated in this way and d independent random phases θ j are then applied to generate a random pure state. It is worth observing that there will be no privileged direction in \(\mathcal {H}\) only because the RDPD is unbiased. This pure state generation procedure gives |ψ〉 distributed with a Haar measure. Another manner of obtaining samples with similar properties is by using the rows or columns of random unitary matrices, which we shall discuss in the next section.

3 Standard Method

The states of a d−level quantum system are described, in the most general scenario, by a density matrix ρ [40, 41], which is a Hermitian positive semidefinite matrix (notation: ρ ≥ 0) with unit trace (Tr(ρ) = 1). Any such matrix can be written in the form of a spectral decomposition:

$$ \rho={\textstyle {\sum}_{j=1}^{d}}r_{j}|r_{j}\rangle\langle r_{j}|, $$
(5)

with the real eigenvalues of ρ being nonnegative (r j ≥ 0 for all j = 1, ⋯ , d) and summing up to one (\({\sum }_{j=1}^{d}r_{j}=1\)). That is to say, \(\{r_{j}\}_{j=1}^{d}\) is a probability distribution [32, 35]. The eigenvectors of ρ, \(\{|r_{j}\rangle \}_{j=1}^{d}\), form an orthonormal basis for the vector space \(\mathbb {C}^{d}\), i.e., 〈r j |r k 〉 = δ j k and \({\sum }_{j=1}^{d}|r_{j}\rangle \langle r_{j}|=\mathbb {I}_{d}\), where \(\mathbb {I}_{d}\) is the dxd identity matrix.

Let us briefly look over the number of real parameters needed for a complete description of an arbitrary density matrix. In order to describe the probability distribution \(\{r_{j}\}_{j=1}^{d}\), the eigenvalues of ρ, we need d−1 real numbers. Besides, as any two bases for the vector space \(\mathbb {C}^{d}\) are connected by an unitary matrix U (i.e., \(UU^{\dagger }=\mathbb {I}_{d}\)), one can write

$$ |r_{j}\rangle=U|c_{j}\rangle, $$
(6)

for j = 1, ⋯ , d, with \(\{|c_{j}\rangle \}_{j=1}^{d}\) being the computational basis, as shown in Section 2. Therefore, the bases \(\{|r_{j}\rangle \}_{j=1}^{d}\) is completely determined by U. Once d 2−d real parameters are sufficient to specify completely an arbitrary unitary matrix U with dimensions dxd [36], it follows that d 2 − 1 independent real parameters are sufficient for a thorough description of any density matrix.

From the last two paragraphs, we see that the numerical generation of a RQS (using the density matrix as written in (5)) can be cast in terms of the creation of a RDPD and of a random unitary matrix (RU) [36, 42–44]. We call it the standard method because it would be a natural first choice giving the defining properties of a density matrix. Moreover, it utilizes as few real parameters as possible. This is a nice characteristic in the view that for doing some statistics with RQS, one in general needs to generate many of them, what can be a very time-consuming task for large values of the system dimension d.

From the several possibilities available [36], in this article, we choose the Hurwitz parametrization for generating RUs [43]. In this parametrization, one writes any dxd unitary matrix U in terms of unitaries

$$ U^{(i,j)}(\phi_{ij},\psi_{ij},\chi_{ij}) $$
(7)

in bi-dimensional sub-spaces. The non-null elements of such elementary transformations are:

$$\begin{array}{@{}rcl@{}} & & U_{k,k}^{(i,j)}=1\text{ for}~ k=1,\cdots,d\text{ and}~ k\ne i,j\text{;} \\ & & U_{i,i}^{(i,j)}=\cos(\phi_{ij})\exp(i\psi_{ij})\text{;}~ U_{i,j}^{(i,j)}=\sin(\phi_{ij})\exp(i\chi_{ij})\text{;} \\ & & U_{j,i}^{(i,j)}=-(U_{i,j}^{(i,j)})^{*}\text{;}~ U_{j,j}^{(i,j)}=\cos(\phi_{ij})\exp(-i\psi_{ij}). \end{array} $$
(8)

A general unitary transformation, for a d-level quantum system, can then be written as

$$ U=\exp(i\alpha)U_{1}U_{2}U_{3}{\cdots} U_{d-1}, $$
(9)

with the sub-matrices being

$$\begin{array}{@{}rcl@{}} & & U_{1}=U^{(1,2)}(\phi_{12},\psi_{12},\chi_{12}), \\ & & U_{2}=U^{(2,3)}(\phi_{23},\psi_{23},0)U^{(1,3)}(\phi_{13},\psi_{13},\chi_{13}), \\ & & U_{3}=U^{(3,4)}(\phi_{34},\psi_{34},0)U^{(2,4)}(\phi_{24},\psi_{24},0) \\ && \hspace{1.0cm} U^{(1,4)}(\phi_{14},\psi_{14},\chi_{14}), \\ & & {\vdots} \\ & & U_{d-1}=U^{(d-1,d)}(\phi_{d-1,d},\psi_{d-1,d},0) \\ && \hspace{1.2cm} U^{(d-2,d)}(\phi_{d-2,d},\psi_{d-2,d},0){\cdots} \\ && \hspace{1.2cm} U^{(1,d)}(\phi_{1,d},\psi_{1,d},\chi_{1,d}). \end{array} $$
(10)

The random numbers appearing in the last equations are distributed uniformly in the following ranges of values:

$$\begin{array}{@{}rcl@{}} & & 0\le\alpha<2\pi\text{;}~~ 0\le\psi_{ij}<2\pi\text{;}~~ 0\le\chi_{ij}<2\pi\text{;}\\ & & \phi_{ij}=\arcsin(\xi_{ij}^{1/2i})\text{,}~~ 0\le\xi_{ij}<1\text{,}~~ i=1,2,\cdots,d-1 . \end{array} $$
(11)

It is worthwhile mentioning that, although not advantageous, it is possible to use the rows or columns of such a random unitary matrix as random state vector.

4 Bloch Vector Parametrization Method

The Hermitian-traceless-orthonormal generators of the special unitary group S U(d), Γ j (j = 1, ⋯ , d 2 − 1), and \(\mathbb {I}_{d}\) can be used as a basis in terms of which we can write any dxd density matrix in the so called Bloch vector parametrization [36]:

$$ \rho = \sum\limits_{j=0}^{d^{2}-1} \gamma_{j}{\Gamma}_{j}, $$
(12)

where \(\vec {\gamma }=(\gamma _{1},\cdots ,\gamma _{d^{2}-1})\) is the Bloch’s vector. One can use Tr(ρ) = 1 to see that γ 0 = 1/d and Tr(Γ j Γ k ) = 2δ j k to show that the coefficients in (12) are half of the mean values of the aforementioned generators of S U(d), i.e., \(\gamma _{j}=2^{-1}\langle {\Gamma }_{j} \rangle \in \mathbb {R}\).

For producing random quantum states using the Bloch vector parametrization, d 2 − 1 real random numbers γ j must be generated. The main difficultly here is that for d ≥ 3, there is no known explicit determination of the range of values for the parameters γ j that will lead to a physical state. Thus, given a basis for S U(d), we may use the spectrum of each Γ j to determine the range from which we shall sample the corresponding γ j . In the context of RQS generation, one attractive choice for the generators of S U(d) are the generalized Gell Mann matrices:

$$\begin{array}{@{}rcl@{}} && |c_{j}\rangle\langle c_{k}| + |c_{k}\rangle\langle c_{j}| \text{ for } 1\leq j < k \leq d, \end{array} $$
(13)
$$\begin{array}{@{}rcl@{}} && -i | c_{j} \rangle\langle c_{k}| +i | c_{k} \rangle\langle c_{j} | \text{ for } 1\leq j < k \leq d, \end{array} $$
(14)
$$\begin{array}{@{}rcl@{}} && \frac{ \textstyle {\sum}_{j=1}^{l}|c_{j}\rangle\langle c_{j}| -l | c_{l+1}\rangle\langle c_{l+1} |} {\sqrt{l(l+1)/2}} \text{ for } 1\leq l \leq d-1. \end{array} $$
(15)

A simple analysis shows that for the generators in (13) and (14) we have γ j ∈ [−1/2, 1/2] while for those in (15) \(\gamma _{j}\in [-\sqrt {l/(2(l+1))},1/\sqrt {2l(l+1)}]\).

Although the condition Tr(ρ) = 1 is promptly satisfied, after generating the entire Bloch’s vector, we must yet do a positivity test. This task requires much computational time, what makes this method impractical for the task under scrutiny here.

5 Overparametrized Method

The basic motivational idea for this method comes from the simple observation that, for any complex matrix A = (A j k ), we have: 〈ψ|A † A|ψ〉 = ||A|ψ〉||2 = |||ϕ〉||2 ≥ 0, where |ψ〉 is any vector of \(\mathbb {C}^{d}\) and \(|||\phi \rangle || := \sqrt {\langle \phi |\phi \rangle }\) is the Euclidean norm of the vector \(|\phi \rangle \in \mathbb {C}^{d}\). That is to say, for a general complex matrix A, the matrix A † A is guaranteed to be positive semidefinite (A † A ≥ 0). Thus, if A is normalized, i.e., if we define

$$ \mathcal{A} := \frac{A}{||A||_{2}}, $$
(16)

it is possible to write a valid density operator as:

$$ \rho=\mathcal{A}^{\dagger}\mathcal{A}. $$
(17)

Above \(||A||_{2} := \sqrt {\langle A|A\rangle }\) is the Hilbert-Schmidt norm of A, with 〈A|B〉 := Tr(A † B) being the Hilbert-Schmidt inner product between the matrices A and B [41].

The simple formula for ρ in (17) has found applications in quantum information science [15, 23, 37, 45, 46]. Once the complete description of a general complex dxd matrix A requires 2d 2 real parameters, one notes that this parametrization, despite being simple and friendly for numerical implementations, uses more real numbers than necessary, as discussed above. Thus, it is dubbed as the overparametrized method. The numerical generation of RQS via this method is further explained in the next sub-section.

5.1 An Issue on the Domains of Re(A j k ) and Im(A j k )

Let us start our analysis of the production of RQS via the overparametrized method by considering the simplest quantum system, a two-level system also known as quantum bit, or qubit for short. The advantage of using this system as our starting point is that it can be visualized straightforwardly in the \(\mathbb {R}^{3}\). For that purpose, we simply need to write a density operator ρ using the 2x2 identity matrix \(\mathbb {I}_{2}\) and the Pauli matrices σ j (j = 1, 2, 3) as a basis (the case d = 2 in the Bloch method):

$$ \rho=2^{-1}\mathbb{I}_{2}+{\textstyle {\sum}_{j=1}^{3}}2^{-1}x_{j}\sigma_{j}, $$
(18)

where x j = Tr(ρ σ j ) is the value of the component of the system’s “polarization” in the direction j = 1, 2, 3 ≡ x, y, z. The real numbers (x 1, x 2, x 3) ≡ (x, y, z) are used as the Cartesian coordinates in \(\mathbb {R}^{3}\). Enforcing the ρ in (18) to be a density matrix leads to the following restrictions [40]: −1 ≤ x j ≤ 1 and \({\sum }_{j=1}^{3}{x_{j}^{2}}\le 1\). Therefore, the points (x 1, x 2, x 3) must lie within a ball with radius equal to one and centered at (0, 0, 0), known as the Bloch’s ball (BB).

There are several functions one may be interested in when working in quantum information science. Some relevant examples are quantifiers for total correlation [47], quantum entanglement [48], quantum discord [49], quantum coherence [50, 51], and quantum channel capacities [52]. All of these quantities can, in general, be defined using distance measures in the quantum state space. For our purposes in this article, the Hilbert-Schmidt distance (HSD) fits well. The HSD between two density matrices ρ and ζ is defined as the Hilbert-Schmidt norm of their subtraction [40, 41]:

$$ d_{hs}(\rho,\zeta) := ||\rho-\zeta||_{2}. $$
(19)

If λ j are the real eigenvalues of the Hermitian matrix ρ − ζ, then

$$ d_{hs}(\rho,\zeta) = \sqrt{\text{Tr}\left( (\rho-\zeta)^{\dagger}(\rho-\zeta)\right)}=\sqrt{{\textstyle {\sum}_{j=1}^{d}}{\lambda_{j}^{2}}}. $$
(20)

For the calculations involved in this article, the so called Mersenne Twister method [53] is used as the pseudo-random number generator (pRNG) and the LAPACK subroutines [54] are utilized for computing eigenvalues. With these tools at hand, when the standard method described in Section 3 is applied for generating one-qubit pseudo-random quantum states, the distribution of such states in the Bloch’s ball and the histogram for the probability of the possible values of HSD are those shown in the upper green panel of Fig. 1. It is worth mentioning that the higher density of states observed closer to the center of this figure can be understood by noticing that the direction in \(\mathbb {R}^{3}\) defined by U is random and that r 1 and r 2 = 1 − r 1 are uniformly distributed in the interval [0, 1].

Fig. 1
figure 1

On the left is presented the distribution in the Bloch’s ball of 2000 pseudo-random one-qubit states generated using standard method (upper green panel) and using the overparametrized method with the ranges for the matrices elements as utilized in Refs. [15, 37], i.e., \(A_{jk}^{r}\text {,} A_{jk}^{i}\in [0,1]\) (gray panel in the middle) and with \(A_{jk}^{r}\text {,} A_{jk}^{i}\in [-1,1]\) (pink panel at the bottom). One the right-hand side is shown the probability distribution for the Hilbert-Schmidt distance of one million pseudo-random quantum states generated using the corresponding method (see the text for more details)

Full size image

Let us consider the same kind of computation, but applying now the overparametrized method for generating the pseudo-RQS. For that purpose, the pRNG can be utilized for the sake of obtaining pseudo-random numbers for generating the real,

$$ \text{Re}(A_{jk}) =: A_{jk}^{r}, $$
(21)

and imaginary,

$$ \text{Im}(A_{jk}) =: A_{jk}^{i}, $$
(22)

parts of the matrix elements of A = (A j k ). The first issue we want to deal with here is with regard to the domains that one may use for those numbers. For instance, we can follow Refs. [15, 37, 55] and generate the matrix elements A j k using uniformly distributed random numbers and setting

$$ A_{jk}^{r}\text{,} A_{jk}^{i}\in[0,1]. $$
(23)

As shown at the right hand side of the gray panel at the middle of Fig. 1, the probability distribution for the HSD obtained in this way is, to some extent, qualitatively similar to that obtained using the standard method. This may lead to the impression that our choice for the domain of the matrix elements is fine. However, a rapid inspection of the distribution of states in the Bloch’s ball obtained using the OPM with \(A_{jk}^{r}\text {,} A_{jk}^{i}\in [0,1]\) reveals a misfortune. Even though the polarization in the y and z directions have approximately equal chance to be positive or negative, only positive values for the polarization in the x direction are generated. There is no need to say that such a restriction over the possible values of physical observables of the system is not a desirable feature for a method supposed to generate random quantum states.

We notice that a simple solution for this problem is generating the matrix elements A j k with

$$ A_{jk}^{r}\text{,} A_{jk}^{i}\in[-1,1]. $$
(24)

With this change, for this case, the distribution of states in the BB becomes even more uniform than that that we get using the standard method, as shown in the pink panel at the bottom of Fig. 1. We want to emphasize already at this point that increasing the range of values for \(A_{jk}^{r}\) and \(A_{jk}^{i}\) does not causes any significant modification neither of these results nor of those that shall be reported in the next sub-section.

5.2 A Too Fast Concentration of Measure for the OPM

In the previous sub-section, we showed that the application of the overparametrized method with the real and imaginary parts of A j k drawn randomly and uniformly from the interval [−1, 1] yields an uniform distribution of one-qubit pseudo-random density matrices. This encouraging result leads naturally to the question of if such a scheme can be applied appropriately for random sampling in high-dimensional quantum systems. In this section, we investigate this question and present strong evidences for answering it in the negative.

It is known for some time now that in high dimensional spaces, random variables tend to concentrate around their mean values [56]. In the last few years, this phenomenon of concentration of measure, that is formalized in Levy’s Lemma, has gained great importance and utility in quantum information science (see for instance Ref. [57] and the references therein).

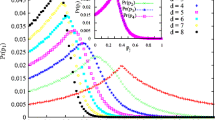
Notwithstanding, as shown in the gray panel on the right hand side of Fig. 2, the OPM leads to a too fast concentration of measure for the Hilbert-Schmidt distance in the quantum state space as the system’s dimension d increases. We note that such a concentration of measure is much more slow in our benchmarking method: the standard method with the Hurwitz’s parametrization for unitary matrices. It is worth observing that, in part, the shift in the probability distribution for the HSD observed with the standard method (green panel on the left hand side of Fig. 2) can be understood as being due to the fact that as d increases, the same number of points will be spread in a “bigger” space, diminishing thus the chance for closer pairs of configurations to be generated.

Fig. 2
figure 2

Probability distribution for the different possible values of the Hilbert-Schmidt distance for one million pairs of quantum states generated using the standard method (green panel on the left) or generated via the overparametrized method with \(A_{jk}^{r}\text {,} A_{jk}^{i}\in [-1,1]\) (gray panel on the right). We see that, in contrast to what happens in the standard method, there is a too fast concentration of measure in the OPM as the system’s dimension d increases. We observe that although only some values of d are shown in this figure (1, 2, 3, and 4 qubits), the mentioned effect is smooth and gradual

Full size image

It is important mentioning that if instead of generating A as described above, we draw it from the Ginibre ensemble [58, 59], i.e., if we produce \(A_{jk}^{r}\) and \(A_{jk}^{i}\) using random numbers normally distributed (and with average equal to zero and variance equal to one), very similar results are obtained, as is shown in Table 1. Thus the effect seems to be a characteristic trait of the overparametrized method, being independent on how it is applied.

Table 1 Mean value (〈d h s 〉) and standard deviation (Δd h s ) of the Hilbert-Schmidt distance for one million pairs of d-dimensional quantum states randomly generated using the overparametrized method with uniformly or normally distributed random numbers or generated using the standard method
Full size table

We also see in Table 1 that, even though the concentration of measure is ubiquitous, while the width of the probability distribution for the HSD obtained via the OPM applied to four qubits is less than 6 % of that obtained in the one-qubit case, for the standard method the corresponding percentage is almost 74 %. We notice another bold difference between the two methods: as d increases, they shift 〈d h s 〉, the “typical” value of the HSD, in opposite directions (see also Fig. 2).

5.3 Ginibre and Bures Methods

For completeness, in this sub-section, we briefly describe two other methods for RQS generation whose starting point is also the sampling of matrices from the Ginibre ensemble. Let us begin with a generalization of the OPM, that will be named here as the Ginibre method. If the d′xd Ginibre matrix A is a square matrix as the ones considered in Section 5.2, i.e., if d′ = d, the RQS are generated with a Hilbert-Schmidt measure. On the other hand, in the general case where the number of lines and columns of A need not to coincide, the RQS are said to be generated with an induced measure [58]. Using the Ginibre method to generate a sample with one million pairs of states for each pair (d′, d), we show in Fig. 3 the dependence with d′ of the average and standard deviation of the Hilbert-Schmidt distance for some values of d. We see a strong dependence of both quantities with d′. This raises an additional practical question about this method. Which value of the Ginibre matrix left dimension d′ should be used and how to justify the choice?

Fig. 3
figure 3

Average of the Hilbert-Schmidt distance, 〈d h s 〉, and the associated standard deviation, Δd h s , as a function of the Ginibre matrix left dimension \(d^{\prime }\) for some values of its right dimension d. A sample with one million pairs of dxd density matrices was created using the Ginibre method for each pair \((d^{\prime },d)\). We see that both 〈d h s 〉 and Δd h s decrease with \(d^{\prime }\) for a specified value of d

Full size image

Now we describe the other method, which shall be dubbed as the Bures’ method because it leads to RQS with a Bures measure. This is accomplished by defining [60]

$$ \rho=\frac{(\mathbb{I}_{d}+U)AA^{\dagger}(\mathbb{I}_{d}+U^{\dagger})}{\text{Tr}((\mathbb{I}_{d}+U)AA^{\dagger}(\mathbb{I}_{d}+U^{\dagger}))}, $$
(25)

with A being a dxd Ginibre matrix and U is dxd a random unitary matrix. It is note worthy that 3d 2−d real parameters are necessary to create a RQS via this method. For one million pairs of states generated in this way, we show in Fig. 4 the center and width of the probability distribution for the Hilbert-Schmidt distance as a function of the system dimension d. A behavior similar to that observed for the overparametrized and Ginibre methods, discussed respectively in the last sub-section and in the last paragraph, is seem here. However, the rate of concentration of measure is a little less pronounced when compared with that for the OPM. For the Bures’ method, the width of the probability distribution for four qubits is approximately 8 % of that for one qubit.

Fig. 4
figure 4

Average Hilbert-Schmidt distance 〈d h s 〉 (black points) as a function of the system dimension d. A sample with one million pairs of density matrices was generated, for each value of d, using the Bures’ method. In the shadowed cyan area are shown values of the HSD standing between 〈d h s 〉−Δd h s and 〈d h s 〉+Δd h s

Full size image

6 Final Remarks

In this article, we presented a brief survey of some methods that may be used for the numerical generation of random quantum states. We gave particular emphasis to the overparametrized method, which is frequently used in quantum information science. After utilizing a qubit system to identify and solve a physically relevant problem related to the domains of the matrix elements used so far in the literature in implementations of the OPM, we considered its possible application for random sampling in high-dimensional quantum systems. In this last scenario, we showed that the overparametrized and related methods lead to a too rapid concentration of measure that may prevent any fair random sampling of quantum states, even for quantum systems with moderate dimension.