1 Introduction

Recently, wide-bandgap II–VI semiconductor compounds (ZnS, ZnO, ZnSe, ZnTe, CdS, CdSe, and CdTe) are the most significant materials for high-performance optoelectronic devices such as light-emitting diodes (LEDs) and laser diodes (LDs) operating in the blue or ultraviolet spectral range. The high ionic character of these compounds also makes them ideal candidates for high electro-optical and electromechanical coupling [1].

Among these compounds, blende-type zinc sulfide (bt-ZnS) has been focus of current researches [2–5] due to its prevalent technological applications. Besides, numerous theoretical efforts have also been devoted to clarify the structural, elastic, optical, and relevant properties of bt-ZnS during the last decade [6–14]. Chen et al. employed [8] plane-wave (PW) pseudo potential scheme of density functional theory (DFT) for phase transition and elastic constants of ZnS. In addition, Kheneta et al. [9] computed some structural, electronic, and optical properties of bt-ZnX (X = Se, S, and Te) by using full-potential linear augmented plane-wave method plus local orbitals (FP-APW + lo). As well, Rong et al. [10] applied generalized gradient approximation (GGA) of DFT to their work for investigating the pressure dependence elastic properties of bt-ZnS and wurtzite ZnS (w-ZnS). Further, Yang et al. [12] utilized local density approximation (LDA) of DFT to study the pressure dependence of elastic and dynamical properties of bt-ZnS and ZnSe.

Recent and progressive theoretical attempts on bt-ZnS [6–14] inspired us to perform this work by addressing the high-pressure structural, elastic, mechanical, and other related properties of bt-ZnS with a different method. Unlike the theoretical approaches used in literature, this work has been carried out by applying a mixed-type interatomic potential with geometry optimization calculations to elucidate the mentioned properties of bt-ZnS under pressures up to 20 GPa. The next part of the paper gives the details of our theoretical calculations with the employed interatomic potential and structure optimization in “Section II”. We also compare our results with the experimental data and other theoretical findings through the results and discussion part of the paper in “Section III”. Finally, “Section IV” summarizes the main findings of this work in the conclusions.

2 Details of Theoretical Calculations

Simple empirical potential models are the main modeling intermediaries for various materials since they can produce successful computing results. These potentials can well describe the defect energies, lattice constants, and elastic properties of oxides [15], fluorides [16], and other compounds [17, 18]. Most of these potentials are composed of Coulomb interactions, short-range pair interactions, and ionic polarization treated by the shell model of Dick and Overhauser [19]. The sum of the Coulomb terms, short-range interactions, and ionic polarization expresses the total energy for these potentials. If we assume the electron cloud of an ion is simulated by a massless shell of charge Y and the nucleus by a core of charge X, then the total charge becomes q = X + Y. In shell model, a harmonic force with spring constant K couples the core and the shell of the ion. So, for modeling the short-range pair interaction acting between the shells, we can use a typical Buckingham potential, as presented in Eq. (1):

$$ {V}_{ij}^{\mathrm{Buckingham}}=A \exp \left(-\frac{r_{ij}}{\rho}\right)-C{r}_{ij}^{-6}. $$
(1)

The first part of the Eq. (1) represents the Born–Mayer term, whereas the second part stands for Van der Waals energies. Beyond, in our work, we applied the original form of a mixed-type interatomic potential of Hamad et al. [20] for short-range interactions, which includes the Buckingham and Lennard–Jones 9–6 potentials form as in Eq. (2):

$$ {V}_{ij}^{\mathrm{short}}=A \exp \left(-\frac{r_{ij}}{\rho}\right)+B{r}_{ij}^{-9}-C{r}_{ij}^{-6}. $$
(2)

We also considered the semi-covalent nature of ZnS by using a three-body potential for S-Zn-S angel as in its original form [20] and defined by Eq. (3):

$$ {V}_{ijk}=\left(\frac{1}{2}\right){K}_{\mathrm{TB}}{\left({\theta}_{ijk}-{\theta}_0\right)}^2. $$
(3)

In Eq. (3), θ 0 and K TB indicate the equilibrium constant angle between S-Zn-S and fitting constant of Hamad et al. [20], respectively. Finally, sulfur anion polarizability treated by the shell model of ref. [19] can be written as in the Eq. (4):

$$ {V}_{ij}^{\mathrm{core}\hbox{-} \mathrm{shell}}=\left(\frac{1}{2}\right)K{r_{ij}}^2. $$
(4)

In Eq. (4), r ij accounts for the core-shell separation, and K denotes the spring constant. Although extra details of presently employed potential and its parameterization procedure can be found in ref. [20], Table 1 lists the original potential parameters of ref. [20] used in our calculations.

Table 1 Mixed-type theoretical interatomic potential used in this work. Parameters of the potential were taken from its original ref. [20]
Full size table

All theoretical calculations were carried out with the General Utility Lattice Program (GULP) 4.0.1 molecular dynamics code [21]. This useful code allows optimizing the structures at constant pressure (all internal and cell variables are included) or at constant volume (unit cell remains frozen). To avoid the constraints, constant pressure optimization was applied to the geometry of bt-ZnS cell with the Newton–Raphson method based on the Hessian matrix calculated from the second derivatives. The cell geometry of bt-ZnS was assigned as the same as with the experimental data of ref. [22] as a = b = c = 5.40 Å and α = β = γ = 90° with space group F − 43m and its corresponding experimental X-Ray diffraction pattern [22] is also given in Fig. 1.

Fig. 1
figure 1

Experimental X-Ray diffraction data [22] of presently investigated bt-ZnS crystal

Full size image

During our geometry optimization calculations, the Hessian matrix was recursively updated using the BFGS [23–26] algorithm. After setting the necessities for the geometry optimization of bt-ZnS, we devised multiple runs at zero Kelvin temperature and checked the pressure ranges between 0 and 20 GPa in the steps of 5 GPa.

3 Results and Discussion

As is well emphasized, pressure can cause a change in the volume of an examined crystal and triggers the phase transition in this crystal. In general, at a particular pressure value, II–VI compounds undergo a first-order phase transition from the stable blende-type (bt) B3 phase to B1 (rocksalt) phase at a critical phase transition pressure (P T) [7–9, 11, 14]. Figure 2 depicts the present pressure–volume (P–V) diagram of bt-ZnS for the entire pressure range. As it is clear from Fig. 2, the volume of bt-ZnS shows its first discontinuity at 17 GPa. This discontinuity in the volume of bt-ZnS at 17 GPa originates from the structural B3 → B1 the phase transition. When compared with the former results (Table 2), our P T value with 17 GPa agrees well with both earlier experimental and theoretical data.

Fig. 2
figure 2

P–V diagram of bt-ZnS up to 30 GPa

Full size image
Table 2 Comparing the previous and present results of the considered parameters of bt-ZnS
Full size table

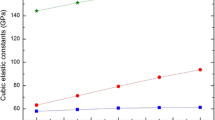
The typical cubic elastic constants namely C11, C12, and C44 describe the mechanical hardness of a material and desirable for evaluating the stability of the material. These elastic constants derived from the total energy calculations represent the single crystal elastic properties. However, Voigt–Reuss–Hill average values afford confident results for the elastic constants of polycrystal materials [23–26]. To capture correct values of elastic constants and other connected parameters of bt-ZnS, we considered the Voigt–Reuss–Hill values. Figure 3 outlines the pressure dependency of the typical cubic elastic constants between the 0 and 20 GPa. It is easy to see from Fig. 3 that the calculated values of elastic constants C11, C12, and C44 are positive where C11 and C12 have smooth increments as a function of increasing pressure. Additionally, the increment of the elastic constant C11 is higher than both elastic constants C12 and C44. Physically, C11 explains the longitudinal elastic behavior, whereas C12 and C44 represent the off-diagonal and shear elastic characteristics of cubic crystals because of shearing, respectively. Therefore, a longitudinal strain produces a change in volume without a change in shape. This volume change substantially related to pressure causes a larger change in C11. In contrast, a transverse strain or shearing causes a change in shape without a change in volume. For this reason, C12 and C44 are less sensitive to pressure than C11. It should be also noted that C11 and C12 coincide at P T = 17 GPa. Apart from the increment of elastic constants C11, C12, and C44 that exposes a sluggish decrease (shear instability) under pressure, their magnitudes never fall to zero even at P T due to first-order phase transition. Our results for the pressure behavior and magnitudes of C11, C12, and C44 are also compatible with the former findings of refs. [7, 28, 30].

Fig. 3
figure 3

Typical cubic elastic constants of bt-ZnS under pressure

Full size image

According to the Born structural stability, the magnitudes of typical cubic elastic constants must satisfy the criteria C11–C12 > 0, C11 > 0, C44 > 0, C11 + 2C12 > 0, and cubic stability, i.e., C12 > B > C11 condition [15, 23–26]. As another result, calculated values of C11, C12, and C44 elastic constants of bt-ZnS satisfy both the structural and cubic stability conditions meaning that the crystal structure of bt-ZnS is stable under zero pressure and temperature.

Figure 4 displays the pressure behavior of bulk modulus (B), shear modulus (G), and Young modulus (E) of bt-ZnS for the investigated pressure range. These three elastic moduli (B, G, and E) are essential parameters for controlling the mechanical properties of materials [15, 23–26]. Among them, bulk modulus (\( B \)) is the only elastic modulus of matter that conveys much information about the bonding strength. It is also a measure of the matter’s resistance to external deformation and occurs in many formulas describing diverse mechanical–physical properties [15, 23–26]. The shear modulus (G), however, defines the resistance to shape change caused by a shearing force and Young’s modulus (E) is the resistance to uniaxial tensions. From the standard physical definition of bulk modulus with B = ΔP / ΔV, one can expect an increment for B due to its direct proportion to the applied pressure. In Fig. 4, the bulk modulus of bt-ZnS demonstrates uniform increment up to 20 GPa as expected. Further, G has a sharp decrease under pressure due its strict correlation with C44.

Fig. 4
figure 4

Pressure dependence of bulk, shear, and Young moduli of bt-ZnS

Full size image

Ductility and brittleness play a key role during materials manufacturing. Thus, we also evaluated the ductile (brittle) nature of bt-ZnS crystal under pressure. The terms brittle and ductile signify the two discrete mechanical properties of solids when they subjected to external stress. In general, brittle materials are not deformable or less deformable before fracture. Contrarily, ductile materials are deformable a lot before fracture. For a separation, Pugh ratio is a determinative limit for ductile (brittle) behavior of materials and has a common use in literature. If the B/G ratio of a material is about 1.75 and higher, the material is ductile; otherwise, the material becomes brittle [15]. Another reliable assessment criterion for ductility and brittleness is Cauchy pressure, which is expressed with C P = C12–C44. The negative (positive) values of the Cauchy pressure reflect the brittle (ductile) nature of the compounds [15]. Hence, we cross-checked our results with Pugh ratio and Cauchy pressure norms. Under zero pressure and temperature, our numerical value for B/G is 2.59 and has a positive Cauchy pressure, which manifests the ductile nature of bt-ZnS crystal similar to w-ZnS [31]. As well, in Fig. 5, B/G ratio has a linear increment under pressure and reaches its maximum value at 20 GPa.

Fig. 5
figure 5

B/G ratio behavior of bt-ZnS under pressure

Full size image

Poisson ratio (ν) is the ratio between the transverse strain and longitudinal strain in the elastic loading direction. It can provide details about the bonding force behavior in solids [26]. The values of ν = 0.25 and ν = 0.5 portray the lower limit and upper limit of central forces, respectively. The present Poisson ratio value for bt-ZnS with 0.39 slightly overestimates the experimental value of 0.27 (Table 2) and increases with increasing pressure as in Fig. 6. This result for ν suggests that interatomic forces in bt-ZnS crystals are mainly central forces.

Fig. 6
figure 6

Pressure dependence of Poisson ratio of bt-ZnS

Full size image

In solids, low-temperature acoustic modes initiate the vibrational excitations. Because of this case, two typical elastic waves namely the longitudinal wave and shear wave arise [15, 23–26], where V P and V S symbolize these wave velocities, respectively. Table 2 gives the numerical values of both velocities, and Fig. 7 illustrates the pressure behavior of V P and V S of bt-ZnS. In Fig. 7, V P displays a gradual increment, whereas V S has an apparent decrease under pressure.

Fig. 7
figure 7

Elastic wave velocities of bt-ZnS versus pressure

Full size image

The static (ε 0) and high-frequency (ε ∞) dielectric constants of materials are essential parameters for the device fabrication of modern electronics. These constants are responsible for the behavior of charge carriers, dopants, defects, and impurities [23]. Figure 8 depicts the plots of both dielectric constants (ε 0 and ε ∞) behavior of bt-ZnS under surveyed pressure range. The dielectric constant ε 0 indicates an evident decrease under pressure. On the other hand, ε ∞ has a slow increment under increasing pressure. A quantitative assessment from Table 2 implies that our numerical values of both dielectric constants underestimate the experiments and are of about previous theoretical results of ref. [27].

Fig. 8
figure 8

Static and high-frequency dielectric constants of bt-ZnS against pressure

Full size image

The Kleinman parameter (ζ) for cubic materials describes the relative ease of bond bending to the bond stretching. Minimizing bond bending leads to ζ = 0, minimizing bond stretching leads to ζ = 1 [15, 24], and ζ links to typical cubic elastic constants [29] as in Eq. (5):

$$ \zeta =\left({C}_{11}+8{C}_{12}\right)/\left(7{C}_{11}+2{C}_{12}\right) $$
(5)

Figure 9 displays the Kleinman parameter of bt-ZnS upon the pressure increment. Under pressure, ζ increases with increasing pressure. Our obtained numerical value for ζ is 0.73 and reveals the bond-stretching character in bt-ZnS under zero pressure and temperature. This result for ζ of bt-ZnS is highly consistent with the experimental measurements and better than other existing theoretical results (Table 2).

Fig. 9
figure 9

Behavior of Kleinman parameter of bt-ZnS under pressure

Full size image

4 Conclusion

In summary, a different theoretical calculation was reported by employing an existing mixed-type interatomic potential to obtain the structural, elastic, and mechanical behavior of bt-ZnS under pressure. This applied potential mainly developed for the surface energies of bt-ZnS well reproduces the investigated high-pressure characteristics of this compound. Presently obtained values of phase transition pressure, typical cubic elastic constants, Kleinman parameter, and both dielectric constants are in good agreement with the experiments and better than those of several early theoretical data. We hope that our results may contribute to both current and future works regarding the pressure dependence elastic and relevant properties of bt-ZnS.