1 Introduction

Atherosclerosis (stenosis) is a prevalent disease among cardiovascular diseases that leads to the death of millions of people. It is hardening and reducing of elasticity of arterial walls. It occurs due to the deposits of cholesterol and fatty and oily substances sticking to the artery wall. The plaque buildup of such substances inside the lumen of the artery is called stenosis. It constricts the arterial cross-section, restricting blood flow to the various body parts. In very severe cases of this disease, the blood vessel is blocked, and the blood flow to the heart muscles or brain is stopped, affecting the brain tissues and giving dangerous consequences such as a heart attack (coronary artery disease) or brain stroke (carotid artery disease). The artery may also be affected because of several stenoses (multi-stenosed artery). Many researchers have studied the characteristics of blood flow through the stenosed artery. Srivastava et al. [1] provided the analytical study of blood flow through the stenosed artery by utilizing the two-phase flow model. Hisham et al. [2] worked on the time-dependent flow of pseudoblood in a stenotic artery. Sharma et al. [3] analyzed the variable properties of blood flow across a curved artery with permeable walls under the magnetic effects.

The study of blood flow through the stenosed vessels is vital and gained the attention of many researchers because of the blood circulation and mechanical properties of the vessel wall. The blood behaves like a Newtonian fluid and non-Newtonian fluid (pseudoplastic) in the vessels of various diameters. Several theoretical works on blood flow in diseased arteries are provided by Nadeem and Akbar [4,5,6]. Kumar et al. [7] analyzed the behavior of two-layered fluid flow through narrowed arteries by accounting for the variable slip velocity on the boundary wall. The non-Newtonian nature of blood flow via permeable stenotic artery with the magnetic influence is investigated by Ellahi et al. [8]. Srivastava [9] investigated the Herschel-Bulkley fluid flow analytically through an inclined constricted artery with magnetic power. Prasad and Yasa [10] studied the micropolar fluid flow through the non-uniform multi-stenosed permeable tube under the slip effects on the boundary. Salman et al. [11] examined the Casson fluid flow in a cylindrical artery with multi-stenosed walls with electroosmotic results. Tripathi and Sharma [12] reviewed the radiation and chemical effects on the two-phase blood flow via the vertical stenotic artery.

The Rabinowitsch fluid is included in the group of pseudoplastic fluids (shear thinning). The Rabinowitsch fluid model efficiently describes the impacts of lubricant additives (long-chain polymer solution), minimizing the shearing rate sensitivity of the lubricants. It fits the wide range of data of the shear rate, and the experimental verification of the theoretical results for this model is firstly given by Wada and Hayashi [13, 14]. This model describes the shear thinning and shear thickening (non-Newtonian) nature of fluids depending upon the non-linearity factor that appears in the stress–strain relationship of this model, known as the coefficient of pseudoelasticity. The Rabinowitsch fluid behaves as pseudoplastic, Newtonian, and dilatant fluids for positive, zero, and negative coefficient values of pseudoplasticity. Many researchers have worked on this model to study the non-Newtonian characteristics of fluid flow through various channels. The applications of the Rabinowitsch fluid model for peristaltic analysis are provided by several researchers [15,16,17,18]. Akbar and Butt examined heat transfer of Rabinowitsch fluid flow through the artery affected due to cilia [19].

The parameters involved in studying fluid flow are responsible for the output results. The influence of parameters on output is determined by local sensitivity analysis (LSA). The LSA evaluates the impact of the input parameter of the interest (PoI) on the output quantity. We classify the much more influential and less effective parameters by the local parameter-based sensitivity analysis. Khan et al. identified the impacts of parameters on blood flow in stenosed carotid artery by using LSA [20]. The LSA is applied in the examination of abnormalities of blood vessels, i.e., aneurysms and stenosis, by Gul et al. [21].

In view of the above literature survey, it is clear that no study is available on the LSA of Rabinowitsch fluid flow through the multi-stenosed artery. In this work, we investigated the Rabinowitsch fluid model to analyze the non-Newtonian nature of blood (shear thinning) flow through the diseased artery constricted due to various shapes of multiple stenoses (bell shape, W shape, elliptical shape). The artery has a porous wall and slips effects the boundary. LSA assesses the more effective parameters involved in the study.

1.1 Mathematical modeling

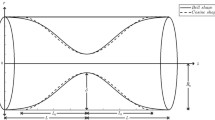
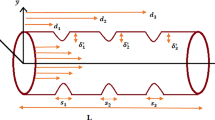
Consider an incompressible, steady, and axisymmetric blood flow across a cylindrical artery of finite length. The artery is diseased due to the multiple stenoses of various shapes (bell shape, W shape, elliptical shape) on its walls. The blood is considered as Rabinowitsch fluid flowing through an artery having permeable walls and slip effects on its boundary (see Fig. 1). The problem is interpreted in the cylindrical coordinate system \((\overline{r },\overline{\theta }, \overline{z })\). The geometry of the arterial wall deformed due to the existence of different shapes and multiple stenoses can be mathematically written as follows [22, 23]:

Fig. 1
figure 1

Geometry of the problem

Full size image
$$\overline\eta\left(\mathrm z\right)=\left\{\begin{array}{l}R-\delta_1^\ast e^{\overline{A_1}(z)}, \;\;\;\;\;\;d_1\leq\overline z\leq d_1+s_1\\R-\frac{12\delta_2^\ast}{10s_2^4}\overline{A_2}\left(z\right) \;\;\;d_2\leq\overline z\leq d_2+s_2\\R-\delta_3^\ast\overline{A_3}\left(z\right) \;\;\;\;\;\;d_3\leq\overline z\leq d_3+s_3\\R \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;Otherwise,\end{array}\right.$$
(1)

where

$$\left.\begin{array}{c}\overline{{A }_{1}}\left(z\right)=-\frac{{{m}^{2}\epsilon }^{2}}{{s}_{1}^{2}}{\left(\overline{z }-1.5{s}_{1}\right)}^{2} ,\\ \overline{{A }_{2}}\left(z\right)=11\left(\overline{z }-{d}_{2}\right){{s}_{2}}^{3}-47{\left(\overline{z }-{d}_{2}\right)}^{2}{{s}_{2}}^{2}+72{\left(\overline{z }-{d}_{2}\right)}^{3}{s}_{2}-36{\left(\overline{z }-{d}_{2}\right)}^{4}, \\ \overline{{A }_{3}}\left(z\right)=sin\left(\frac{\pi \left(\overline{z }-{d}_{3}\right)}{{s}_{3}}\right) .\end{array}\right\}$$
(2)

\(R\) is the radius of the non-stenotic region of the artery, \({s}_{l}\) is the width of stenosis, \({d}_{l}\) is the position of stenosis, \({\delta }_{l}^{*}\) is the height of stenosis, \(m\) is parametric constant, \(l=1, 2, 3\). \(\epsilon\) is the relative length of constriction, and it is the ratio of radius \(R\) to the half of the stenosis width \({s}_{1}\), i.e., \(\epsilon =\frac{R}{{~}^{{s}_{1}}\!\left/ \!{~}_{2}\right.}\).

The governing equations (continuity and momentum) of steady incompressible fluid flow are as follows [24]:

$$\frac{\partial \overline{u} }{\partial \overline{r} }+\frac{\overline{u} }{\overline{r} }+\frac{\partial \overline{w} }{\partial \overline{z} }=0,$$
(3)
$$\rho \left(\overline{u}\frac{\partial }{\partial \overline{r} }+\overline{w}\frac{\partial }{\partial \overline{z} }\right)\overline{u }=-\frac{\partial \overline{p} }{\partial \overline{r} }+\frac{1}{r}\frac{\partial \left(\overline{r }{\overline{s} }_{\overline{rr} }\right)}{\partial \overline{r} }+\frac{\partial \left({\overline{s} }_{\overline{rz} }\right)}{\partial \overline{z} }-\frac{{\overline{s} }_{\overline{\theta \theta }} }{\overline{r} } ,$$
(4)
$$\rho \left(\overline{u}\frac{\partial }{\partial \overline{r} }+\overline{w}\frac{\partial }{\partial \overline{z} }\right)\overline{w }=-\frac{\partial \overline{p} }{\partial \overline{z} }+\frac{1}{r}\frac{\partial \left(\overline{r }{\overline{s} }_{\overline{rz} }\right)}{\partial \overline{r} }+\frac{\partial \left({\overline{s} }_{\overline{zz} }\right)}{\partial \overline{z} }.$$
(5)

The stress tensor relationship of Rabinowitsch fluid model, i.e., shear stress and shear strain for Rabinowitsch fluid are related as follows [14]:

$${\overline{s} }_{\overline{rz} }+\overline{k }( {{\overline{s} }_{\overline{rz} })}^{3}=\mu \left(\frac{\partial \overline{w} }{\partial \overline{r} }\right) ,$$
(6)

where \(\overline{k }\) is known as the coefficient of pseudoplasticity.

We introduce the dimensionless variables to process the equations into non-dimensional form that enables us to solve them analytically.

$$\left.\begin{array}{c}r=\frac{\overline{r}}{R } , z=\frac{\overline{z}}{{s }_{l}} , u=\frac{L\overline{u}}{{u }_{0}{\delta }_{l}^{*}}, w=\frac{\overline{w}}{{u }_{0}} , p=\frac{{R}^{2}\overline{p}}{{s }_{l}{u}_{0}\mu } ,\\ \eta \left(z\right)=\frac{\overline{\eta }(z)}{R} , {h}_{l}=\frac{{d}_{l}}{{s}_{l}} ,{\delta }_{l}=\frac{{\delta }_{l}^{*}}{R} , k=\frac{{u}_{0}^{2}{\mu }^{2}\overline{k}}{{R }^{2}}, {s}_{ij}=\frac{R {\overline{s} }_{\overline{ij}}}{{u }_{0}\mu } . \end{array}\right\}$$
(7)

The conditions accounted for the study of a mild case of stenosis are as follows [22]:

$${\delta }_{l}=\frac{{\delta }_{l}^{*}}{R}\ll 1,\;\frac{R}{{s}_{l}}\sim^\circ 1.$$
(8)

By settling the dimensionless variables given in (7) in Eqs. (1)–(6) and then using the conditions of mild stenosis provided in (8), we acquired the following:

$$\eta\left(z\right)=\left\{\begin{array}{cc}\begin{array}{c}1-{\delta }_{1}{e}^{{A}_{1}\left(z\right)},\\ 1-\frac{12 }{10}{{\delta }_{2} A}_{2}\left(z\right)\\ \begin{array}{c}1-{\delta }_{3} {A}_{3}\left(z\right)\\ 1\end{array}\end{array}& \begin{array}{c}{h}_{1}\le z\le {h}_{1}+1\\ {h}_{2}\le z\le {h}_{2}+1\\ \begin{array}{c}{h}_{3}\le z\le {h}_{3}+1\\ Otherwise,\end{array}\end{array}\end{array}\right\}$$
(9)

where

$$\left.\begin{array}{c}{A}_{1}\left(z\right)=-{{m}^{2}\epsilon }^{2}{\left(z-1.5\right)}^{2} ,\\ {A}_{2}\left(z\right)=11\left(z-{h}_{2}\right)-47{\left(z-{h}_{2}\right)}^{2}+72{\left(z-{h}_{2}\right)}^{3}-36{\left(z-{h}_{2}\right)}^{4}, \\ {A}_{3}\left(z\right)=sin\left(\pi \left(z-{h}_{3}\right)\right) .\end{array}\right\}$$
(10)

Equation (3) is satisfied, and Eqs. (4) and (5) become the following:

$$\frac{\partial p}{\partial r}=0,$$
(11)
$$r\frac{dp}{dz}=\frac{\partial \left(r {s}_{rz}\right)}{\partial r}.$$
(12)

The non-dimensional form of stress tensor relationship for Rabinowitsch fluid model is as follows:

$${s}_{rz}+k({{s}_{rz})}^{3}=\frac{\partial w}{\partial r}.$$
(13)

The corresponding boundary conditions of a permeable wall in the dimensionless form are as follows [25]:

$$\frac{\partial\mathrm w}{\partial\mathrm r}=0\;at\;r=0\;and\;w=\frac{\sqrt{D_a}}\alpha\frac{\partial w}{\partial r}-D_a\frac{dp}{dz}\;at\;r=\eta,$$
(14)

where \(\alpha\) and \({D}_{a}\) represent the slip parameter and Darcy number, respectively.

1.2 Analytical solution

On integrating Eq. (12) along with the boundary condition \({s}_{rz}=0\) on the axis of symmetry of the channel i.e., \(r=0\), we have the following:

$${s}_{rz}=\frac{r}{2}\frac{dp}{dz} .$$
(15)

By utilizing Eq. (15) in Eq. (13) and then integrating along with boundary conditions provided in (14), we obtain the solution of axial velocity as follows:

$$w\left(r,z\right)=\frac{dp}{dz}\left[\frac{\sqrt{{D}_{a}} \eta }{8\alpha }\left(4+k{\left(\frac{dp}{dz}\right)}^{2}{\eta }^{2}\right)+\left(\frac{{r}^{2}-{\eta }^{2}}{4}\right)+k\left(\frac{{r}^{4}-{\eta }^{4}}{32}\right){\left(\frac{dp}{dz}\right)}^{2}-{D}_{a}\right] ,$$
(16)

where the pressure gradient \(\frac{dp}{dz}\) is acquired from the volume flow rate as follows:

$$Q=2\pi \underset{0}{\overset{\eta }{\int }}rwdr.$$
(17)

Equation (17) gives an expression which is cubic in \(\frac{dp}{dz}\), by solving this expression for real roots, we get the mathematical expression of the pressure gradient as follows:

$$\frac{dp}{dz}=\frac{6{\times 2}^{1/3}\left(\pi \alpha {\eta }^{4}-4\pi {\eta }^{3}\sqrt{{D}_{a}}+8\pi \alpha {\eta }^{2}{D}_{a}\right)}{{\left({\mathrm{B}}_{1}+\sqrt{{{{\mathrm{B}}_{1}}^{2}+\mathrm{B}}_{2}}\right)}^{1/3}}+\frac{{\left({\mathrm{B}}_{1}+\sqrt{{{{\mathrm{B}}_{1}}^{2}+\mathrm{B}}_{2}}\right)}^{1/3}}{3{\times 2}^{1/3}(-k\pi \alpha {\eta }^{6}+6k\pi {\eta }^{5}\sqrt{{D}_{a}})},$$
(18)

where

$$\begin{array}{c}{\mathrm{B}}_{1}=1296{k}^{2}{\pi }^{2}Q{\alpha }^{3}{\eta }^{12}-15552{k}^{2}{\pi }^{2}Q{\alpha }^{2}{\eta }^{11}\sqrt{{D}_{a}}+46656{k}^{2}{\pi }^{2}Q\alpha {\eta }^{10}{D}_{a} ,\\ {\mathrm{B}}_{2}=-23328{\left(-k\pi \alpha {\eta }^{6}+6k\pi {\eta }^{5}\sqrt{{D}_{a}}\right)}^{3}{\left(\pi \alpha {\eta }^{4}-4\pi {\eta }^{3}\sqrt{{D}_{a}}+8\pi \alpha {\eta }^{2}{D}_{a}\right)}^{3}.\end{array}$$

The shear stress at the stenotic arterial wall is as follows:

$${\uptau }_{\mathrm{w}}={\left.-\frac{\partial \mathrm{w}}{\partial \mathrm{r}}\right|}_{\mathrm{r}=\upeta }=-\frac{\eta }{8}\frac{dp}{dz}\left(4+k{\left(\eta \frac{dp}{dz}\right)}^{2}\right).$$
(19)

2 Results and discussion

This section consists of a graphical analysis of analytical solutions obtained in the earlier fragment. This study involves the stenosis of various shapes, i.e., bell shape, W shape, and an elliptical shape with heights \({\delta }_{1}\), \({\delta }_{2}\), and \({\delta }_{3}\). For simplicity, we considered that each stenosis has an equal height represented by \({\delta }_{l}\). The graphical behavior of flow velocity, pressure gradient, wall shear stress, and streamlines depending on important involved physical parameters flow rate \(Q\), height of stenosis \({\delta }_{l}\), slip parameter \(\alpha\), and Darcy number \({D}_{a}\) is discussed in this segment. The computer code is generated in Wolfram Mathematica 12 to plot these graphs.

Figures 2, 3, 4, and 5 describe the impact of various parameters on the fluid’s velocity \(w(r,z)\). Figure 2 explains the impact of the volumetric flux rate on the velocity graph. The flow velocity increases for quickly flowing fluid. Figure 3 depicts the effect of height of stenosis on the axial velocity. It shows that the fluid velocity increments with a growing height of stenosis. Figure 4 elucidates the influence of the slip parameter on the velocity profile. It reveals that the flow velocity lessens with the enhancing value of the slip parameter. It is noted that the fluid velocity reverses its behavior and increases in the vicinity of the boundary wall because of the slip effects. Figure 5 describes the reliance of velocity \(w\) on the Darcy number \({D}_{a}\). It displays that the velocity of fluid enhances with the rise in Darcy number, but its nature reverses near the conduit boundary because of the permeability effect. Figure 6 is a pictorial representation of flow velocity against the axis of the channel for various values of \(r\). It explains that velocity of flow has larger values in the narrowed region as compared to velocity near the conduit axis, and it increases quickly in the stenotic region. The effect of the coefficient of pseudoplasticity \(k\) on the velocity is examined in Table 1 for \(1\le k\le 10\). It is observed from Table 1 that the flow velocity is not strongly disturbed in a radial direction with an incrementing value of \(k\), and it has a very small effect on the output value of axial velocity \(w\). Moreover, the flow has the smallest and highest values at the centerline and arterial wall, respectively.

Fig. 2
figure 2

Impact of flow rate \(Q\) on the velocity profile

Full size image
Fig. 3
figure 3

Impact of stenosis height \({\delta }_{l}\) on the velocity profile

Full size image
Fig. 4
figure 4

Impact of slip parameter \(\alpha\) on the velocity profile

Full size image
Fig. 5
figure 5

Impact of Darcy number \({D}_{a}\) on the velocity profile

Full size image
Fig. 6
figure 6

Velocity profile against the axis of the channel for r

Full size image
Table 1 Changing values of axial velocity for increasing values of \(k\) with \(r=0, 0.5, 1\), and \(z=1.5, 3.5\)
Full size table

Figures 7, 8, 9, and 10 show the behavior of pressure gradient for various parameters. Figure 7 shows that the pressure gradient increases with a higher value of flow rate \(Q\). Figure 8 provides the impact of stenosis height on the pressure gradient. It delineates that the pressure gradient remains the same in the non-stenotic region but rises in the stenotic region with the growing values of \({\delta }_{l}\). Figures 9 and 10 illustrate the influence of the slip parameter and Darcy number on the pressure gradient. It gets higher values with the improving slip effects on the boundary wall and diminishes for advancing values of Darcy number. Figures 11, 12, 13, and 14 explain the wall shear stress (WSS) \({\tau }_{w}\) relation with the physical parameters. Figure 11 reveals that the WSS increases with increasing flow rate. Figure 12 indicated that WSS has enlarging values in the stenotic segment of the channel for increasing stenosis height and remains the same in the non-stenotic region. Figures 13 and 14 display that the WSS reduces for enhancing the value of slip parameter but has an opposite behavior in the case of Darcy number. Figures 15, 16, 17, 18, 19, and 20 provide the streamline analysis of fluid flow and describe the flow pattern in the multi-stenosed artery of various shapes. They show that the streamlines close to the arterial wall split into contours in the stenotic region. Figures 15, 16, 17, and 18 delineate that the size of contours decreases with an increase in the flow rate, but in the case of greater stenosis height, the opposite behavior appears. Figures 19 and 20 depict that the size of contours improves for a higher value of Darcy number. The shape of these contours is affected by the various shapes of stenosis.

Fig. 7
figure 7

Pressure gradient for the flow rate \(Q\)

Full size image
Fig. 8
figure 8

Pressure gradient for the stenosis height \({\delta }_{l}\)

Full size image
Fig. 9
figure 9

Pressure gradient for the slip parameter \(\alpha\)

Full size image
Fig. 10
figure 10

Pressure gradient for Darcy number \({D}_{a}\)

Full size image
Fig. 11
figure 11

Impact of flow rate \(Q\) on the wall shear stress

Full size image
Fig. 12
figure 12

Impact of stenosis height \({\delta }_{l}\) on the wall shear stress

Full size image
Fig. 13
figure 13

Impact of slip parameter \(\alpha\) on the wall shear stress

Full size image
Fig. 14
figure 14

Impact of Darcy number \({D}_{a}\) on the wall shear stress

Full size image
Fig. 15
figure 15

Streamlines for the flow rate \(Q\)=1.2

Full size image
Fig. 16
figure 16

Streamlines for the flow rate \(Q\)=1.3

Full size image
Fig. 17
figure 17

Streamlines for the stenosis height \({\delta }_{l}\) =0.13

Full size image
Fig. 18
figure 18

Streamlines for the stenosis height \({\delta }_{l} =0.2\)

Full size image
Fig. 19
figure 19

Streamlines for Darcy number Da = 0.42

Full size image
Fig. 20
figure 20

Streamlines for Darcy number \({D}_{a}=0.43\)

Full size image

2.1 Local sensitivity analysis

This section consists of the LSA, which is a method of examining the more and less effective parameter of the study. In this method, input PoI are perturbed in the proximity of the nominal values to analyze the effect on output quantity. In this study, the slip parameter \(\alpha\), Darcy number \({D}_{a}\), and stenosis height \({\delta }_{l}\) are significant PoI and axial velocity \(w(r,z)\) is the output quantity. The PoI are perturbed by 1.8% of their nominal values, and the sensitivity index is calculated for the various mesh points by using the subsequent relationship [26] as follows:

$${S}_{PoI}^{\;j}=\frac{\partial \vartheta }{\partial r}=\frac{\vartheta (r+\Delta r)-\vartheta (r)}{\Delta r},$$
$${N}_{PoI}=\frac{1}{n}\sum {S}_{PoI}^{j} .$$

where \({S}_{PoI}^{j}\) is the sensitivity index of the input parameter of interest at jth mesh point, \(n\) represents mesh elements, and \({N}_{PoI}\) is a sensitivity magnitude of the input parameter of interest. The value of the sensitivity index at each mesh element is provided in Table 2. Figure 21 gives the comparison of the magnitude of the sensitivity index for each PoI. It shows that the slip parameter \(\alpha\) is much impactful parameter and stenosis height \({\delta }_{l}\) is less effective parameter. It makes the sense that \(\alpha\) has a greater effect on the value of flow velocity as compared to \({D}_{a}\) and \({\delta }_{l}\), while \({\delta }_{l}\) is the least influential parameter among PoI.

Table 2 LSA of significant physical parameters with \(n=12\) and \({S}_{PoI}=\left|\frac{{(w}_{OLD}-{w}_{NEW})\times 100}{1.8\times (nominal\;value\;of\;PoI)}\right|\)  
Full size table
Fig. 21
figure 21

Comparison of sensitivity magnitude

Full size image

3 Conclusion

We have studied the non-Newtonian blood flow behavior in the present work by considering the Rabinowitsch fluid model. We evaluated the cylindrical artery having multiple stenoses of different shapes, i.e., bell shape, W shape, and elliptical shape. The stenosed artery is considered to have a porous wall and slip effects on the boundary. The study involves various significant physical parameters. The LSA is studied in this work to classify these crucial parameters having the least and most potent influence on the fluid’s velocity. The main consequences of the study are provided as follows:

  1. 1.

    The velocity of flow rises for quick flow and growing height of stenosis. The adjacent conduit wall has reverse behavior as it depicts near the central axis for both slip parameter \(\alpha\) and Darcy number \({D}_{a}\). It has the opposite nature for \(\alpha\) and \({D}_{a}\).

  2. 2.

    The flow velocity has a minimum value at the axis of the channel and gets the maximum value at the boundary wall.

  3. 3.

    The axial velocity gets greater values in the constricted region while it overgrows in the stenotic area.

  4. 4.

    The pressure gradient increases for greater values of flow rate, stenosis height, and slip parameter, but it gives the opposite behavior for Darcy number.

  5. 5.

    The wall shear stress enhances higher flow rate values, stenosis height, and Darcy number, but it reduces for improving values of slip parameter.

  6. 6.

    The local sensitivity analysis clarified that the slip parameter is much more influential. It has a more significant impact on the flow velocity.

  7. 7.

    The stenosis height is the less effective parameter and has a minor effect on the flow velocity than the Darcy number and slip parameter. The Darcy number is more effective than stenosis height but less influential than the slip parameter.

  8. 8.

    The LSA allows us to conclude that the slip parameter and Darcy number have greater importance in studying blood flow through permeable stenosed arteries influenced by slip effects.

  9. 9.

    It is noted from streamlines that contours are generated in the narrower region, and the shape of various stenosis affects the shape of contours. Also, the size of contours increases for the rising value of stenosis height and Darcy number, but the behavior reverses for quick flow.