Fundamental group of complex hypocycloids

Abstract

The Zariski–van Kampen theorem allows us to provide a presentation of the fundamental group for the complement of algebraic plane curves. However, certain computations require arduous work, as exemplified in the case of hypocycloids. In this paper we present the following result: Theorem 1. The fundamental group of any complex hypocycloid with N cusps is the Artin group of the N-gon. The main idea of the proof is take advantage of the symmetries inherent in the hypocycloid, allowing us to partition the domain to determine the generators of the fundamental group.

1 Introduction

The parametric equation of a complex hypocycloid has the form:

$$\begin{aligned} D_{N,\ell }=\left( \frac{\ell \cos (k \theta )+k\cos (\ell \theta )}{N},\frac{\ell \sin (k \theta )-k \sin (\ell \theta )}{N}\right) , \end{aligned}$$

with $\theta \in \mathbb {C}$, $N, \ell \in \mathbb {N}$, N and $\ell$ coprime, $\ell < \frac{N}{2}$ and $k=N-\ell$. Note that due to the periodicity of $\sin$ and $\cos$, we can consider $\theta \in [0,2\pi ] \times i\mathbb {R}\subset \mathbb {C}$ which establishes a surjection and a closed parametrization. Some examples of hypocycloids are given in Figs. 1 and 2.

Fig. 1

To the left $N=4$ and $\ell =1$, to the right $N=5$ and $\ell =1$

Fig. 2

To the left $N=5$ and $\ell =2$, to the right $N=13$ and $\ell =6$

Let:

$$\begin{aligned} X_{N,\ell }=\frac{\ell \cos (k \theta )+k\cos (\ell \theta )}{N}{} & {} \text {and}{} & {} Y_{N,\ell }=\frac{\ell \sin (k \theta )-k \sin (\ell \theta )}{N}. \end{aligned}$$

On the other hand, the Artin group of the N-gon has the form:

$$\begin{aligned} \left\langle \alpha _i,\ i\in \mathbb {Z}/ N \ \begin{array}{|l} \alpha _i\alpha _j=\alpha _j\alpha _i \ j\ne i, i-1\\ \alpha _i\alpha _{i+1}\alpha _i=\alpha _{i+1}\alpha _i\alpha _{i+1} \ \end{array} \right\rangle . \end{aligned}$$

Theorem 1 was first conjectured by José Ignacio Cogolludo Agustín and Enrique Artal Bartolo in [2], in the same paper they prove the conjecture for specific cases:

• $N=3$ and $\ell =1$.

• $N=4$ and $\ell =1$.

• $N=5$ and $\ell =2$.

• $N=8$ and $\ell =3$.

In [1] Artal, Cogolludo and Jorge Martín Morales prove the conjecture for a significant family of hypocycloids: $\ell =k-1$; for the proof they use the Wirtinger presentation of the group.

The paper is organized as follows: In Sect. 1 we introduce the Zariski–van Kampen theorem and give the relations for cusps, nodes and tangent points. In Sect. 2 we recall some results of [2] about the topology of the hypocycloids, and present new results about the topology as the tangent points and the tangent cusps. We make a partition of the domain and prove our key theorem in order to distinguish the different generators of the fundamental group, also we relate the partition with the singular and tangent points. In Sect. 3 we prove Theorem 1. In Sect. 4, we give two examples, deltoid and $D_{8,1}$ to summarize our results.

2 Zariski–van Kampen theorem

The Zariski–van Kampen theorem was proved by Oscar Zariski in 1929 [7]; a most recent proof can be found in [4] by Alexandru Dimca, we refer [2] and [1] for a good introduction of the subject. For the sake of completeness we are going to give an introduction.

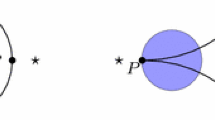
Let $C \subset \mathbb {C}^2$ be a plane algebraic curve defined by a reduced polynomial $f(x,y)=0$ where the degree of f in y is d and the coefficient of $y^d$ is constant. Consider $P:\mathbb {C}^2 \setminus C \rightarrow \mathbb {C}$ as the projection into the first coordinate x; let $Z=\{z_1,\ldots ,z_r\}$ be the set of projections under P of the singularities and of the points at witch the tangent to C exists and is vertical. Note that the points tangent to the vertical lines are not singularities, but we include them for the application of the Zariski–van Kampen theorem.

By restricting $P|_{\mathbb {C}^2\setminus (C\cup P^{-1}(Z))}$ we obtain a locally trivial fibration, where each fiber F is $\mathbb {C}$ minus d points. Let us assume that the base point in the projection space $\mathbb {C}\setminus Z$ and the base point in the total space $\mathbb {C}^2\setminus C$ is the same point b. Considering the fixed fiber $F_b=P^{-1}(b)$, the Zariski–van Kampen theorem holds:

Theorem 2

The fundamental group of $C^2 \setminus C$ with base point b, is the quotient group of $\pi _1(F_b,b)$ by the subgroup normally generated by $\{\alpha _i^{\gamma _j}\alpha _i^{-1}\}$ were $\alpha _i$ runs along the generators of the free group $\pi _1(F_b,b)$, $\gamma _j$ runs along the generators of the free group $\pi _1(\mathbb {C}\setminus Z,b)$ and $\alpha _i^{\gamma _j}$ represents the monodromy action. Stated differently, it admits the following presentation:

$$\begin{aligned} \pi _1(\mathbb {C}^2\setminus C,b)=\left\langle \alpha _1,\ldots ,\alpha _d | \alpha _i^{\gamma _j}=\alpha _i \right\rangle . \end{aligned}$$

The Zariski–van Kampen theorem operates as follows: $\pi _1(F_b,b)$ represents a free group with d elements and base point b, similarly $\pi _1(\mathbb {C}\setminus Z,b)$ represents a free group with r elements and the same base point. By selecting two generators, namely $\alpha$ from $\pi _1(F_b,b)$ and $\gamma$ from $\pi _1(\mathbb {C}\setminus Z,b)$, we use $\gamma$ to “induce the movement” of the fiber $F_b$; this process can be properly done using either the isotopy extension lemma or a pullback; the “movement” is geometrically represented by the braid action, at the end, the element $\alpha$ is transformed into a conjugate, thereby establishing a connection between the monodromy action and the braid action onto the free group (see Fig. 3).

Fig. 3

Example of the pullback of $\gamma$ and $F_b$ where $\pi _1(F_b,b)$ has four generators; $\gamma$ represents a loop with the same initial and endpoint. As a consequence, this yields the relations $\alpha _i=\alpha _i^{\gamma }$ were the monodromy actions are: $\alpha _1^{\gamma }=\alpha _1$, $\alpha _2^{\gamma }=\alpha _2\alpha _3\alpha _2^{-1}$, $\alpha _3^{\gamma }=\alpha _2$ and $\alpha _4^{\gamma }=\alpha _4$

The most common examples are the polynomials $y^p-x^q=0$ (see [6]). According to the Zariski–van Kampen theorem, for each example, we choose a non-singular point b as the base point and consider the fiber $F_b$. The generators correspond to the generators of $\pi _1(F_b, b)$. We are particularly interested in specific cases provided in the following list. It includes the polynomials and the relations established by the monodromy action:

• Tangent point has an equation $x-y^2=0$ and gives us the relation $\alpha _1=\alpha _2$.

• Ordinary node has an equation $x^2-y^2=0$ and gives us the relation $\alpha _1\alpha _2=\alpha _2\alpha _1$.

• Transversal cusp has an equation $x^3-y^2=0$ and gives us the relation $\alpha _1\alpha _2\alpha _1=\alpha _2\alpha _1\alpha _2$.

• Tangent cusp has an equation $x^2-y^3=0$ and gives us the relations $\alpha _1\alpha _2\alpha _1=\alpha _2\alpha _1\alpha _2$ and $\alpha _1=\alpha _3$.

Note that, the generators used in the last list are special generators, the base point b is usually taken real in order to obtain convenient generators for a better understanding of the braid action. The basic idea of these can be see in the generators $\alpha _2$ and $\alpha _3$ from Fig. 3.

In the next section, we are going to observe that these singular points are the only ones that appear on hypocycloids.

The Zariski–van Kampen Theorem allows us to provide a presentation even in cases where there are multiple singular points. Moreover, when all the singular points of a curve are real, it allows a visual depiction. To illustrate this, we are going to use the deltoid example. This example was explored by Zariski in [7] and also by Artal and Cogolludo in [2] using a different method.

Example 3

The deltoid is represented by the affine equation:

$$\begin{aligned} 3(x^2+y^2)^2+24x(x^2+y^2)+6(x^2+y^2)-32x^3-1=0. \end{aligned}$$

We can observe that it is a curve of degree 4, which means that the Zariski–van Kampen presentation has 4 generators, namely $\alpha _i$ for $i=1,2,3,4$. The curve possesses three cusps and one tangent point as its singularities. By selecting the base point for the Zariski–van Kampen theorem between the tangent point and the two cusps on the left (see Fig. 4), we can identify the 4 generators.

Fig. 4

Four generators of Deltoid

We also have three projections of the singular points. Moving to the left, we encounter one projection for both cusp points. Moving around a meridian of this projection, we obtain two relations. The first relation corresponds to the generators $\alpha _1$ and $\alpha _3$, while the second relation corresponds to $\alpha _2$ and $\alpha _4$. Locally the cusps have the equation $x^3-y^2=0$, resulting in the following relations:

$$\begin{aligned} \alpha _1\alpha _3\alpha _1=\alpha _3\alpha _1\alpha _3{} & {} \text {and}{} & {} \alpha _2\alpha _4\alpha _2=\alpha _4\alpha _2\alpha _4. \end{aligned}$$

Moving to the right, we encounter one projection for the cusp. Moving around a meridian of this projection, we obtain one relation for the generators $\alpha _1$ and $\alpha _ 2$. Additionally, we have the last projection for the tangent point. Moving around a meridian of this projection, we obtain one relation for the generators $\alpha _3$ and $\alpha _4$. Locally, cusps have the equation $x^3-y^2=0$ and tangent points have the equation $x-y^2=0$, this leads to the following relations:

$$\begin{aligned} \alpha _1\alpha _2\alpha _1&=\alpha _2\alpha _1\alpha _2{} & {} \text {and}{} & {} \alpha _3=\alpha _4. \end{aligned}$$

Summarizing, the fundamental group can be expressed as follows:

$$\begin{aligned} \left\langle \alpha _1, \alpha _2, \alpha _3 \ \begin{array}{|l} \alpha _1\alpha _2\alpha _1=\alpha _2\alpha _1\alpha _2 \\ \alpha _2\alpha _3\alpha _2=\alpha _3\alpha _2\alpha _3 \\ \alpha _3\alpha _1\alpha _3=\alpha _1\alpha _3\alpha _1 \end{array} \right\rangle . \end{aligned}$$

Remark 4

One of the challenges in applying the Zariski–van Kampen theorem is determining which generators are related when the curve contains complex singular points. In such cases, a purely real picture may not be sufficient.

3 Topology and partitions of hypocycloids

In [2], the topology and singularities of complex hypocycloids were studied using Chebyshev polynomials. The research presents results for both the projective curve and the affine curve. The following theorem is part of their results focusing only on the affine curve:

Theorem 5

The complex hypocycloid is a curve of degree 2k with the following properties:

• The curve is invariant under the action of the dihedral group $D_{2N}$.

• The singular points of the complex hypocycloid are N ordinary cusps, $N(\ell -1)$ ordinary real nodes and $N(k-\ell -1)$ ordinary complex nodes.

Some other points to remark in the proof of Proposition 2.1 which appear in [2] are:

• The cusps occur in $\theta _n=\frac{2\pi n}{N}$ with $n=1,\ldots ,N$, that is, $D_{N,\ell }(\frac{2\pi n}{N})$ is a cusp.

• The complex line with angle $\frac{\pi n}{N}$ with $n=1,\ldots ,N$ are the reflection lines of $D_{N,\ell }$.

• The nodes occur in the previous complex lines.

• If we rotate and reparametrize the hypocycloid with and angle $\frac{\pi }{N}$ we obtain the equation:

  $$\begin{aligned} \tilde{D}_{N,\ell } =\left( \frac{\ell \cos (k \theta )-k\cos (\ell \theta )}{N},\frac{\ell \sin (k \theta )+k \sin (\ell \theta )}{N}\right) . \end{aligned}$$

• If we consider the matrices:

  $$\begin{aligned} r=\left( \begin{array}{rr} \cos (\frac{2\pi k}{N}) &{} -\sin (\frac{2\pi k}{N}) \\ \sin (\frac{2\pi k}{N}) &{} \cos (\frac{2\pi k}{N}) \\ \end{array} \right){} & {} \text {and}{} & {} s=\left( \begin{array}{rr} 1 &{} 0 \\ 0 &{} -1 \\ \end{array} \right) , \end{aligned}$$

  of rotation and reflection respectively, those satisfy:

  $$\begin{aligned} rD_{N,\ell }(\theta )&=D_{N,\ell } \left( \theta +\frac{2\pi }{N} \right){} & {} \text {and}{} & {} sD_{N,\ell }(\theta )=D_{N,\ell }(-\theta ). \end{aligned}$$

  Additionally, it can be proved that:

  $$\begin{aligned} r\tilde{D}_{N,\ell }(\theta )&=\tilde{D}_{N,\ell }\left( \theta +\frac{2\pi }{N} \right){} & {} \text {and}{} & {} s\tilde{D}_{N,\ell }(\theta )=\tilde{D}_{N,\ell }(-\theta ). \end{aligned}$$

The next results are original and generally focus on taking advantage of the symmetries of the hypocycloid to find the generators and relations. It is important to note that there are two types of cusps: transversal cusps and tangent cusps. Each of these types yields different relations, emphasizing the need to distinguish between them when analyzing hypocycloids.

Proposition 6

If N is a multiple of 4, then, the hypocycloid $D_{N,\ell }$ has two tangent cusps.

Proof

The tangent cusps have angles $\frac{\pi }{2}$ and $\frac{3\pi }{2}$, on the other side, for an hypocycloid $D_{N,\ell }$ the cusps have angles $\frac{2\pi n}{N}$ with $n=1,\ldots ,N$, by selecting $N=4N'$ and $n=N'$ we have:

$$\begin{aligned} \frac{2\pi n}{N}=\frac{2\pi N'}{N}=\frac{4\pi N'}{2N}=\frac{\pi N}{2N}=\frac{\pi }{2}, \end{aligned}$$

this is the first tangent cusp. The second one can be obtained by reflection. $\square$

It should be noted that even though the vertical tangent points are not singularities, they still need to be taken into account when applying the Zariski–van Kampen theorem. Therefore, we have the following result:

Proposition 7

Let $D_{N,\ell }$ the complex hypocycloid, then:

• If N is multiple of 4 there are $k- \ell -2$ tangent points. The set of points is $\{\theta _n=\frac{2n\pi }{k-\ell }+\frac{\pi }{k-\ell }\}$ minus the two points corresponding with tangent cusps.

• If N is not multiple of 4 there are $k-\ell$ tangent points. The set of points is $\{\frac{2n\pi }{k-\ell }+\frac{\pi }{k-\ell }\}$.

The location

Proof

If we make $X'_{N,\ell }$ and $Y'_{N,\ell }$ equal to zero:

$$\begin{aligned}&\sin (k\theta )+\sin (\ell \theta )=0{} & {} \text {and}{} & {} \cos (k\theta )-\cos (\ell \theta )=0 \\ \Rightarrow&2\sin \left( \frac{k+\ell }{2}\theta \right) \cos \left( \frac{k-\ell }{2}\theta \right) =0{} & {} \text {and}{} & {} 2\sin \left( \frac{k+\ell }{2}\theta \right) \sin \left( \frac{k-\ell }{2}\theta \right) =0, \end{aligned}$$

the points $\cos (\frac{k-\ell }{2}\theta )=0$ make $X'_{\ell ,N}=0$ and $Y'_{\ell ,N}\ne 0$, these are the tangent points:

$$\begin{aligned}&\frac{k-\ell }{2}\theta _n=n\pi +\frac{\pi }{2} \\ \Rightarrow&\theta _n = \frac{2n\pi }{k-\ell }+\frac{\pi }{k-\ell }, \end{aligned}$$

with $n=1,\ldots ,k-\ell$. When N is a multiple of 4, by the preceding proposition we know that there is some $t\in \{1,\ldots ,N\}$ such that the angle of $D_{N,\ell }(\frac{2t\pi }{N})$ is $\frac{\pi }{2}$, that means:

$$\begin{aligned} \frac{2t\ell \pi }{N}=\frac{\pi }{2}+2\pi m, \end{aligned}$$

(1)

for some integer m. Observe that the tangent points coincide with the cusp points when:

$$\begin{aligned}&\frac{(2n+1)\pi }{k-\ell }=\frac{2t\pi }{N}+2\pi s \\ \Leftrightarrow&N(2n+1)=2t(k-\ell )+2N(k-\ell )s \\ \Leftrightarrow&(2N)n=[2t(k-\ell )-N] + [2N(k-\ell )] s. \end{aligned}$$

The greatest common divisor of 2N and $2N(k-\ell )$ is 2N and, moreover:

$$\begin{aligned} \frac{2t(k-\ell )-N}{2N}&=\frac{2tN-4t\ell -N}{2N}=\frac{2tN}{2N}-\frac{4t\ell }{2N}-\frac{1}{2} \\&=t-\frac{1}{2}-\frac{2t\ell }{N}=t-\frac{1}{2}-(\frac{1}{2}+2m){} & {} \text {by} (1) \\&=t-1-2m \in \mathbb {Z}, \end{aligned}$$

i.e. 2N divides $2t(k-\ell )-N$ so we have integer solutions for n and s (results related to Diophantine equations can be found in [3]). In other words, if N is a multiple of 4, one of the tangent points correspond with a tangent cusp, then, the number of tangent points in this case is $k-\ell -2$. $\square$

Note that we can use the Riemann–Hurwitz formula to determine the number of vertical tangencies. However, to obtain the correct relations in the Zariski–van Kampen theorem, we need to specify the location of these tangencies.

Remark 8

We can exclude from our analysis the consideration when N is multiple of 4 by rotating the hypocycloids and avoiding the tangent cusps. This provides an alternative way to establish similar results.

To distinguish the generators of the fundamental group we are going to make a partition of the domain. Let us define:

$$\begin{aligned} A_n=\left[ \frac{2\pi (n-1)}{N},\frac{2 \pi n}{N}\right) \times i\mathbb {R}\subset \mathbb {C},{} & {} n=1,\ldots ,N. \end{aligned}$$

The next theorem is the key to distinguish N of the generators of the hypocycloid $D_{N,\ell }$.

Theorem 9

$X_{N,\ell }|_{A_n}: A_n \rightarrow \mathbb {C}$ is surjective for $n=1,\ldots , N$.

It is equivalent to say that $X_{N,\ell }-X_0=0$ has at less one solution in every $A_n$ for $n=1,\ldots , N$ and for any $X_0$ of $\mathbb {C}$.

Proof

Observe that:

$$\begin{aligned} X_{N,\ell }-X_0&=\frac{\ell \cos (k \theta )+k\cos (\ell \theta )}{N}-X_0 \\&=\frac{\ell e^{ki\theta }+\ell e^{-ki\theta }+ke^{\ell i\theta }+k e^{-\ell i\theta }}{2N}-X_0 \\&=\frac{1}{2Ne^{ki\theta }}(\ell e^{2ki\theta }+\ell +ke^{(k+\ell ) i\theta }+k e^{(k-\ell ) i\theta }-2NX_0e^{ki\theta }). \\ \text {Let } x=e^{i\theta },&\\&=\frac{1}{2Nx^k}(\ell x^{2k}+\ell +k x^{N}+ k x^{k-\ell }-2NX_0 x^{k}), \end{aligned}$$

as $k>\ell$ all the indices in the polynomial are positive. We are going to consider the solutions in $A_1$, the rest are similar. Using the transformation $x=e^{i\theta }$ it is enough to find the solutions of:

$$\begin{aligned} h(x)=\ell x^{2k}+k x^N -2NX_0 x^k +kx^{k-\ell }+\ell \end{aligned}$$

in the region of Fig. 5 with $R \rightarrow \infty$.

Fig. 5

Region to find solutions, R must tend to infinity

To do this we are going to use the principle of the argument, it can be found in [5, Theorem 6.2.4]; observe that:

$$\begin{aligned} arg [h(x)]&=arg [x^{2k}(\ell +kx^{N-2k}-2NX_0x^{-k}+kx^{-k-\ell }+\ell x^{-2k})] \\&= arg [x^{2 ^k}]+ arg[\ell +kx^{N-2k}-2NX_0x^{-k}+kx^{-k-\ell }+\ell x^{-2k}]. \end{aligned}$$

We let $f(x)=x^{2k}$ and $g(x)=[\ell +kx^{N-2k}-2NX_0x^{-k}+kx^{-k-\ell }+\ell x^{-2k}]$, and we are going to divide the curve in 3 parts:

• (1) Real line.

  $$\begin{aligned} \lim _{R\rightarrow \infty }arg[h(R)]&=\lim _{R\rightarrow \infty }arg[f(R)]+\lim _{R\rightarrow \infty }arg[g(R)]]\\&=\lim _{R\rightarrow \infty }arg[g(R)]\\&=arg[\ell ]\\&=0. \end{aligned}$$

  The real line does not bring any changes in the argument.

• (2) The line with angle $\frac{2\pi }{N}$. In this case, using $Re^{i\frac{2\pi }{N}}$ and similarly as the preceding case, it does not bring any change in the argument.

• (3) The curve $\gamma (t)=Re^{it}$ with $t\in [0,\frac{2\pi }{N}]$. First consider:

  $$\begin{aligned} \lim _{R\rightarrow \infty }arg[g(\gamma (t))]= arg(\ell )=0. \end{aligned}$$

  The first equality holds because all the exponents of g are negative. Also:

  $$\begin{aligned} \frac{1}{i} \Delta arg [f(x)]&=\frac{1}{i}\int _{f(\gamma )}\frac{dz}{z}=\frac{1}{i}\int _0 ^{\frac{2\pi }{N}}\frac{2k(Re^{it}) ^{2k-1}}{(Re^{it}) ^{2k}}Rie^{it}dt \\&=\int _{0}^{\frac{2\pi }{N}}2kdt=2k\frac{2\pi }{N}=\frac{4\pi k}{N}>2\pi , \end{aligned}$$

  the change in the argument is at least $2\pi$.

By the principle of the argument there are at least one solution in $A_1$. $\square$

In a similar way we can prove for $Y_{N,\ell }$.

Theorem 10

$Y_{N,\ell }|_{A_n}: A_n \rightarrow \mathbb {C}$ is surjective for $n=1,\ldots , N$.

Once we partition the domain, it becomes necessary to determine the location of singular points, it does not need to be the exact location, only their respective regions $A_i$. Let’s begin by considering the tangent points.

Proposition 11

Each $A_i$ intersects $\{\frac{2n\pi }{k-\ell }+\frac{\pi }{k-\ell }\}$ in at most one point.

Proof

If we take two consecutive points (n and $n+1$), as $N>k-\ell$:

$$\begin{aligned}&\left| \frac{2n\pi }{k-\ell }+\frac{\pi }{k-\ell }-\left( \frac{2(n+1)\pi }{k-\ell }+\frac{\pi }{k-\ell } \right) \right| 2\pi \left| \frac{n}{k-\ell }-\frac{n+1}{k-\ell } \right| =\frac{2\pi }{k-\ell }>\frac{2\pi }{N}. \end{aligned}$$

$\square$

Remark 12

In the case when N is a multiple of 4, the last proposition includes the tangent cusps.

The cusp points are easy to locate because every $A_i$ starts in one, the remaining points are the nodes, in these cases we need to use the reflection complex lines to locate.

Lemma 13

For every pair $D_{N,\ell }(A_n)$ and $D_{N,\ell }(A_m)$ there is a reflection line such that $D_{N,\ell }(A_m)$ is reflection of $D_{N,\ell }(A_n)$.

Proof

Using rotations it is enough to prove it for $A_1$ and $A_n$; take the middle point in the image under $D_{N,\ell }$ of $A_1$ this has an angle $\frac{\pi \ell }{N}$ while the middle point in the image of $A_n$ has angle $\frac{2\pi (n-1)\ell }{N}+\frac{\pi \ell }{N}$, if we take the middle angle between these two, we have:

$$\begin{aligned} \frac{\ell \pi }{N}+\frac{1}{2}\left( \frac{2\pi (n-1)\ell }{N}+\frac{\pi \ell }{N}-\frac{\pi \ell }{N}\right) =\frac{\ell \pi }{N}+\frac{\pi (n-1)\ell }{N}= \frac{\ell n \pi }{N}, \end{aligned}$$

which, as we mention early, it’s an angle corresponding to a reflection complex line. $\square$

As we saw in Theorem 5, the nodes belong to the reflection complex lines, but we need to know which $A_i$ intersects in order to give the relations for the Zariski–van Kampen theorem.

Theorem 14

Every pair $D_{N,\ell }(A_n)$ and $D_{N,\ell }(A_m)$ intersects in a node if $m\ne n-1,n, n+1$.

Proof

If we take the complex lines of last lemma for $D_{\ell ,N}(A_n)$ and $D_{\ell ,N}(A_m)$ and rotate in such a way that agree with x axis, we can suppose, without loss of generality, that if $\theta \in A_n$ then $-\theta \in A_m$. Observe that, after the rotation, the equation could be of the form $D_{N,\ell }$ or $\tilde{D}_{N,\ell }$, in both cases the proof is similar so we are only consider the case $D_{N,\ell }$. By Theorem 10$Y_{N,\ell }(\theta )=0$ has a solution in $A_n$, say $\theta _0$ and observe that, as $X_{N,\ell }$ is an even function, then:

$$\begin{aligned} D_{N,\ell }(\theta _0)=(X_{N,\ell }(\theta _0),0)=(X_{N,\ell }(-\theta _0),0)=D_{N,\ell }(-\theta _0) \end{aligned}$$

that means, $D_{N,\ell }(A_n)$ and $D_{N,\ell }(A_m)$ intersect in $D_{N,\ell }(\theta _0)$. Furthermore, as $m\ne n-1,n, n+1$, this point can’t be a cusp or tangent, the only option is a node. $\square$

The advantage of the last theorem is that it includes complex nodes, so even when we can not see the exact location, we know how they are related. The last part is to show that the nodes does not give us more relations, to do this it’s enough to count all the possible relations so we need the next lemma:

Lemma 15

If $D_{N,\ell }(A_n)$ and $D_{N,\ell }(A_m)$ intersects in a complex node, then $D_{N,\ell }(A_n)$ and $D_{N,\ell }(A_m)$ intersect in the conjugate node.

Proof

Let $\theta _n\in A_n$ and $\theta _m\in A_m$ such that $D_{N,\ell }(\theta _n)=D_{N,\ell }(\theta _m)$ (this is a node point), using that $\sin (\overline{z})=\overline{\sin (z)}$ and $\cos (\overline{z})=\overline{\cos (z)}$ we have:

$$\begin{aligned} D_{N,\ell }(\overline{\theta _n})&=(X_{N,\ell }(\overline{\theta _n}),Y_{N,\ell }(\overline{\theta _n})) \\&=(\overline{X_{N,\ell }(\theta _n)},\overline{Y_{N,\ell }(\theta _n)})\\&=(\overline{X_{N,\ell }(\theta _m)},\overline{Y_{N,\ell }(\theta _m)})\\&=(X_{N,\ell }(\overline{\theta _m}),Y_{N,\ell }(\overline{\theta _m})) \\&= D_{N,\ell }(\overline{\theta _m}). \end{aligned}$$

$\square$

The next proposition guarantees that there are no more relations given by nodes.

Proposition 16

A node point is an intersection of $D_{N,\ell }(A_n)$ and $D_{N,\ell }(A_m)$ for some n and m.

Proof

It is enough to count all the intersections of $D_{N,\ell }(A_n)$ and $D_{N,\ell }(A_m)$ $m\ne n-1,n, n+1$ and see that agree with the number of nodes given in Theorem 5. First we are going to count the real intersections. For each $D_{N,\ell }(A_n)$ we have $(\ell -1)$ cusp between the two cusps corresponding for $D_{N,\ell }(A_n)$, each of these cusps are related with another 2 so we have $2(\ell -1)$ intersections, counting the N parts and considering that the intersections are counted twice we have:

$$\begin{aligned} \frac{2N(\ell -1)}{2}=N(\ell -1), \end{aligned}$$

this is exactly the number of real nodes given in Theorem 5. For the complex intersections observe that each $D_{N,\ell }(A_n)$ is related with $N-3$ $D_{N,\ell }(A_m)$, if we only count one node for each intersection we have:

$$\begin{aligned} \frac{N(N-3)}{2} \end{aligned}$$

nodes, now we subtract the real nodes to only count the complex nodes we have:

$$\begin{aligned} \frac{N(N-3)}{2}-N(\ell -1) \end{aligned}$$

and finally we count 2 complex nodes for each intersection by Lemma 15 to obtain:

$$\begin{aligned} 2\left[ \frac{N(N-3)}{2}-N(\ell -1) \right]&=N(N-3)-2N(l\ell -1)\\&=N(k+\ell -3-2\ell +2) \\&=N(k-\ell -1), \end{aligned}$$

this is exactly the number of complex nodes given in Theorem 5. $\square$

4 Fundamental group of the complement of hypocycloids

In this section we are going to prove Theorem 1; we divide the proof in several lemmas, one for each kind of singular point. By the results of Theorem 5 we know that the hypocycloids have degree 2k so the fundamental group has the general form:

$$\begin{aligned} \left\langle \beta _i,\ i\in \{1,\ldots ,2k\} \ \begin{array}{|l} R \end{array} \right\rangle , \end{aligned}$$

where R represents a set of relations given by the singular and tangent points. First, we are going to reduce the generators using equality relations.

Lemma 17

There are N among the 2k generators such that

$$\begin{aligned} \left\langle \beta _i,\ i\in \{1,\ldots ,2k\} \ \begin{array}{|l} R \end{array} \right\rangle = \left\langle \alpha _i,\ i\in \{1,\ldots ,N\} \ \begin{array}{|l} R' \end{array} \right\rangle \end{aligned}$$

with $R'$ the same relations as R except for equality relations and for replacements of $\beta _i$ with $\alpha _j$ in the relations.

Proof

If we take the base point $b\in \mathbb {C}$ such that it is not singular nor tangent, the vertical complex line $x=b$, denoted $L_b$, intersects $D_{N,\ell }(\mathbb {C})$ in 2k points; by Theorem 9 there are $\theta _n \in A_n$ for $n=1,\ldots ,N$ such that $X_{N,\ell }(\theta _n)=b$, the points $D_{N,\ell }(\theta _n)$ belong to $L_b \cap D_{N,\ell }(\mathbb {C})$. We recall that, according to Zariski–van Kampen theorem, a loop surrounding these points and joining the base point b with a path represents a generator of the fundamental group. Reordering if it was necessary, we can suppose that the first N generators of the fundamental group $\pi _1(D_{N,\ell })$ are the ones that correspond to each $D_{N,\ell }(\theta _n)$, we are going to call it $\alpha _n$. In order to use the equality relations we must distinguish two cases: N multiple of 4 and N is not a multiple of 4. In the last one we have $k-\ell$ tangent points (by Proposition 7) which correspond to equalities by the Zariski–van Kampen theorem. If N is multiple of 4 there are $k-\ell -2$ tangent points (by Proposition 7) and 2 tangent cusps, these, by the Zariski–van Kampen theorem, give us two types of relations, the first ones of the form $\alpha =\beta$ and the second ones of the form $\alpha \beta \alpha =\beta \alpha \beta$; if we consider only the equality relations, in total we have $k-\ell$ equalities. In both cases, these equalities occur in $t_i=\frac{2i\pi }{k-\ell }+\frac{\pi }{k-\ell }$, by the Proposition 11, these points belong to different $A_n$. To use Zariski–van Kampen theorem and give the equality between two generators, we need a path in the x axis from b to the projection of $D_{N,\ell }(t_n)$, we are going to suppose that $\theta _i$ and $t_j$ belong to the same $A_n$, if we take $A_n$ minus the singular points, it is arcwise connected so there is a path r(s) from $\theta _i$ to $t_j$, we take the projection of $D_{N,\ell }(r(s))$ in the x axis and this is the desired path. Following that path, then traverse around the projection of the singular point and travel the path in the opposite direction, we are given a equality relation between the $\alpha _i$ generator corresponding to $D_{N,\ell }(\theta _i)$ and one of the remaining $k-\ell$ generators $\beta _j$. $\square$

Once we finish with equality relations, the only relations that appear are given by cusps and nodes. Now we are going to analyze the cusp points.

Lemma 18

For each cusp point, we have the relation $\alpha _i\alpha _{i+1}\alpha _i=\alpha _{i+1}\alpha _i\alpha _{i+1}$ with $i \bmod {N}$.

Proof

Similar to the last lemma, by Theorem 9 there is $\theta _i \in A_i$ such that $X_{N,\ell }(\theta _i)=b$; also there is $t_i\in A_i$ such that $D_{N,\ell }(t_i)$ is the cusp point between $D_{N,\ell }(A_i)$ and $D_{N,\ell }(A_{i+1})$. To use Zariski–van Kampen theorem and give the relation between two generators we need a path in the x axis from b to the projection of $D_{N,\ell }(t_i)$. If we take $A_i$ minus the singular points, it is arcwise connected, so there is a path r(s) from $\theta _i$ to $t_i$, we take the projection of $D_{N,\ell }(r(s))$ in the x axis and this is the desired path. Following that path we are given a cusp relation between the $\alpha _i$ generator corresponding to $D_{N,\ell }(\theta _i)$ and the $\alpha _{i+1}$ generator corresponding to $D_{N,\ell }(\theta _{i+1})$. $\square$

The last lemma includes the case N multiple of 4, and together with the Lemma 17 exhaust all the relations of the tangent cusps. Until now we have:

$$\begin{aligned} \left\langle \alpha _i,\ i\in \mathbb {Z}/ N \ \begin{array}{|l} R''\\ \alpha _i\alpha _{i+1}\alpha _i=\alpha _{i+1}\alpha _i\alpha _{i+1} \ \end{array} \right\rangle , \end{aligned}$$

with $R''$ a set of relations given by the nodes. We are going to analyze the last set of relations.

Lemma 19

For each pair $\alpha _i$ and $\alpha _j$ with $j \ne i-1,i+1$ we have the relation $\alpha _i\alpha _j=\alpha _j\alpha _i$.

Proof

By Theorem 14, if $j\ne i-1,i+1$ then two different $D_{N,\ell }(A_i)$ and $D_{N,\ell }(A_j)$ intersect in a node, we can suppose that $t_i\in A_i$ is such that $D_{N,\ell }(t_i)$ is this node; also, by Theorem 9 there is $\theta _i \in A_i$ such that $X_{N,\ell }(\theta _i)=b$. If we take $A_i$ minus the singular points, it is arcwise connected, so there is a path r(s) from $\theta _i$ to $t_i$, we take the projection of $D_{N,\ell }(r(s))$ in the x axis. Following that path we are given the relation $\alpha _i\alpha _j=\alpha _j\alpha _i$ between the $\alpha _i$ generator corresponding to $D_{N,\ell }(\theta _i)$ and $\alpha _{j}$ generator corresponding to $D_{N,\ell }(\theta _{j})$. $\square$

By Proposition 16 we exhaust all the nodes so there are no more relations. All the preceding results prove the Theorem 1.

5 Examples

Even when the results are in general for all the hypocycloids, we are going to give a pair of examples. The first is the deltoid but using the ideas given in this work.

Example 20

$D_{3,1}$ is a curve of degree 4 so it has 4 generators, it has 3 transversal cusps, 1 tangent points and no other singularities. If we take a vertical line next to the right cusp, we can only see 2 of the 4 points corresponding to generators (see Fig. 6). The difference with Example 3 is that we can not see 2 of the generators, so we represent them on the same line. We can make a partition of the domain of $D_{3,1}$ into 3 parts $A_1$, $A_2$ and $A_3$. By Theorem 9 we can distinguish 3 generators, one for each $A_i$, we are going to call it $\alpha _i$ with $i=1,2,3$.

Fig. 6

Dashed lines represent the path followed by $\alpha _2$ to the cusp

By Proposition 11 we have 1 tangent point, this means that there is 1 equality relation, this tangent point belongs to $A_2$ so the missing generator must be equal to $\alpha _2$ by Lemma 17. By the definition of $A_i$ we can observe that two consecutive generators go to one common cusp, using Lemma 18 there is a cusp relation between each consecutive $\alpha _i$ (In the Fig. 7 we represent the path followed by $\alpha _2$ to the cusp), this gives the relations:

$$\begin{aligned} \alpha _i\alpha _{i+1}\alpha _i=\alpha _{i+1}\alpha _i\alpha _{i+1}, \end{aligned}$$

module 3.

The second example is $D_{8,1}$. This example cannot be derived from the results of [1] or [2], so we consider it a new example.

Example 21

$D_{8,1}$ is a curve of degree 14 so it has 14 generators, it has 6 transversal cusps, 2 tangent cusps, 40 complex nodes, 4 tangent points and no other singularities. If we take a vertical line next to the right cusp, we can only see 2 of the 14 points corresponding to generators (see Fig. 5), the other 12 are represented in the same line. We can make a partition of the domain of $D_{8,1}$ into 8 parts $A_i$ with $i=1,..,8$ and by Theorem 9 we can distinguish 8 generators, one for each $A_i$, we are going to call it $\alpha _i$ with $i=1,\ldots ,8$.

Fig. 7

Dashed lines represent the path followed by generators $\alpha _2$ and $\alpha _7$ to the corresponding cusp point

By Proposition 11 we have 4 tangent points and the 2 tangent cusps in different $A_i$ (the only ones without a tangent point are $A_3$ and $A_7$) this means that there are 6 equality relations, in other words, the 6 generators missing must be equal to one $\alpha _i$ different (the generators without equality relation are $\alpha _3$ and $\alpha _7$). By the definition of $A_i$ we can observe that two consecutive generators go to one common cusp, by Lemma 18 this gives the relations:

$$\begin{aligned} \alpha _i\alpha _{i+1}\alpha _i=\alpha _{i+1}\alpha _i\alpha _{i+1}, \\ \end{aligned}$$

module 8 (in the Fig. 5 we represent by dashed lines the paths of two of the generators to the corresponding cusp). The forty complex nodes live in complex lines with angles $\frac{\pi n}{8}$ with $n=1,\ldots ,8$, by Theorem 14 every pair $D_{8,1}(A_n)$ and $D_{8,1}(A_m)$ intersects in a node if n and m are not consecutive module 8, by Lemma 19 this gives us the relations:

$$\begin{aligned} \alpha _n\alpha _m=\alpha _m\alpha _n. \end{aligned}$$

Finally, by Lemma 15 there are 2 intersections for each pair $D_{8,1}(A_n)$ and $D_{8,1}(A_m)$, and by Proposition 16 this gives us $8(8-3)=40$ intersections, in other words, this exhausts the relations given by nodes so there are no more relations.