Dunford-Pettis type properties in $L_1$ of a vector measure

Abstract

Let $\nu$ be a countably additive vector measure defined on a $\sigma$-algebra and taking values in a Banach space. In this paper we deal with the following three properties for the Banach lattice $L_1(\nu )$ of all $\nu$-integrable real-valued functions: the Dunford-Pettis property, the positive Schur property and being lattice-isomorphic to an AL-space. We give new results and we also provide alternative proofs of some already known ones.

1 Introduction

Let X be a Banach space with (topological) dual $X^*$, let $(\Omega ,\Sigma )$ be a measurable space and let $\nu :\Sigma \rightarrow X$ be a (countably additive) vector measure. A $\Sigma$-measurable function $f:\Omega \rightarrow \mathbb {R}$ is called $\nu$-integrable if it is $|x^*\nu |$-integrable for all $x^*\in X^*$ and, for each $A\in \Sigma$, there is $\int _A f \, d\nu \in X$ such that

$$\begin{aligned} x^*\left( \int _A f \, d\nu \right) =\int _A f\,d(x^*\nu ) \quad \text {for all } x^*\in X^*. \end{aligned}$$

Here $x^*\nu$ is the signed measure obtained as the composition of $\nu$ with $x^*$ and $|x^*\nu |$ denotes its variation. By identifying functions which coincide except to a $\nu$-null set (where $A\in \Sigma$ is said to be $\nu$-null if $\nu (B)=0$ for every $B\in \Sigma$ with $B\subseteq A$), the set $L_1(\nu )$ of all (equivalence classes of) $\nu$-integrable functions is a Banach lattice with the $\nu$-a.e. order and the norm

$$\begin{aligned} \Vert f\Vert _{L_1(\nu )}:=\sup _{x^*\in B_{X^*}}\int _\Omega |f|\,d|x^*\nu |. \end{aligned}$$

Here $B_{X^*}$ denotes the closed unit ball of $X^*$. Let us agree to say that $L_1(\nu )$ is the $L_1$ space of the vector measure $\nu$.

Every Banach lattice with order continuous norm and a weak unit is lattice-isometric to the $L_1$ space of a vector measure, [11, Theorem 8] (cf. [19, Proposition 2.4]). Such a representation is not unique. For instance, the usual space $L_1[0,1]$ is equal to $L_1(\nu _i)$ for each one of the following $X_i$-valued vector measures $\nu _i$ defined on the Borel $\sigma$-algebra of [0, 1]:

• $X_1:={\mathbb {R}}$ and $\nu _1(A):=\lambda (A)$ (the Lebesgue measure of A);

• $X_2:=L_1[0,1]$ and $\nu _2(A):=\chi _A$ (the characteristic function of A);

• $X_3:=c_0$ and $\nu _3(A):=(\int _A r_n \, d\lambda )_{n\in \mathbb {N}}$, where $(r_n)_{n\in \mathbb {N}}$ is the sequence of Rademacher functions.

The structure of the space $L_1(\nu )$ can be greatly conditioned by certain properties of $\nu$. For complete information on these spaces and their important role in Banach lattices and operator theory, we refer the reader to the monograph [33] and the papers [6, 14, 15, 28, 34, 36, 38].

The inclusion map

$$\begin{aligned} \iota _\nu : L_1(|\nu |) \rightarrow L_1(\nu ) \end{aligned}$$

is a well-defined injective lattice-homomorphism, where $|\nu |$ is the variation of $\nu$ (see, e.g., [33, Lemma 3.14]). If $\iota _\nu$ is surjective, then it is a lattice-isomorphism and, moreover, we have $|\nu |(\Omega )<\infty$. Curbera [12] addressed the question of when the $L_1$ space of a vector measure is lattice-isomorphic to an AL-space. Recall that a Banach lattice E is said to be an AL-space if its norm satisfies $\Vert x+y\Vert =\Vert x\Vert +\Vert y\Vert$ whenever $x,y\in E$ are disjoint, which is equivalent to saying that E is lattice-isometric to the usual space $L_1(\mu )$ of a non-negative measure $\mu$ (see, e.g., [3, Theorem 4.27]). It turns out that $L_1(\nu )$ is lattice-isomorphic to an AL-space if and only if $\iota _\nu$ is surjective, [12, Proposition 2]. This is also equivalent to the fact that the integration operator of $\nu$, that is, the norm 1 operator

$$\begin{aligned} I_\nu :L_1(\nu )\rightarrow X,\quad I_\nu (f):=\int _\Omega f \, d\nu \quad \text {for all } f\in L_1(\nu ), \end{aligned}$$

is cone absolutely summing (i.e., the series $\sum _{n=1}^\infty I_\nu (f_n)$ is absolutely convergent whenever $\sum _{n\in \mathbb {N}}f_n$ is unconditionally convergent and $f_n \in L_1(\nu )^+$ for all $n\in \mathbb {N}$), [10, Proposition 3.1]. As usual, given a Banach lattice E, we denote by $E^+$ its positive cone, that is, $E^+:=\{x\in E: x\ge 0\}$. At this point we should stress that if a Banach lattice is isomorphic (just as a Banach space) to an AL-space, then it is lattice-isomorphic to an AL-space [1] (cf. [16, Proposition 2.1]).

An operator between Banach spaces is said to be Dunford-Pettis (or completely continuous) if it maps weakly null sequences to norm null ones. The space $L_1(\mu )$ of a non-negative measure $\mu$ has the Dunford-Pettis property, that is, every weakly compact operator from $L_1(\mu )$ to an arbitrary Banach space is Dunford-Pettis (see, e.g., [2, Theorem 5.4.5] or [3, Theorem 5.85]). In general, this is not true for the $L_1$ space of a vector measure. Indeed, reflexive infinite-dimensional Banach spaces fail the Dunford-Pettis property and, as we have already mentioned, spaces like $\ell _p$ and $L_p[0,1]$ for $1<p<\infty$ can be seen as $L_1$ spaces of a vector measure. On the other side, there are $L_1$ spaces of a vector measure having the Dunford-Pettis property which are not lattice-isomorphic to an AL-space, like $c_0$. Curbera showed in [13, Theorem 4] that $L_1(\nu )$ has the Dunford-Pettis property if $\nu$ has $\sigma$-finite variation and X has the Schur property (i.e., every weakly null sequence in X is norm null). In fact, he proved that:

• (i) $L_1(\nu )$ has the positive Schur property whenever X has the Schur property.

• (ii) If $L_1(\nu )$ has the positive Schur property and $\nu$ has $\sigma$-finite variation, then $L_1(\nu )$ has the Dunford-Pettis property (cf. [6, Section 3.2]).

Recall that a Banach lattice E is said to have the positive Schur property if every weakly null sequence in $E^+$ is norm null. Note that statement (i) can be deduced at once from the fact that $L_1(\nu )$ has the positive Schur property if and only if the integration operator $I_\nu$ is almost Dunford-Pettis (i.e., $(I_\nu (f_n))_{n\in \mathbb {N}}$ is norm null for every weakly null sequence $(f_n)_{n\in \mathbb {N}}$ in $L_1(\nu )^+$), see [6, Theorem 5.12].

The integration operator is undoubtedly a key point in the theory of $L_1$ spaces of a vector measure. Note that its properties depend on $\nu$ rather than on the space $L_1(\nu )$ itself. For instance, going back to the example at the beginning, we have:

• $I_{\nu _1}$ is the functional given by $I_{\nu _1}(f)=\int _{[0,1]} f \, d\lambda$;

• $I_{\nu _2}$ is the identity operator on $L_1[0,1]$;

• $I_{\nu _3}: L_1[0,1]\rightarrow c_0$ is the operator given by $I_{\nu _3}(f)=(\int _{[0,1]} r_n f \, d\lambda )_{n\in \mathbb {N}}$, which is strictly singular but fails to be weakly compact.

It is known that $L_1(\nu )$ is lattice-isomorphic to an AL-space whenever $I_\nu$ is compact (see [30, Theorem 1], cf. [32, Theorem 2.2] and [7, Theorem 3.3]), absolutely p-summing for $1\le p <\infty$ (see [31, Theorem 2.2]) or, more generally, Dunford-Pettis and Asplund (see [35, Theorem 3.3]). Recall that an operator between Banach spaces is said to be Asplund if it factors through a Banach space which is Asplund (i.e., all of its separable subspaces have separable dual). In particular, $L_1(\nu )$ is lattice-isomorphic to an AL-space if $I_\nu$ is Dunford-Pettis and X is Asplund, [7, Theorem 1.3]. This is a partial answer to the following question posed by Okada, Ricker and Rodríguez-Piazza [31]:

Question 1.1

Suppose that $I_\nu$ is Dunford-Pettis and that X contains no subspace isomorphic to $\ell _1$. Is $L_1(\nu )$ lattice-isomorphic to an AL-space?

They showed that this is the case if, in addition, X has an unconditional Schauder basis, [31, Theorem 1.2]. Note that any Banach space with an unconditional Schauder basis and no subspace isomorphic to $\ell _1$ has separable dual (see, e.g., [2, Theorem 3.3.1]). To the best of our knowledge, Question 1.1 remains open.

In this paper we deal with $L_1$ spaces of a vector measure with focus on the property of being isomorphic to an AL-space, the positive Schur property and the Dunford-Pettis property. Our aim is twofold: we include new results and we also present alternative proofs of some already known ones which hopefully might led to a better understanding of the theory. The structure of the paper is as follows.

In Sect. 2 we collect some known preliminary facts on $L_1$ spaces of a vector measure that will be needed later.

In Sect. 3 we revisit the aforementioned positive answer to Question 1.1 for Asplund spaces (Corollary 3.8) and the related result for integration operators which are Dunford-Pettis and Asplund (Corollary 3.11).

In Sect. 4 we show that the positive Schur property of $L_1(\nu )$ can be characterized by means of a Dunford-Pettis type property with respect to the so-called “vector duality” induced by the integration operator, that is, the continuous bilinear map

$$\begin{aligned} L_1(\nu )\times L_\infty (\nu ) \rightarrow X, \qquad (f,g) \mapsto I_\nu (fg)=\int _\Omega fg \, d\nu \end{aligned}$$

(Theorem 4.3). We also give another proof of the aforementioned result of [13] stating that $L_1(\nu )$ has the Dunford-Pettis property if it has the positive Schur property and $\nu$ has $\sigma$-finite variation (Corollary 4.5). It seems to be an open question whether the assumption on the variation can be dropped, namely:

Question 1.2

Suppose that $L_1(\nu )$ has the positive Schur property. Does $L_1(\nu )$ have the Dunford-Pettis property?

Finally, in Example 4.6 we discuss a class of vector measures $\nu$ such that $L_1(\nu )$ has the positive Schur property and the Dunford-Pettis property, but fails to be lattice-isomorphic to an AL-space, among other interesting properties.

2 Preliminaries

All Banach spaces considered in this paper are real. An operator is a continuous linear map between Banach spaces. Given an operator T, its adjoint is denoted by $T^*$. By a subspace of a Banach space we mean a norm closed linear subspace. Let Z be a Banach space. The norm of Z is denoted by $\Vert \cdot \Vert _Z$, or simply $\Vert \cdot \Vert$, and we write $B_Z:=\{z\in Z: \Vert z\Vert \le 1\}$ (the closed unit ball of Z). The evaluation of $z^*\in Z^*$ at $z\in Z$ is denoted by either $z^*(z)$ or $\langle z^*,z\rangle$. By a projection from Z onto a subspace $Y \subseteq Z$ we mean an operator $P:Z\rightarrow Z$ such that $P(Z)=Y$ and P is the identity when restricted to Y. The subspace of Z generated by a set $H \subseteq Z$ is denoted by $\overline{\textrm{span}}(H)$.

In this section we gather, for the reader’s convenience, some known facts on $L_1$ spaces of a vector measure. A basic reference on this topic is [33, Chapter 3].

Throughout this section X is a Banach space, $(\Omega ,\Sigma )$ is a measurable space and $\nu \in \textrm{ca}(\Sigma ,X)$. As usual, we denote by $\textrm{ca}(\Sigma ,X)$ the set of all countably additive X-valued vector measures defined on $\Sigma$. The range of $\nu$ is the set

$$\begin{aligned} {\mathcal {R}}(\nu ):=\{\nu (A): \, A\in \Sigma \}\subseteq X. \end{aligned}$$

The variation and semivariation of $\nu$ are denoted by $|\nu |$ and $\Vert \nu \Vert$, respectively. The family of all $\nu$-null sets is denoted by ${\mathcal {N}}(\nu )$. By a Rybakov control measure of $\nu$ we mean a finite non-negative measure of the form $\mu =|x^*\nu |$ for some $x^*\in X^*$ such that ${\mathcal {N}}(\mu ) = {\mathcal {N}}(\nu )$ (see, e.g., [18, p. 268, Theorem 2]). Throughout this section $\mu$ is a fixed Rybakov control measure of $\nu$.

2.1 $L_\infty$ of a vector measure

A function $f:\Omega \rightarrow \mathbb {R}$ is called $\Sigma$-simple if it is a linear combination of functions of the form $\chi _A$, where $A\in \Sigma$. Clearly, all $\Sigma$-simple functions are $\nu$-integrable. The set of all $\Sigma$-simple functions is norm dense in $L_1(\nu )$ (see, e.g., [33, Theorem 3.7(ii)]), so one has

$$\begin{aligned} \overline{I_\nu (L_1(\nu ))} = \overline{\textrm{span}}({\mathcal {R}}(\nu )). \end{aligned}$$

(2.1)

More generally, every $\nu$-essentially bounded $\Sigma$-measurable function $f:\Omega \rightarrow \mathbb {R}$ is $\nu$-integrable. By identifying functions which coincide $\nu$-a.e., the set $L_\infty (\nu )$ of all (equivalence classes of) $\nu$-essentially bounded $\Sigma$-measurable functions is a Banach lattice with the $\nu$-a.e. order and the $\nu$-essential supremum norm $\Vert \cdot \Vert _{L_\infty (\nu )}$. Of course, $L_\infty (\nu )$ is equal to the usual spaces $L_\infty (|\nu |)$ and $L_\infty (\mu )$. The inclusion map

$$\begin{aligned} j_\nu : L_\infty (\nu ) \rightarrow L_1(\nu ) \end{aligned}$$

is an injective operator. Moreover, it is weakly compact. Indeed, $j_\nu (B_{L_\infty (\nu )})$ coincides with the order interval $[-\chi _\Omega ,\chi _\Omega ]$ in $L_1(\nu )$, so it is weakly compact as $L_1(\nu )$ has order continuous norm (see, e.g., [3, Theorem 4.9]). Hence, $I_\nu (j_\nu (B_{L_\infty (\nu )}))$ is weakly compact in X. We have the following characterization of relative norm compactness of ${\mathcal {R}}(\nu )$ (see, e.g., [33, Proposition 2.41]):

Proposition 2.1

The following statements are equivalent:

• (i) ${\mathcal {R}}(\nu )$ is relatively norm compact.

• (ii) $I_\nu (j_\nu (B_{L_\infty (\nu )}))$ is norm compact.

2.2 Composition of a vector measure with an operator

We will use several times the following fact (see, e.g., [33, Lemma 3.27]):

Proposition 2.2

Let $T:X\rightarrow Y$ be an operator between Banach spaces. Then:

• (i) The composition ${\tilde{\nu }}:=T\circ \nu :\Sigma \rightarrow Y$ is a countably additive vector measure.

• (ii) Every $\nu$-integrable function is ${\tilde{\nu }}$-integrable.

• (iii) The inclusion map $u: L_1(\nu ) \rightarrow L_1({\tilde{\nu }})$ is an operator and $I_{{\tilde{\nu }}}\circ u=T\circ I_\nu$.

2.3 L-weakly compact sets and the positive Schur property

Let E be a Banach lattice. Given a set $W \subseteq E$, we denote by $\textrm{Sol}(W)$ its solid hull, that is, the set of all $x\in E$ such that $|x|\le |y|$ for some $y\in W$. It is known that if W is relatively weakly compact, then every disjoint sequence in $\textrm{Sol}(W)$ is weakly null (see, e.g., [3, Theorem 4.34]). The set W is said to be L-weakly compact if it is bounded and every disjoint sequence in $\textrm{Sol}(W)$ is norm null. Every L-weakly compact set is relatively weakly compact (see, e.g., [3, Theorem 5.55]), but the converse does not hold in general. The following result is well-known (see [26, Corollaries 2.3.5 and 3.6.8], [39, Theorem 1.16] and [41, Lemma 3]):

Proposition 2.3

Let E be a Banach lattice. The following statements are equivalent:

• (i) E has the positive Schur property.

• (ii) Every disjoint weakly null sequence in E is norm null.

• (iii) Every disjoint weakly null sequence in $E^+$ is norm null.

• (iv) Every relatively weakly compact subset of E is L-weakly compact.

Proposition 2.4 below characterizes L-weakly compact sets in the $L_1$ space of a vector measure. We first need to introduce some terminology. Given $f\in L_1(\nu )$, the map $\nu _f:\Sigma \rightarrow X$ defined by

$$\begin{aligned} \quad \nu _f(A):=I_\nu (f\chi _A)=\int _A f \, d\nu \quad \text {for all } A\in \Sigma \end{aligned}$$

is a countably additive vector measure by the Orlicz-Pettis theorem (see, e.g., [18, p. 22, Corollary 4]). Note that $\Vert \nu _f\Vert (A)=\Vert f\chi _A\Vert _{L_1(\nu )}$ for all $A\in \Sigma$. Moreover, $\nu _f$ is $\mu$-continuous, that is, for every $\varepsilon >0$ there is $\delta >0$ such that $\Vert \nu _f(A)\Vert \le \varepsilon$ for every $A\in \Sigma$ with $\mu (A)\le \delta$ (see, e.g., [18, p. 10, Theorem 1]). A set $F \subseteq L_1(\nu )$ is said to be equi-integrable if the set $\{\nu _f:f\in F\}$ is uniformly $\mu$-continuous, that is, for every $\varepsilon >0$ there is $\delta >0$ such that

$$\begin{aligned} \sup _{f\in F}\Vert \nu _f(A)\Vert \le \varepsilon \quad \text {for every } A\in \Sigma \text {with }\mu (A)\le \delta . \end{aligned}$$

The following result can be found in [26, Proposition 3.6.2] and [33, Lemma 2.37] within a more general framework.

Proposition 2.4

Let $F \subseteq L_1(\nu )$ be a set. The following statements are equivalent:

• (i) F is L-weakly compact.

• (ii) F is bounded and equi-integrable.

• (iii) F is approximately order bounded, i.e., for every $\varepsilon >0$ there is $\rho >0$ such that $F \subseteq j_\nu (\rho B_{L_\infty (\nu )})+\varepsilon B_{L_1(\nu )}$.

We refer the reader to the recent works [4, 9, 22] for further results related to the positive Schur property in Banach lattices.

2.4 Characterization of Dunford-Pettis integration operators

Proposition 2.6 below was first proved in [6, Theorem 5.8]. We include here a more direct proof for the reader’s convenience. One part follows the argument used in [13, Theorem 4] to show that $L_1(\nu )$ has the positive Schur property if X has the Schur property. The following auxiliary lemma will also be used later.

Lemma 2.5

Let $(f_n)_{n\in \mathbb {N}}$ be a sequence in $L_1(\nu )$ such that the sequence $(\nu _{f_n}(A))_{n\in \mathbb {N}}$ is norm convergent for every $A\in \Sigma$. Then $(f_n)_{n\in \mathbb {N}}$ is equi-integrable.

Proof

This follows from the Vitali-Hahn-Saks theorem (see, e.g., [18, p. 24, Corollary 10]) applied to the sequence of $\mu$-continuous vector measures $(\nu _{f_n})_{n\in \mathbb {N}}$. $\square$

Proposition 2.6

The following statements are equivalent:

• (i) $L_1(\nu )$ has the positive Schur property and ${\mathcal {R}}(\nu )$ is relatively norm compact.

• (ii) $I_\nu$ is Dunford-Pettis.

Proof

(i)$\Rightarrow$(ii): Let $F \subseteq L_1(\nu )$ be a relatively weakly compact set. We will show that $I_\nu (F)$ is relatively norm compact by checking that for each $\varepsilon >0$ there is a norm compact set $K_\varepsilon \subseteq X$ such that $I_\nu (F) \subseteq K_\varepsilon +\varepsilon B_X$. Fix $\varepsilon >0$. Since F is approximately order bounded (by Propositions 2.3 and 2.4), there is $\rho >0$ such that $F \subseteq j_\nu (\rho B_{L_\infty (\nu )})+\varepsilon B_{L_1(\nu )}$. Therefore, $I_\nu (F) \subseteq K_\varepsilon +\varepsilon B_{X}$, where $K_\varepsilon := I_\nu (j_\nu (\rho B_{L_\infty (\nu )}))$ is norm compact by Proposition 2.1.

(ii)$\Rightarrow$(i): Since $j_\nu (B_{L_\infty (\nu )})$ is weakly compact in $L_1(\nu )$ (see the paragraph preceding Proposition 2.1) and $I_\nu$ is Dunford-Pettis, the set $I_\nu (j_\nu (B_{L_\infty (\nu )}))$ is norm compact and so ${\mathcal {R}}(\nu )$ is relatively norm compact (Proposition 2.1). To prove that $L_1(\nu )$ has the positive Schur property it suffices to check that every weakly convergent sequence is equi-integrable (Propositions 2.3 and 2.4). Let $(f_n)_{n\in \mathbb {N}}$ be a sequence in $L_1(\nu )$ which converges weakly to some $f\in L_1(\nu )$. Then for each $A\in \Sigma$ the sequence $(f_n\chi _A)_{n\in \mathbb {N}}$ converges weakly to $f\chi _A$ in $L_1(\nu )$ (bear in mind that the map $h \mapsto h\chi _A$ is an operator on $L_1(\nu )$). Since $I_\nu$ is Dunford-Pettis, for each $A\in \Sigma$ the sequence $(I_{\nu }(f_n\chi _A))_{n\in \mathbb {N}}=(\nu _{f_n}(A))_{n\in \mathbb {N}}$ converges in norm to $I_{\nu }(f\chi _A)=\nu _f(A)$. Now, Lemma 2.5 applies to conclude that $(f_n)_{n\in \mathbb {N}}$ is equi-integrable. $\square$

2.5 The “vector duality” induced by the integration operator

The following result (see, e.g., [33, Proposition 3.31]) shows, in particular, that we have a continuous bilinear map

$$\begin{aligned} L_1(\nu )\times L_\infty (\nu )\rightarrow X \end{aligned}$$

defined by

$$\begin{aligned} \quad (f,g) \mapsto I_\nu (fg)=\int _\Omega fg \, d\nu . \end{aligned}$$

Proposition 2.7

Let $f\in L_1(\nu )$. Then:

• (i) For every $g\in L_\infty (\nu )$ the product $fg\in L_1(\nu )$ and

  $$\begin{aligned} \Vert fg\Vert _{L_1(\nu )}\le \Vert f\Vert _{L_1(\nu )}\Vert g\Vert _{L_\infty (\nu )}. \end{aligned}$$

• (ii) The norm of f in $L_1(\nu )$ is

  $$\begin{aligned} \Vert f\Vert _{L_1(\nu )}=\sup _{g\in B_{L_\infty (\nu )}}\Vert I_\nu (fg)\Vert _X. \end{aligned}$$

There are some elements of $L_1(\nu )^*$ which admit a simple description and are helpful for dealing with the weak topology of $L_1(\nu )$. By Proposition 2.7, for each $(g,x^*)\in B_{L_\infty (\nu )}\times B_{X^*}$ we can define a functional $\gamma _{(g,x^*)} \in B_{L_1(\nu )^*}$ by the formula

$$\begin{aligned} \gamma _{(g,x^*)}(f):=x^*(I_\nu (fg))=\int _\Omega fg \, d(x^*\nu ) \quad \text {for all } f\in L_1(\nu ), \end{aligned}$$

and the set

$$\begin{aligned} \Gamma _\nu :=\{\gamma _{(g,x^*)}: \, (g,x^*)\in B_{L_\infty (\nu )}\times B_{X^*}\} \subseteq B_{L_1(\nu )^*} \end{aligned}$$

is norming for $L_1(\nu )$, that is,

$$\begin{aligned} \Vert f\Vert _{L_1(\nu )}=\sup _{\gamma \in \Gamma _\nu } \gamma (f) \quad \text {for all } f\in L_1(\nu ). \end{aligned}$$

(2.2)

Let $\sigma (L_1(\nu ),\Gamma _\nu )$ be the (locally convex Hausdorff) topology on $L_1(\nu )$ of pointwise convergence on $\Gamma _\nu$, which is weaker than the weak topology. Proposition 2.8 below was first proved in [29, Proposition 17]. It was pointed out in [25, Section 4.7] that it can also be seen as a corollary of the Rainwater-Simons theorem (see, e.g., [20, Theorem 3.134]) and the fact that $\Gamma _\nu$ is a James boundary for $L_1(\nu )$ (i.e., the supremum in (2.2) is a maximum) whenever ${\mathcal {R}}(\nu )$ is relatively norm compact. We refer the reader to [6, Section 4] and [8, Section 2] for more information on this topic.

Proposition 2.8

Suppose that ${\mathcal {R}}(\nu )$ is relatively norm compact. Then every bounded and $\sigma (L_1(\nu ),\Gamma _\nu )$-convergent sequence in $L_1(\nu )$ is weakly convergent.

3 Dunford-Pettis integration operators

Let ${\mathcal {A}}$ be an operator ideal. Following [31], a Banach space X is said to be ${\mathcal {A}}$-variation admissible if for every measurable space $(\Omega ,\Sigma )$ and for every $\nu \in \textrm{ca}(\Sigma ,X)$ such that $I_\nu \in {\mathcal {A}}$, we have $|\nu |(\Omega )<\infty$. The interest of this concept is based on the following result, [31, Proposition 1.1], which provides a tool for proving that $L_1$ is lattice-isomorphic to an AL-space under some additional assumptions.

Proposition 3.1

Let ${\mathcal {A}}$ be an operator ideal and let X be a Banach space. If X is ${\mathcal {A}}$-variation admissible, then for every measurable space $(\Omega ,\Sigma )$ and for every $\nu \in \textrm{ca}(\Sigma ,X)$ such that $I_\nu \in {\mathcal {A}}$, the inclusion map $\iota _\nu : L_1(|\nu |) \rightarrow L_1(\nu )$ is a lattice-isomorphism.

The next proposition is elementary.

Proposition 3.2

Let ${\mathcal {A}}$ be an operator ideal and let X and Y be Banach spaces.

• (i) If X and Y are isomorphic, then X is ${\mathcal {A}}$-variation admissible if and only if Y is ${\mathcal {A}}$-variation admissible.

• (ii) If X is ${\mathcal {A}}$-variation admissible, then every subspace of X is ${\mathcal {A}}$-variation admissible.

Proof

Let $(\Omega ,\Sigma )$ be a measurable space.

(i) If $T:X\rightarrow Y$ is an isomorphism and $\nu \in \textrm{ca}(\Sigma ,X)$, then we can apply Proposition 2.2 to deduce that a function is $\nu$-integrable if and only if it is ${\tilde{\nu }}$-integrable, where we write ${\tilde{\nu }}:=T\circ \nu \in \textrm{ca}(\Sigma ,Y)$, and that the identity map $u: L_1(\nu )\rightarrow L_1({\tilde{\nu }})$ is an isomorphism satisfying $I_{{\tilde{\nu }}}\circ u=T\circ I_\nu$. Hence, $I_\nu \in {\mathcal {A}}$ if and only if $I_{{\tilde{\nu }}}\in {\mathcal {A}}$. Moreover, we have $\Vert T^{-1}\Vert ^{-1}\cdot |\nu |(\Omega ) \le |{\tilde{\nu }}|(\Omega )\le \Vert T\Vert \cdot |\nu |(\Omega )$.

(ii) Let $Z\subseteq X$ be a subspace and let $i:Z\rightarrow X$ be the inclusion operator. Fix $\nu \in \textrm{ca}(\Sigma ,Z)$ such that $I_\nu \in {\mathcal {A}}$ and define ${\tilde{\nu }}:=i\circ \nu \in \textrm{ca}(\Sigma ,X)$. Then a function is $\nu$-integrable if and only if it is ${\tilde{\nu }}$-integrable, the identity map $u: L_1(\nu )\rightarrow L_1({\tilde{\nu }})$ is an isometry and $I_{{\tilde{\nu }}}=i\circ I_\nu \circ u^{-1} \in {\mathcal {A}}$ (Proposition 2.2). Since X is ${\mathcal {A}}$-variation admissible, we have $|\nu |(\Omega )=|{\tilde{\nu }}|(\Omega )<\infty$. $\square$

In this section we focus on the operator ideal ${\mathcal {A}}_{cc}$ of all Dunford-Pettis operators. Our main goal is to provide a somehow simpler proof of the fact that Asplund spaces are ${\mathcal {A}}_{cc}$-variation admissible, [7, Theorem 1.3], see Corollary 3.8 below.

Part (i) of the following result was already pointed out in [31]:

Proposition 3.3

Let X be a Banach space.

• (i) If X is ${\mathcal {A}}_{cc}$-variation admissible, then X contains no subspace isomorphic to $\ell _1$.

• (ii) If every separable subspace of X is ${\mathcal {A}}_{cc}$-variation admissible, then X is ${\mathcal {A}}_{cc}$-variation admissible.

Proof

(i) By Proposition 3.2, its suffices to check that $\ell _1$ is not ${\mathcal {A}}_{cc}$-variation admissible. Since $\ell _1$ is infinite-dimensional, the Dvoretzky-Rogers theorem (see, e.g., [17, Theorem 1.2]) ensures the existence of an unconditionally convergent series $\sum _{n=1}^\infty x_n$ in $\ell _1$ which is not absolutely convergent. Now, define $\nu :{\mathcal {P}}(\mathbb {N})\rightarrow \ell _1$ by $\nu (A):=\sum _{n\in A}x_n$ for all $A \in {\mathcal {P}}(\mathbb {N})$ (the power set of $\mathbb {N}$). Then $\nu \in \textrm{ca}({\mathcal {P}}(\mathbb {N}),\ell _1)$ satisfies $|\nu |({\mathcal {P}}(\mathbb {N}))=\sum _{n=1}^\infty \Vert x_n\Vert =\infty$, while $I_\nu$ is Dunford-Pettis by the Schur property of $\ell _1$ (see, e.g., [2, Theorem 2.3.6]). Hence, $\ell _1$ is not ${\mathcal {A}}_{cc}$-variation admissible.

(ii) Let $(\Omega ,\Sigma )$ be a measurable space and let $\nu \in \textrm{ca}(\Sigma ,X)$ such that $I_\nu$ is Dunford-Pettis. Then ${\mathcal {R}}(\nu )$ is relatively norm compact (Proposition 2.6), so it is separable. Hence, the subspace $Z:=\overline{\textrm{span}}({\mathcal {R}}(\nu ))=\overline{I_\nu (L_1(\nu ))}$ (see (2.1) at page 4) is separable. Then Z is ${\mathcal {A}}_{cc}$-variation admissible by assumption. Since $\nu$ takes values in Z and $I_\nu$ is Dunford-Pettis, we deduce that $|\nu |(\Omega )<\infty$. $\square$

3.1 Schauder decompositions and the variation of a vector measure

Let X be a Banach space. A Schauder decomposition of X is a sequence $(X_n)_{n\in \mathbb {N}}$ of (non-zero) subspaces of X such that each $x\in X$ can be written in a unique way as a convergent series of the form $x=\sum _{n=1}^\infty x_n$, where $x_n\in X_n$ for all $n\in \mathbb {N}$. In this case, for each $n\in \mathbb {N}$ there is a projection $S_n$ from X onto $X_n$ such that $x=\sum _{n=1}^\infty S_n(x)$ for all $x\in X$. For each $k\in \mathbb {N}$, the operator $P_k:=\sum _{n=1}^k S_n$ is a projection from X onto the subspace $\bigoplus _{n=1}^k X_n$, we have $\sup _{k\in \mathbb {N}}\Vert P_k\Vert <\infty$ and the formula $|||x|||=\sup _{k\in \mathbb {N}}\Vert P_k(x)\Vert$ defines an equivalent norm on X. Note that $P_{k'}\circ P_{k}=P_{k}\circ P_{k'}=P_{\min \{k,k'\}}$ for all $k,k'\in \mathbb {N}$ and $\Vert P_k(x)-x\Vert \rightarrow 0$ as $k\rightarrow \infty$ for every $x\in X$. Of course, if X has a Schauder basis $(e_n)_{n\in \mathbb {N}}$, then the sequence of 1-dimensional subspaces generated by each $e_n$ is a Schauder decomposition of X.

The following lemma will be a key tool for proving Theorem 3.6 below.

Lemma 3.4

Let X be a Banach space, let $(\Omega ,\Sigma )$ be a measurable space and let $\nu \in \textrm{ca}(\Sigma ,X)$. Suppose that:

• $|\nu |(\Omega )=\infty$ and ${\mathcal {R}}(\nu )$ is relatively norm compact.

• X has a Schauder decomposition $(X_n)_{n\in \mathbb {N}}$ such that $|P_k\circ \nu |(\Omega )<\infty$ for all $k\in \mathbb {N}$, where $P_k$ is the associated projection from X onto $\bigoplus _{n=1}^k X_n$.

Then there exist a sequence $(B_j)_{j\in \mathbb {N}}$ of pairwise disjoint elements of $\Sigma \setminus {\mathcal {N}}(\nu )$, a strictly increasing sequence $(k_j)_{j\in \mathbb {N}}$ in $\mathbb {N}$ and $\varepsilon >0$ such that the functions $f_j:=\frac{1}{\Vert \nu \Vert (B_j)}\chi _{B_j} \in L_1(\nu )$ and the projections $R_j:=P_{k_{j+1}}-P_{k_{j}}$ satisfy:

• (i) $\Vert I_\nu (f_jg)-R_{j}(I_\nu (f_jg))\Vert \le 2^{-j}$ for all $g\in B_{L_\infty (\nu )}$ and $j\in \mathbb {N}$.

• (ii) There is $j_0\in \mathbb {N}$ such that $\Vert I_\nu (f_j)-I_\nu (f_{j'})\Vert \ge \varepsilon$ for all distinct $j,j' \ge j_0$.

Proof

Write $Q_k:=\textrm{id}_X-P_k$ for all $k\in \mathbb {N}$ (where $\textrm{id}_X$ stands for the identity operator on X). Since $\sup _{k\in \mathbb {N}}\Vert Q_k\Vert <\infty$ and $\Vert Q_k(x)\Vert \rightarrow 0$ as $k\rightarrow \infty$ for every $x\in X$, the sequence $(Q_k)_{k\in \mathbb {N}}$ converges to 0 uniformly on each norm compact subset of X. By renorming, we can assume without loss of generality that $\Vert P_k\Vert =1$ for all $k\in \mathbb {N}$.

Since $|\nu |(\Omega )=\infty$, there is a sequence $(C_l)_{l\in \mathbb {N}}$ of pairwise disjoint elements of $\Sigma \setminus {\mathcal {N}}(\nu )$ such that $\sum _{l=1}^\infty \Vert \nu (C_l)\Vert =\infty$, [27, Corollary 2]. Fix $\rho >2$ and, for each $l\in \mathbb {N}$, take $A_l \in \Sigma {\setminus } {\mathcal {N}}(\nu )$ such that $A_l \subseteq C_l$ and $\rho \Vert \nu (A_l)\Vert \ge \Vert \nu \Vert (C_l)$. Then $\sum _{l=1}^\infty \Vert \nu (A_l)\Vert =\infty$ and

$$\begin{aligned} \Vert \nu (A_l)\Vert \ge \rho ^{-1}\Vert \nu \Vert (A_l) \quad \text {for all } l\in \mathbb {N}. \end{aligned}$$

(3.1)

Claim. There exist two strictly increasing sequences $(k_j)_{j\in \mathbb {N}}$ and $(l_j)_{j\in \mathbb {N}}$ in $\mathbb {N}$ such that for every $j\in \mathbb {N}$ we have:

($\alpha$):

$\Vert P_{k_{j}}(I_\nu (\chi _{A_{l_{j+1}}}g))\Vert \le 2^{-j-1}\Vert \nu \Vert (A_{l_{j+1}})$ for all $g\in B_{L_\infty (\nu )}$;

($\beta$):

$\Vert Q_{k_{j}}(I_\nu (\chi _{A_{l_j}}g))\Vert \le 2^{-j} \Vert \nu \Vert (A_{l_j})$ for all $g\in B_{L_\infty (\nu )}$.

Indeed, we proceed by induction. Set $l_1:=1$ and consider

$$\begin{aligned} K_1:=\big \{I_\nu (\chi _{A_{1}}g): \, g \in B_{L_\infty (\nu )}\big \} \subseteq X. \end{aligned}$$

Since ${\mathcal {R}}(\nu )$ is relatively norm compact, so is $K_1$ (Proposition 2.1) and therefore we can pick $k_1\in \mathbb {N}$ such that

$$\begin{aligned} \sup _{x \in K_{1}}\Vert Q_{k_1}(x)\Vert \le \frac{\Vert \nu \Vert (A_{1})}{2}. \end{aligned}$$

Hence, ($\beta$) holds for $j=1$. Suppose now that $k_N,l_N\in \mathbb {N}$ are already chosen for some $N\in \mathbb {N}$. Since ${\tilde{\nu }}:=P_{k_N} \circ \nu$ satisfies $|{\tilde{\nu }}|(\Omega )<\infty$ and $\sum _{l=1}^\infty \Vert \nu \Vert (A_l)=\infty$, there is $l_{N+1}\in \mathbb {N}$ with $l_{N+1}>l_N$ such that

$$\begin{aligned} |{\tilde{\nu }}|(A_{l_{N+1}}) \le 2^{-N-1}\Vert \nu \Vert (A_{l_{N+1}}). \end{aligned}$$

(3.2)

Observe that for each $g\in B_{L_\infty (\nu )}$ we have

$$\begin{aligned} \Vert P_{k_N}(I_\nu (\chi _{A_{l_{N+1}}}g))\Vert{} & {} {\mathop {=}\limits ^{(*)}} \Vert I_{{\tilde{\nu }}}(\chi _{A_{l_{N+1}}}g)\Vert \le \Vert \chi _{A_{l_{N+1}}}g\Vert _{L_1({\tilde{\nu }})} {\mathop {\le }\limits ^{(**)}} \Vert \chi _{A_{l_{N+1}}}\Vert _{L_1({\tilde{\nu }})} \\{} & {} = \Vert {\tilde{\nu }}\Vert (A_{l_{N+1}}) \le |{\tilde{\nu }}|(A_{l_{N+1}}) {\mathop {\le }\limits ^{(3.2)}} 2^{-N-1}\Vert \nu \Vert (A_{l_{N+1}}), \end{aligned}$$

where $(*)$ and $(**)$ follow from Propositions 2.2 and 2.7(i), respectively. Hence, ($\alpha$) holds for $j=N$. Now, we consider the relatively norm compact subset of X defined by

$$\begin{aligned} K_{N+1}:=\big \{I_\nu (\chi _{A_{l_{N+1}}}g): \, g \in B_{L_\infty (\nu )}\big \} \end{aligned}$$

(apply Proposition 2.1 again) and we choose $k_{N+1}\in \mathbb {N}$ with $k_{N+1}>k_N$ such that

$$\begin{aligned} \sup _{x \in K_{N+1}}\Vert Q_{k_{N+1}}(x)\Vert \le 2^{-N-1}\Vert \nu \Vert (A_{l_{N+1}}). \end{aligned}$$

Therefore, ($\beta$) holds for $j=N+1$. This finishes the proof of the Claim.

For each $j\in \mathbb {N}$, define $B_j:=A_{l_{j+1}}$ and let $f_j$ and $R_j$ be as in the statement. To check property (i), take $j\in \mathbb {N}$ and $g\in B_{L_\infty (\nu )}$. Then ($\alpha$) and ($\beta$) imply

$$\begin{aligned} \Vert I_\nu (f_jg)-R_{j}(I_\nu (f_jg))\Vert= & {} \Vert Q_{k_{j+1}}(I_\nu (f_jg)) + P_{k_{j}}(I_\nu (f_j g))\Vert \\\le & {} \Vert Q_{k_{j+1}}(I_\nu (f_jg))\Vert + \Vert P_{k_{j}}(I_\nu (f_j g))\Vert \\ {}\le & {} \frac{1}{2^{j+1}}+\frac{1}{2^{j+1}}=\frac{1}{2^j}. \end{aligned}$$

Finally, we will check that (ii) holds for an arbitrary $0<\varepsilon <\rho ^{-1}$. Choose $j_0\in \mathbb {N}$ large enough such that $\rho ^{-1}-2^{-j_0}\ge \varepsilon$. Take $j'>j\ge j_0$ in $\mathbb {N}$. Then

$$\begin{aligned} \Vert I_\nu (f_j)-I_\nu (f_{j'})\Vert\ge & {} \Vert P_{k_{j+1}}(I_\nu (f_j)-I_\nu (f_{j'}))\Vert \\{} & {} (\text {because } \Vert P_{k_{j+1}}\Vert =1) \\= & {} \Vert I_\nu (f_j)-Q_{k_{j+1}}(I_\nu (f_j))-P_{k_{j+1}}(I_\nu (f_{j'}))\Vert \\\ge & {} \Vert I_\nu (f_j)\Vert -\Vert Q_{k_{j+1}}(I_\nu (f_j))\Vert -\Vert P_{k_{j+1}}(I_\nu (f_{j'}))\Vert \\= & {} \Vert I_\nu (f_j)\Vert -\Vert Q_{k_{j+1}}(I_\nu (f_j))\Vert -\Vert P_{k_{j+1}}(P_{k_{j'}}(I_\nu (f_{j'})))\Vert \\{} & {} (\text {because } P_{k_{j+1}}\circ P_{k_{j'}}=P_{k_{j+1}}) \\\ge & {} \rho ^{-1}-\Vert Q_{k_{j+1}}(I_\nu (f_j))\Vert -\Vert P_{k_{j'}}(I_\nu (f_{j'}))\Vert \\{} & {} (\text {by } (3.1 \text {and } \Vert P_{k_{j+1}}\Vert =1) \\\ge & {} \rho ^{-1}-\frac{1}{2^{j+1}} -\frac{1}{2^{j'+1}} \\{} & {} (\text {by } (\alpha ) \text { and } (\beta ) \text { with } g=\chi _\Omega ) \\> & {} \rho ^{-1}-\frac{1}{2^{j_0}} \ge \varepsilon . \end{aligned}$$

The proof is finished. $\square$

3.2 Asplund spaces are ${\mathcal {A}}_{cc}$-variation admissible

Let $(X_n)_{n\in \mathbb {N}}$ be a Schauder decomposition of a Banach space X. By a block sequence with respect to $(X_n)_{n\in \mathbb {N}}$ we mean a sequence $(x_j)_{j\in \mathbb {N}}$ in X for which there is a sequence $(I_j)_{j\in \mathbb {N}}$ of non-empty finite subsets of $\mathbb {N}$ such that $\max (I_j)<\min (I_{j+1})$ and $x_j\in \bigoplus _{n\in I_j}X_n$ for all $j\in \mathbb {N}$. We say that $(X_n)_{n\in \mathbb {N}}$ is shrinking if $\Vert P_k^*(x^*)-x^*\Vert \rightarrow 0$ as $k\rightarrow \infty$ for every $x^*\in X^*$, where $P_k$ is the associated projection from X onto $\bigoplus _{n=1}^k X_n$. When X has a Schauder basis $(e_n)_{n\in \mathbb {N}}$ and each $X_n$ is the subspace generated by $e_n$, then $(X_n)_{n\in \mathbb {N}}$ is shrinking if and only if $(e_n)_{n\in \mathbb {N}}$ is shrinking in the usual sense.

The following fact belongs to the folklore and can be proved as in the case of Schauder bases (see, e.g., [2, Proposition 3.2.7]).

Proposition 3.5

Let $(X_n)_{n\in \mathbb {N}}$ be a Schauder decomposition of a Banach space X. The following statements are equivalent:

• (i) $(X_n)_{n\in \mathbb {N}}$ is shrinking.

• (ii) Every bounded block sequence with respect to $(X_n)_{n\in \mathbb {N}}$ is weakly null.

Theorem 3.6

Let X be a Banach space having a shrinking Schauder decomposition $(X_n)_{n\in \mathbb {N}}$ such that $X_n$ is finite-dimensional for all $n\in \mathbb {N}$. Then X is ${\mathcal {A}}_{cc}$-variation admissible. In particular, every Banach space having a shrinking Schauder basis is ${\mathcal {A}}_{cc}$-variation admissible.

Proof

Let $(\Omega ,\Sigma )$ be a measurable space and let $\nu \in \textrm{ca}(\Sigma ,X)$ such that $I_\nu$ is Dunford-Pettis. Then ${\mathcal {R}}(\nu )$ is relatively norm compact (Proposition 2.6). Fix $k\in \mathbb {N}$ and denote by $P_k$ the associated projection from X onto $\bigoplus _{n=1}^k X_n$. Since $\bigoplus _{n=1}^k X_n$ is finite-dimensional, we have $|P_k \circ \nu |(\Omega )<\infty$. By renorming, we can assume that $\Vert P_k\Vert =1$ for all $k\in \mathbb {N}$.

Suppose, by contradiction, that $|\nu |(\Omega )=\infty$. Let $(f_j)_{j\in \mathbb {N}}$ and $(R_j)_{j\in \mathbb {N}}$ be as in Lemma 3.4. Since $(I_\nu (f_j))_{j\in \mathbb {N}}$ is not norm convergent (by property (ii) in Lemma 3.4) and $I_\nu$ is Dunford-Pettis, the sequence $(f_j)_{j\in \mathbb {N}}$ is not weakly convergent in $L_1(\nu )$. In addition, $\Vert f_j\Vert _{L_1(\nu )}=1$ for all $j\in \mathbb {N}$. By Proposition 2.8, there is $g\in B_{L_\infty (\nu )}$ such that the sequence $(I_\nu (f_j g))_{j\in \mathbb {N}}$ is not weakly null in X. Then $(R_j(I_\nu (f_j g)))_{j\in \mathbb {N}}$ is a bounded block sequence with respect to $(X_n)_{n\in \mathbb {N}}$ which cannot be weakly null, by property (i) in Lemma 3.4. This contradicts that $(X_n)_{n\in \mathbb {N}}$ is shrinking (Proposition 3.5). $\square$

The last ingredient of our proof that Asplund spaces are ${\mathcal {A}}_{cc}$-variation admissible is the following deep result of Zippin [43] (cf. [21, Theorem III.1] and [40]):

Theorem 3.7

(Zippin) Every Banach space having separable dual is isomorphic to a subspace of a Banach space having a shrinking Schauder basis.

Corollary 3.8

Every Asplund space is ${\mathcal {A}}_{cc}$-variation admissible.

Proof

By Proposition 3.3(ii), it suffices to prove that every Banach space having separable dual is ${\mathcal {A}}_{cc}$-admissible. Since every Banach space having a shrinking Schauder basis is ${\mathcal {A}}_{cc}$-variation admissible (Theorem 3.6), the conclusion follows from Theorem 3.7 and Proposition 3.2(ii). $\square$

3.3 An application of the Davis-Figiel-Johnson-Pełczyński factorization

We begin by recalling the refinement of the DFJP factorization developed by Lima, Nygaard and Oja in [23]. Let Z and X be Banach spaces, let $T:Z\rightarrow X$ be a (non-zero) operator and consider the set

$$\begin{aligned} K:=\frac{1}{\Vert T\Vert }\overline{T(B_Z)} \subseteq B_X. \end{aligned}$$

Fix $a \in (1,\infty )$ and write

$$\begin{aligned} f(a):=\left( \sum _{n=1}^\infty \frac{a^{n}}{(a^{n}+1)^2}\right) ^{1/2}. \end{aligned}$$

For each $n\in \mathbb {N}$, let $\Vert \cdot \Vert _n$ be the Minkowski functional of $K_n:=a^{n/2} K +a^{-n/2} B_X$, that is,

$$\begin{aligned} \Vert x\Vert _n:=\inf \{t>0: x\in tK_n\} \quad \text {for all } x\in X. \end{aligned}$$

The following theorem can be found in [23, Lemmas 1.1 and 2.1, Theorem 2.2], with the exception of part (vi), which can be obtained similarly as for the usual DFJP factorization (see, e.g., [5, §3]).

Theorem 3.9

Under the previous assumptions, the following statements hold:

• (i) $Y:=\{x\in X: \ \sum _{n=1}^\infty \Vert x\Vert _n^2 <\infty \}$ is a Banach space with the norm

  $$\begin{aligned} \Vert x\Vert _Y:=\left( \sum _{n=1}^\infty \Vert x\Vert _n^2\right) ^{1/2}. \end{aligned}$$

• (ii) $K \subseteq f(a) B_{Y}$ and the identity map $J: Y \rightarrow X$ is an operator.

• (iii) T factors as

  

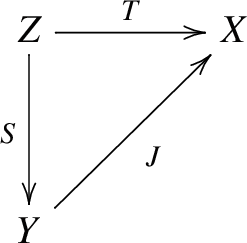  (3.3)

  where S is an operator.

• (iv) J is a norm-to-norm homeomorphism when restricted to K. In fact:

  $$\begin{aligned} \Vert x\Vert _Y^2 \le \Big (\frac{1}{4}+\frac{1}{\ln a}\Big ) \Vert x\Vert \quad \text {for all } x\in K. \end{aligned}$$

  Therefore, if T is Dunford-Pettis, then S is Dunford-Pettis as well.

• (v) If T is weakly compact, then Y is reflexive.

• (vi) If T is Asplund, then Y is Asplund.

• (vii) If a is the unique element of $(1,\infty )$ satisfying $f(a)=1$, then $\Vert S\Vert =\Vert T\Vert$ and $\Vert J\Vert =1$. In this case, (3.3) is called the DFJP-LNO factorization of T.

In [28] the DFJP-LNO factorization was applied to the integration operator of a vector measure. Our next proposition gathers some of the results obtained in [28, Theorems 3.7 and 4.5]:

Proposition 3.10

Let X be a Banach space, let $(\Omega ,\Sigma )$ be a measurable space, let $\nu \in \textrm{ca}(\Sigma ,X)$ and let

be the DFJP-LNO factorization of $I_\nu$. Define ${\tilde{\nu }}:\Sigma \rightarrow Y$ by ${\tilde{\nu }}(A):=S(\chi _A)$ for all $A\in \Sigma$. Then:

• (i) ${\tilde{\nu }} \in \textrm{ca}(\Sigma ,Y)$, $\nu =J\circ {\tilde{\nu }}$ and ${\mathcal {N}}(\nu )={\mathcal {N}}({\tilde{\nu }})$.

• (ii) $L_1({\tilde{\nu }})=L_1(\nu )$, with $\Vert f\Vert _{L_1(\nu )}=\Vert f\Vert _{L_1({\tilde{\nu }})}$ for all $f\in L_1(\nu )$, and $S=I_{{\tilde{\nu }}}$.

• (iii) ${\tilde{\nu }}$ has finite (resp., $\sigma$-finite) variation whenever $\nu$ does.

Corollary 3.11

Let X be a Banach space, let $(\Omega ,\Sigma )$ be a measurable space and let $\nu \in \textrm{ca}(\Sigma ,X)$. If $I_\nu$ is Asplund and Dunford-Pettis, then $|\nu |(\Omega )<\infty$ and the inclusion map $\iota _\nu : L_1(|\nu |) \rightarrow L_1(\nu )$ is a lattice-isomorphism.

Proof

Let Y, J and ${\tilde{\nu }}$ be as in Proposition 3.10. Since $I_{{\tilde{\nu }}}$ is Dunford-Pettis and Y is Asplund (Theorem 3.9, parts (iv) and (vi)), we can apply Corollary 3.8 to get $|{\tilde{\nu }}|(\Omega )<\infty$, hence $|\nu |(\Omega )=|J\circ {\tilde{\nu }}|(\Omega ) \le |{\tilde{\nu }}|(\Omega )<\infty$. This shows that every Banach space is ${\mathcal {A}}$-variation admissible, where ${\mathcal {A}}$ denotes the operator ideal of all Asplund and Dunford-Pettis operators. The last statement follows from Proposition 3.1. $\square$

4 Dunford-Pettis type properties

4.1 A remark on equimeasurability

Let $(\Omega ,\Sigma ,\mu )$ be a finite measure space. A set $H \subseteq L_\infty (\mu )$ is said to be equimeasurable if for every $\varepsilon >0$ there is $A\in \Sigma$ with $\mu (\Omega {\setminus } A)\le \varepsilon$ such that $\{h\chi _A:h\in H\}$ is relatively norm compact in $L_\infty (\mu )$. Theorem 4.1 below is a particular case of [5, Theorem 5.5.4]. We include a direct proof for the sake of completeness.

Theorem 4.1

Let $(\Omega ,\Sigma ,\mu )$ be a finite measure space. If $H \subseteq L_\infty (\mu )$ is relatively weakly compact, then it is equimeasurable.

Proof

By the Davis-Figiel-Johnson-Pełczyński factorization (see, e.g., [3, Theorem 5.37]), there exist a reflexive Banach space Y and an operator $T:Y \rightarrow L_\infty (\mu )$ such that $T(B_Y) \supseteq H$. Let $i: L_1(\mu ) \rightarrow L_\infty (\mu )^*$ be the inclusion operator and let $S:=T^*\circ i: L_1(\mu ) \rightarrow Y^*$. Since $Y^*$ is reflexive, S is representable, that is, there is $g\in L_\infty (\mu ,Y^*)$ such that

$$\begin{aligned} S(f)=\text {(Bochner)-}\int _\Omega fg \, d\mu \quad \text {for all } f\in L_1(\mu ) \end{aligned}$$

(see, e.g., [18, p. 75, Theorem 12]).

Fix $\varepsilon >0$. Since g is strongly $\mu$-measurable, Egorov’s theorem ensures the existence of $A\in \Sigma$ with $\mu (\Omega {\setminus } A)\le \varepsilon$ and a sequence $g_n:\Omega \rightarrow Y^*$ of $\Sigma$-simple $Y^*$-valued functions such that

$$\begin{aligned} \Vert g(t)-g_n(t)\Vert \le \frac{1}{n} \quad \text {for every }t\in A \text { and for every } n\in \mathbb {N}. \end{aligned}$$

(4.1)

For each $n\in \mathbb {N}$, let us consider the operator $S_n:L_1(\mu )\rightarrow Y^*$ defined by

$$\begin{aligned} S_n(f)=\text {(Bochner)-}\int _A fg_n \, d\mu \quad \text {for all } f\in L_1(\mu ). \end{aligned}$$

Note that $S_n$ is a finite-rank operator, because $g_n$ is the sum of finitely many functions of the form $y^*\chi _B$, where $y^*\in Y^*$ and $B\in \Sigma$. Hence, $S_n$ is compact. Moreover, if $P_A:L_1(\mu )\rightarrow L_1(\mu )$ is the projection defined by $P_A(f):=f\chi _A$ for all $f\in L_1(\mu )$, then the operator $S\circ P_A: L_1(\mu )\rightarrow Y^*$ satisfies

$$\begin{aligned} \Vert S\circ P_A-S_n\Vert =\sup _{f\in B_{L_1(\mu )}}\left\| \text {(Bochner)-}\int _A f (g-g_n) \, d\mu \right\| {\mathop {\le }\limits ^{(4.1)}} \frac{1}{n}. \end{aligned}$$

It follows that $(S_n)_{n\in \mathbb {N}}$ converges to $S\circ P_A$ in the operator norm. In particular, $S\circ P_A$ is compact and, therefore, $(S\circ P_A)^*: Y \rightarrow L_\infty (\mu )$ is compact as well (by Schauder’s theorem).

For every $y\in Y$ and for every $f\in L_1(\mu )$ we have

$$\begin{aligned} \langle (S\circ P_A)^*(y),f \rangle = \langle y,(S\circ P_A)(f) \rangle = \langle y,T^*(i(f\chi _A)) \rangle \\ = \langle T(y),f\chi _A \rangle = \int _AfT(y)\, dy=\langle T(y)\chi _A,f \rangle . \end{aligned}$$

Therefore $(S\circ P_A)^*(y)=T(y)\chi _A$ for all $y \in Y$. It follows that

$$\begin{aligned} \{h\chi _A: \, h\in H\} \subseteq \{T(y)\chi _A: \, y\in B_Y\}= (S\circ P_A)^*(B_Y) \end{aligned}$$

and so $\{h\chi _A: \, h\in H\}$ is relatively norm compact in $L_\infty (\mu )$. $\square$

4.2 A Dunford-Pettis type property for $L_1$ of a vector measure

Recall that a Banach space Z has the Dunford-Pettis property if and only if $z_n^*(z_n)\rightarrow 0$ as $n\rightarrow \infty$ for all weakly null sequences $(z_n)_{n\in \mathbb {N}}$ and $(z_n^*)_{n\in \mathbb {N}}$ in Z and $Z^*$, respectively (see, e.g., [2, Theorem 5.4.4]).

We next show that the $L_1$ space of an arbitrary vector measure enjoys a Dunford-Pettis type property with respect to the “vector duality” induced by the integration operator (Subsection 2.5).

Theorem 4.2

Let X be a Banach space, let $(\Omega ,\Sigma )$ be a measurable space and let $\nu \in \textrm{ca}(\Sigma ,X)$. Let $(f_n)_{n\in \mathbb {N}}$ be a sequence in $L_1(\nu )$ and let $(g_n)_{n\in \mathbb {N}}$ be a weakly null sequence in $L_\infty (\nu )$.

• (i) If $(f_n)_{n\in \mathbb {N}}$ is weakly null, then $(I_\nu (f_ng_n))_{n\in \mathbb {N}}$ is weakly null.

• (ii) If $(f_n)_{n\in \mathbb {N}}$ is bounded and equi-integrable, then $(I_\nu (f_ng_n))_{n\in \mathbb {N}}$ is norm null.

Proof

(i) Fix $x^*\in X^*$. Let $h_{x^*} \in L_\infty (|x^* \nu |)$ be the Radon-Nikodým derivative of $x^*\nu$ with respect to $|x^*\nu |$. For each $n\in \mathbb {N}$ we have

$$\begin{aligned} x^*\big (I_\nu (f_n g_n)\big )=\int _\Omega f_n g_n \, d(x^*\nu )=\int _\Omega f_n h_{x^*} g_n \, d|x^*\nu |. \end{aligned}$$

(4.2)

Since $(f_n)_{n\in \mathbb {N}}$ is weakly null in $L_1(\nu )$ and the inclusion map $L_1(\nu )\rightarrow L_1(|x^*\nu |)$ is an operator, $(f_n)_{n\in \mathbb {N}}$ is weakly null in $L_1(|x^*\nu |)$ and so the same holds for $(f_n h_{x^*})_{n\in \mathbb {N}}$. In the same way, $(g_n)_{n\in \mathbb {N}}$ is weakly null in $L_\infty (|x^* \nu |)$, so we can apply the Dunford-Pettis property of $L_1(|x^*\nu |)$ and (4.2) to conclude that $x^*(I_\nu (f_n g_n))\rightarrow 0$ as $n\rightarrow \infty$. Since $x^*\in X^*$ is arbitrary, $(I_\nu (f_ng_n))_{n\in \mathbb {N}}$ is weakly null.

(ii) Define $\alpha :=\sup _{n\in \mathbb {N}}\Vert f_n\Vert _{L_1(\nu )}$ and $\beta :=\sup _{n\in \mathbb {N}}\Vert g_n\Vert _{L_\infty (\nu )}$. Let $\mu$ be a Rybakov control measure of $\nu$. Fix $\varepsilon >0$. Since $F:=\{f_n: n\in \mathbb {N}\}$ is equi-integrable, we can choose $\delta >0$ such that

$$\begin{aligned} \sup _{f\in F}\Vert f\chi _B\Vert _{L_1(\nu )}\le \varepsilon \quad \text {for every } B\in \Sigma \text {with } \mu (B)\le \delta . \end{aligned}$$

(4.3)

By Theorem 4.1, the set $\{g_n:n\in \mathbb {N}\}$ is equimeasurable, so there is $A\in \Sigma$ with $\mu (\Omega {\setminus } A)\le \delta$ such that $\{g_n \chi _A: n\in \mathbb {N}\}$ is relatively norm compact in $L_\infty (\nu )$. Since the sequence $(g_n \chi _A)_{n\in \mathbb {N}}$ is weakly null in $L_\infty (\nu )$ (bear in mind that the map $g \mapsto g\chi _A$ is an operator on $L_\infty (\nu )$), we conclude that $(g_n \chi _A)_{n\in \mathbb {N}}$ is norm null in $L_\infty (\nu )$. Choose $n_0\in \mathbb {N}$ such that

$$\begin{aligned} \sup _{n\ge n_0} \Vert g_n\chi _A\Vert _{L_\infty (\nu )} \le \varepsilon . \end{aligned}$$

(4.4)

Now, for every $f\in F$ and for every $n\in \mathbb {N}$ with $n\ge n_0$ we have

$$ \begin{aligned} \big \Vert I_\nu (fg_n)\big \Vert{} & {} \le \big \Vert I_\nu (fg_n\chi _{\Omega \setminus A})\big \Vert +\big \Vert I_\nu (f g_n\chi _A)\big \Vert \\{} & {} {\mathop {\le }\limits ^{(\text {Prop.}~2.7(i))}} \Vert f\chi _{\Omega \setminus A}\Vert _{L_1(\nu )} \Vert g_n\Vert _{L_\infty (\nu )}+\Vert f\Vert _{L_1(\nu )} \Vert g_n\chi _A\Vert _{L_\infty (\nu )}\\{} & {} {\mathop {\le }\limits ^{(4.3) \& (4.4)}} (\beta +\alpha )\varepsilon . \end{aligned}$$

As $\varepsilon >0$ is arbitrary, the sequence $(I_\nu (f_ng_n))_{n\in \mathbb {N}}$ is norm null. $\square$

4.3 The positive Schur property as a Dunford-Pettis type property

As a natural outcome of our previous work we get the following characterization:

Theorem 4.3

Let X be a Banach space, let $(\Omega ,\Sigma )$ be a measurable space and let $\nu \in \textrm{ca}(\Sigma ,X)$. The following statements are equivalent:

• (i) $L_1(\nu )$ has the positive Schur property.

• (ii) For all weakly null sequences $(f_n)_{n\in \mathbb {N}}$ and $(g_n)_{n\in \mathbb {N}}$ in $L_1(\nu )$ and $L_\infty (\nu )$, respectively, the sequence $(I_\nu (f_ng_n))_{n\in \mathbb {N}}$ is norm null.

Proof

(i)$\Rightarrow$(ii): This follows from Theorem 4.2, because the positive Schur property of $L_1(\nu )$ is equivalent to the fact that every relatively weakly compact subset of $L_1(\nu )$ is equi-integrable (Propositions 2.3 and 2.4).

(ii)$\Rightarrow$(i): By Propositions 2.3 and 2.4, it suffices to prove that every disjoint weakly null sequence $(f_n)_{n\in \mathbb {N}}$ in $L_1(\nu )$ is equi-integrable. Let $(A_n)_{n\in \mathbb {N}}$ be a sequence of pairwise disjoint elements of $\Sigma$ such that $f_n\chi _{A_n}=f_n$ for all $n\in \mathbb {N}$. Observe that $(\chi _{A_n})_{n\in \mathbb {N}}$ is weakly null in $L_\infty (\nu )$. Indeed, we can assume without loss of generality that $A_n\not \in {\mathcal {N}}(\nu )$ for all $n\in \mathbb {N}$. Then $(\chi _{A_n})_{n\in \mathbb {N}}$ is a basic sequence in $L_\infty (\nu )$ which is equivalent to the usual basis of $c_0$. In particular, $(\chi _{A_n})_{n\in \mathbb {N}}$ is weakly null in $L_\infty (\nu )$.

Fix $A\in \Sigma$. Define ${\tilde{f}}_n:=f_n\chi _A$ for all $n\in \mathbb {N}$. Note that

$$\begin{aligned} I_\nu ({\tilde{f}}_n\chi _{A_n})=I_\nu ({\tilde{f}}_n)=\nu _{f_n}(A) \quad \text {for all } n\in \mathbb {N}. \end{aligned}$$

(4.5)

Since $({\tilde{f}}_n)_{n\in \mathbb {N}}$ is weakly null in $L_1(\nu )$ (because $(f_n)_{n\in \mathbb {N}}$ is weakly null and the map $h \mapsto h\chi _A$ is an operator on $L_1(\nu )$) and $(\chi _{A_n})_{n\in \mathbb {N}}$ is weakly null in $L_\infty (\nu )$, condition (ii) and (4.5) imply that the sequence $(\nu _{f_n}(A))_{n\in \mathbb {N}}$ is norm null. As $A\in \Sigma$ is arbitrary, we can apply Lemma 2.5 to conclude that $(f_n)_{n\in \mathbb {N}}$ is equi-integrable. $\square$

Of course, Theorems 4.2 and 4.3 provide another point of view for the positive Schur property of the $L_1$ space of a vector measure taking values in a Banach space with the Schur property, [13, proof of Theorem 4].

4.4 Vector measures with $\sigma$-finite variation

The analysis of the Dunford-Pettis property is simpler for $L_1$ spaces of a vector measure with $\sigma$-finite variation.

Proposition 4.4

Let X be a Banach space, let $(\Omega ,\Sigma )$ be a measurable space and let $\nu \in \textrm{ca}(\Sigma ,X)$ with $\sigma$-finite variation. If $(f_n)_{n\in \mathbb {N}}$ is a bounded and equi-integrable sequence in $L_1(\nu )$ and $(\varphi _n)_{n\in \mathbb {N}}$ is a weakly null sequence in $L_1(\nu )^*$, then $\varphi _n(f_n)\rightarrow 0$ as $n\rightarrow \infty$.

Proof

The sequence $(f_n)_{n\in \mathbb {N}}$ is approximately order bounded (Proposition 2.4). Hence, we can assume without loss of generality that $f_n\in j_\nu (B_{L_\infty (\nu )})$ for all $n\in \mathbb {N}$. Define $\alpha :=\sup _{n\in \mathbb {N}}\Vert \varphi _n\Vert _{L_1(\nu )^*}$. Let $(A_m)_{m\in \mathbb {N}}$ be an increasing sequence in $\Sigma$ such that $\Omega =\bigcup _{m\in \mathbb {N}}A_m$ and $|\nu |(A_m)<\infty$ for all $m\in \mathbb {N}$. Fix $\varepsilon >0$. Choose $m\in \mathbb {N}$ large enough such that

$$\begin{aligned} \Vert \nu \Vert (\Omega \setminus A_m)\le \varepsilon . \end{aligned}$$

(4.6)

Define $\mu (A):=|\nu |(A\cap A_m)$ for all $A\in \Sigma$, so that $\mu$ is a finite non-negative measure. Consider the inclusion operator $\iota : L_1(\mu ) \rightarrow L_1(\nu )$ (see, e.g., [33, Lemma 3.14]) and $\iota ^*:L_1(\nu )^*\rightarrow L_\infty (\mu )$. Define $g_n:=\iota ^*(\varphi _n)\in L_\infty (\mu )$ for all $n\in \mathbb {N}$, so that $(g_n)_{n\in \mathbb {N}}$ is weakly null in $L_\infty (\mu )$.

The sequence $(f_n\chi _{A_m})_{n\in \mathbb {N}}$ is bounded and equi-integrable in $L_1(\mu )$ and

$$\begin{aligned} \langle g_n,f_n \chi _{A_m}\rangle = \int _{A_m} f_n g_n \, d\mu =\varphi _n(f_n \chi _{A_m}) \quad \text {for all } n\in \mathbb {N}. \end{aligned}$$

Therefore, the Dunford-Pettis property of $L_1(\mu )$ (cf. Theorem 4.2(ii)) ensures that $\varphi _n(f_n \chi _{A_m})\rightarrow 0$ as $n\rightarrow \infty$. Take $n_0\in \mathbb {N}$ such that

$$\begin{aligned} |\varphi _n(f_n \chi _{A_m})|\le \varepsilon \quad \text {whenever } n\ge n_0. \end{aligned}$$

Since

$$\begin{aligned} |\varphi _n(f_n\chi _{\Omega \setminus A_m})| \le \alpha \Vert f_n\chi _{\Omega \setminus A_m}\Vert _{L_1(\nu )} \le \alpha \Vert \nu \Vert (\Omega \setminus A_m)\le \alpha \varepsilon \quad \text {for all } n\in \mathbb {N}\end{aligned}$$

(by Proposition 2.7(i) and (4.6)), we have

$$\begin{aligned} | \varphi _n(f_n)|\le |\varphi _n(f_n\chi _{A_m})| + |\varphi _n(f_n\chi _{\Omega \setminus A_m})| \le (1+\alpha )\varepsilon \quad \text {whenever } n\ge n_0. \end{aligned}$$

This shows that $\varphi _n(f_n)\rightarrow 0$ as $n\rightarrow \infty$. $\square$

By putting together Propositions 2.3, 2.4 and 4.4, we get the already mentioned result from [13]:

Corollary 4.5

Let X be a Banach space, let $(\Omega ,\Sigma )$ be a measurable space and let $\nu \in \textrm{ca}(\Sigma ,X)$ with $\sigma$-finite variation. If $L_1(\nu )$ has the positive Schur property, then it has the Dunford-Pettis property.

Let E be a Banach space with a normalized 1-unconditional Schauder basis, say $(e_n)_{n\in \mathbb {N}}$. The E-sum of countably many copies of $L_1[0,1]$ is the Banach lattice Z of all sequences $(h_n)_{n\in \mathbb {N}}$ in $L_1[0,1]$ such that the series $\sum _{n=1}^\infty \Vert h_n\Vert _{L_1[0,1]} \, e_n$ converges unconditionally in E, equipped with the norm

$$\begin{aligned} \left\| (h_n)_{n\in \mathbb {N}}\right\| _{Z}:= \left\| \sum _{n=1}^\infty \Vert h_n\Vert _{L_1[0,1]} \, e_n\right\| _E \end{aligned}$$

and the coordinatewise order. If E has the the Schur property, then Z has the positive Schur property, but it is not lattice-isomorphic to an AL-space unless E is isomorphic to $\ell _1$, [42, Section 3].

The following construction provides more examples of Banach lattices with such features:

Example 4.6

Let X be a Banach space and let $\sum _{n=1}^\infty x_n$ be an unconditionally convergent series in X with $x_n\ne 0$ for all $n\in \mathbb {N}$. Let $\lambda$ be the Lebesgue measure on the $\sigma$-algebra $\Sigma$ of all Borel subsets of [0, 1]. Write $I_n:=(2^{-n},2^{-n+1}]$ for all $n\in \mathbb {N}$. Then:

• (i) The formula

  $$\begin{aligned} \nu (A):=\sum _{n=1}^\infty 2^n\lambda (A\cap I_n)x_n, \quad A\in \Sigma , \end{aligned}$$

  defines a vector measure $\nu \in \textrm{ca}(\Sigma ,X)$.

• (ii) ${\mathcal {N}}(\nu )={\mathcal {N}}(\lambda )$. Hence, $\nu$ is atomless and $L_1(\nu )$ is separable.

• (iii) ${\mathcal {R}}(\nu )$ is relatively norm compact.

• (iv) $|\nu |$ is $\sigma$-finite and $|\nu |([0,1])=\sum _{n=1}^\infty \Vert x_n\Vert$.

• (v) If $\sum _{n=1}^\infty x_n$ is not absolutely convergent, then $L_1(\nu )$ is not lattice-isomorphic to an AL-space.

• (vi) If X has the Schur property, then $L_1(\nu )$ has the positive Schur property and the Dunford-Pettis property.

• (vii) If $\sum _{n=1}^\infty x_n$ is not absolutely convergent and X has the Schur property, then $L_1(\nu )$ is not lattice-isomorphic to $L_1({\tilde{\nu }})$ for any $\sigma$-algebra ${\tilde{\Sigma }}$ and any ${\tilde{\nu }} \in \textrm{ca}({\tilde{\Sigma }},c_0)$ such that ${\mathcal {R}}({\tilde{\nu }})$ is relatively norm compact.

Proof

Since $\sum _{n=1}^\infty x_n$ is unconditionally convergent, for every $(a_n)_{n\in \mathbb {N}}\in \ell _\infty$ the series $\sum _{n=1}^\infty a_nx_n$ is unconditionally convergent and the map

$$\begin{aligned} T:\ell _\infty \rightarrow X, \quad T((a_n)_{n\in \mathbb {N}}):=\sum _{n=1}^\infty a_n x_n, \end{aligned}$$

is a compact operator (see, e.g., [17, Theorem 1.9]). This shows that the map $\nu$ is well-defined and has relatively norm compact range (note that $2^n \lambda (A\cap I_n) \le 1$ for all $n\in \mathbb {N}$). Since the map $\Sigma \ni A\mapsto 2^n\lambda (A\cap I_n)x_n \in X$ is countably additive for each $n\in \mathbb {N}$, the Vitali-Hahn-Saks theorem (see, e.g., [18, p. 24, Corollary 10]) ensures that $\nu$ is countably additive. This proves parts (i) and (iii).

(ii) The equality ${\mathcal {N}}(\nu )={\mathcal {N}}(\lambda )$ is obvious. Since $\lambda$ is atomless, so is $\nu$. Let ${\mathcal {C}} \subseteq \Sigma$ be a countable set such that for every $A\in \Sigma$ we have $\inf _{C\in {\mathcal {C}}}\lambda (A\triangle C)=0$. Then for every $A\in \Sigma$ we also have $\inf _{C\in {\mathcal {C}}}\Vert \nu \Vert (A\triangle C)=0$ (notice that $\nu$ is $\lambda$-continuous). This implies that $L_1(\nu )$ is separable, because the set of all $\Sigma$-simple functions is norm dense in $L_1(\nu )$.

(iv) It is easy to check that $|\nu |(A)=\sum _{n=1}^\infty 2^n\lambda (A\cap I_n)\Vert x_n\Vert$ for every $A\in \Sigma$.

(v) This follows from [12, Proposition 2] and (iv).

(vi) We already know that the Schur property of X implies that $L_1(\nu )$ has the positive Schur property, [13, proof of Theorem 4]. Now, (iv) and Corollary 4.5 ensure that $L_1(\nu )$ has the Dunford-Pettis property.

(vii) Suppose, by contradiction, that there exist a $\sigma$-algebra ${\tilde{\Sigma }}$ and ${\tilde{\nu }}\in \textrm{ca}({\tilde{\Sigma }},c_0)$ such that ${\mathcal {R}}({\tilde{\nu }})$ is relatively norm compact and $L_1(\nu )$ is lattice-isomorphic to $L_1({\tilde{\nu }})$. Then $L_1({\tilde{\nu }})$ has the positive Schur property (by (vi)) and we can apply Proposition 2.6 to infer that the integration operator $I_{{\tilde{\nu }}}:L_1({\tilde{\nu }}) \rightarrow c_0$ is Dunford-Pettis. Now, Proposition 3.1 and Theorem 3.6 (the usual basis of $c_0$ is shrinking) imply that $L_1({\tilde{\nu }})$ is lattice-isomorphic to an AL-space, which contradicts (v). $\square$

Remark 4.7

Part (vii) of Example 4.6 should be compared with [12, Theorem 1]. That result states that if X is a Banach space, $(\Omega ,\Sigma )$ is a measurable space, the vector measure $\nu \in \textrm{ca}(\Sigma ,X)$ is atomless and $L_1(\nu )$ is separable, then there is ${\tilde{\nu }}\in \textrm{ca}(\Sigma ,c_0)$ such that $L_1(\nu )$ and $L_1({\tilde{\nu }})$ are lattice-isometric (cf. [24, Theorem 5] for another proof). For variants in the non-separable setting, see [36] and [37]. In [24, Theorem 5] it was claimed that if, in addition, ${\mathcal {R}}(\nu )$ is relatively norm compact, then ${\tilde{\nu }}$ can be chosen so that ${\mathcal {R}}({\tilde{\nu }})$ is relatively norm compact as well. Unfortunately, this turns out to be false in general, as shown in Example 4.6(vii).