1 Introduction

The inequalities involving circular and hyperbolic functions has caused wide interests of many researchers, see also  [1, 2, 5,6,7,8,9,10,11, 13,14,15,16,17,18,19,20,21,22,23,24, 26,27,34, 36,37,43, 45,46,50] and the references therein. In particular, the following inequalities involving trigonometric functions

$$\begin{aligned} {\left( \dfrac{\sin x}{x}\right) ^2 + \dfrac{\tan x}{x} > 2,} \end{aligned}$$
(1)

and

$$\begin{aligned} {2 \dfrac{ \sin x}{x} + \dfrac{\tan x}{x} > 3, } \end{aligned}$$
(2)

have been obtained by Wilker [32] and Huygen [12], and are referred as Wilker and Huygens type inequalities. The following inequalities

$$\begin{aligned} { \left( \dfrac{\sinh x}{x}\right) ^2 + \dfrac{\tanh x}{x} > 2, } \end{aligned}$$
(3)

and

$$\begin{aligned} { 2 \dfrac{ \sinh x}{x} + \dfrac{\tanh x}{x} > 3, } \end{aligned}$$
(4)

are the counterparts of Eqs. (1) and (2) for the hyperbolic functions, where the proofs are referred to [44] and [25], respectively. Wilker and Huygens type inequalities have also been established for the lemniscate functions and Jacobian elliptic and theta functions [26, 31], for circular functions [49, 50], for hyperbolic functions [6], and so on. The Wilker and Huygens type inequalities involving inverse trigonometric functions

$$\begin{aligned} { f_1(x) = \left( \dfrac{\arcsin x}{x}\right) ^2 + \dfrac{\arctan x}{x} ~~\text{ and }~~ f_2(x) = 2\left( \dfrac{\arcsin x}{x}\right) + \dfrac{\arctan x}{x} } \end{aligned}$$
(5)

have also been discussed in many references [2,3,4,5,6, 15, 18, 19, 22, 25, 26, 31, 35, 49, 50].

For \(x \in (0,1)\), the following inequalities

$$\begin{aligned} \begin{array}{ll} { R_1(x)\triangleq 2 + \dfrac{\pi ^2+\pi -8}{\pi } x^3 \arctan x> f_1(x) > 2 + \dfrac{17}{45} x^3 \arctan x \triangleq L_1(x), } \end{array} \end{aligned}$$
(6)

and

$$\begin{aligned} { R_2(x) \triangleq 3 + \dfrac{5\pi -12}{\pi } x^3 \arctan x> f_2(x) >3 + \dfrac{7}{20} x^3 \arctan x \triangleq L_2(x), } \end{aligned}$$
(7)

are obtained in [3] and [19], where \(\dfrac{17}{45}\) and \(\dfrac{\pi ^2+\pi -8}{\pi }\), \(\dfrac{5\pi -12}{\pi }\) and \(\dfrac{7}{20}\) are the best constants in Eqs. (6) and (7), respectively.

This paper provides much sharper bounds by using the following two-parameter functions

$$\begin{aligned} { \begin{array}{ll} G_{i,n}(x,\alpha ) = (1+i) + A_{i,n}(x) \arctan (\alpha x), ~i=1,2, \\ H_{i,n}(x,\alpha ) = (1+i) + B_{i,n}(x) \arcsin (\alpha x), ~i=1,2, \end{array} } \end{aligned}$$
(8)

where \(A_{i,n}(x)\) and \(B_{i,n}(x)\) are polynomials of degree n satisfying either Eqs. (9) or (10)

$$\begin{aligned} D_j(0)= & {} D_j^{'}(0)=\cdots =D_j^{(n)}(0)=0, ~~j=1,2,3,4. \end{aligned}$$
(9)
$$\begin{aligned} D_j(0)= & {} D_j^{'}(0)=\cdots =D_j^{(n-1)}(0)=D_j(1)=0, ~~j=1,2,3,4. \end{aligned}$$
(10)

where \( { D_i(x)=f_i(x)- G_{i,n}(x,\alpha ), ~~D_{i+2}(x)=f_i(x)- H_{i,n}(x,\alpha ), ~~i=1,2 }\).

This paper takes the \(n=3\) case as an example, the cases of \(n>3\) can also be done in a similar way. Firstly, one obtains that

$$\begin{aligned} \begin{array}{ll} \bar{G}_{1,3}(x,\alpha ) &{}= 2 + \dfrac{17}{45 \alpha } x^3 \arctan (\alpha x), \\ \bar{G}_{2,3}(x,\alpha ) &{}=2 + \dfrac{\pi ^2+\pi -8}{4 \arctan (\alpha )} x^3 \arctan (\alpha x). \\ \bar{G}_{3,3}(x,\alpha ) &{}= 3 + \dfrac{7}{20 \alpha } x^3 \arctan (\alpha x), \\ \bar{G}_{4,3}(x,\alpha )&{} =3 + \dfrac{5 \pi -12}{4 \arctan (\alpha )} x^3 \arctan (\alpha x). \\ \bar{H}_{1,3}(x,\alpha ) &{}= 2 + \dfrac{\pi ^2+\pi -8}{4 \arcsin (\alpha )} x^3 \arcsin (\alpha x), \\ \bar{H}_{2,3}(x,\alpha ) &{}=3 + \dfrac{5 \pi -12}{4 \arcsin (\alpha )} x^3 \arcsin (\alpha x), \\ R_3(x)&{}=2-\dfrac{45\pi ^2+11\pi -360}{45\pi } \cdot x^3 \cdot \arctan (x) \\ &{}\quad +\dfrac{ 45 \pi ^2+28 \pi -360}{45 \pi } \cdot x^3 \cdot \arcsin (x), \\ L_3(x)&{}=2+\dfrac{173}{945} \cdot x^3 \cdot \arctan (x)+\dfrac{184}{945} \cdot x^3 \cdot \arcsin (x). \end{array} \end{aligned}$$
(11)

Secondly, by using the Maple software, it can be verified that

$$\begin{aligned} \begin{array}{ll} F_1(x)=\bar{G}_{1,3}(x,\alpha )-f_1(x), ~~F_2(x)=\bar{G}_{2,3}(x,\alpha )-f_1(x), \\ F_3(x)=\bar{G}_{3,3}(x,\alpha )-f_2(x), ~~F_4(x)=\bar{G}_{4,3}(x,\alpha )-f_2(x), \\ F_1(0)=F_1'(0)=\cdots =F_1^{(5)}(0)=0, ~~F_1^{(6)}(0)=\frac{272 \alpha ^2}{3}-\frac{144}{7}, \\ F_2(0)=F_2'(0)=F_2''(0)=F_2'''(0)=0, ~~F_2^{(4)}(0)=\frac{48 \alpha -6 \pi ^2 \alpha -6 \pi \alpha +\frac{136 \arctan (\alpha )}{15}}{\arctan (\alpha )}, \\ F_3(0)=F_3'(0)=\cdots =F_3^{(5)}(0)=0, ~~F_3^{(6)}(0)=-84 \alpha ^2+\frac{270}{7}, \\ F_4(0)=F_4'(0)=F_4''(0)=F_4'''(0)=0, ~~F_4^{(4)}(0)=\frac{6 (25 \pi \alpha -7 \arctan (\alpha )-60 \alpha )}{5 \arctan (\alpha )}. \end{array} \end{aligned}$$

By solving \(F_1^{(6)}(0)=0\), \(F_2^{(4)}(0)=0\), \(F_3^{(6)}(0)\) and \(F_4^{(4)}(0)=0\), one obtains the values of \(\alpha \) in \(G_{i,3}(x,\alpha )\). The main results are as follows.

Theorem 1

For \(x \in (0,1)\), one obtains the following inequalities

$$\begin{aligned} \begin{array}{ll} { \bar{G}_{1,3}\left( x, \sqrt{\dfrac{27}{119}} \right)< f_1(x) < \underset{\alpha \rightarrow 0_{+}}{\lim } \bar{G}_{2,3}(x,\alpha ) =2 + \dfrac{\pi ^2+\pi -8}{4} x^4. } \end{array} \end{aligned}$$
(12)

Theorem 2

For \(x \in (0,1)\), one obtains the following inequalities

$$\begin{aligned} \begin{array}{ll} { \bar{G}_{3,3}\left( x,\dfrac{3 \sqrt{10}}{14}\right)< f_2(x) < \underset{\alpha \rightarrow 0_{+}}{\lim } \bar{G}_{4,3}(x,\alpha ) = 3+\dfrac{5 \pi -12}{4} x^4. } \end{array} \end{aligned}$$
(13)

Theorem 3

For \(x \in (0,1)\), one obtains the following inequalities

$$\begin{aligned} \begin{array}{ll} f_1(x)< \bar{H}_{1,3}(x,1)= 2 + \dfrac{\pi ^2+\pi -8}{2 \pi } x^3 \arcsin (x), \\ f_2(x)<\bar{H}_{2,3}(x,1)=3 + \dfrac{5 \pi -12}{2 \pi } x^3 \arcsin (x). \end{array} \end{aligned}$$
(14)

Theorem 4

For \(x \in (0,1)\), one obtains the following inequalities

$$\begin{aligned} \begin{array}{ll} { L_3(x)< f_1(x) < R_3(x). } \end{array} \end{aligned}$$
(15)
Fig. 1
figure 1

Error plots of a the bounds of \(f_1(x)\) from Eqs. (6), (12), (14) and (15); and b the bounds of \(f_2(x)\) from Eqs. (7), (13) and (14)

Full size image

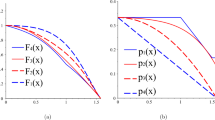
As shown in Fig. 1, the bounds of \(f_i(x)\) from Eqs. (12–14) achieve much better approximation effect than those of Eqs. (6) and (7), see also Eqs. (31) and (32) and the corresponding proofs in Sect. 3.

2 Proofs of Theorems 1–4

Firstly, we have the following lemmas.

Lemma 1

The following inequalities

$$\begin{aligned} \begin{array}{ll} l_1(x)< \arctan (x)< l_2(x) ~~\text{ and }~~ l_3(x)< \arctan (x) < l_4(x), \end{array} \end{aligned}$$
(16)

hold for all \(x \in (0,1)\), where

$$\begin{aligned} \begin{array}{ll} l_1(x)=x-\dfrac{1}{3} x^3+\dfrac{1}{5} x^5-\dfrac{1}{7} x^7+\left( \dfrac{\pi }{4}-\dfrac{76}{105}\right) x^9, \\ l_2(x)=x-\dfrac{1}{3} x^3+\dfrac{1}{5} x^5-\dfrac{1}{7} x^7-\left( \dfrac{491}{70}-\dfrac{9 \pi }{4}\right) x^8 + \left( \dfrac{1321}{210}-2 \pi \right) x^9, \\ l_3(x) = x-\dfrac{1}{3} x^3+\dfrac{1}{5} x^5-\dfrac{1}{7} x^7+ \dfrac{1}{9} x^9 + \left( \dfrac{11 \pi }{4}-\dfrac{5471}{630}\right) x^{10} + \left( \dfrac{989}{126}-\dfrac{5 \pi }{2}\right) x^{11}, \\ l_4(x) =x-\dfrac{1}{3} x^3+\dfrac{1}{5} x^5-\dfrac{1}{7} x^7+ \dfrac{1}{9} x^9 + \left( \dfrac{\pi }{4}-\dfrac{263}{315}\right) x^{11}. \end{array} \end{aligned}$$

Proof

Let \(H_i(x)=\arctan (x)-l_i(x)\), \(i=1,2,3,4\). Let

$$\begin{aligned} \begin{array}{ll} x_1=\sqrt{\dfrac{1052-315 \pi }{3(105 \pi -304)} } \approx 0.89, \\ x_2=- \dfrac{(35-\sqrt{-62265431-6350400 \pi ^2+39770640 \pi } )}{6(420 \pi -1321)} \approx 0.78, \\ x_3=\dfrac{-63+\sqrt{-48024900 \pi ^2+302439060 \pi -476148103}}{22(315\pi -989)} \approx 0.823, \\ x_4=\dfrac{\sqrt{11} \sqrt{(1052-315 \pi ) (3465\pi -10312)}}{11 (1052-315 \pi ) } \approx 0.914. \end{array} \end{aligned}$$

It can be verified that

$$\begin{aligned} \begin{array}{ll} H_i(0)=H_i(1)=0, ~~i=1,2,3,4, \\ H_1^{'}(x)= - \dfrac{x^8 \cdot ( (315 \pi -912) x^2+(315 \pi -1052) )}{140 (x^2+1) }, \\ H_2^{'}(x)=- \dfrac{x^7 \cdot (1-x) \cdot ( (1260 \pi -3963)x^2-35 x+1260 \pi -3928 )}{70 (x^2+1) }, \\ H_3^{'}(x)= \dfrac{ x^9 \cdot (x-1) \cdot ((3465 \pi -10879) x^2+63 x+3465 \pi -10942)}{126 (x^2+1)}, \\ H_4^{'}(x)=-\dfrac{x^{10} \cdot ((3465 \pi -11572) x^2+3465 \pi -10312)}{1260 (x^2+1)}, \end{array} \end{aligned}$$
(17)

such that \(x_i\) is the unique root of \(H_i^{'}(x)\) within (0, 1), \(i=1,2,3,4\), and

$$\begin{aligned} { H_i^{'}(x) } \left\{ \begin{array}{ll} {>0, } &{} { x \in (0,x_i), } \\ { =0, } &{} { x=x_i, } \\ {<0, } &{} { x \in (x_i,1), } \end{array} \right. i=1,3, ~\text{ and }~ { H_j^{'}(x) } \left\{ \begin{array}{ll} { <0, } &{} { x \in (0,x_j), } \\ { =0, } &{} { x=x_j, } \\ { >0, } &{} { x \in (x_j,1). } \end{array} \right. ~j=2,4. \end{aligned}$$
(18)

Combining Eq. (17) with Eq. (18), \(\forall x \in (0,1)\), one has that

$$\begin{aligned} \begin{array}{ll} \arctan (x)-l_i(x) = H_i(x)> \min \{H_i(0),H_i(1)\} =0, ~~i=1,3, \\ \arctan (x)-l_j(x) = H_j(x) < \max \{H_j(0),H_j(1)\}=0, ~~j=2,4, \end{array} \end{aligned}$$

where leads to Eq. (16), and the proof is completed.

Lemma 2

The following inequalities

$$\begin{aligned} l_5(x)< \arcsin (x)< l_7(x)<l_6(x) ~~\text{ and }~~l_8(x)< \arcsin (x) < l_9(x). \end{aligned}$$
(19)

hold for all \( x \in (0,1)\), where

$$\begin{aligned} \begin{array}{ll} l_5(x)=x+\dfrac{1}{6} x^3+\dfrac{3}{40} x^5+\dfrac{5}{112} x^7, \\ l_6(x)=x+\dfrac{1}{6} x^3+\dfrac{3}{40} x^5+ \left( \dfrac{\pi }{2}-\dfrac{149}{120}\right) x^7, \\ l_7(x)=x+\dfrac{1}{6} x^3+\dfrac{3}{40} x^5+\dfrac{5}{112} x^7 + \left( \dfrac{\pi }{2} -\dfrac{2161}{1680}\right) x^9, \\ l_8(x)=x+\dfrac{1}{6} x^3+\dfrac{3}{40} x^5+\dfrac{5}{112} x^7+\dfrac{35}{1152} x^9 + \dfrac{63}{2816}x^{11}, \\ l_9(x)=x+\dfrac{1}{6} x^3+\dfrac{3}{40} x^5+\dfrac{5}{112} x^7+\dfrac{35}{1152} x^9 +\left( \dfrac{\pi }{2}-\dfrac{53089}{40320}\right) x^{11}. \end{array} \end{aligned}$$

Proof

Let \(E_i(x)=\arcsin (x)-l_{i+4}(x)\), \(i=1,2,\ldots ,5\). For \(x \in (0,1)\), it can be verified that

$$\begin{aligned} { \begin{array}{ll} \arcsin ^{(8)}(x)&{} = \dfrac{315 x (16 x^6+168 x^4+210 x^2+35)}{(\sqrt{1-x^2})^{15}}>0, \\ \arcsin ^{(9)}(x) &{}= \dfrac{315(128 x^8+1792 x^6+3360 x^4+1120 x^2+35)}{\left( \sqrt{1-x^2}\right) ^{17}}>0, \\ \arcsin ^{(10)}(x) &{}= \dfrac{2835 x (128 x^8+2304 x^6+6048 x^4+3360 x^2+315)}{\left( \sqrt{1-x^2}\right) ^{19}}>0, \\ \arcsin ^{(12)}(x) &{}= \dfrac{155925 x }{\left( \sqrt{1-x^2}\right) ^{25}} \cdot (256 x^{10}+7040 x^8+31680 x^6 \\ &{}\quad +36960 x^4+11550 x^2+693)>0, \\ \arcsin ^{(13)}(x) &{}= \dfrac{ 467775 }{\left( \sqrt{1-x^2}\right) ^{25}} \cdot (1024 x^{12}+33792 x^{10}+190080 x^8 \\ &{}\quad +295680 x^6+138600 x^4+16632 x^2+231)>0, \\ E_1(0)&{}=E_1^{'}(0)=\cdots =E_1^{(8)}(0)=0, ~~E_1^{(9)}(0)=11025 \ne 0,~ E_1(1)\ne 0, \\ E_2(0)&{}=E_2^{'}(0)=\cdots =E_2^{(6)}(0)=E_2(1)=0, ~E_2^{(7)}(0)\ne 0, ~E_2^{'}(1) \ne 0, \\ E_3(0)&{}=E_2^{'}(0)=\cdots =E_2^{(8)}(0)=E_2(1)=0, ~E_2^{(9)}(0)\ne 0, ~E_3^{'}(1) \ne 0, \\ E_4(0)&{}=E_4^{'}(0)=\cdots =E_4^{(12)}(0)=0, ~~E_4^{(13)}(0) \ne 0,~ E_4(1) \ne 0, \\ E_5(0)&{}=E_5^{'}(0)=\cdots =E_5^{(10)}(0)=E_5(1)=0, ~E_5^{(11)}(0)\ne 0, ~E_5^{'}(1) \ne 0. \end{array} } \end{aligned}$$
(20)

From Eq. (20), for \(x \in (0,1)\), there exists \(\phi _i(x) \in (0,1)\), \(i=1,2,\ldots ,5\), such that

$$\begin{aligned} { \begin{array}{ll} E_1(x)=\dfrac{E_1^{(9)}(\phi _1(x))}{9!}\cdot (x-0)^9> 0, \\ E_2(x)=\dfrac{E_2^{(8)}(\phi _2(x))}{8!}\cdot (x-0)^7 \cdot (x-1)< 0, \\ E_3(x)=\dfrac{E_3^{(10)}(\phi _3(x))}{10!}\cdot (x-0)^9 \cdot (x-1)< 0, \\ E_4(x)=\dfrac{E_4^{(13)}(\phi _4(x))}{13!}\cdot (x-0)^{13} > 0, \\ E_5(x)=\dfrac{E_5^{(12)}(\phi _5(x))}{12!}\cdot (x-0)^{11} \cdot (x-1) < 0. \end{array} } \end{aligned}$$
(21)

On the other hand, we have that

$$\begin{aligned} { \begin{array}{ll} l_6(t)-l_7(x)=\dfrac{ (840 \pi -2161) \cdot x^7 \cdot (1-x^2)}{1680}>0, ~~\forall x \in (0,1), \end{array} } \end{aligned}$$
(22)

Combining Eq. (21) with Eq. (22), we obtain Eq. (19), and the proof is completed.

2.1 Proof of Theorem 1

Combining with Lemmas 1 and 2, for \(\forall x \in (0,1)\), by using the Maple software, let

$$\begin{aligned} \begin{array}{ll} \gamma _{1,0}= \dfrac{\pi }{4}-\dfrac{942547}{1332800} \approx 0.078>0, \gamma _{1,1}=0, \gamma _{1,2}=\dfrac{1626873}{222044480} \approx 0.0073>0, \\ \gamma _{1,3}=-\,\, \dfrac{6561 \sqrt{357} (-982+315\pi )}{8257279100} \approx -0.00011<0, \\ \gamma _{1,4}= -\dfrac{2274934729}{528465862400}+\dfrac{118098 \pi }{58980565} \approx 0.001>0; \\ \gamma _{1,5}=-\dfrac{\pi ^2}{4} -\dfrac{\pi }{4} +\dfrac{107}{45}) \approx -0.87<0, \\ \gamma _{1,6}= \left( -\dfrac{\pi ^2}{4} +\dfrac{3 \pi }{4} -\dfrac{563}{2520}\right) \approx -0.33<0, \\ \gamma _{1,7} =\left( -\dfrac{\pi ^2}{4} +3 \pi -\dfrac{18239}{2520}\right) \approx -0.28<0, \\ \gamma _{1,8} =\left( -\dfrac{(60 \pi -131) (60 \pi -149)}{14400}\right) \approx -0.15<0, \\ \gamma _{1,9}=\left( -\dfrac{(60 \pi -149)^2}{14400}\right) \approx -0.108<0, \end{array} \end{aligned}$$

it can be verified that

$$\begin{aligned} \begin{array}{ll} { f_1(x)-\bar{G}_{1,3}\left( x,\sqrt{\dfrac{27}{119}}\right) } \\ \quad { = \dfrac{(\arcsin x )^2}{x^2} + \dfrac{\arctan x}{x} - \dfrac{17}{45 \sqrt{\dfrac{27}{119}}} x^3 \arctan \left( \sqrt{\dfrac{27}{119}} x\right) - 2 } \\ \quad {> \dfrac{l_3(x)^2}{x^2} + \dfrac{l_1(x)}{x} - \dfrac{17}{45 \sqrt{\dfrac{27}{119}}} x^3 \cdot l_2\left( \sqrt{\dfrac{27}{119}} x\right) -2 } \\ \quad = \left( \overset{4}{\underset{i=0}{\sum }} \gamma _{1,i} x^i \right) \cdot x^8> \left( \gamma _{1,0}+\gamma _{1,3}\right) \cdot x^8 \approx (0.078 -0.00011 ) \cdot x^8 >0, \end{array} \end{aligned}$$
(23)

and

$$\begin{aligned} \begin{array}{ll} f_1(x)-\left( 2 + \dfrac{\pi ^2+\pi -8}{4} x^4\right) \\ \quad = \dfrac{(\arcsin x )^2}{x^2} + \dfrac{\arctan x}{x}-2- \dfrac{\pi ^2+\pi -8}{4} x^4 \\ \quad< \dfrac{l_4(x)^2}{x^2} + \dfrac{l_2(x)}{x}-2- \dfrac{\pi ^2+\pi -8}{4} x^4 = (1-x)\cdot x^4 \\ \quad \cdot (\gamma _{1,5} (1+x)+\gamma _{1,6} x^2 +\gamma _{1,7} x^3 +\gamma _{1,8} (x^4+x^5) +\gamma _{1,9} (x^6 + x^7) ) <0. \end{array} \end{aligned}$$
(24)

Combining Eq. (23) with Eq. (24), one obtains Eq. (12), and the proof of Theorem 1 is completed.

2.2 Proof of Theorem 2

Combining with Lemmas 1 and 2, for \(\forall x \in (0,1)\), by using the Maple software, let

$$\begin{aligned} \begin{array}{ll} \gamma _{2,0}=\dfrac{\pi }{4}-\dfrac{60799}{82320} \approx 0.0468>0, \gamma _{2,1}=0, \gamma _{2,2}=\dfrac{18225}{3764768} \approx 0.0048>0, \\ \gamma _{2,3}=-\,\,\dfrac{10935 \sqrt{10}(315 \pi -982)}{210827008} \approx -\,\,0.00124<0, \\ \gamma _{2,4}= \dfrac{820125 \pi }{26353376}-\dfrac{72225675}{737894528} \approx -\,\,0.000113<0, \\ \gamma _{2,5}= -\dfrac{5 \pi }{4}+\dfrac{67}{20} \approx -\,\,0.576<0, \gamma _{2,6}= -\dfrac{\pi }{4} +\dfrac{76}{105} \approx -\,\,0.0615<0, \\ \gamma _{2,7}= 2 \pi -\dfrac{1321}{210} \approx -\,\,0.0072<0, \end{array} \end{aligned}$$

it can be verified that

$$\begin{aligned} \begin{array}{ll} f_2(x)- \bar{G}_{3,3}\left( x,\dfrac{3 \sqrt{10}}{14} \right) \\ \quad = \dfrac{2 \arcsin x}{x} + \dfrac{\arctan x}{x}-3 - \dfrac{49}{30 \sqrt{10} } x^3 \arctan \left( \dfrac{3 \sqrt{10}}{14} x\right) \\ \quad> \dfrac{2 l_3(x)}{x} + \dfrac{l_1(x)}{x}-3 - \dfrac{49}{30 \sqrt{10} } x^3 \cdot l_2\left( \dfrac{3 \sqrt{10}}{14} x\right) \\ \quad = ( \overset{4}{\underset{i=0}{\sum }} \gamma _{2,i} x^i ) \cdot x^8> (\gamma _{2,0} + \gamma _{2,3} + \gamma _{2,4} ) \cdot x^8 \\ \quad \approx (0.0468 -\,\,0.00124 -\,\,0.000113 ) \cdot x^8>0.04 x^8 >0, \end{array} \end{aligned}$$
(25)

and

$$\begin{aligned} \begin{array}{ll} f_2(x)-\left( 3+\dfrac{5 \pi -12}{4} x^4\right) = \dfrac{2 \arcsin x}{x} + \dfrac{\arctan x}{x}-3 -\dfrac{5 \pi -12}{4} x^4 \\ \quad< \dfrac{2 l_4(x)}{x} + \dfrac{l_2(x)}{x}-3 -\dfrac{5 \pi -12}{4} x^4 \\ \quad = \left( \gamma _{2,5}(1+x) + \gamma _{2,6} x^2 + \gamma _{2,7} x^3 \right) \cdot (1-x)\cdot x^4 <0. \end{array} \end{aligned}$$
(26)

Combining Eq. (25) with Eq. (26), one obtains Eq. (13) and completes the proof of Theorem 2.

2.3 Proof of Theorem 3

Combining with Lemma 1 and Lemma 2, for \(x \in (0,1)\), by using the Maple software, let

$$\begin{aligned} \gamma _{3,0}= & {} -\,\,\dfrac{45 \pi ^2+11 \pi -360}{ 90\pi } \approx -\,\,0.4<0, \\ \gamma _{3,1}= & {} \dfrac{1050 \pi ^2-7073 \pi +11760}{2520 \pi } \approx -0.01<0, \\ \gamma _{3,2}= & {} \dfrac{6720 \pi ^2-24749 \pi +11760}{2520\pi }\approx 0.042>0 , \\ \gamma _{3,3}= & {} \dfrac{(60 \pi -149)(191 \pi -480)}{14400\pi }\approx 0.11>0, \\ \gamma _{3,4}= & {} -\,\,\dfrac{(60 \pi -149)^2}{14400} \approx -\,\,0.1<0, \\ \gamma _{3,5}= & {} -\,\,\dfrac{43\pi -120}{20 \pi } \approx -\,\,0.24<0, \\ \gamma _{3,6}= & {} -\,\, \dfrac{2201\pi -5880}{840 \pi } \approx -\,\,0.39<0, \\ \gamma _{3,7}= & {} \dfrac{(1890 \pi ^2-8093 \pi +5880)}{840 \pi }\approx -0.33<0, \\ \gamma _{3,8}= & {} \dfrac{(5 \pi -12) (60 \pi -149)}{240 \pi } \approx 0.19>0, \\ \gamma _{3,9}= & {} \dfrac{(5 \pi -12) (840 \pi -2161)}{3360 \pi } \approx 0.16 >0 , \end{aligned}$$

it can be verified that

$$\begin{aligned} \begin{array}{ll} l_4(x)-\dfrac{(\pi ^2+\pi -8)}{2 \pi } x^5> x -\dfrac{(\pi ^2+\pi -8)}{2 \pi } x> 0.2 x >0, \\ \quad f_1(x)-\left( 2 + \dfrac{\pi ^2+\pi -8}{2 \pi } x^3 \arcsin (x)\right) \\ \quad = \dfrac{\arcsin (x)}{x^2} \left( \arcsin (x)-\dfrac{(\pi ^2+\pi -8)}{2 \pi } x^5\right) + \dfrac{\arctan (x)}{x}-2 \\ \quad< \dfrac{l_4(x)}{x^2} \cdot (l_4(x)-\dfrac{(\pi ^2+\pi -8)}{2 \pi } x^5) + \dfrac{l_2(x)}{x}-2 = x^4 \cdot (1-x) \\ \quad \cdot \left( \gamma _{3,0} (1+x)+ \gamma _{3,1} x^2 + \gamma _{3,2} x^3 + \gamma _{3,3} (x^4+x^5) + \gamma _{3,4} (x^6+x^7)\right) \\ \quad<\left( \gamma _{3,0} (1+x) + \gamma _{3,2} x^3 + \gamma _{3,3} (x^4+x^5) ) \cdot (x^4 \cdot (1-x)\right) \\ \quad< \left( \gamma _{3,0} + \gamma _{3,2} + \gamma _{3,3} (1+1)\right) \cdot (x^4 \cdot (1-x)) \\ \quad \approx \left( -\,\,0.4 + 0.042 + 0.11 \cdot 2 \right) \cdot \left( x^4 \cdot (1-x)\right) \\ \quad = -\,\,0.138 \cdot \left( x^4 \cdot (1-x)\right) <0, \end{array} \end{aligned}$$
(27)

and

$$\begin{aligned} \begin{array}{ll} \dfrac{2 }{x} - \dfrac{5 \pi -12}{2 \pi } x^3> 2 -\dfrac{5 \pi -12}{2 \pi } = \dfrac{12-\pi }{2 \pi }>0, \\ \quad f_2(x)-\left( 3 + \dfrac{5 \pi -12}{2 \pi } x^3 \arcsin (x)\right) \\ \quad = \dfrac{2 \arcsin x}{x} + \dfrac{\arctan x}{x}-\left( 3 + \dfrac{5 \pi -12}{2 \pi } x^3 \arcsin (x)\right) \\ \quad = \left( \dfrac{2 }{x} - \dfrac{5 \pi -12}{2 \pi } x^3\right) \cdot \arcsin (x) + \dfrac{\arctan x}{x}-3 \\ \quad< \left( \dfrac{2 }{x} - \dfrac{5 \pi -12}{2 \pi } x^3\right) \cdot l_5(x) + \dfrac{l_2(x)}{x}-3 = x^4 \cdot (1 -x) \\ \quad \cdot \left( \gamma _{3,5} (1+x) + \gamma _{3,6} x^2 + \gamma _{3,7} x^3 +\gamma _{3,8} (x^4+x^5) + \gamma _{3,9} (x^6+x^7)\right) \\ \quad< \left( \gamma _{3,6} x^3 + \gamma _{3,7} x^3 +\gamma _{3,8} (x^3+x^3) + \gamma _{3,9} (x^3+x^3)\right) \cdot x^4 \cdot (1 -x) \\ \quad = \left( \gamma _{3,6} + \gamma _{3,7} +\gamma _{3,8} (1+1) + \gamma _{3,9} (1+1)\right) \cdot x^7 \cdot (1 -x) \\ \quad \approx \left( -\,\,0.39 -\,\,0.33 + 0.19 \cdot 2 + 0.16 \cdot 2 \right) \cdot x^7 (1 -x) \\ \quad = -\,\,0.02 \cdot x^7 \cdot (1 -x)<0. \end{array} \end{aligned}$$
(28)

Combining Eq. (27) with Eq. (28), Theorem 3 has been proved.

2.4 Proof of Theorem 4

Combining with Lemma 1 and Lemma 2, by using the Maple software, let

$$\begin{aligned}&\gamma _{4,0} = 3.33220478976 \cdot 10^{11}, \\&\gamma _{4,1} = 6491429683200 \pi -20499054428160 \approx -1.05 \cdot 10^{11}<0, \\&\gamma _{4,2} = -\,\,5901299712000 \pi +18714755727360 \approx 1.75 \cdot 10^{11}>0, \\&\gamma _{4,3} =0,~~ \gamma _{4,4} =-2.8913892480\cdot 10^{10}<0, \\&\gamma _{4,5} =-\,\,1188378132480 \pi +3752736948224 \approx 1.93\cdot 10^{10}>0, \\&\gamma _{4,6} =1080343756800 \pi -3387894188800 \approx 6.1 \cdot 10^9>0, \\&\gamma _{4,7} =0,~~ \gamma _{4,8} =6894079500, ~~ \gamma _{4,9} =0, ~~ \gamma _{4,10} =3208936500, \\&\gamma _{4,11} =0, ~~ \gamma _{4,12}=1181472075, \\&\gamma _{5,0}=812851200 \pi ^2+347504640 \pi -6502809600 \approx 2.61 \cdot 10^9>0, \\&\gamma _{5,1}=609638400 \pi ^2+31137792 \pi -4877107200 \approx 1.23 \cdot 10^9>0, \\&\gamma _{5,2}=-\,\,1117670400 \pi ^2+5744145792 \pi -7315660800 \approx -3.008 \cdot 10^8<0, \\&\gamma _{5,3}=-\,\,1519862400 \pi ^2+6433591072 \pi -6265728000 \approx -1.05 \cdot 10^9<0, \\&\gamma _{5,4}=432 (940800 \pi ^2-4672640 \pi +5784153) \pi \approx 5.29\cdot 10^8>0, \\&\gamma _{5,5}=(20160 \pi -50639)\cdot (20160 \pi -53089) \pi \approx 4.08 \cdot 10^8>0, \\&\gamma _{5,6}= (20160 \pi -53089)^2 \pi \approx 3.29 \cdot 10^8>0, \\&\gamma _{4,0}+ \gamma _{4,1}> 3.1 \cdot 10^{11}>0, ~~\gamma _{4,2}+ \gamma _{4,4}> 1.4 \cdot 10^{11}>0, \\&\gamma _{5,0} + \gamma _{5,2} + \gamma _{5,3}> 1.0 \cdot 10^{9}>0, \end{aligned}$$

for \(x \in (0,1)\), it can be verified that

$$\begin{aligned} \begin{array}{ll} \arcsin (x)-\dfrac{184}{945} \cdot x^5> l_5(x)-\dfrac{184}{945} \cdot x^5 \\ \quad =\dfrac{x (135 x^6-362 x^4+504 x^2+3024)}{3024}>0, \\ \quad f_1(x)-L_3(x) \\ \quad = \dfrac{\arcsin (x)}{x^2} \cdot \left( \arcsin (x)-\dfrac{184}{945} \cdot x^5 \right) + \dfrac{\arctan (x)}{x}\left( 1 -\dfrac{173}{945} \cdot x^4\right) -2 \\ \quad> \dfrac{l_8(x)}{x^2} \cdot \left( l_8(x)-\dfrac{184}{945} \cdot x^5 \right) + \dfrac{l_3(x)}{x}\left( 1 -\dfrac{173}{945} \cdot x^4\right) -2 \\ \quad = \dfrac{x^8}{2360519884800} \cdot (\overset{12}{\underset{i=0}{\sum }} \gamma _{4,i} \cdot x^i) \\ \quad> \dfrac{x^8}{2360519884800} \cdot \left( (\gamma _{4,0}+ \gamma _{4,1}) + (\gamma _{4,2}+ \gamma _{4,4}) x^2 \right) >0, \end{array} \end{aligned}$$
(29)

and

$$\begin{aligned} \begin{array}{ll} \dfrac{45\pi ^2+11\pi -360}{45\pi } \approx -0.839, \\ \quad \arcsin (x)-\dfrac{ 45 \pi ^2+28 \pi -360}{45 \pi } \cdot x^5> l_5(x)-\dfrac{ 45 \pi ^2+28 \pi -360}{45 \pi } \cdot x^5 \\ \quad> x+\dfrac{1}{6} x^3+\dfrac{3}{40} x^5 -\dfrac{ 45 \pi ^2+28 \pi -360}{45 \pi } \cdot x^5 \\ \quad> \left( 1+\dfrac{1}{6} +\dfrac{3}{40} -\dfrac{ 45 \pi ^2+28 \pi -360}{45 \pi }\right) \cdot x^5 \approx 0.0243 \cdot x^5>0, \\ \quad f_1(x)-R_3(x) = \dfrac{\arctan (x)}{x} \left( 1+\dfrac{45\pi ^2+11\pi -360}{45\pi } \cdot x^4 \right) \\ \quad + \dfrac{\arcsin (x)}{x^2} \left( \arcsin (x)-\dfrac{ 45 \pi ^2+28 \pi -360}{45 \pi } \cdot x^5\right) -2 \\ \quad< \dfrac{l_4(x)}{x} \left( 1+\dfrac{45\pi ^2+11\pi -360}{45\pi } \cdot x^4 \right) \\ \quad + \dfrac{l_9(x)}{x^2} \left( l_9(x)-\dfrac{ 45 \pi ^2+28 \pi -360}{45 \pi } \cdot x^5\right) -2 \\ \quad =\dfrac{x^6\cdot (x^2-1)}{1625702400 \pi }\cdot (\overset{6}{\underset{i=0}{\sum }} \gamma _{5,i} \cdot x^{2i}) \\ \quad< \dfrac{x^6\cdot (x^2-1)}{1625702400 \pi }\cdot ( \gamma _{5,0} + \gamma _{5,2} + \gamma _{5,3}) <0. \end{array} \end{aligned}$$
(30)

Combining Eq. (29) with Eq. (30), Theorem 4 has been proved.

3 More discussions

Firstly, the new method can recover previous results in Eqs. (6) and (7) in [3, 19]. It can be verified that \(\bar{G}_{1,3}(x,1)=L_1(x)\) and \(\bar{G}_{2,3}(x,1)=R_1(x)\), \(\bar{G}_{3,3}(x,1)=L_2(x)\) and \(\bar{G}_{4,3}(x,1)=R_2(x)\), so both Eqs. (6) and (7) are recovered.

Secondly, the new method can achieve much better approximation performance. Let \(D_3(x)=\dfrac{R_1(x)-\bar{G}_{2,3}(x,0)}{x^3}\) and \(D_4(x)=L_1(x)-\bar{G}_{1,3}(x,\sqrt{\dfrac{27}{119}})\). We have that \(D_4^{'}(x)=\dfrac{-1564 x^2}{45 (x^2+1) (119+27 x^2)}\) and \(D_3^{'}(x)=\dfrac{- (\pi ^2+\pi -8) (\pi x^2+\pi -4)}{4 \pi (x^2+1)}\) has a unique simple root \(x_4 = \sqrt{\dfrac{4-\pi }{\pi }}\) within (0, 1), such that

$$\begin{aligned} \begin{array}{ll} D_3^{'}(x)>0, ~x \in (0,x_4) ~~\text{ and } ~~D_3^{'}(x)<0, ~x \in (x_4,1), \\ D_3(x)>D_3(0)=0, ~x \in (0,x_4] ~~\text{ and } ~~D_3(x)>D_3(1)=0, ~x \in (x_4,1), \\ D_4^{'}(x)<0 ~~\text{ and }~~D_4(x)<D_4(0)=0, ~~x \in (0,1), \end{array} \end{aligned}$$

which leads to

$$\begin{aligned} R_1(x)>\bar{G}_{2,3}(x,0)>f_1(x)>\bar{G}_{1,3}\left( x,\sqrt{\dfrac{27}{119}}\right) >L_1(x),~~ x \in (0,1). \end{aligned}$$
(31)

Let \(D_5(x)=\dfrac{R_2(x)-\bar{G}_{4,3}(x,0)}{x^3}\) and \(D_6(x)=L_2(x)- \bar{G}_{3,3}(x,\dfrac{3 \sqrt{10}}{14})\). We have that \(D_6^{'}(x)=\dfrac{-371 x^2}{20 (x^2+1) (98+45 x^2)}\) and \(D_5^{'}(x)=\dfrac{- (5\pi -12)(\pi x^2+\pi -4)}{4 \pi (x^2+1)}\) has a unique simple root \(x_5 = \sqrt{\dfrac{4-\pi }{\pi }}\) within (0, 1), such that

$$\begin{aligned} \begin{array}{ll} D_5^{'}(x)>0, ~x \in (0,x_5) ~~\text{ and } ~~D_5^{'}(x)<0, ~x \in (x_5,1), \\ D_5(x)>D_5(0)=0 ~x \in (0,x_5] ~~\text{ and } ~~D_5(x)>D_5(1)=0, ~x \in (x_5,1), \\ D_6^{'}(x)<0 ~~\text{ and }~~D_6(x)<D_6(0)=0, ~~x \in (0,1), \end{array} \end{aligned}$$

which leads to

$$\begin{aligned} R_2(x)>\bar{G}_{4,3}(x,0)>f_2(x)>\bar{G}_{3,3}\left( x,\dfrac{3 \sqrt{10}}{14}\right) >L_2(x),~~ x \in (0,1). \end{aligned}$$
(32)

From Eqs. (31) and (32), both Eqs. (12) and (13) achieve better approximation effect than those of Eqs. (6) and (7), see also the error plots shown in Fig. 1.

Finally, we have tested the errors for approximating the integral of \(f_i(x)\) by using the bounds in Eqs. (6, 7) and (12–14). Table 1 shows that the approximation errors from (12–14) are much better than those of Eqs. (6, 7).

Table 1 Errors for approximating the integral of \(f_i(x)\) from different bounds
Full size table

As for future work, there is still great scope for further development. In principle, more forms of the two-parameter functions, or even three-parameter functions, can be used for sharpening the bounds of Wilker and Huygens type inequalities. On the other hand, the idea can be extended for more other types of inequalities.