A counterexample to the Fortune’s Formula investing method

Abstract

The classical Kelly investment method consists in betting a fixed fraction $f^*$ of wealth which maximizes the expected log growth rate. The strategy was introduced in 1956 by Kelly and applied effectively to financial investments by Edward O. Thorp and others. In this paper, we determine a large class of n-valued financial games, $n\ge 3$, where the use of a simplified parameter $\widehat{f}$ (the so-called Fortune’s Formula) instead of $f^*$, applied by investors and recommended in investor’s guides and services, as well as in some research papers, leads to ruin. Our theory is completed with an example and simulations.

1 Preface

This article has been written as a result of my search for an optimal method of money management by an investor performing consecutive transactions.

One of the popular solutions, which is recommended in the books and reputable websites about investing , is the so-called Kelly Criterion, based on the 1956 article by Kelly [6]. The author considers there a simple (two-valued: one win and one loss only) investment case with a positive expected value, and proposes a method of money management, which maximizes the growth of wealth in the long run.

However, in practice the investor is faced with more complicated scenarios. For this reason, Thorp [13, p. 129] has proposed the investor should first simplify the distribution of his outcomes to the case described in Kelly’s article, and next apply the solution given there. This method, called today ‘Fortune’s Formula’, was popularized in the 2005 book by Poundstone [10], and was discussed further in the paper [9] (see also [4, Appendix A1]).

During my research, however, I have found many cases showing the investor does not maximize his wealth using the Thorp’s method.

Hence, I was also curious to know whether the use of Fortune’s Formula could have any negative effects. The point is that investors usually identify just this method with the original solution of Kelly and its positive properties: namely that, in the long run, the investor maximizes the growth of his assets and never goes bankrupt.

Thus, there is a natural question:

Whether the use of Fortune’s Formula in investing can lead to the exact opposite, i.e. undesirable consequences: ruin of an investor despite the fact that he is applying a strategy with a positive expected value?

During my research, it turned out this question has a positive answer, and I have found a method of generating such cases.

2 Introduction and the main result

Throughout this paper, we study a class of two-person economic games with a fixed finite set of outcomes and with a positive expected value. The symbol $W_0$ denotes investor’s starting capital.

Suppose an investor (a player) knows the distribution of profits and losses of a given game $\Gamma$ and can play it repeatedly, and that his opponent (e.g., a market) is infinitely rich. Hence, the investor is able to decide what proportion of wealth to risk in a single bet. A natural problem is thus to determine a betting fraction $f^*$ that maximizes the investor’s expected terminal wealth.

One of the solutions, called the Kelly Criterion, says that

(KC)   The investor should maximize (after each bet) the expected log growth rate of his wealth

([6, p. 919], cf. [19, p. 511]). This general solution, when applied properly, has many positive properties [8, pp. 563–574], similar to the two-valued Kelly case mentioned in Sect. 1, e.g., the KC maximizes the rate wealth growth and minimizes the expected time to a preassigned goal [1]; moreover, the investor applying the KC never risks ruin [5] (cf. the Proposition below).

To be honest with the reader who is not a specialist in the Kelly criterion, we must mention this method has also some bad properties, listed in [8, 565–575]. Probably Samuelson, the Nobel Prize winner in economy, was the first critic of the criterion by showing that the KC is optimal for the log-utility function only [11], and that, in short runs, the KC may generate big losses [12].

However, many investors use simplified histograms of outcomes reduced to two values, one gain and one loss only, with respective average probabilities, and apply the KC just to this case [7, 13, 21, 22]. Moreover, the reliable services Morningstar [24] and Motley Fool [25] recommend the simplified rule for investments, which takes the form: The optimal Kelly bet equals

$$\begin{aligned} \widehat{f}:=edge/odds, \end{aligned}$$

where edge is the expected gain from the current bet, and odds is the multiple of the amount of the bet that the winning bettor stands to receive (see Sect. 3.2 for details).

The main goal of this paper is to indicate a class of financial games where an automatic application of the above rule may lead an investor to ruin. More exactly, we have the following result.

Main Theorem

For an arbitrary pair (N, M) of integers with $N\ge 2$, $M\ge 1$ there is a class of random variables X (with corresponding probability distributions), representing N gains and M losses of a financial game, with the expected value E(X) positive, such that the use of the simplified parameter $\widehat{f}$ in investing can lead to ruin.

Thus, our result supplements the Samuelson’s criticism of the Kelly Criterion but from another perspective.

The next sections of this paper are organized as follows. In Sect. 3 we address the construction of a function describing the log growth rate of the investor’s wealth, and a process of reduction of n-valued games to two-valued games (Fortune’s Formula). We also outline the theory of the Kelly Criterion for n-valued games and the problem of determining an exact value of the optimal betting fraction $f^*$. In Sect. 4, Theorem 1, we present a three-valued version of the main Theorem along with a counterexample and simulations illustrating Theorem 1. This version is too technical to present it here, yet it is the basis of the proof of the general case stated in the main Theorem above and, moreover, it allows us to generate many concrete examples. In Sect. 5, we give proofs of our results.

3 Notation and preliminary results

As at the beginning of Sect. 2, we shall assume the investor knows the distribution of profits and losses of a given game $\Gamma$; f is the fraction of wealth the investor risks in a single trial $(0<f<1)$, and $W_k(f)$ denotes the investor’s wealth after k trials when applying the parameter f, $k=1,2,\ldots ,K$. Further, $d_k$ denotes the gain/loss in the kth transaction, and $\delta$ denotes the modulus of the greatest loss among all of the K transactions; we also assume that the outcomes $d_k$ are i.i.d.

3.1 The construction of function $G_{(N,M)}$

We present below a step-by-step construction of a function whose properties allow us to determine the optimal betting fraction $f^*$ in the Kelly Criterion. It is interesting to note that the normalization process, of dividing all the outcomes $d_k$ by the modulus of the biggest loss, is the result of this construction, and not an a priori requirement (see [20, p. 122], cf. the remarks in [15, p. 216]).

Set $W_0(f)=W_0$. By the definition of f, in the kth transaction we risk (i.e., we may lose) $f\cdot W_{k-1}(f)$ of our wealth. On the other hand, we may lose at most $\delta >0$ on each share, whence the number of shares we buy equals $S_k:=\frac{f\cdot W_{k-1}(f)}{\delta }$. But since our kth gain/loss equals $d_k$, the financial result of our kth transaction equals¹$S_k d_k = f \cdot W_{k-1}(f)\cdot \frac{d_k}{\delta }$. Hence, after the kth transaction our capital equals

$$\begin{aligned} W_k(f)= W_{k-1}(f)+ S_k d_k = W_{k-1}(f) \left( 1+f\frac{d_k}{\delta }\right) , \end{aligned}$$

(1)

$k=1,2,\ldots ,K$, whence, inductively,

$$\begin{aligned} W_K(f)=W_0\prod _{k=1}^K \left( 1+f\frac{d_k}{\delta }\right) . \end{aligned}$$

(2)

Notice that, although $d_k$ and $\delta$ are expressed in concrete financial units, each fraction $d_k/\delta$ is a dimensionless number (i.e., a pure number without any physical units).

Now let $\mathcal {D}$ denote the string $(d_k/\delta )_{k=1}^K$, and let

$$\begin{aligned} X_{(N,M)}=\left( A_1,\ldots , A_N, -B_1,\ldots ,-B_M\right) \end{aligned}$$

(3)

be the strictly decreasing sequence of the values of $\mathcal {D}$ with $A_N\ge 0>-B_1$; notice that

$$\begin{aligned} B_M=1. \end{aligned}$$

(4)

Further, let $n_i$ and $m_j$, respectively, denote the cardinalities of the sets $\{k: d_k/\delta =A_i\}$ and $\{k: d_k/\delta =B_j\}$, $i\le N$, $j\le M$. Then (2) is going into

$$\begin{aligned} W_K(f)=W_0\prod _{i=1}^N(1+fA_i)^{n_i}\prod _{j=1}^M(1-fB_j)^{m_j}, \end{aligned}$$

whence the Kth geometric mean $H_K(f)$ of $W_K(f)/W_0$ equals

$$\begin{aligned} H_K(f)=\prod _{i=1}^N(1+fA_i)^{\nu _i}\prod _{j=1}^M(1-fB_j)^{\mu _j}, \end{aligned}$$

(5)

where $\nu _i=n_i/K$ and $\mu _j=m_j/K$, with $\nu _1+\cdots +\nu _N+\mu _1+\cdots +\mu _M=1$. If the number K is sufficiently large (in the sense of the law of large numbers), or if we make only an ‘ex-post analysis’ of the game $\Gamma$, we replace in (5) the frequencies $\nu _i$ and $\mu _j$ by respective probabilities $p_i$ and $q_j$. Then the string X defined in (3) becomes the random variable of the game $\Gamma$ with the probability distribution

$$\begin{aligned} \mathcal {P}_{(N,M)}=(p_1,\ldots , p_N, q_1,\ldots , q_M). \end{aligned}$$

(6)

Now, taking logarithms (in base e), we obtain a formula describing the log growth rate of the investor’s wealth (depending on f):

$$\begin{aligned} \begin{aligned} G_{(N,M)}(f)=&~E(\log (1+fX)) \\ =&\sum _{i=1}^Np_i\log (1+fA_i) + \sum _{j=1}^Mq_j \log (1-fB_j). \end{aligned} \end{aligned}$$

(7)

In the particular case $N=1$ or $N=2$, with $M=1$, we shall write G instead of $G_{(N,1)}$; similarly for X and $\mathcal {P}$.

Remark 1

We will discuss now a peculiar situation that appears in the proof of the Main Theorem, based on part (b) of the Proposition in the next subsection. From the general form (7) of $G_{(N,M)}$ it follows this function depends continuously on all the parameters defining it. Let us consider the case when $M\ge 2$ and f is a continuous function of$(B_1,\ldots ,B_M)$, with $0<B_1<\ldots <B_M=1$ and each $B_j$ converging to $B_j^0\in (0,1]$,² and such that $f\rightarrow f^0:=f(B_1^0,\ldots ,B_{M-1}^0,1)\in (0,1)$; then we are dealing with an infinite family of functions $G_{(N;B_1,\ldots ,B_{M-1},1)}$, and not a one of them. We thus obtain $G_{(N;B_1,\ldots ,B_{M-1},1)}(f)\rightarrow G_{(N;B_1^0,\ldots ,B_{M-1}^0,1)}(f^0)$, and if $G_{(N;B_1^0,\ldots ,B_{M-1}^0,1)}(f^0)<0$, then, by continuity of $G_{(N,\cdot ,\ldots ,\cdot ,1)}(f(\cdot ,\ldots ,\cdot ,1))$, there are infinite many systems$(B_1,\ldots ,B_{M-1},1)$ with $0<B_1<\ldots <B_M=1$ and $B_j\not =B_j^0$ for all $j\le M-1$, such that $G_{(N;B_1,\ldots ,B_{M-1},1)}(f(B_1,\ldots ,B_{M-1},1))<0$. Then, for our purposes, we can choose one of such functions $G_{(N;B_1,\ldots ,B_{M-1},1)}$.

3.2 The Kelly criterion for n-valued games

The Kelly criterion applies easily to two-valued games, where the determination of the betting fraction $f^*$ is very simple: If $X=(A,-B)$, with $A,B>0$, is a random variable of the game with the probability distribution $\mathcal {P}=(p,q)$ and $E(X)>0$, then

$$\begin{aligned} f^*=\frac{E(X)}{A}=p- \frac{qB}{A}\in (0,1) \quad \mathrm {and}\quad G(f^*)>0. \end{aligned}$$

(8)

Indeed, by (7), the log growth rate of the investor’s wealth equals

$$\begin{aligned} G(f)=p\log (1+Df)+q\log (1-f), \end{aligned}$$

(9)

where $D=A/B$. Hence, by the KC, solving equation $G'(f)=0$ and noting that G is concave on [0, 1) with $G'(0)=E(X)>0$ we obtain (8).

One should note that formula (8), for $A=B=1$, appears (implicitly) for the first time in the 1956 paper by Kelly [6, p. 920] (here $f^*=p-q=E(X)$), and its general form can be obtained from the form of G(f) [as in (9)] on page 129 of the 1984 book [17] by Thorp.

For n-valued games, with $n>2$, the $f^*$-problem is much more complex: in Sect. 3.1, formula (7), we showed that the log growth rate of the investor’s wealth equals

$$\begin{aligned} G_{(N,M)}(f)= \sum _{i=1}^Np_i\log (1+fA_i) + \sum _{j=1}^Mq_j \log (1-fB_j), \end{aligned}$$

where $N+M=n$ with $N,M\ge 1$, the gains $A_i$ and losses $B_j$ (i.e., the elements of the random variable X of the game) are positive and pairwise distinct, respectively, and the probabilities $p_i$ and $q_j$ are positive and sum up to 1; we have also shown we may assume that $\max _{j\le M} B_j=1$, in general.³ It is easy to check that the function $G_{(N,M)}$ is concave on [0, 1) and since, by our general hypothesis, $G_{(N,M)}'(0)=E(X)>0$, we obtain that

$(P_1)$ :

$G_{(N,M)}$attains its maximum at some$f^*=f^*_{(N,M)}\in (0,1)$, which is a unique solution of the equation$G_{(N,M)}'(f)=0$;

and that

$(P_2)$ :

$G_{(N,M)}(f^*)>0$.

The determination of an exact value of $f^*$ is thus equivalent to solving of a polynomial equation of the $n-1$ degree. The task is complicated even for $n=4$ and $n=5$ and, by the celebrated Galois theory, has no general solution for $n\ge 6$ by means of the parameters defining the game [14]. Although the Cover’s algorithm [3] gives us a numerical value of $f^*$, it does not tell us about the dependence of $f^*$ on the form of X.

The knowledge about the value of $f^*$ is important to investors because of the following property, which is a simple consequence of a more general result obtained in 1961 by Breiman [1, Proposition 3] (cf. [16, Theorem 5] or [18, Theorem 1] for two-valued games):

Proposition

Let $f \in (0,1)$, let $W_k(f)$ denote the investor’s wealth after k trials applying f, and let $\mathrm {Pr}[A]$ mean “the probability of event A”.

• (a) If $G_{(N,M)}(f) > 0$, then $\lim _{k\rightarrow \infty } W_k(f) = \infty$, almost surely, i.e., for each $M > 0$, $\mathrm {Pr}[\liminf _{k\rightarrow \infty }W_k(f) > M]=1$.

• (b) If $G_{(N,M)}(f) < 0$, then $\lim _{k\rightarrow \infty } W_k(f) = 0$, almost surely, i.e., for each $\varepsilon > 0$, $\mathrm {Pr}[\liminf _{k\rightarrow \infty }W_k(f) < \varepsilon ]=1$.

In other words, applying $f_1$ with $G_{(N,M)}(f_1) > 0$ the investor’s capital can grow unlimitedly, while applying $f_2$ with $G_{(N,M)}(f_2) < 0$ the investor will achieve ruin in proper time.

3.3 The Fortune’s Formula: a simplification of the $f^*$-problem

The $f^*$-problem has thus caused the need of replacing the exact value of $f^*$ by a simpler parameter but ’almost as good as’ $f^*$. Some traces of this idea can be found at the end of page 926 of the Kelly paper [6]. Probably Thorp is the author of such a parameter, $\widehat{f}$, but the historians Christensen [2] and Poundstone [10] do not mention about that. The parameter $\widehat{f}$ is of the form edge / odds, defined already in Sect. 2. This formula, called by Poundstone the Fortune’s Formula [10, p. 72], has more exact form, similar to (8): if X denotes the random variable of the game $\Gamma$ and $\widetilde{A}:=E(X>0)$ denotes the average of profits of the game, then

$$\begin{aligned} \widehat{f}=edge/odds=E(X)/\widetilde{A}. \end{aligned}$$

(10)

Poundstone, in his book [10], writes about the career $\widehat{f}$ has made in the world of investors, and the pioneering role of Thorp in that field. The use of $\widehat{f}$ in investing is recommended in the books by Kaufman [7, p. 624], Schwager [13, pp. 194–198] (in an interview with Thorp), on internet sites [21, 22], and in research papers, e.g. [4, 9].

By (8) and (10), for two-valued games we have the identity $\widehat{f}=f^*$ , yet $\widehat{f}\not = f^*$, in general, and it has never been proved that $G_{(N,M)}(\widehat{f})>0$ for every n-valued game with $n\ge 3$. Moreover, in the counterexample in Sect. 4 below we illustrate numerically that the uncritical use of $\widehat{f}$ in investing may have a negative consequence.

4 The results

The main result of this paper is the main Theorem stated in Sect. 2. In Theorem 1 below, we present a detailed 3-valued version of the main Theorem. The parameters of Theorem 1 will be applied essentially in the proof of the general case (see Sect. 5). In Sects. 4.1 and 4.2, we present a numerical counterexample to the Fortune’s Formula investment method, based on Theorem 1.

Let $(A_1,A_2)$ be a pair of positive numbers with $A_1>1>A_2$ such that

$$\begin{aligned} (A_1-1)(1-A_2)>2. \end{aligned}$$

(11)

We shall consider the random variable $X=(A_1,A_2,-1)$ of a game with probability distribution $\mathcal {P}_s=(p_1(s),p_2(s),q_1(s))$ of the form

$$\begin{aligned} p_1(s)&=(0.5+s)\cdot \frac{1-A_2}{A_1-A_2}, \nonumber \\ p_2(s)&=(0.5+s)\cdot \frac{A_1-1}{A_1-A_2}, \\ q(s)&=0.5-s,\nonumber \end{aligned}$$

(12)

where $0<s<0.5$. Moreover, $E_s(X)$ denotes the expected value of X with respect to $\mathcal {P}_s$, and $G_s(f)$, defined in (7) for $N=2$ and $M=1$, has a similar meaning.

Theorem 1

Let $X=(A_1,A_2,-1)$ be the random variable fulfilling inequality (11). Then there is $s_1 \in (0,0.5)$ such that, for every $s \in (0, s_1)$ and the probability distribution $\mathcal {P}_s$ of the form (12),

• (i) $E_s(X)=2s=\widehat{f}_s>0$ and $G_s(\widehat{f}_s)<0$, whence (by the Proposition, part (b)) the investor applying $\widehat{f}_a$ will achieve ruin almost surely (a.s.) despite the fact that

• (ii) $G_s(f^*_s)>0$ for a positive $f^*_s < \widehat{f}_s$ maximizing $G_s$, whence (by the Proposition, part (a)) the capital of the investor applying $f^*_s$ will grow unlimitedly a.s.

Moreover, there is $s_0\in (0,1/2)$ such that $G_{s_0}(\widehat{f}_{s_0})<0$ is the minimum of the numbers $G_s(\widehat{f}_s)$, $s\in (0,1/2)$.

4.1 The counterexample

Now we shall present only one numerical illustration of Theorem 1, because other counterexamples can be obtained by means of the method described below.

Let us consider a game with two wins $d_1=\$216$, $d_2=\$3$ and one loss $d_3=- \$24$, and with some probabilities $p_1,p_2,q$, respectively. Then, by definition, $\delta =|d_3|=\$~24$, whence $A_1=d_1/\delta = 9$, $A_2=d_2/\delta =0.125$, and $B_1=-d_3/\delta =1$. Since the pair $(A_1,A_2)$ fulfills inequality (11), Theorem 1 can be applied with a suitable probability distribution.

We shall apply the notation as for Theorem 1, yet in this case we do not use the subscript s, i.e., we simply write E(X) instead of $E_s(X)$, etc.

Claim

Let $\Gamma$ denote a game with $X=(A_1,A_2,-1)=(9,0.125,-1)$ and $\mathcal {P}=(\frac{4.6214}{71}, \frac{42.2528}{71}, 0.3398)$, and let G denote a function of the form (7) defined by the pair $(X,\mathcal {P})$:

$$\begin{aligned} G(f)=\frac{4.6214}{71}\log (1+9f) + \frac{42.2528}{71}\log (1+0.125f)+0.3398\log (1-f). \end{aligned}$$

(13)

Then:

• (i) $E(X)=0.3204=\widehat{f}>0$,

• (ii) $G(\widehat{f})=-0.01961 <0$, and

• (iii) G attains its maximum at $f^*=0.1032$ with $G(f^*)=0.0133>0$.

Hence, by Theorem 1, the investor applying $\widehat{f}=0.3204$ achieves ruin a.s., while applying $f^*=0.1032$ the investor’s capital can grow unlimitedly.

Figures 1 and 2 contain simulations of the game $\Gamma$ for the above parameters $\widehat{f}$ and $f^*$ illustrating the ruin and increase of wealth, respectively.

Comparing the values of the parameters $\widehat{f}$ and $f^*$ we obtain

$$\begin{aligned} \widehat{f}/f^*=0.3204/0.1032= 3.104 \cdots \end{aligned}$$

This shows that $\widehat{f}$ lies far away from $f^*$ and, along with part (ii) of the Claim, disproves the belief that investing using $\widehat{f}$ is as profitable as investing by means of $f^*$ (see, e.g., [4, Appendix A1]).

4.2 Simulations

From part (ii) of the Claim and from part (iii) of Theorem 1 it follows that the investor applying $\widehat{f}$ will achieve ruin almost surely. This is illustrated in Fig. 1 containing five sample simulations of our game $\Gamma$ obtained by means of the inductive formula (1), with starting capital of 1000 units and 300 trials. Figure 2 shows the wealth paths of the investor applying $f^*=0.1032$. We have accepted only the simulations passed positively through the Bartels Rank Test of randomness [23] applied to the appearance of the outcomes 0.125, 9, and $-1$ in game $\Gamma$ in consecutive trials. Notice high local fluctuations in the graphs caused by the high variance of X, $Var(X)=5.518\cdots$, relative to $E(X)=0.3204$.

Fig. 1

Five simulations of the capital of an investor applying $\widehat{f}=0.3204$, after consecutive k transactions

Fig. 2

Five simulations of the capital of an investor applying $f^*=0.1032$, after consecutive k transactions

5 The proofs

5.1 Proof of Theorem 1

At first, we present an idea of the proof. For clarity we shall simplify notation: we write below $\mathcal {X}$, $\mathcal {G}$, $E(\mathcal {X})$, etc., instead of $X_{(N,M)}$, $G_{(N,M)}$, $E_{(N,M)}(X_{(N,M)})$, etc.

Let $\Gamma$ be a fixed game defined uniquely by a random variable

$$\begin{aligned} \mathcal {X}=(A_1,\ldots , A_N,-B_1,\ldots , -B_M), \end{aligned}$$

where the string $\mathcal {X}$ is strictly decreasing with $A_N\ge 0>-B_1$ and $B_M=1$, and by the respective probability distribution $\mathcal {P}=(p_1,\ldots , p_N,q_1,\ldots ,q_M)$, $N,M\ge 1$ and$N+M>2$. We also assume that the expected value $E(\mathcal {X})=\sum _{i=1}^Np_iA_i - \sum _{j=1}^M q_jB_j$ is positive.

From the Taylor formula for $\log (1+x)$ we obtain the inequality $\log (1+ x) \le x-\frac{x^2}{2}+\frac{x^3}{3}$, for $x>-1$, with equality only for $x=0$. Hence, for every $f\in (0,1)$, $A_i$ and $B_j$,

$$\begin{aligned}&\log (1+fA_i)\le f\cdot A_i -\frac{f^2\cdot A_i^2}{2}+\frac{f^3\cdot A_i^3}{3}, \quad \mathrm {and} \end{aligned}$$

(14)

$$\begin{aligned}&\log (1-fB_j)<-f\cdot B_j -\frac{f^2\cdot B_j^2}{2}-\frac{f^3\cdot B_j^3}{3}. \end{aligned}$$

(15)

Applying inequalities (14) and (15) to the form of $\mathcal {G}=G_{(N,M)}$ in (7) we obtain a basic inequality:

$$\begin{aligned} \mathcal {G}(f)<f\cdot E(\mathcal {X})-\frac{f^2}{2}\cdot E(\mathcal {X}^2) + \frac{f^3}{3}\cdot E(\mathcal {X}^3), \quad f\in (0,1), \end{aligned}$$

(16)

where $E(\mathcal {X}^2)$ and $E(\mathcal {X}^3)$ denote the second and third moment of $\mathcal {X}$, respectively. Set$m=E(\mathcal {X})$ and $f=\widehat{f}=m/\widetilde{A}$, where $\widetilde{A}=E(\mathcal {X}>0)$ is the average gain of $\Gamma$ [see (10)]. Then, by (16),

$$\begin{aligned} \mathcal {G}(\widehat{f})< \frac{m^2}{\widetilde{A}}\left( 1- \frac{E(\mathcal {X}^2)}{2\widetilde{A}}+m\frac{E(\mathcal {X}^3)}{3\widetilde{A}^2} \right) . \end{aligned}$$

(17)

Hence, we obtain

Main idea

If $1- \frac{E(\mathcal {X}^2)}{2\widetilde{A}} + m\frac{E(\mathcal {X}^3)}{3\widetilde{A}^2}<0$ then $\mathcal {G}(\widehat{f})<0$, too. It is thus enough to find a pair $(\mathcal {X},\mathcal {P})$ such that $1- \frac{E(\mathcal {X}^2)}{2\widetilde{A}}<0$ and the value $m\frac{E(\mathcal {X}^3)}{3\widetilde{A}^2}$ is sufficiently small to get $\mathcal {G}(\widehat{f})<0$.

The proof of Theorem 1, presented below, is thus based on the Main Idea and consists in finding suitable estimates of $E(X^2)$ and $E(X^3)$, where the random variable $X=\mathcal {X}=X_{2,1}$ is fixed and $\mathcal {P}=\mathcal {P}_{2,1}$ depends on a parameter allowing to get $m=E(X)$ as small as possible.

Let, as in the hypothesis of Theorem 1, $X=(A_1,A_2,-1)$ with $A_1>1>A_2>0$, and let $\mathcal {P}=(p_1,p_2,q)$, with $p_1,p_2,q$ positive, be an arbitrary fixed probability distribution. Our considerations will be simpler for

$$\begin{aligned} \widetilde{A} =1. \end{aligned}$$

(18)

In our case, $\widetilde{A}= \frac{p_1}{p_1+p_2}\cdot A_1 + \frac{p_2}{p_1+p_2}\cdot A_2= \frac{p_1}{1-q}\cdot A_1 + \frac{p_2}{1-q}\cdot A_2$. Hence, from the assumption (18) we obtain a system of two equations:

$$\begin{aligned} \begin{aligned} p_1A_1 +p_2A_2&= 1-q \\ p_1 + p_2&= 1-q. \end{aligned} \end{aligned}$$

(19)

Let us treat $p_1,p_2$ as unknown values and q as a parameter. Then (19) has a solution

$$\begin{aligned} p_1=(1-q)\cdot \frac{1-A_2}{A_1-A_2}\quad \mathrm {and}\quad p_2=(1-q)\cdot \frac{A_1-1}{A_1-A_2}. \end{aligned}$$

(20)

Moreover, from the assumption $E(X)>0$ and from (19) we obtain

$$\begin{aligned} E(X)= & {} p_1A_1 +p_2A_2 -q = 1-2q>0. \end{aligned}$$

(21)

It follows that $q<0.5$, thus $q=0.5-s$ for some $s\in (0,1/2)$. Hence, by (20), we obtain (12):

$$\begin{aligned} \begin{aligned} p_1&=p_1(s)=(0.5+s)\cdot \frac{1-A_2}{A_1-A_2}, \\ p_2&=p_2(s)=(0.5+s)\cdot \frac{A_1-1}{A_1-A_2}, \\ q&=q(s)=0.5-s. \end{aligned} \end{aligned}$$

Since now $\mathcal {P}=(p_1(s),p_2(s),q(s))$ depends on s, we write $\mathcal {P}_s$ instead of $\mathcal {P}$, and $E_s(X)$ denotes the expected value of X with respect to $\mathcal {P}_s$; similarly for $E_s(X^2)$ and $E_s(X^3)$. Consequently, by formula (10) and the assumption $\widetilde{A}=1$ we obtain $\widehat{f}_s = E_s(X)/\widetilde{A} =E_s(X)$. Hence, by (21) and the proved above identities (12),

$$\begin{aligned} E_s(X)=2s=\widehat{f}_s. \end{aligned}$$

(22)

Lower estimate of$E_s(X^2)$. Set $\alpha =\frac{1-A_2}{A_1-A_2}$ and $\beta =\frac{A_1-1}{A_1-A_2}$, and notice that $q=1-(0.5+s)$. Then, since $0.5 +s> 0.5$ and $\alpha A_1^2+\beta A_2^2 = A_1+A_2 -A_1A_2$, by identities (12),

$$\begin{aligned} E_s(X^2)= & {} (0.5+s)\left( \alpha A_1^2+\beta A_2^2 \right) +1 -(0.5+s) \nonumber \\> & {} 0.5 (A_1+A_2-A_1A_2-1 ) +1 \nonumber \\= & {} 0.5 (A_1-1)(1-A_2)+1. \end{aligned}$$

(23)

Upper estimate of$E_s(X^3)$. By (12) and the form of $\alpha$ and $\beta$ again, and since $s<0.5$ and $-q<0$,

$$\begin{aligned} E_s(X^3)< & {} \alpha A_1^3 + \beta A_2^3 =\frac{1}{A_1-A_2}\left( (1-A_2)\cdot A_1^3 + (A_1-1)\cdot A_2^3 \right) \nonumber \\= & {} A_1^2 + A_1A_2 + A_2^2 - A_1A_2\cdot (A_1+A_2) \nonumber \\= & {} A_1^2 - (A_1-1)\cdot (A_1A_2+A_2^2) {\mathop {<}\limits ^{A_1>1}} A_1^2. \end{aligned}$$

(24)

Set $m(s)=m$; thus $m(s)=E_s(X)$. From (22), (23) and (24) we obtain

$$\begin{aligned} 1-\frac{E_s(X^2)}{2}+ m(s)\cdot \frac{E_s(X^3)}{3}< \Psi (s) := - \frac{(A_1-1)(1-A_2)-2}{4} +2s\cdot \frac{A_1^2}{3}. \end{aligned}$$

(25)

Now, if $(A_1-1)(1-A_2)>2$ [condition (11) of Theorem 1], the equation $\Psi (s)=0$ has a solution $s_1$ such that

$$\begin{aligned} 0<s_1=\frac{3}{8}\cdot \frac{(A_1-1)(1-A_2)-2}{A_1^2}< 3/8 \end{aligned}$$

because $(A_1-1)(1-A_2)-2<A_1$ and $A_1^2>1$; hence $\Psi (s)<0$ on the interval $(0,s_1)$ with $s_1\in (0,1/2)$. But, by (22), (17) and (25), we have $G_s(\widehat{f}_s)<4s^2\cdot \Psi (s)$, thus $G_s(\widehat{f}_s)<0$ for every $s\in (0,s_1)$. This proves part (i) of Theorem 1.

Part (ii) follows from properties $(P_1)$ and $(P_2)$ in Sect. 3.2:

• (a) $G'_s(0)=E_s(X) (=2s)>0$ for every $s\in (0,s_1)$, whence $G_s$ is increasing on the right neighborhood of 0,

• (b) $G_s$ is concave (as $G''(f)<0$ on (0, 1)), and

• (c) $G_s(1^-)=-\infty$;

hence there is $f^*_s\in (0,1)$ such that $G_s$ attains its maximum at $f^*_s$ with $G_s(f^*_s)>0$ (the latter follows from $G'_s(0)>0$), cf. Fig. 2.

The last part of Theorem 1 follows from the continuity of the function $s\mapsto G_s(\widehat{f}_s)$ on the compact interval [0, 1 / 2].

5.2 Proof of the Claim

Since the pair $(A_1,A_2)=(9,1/8)$ fulfills inequality (11), by Theorem 1, we shall consider the probability distribution $\mathcal {P}_s$ of the form:

$$\begin{aligned} p_1(s)= & {} (0.5+s)\frac{7}{71}, \\ p_2(s)= & {} (0.5+s)\frac{64}{71}, \, \hbox { and} \\ q_1(s)= & {} 0.5-s. \end{aligned}$$

Hence, by (7) for $N=2$ and $M=1$ and by Theorem 1, we have to find ’bad’ functions $G_s$ of the form

$$\begin{aligned} G_s(f)&= (0.5+s)\frac{7}{71}\log (1+9f)+ (0.5+s)\frac{64}{71}\log (1+0.125f) \nonumber \\&\quad +(0.5-s)\log (1-f). \end{aligned}$$

(26)

From the proof of the last part of Theorem 1 it follows that a continuous function $\varphi$ defined by the formula

$$\begin{aligned} \varphi (s):= G_s(\widehat{f}_s),\quad s\in [0,1/2], \end{aligned}$$

attains its minimum at some $s_0\in (0,1/2)$ with $G_{s_0}(\widehat{f}_{s_0})<0$. In our case, by (22) and (26), we obtain:

$$\begin{aligned} \begin{aligned} \varphi (s)=&~(0.5+s)\frac{7}{71}\log (1+18s)+(0.5+s)\frac{64}{71}\log (1+0.25s) \\&+ (0.5-s)\log (1-2s). \end{aligned} \end{aligned}$$

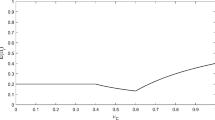
The graph of $\varphi$ is given in Fig. 3. Analyzing it numerically we obtain that $\varphi$ is strictly negative on the open interval (0, 0.2679), and that $s_0=0.1602$ with $\varphi (s_0)=-0.01961$. Hence, setting $G=G_{s_0}$, $E(X)=E_{s_0}(X)$ and $\widehat{f}= \widehat{f}_{s_0}$, by Theorem 1 and the form of $\varphi$, we obtain parts (i) and (ii) of the Claim:

$$\begin{aligned} \widehat{f}=E(X)=2s_0=0.3204, \quad \mathrm {and} \quad G(\widehat{f})=\varphi (s_0)=-0.01961<0. \end{aligned}$$

(27)

Fig. 3

The graph of $\varphi$

Fig. 4

The graph of $G_{0.1602}$

By (26), $G=G_{0.1602}$ is thus of the form (13) and it is the ‘worst’ element of the class $\{G_s\}$ in the terms of the value of $G_s(\widehat{f}_s)$. Its graph is given in Fig. 4 and proves part (iii) of the Claim: G attains its maximum at $f^*=0.1032$ with

$$\begin{aligned} G(f^*)=0.0133 >0. \end{aligned}$$

(28)

5.3 Proof of the main Theorem

By Theorem 1, we shall consider the case $n=N+M>3$, where $N ~\text {(gains)}\ge 2$ and $M ~\text {(losses)}\ge 1$.

Let $X=(A_1, A_2, -1)$ and $\mathcal {P}=(p_1, p_2, q)$ be the random variable and probability distribution defined in Theorem 1, and let G be a function of the form (13). Thus,

$$\begin{aligned}&\displaystyle G(f) = p_1\log (1+fA_1)+p_2\log (1+fA_2) + q\log (1-f), \end{aligned}$$

(29)

$$\begin{aligned}&\displaystyle E(X)=p_1A_1+p_2A_2-q>0, ~\text {and} \end{aligned}$$

(30)

$$\begin{aligned}&\displaystyle G(\widehat{f})<0<G(f^*), \end{aligned}$$

(31)

with the parameters $A_1,A_2,p_1,p_2,q, \widehat{f}, f^*$ fixed, e.g., as in the Claim. By means of these values, we shall construct a new random variable $X_{(N,M)}$ with corresponding probability distribution $\mathcal {P}_{(N,M)}$ of the form

$$\begin{aligned} X_{(N,M)} = (\alpha _1, \ldots , \alpha _N, -\beta _1, \ldots , -\beta _M), \end{aligned}$$

(32)

where $\alpha _i > 0$ and $0 < \beta _j \le 1$ for all $i\le M,j\le N$, with $\beta _M=1$, and

$$\begin{aligned} \mathcal {P}_{(N,M)} = (\pi _1, \ldots , \pi _N, q_1, \ldots , q_M), \end{aligned}$$

(33)

such that $X_{(2,1)}=X$, and $\mathcal {P}_{(2,1)}=\mathcal {P}$. Then the function $G_{(N,M)}$ below of the form (7), defined by $X_{(N,M)}$ and $\mathcal {P}_{(N,M)}$:

$$\begin{aligned} G_{(N,M)}(f)= \sum _{i=1}^N\pi _i\log (1+f\alpha _i) + \sum _{j=1}^Mq_j \log (1-f\beta _j),\quad f\in [0,1), \end{aligned}$$

(34)

is the sum of the ‘win’ $W_N$ and ‘loss’ $L_M$ functions:

$$\begin{aligned} G_{(N,M)}(f)=W_N(f)+L_M(f), \end{aligned}$$

(35)

where

$$\begin{aligned} W_N(f):=\sum _{i=1}^N\pi _i\log (1+f\alpha _i) \quad \text {and}\quad L_M(f):=\sum _{j=1}^Mq_j \log (1-f\beta _j). \end{aligned}$$

(36)

We obviously have $G=G_{(2,1)}=W_2+L_1$, see (29), thus $G_{(N,M)}$ is a generalization of G.

Plan of the proof We are looking for $X_{(N,M)}$ and $\mathcal {P}_{(N,M)}$ fulfilling the following two conditions below:

$$\begin{aligned} E(X_{(N,M)}>0)=E(X>0) =\widehat{A}=1; ~(\text {see}~ (18)), \end{aligned}$$

(37)

and

$$\begin{aligned} E(X_{(N,M)})=E(X)+\theta _M, \end{aligned}$$

(38)

where

$$\begin{aligned} \theta _M\ge 0, ~\text {with}~ \theta _M=0~\text {iff}~M=1~ \text {and}~ \theta _M~\text {independent of}~ N, \end{aligned}$$

(39)

and such that

$$\begin{aligned} G_{(N,M)} < G~\text {in a neighborhood of} ~ \widehat{f}. \end{aligned}$$

(40)

Then, by (10), (37) and (38), we would have

$$\begin{aligned} \widehat{f}_{(N,M)}=\widehat{f}+\theta _M, \end{aligned}$$

(41)

and hence, by (31), (40) and (41), for $\theta _M$ sufficiently close to 0,

$$\begin{aligned} G_{(N,M)}(\widehat{f}_{(N,M)})<0. \end{aligned}$$

(42)

Remark 2

The latter inequality finishes the proof of the main Theorem. Indeed, by (30) and (38), we obtain $E(X_{(N,M)})>0$, whence, by property$(P_2)$ in Sect. 3.2, $G_{(N,M)}({f^*}_{(N,M)})>0$; this, along with (42), yields

$$\begin{aligned} G_{(N,M)}(\widehat{f}_{(N,M)})<0<G_{(N,M)}({f^*}_{(N,M)}), \end{aligned}$$

and we can apply the Proposition in Sect. 3.2 for $f_1=f^*_{(N,M)}$ and $f_2=\widehat{f}_{(N,M)}$.

The proof Set $k=\frac{N-1}{2}$ for N odd (then $k\ge 1$ because $N\ge 2$), and $k=\frac{N-2}{2}$ for N even (then $k\ge 0$). Let us fix two finite sequences ${\{c_i\}}^k_{i=1}$ and ${\{b_j\}}^M_{j=1}$ of real numbers such that

$$\begin{aligned} 0<c_1<\cdots<c_k<A_1-A_2 ~(\text {thus}~{\{c_i\}}^k_{i=1}=\emptyset ~\text {for}~k=0, \text { by definition}), \end{aligned}$$

(43)

and

$$\begin{aligned} 1>b_1>\cdots>b_{M-1}>b_M=0\quad \text {for}~ M\ge 2, ~\text {and}~ b_M=0 ~\text {for}~ M=1. \end{aligned}$$

(44)

We shall consider the cases N odd and N even separately.

Case N odd. Set

$$\begin{aligned} \alpha _i= & {} {\left\{ \begin{array}{ll} A_1+c_{k+1-i} &{}\quad \text {for}~ i =1, \ldots , k \\ A_1-c_{i-k} &{}\quad \text {for}~ i =k+1, \ldots , 2k \\ A_2 &{}\quad \text {for}~ i =2k+1=N, \end{array}\right. } \\ \pi _i= & {} {\left\{ \begin{array}{ll} p_1/2k~&{}\quad \text {for}~ i =1, \ldots , 2k=N-1 \\ p_2 &{}\quad \text {for}~ i =2k+1=N, \end{array}\right. } \end{aligned}$$

$\beta _j = 1 - b_j$ (with $\beta _M = 1-0 = 1$), and $q_j = \frac{q}{M}$ for all $1 \le j \le M$.

Then, by (32) and (33),

$$\begin{aligned} X_{(N,M)}= & {} \Bigg (\underbrace{\underbrace{A_1+c_k, \ldots , A_1+c_1}_{k}, \underbrace{A_1-c_1,L \ldots , A_1-c_k}_{k}, A_2}_{2k+1=N}, \nonumber \\&\underbrace{-1+b_1, \ldots , -1+b_{M-1}, -1}_{M}\Bigg ), \end{aligned}$$

(45)

and

$$\begin{aligned} \mathcal {P}_{(N,M)} = \Bigg (\underbrace{\frac{p_1}{2k}, \ldots , \frac{p_1}{2k}, p_2}_{2k+1=N},\underbrace{\frac{q}{M}, \ldots , \frac{q}{M}}_{M}\Bigg ). \end{aligned}$$

(46)

Hence, by (35), (36) and the formulas defining $\alpha _i, \pi _i, \beta _j$, $q_j$, we obtain $G_{(N,M)}(f)=W_N(f)+L_M(f)$, where

$$\begin{aligned} W_N(f)&= \frac{p_1}{2k} \sum _{i=1}^k (\log ((1+fA_1)+fc_i)+\log ((1+fA_1)-fc_i)) \nonumber \\&\quad + p_2\log (1+fA_2), \end{aligned}$$

(47)

and

$$\begin{aligned} L_M(f)=\frac{q}{M}\sum _{j=1}^M\log (1-f+fb_j). \end{aligned}$$

(48)

Now shall show that $X_{(N,M)}$, $\mathcal {P}_{(N,M)}$ and $G_{(N,M)}$ fulfill our requirements (37), (38), (40), (41), and (42).

Indeed, by (45) and (46),

$$\begin{aligned} \begin{aligned} E(X_{(N,M)}>0)=&~\frac{p_1}{2k} \sum _{i=1}^k (A_1+c_i +A_1-c_i) + p_2A_2 \\ =&p_1A_1+p_2A_2= E(X>0)=1, \end{aligned} \end{aligned}$$

which proves (37), and, by (30),

$$\begin{aligned} E(X_{(N,M)})&= E(X>0) + \frac{q}{M}\sum _{j=1}^M(-1+b_j)=E(X>0)-q+\theta _M\nonumber \\&= E(X)+\theta _M >0, \end{aligned}$$

(49)

where the parameter

$$\begin{aligned} \theta _M:=\frac{q}{M}\sum _{j=1}^{M}b_j ~(\text {with }\theta _1=0 ~\text {because }b_M=0,~\text {see } (44)) \end{aligned}$$

(50)

is nonnegative and independent of N, which proves (38); then, obviously, (41) holds true, too, with $\widehat{f}+\theta _M\in (0,1)$.

For the proof of (40), we shall evaluate the difference $G_{(N,M)}(f)-G(f)$, where the parameter $f\in (0,1)$ is arbitrary fixed. By (29) and (35), we have $G=G_{(2,1)}=W_2+L_1$, where $W_2(f)=p_1\log (1+fA_1)+p_2\log (1+fA_2)$, thus from the identity

$$\begin{aligned} \log (u+v)+\log (u-v)=2\log u + \log (1-(v/u)^2),\quad \text { for }u>v>0, \end{aligned}$$

(51)

applied in (47) for $u=1+fA_1$ and $v=fc_i$ (and keeping in mind that $W_N(f)$ and $W_2(f)$ have the common component $p_2\log (1+fA_2)$) we obtain

$$\begin{aligned} W_N(f) -W_2(f)= & {} \frac{p_1}{2k}\sum _{i=1}^{k} \left( 2\log (1+fA_1) +\log \left( 1- \left( \frac{fc_i}{1+fA_1}\right) ^2\right) \right) \nonumber \\&-\,p_1\log (1+fA_1) = T_N(f), \end{aligned}$$

(52)

where

$$\begin{aligned} T_N(f):=\frac{p_1}{2k}\sum _{i=1}^{k}\log \left. \left( 1- \left( \frac{fc_i}{1+fA_1}\right) ^2\right) \right) . \end{aligned}$$

(53)

By (43), we have $0<\frac{fc_i}{1+fA_1}<1$, thus $\log (1-(\frac{fc_i}{1+fA_1})^2)$ is well defined and is negative for all $1\le i\le N$. Hence

$$\begin{aligned} T_N(f)<0. \end{aligned}$$

(54)

Moreover, by (48) and (50),

$$\begin{aligned} L_M(f)-L_1(f)= & {} \frac{q}{M}\sum _{j=1}^{M}\log (1-f+fb_j) - \frac{q}{M}\sum _{j=1}^{M}\log (1-f) \nonumber \\= & {} \frac{q}{M}\sum _{j=1}^{M}\log \left( 1+ \frac{fb_j}{1-f}\right) < \frac{f}{1-f}\cdot \theta _M \quad \text { for } M>1. \end{aligned}$$

(55)

Now, by (52), (54) and (55), we obtain a basic inequality involving functions $G_{N,M}$ and G:

$$\begin{aligned} G_{(N,M)}(f) < G(f)+ \frac{f}{1-f}\cdot \theta _M, \end{aligned}$$

(56)

where $f\in (0,1)$ is arbitrary fixed.

Subcase$M=1$ For one loss only, i.e., when $M=1$, by (50) and the just proved identity (41) [see the lines below (50)], we have $\theta _1=0$ and

$$\begin{aligned} \widehat{f}_{N,1}=\widehat{f}. \end{aligned}$$

(57)

Thus, by (56),

$$\begin{aligned} G_{(N,1)}(f) <G(f) \quad \text { for all } f\in (0,1), \end{aligned}$$

(58)

and we obtain

$$\begin{aligned} G_{(N,1)}(\widehat{f}_{N,1}){\mathop {=}\limits ^{(57)}} G_{(N,1)}(\widehat{f}){\mathop {<}\limits ^{(58)}} G(\widehat{f}) {\mathop {<}\limits ^{(31)}} 0 \text { with } E(X_{(N,1)})>0 ~(\text {by } (49)). \end{aligned}$$

(59)

By inequalities (59) and Remark 2, the proof of subcase $M=1$ is complete.

Subcase$M\ge 2$ Identity (41) and inequality (56) yield

$$\begin{aligned} G_{(N,M)}(\widehat{f}_{(N,M)})&{\mathop {=}\limits ^{(41)}}&~G_{(N,M)}(\widehat{f}+\theta _M)\nonumber \\&{\mathop {<}\limits ^{(56)}}&G(\widehat{f}+\theta _M)+\frac{\widehat{f}+\theta _M}{1-\widehat{f}- \theta _M}\theta _M. \end{aligned}$$

(60)

By (50), $\theta _M$ depends continuously on $b_j$’s, $j=1,\ldots ,M$, so, by (41), $\widehat{f}_{(N,M)}$ does too. Hence we can write $\widehat{f}_{(N,M)}=F(\beta _1,\ldots ,\beta _M)$, where F is a continuous function and $\beta _j=1-b_j$ for all $j\le M$. Notice also that, by (35), (36) and (48), $G_{(N,M)}:=G_{(N;\beta _1,\ldots ,\beta _M)}$ is a function depending continuously on $b_j$’s (hence on $\beta _j$’s) too.

Now, taking $\theta _M\rightarrow 0$ with $b_{M-1}$ strictly positive⁴ [see (44) and (50)] we obtain $b_j\rightarrow 0$ (hence $\beta _j\rightarrow 1$) for all $j\le M$ and, by (60) and (41),

$$\begin{aligned} \lim _{\theta _M\rightarrow 0}G_{(N,M)}(\widehat{f}_{(N,M)})\le G(\widehat{f}) {\mathop {<}\limits ^{(\text {}31)}}0. \end{aligned}$$

(61)

By Remark 1, inequality (61) implies there is a system $(\beta _1,\ldots ,\beta _{M})$, with $\beta _j=1-b_j$ for all $j\le M$ and $\beta _1>\cdots>\beta _{M-1}>\beta _M=0$ (whence $\theta _M>0$), such that, for the parameter $\widehat{f}_{(N,M)}:=\widehat{f}+\theta _M\in (0,1)$, we have $G_{(N,M)}(\widehat{f}_{(N,M)})=G_{(N;\beta _1,\ldots ,\beta _M)} (\widehat{f}_{(N,M)}) <0$. By (49), we also have $E(X_{(N,M)})>0$. Now we apply Remark 2, which finishes the proof of subcase $M\ge 2$.

Case N even We thus have $N=2k+2$ with $k \ge 0$. Similarly as for N odd, by means of the numbers defined in (43) and (44), we shall construct a random variable $X_{(N,M)}$ and probability distribution $\mathcal {P}_{(N,M)}$ such that, the function $G_{(N,M)}$ determined by the pair $(X_{(N,M)},\mathcal {P}_{(N,M)})$ fulfills inequality (56). Then we can follow the arguments as in case N odd to complete the proof.

To this end, for $k=0$ (whence $M \ge 2$ because $N + M > 3$, by hypothesis), by (32) and (33), we set

$$\begin{aligned} X_{(2,M)} = (A_1, A_2, -1 + b_1, \ldots , -1 + b_{M-1}, -1), \end{aligned}$$

and

$$\begin{aligned} \mathcal {P}_{(2,N)} = \Bigg (p_1, p_2, \underbrace{\frac{q}{M},\ldots , \frac{q}{M}}_{M}\Bigg ). \end{aligned}$$

Then

$$\begin{aligned} G_{(2,M)}(f)= & {} p_1\log (1+fA_1)+ p_2\log (1+fA_2)\nonumber \\&+ \frac{q}{M}\sum _{j=1}^{M}\log (1-f+fb_j). \end{aligned}$$

(62)

For $k\ge 1$ (then $N\ge 4$ and $M\ge 1$), since $A_1 + c_1> A_1 > A_1 - c_1$, we can define a random variable $X_{(N,M)}$ with strictly increasing values as follows:

$$\begin{aligned} \begin{aligned} X_{(N,M)} =&\Bigg (\underbrace{\underbrace{A_1+c_k, \ldots , A_1+c_1}_{k}, A_1, \underbrace{A_1-c_1, \ldots , A_1-c_k}_{k}, A_2}_{2k+2=N}, \\&\underbrace{-1+b_1, \ldots , -1 + b_{M-1}, -1}_{M}\Bigg ), \end{aligned} \end{aligned}$$

and the corresponding probability distribution we define as:

$$\begin{aligned} \mathcal {P}_{(N,M)} = \Bigg (\underbrace{\underbrace{\frac{p_1}{4k}, \ldots , \frac{p_1}{4k}}_{k}, \frac{p_1}{2}, \underbrace{\frac{p_1}{4k}, \ldots , \frac{p_1}{4k}}_{k}, p_2}_{2k+2=N}, \underbrace{\frac{q}{M}, \ldots , \frac{q}{M}}_{M}\Bigg ). \end{aligned}$$

Then $G_{(N,M)}$ takes the form

$$\begin{aligned} G_{(N,M)}(f)= & {} \frac{p_1}{4k}\left( \sum _{i=1}^k \log (1+fA_1+fc_i)+\log (1+fA_1-fc_i)\right) +\frac{p_1}{2} \nonumber \\&+\, p_2\log (1+A_2) + \frac{q}{M}\sum _{j=1}^M\log (1-f+fb_j). \end{aligned}$$

(63)

It is easy to check that, both for $k=0$ and $k\ge 1$, as in case N odd, $E(X_{(N,M)}>0)=1$ and $E(X_{(N,M)})=E(X)+\theta _M$, where $\theta _M$ is defined in (50). Thus (41) holds true, i.e., $\widehat{f}_{(N,M)}=\widehat{f}+\theta _M$ with $\theta _1=0$.

Moreover, since the ‘loss’ part of $G_{(N,M)}$ does not depend on k, we obtain inequality (55) for N even: $L_M(f)-L_1(f)<f\theta _M/1-f$ for $M>1$. For the ‘win’ part of $G_{(N,M)}$, we obviously have $W_N(f)-W_2(f)=0$ when $k=0$, while for $k\ge 1$, following the method of proof for N odd, it is easy to check that

$$\begin{aligned} W_N(f)-W_1(f)=\frac{p_1}{4k}\sum _{i=1}^k\log \left( 1- \left( \frac{fc_i}{1_fA_1}\right) ^2\right) =\frac{1}{2}T_N(f), \end{aligned}$$

whence, by (54), $W_N(f)-W_1(f)<0$ for all $f\in (0,1)$. Summing up,

$$\begin{aligned} G_{(N,M)}(f)= {\left\{ \begin{array}{ll} L_M(f)-L_1(f)<\frac{f}{1-f}\cdot \theta _M, \text { for } N=2 \text { with } \theta _M>0, \\ \frac{1}{2}T_N(f) + L_M(f)-L_1(f) < \frac{f}{1-f}\cdot \theta _M, \text { for } N\ge 4 \text { with } \theta _M\ge 0. \end{array}\right. } \end{aligned}$$

We thus have obtained inequality (56), as claimed. Now, applying the same arguments as for $M=1$ and $M>1$ in case N odd we conclude the proof.

The proof of the main Theorem is complete.