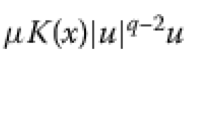Existence of solutions for a class of biharmonic equations with critical nonlinearity in $\mathbb {R}^N$

Abstract

In this paper, we consider the existence and multiplicity of solutions of biharmonic equations with critical nonlinearity in $\mathbb {R}^N:$ $\varepsilon ^4\Delta ^2u + V(x)u = |u|^{2^{**}-2}u + h(x,u)$, $(t, x) \in \mathbb {R} \times \mathbb {R}^N$. Under suitable assumptions, we prove that it has at least one solution and, if h(x, .) is odd, for any $m \in \mathbb {N}$, it has at least m pairs of solutions.

1 Introduction

The main purpose of this paper is to study the existence and multiplicity of solutions of the following singularly perturbed biharmonic equations with critical nonlinearity of the form

$$\begin{aligned} \left\{ \begin{array}{lll}\varepsilon ^4\Delta ^2u + V(x)u = |u|^{2^{**}-2}u + h(x,u),\quad x\in \mathbb {R}^N,\\ u(x) \rightarrow 0, \quad \text {as}\ |x| \rightarrow \infty , \end{array}\right. \end{aligned}$$

(1.1)

where $\varepsilon > 0$ and $N \ge 5$, $2^{**}=\frac{2N}{N-4}$ is the Sobolev critical exponent, V(x) and h(x, u) are functions satisfying the following assumptions throughout this paper:

• (V) $V(x) \in C(\mathbb {R}^N, \mathbb {R})$; $V(x_0) = \min _{x \in \mathbb {R}^N} V = 0$ and there is $a > 0$ such that the set $V^a = \{x \in \mathbb {R}^N: V(x) < a\}$ has finite Lebesgue measure;

• (H) ($h_1$) $h \in C(\mathbb {R}^N \times \mathbb {R}, \mathbb {R})$ and $h(x, t) = o(|t|)$ uniformly in x as $t \rightarrow 0$;

  ($h_2$) there are $C_0 > 0$ and $q \in (2, 2^{**})$ such that $|h(x, t) | \le C_0 (1 + t^{q-1})$;

  ($h_3$) there exist $a_0 > 0$, $p > 2$ and $2^{**}>\mu > 2$ such that $H(x, t) \ge a_0 t^{p}$ and $\mu H(x, t) \le h(x, t)t$, where $H(x, t) = \int _0^t h(x, s)ds$ for all (x, t).

In the last years, many authors have studied Schrödinger equation

$$\begin{aligned} -\varepsilon ^2\Delta u + V(x)u = f(x,u),\quad x \in \mathbb {R}^N. \end{aligned}$$

(1.2)

Different approaches have been taken to attack this problem under various hypotheses on the potential and the nonlinearity. See for examples [19, 20, 25, 29, 30] and the references therein. Observe that in all these papers the nonlinearities are assumed to be subcritical

$$\begin{aligned} |f(x, u)| \le c(1 + |u|^{p-1})\ \ \text {with}\ p \in (2, 2^*), \end{aligned}$$

(1.3)

together with some other technical conditions of course. Under the condition $V(x) > 0$, there have been enormous investigations on problem (1.2). Much of the impetus for these studies seems to have originated from the pioneering paper [25] by Floer and Weinstein in which the one-dimensional case $(N = 1)$ with a cubic nonlinearity was studied by assuming that V(x) is a bounded potential having a single non-degenerate minimum point $x_0$ while $\inf _{\mathbb {R}} V > 0$. As a matter of fact, based on a Lyapounov–Schmidt reduction technique, it was shown there that (1.2) admits, for $\varepsilon > 0$ sufficiently small, a family of spike-like solutions which in the semiclassical limit (i.e. as $\varepsilon \rightarrow 0$) concentrate around $x_0$; see also [29, 30]. The extension of this important result to higher dimensions with condition (1.3) and V(x) having a finite set of non-degenerate critical points was achieved in [29] while this last hypothesis was eventually removed in [21]; for complementary results obtained by perturbation or variational methods see [3, 32], as well as the recent monograph [4]. For more results, we refer the reader to [5, 17, 24]. If the nonlinearities are assumed to be critical, Clapp and Ding [18] studied problem: $-\Delta u + \lambda V(x)u = \mu u + u^{2^*- 1}$ and $V(x) \ge 0$ and has a potential well and is invariant under an orthogonal involution of $\mathbb {R}^N$, they established existence and multiplicity of solutions which change sign exactly once and these solutions localize near the potential well for real numbers $\mu$ small and $\lambda$ large. Ding and Lin [22] showed the existence and multiplicity of semiclassical solutions of perturbed nonlinear Schrödinger equations with critical nonlinearity. Ding and Wei [23] established the existence and multiplicity of semiclassical bound states of the nonlinear Schrödinger equations under the assumption of V(x) changes sign and f is superlinear with critical or supercritical growth as $|u| \rightarrow \infty$. For some other important results the interested reader is also referred to [6–8, 10, 12–16, 27, 28, 35–38].

Although there are many works dealing with problem (1.2), just few works can be found dealing with biharmonic or even polyharmonic Schrödinger equations. We would like to cite [1, 2], where the authors have obtained nontrivial solutions to semilinear biharmonic problems with nonlinearities and also [33], where Salvatore and Squassina obtained infinitely many solutions for a polyharmonic Schrödinger equations with nonhomogenous boundary data on unbounded domains. Recently in [31], Pimenta and Soares studied

$$\begin{aligned} \left\{ \begin{array}{lll} \varepsilon ^4\Delta ^2u + V(x)u = h(u),\quad x\in \mathbb {R}^N,\\ u \in H^2(\mathbb {R}^N), \end{array}\right. \end{aligned}$$

(1.4)

where $\varepsilon > 0$ and $N \ge 5$, $V \in C(\mathbb {R}^N)\cap L^\infty (\mathbb {R}^N)$ and there exist a bounded domain $\Omega \subset \mathbb {R}^N$ and $x_0 \in \Omega$ such that $0 < V(x_0) = V_0 = \inf _{\mathbb {R}^N}V < \inf _{\partial \Omega }V$. They obtained a ground state solution and concentration of nontrivial solutions by a penalization-type method, where h is a subcritical and superlinear function.

In this paper, motivated by [22, 23], we study the existence and multiplicity of semiclassical solutions of perturbed biharmonic equation with critical nonlinearity (1.1). To the best of our knowledge, the existence and multiplicity of solutions to problem (1.1) on $\mathbb {R}^N$ has not been studied before by variational methods. Because of lack of a general form of the maximum principle to the biharmonic operator and the impossibility of splitting $u = u^+ + u^-$ in $H^2(\mathbb {R}^N)$, we obtain only nontrivial solutions for (1.1). Furthermore, differently from [22, 23] we use Lions’ second concentration compactness principle and concentration compactness principle at infinity to prove that the $(PS)_c$ condition holds. Let us point out that although the idea was used before for other problems, the adaptation to the procedure to our problem is not trivial at all, since due to the appearance of the biharmonic operator, we must consider our problem in a suitable space and so we need more delicate estimates.

For problem (1.1), we want to obtain the following results.

Theorem 1.1

Let (V) and (H) be satisfied. Then, for any $\sigma > 0$, there is $\mathcal {E}_\sigma > 0$ such that if $\varepsilon \le \mathcal {E}_\sigma$, then problem (1.1) has at least one nontrivial solutions $u_\varepsilon$ satisfying

$$\begin{aligned} \frac{\mu -2}{2}\int _{\mathbb {R}^N}H(x, u_\varepsilon )dx + \frac{2}{N}\int _{\mathbb {R}^N}|u_\varepsilon |^{2^{**}}dx \le \sigma \varepsilon ^N \end{aligned}$$

(1.5)

and

$$\begin{aligned} \frac{\mu -2}{2\mu }\int _{\mathbb {R}^N}\left( \varepsilon ^4|\Delta u_\varepsilon |^2 + V(x)u_\varepsilon ^2\right) dx \le \sigma \varepsilon ^N. \end{aligned}$$

(1.6)

Theorem 1.2

Let (V) and (H) be satisfied. Moreover, assume that h(x, t) is odd in t. Then, for any $m \in N$ and $\sigma > 0$ there is $\mathcal {E}_{m\sigma } > 0$ such that problem (1.1) has at least m pairs of solutions $u_\varepsilon$ which satisfies the estimates (1.5) and (1.6).

2 Main results

We set $\lambda = \varepsilon ^{-4}$ and rewrite (1.1) in the following form

$$\begin{aligned} \left\{ \begin{array}{lll} \Delta ^2 u + \lambda V(x)u = \lambda |u|^{2^{**}-1}u + \lambda h(x,u),\quad x\in \mathbb {R}^N,\\ u(x) \rightarrow 0, \qquad as \quad |x| \rightarrow \infty . \end{array}\right. \end{aligned}$$

(2.1)

In order to prove our results, we introduce the space

$$\begin{aligned} E := \left\{ u \in H^2(\mathbb {R}^N): \int _{\mathbb {R}^N} V(x)|u|^2dx < \infty \right\} \end{aligned}$$

which is a Hilbert space with the inner product

$$\begin{aligned} \langle u, v\rangle = \int _{\mathbb {R}^N} (\Delta u\Delta v + V(x)uv)dx \end{aligned}$$

and the associated norm $\Vert u\Vert ^2 = \langle u, u\rangle$. By the assumption (V), we know that the embedding $E \hookrightarrow H^2(\mathbb {R}^N)$ is continuous (see [22, 23]). Note that the norm $\Vert \cdot \Vert$ is equivalent to the one $\Vert \cdot \Vert _\lambda$ defined by

$$\begin{aligned} \Vert u\Vert _\lambda ^2 = \int _{\mathbb {R}^N} (|\Delta u|^2 + \lambda V(x)|u|^2)dx \end{aligned}$$

for each $\lambda > 0$. It is obvious that for each $s \in [2, 2^{**}]$, there is $c_s > 0$ (independent of $\lambda$) such that if $\lambda \ge 1$

$$\begin{aligned} |u|_s \le c_s\Vert u\Vert \le c_s \Vert u\Vert _\lambda \quad \text {for all}\ u \in E. \end{aligned}$$

(2.2)

Consider the functional

$$\begin{aligned} J_\lambda (u):= & {} \frac{1}{2}\int _{\mathbb {R}^N}(|\Delta u|^2 + \lambda V(x)|u|^2)dx - \frac{\lambda }{2^{**}}\int _{\mathbb {R}^N}|u|^{2^{**}}dx - \lambda \int _{\mathbb {R}^N}H(x, u)dx\\= & {} \frac{1}{2}\Vert u\Vert _\lambda ^2 - \frac{\lambda }{2^{**}}\int _{\mathbb {R}^N}|u|^{2^{**}}dx - \lambda \int _{\mathbb {R}^N}H(x, u)dx. \end{aligned}$$

Under the assumptions $(h_1)$ and $(h_2)$, $J_\lambda \in C^1 (E, \mathbb {R})$ (see [38], Theorem 1.22) and its critical points are solutions of (2.1).

After the rescalings, the Theorems 1.1 and 1.2 can be restated as following:

Theorem 2.1

Let (V) and (H) be satisfied. Then, for any $\sigma > 0$, there is $\Lambda _\sigma > 0$ such that if $\lambda \ge \Lambda _\sigma$, then problem (1.1) has at least one nontrivial solutions $u_\lambda$ satisfying

$$\begin{aligned} \frac{\mu -2}{2}\int _{\mathbb {R}^N}H(x, u_\lambda )dx + \frac{2}{N}\int _{\mathbb {R}^N}|u_\lambda |^{2^{**}}dx \le \sigma \lambda ^{-\frac{N}{4}} \end{aligned}$$

(2.3)

and

$$\begin{aligned} \frac{\mu -2}{2\mu }\int _{\mathbb {R}^N}\left( |\Delta u_\lambda |^2 + \lambda V(x)u_\lambda ^2\right) dx \le \sigma \lambda ^{1-\frac{N}{4}}. \end{aligned}$$

(2.4)

Theorem 2.2

Let (V) and (H) be satisfied. Moreover, assume that h(x, t) is odd in t. Then, for any $m \in \mathbb {N}$ and $\sigma > 0$ there is $\Lambda _{m\sigma } > 0$ such that if $\lambda \ge \Lambda _{m\sigma }$, then problem (1.1) has at least m pairs of solutions $u_\lambda$ which satisfy the estimates (2.3) and (2.4).

3 $(PS)_c$ condition

Recall that we say that a sequence $(u_n)$ is a (PS) sequence at level c ($(PS)_c$-sequence, for short) if $J_\lambda (u_n) \rightarrow c$ and $J_{\lambda }'(u_n) \rightarrow 0$. $\Phi _\lambda$ is said to satisfy the $(PS)_c$ condition if any $(PS)_c$-sequence contains a convergent subsequence.

Denote $\mathcal {M}^+$ as a cone of positive finite Radon measure. We omit the proof of the following result since it is similar to that one of Lions [26] and Smets [34].

Lemma 3.1

Let $\{u_n\} \subset H^2(\mathbb {R}^N)$ be a bounded sequence, going if necessary to subsequence, we may assume that $u_n \rightharpoonup u$ in $H^2(\mathbb {R}^N)$, $|\Delta u_n|^2 \rightharpoonup \mu$ in $\mathcal {M}^+$, $|u_n|^{2^{**}} \rightharpoonup \nu$ in $\mathcal {M}^+$. Define

$$\begin{aligned} \mu _\infty:= & {} \lim _{R\rightarrow \infty }\overline{\lim _{n\rightarrow \infty }}\int _{\mathbb {R}^N \cap |x|>R}|\Delta u_n|^2dx,\\ \nu _\infty:= & {} \lim _{R\rightarrow \infty }\overline{\lim _{n\rightarrow \infty }}\int _{\mathbb {R}^N \cap |x|>R}|u_n|^{2^{**}}dx.\end{aligned}$$

Then there exist an at most, countable index set J and a collection of points $\{x_j\}$, $j \in J$, in $\mathbb {R}^N$ such that

• (i) $\mu _\infty \ge S\nu _\infty ^{2/2^{**}};$

• (ii) $\nu = |u|^{2^{**}} + \sum \delta _{x_j}\nu _j$, $\nu _j > 0$, $\mu = |\Delta u|^2 + \sum \delta _{x_j}\mu _j^{2/2^{**}};$

• (iii) $\mu _j \ge S\nu _j^{2/2^{**}};$

• (iv) $\lim _{n\rightarrow \infty }\int _{\mathbb {R}^N}|u_n|^{2^{**}}dx = \int _{\mathbb {R}^N}|u|^{2^{**}}dx + \nu _\infty$,

where S is the best Sobolev constant, i.e. $S = \inf \left\{ \int _{\mathbb {R}^N}|\Delta u|^2dx: \int _{\mathbb {R}^N}|u|^{2^{**}}dx = 1\right\}$, $x_j \in \mathbb {R}^N$, $\delta _{x_j}$ are Dirac measures at $x_j$ and $\mu _j$, $\nu _j$ are constants.

Lemma 3.2

Let (V) and (H) be satisfied. Let $\{u_n\} \subset E$ be a $(PS)_{c}$-sequence. Thus, $c \ge 0$ and there exists a constant M(c) which is independent of $\lambda \ge 0$ such that

$$\begin{aligned} \limsup _{n \rightarrow \infty } \Vert u_n\Vert _{\lambda }^2 \le M(c). \end{aligned}$$

Proof

Let $\{u_n\}$ be a sequence in E such that

$$\begin{aligned} c + o(1)= & {} J_\lambda (u_n) = \frac{1}{2}\Vert u_n\Vert _\lambda ^2 - \frac{\lambda }{2^{**}}\int _{\mathbb {R}^N}|u_n|^{2^{**}}dx - \lambda \int _{\mathbb {R}^N}H(x, u_n)dx,\end{aligned}$$

(3.1)

$$\begin{aligned} o(1)= & {} \nonumber \langle J_\lambda '(u_n), v\rangle = \int _{\mathbb {R}^N}\left( \Delta u_n \cdot \Delta v + \lambda V(x)u_nv\right) dx \\&\text {} - \lambda \int _{\mathbb {R}^N}|u_n|^{2^{**}-2}u_nvdx - \lambda \int _{\mathbb {R}^N}h(x, u_n)vdx. \end{aligned}$$

(3.2)

By (3.1) and (3.2) we have

$$\begin{aligned} J_\lambda (u_n) - \frac{1}{\mu } J'_\lambda (u_n)u_n= & {} \nonumber \left( \frac{1}{2} - \frac{1}{\mu }\right) \int _{\mathbb {R}^N}(|\Delta u_n|^2 + \lambda V(x)|u_n|^2)dx\\&\nonumber +\, \left( \frac{1}{\mu } - \frac{1}{2^{**}}\right) \lambda \int _{\mathbb {R}^N}|u_n|^{2^{**}}dx\\&+ \,\lambda \int _{\mathbb {R}^N}\left( \frac{1}{\mu }h(x, u_n)u_n - H(x, u_n)\right) dx. \end{aligned}$$

(3.3)

On the other hand, condition $(h_3)$ implies that

$$\begin{aligned} \frac{1}{\mu }h(x, u_n)u_n - H(x, u_n) \ge 0. \end{aligned}$$

Thus, it follows from (3.3) that

$$\begin{aligned} \left( \frac{1}{2} - \frac{1}{\mu }\right) \Vert u_n\Vert _{\lambda }^2 \le c + o(1) + \epsilon _n\Vert u_n\Vert _\lambda , \end{aligned}$$

thus $\Vert u_n\Vert _\lambda$ is bounded as $n \rightarrow \infty$. Passing to the limit in the last inequality, it follows that $c \ge 0$. This completes the proof of Lemma 3.2. $\square$

Lemma 3.3

Suppose that (V) and (H) hold. For any $\lambda \ge 1$, $J_\lambda$ satisfies $(PS)_c$ condition, for all $c \in \left( 0,\, \alpha _0\lambda ^{1-\frac{N}{4}}\right)$, where $\alpha _0 = \left( \frac{1}{\mu }-\frac{1}{2^{**}}\right) S^{\frac{N}{4}}$, that is any $(PS)_c$-sequence $(u_n) \subset E$ has a strongly convergent subsequence in E.

Proof

Let $\{u_n\}$ be a $(PS)_c$ sequence, by Lemma 3.2, $\{u_n\}$ is bounded in E. Hence, up to a subsequence, we may assume that

(3.4)

where $\mu$ and $\nu$ are a nonnegative bounded measures on $\mathbb {R}^N$. Let $x_j$ be a singular point of the measures $\mu$ and $\nu$. We define a function $\phi _j(x) \in C_0^\infty (\mathbb {R}^N)$ such that $\phi _j(x) = 1$ in $B(x_j, \varepsilon )$, $\phi _j(x) = 0$ in $\mathbb {R}^N {\setminus } B(x_j, 2\varepsilon )$, $|\nabla \phi _j| \le 2/\varepsilon$ and $|\Delta \phi _j| \le 2/\varepsilon ^2$ in $\mathbb {R}^N$. Obviously, $\langle J_\lambda '(u_n), u_n\phi _j\rangle \rightarrow 0$, i.e.

$$\begin{aligned} \int _{\mathbb {R}^N}|\Delta u_n|^2\phi _j dx= & {} - \int _{\mathbb {R}^N} \Delta u_n \Delta \phi _j u_n dx-2\int _{\mathbb {R}^N} \Delta u_n \nabla u_n\nabla \phi _j dx \nonumber \\&- \int _{\mathbb {R}^N}\lambda V(x)|u_n|^2\phi _j dx + \lambda \int _{\mathbb {R}^N}h(x,u_n)u_n\phi _j dx \nonumber \\&+\, \lambda \int _{\mathbb {R}^N} |u_n|^{2^{**}}\phi _j dx+o(1). \end{aligned}$$

(3.5)

On the other hand, by Hölder’s inequality we obtain

$$\begin{aligned}&\limsup _{n\rightarrow \infty } \Bigg |\int _{\mathbb {R}^N} \Delta u_n \Delta \phi _j u_n dx\Bigg |\nonumber \\&\quad \le \limsup _{n\rightarrow \infty } \Bigg (\int _{\mathbb {R}^N}|\Delta u_n|^2dx\Bigg )^{1/2} \Bigg (\int _{\mathbb {R}^N}|u_n\Delta \phi _j|^2 dx\Bigg )^{1/2}\nonumber \\&\quad \le \limsup _{n\rightarrow \infty } C_1\Bigg (\int _{B(x_j,2\varepsilon )}|u_n|^2|\Delta \phi _j|^2 dx\Bigg )^{1/2}\nonumber \\&\quad \le C_1\Bigg (\int _{B(x_j,2\varepsilon )}|\Delta \phi _j|^{N/2}dx\Bigg )^{2/N} \Bigg (\int _{B(x_j,2\varepsilon )}|u|^{2^{**}} dx\Bigg )^{1/2^{**}}\nonumber \\&\quad \le C_2\Bigg (\int _{B(x_j,2\varepsilon )}|u|^{2^{**}} dx\Bigg )^{1/2^{**}} \rightarrow 0\quad \text {as } \varepsilon \rightarrow 0. \end{aligned}$$

(3.6)

Similarly, it follows from the definition of $\phi$ and (3.4) that

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0}\lim _{n \rightarrow \infty }\int _{\mathbb {R}^N} \Delta u_n \nabla u_n\nabla \phi _j dx = 0 \end{aligned}$$

(3.7)

and

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0}\lim _{n \rightarrow \infty }\int _{\mathbb {R}^N}h(x,u_n)u_n\phi _j dx = 0. \end{aligned}$$

(3.8)

Consequently, using (3.4) and (3.6)–(3.8), we can let $n \rightarrow \infty$ in (3.5) to obtain

$$\begin{aligned} \int _{\mathbb {R}^N}\phi _j d\mu \le \lambda \int _{\mathbb {R}^N} \phi _j d\nu . \end{aligned}$$

Letting $\varepsilon \rightarrow 0$, we obtain $\mu _j\le \lambda \nu _j$. Combining this with Lemma 3.1 $\mathrm{(iii)}$, we obtain $\nu _j \ge \lambda ^{-1}S \nu _j^{\frac{2}{2^{**}}}$. This result implies that

$$\begin{aligned} \mathrm{(I)} \quad \nu _j = 0 \qquad \text {or}\ \quad \mathrm{(II)} \quad \nu _j \ge \left( \lambda ^{-1}S\right) ^{\frac{N}{4}}. \end{aligned}$$

To obtain the possible concentration of mass at infinity, similarly, we define a cut off function $\phi _R \in C^\infty (\mathbb {R}^N)$ such that $\phi _R(x)=0$ on $|x| < R$ and $\phi _R(x)=1$ on $|x| > R+1$. Note that $\langle J_\lambda '(u_n), u_n\phi _R\rangle \rightarrow 0$, this fact imply that

$$\begin{aligned} \int _{\mathbb {R}^N}|\Delta u_n|^2\phi _R dx= & {} - \int _{\mathbb {R}^N} \Delta u_n \Delta \phi _R u_n dx-2\int _{\mathbb {R}^N} \Delta u_n \nabla u_n\nabla \phi _R dx \nonumber \\&- \int _{\mathbb {R}^N}\lambda V(x)|u_n|^2\phi _R dx + \lambda \int _{\mathbb {R}^N}h(x,u_n)u_n\phi _R dx\nonumber \\&+\,\lambda \int _{\mathbb {R}^N} |u_n|^{2^{**}}\phi _R dx+o_n(1). \end{aligned}$$

(3.9)

It is easy to prove that

$$\begin{aligned} \lim _{R \rightarrow \infty }\lim _{n \rightarrow \infty }\int _{\mathbb {R}^N} \Delta u_n \Delta \phi _R u_n dx = 0 \end{aligned}$$

and

$$\begin{aligned} \lim _{R \rightarrow \infty }\lim _{n \rightarrow \infty }\int _{\mathbb {R}^N} \Delta u_n \nabla u_n\nabla \phi _R dx = 0. \end{aligned}$$

Letting $R \rightarrow \infty$, we obtain $\mu _\infty \le \lambda \nu _\infty$. Thus $\nu _\infty \ge \lambda ^{-1}S \nu _\infty ^{\frac{2}{2^{**}}}$. This result implies that

$$\begin{aligned} \mathrm{(III)} \quad \nu _\infty = 0 \ \qquad \qquad \text {or}\ \quad \mathrm{(IV)} \quad \nu _\infty \ge \left( \lambda ^{-1}S\right) ^{\frac{N}{4}}. \end{aligned}$$

Next, we claim that $\mathrm{(II)}$ and $\mathrm{(IV)}$ cannot occur. If the case $\mathrm{(IV)}$ holds, then by condition (H), we have that

$$\begin{aligned} c= & {} \lim _{n \rightarrow \infty }\left( J_\lambda (u_n) - \frac{1}{\mu }\langle J'_\lambda (u_n), u_n\rangle \right) \\= & {} \lim _{n \rightarrow \infty }\left\{ \left( \frac{1}{2} - \frac{1}{\mu }\right) \int _{\mathbb {R}^N}(|\Delta u_n|^2 + \lambda V(x)|u_n|^2)dx + \left( \frac{1}{\mu } - \frac{1}{2^{**}}\right) \lambda \int _{\mathbb {R}^N}|u_n|^{2^{**}}dx\right. \\&\left. +\, \lambda \int _{\mathbb {R}^N}\left( \frac{1}{\mu }h(x, u_n)u_n - H(x, u_n)\right) dx\right\} \\\ge & {} \lim _{n \rightarrow \infty }\left( \frac{1}{\mu }-\frac{1}{2^{**}}\right) \lambda \int _{\mathbb {R}^N} |u_n|^{2^{**}}dx \ge \lim _{n \rightarrow \infty }\left( \frac{1}{\mu }-\frac{1}{2^{**}}\right) \lambda \int _{\mathbb {R}^N} |u_n|^{2^{**}}\phi _Rdx. \end{aligned}$$

Hence, by condition (IV) we obtain

$$\begin{aligned} \left( \frac{1}{\mu }-\frac{1}{2^{**}}\right) \lambda \nu _\infty \ge \alpha _0\lambda ^{1-\frac{N}{4}}, \end{aligned}$$

where $\alpha _0 = \left( \frac{1}{\mu }-\frac{1}{2^{**}}\right) S^{\frac{N}{4}}$.

This is impossible. Consequently, $\nu _\infty = 0$. Similarly, we can prove that $\mathrm{(II)}$ cannot occur. Thus

$$\begin{aligned} \int _{\mathbb {R}^N}|u_n|^{2^{**}}dx \rightarrow \int _{\mathbb {R}^N}|u|^{2^{**}}dx. \end{aligned}$$

(3.10)

Thus, from Brezis-Lieb Lemma [11], we have

$$\begin{aligned} \Vert u_n\Vert _\lambda= & {} \nonumber \langle J_\lambda '(u_n), u_n\rangle = \Vert u_n\Vert _\lambda ^2 - \lambda \int _{\mathbb {R}^N}|u_n|^{2^{**}}dx - \lambda \int _{\mathbb {R}^N}h(x, u_n)u_ndx\\= & {} \Vert u_n-u\Vert _\lambda ^2 + \Vert u\Vert _\lambda ^2 - \lambda \int _{\mathbb {R}^N}|u_n|^{2^{**}}dx - \lambda \int _{\mathbb {R}^N}h(x, u_n)u_ndx\\= & {} \Vert u_n - u\Vert _\lambda ^2 + \Vert u_n\Vert _\lambda , \end{aligned}$$

here we use $J_\lambda '(u) = 0$. Thus we prove that $\{u_n\}$ strongly converges to u in E. This completes the proof of Lemma 3.3. $\square$

4 Proofs of Theorem 2.1

In the following, we always consider $\lambda \ge 1$. By the assumptions (V) and (H), one can see that $J_\lambda (u)$ has mountain pass geometry.

Lemma 4.1

Assume (V) and (H) hold. There exist $\alpha _\lambda , \rho _\lambda > 0$ such that $J_\lambda (u) > 0$ if $u \in B_{\rho _\lambda }{{\setminus }}\{0\}$ and $J_\lambda (u) \ge \alpha _\lambda$ if $u \in \partial B_{\rho _\lambda }$, where $B_{\rho _\lambda } = \{u\in E: \Vert u\Vert _\lambda \le \rho _\lambda \}$.

Proof

By conditions $(h_1)$ and $(h_2)$, for any $\delta > 0$ small enough there is $C_\delta > 0$ such that

$$\begin{aligned} \frac{1}{2^{**}}\int _{\mathbb {R}^N}|u|^{2^{**}}dx + \int _{\mathbb {R}^N}H(x, u)dx \le \delta |u|_2^2 + C_\delta |u|_{2^{**}}^{2^{**}}. \end{aligned}$$

So, choosing $\delta \le (4\lambda c_2^2)^{-1}$, from condition (V) it follows that

$$\begin{aligned} J_\lambda (u)\ge & {} \frac{1}{2}\Vert u\Vert _\lambda ^2 - \lambda \delta |u|_2^2 -\lambda C_\delta |u|_{2^{**}}^{2^{**}}\\\ge & {} \frac{1}{4}\Vert u\Vert _\lambda ^2 - \lambda C_\delta |u|_{2^{**}}^{2^{**}}. \end{aligned}$$

Because $2 < 2^{**}$, we know that the conclusion of Lemma 4.1 holds. This completes the proof of Lemma 4.1. $\square$

Lemma 4.2

Under the assumption of Lemma 4.1, for any finite dimensional subspace $F \subset E$,

$$\begin{aligned} J_\lambda (u) \rightarrow -\infty \ \ \ as\ \ u\in F, \ \Vert u\Vert _\lambda \rightarrow \infty . \end{aligned}$$

Proof

Using conditions (V) and$(h_3)$, we can get

$$\begin{aligned} J_\lambda (u) \le \frac{1}{2}\Vert u\Vert _\lambda ^2 - \lambda a_0|u|_p^p \end{aligned}$$

for all $u \in E$. Since all norms in a finite-dimensional space are equivalent and $p > 2$, this completes the proof of Lemma 4.2. $\square$

Since $J_\lambda (u)$ does not satisfy $(PS)_c$ condition for all $c > 0$, thus, in the following we will find special finite-dimensional subspaces by which we construct sufficiently small minimax levels.

Recall that the assumption (V) implies there is $x_0 \in \mathbb {R}^N$ such that $V(x_0) = \min _{x\in \mathbb {R}^N} V(x) = 0$. Without loss of generality we assume from now on that $x_0 = 0$.

Observe that, by condition $(h_3)$, we have

$$\begin{aligned} \frac{\lambda }{2^{**}}\int _{\mathbb {R}^N}|u|^{2^{**}}dx + \lambda \int _{\mathbb {R}^N}H(x, u)dx \ge a_0\lambda \int _{\mathbb {R}^N} |u|^pdx. \end{aligned}$$

Define the function $I_\lambda \in C^1(E, \mathbb {R})$ by

$$\begin{aligned} I_\lambda (u) := \frac{1}{2}\int _{\mathbb {R}^N}(|\Delta u|^2 + \lambda V(x)|u|^2)dx - a_0\lambda \int _{\mathbb {R}^N} |u|^pdx. \end{aligned}$$

Then $J_\lambda (u) \le I_\lambda (u)$ for all $u \in E$ and it suffices to construct small minimax levels for $I_\lambda$.

Note that

$$\begin{aligned} \inf \left\{ \int _{\mathbb {R}^N} |\Delta \phi |^2dx: \phi \in C_0^\infty (\mathbb {R}^N), |\phi |_2 = 1\right\} = 0. \end{aligned}$$

For any $\delta > 0$ one can choose $\phi _\delta \in C_0^\infty (\mathbb {R}^N)$ with $|\phi _\delta |_p = 1$ and supp $\phi _\delta \subset B_{r_\delta } (0)$ so that $|\Delta \phi _\delta |_p^p < \delta$. Set

$$\begin{aligned} f_\lambda (x) = \phi _\delta (\lambda ^{\frac{1}{4}}x), \end{aligned}$$

(4.1)

then

$$\begin{aligned} {\text { supp}}\,f_\lambda \subset B_{\lambda ^{-\frac{1}{4}}r_\delta }(0). \end{aligned}$$

Thus, for $t \ge 0$,

$$\begin{aligned} I_\lambda (tf_\lambda )= & {} \frac{t^2}{2}\int _{\mathbb {R}^N}(|\Delta f_\lambda |^2 + \lambda V(x)|f_\lambda |^2)dx - t^pa_0\lambda \int _{\mathbb {R}^N} |f_\lambda |^pdx\\= & {} \lambda ^{1-\frac{N}{4}}\left( \frac{t^2}{2}\int _{\mathbb {R}^N}\left( |\Delta \phi _\delta |^2 + V\left( \lambda ^{-\frac{1}{4}}x\right) |\phi _\delta |^2\right) dx - t^pa_0\int _{\mathbb {R}^N} |\phi _\delta |^pdx\right) \\= & {} \lambda ^{1-\frac{N}{4}}\Psi _\lambda (t\phi _\delta ), \end{aligned}$$

where $\Psi _\lambda \in C^1(E, \mathbb {R})$ defined by

$$\begin{aligned} \Psi _\lambda (u) := \frac{1}{2}\int _{\mathbb {R}^N}\left( |\Delta u|^2 + V\left( \lambda ^{-\frac{1}{4}}x\right) |u|^2\right) dx - a_0\int _{\mathbb {R}^N} |u|^pdx. \end{aligned}$$

Obviously,

$$\begin{aligned} \max _{t \ge 0} \Psi _\lambda (t\phi _\delta ) = \frac{p-2}{2p(pa_0)^{\frac{2}{p-2}}} \left[ \int _{\mathbb {R}^N}\left( |\Delta \phi _\delta |^2 + V\left( \lambda ^{-\frac{1}{4}}x\right) |\phi _\delta |^2\right) dx\right] ^{\frac{p}{p-2}}. \end{aligned}$$

On the one hand, since $V(0) = 0$ and supp $\phi _\delta \subset B_{r_\delta }(0)$, there is $\Lambda _{\delta } > 0$ such that

$$\begin{aligned} V\left( \lambda ^{-\frac{1}{4}}x\right) \le \frac{\delta }{|\phi _\delta |_2^2},\ \text {for all }\ |x| \le r_\delta \ \text {and}\ \lambda \ge \Lambda _{\delta }. \end{aligned}$$

Then

$$\begin{aligned} \max _{t\ge 0} \Psi _\lambda (t\phi _\delta ) \le \frac{p-2}{2p(pa_0)^{\frac{2}{p-2}}} \left( 2\delta \right) ^{\frac{p}{p-2}}. \end{aligned}$$

(4.2)

Therefore, for all $\lambda \ge \Lambda _\delta$,

$$\begin{aligned} \max _{t\ge 0} J_\lambda (t\phi _\delta ) \le \frac{p-2}{2p(pa_0)^{\frac{2}{p-2}}} \left( 2\delta \right) ^{\frac{p}{p-2}}\lambda ^{1-\frac{N}{4}}. \end{aligned}$$

(4.3)

Thus we have the following lemma.

Lemma 4.3

Under the assumption of Lemma 4.1, for any $\sigma > 0$ there exists $\Lambda _\sigma > 0$ such that for each $\lambda \ge \Lambda _\sigma$, there is $\widehat{f}_\lambda \in E$ with $\Vert \widehat{f}_\lambda \Vert _\lambda > \rho _\lambda$, $J_\lambda (\widehat{f}_\lambda ) \le 0$ and

$$\begin{aligned} \max _{t\in [0, 1]} J_\lambda (t\widehat{f}_\lambda ) \le \sigma \lambda ^{1-\frac{N}{4}}. \end{aligned}$$

(4.4)

Proof

Choose $\delta > 0$ so small that

$$\begin{aligned} \frac{p-2}{2p(pa_0)^{\frac{2}{p-2}}} \left( 2\delta \right) ^{\frac{p}{p-2}} \le \sigma \end{aligned}$$

and let $f_\lambda \in E$ be the function defined by (4.1). Taking $\Lambda _\sigma = \Lambda _\delta$. Let $\widehat{t}_\lambda > 0$ be such that $\widehat{t}_\lambda \Vert f_\lambda \Vert _\lambda > \rho _\lambda$ and $J_\lambda (tf_\lambda ) \le 0$ for all $t \ge \widehat{t}_\lambda$. By (4.3), setting $\widehat{f}_\lambda = \widehat{t}_\lambda f_\lambda$, we know that the conclusion of Lemma 4.3 holds. $\square$

For any $m^{*} \in N$, one can choose $m^{*}$ functions $\phi _\delta ^i \in C_0^\infty (\mathbb {R}^N)$ such that supp $\phi _\delta ^i\cap$ supp $\phi _\delta ^k = \emptyset$, $i \ne k$, $|\phi _\delta ^i|_p = 1$ and $|\Delta \phi _\delta ^i|_2^2 < \delta$. Let $r_\delta ^{m^{*}} > 0$ be such that supp $\phi _\delta ^{i} \subset B_{r_\delta ^{m^{*}}}^{i}(0)$ for $i = 1,2,\ldots ,m^{*}$. Set

$$\begin{aligned} f_\lambda ^i(x) = \phi _\delta ^i (\lambda ^{\frac{1}{4}}x), \ \ \text {for}\ j = 1,2,\ldots ,m^{*} \end{aligned}$$

and

$$\begin{aligned} H_{\lambda \delta }^{m^{*}} = \text {span}\{f_\lambda ^1, f_\lambda ^2, \cdots , f_\lambda ^{m^{*}}\}. \end{aligned}$$

Observe that for each $u = \displaystyle \sum _{i=1}^{m^{*}}c_i f_\lambda ^i \in H_{\lambda \delta }^{m^{*}}$,

$$\begin{aligned} \int _{\mathbb {R}^N} |\Delta u|^2dx= & {} \sum _{i=1}^{m^{*}}|c_i|^2\int _{\mathbb {R}^N} |\Delta f_\lambda ^i|^2dx,\\ \int _{\mathbb {R}^N} V(x)| u|^2dx= & {} \sum _{i=1}^{m^{*}}|c_i|^2\int _{\mathbb {R}^N}V(x) |f_\lambda ^i|^2dx,\\ \frac{1}{2^{**}}\int _{\mathbb {R}^N} |u|^{2^{**}}dx= & {} \frac{1}{2^{**}}\sum _{i=1}^{m^{*}}|c_i|^{2^{**}}\int _{\mathbb {R}^N} |u|^{2^{**}}dx \end{aligned}$$

and

$$\begin{aligned} \int _{\mathbb {R}^N} H(x, u)dx = \sum _{i=1}^{m^{*}}\int _{\mathbb {R}^N}H(x, c_if_\lambda ^i)dx. \end{aligned}$$

Thus

$$\begin{aligned} J_\lambda (u) = \sum _{i=1}^{m^{*}}J_{\lambda }(c_i f_\lambda ^i) \end{aligned}$$

and as before

$$\begin{aligned} J_\lambda (c_i f_\lambda ^i) \le \lambda ^{1 - \frac{N}{4}}\Psi _\lambda (|c_i| f_\lambda ^i). \end{aligned}$$

Set

$$\begin{aligned} \beta _\delta := \max \{|\phi _\delta ^i|_2^2: i = 1,2,\ldots ,m^{*}\} \end{aligned}$$

and choose $\Lambda _{m^{*}\delta } > 0$ so that

$$\begin{aligned} V(\lambda ^{- \frac{1}{4}}x) \le \frac{\delta }{\beta _\delta } \ \text {for all }\ |x| \le r_\delta ^{m^{*}}\ \text {and}\ \lambda \ge \Lambda _{m^{*}\delta }. \end{aligned}$$

As before, we can obtain the following

$$\begin{aligned} \max _{u\in H_{\lambda \delta }^{m^{*}}} J_\lambda (u) \le \frac{m^{*}(p-2)}{2p(pa_0)^{\frac{2}{p-2}}} \left( 2\delta \right) ^{\frac{p}{p-2}}\lambda ^{-\frac{1}{4}} \end{aligned}$$

(4.5)

for all $\lambda \ge \Lambda _{m^{*}\delta }$.

Using this estimate we have the following.

Lemma 4.4

Under the assumption of Lemma 4.1, for any $m^{*} \in N$ and $\sigma > 0$ there exists $\Lambda _{m^{*}\sigma } > 0$ such that for each $\lambda \ge \Lambda _{m^{*}\sigma }$, there exists an $m^{*}$-dimensional subspace $F_{\lambda m^{*}}$ satisfying

$$\begin{aligned} \max _{u\in F_{\lambda \delta }} J_\lambda (u) \le \sigma \lambda ^{1-\frac{N}{4}}. \end{aligned}$$

Proof

Choose $\delta > 0$ so small that

$$\begin{aligned} \frac{m^{*}(p-2)}{2p(pa_0)^{\frac{2}{p-2}}} \left( 2\delta \right) ^{\frac{p}{p-2}} \le \sigma \end{aligned}$$

and take $F_{\lambda m^{*}} = H_{\lambda \delta }^{m^{*}}$. By (4.5), we know that the conclusion of Lemma 4.4 holds. $\square$

We now establish the existence and multiplicity results.

Proof of Theorem 2.1

Using Lemma 4.3, we choose $\Lambda _{\sigma } > 0$ and define for $\lambda \ge \Lambda _\sigma$, the minimax value

$$\begin{aligned} c_\lambda := \inf _{\gamma \in \Gamma _\lambda }\max _{t\in [0,1]} J_\lambda (t\widehat{f}_\lambda ) \end{aligned}$$

where

$$\begin{aligned} \Gamma _\lambda := \{\gamma \in C([0, 1], E): \gamma (0) = 0 \ \text {and}\ \gamma (1) = \widehat{f}_\lambda \}. \end{aligned}$$

By Lemma 4.1, we have $\alpha _\lambda \le c_\lambda \le \sigma \lambda ^{1-\frac{N}{4}}$. In virtue of Lemma 3.3, we know that $J_\lambda$ satisfies the $(PS)_{c_\lambda }$ condition, there is $u_\lambda \in E$ such that $J'_\lambda (u_\lambda ) = 0$ and $J_\lambda (u_\lambda ) = c_\lambda$, hence the existence is proved. Moreover, fixing $\nu > 0$, it results

$$\begin{aligned} \sigma \lambda ^{1-\frac{N}{4}}\ge & {} J_\lambda (u_\lambda ) = J_\lambda (u_\lambda ) - \frac{1}{\nu }J_\lambda '(u_\lambda )u_\lambda \\\ge & {} \left( \frac{1}{2} - \frac{1}{\nu }\right) \int _{\mathbb {R}^N}(|\Delta u_\lambda |^2 + \lambda V(x)|u_\lambda |^2)dx + \left( \frac{1}{\nu } - \frac{1}{2^{**}}\right) \lambda \int _{\mathbb {R}^N}|u_\lambda |^{2^{**}}dx\\&+\, \lambda \left( \frac{\mu }{\nu }-1\right) \int _{\mathbb {R}^N}H(x, u_\lambda )dx, \end{aligned}$$

where $\mu$ is the constant in condition (H). Taking $\nu = 2$, we obtain the estimates (2.3) and taking $\nu = \mu$ we obtain the estimate (2.4).

Denote the set of all symmetric (in the sense that $-Z = Z$) and closed subsets of E by $\Sigma$. For each $Z \in \Sigma$, let gen(Z) be the Krasnoselski genus and

$$\begin{aligned} i(Z) := \min _{h\in \Gamma _{m^*}}\text {gen}(h(Z)\cap \partial B_{\rho _\lambda }), \end{aligned}$$

where $\Gamma _{m^*}$ is the set of all odd homeomorphisms $h \in C(E, E)$ and $\rho _\lambda$ is the number from Lemma 4.1. Then i is a version of Benci’s pseudoindex [9]. Let

$$\begin{aligned} c_{\lambda i} := \inf _{i(Z)\ge i}\sup _{u\in Z}J_\lambda (u), 1 \le i \le m^*. \end{aligned}$$

Since $J_\lambda (u) \ge \alpha _\lambda$ for all $u \in \partial B_{\rho _\lambda }$ and since $i(F_{\lambda m^*}) = \dim F_{\lambda m^*} = m^*$,

$$\begin{aligned} \alpha _\lambda \le c_{\lambda 1} \le \cdots \le c_{\lambda m^*} \le \sup _{u \in F_{\lambda m^*}} J_\lambda (u) \le \sigma \lambda ^{1-\frac{N}{4}}. \end{aligned}$$

It follows from Lemma 3.3 that $J_\lambda$ satisfies the $(PS)_{c_\lambda }$ condition at all levels $c_{\lambda _i}$. By the usual critical point theory, all $c_i$ are critical levels and $J_\lambda$ has at least $m^*$ pairs of nontrivial critical points. We see that these solutions satisfy the estimate (2.3) and (2.4). $\square$