Introduction

Understanding rational numbers is important inside and outside school. For many reasons, rational numbers are challenging for students, a major source of difficulty being the whole or natural number bias, hereafter NNB (Ni & Zhou, 2005; Vamvakoussi et al., 2013). The NNB refers to students’ tendency to draw on prior natural number knowledge to interpret new information about non-natural numbers, and to deal with related tasks about non-natural numbers. Many systematic errors, particularly when rational numbers appear in an abstract context, can be attributed to this bias. In this paper, we investigated aspects of students’ understandings of multiplication and division with decimal numbers in an abstract context. We argue that, besides students’ expectations about the effect of multiplication and division (always “makes bigger,” always “makes smaller,” respectively), the NNB has an additional effect. More specifically, the present study intends to provide evidence that students develop expectations also regarding the type (i.e., natural or non-natural number) of the operands and the result of multiplication and division.

Theoretical background

Natural number bias when reasoning with rational numbers

The natural number bias phenomenon has been long known to mathematics educators and mathematics education researchers (Hart, 1981), mainly as a source of systematic errors that appear in cases where rational numbers differ from natural numbers. Many misconceptions underlying systematic errors have been identified in the literature such as that “longer decimals are larger” (e.g., 0.123 > 0.45, Moloney & Stacey, 1997; Nesher & Peled, 1986; Resnick et al., 1989); that a fraction’s magnitude always increases when its denominator, numerator, or both increase (Chinnappan & Forrester, 2014; Meert et al., 2009; Stafylidou & Vosniadou, 2004; Van Hoof et al., 2013); and that every number has a unique successor (Merenluoto & Lehtinen, 2004; Vamvakoussi & Vosniadou, 2010).

When it comes to arithmetic operations, the result of addition or multiplication between two natural numbers (except 0 and 1) is always bigger than the operands. Similarly, the result of subtraction or division between two natural numbers is smaller than the minuend and the dividend, respectively. On the contrary, multiplying or dividing with a number smaller than 1 results in either a smaller or larger outcome, respectively (e.g., 8 × 0.5 is smaller than 8; 5 ÷ 0.3 is bigger than 5). Dating back to the 1980s, it has been documented that when students solve word problems, they tend to perform multiplication if they expect a bigger result and division if they expected a smaller result (Fischbein et al., 1985; Graeber et al., 1989; Harel et al., 1994; Hart, 1981). More recent studies have provided supporting evidence for this tendency in the context of algebraic expressions, using tasks such as, for example, “is 5 × always bigger than 5?” (Vamvakoussi et al., 2013; Van Hoof et al., 2015); and also in the context of arithmetic equalities with missing numbers (e.g., “is it possible to find a number that could make this equality hold: 2÷_=9?” (Christou, 2015; Christou et al., 2020)).

NNB-based errors tend to decrease with age and school experience, but remain present even in educated adults (Obersteiner et al., 2015; Vamvakoussi et al., 2013). Examining a large sample of 4th to 12th graders, Van Hoof et al. (2015) showed that while NNB-based errors in fraction and decimal comparisons practically disappear at the end of secondary school, the NNB effects with respect to operations and density remain salient.

There are different approaches and explanations given about the origins of the NNB (Ni & Zhou, 2005; Rips et al., 2008). Nevertheless, there is consensus among scholars that early informal and formal experiences support the construction of initial, principled understandings of numbers as natural numbers, rooted in the act of counting (Gelman, 2000). According to the perspective that we endorse, these initial understandings are organized into complex conceptual systems (Smith et al., 2005; Vamvakoussi & Vosniadou, 2010) that underlie students’ implicit beliefs about numbers. Initial understandings of numbers as natural numbers are useful in a variety of everyday situations and are also validated during the first years of instruction that focuses on natural number arithmetic. The implicit beliefs underlying these understandings thus acquire an intuitive character in the sense that they are characterized by immediacy and pervasiveness, and are accompanied by a feeling of certainty; they remain strong, even when a mathematically correct model is available to the individual (Fischbein, 1987). In other words, natural number knowledge comes to mind first when dealing with a problem that involves numbers, triggering immediate responses, and continues to influence students’ reasoning, even after years of instruction on non-natural numbers.

Research on the NNB does not address the whole range of potential understandings of number that students may exhibit across various contexts. It typically uses symbolic tasks, where numbers act as abstract entities that take their meaning within a number system (Kilpatrick et al., 2001), through their relations with other numbers and the operations in which they participate (e.g., 10 > 8, 10 = 8 + 2, 10 is an even number). This meaning of numbers, termed “analytic” by Nunes and Bryant (2015), is considerably more challenging to master, than their referential meaning, where the numbers take their meaning from the quantities they represent. One important reason is that when numbers refer to quantities and are represented concretely, students can draw on legitimate actions on quantities to construct meaning for numbers and their operations (see Behr et al., 1992 for a detailed account of various meanings of rational numbers). However, these understandings are not immediately transferred to abstract contexts. Indeed, there is great discrepancy between students’ performance in symbolic and non-symbolic tasks, with the NNB more likely to manifest in the former (Ni & Zhou, 2005). Although it is only one aspect of the great variety of number meanings, the analytic meaning of numbers is important in many contexts, notably algebra.

Rationale of the present study

In this study, we investigated students’ understandings of multiplications and division in an abstract context. A main focus of the study was whether or not students understand that operations between decimal numbers may result in natural numbers, and vice versa. This understanding can be viewed as a component of higher-order number sense (Berch, 2005) pertaining to the analytic meaning of number (Nunes & Bryant, 2015).

To the best of our knowledge, no prior study focused on this issue before. There is evidence indicating that the type of operands (natural/non-natural) may affect students’ selection of operation and their accuracy in evaluating the results of the operations when solving word problems (De Corte & Verschaffel, 1996; De Corte et al., 1988). More direct evidence comes from a study by Switzer (2018) who interviewed fourth to sixth graders asking them which numbers can and cannot act as addends in expressions such as the following 8 = □ + □, where the sum was always a natural number. One-fourth of the students rejected non-natural numbers as possible addends, arguing that non-natural numbers are not relevant when the result is a natural number. For example, some argued that “we are not talking about decimals”, “we are not doing fractions”, “because that (the sum) is a positive integer” (p. 47).

We conjectured that some students expect that the operands and the result of arithmetical operations are of the same type (natural/non-natural). There are two reasons underlying this conjecture, both stemming from a NNB perspective. The first relates to students’ experiences with arithmetical operations in the context of natural number arithmetic, in particular when these operations are not represented concretely and pertain to the analytic meaning of number. In the first years of instruction, such experiences are limited to expressions that include numbers of the same type, namely natural numbers, as also appear in contemporary mathematics curriculums in many countries (Australian Curriculum and Assessment Reporting Authority [ACARA], 2014; Common Core State Standards Initiative [CCSSI], 2010). In the context of operations, expressions illustrate natural numbers interacting to produce a natural number. This is obvious in the case of addition and multiplication, since the set of natural numbers is closed under both these operations (i.e., adding or multiplying natural numbers results in natural numbers). It is not the case for subtraction and division, which may result in non-natural numbers. However, before they are formally introduced to positive rational numbers (typically at third or fourth grade), students have only been taught the Euclidean division that produces a natural number as quotient, with a possible remainder, also a natural number. Additionally, before they are introduced to negative rational numbers (typically at sixth or seventh grade), students have only experienced subtraction as a process of subtracting a smaller natural number from a bigger one, and never the other way around. Thus, students are over-exposed to expressions presenting numbers of the same type—in particular, natural numbers—interacting to produce a same-type number. This also applies to expressions where an operand is missing, and one might also consider the Euclidean division formula (i.e., dividend = divisor × quotient + remainder, for example, 19 = 2 × 9 + 1).

Second, conceptualizing the rational numbers set as a unified system of numbers, where fractions, decimals, and integers are perceived as different representations of rational numbers, is very challenging for students (Kilpatrick et al., 2001). There is evidence indicating that many students in various contexts treat rational numbers as a collection of distinct sets of numbers (i.e., whole numbers, decimals, and fractions) despite their experiences with the number line and also with converting one representational form to another, for example, converting decimals to fractions (Vamvakoussi & Vosniadou, 2010). For instance, middle-grade students were found reluctant to order a series of numbers of different types; instead, they ordered them separately, or explicitly stated that ordering different types of numbers is impossible (Markovits & Sowder, 1991). The aforementioned study by Switzer (2018) indicates that some students were reluctant to “mix together” natural and non-natural numbers in the context of addition. Vamvakoussi and Vosniadou (2010) found that secondary students who were prepared to accept that there are infinitely many numbers in an interval still stated that the intermediates must be of the same type as the interval endpoints.

Vamvakoussi and Vosniadou (2010) argued that this problem contributes to students’ difficulty to re-organize their initial category of number as natural number to form a new category under which natural and non-natural numbers are subsumed. In this long process, students learn to call decimals and fractions “numbers.” However, they do not deem fractions and decimals a member of the same family as the natural numbers, and they also neglect the fact that fractions and (rational) decimals are interchangeable representations of the same numbers, rather than different kinds of numbers (Khoury & Zazkis, 1994; O’Connor, 2001). From this perspective, this phenomenon relates to the NNB, in the sense that new information about non-natural numbers is interpreted based on students’ initial number concepts and is accommodated allowing for natural numbers to retain their privileged status. It should be noted that instruction typically does not facilitate students’ conceptualization of rational numbers as a unified system of numbers that are invariant under different symbolic representations; we will return to this issue in the discussion.

Given students’ tendency to group numbers based on the natural/non-natural distinction as well as based on their representational form (decimals/fractions), and their early over-exposure to expressions that present numbers of the same type interacting to produce a same-type result, we reasoned that students may be constrained by the background assumption that the numbers involved in an operation must be of the same type. Such a constraint could manifest in various arithmetic and algebraic contexts. For example, in school textbooks, algebraic expressions, equations, inequalities, and functions typically contain only natural numbers as coefficients and constants (Greer & Verschaffel, 2007). Presuming that all components must be of the same type could affect students’ expectations about the sign of an algebraic expression, the values over which the variable ranges, etc.

Research questions and predictions

The main hypothesis of this study is that prior knowledge and experience about natural numbers has a twofold effect on students’ understanding of arithmetical expressions related to operations: First, it shapes their expectations regarding the size of the result, in relation to the operands (i.e., multiplication makes bigger, division makes smaller). Second, it affects their assumptions regarding the type of numbers that are involved in the operation. Specifically, we predicted that students tend to assume that the operands and the results are of the same type.

We tested this hypothesis for multiplication and division, using different combinations of natural and decimal numbers as operands and results of the operations. A sample of seventh and eighth graders were presented with a series of arithmetic expressions of multiplication and division between one given and one missing operand number with the results also given (e.g., 8 ÷ _ = 3.3). Some of the expressions were consistent with the assumed expectations (hereafter, congruent items), and some were not (hereafter, incongruent items). Students were asked to evaluate the given equalities (i.e., whether there is a number for which the equality holds).

Question 1 was whether there would be performance differences due to grade. Previous studies with similar tasks showed that sixth graders performed better than fifth graders (Christou, 2015) thus, we expected older students to perform better (Prediction 1).

Question 2 related to the effect of the NNB on students’ evaluations. We predicted that students would make more mistakes in the incongruent items (where an intuitive belief about the size or about the type of the results of the operations would lead to incorrect responses) than in the congruent items, for multiplication as well as for division (Prediction 2).

Question 3 was which of the two factors, namely the size or the type of the numbers involved, would have a stronger effect on students’ accuracy. Since the effect of number type has not been tested before, no prediction was made.

Question 4 was whether students would respond similarly to multiplication and division items. Higher accuracy was expected in multiplication than in division in the size congruent items (Prediction 3) but not necessarily in the size incongruent items. This is because different studies with secondary school students that used similar (but not identical) tasks had contradictory findings. In one study, the students appeared more willing to accept that division “makes bigger” than to accept that multiplication “makes smaller” (Christou, 2015). However, another study had the exact opposite finding (Van Hoof et al., 2015). No prediction was made with respect to type congruency. 

Question 5 was whether there would be individual differences in the way that students would respond in the different categories of items.

Method

Participants

The participants were 91 students from a public school of Greece: two entire seventh-grade classes (43 students, mean age 12.6) and two entire eighth-grade classes (48 students, mean age 13.5); 53 of the overall sample were girls.

Greek students are introduced to fractions and decimal numbers at grade 3. By grade 7, they are supposed to have acquired a good knowledge of operations with rational numbers and to be able to apply them in different mathematical contexts such as in equations and inequalities, functions, and problem solving.

Materials

The participants were administered a questionnaire, designed for the purposes of this study, that included 46 equalities with operations between one given and one missing operand, with the result also given. The task for students was to decide whether or not there was a number that would make the given equality valid. Specifically, the equality was presented in a form such as is 6 × _ = 498 (more examples are presented in Table 1), and students had to select one of two alternatives (possible/not possible). The design of the tasks was based on previous research designs applied in related empirical studies in the field (Christou et al., 2020). Only multiplication and division were involved in this study, and also only natural or decimal numbers appeared in the given tasks. The given operand and result were either of the same type (i.e., both natural numbers or decimals), or of different type (i.e., one natural number, one decimal). Size and type were crossed, producing four types of items:

  1. 1.

    Size congruent/incongruent tasks: Size congruent tasks were in-line with the assumed expectations that multiplication makes bigger and division makes smaller, that is, the result was bigger than the given operand for multiplication (e.g., 6 × _ = 498) and smaller for division (e.g., 735 ÷ _ = 8). On the contrary, the result for size incongruent tasks was smaller than the given operand for multiplication (e.g., 437 × _ = 3) and bigger for division (e.g., 9 ÷ _ = 656).

  2. 2.

    Type congruent/incongruent tasks: Type congruent tasks were in line with the assumed expectation that the operands and the result of an operation should be of the same type. Thus, in type congruent tasks, the given operand and the output were of the same type (e.g., 6.3 × _ = 2.1). On the other hand, in type incongruent tasks, the given operand and the result were of different types (e.g., 4 ÷ _ = 7.6).

Table 1 Examples of items per type of operation and congruency
Full size table

The 40 main tasks were counter-balanced across the abovementioned categories. Because the correct answer was it is possible across all tasks, we also included 6 buffer tasks that involved multiplication or division with zero and for which the correct answer was it is not possible. Greek students are explicitly taught from early on that if the multiplicand or the multiplier is zero, the product is also zero and that if the dividend is zero, the quotient is zero, whereas zero is not allowed as a divisor.

The blank was used, instead of the literal symbol x, as a means to avoid reminding to students that the given equalities could be treated as equations and were all solvable. We also note that we did not include fraction tasks in the questionnaire, because the number of items would be doubled and it would be tiresome for students to complete.

The written instruction read as follows: In the following tasks, you should answer whether you think it is possible to find a value for the missing number that would provide the given result, or not. They were also told that they should choose the alternative that best represents their opinion. They were explicitly instructed to consider any kind of number they know, meaning any type of number they have come across in mathematics, independently of its form. Additionally, it was stressed that they do not have to find the missing number. Typical missing number tasks (i.e., asking for the missing number) are familiar to students because they appear in textbooks throughout primary school. However, we cannot exclude the possibility of a teacher having used tasks like the ones we used in the classroom.

Procedure

The students completed the tests in their classroom during their mathematics course in the presence of their teacher and one researcher. Students understood the tasks, and no clarification question was asked. One teaching hour (45 min) was available for the whole process, including distributing the test papers, instructions, time for students to take a look at the tasks, and prompting them to ask clarification questions. This left students with about 30–35 min to complete the questionnaire. The available time was not exhausted by any of the students.

Results

We first note that the buffer tasks were not included in any of the analyses presented in the following. Participants’ responses were scored as correct or incorrect (0/1). Raw data were included in the analyses; no data manipulation was made. Cronbach’s alpha test measured the reliability of the questionnaire, which was satisfactory (Cronbach’s alpha = 0.871).

Considering question 1, univariate analysis of variance was used with students’ mean accuracy across all tasks as depended variable, and grade as factor. The results showed that, against Prediction 1, the eighth graders did not perform better than the seventh graders (M = .48, SE = .03 vs M = .49, SD = .02) [F(1, 89) = .103, p = .749, np2 = 0.001]; thus, the sample was unified for the analyses that follow.

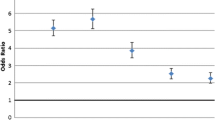
To address question 2 and question 4, generalized estimating equations (GEEs) with mean accuracy as dependent variable were used to test for main effects of size and type congruency as well as operation type, and possible interactions between them—Bonferroni correction was applied. This analysis requires a data set with multiple measurements per subject; therefore, GEE was used because it can test repeated (and therefore probably correlated) measures within subjects (Nussbaum, 2015). Further, the interaction between size and type congruency, as well as pairwise comparisons and odds ratio comparisons, presented in more detail in the following, were used to address question 3. Figure 1 presents mean accuracy by operation (multiplication/division), by size congruency (congruent/incongruent), and by type congruency (congruent/incongruent), with error bars showing the 95% confidence interval.

Fig. 1
figure 1

Mean accuracy by operation, by size congruency, and by type congruency

Full size image

A significant main effect of size congruency χ2(1, N = 3640) = 93.400, p < 0.001, as well as of type congruency χ2(1, N = 3640) = 25.474, p < 0.001 was found, which addresses question 2, and is in-line with Prediction 2 of the study. Specifically, mean accuracy was significantly higher on size congruent (65%) than on size incongruent items (32%), and it was also higher on type congruent (53%) than on type incongruent items (44%). The odds ratios for accuracy for size congruent vs size incongruent items and type congruent vs type incongruent items gave an indication of the relative strength of the bias on the size and the type of the results, and thus address question 3. The odds ratio showed that the strength of size congruency (OR = 3.95, 95% CI [2.19, 7.1]) was larger than that of type congruency (OR = 1.44, 95% CI [0.82, 2.5]). Specifically, estimated odds ratios suggested that the odds of answering a size congruent task correctly were about 4 times the odds of answering a size incongruent item correctly, and the odds of answering a type congruent item correctly was 1.5 times the odds of answering a type incongruent item correctly.

Additionally, there was a significant main effect of size congruency for multiplication and for division χ2(3, N = 3640) = 136.340, p < .001. Pairwise comparisons among the estimated marginal means showed significantly higher accuracy on size congruent than on size incongruent items, evidencing an effect of number size for multiplication (67% vs. 31%, p < .001) as well as for division (62% vs. 33%, p < .001).

There was also a significant main effect of type congruency for both operations χ2(3, N = 3640) = 28.582, p < .001. Again, pairwise comparisons among the estimated marginal means showed higher accuracy on type congruent than on type incongruent items, evidencing an effect of number type for multiplication (52% vs. 46%, p < .05) as well as for division (53% vs. 42%, p < .001).

Finally, considering research question 4, students showed similar accuracies in multiplication (49%) and in division (47%) with no main effect for operation χ2(1, N = 3640) = .525, p = .469.

Individual profiles

The above analyses are based on mean accuracy, and as such, they do not provide information about the individual student’s treatment of the tasks. To identify different groups (clusters) in terms of within-group similarities (question 5), a two-step cluster analysis was applied on mean accuracy in (a) multiplication items and (b) division items—raw data were included in the analyses, and no data manipulation was made.

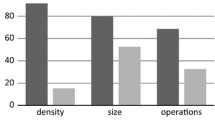
For multiplication, Schwarz’s Bayesian criterion indicated an optimal solution of two clusters. The silhouette coefficient of this solution was 0.6, which is characterized as reasonable, because it is higher than 0.5 in the estimate of cluster cohesion and separation scale that ranges from − 1 to 1 (Kaufman & Rousseeuw, 1990). For the latter, Schwarz’s Bayesian criterion indicated that a solution with three clusters described the data best. The silhouette coefficient was 0.4, which is characterized as fair. Table 2 presents the mean scores and standard deviations of mean accuracy per task category, by cluster, for both operations.

Table 2 Mean scores and St. deviations of accuracy in each cluster by item category and operation
Full size table

For the multiplication items, the members of the first cluster (Clust. M1) can be characterized as the high performers in all four categories of items (at least 0.86 mean accuracy in each category). The second cluster (Clust. M2) included the students who could be characterized as the lower-performing students, with much lower accuracy across all categories of items (lower than 0.18). Students in both clusters performed higher in the size congruent tasks than in the size incongruent tasks, independently of type congruency. These profiles show again that the students were affected more by size congruency, than type congruency with respect to the multiplication items.

Regarding the division items, the first cluster (Clust. D1) comprised, similarly to Clust. M1, students with high accuracy in all division tasks (at least 0.89 mean score in all categories). The second cluster (Clust. D2) comprised students with high accuracy in the size congruent items (mean accuracy higher than 0.66) and low in size incongruent items (mean accuracy lower than 0.17 in both size incongruent task categories). Interestingly, the third cluster (Clust. D3) comprised students who performed higher in the type congruent items (mean accuracy higher than 0.41 in both type congruent categories) than in the type incongruent items (mean accuracy lower than 0.28 in both type incongruent categories). This indicates that, also in division items, number size congruency played a definitive role in most students’ evaluations. However, in the case of division, there were also some students who appear to have systematically based their responses on the number type.

The cluster membership as identified in the two-step cluster analysis presented above was a significant factor for students’ total performance in multiplication items F(1, 85) = 84.306, p < .001, np2 = .498 as well as in division items F(1, 85) = 23.608, p < .001, np2 = .357.

Discussion

In this study, we tested for a twofold effect of the NNB on secondary students’ expectations about multiplication and division. First, we hypothesized that students would expect that multiplication always makes bigger whereas division always makes smaller. Second, we hypothesized that students would expect that the operands and the result of multiplication or division are of the same type (natural/non-natural). To the best of our knowledge, this hypothesis has never been tested before and may extend the range of effects of the natural number bias phenomenon.

The results of the study supported our hypotheses showing that the size as well as the type of numbers involved in the operations affected students’ evaluations of the validity of the given equalities. More specifically, students’ accuracy in the size congruent tasks was higher than in the size incongruent tasks, for multiplication as well as for division. These results are in line with prior research, strengthening previous findings (Christou, 2015; Fischbein et al., 1985; Vamvakoussi et al., 2013; Van Hoof et al., 2015).

Additionally, students’ accuracy in evaluating the type congruent items was higher than in the type incongruent items, for size congruent items in multiplication and division, and for size incongruent tasks in division, but not for size incongruent tasks in multiplication, where students’ performance was very low. These results provide empirical evidence that besides the size of the results, the type of operands also affects students’ responses. It also appears that students focused more on the size of the result than on the type of the numbers when evaluating the given equalities. Cluster analysis further strengthened these results and additionally showed that in division, there were also students who focused on the type of the numbers in a systematic way.

Contrary to Prediction 3, students’ accuracy did not differ significantly in multiplication compared to division in the different categories of tasks. Additionally, contrary to Prediction 1, there was no significant difference between eighth and seventh graders’ performance, indicating that the NNB still affects students’ reasoning at the end of high school (Obersteiner et al., 2015; Vamvakoussi et al., 2013).

The results of the current study provide some empirical evidence that besides the well-known effect of NNB on students’ expectations about the size of the results of multiplication and division, there are also students’ expectations considering the type (i.e., natural or non-natural number) of the operands and the result of multiplication and division which are biased in certain ways. Knowledge of the effects of operations on numbers is considered a fundamental feature of number sense (Berch, 2005), pertaining to the analytic meaning of numbers (Nunes & Bryant, 2015). In the same vein, understanding that operations between numbers of a certain type may result in numbers of a different type is important in developing a good understanding of the properties of numbers and their operations. This knowledge is essential for succeeding in many different mathematical areas such as in estimating, solving, and evaluating the results of equations, understanding functions, etc.

Limitations and further research

A main limitation of the study is that the sample size is small and the participants came from only one school; thus, the findings should be interpreted with caution. Another limitation of this study is that it is based on students’ responses to a written questionnaire and there are no data illustrating students’ reasoning when or immediately after solving the tasks. There are several possible routes that students could have taken, and we discuss them systematically in the following.

First, students could respond to these questions based on their knowledge about how simple equations are solved, circumventing strategies such as trying out numbers or relying on general rules of operations (e.g., multiplication makes bigger), that might lead them to NNB errors. This was taken into consideration in the design of the tasks, by using blanks to represent the missing numbers, instead of the literal symbol x which might steer students towards equation solving, and also, in the instructions, by stressing that the missing number is not to be specified, as well as by providing number combinations in which computing the missing number is not easy. Based on previous experience with secondary students solving similar tasks with variables in individual interviews, we are fairly confident that they do not treat them as tasks on equation solvability; they rather try to respond by trying different numbers (Dimitrakopoulou & Christou, 2018; Van Hoof et al., 2015). In the literature, evoking knowledge on equation solvability has been attributed to experts (Obersteiner et al., 2015). Still, the possibility of students using this strategy cannot be excluded.

Another possibility that cannot be excluded is that some students did try to find the missing number by solving the given equations. This would mean that they recognized the given equalities as equations, which, as we mentioned above, we have reasons to doubt. In addition, we did not find any indication on the questionnaires that students made any calculations. Assuming that there were some students who either solved the equations, or evoked knowledge on equation solvability, an interesting question arises to be further investigated via qualitative methods. Specifically, only two students in our sample managed to answer all tasks correctly. For the great majority of students, even if some students used any of these two strategies, they did not seem to have used it systematically. This implies that although some students may have recognized that knowledge on equations was relevant to the tasks at hand, they failed to use it in all items.

Another concern could be that some students might have been puzzled by the fact that the answer “it is possible” appears far more often than the answer “it is not possible” and might have changed their answers during or after the completion of the questionnaire to balance the set of responses. However, we did not find such indications (i.e., changes in the initial answer, or sudden increases of “it is possible” responses from some point on) in the test papers. In our experience with students dealing with similarly designed sets of tasks, we have never observed any indication of this strategic approach (Christou, 2015; Christou et al., 2020). More importantly, had students implemented such a strategy, we would have not found the expected patterns of responses, at least with respect to size, which is widely documented in the literature.

Future studies with individual interviews are currently designed that could corroborate the findings of this study. Additionally, complementing accuracy data with reaction time data might provide further empirical evidence of natural number reasoning in these tasks and similar tasks, and may clarify some of the issues reported above (see also Gillard et al., 2009; Obersteiner et al., 2015). A plausible prediction would then be that accurate responses to congruent items would be faster than to incongruent items. So far, this methodology has been used only with size congruent/incongruent items, and the results were in-line with this prediction (Meert et al., 2009; Obersteiner et al., 2015; Stafylidou & Vosniadou, 2004; Vamvakoussi et al., 2013; Van Hoof et al., 2013, 2015). The same methodology could also be used with type congruent/incongruent items.

Additionally, the effect of type of operands on students’ evaluations could be investigated for different combinations of other types of non-natural numbers, notably fractions. Based on the same rationale as the one of this study, we would predict that students would tend to expect that operations between fractions could not result to decimals and vice versa.

Educational implications

Addressing the NNB in instruction is a complex endeavor that requires remedial as well as anticipation approaches. Here, we only refer to few implications that are relevant to this study, conducted through the particular theoretical lenses.

An important issue is that the majority of students are typically not aware of their background assumptions about numbers and operations (Fischbein, 1987; Vamvakoussi & Vosniadou, 2010). It is well documented that merely exposing students to situations that are not consistent with their background assumptions is not effective (Merenluoto & Lehtinen, 2004). For example, an intervention based on a refutational text was successful enough to reduce the NNB errors but did not manage to fully address the effects of NNB (Christou & Prokopou, 2020). Hinting towards the correct answer (e.g., advising students to think of any type of number they know, as we did in this study) is also not enough. Indeed, raising students’ awareness requires substantial support for them to externalize their beliefs, compare them with their peers’, acknowledge changes in their thinking, and, in a more general fashion, to reflect on their reasoning (for a similar suggestion, albeit from a different perspective, see Tzur, 2019). Tasks inconsistent with students’ assumed beliefs, such as the incongruent items in this study, could be used in a systematic and structured way to support students to engage in reflection.

However, assuming that students’ background assumptions about numbers have an intuitive character, in terms of Fischbein (1987) account of intuitions, such interventions should not be expected to address the NNB-based errors that may re-surface at another moment or in another context. A possible teaching approach is to alert students to this possibility and support them to adopt or invent inhibition strategies (Christou, 2015; Dimitrakopoulou & Christou, 2018). One such inhibition strategy is to always think of at least one negative or one positive number smaller than 1 in algebraic contexts (e.g., when drawing function graphs, or working with absolute values and square roots).

Instruction plays of course an important role in the development and sustainability of the NNB (Vamvakoussi et al., 2018). Indeed, instruction typically does not support students to reorganize their conceptualization of numbers and operations, grounded in natural numbers; and to develop a unified view of the set of rational numbers (Kilpatrick et al., 2001; Moss, 2005; Vamvakoussi & Vosniadou, 2010). More attention should be paid to the similarities between natural and non-natural numbers that make them members of the same family, such as that they are measures of quantity (e.g., length on the numbers line); they can be compared in terms of magnitude; and they are subject to the same operations, despite procedural differences. The number line can also be used to support students understand that different representations may actually refer to the same number (i.e., the same point on the number line). The content pertaining to these ideas is already included in current curricula. Unfortunately, it is not exploited adequately by textbooks and in the classroom. Consider, for example, that fractions and decimals are typically presented separately, and conversion from one form to another is treated mainly as a procedure, with little attention to the underlying idea that different representations correspond to the same mathematical object.

Further, students are typically exposed to a very limited range of examples of natural numbers, decimals, and fractions “mixing together,” for example, in the context of algebra (Greer & Verschaffel, 2007). In fact, an analysis of the Greek mathematical textbooks for junior high school showed that the great majority of coefficients in the chapters on equations, inequalities, and functions were natural numbers, and only few non-natural number as the solution of the worked-out examples or the tasks for students (Dimitrakopoulou & Christou, 2018).

Anticipating the NNB problem in the context of multiplication and division entails reconsidering the way these operations are introduced in the first years of instruction. Indeed, multiplication is typically introduced as repeated addition, an inadequate model that cannot be used meaningfully in the context of rational numbers, and underlies the idea that multiplication “makes bigger” (Fischbein et al., 1985). On the other hand, division as partition is prevalent in the early years of instruction, while division as quotition is downplayed (Roche & Clarke, 2013). It has been suggested that introducing multiplication as a scalar factor, and division in terms of both quotition and partition could be beneficiary for students in the long run (Prediger, 2008). Taking a different perspective on the same problem, Izsák and Beckmann (2018) have suggested that the deep connections between measurement and multiplication should be exploited in instruction. Introducing multiplication and division with a view to anticipate later expansions of meaning is worth exploring. Plausible alternatives need, of course, to be empirically validated.