1 Introduction

In this brief report, we present the results of a study in which we empirically tested the hypothesis that educated adults hold intuitions about the effect of arithmetical operations which interfere with their reasoning, even in cases when they provide a correct answer to a task.

The effect of operations changes in the shift from natural to rational numbers. More specifically, whenever two natural numbers are added or multiplied, the outcome is always bigger than the two initial numbers (unless 0 or 1 are involved, respectively). Similarly, when two natural numbers are subtracted or divided, the outcome is smaller than the minuend and the dividend, respectively. Within the rational numbers set, none of the above is necessarily true, as the effect of operations depends on the numbers involved. For instance, 5 + (−3) is smaller than 5, and \( {4} \div \frac{1}{2} \)is bigger than 4.

Several researchers point out the possibility that intuitions along the lines of “multiplication makes bigger” and “division makes smaller” as well as “addition makes bigger” and “subtraction makes smaller” are transferred in the domain of rational numbers (e.g., Moss, 2005; see also Tirosh, Tsamir, & Hershkovitz, 2008). Indirect evidence for this claim can be found in students’ difficulties with multiplicative word-problem solving and posing involving rational numbers (Bell, Swan, & Taylor, 1981; De Corte & Verschaffel, 1996; Fischbein, Deri, Nello, & Marino, 1985; Greer, 1994). For instance, students are found to choose division over multiplication, when they anticipate that the outcome of a word problem should be smaller, such as in the problem “When 1 kg of coffee costs €8.00, how much will 0.75 kg of that same coffee cost?” Students are also found to associate the words “more” and “fewer” with addition and subtraction, respectively (e.g., De Corte, Verschaffel, & Pauwels, 1990; Lewis & Mayer, 1987). There is some evidence that adults make mistakes in line with these intuitions as well (e.g., Graeber, Tirosh, & Glover, 1989), but systematic research about this phenomenon is lacking. Moreover, it remains a question whether adults, when they provide a correct answer, are still affected by these intuitions, but successfully inhibit them before answering. Before describing the details of the concrete study that we have conducted, we elaborate on the theoretical background underlying our experimental approach.

2 Theoretical background

In a seminal paper, Fischbein et al. (1985) conjectured that there are primitive, implicit models of the operations, such as the model of addition as putting together, subtraction as taking away, multiplication as repeated addition, and division as equal sharing. Focusing on multiplication and division, they showed that students’ choice of operations in word problems involving multiplication or division reflects the effect of these tacit, underlying models. Thus students may not accept a non-whole number as a multiplier, because it violates the background assumptions of the model of multiplication as repeated addition. Fischbein et al. made specific predictions about students’ expectations about the numbers involved in operations, some of which have been challenged by subsequent research (e.g., De Corte & Verschaffel, 1996).

For the present discussion, it is important to note that the assumed primitive models are compatible with—and based on—natural number operations, in particular, with the characteristic that their effect (i.e., whether the outcome will be larger or smaller) depends merely on the operation and not on the numbers involved.

Particularly relevant for this paper is that Fischbein et al. (1985) argued that students’ implicit ideas about the effect of operations are intuitive in nature. Fischbein (1987) postulated several distinctive characteristics of intuitive reasoning in mathematics, among which two are of particular interest for the present study. The first is perseverance, that is, intuitions are persistent and continue to influence the individual’s thinking, even after exposure to the relevant formal instruction; the second is immediacy, that is, intuitions lead to a fast response to the problem at hand, faster than responding counter to these intuitions. So far, there is no systematic empirical evidence for these claims with respect to the effect of all four arithmetical operations.

In the search for empirical evidence, inspiration may be found in the theories and methodologies that are developed in the field of cognitive psychology. Recently, several authors (Gillard, Van Dooren, Schaeken, & Verschaffel, 2009a; Leron & Hazzan, 2006) have argued that the distinction between intuitive and analytic reasoning as made within the mathematics education research area—and, in particular, as accounted for by Fischbein (1987)—has very strong parallels with the cognitive–psychological dual-process theory. Moreover, they have indicated that in the field of dual-process theory, more systematic methodologies have been developed that could be of value for providing empirical evidence for the intuitive nature of the reasoning that can be observed in various mathematical tasks. Dual process theorists (e.g., Evans & Over, 1996; Kahneman, 2000) assume that humans have an intuitive/heuristic processing system (S1) and an analytic system (S2). S1 is deemed fast, automatic, associative, and undemanding of working memory capacity, whereas S2 is deemed slow, controlled, deliberate, and effortful. Fast S1 heuristics often lead to correct responses, but in other cases they do not. In these latter cases, either an incorrect response is provided, or S2 needs to intervene and override the initial response. Hence, errors may be attributed to S1’s pervasiveness and speed and S2’s failure to intervene.

The differential processing speed—S1 being faster than S2—is one of the processing claims made within the dual process framework, which serves as a basis to identify whether a response is the result of a heuristic process or of an analytic one. Chronometric data have already been successfully used in several studies to establish the intuitive character of students’ erroneous reasoning in various mathematical tasks, in the tradition of Fischbein’s account of intuition (e.g., Babai, Brecher, Stavy, & Tirosh, 2006; Babai, Levyadun, Stavy, & Tirosh, 2006; Gillard, Van Dooren, Schaeken, & Verschaffel, 2009b). In such studies, one typically compares participants’ responses in terms of accuracy and reaction time between congruent and incongruent items. We illustrate the meaning of these latter terms with an example that will also clarify the use of our research items (which are presented in detail in Section 4.2). In the case of the effect of addition, the assumed intuition would be that “addition makes bigger”. Consider then the statements “1 + 10y is always smaller than 1” and “1 + 10y is always greater than 1”. Mathematically speaking, both are false. However, a response based on the assumed intuition would lead to a correct judgment in the first case (i.e., that the statement is false), but to an incorrect judgment in the second (i.e., that the statement is true). In this sense, the first statement is congruent and the second incongruent (with the assumed intuition).

3 Goals and hypotheses

Our study had two goals. Our first goal was to document that intuitions about the effect of operations are persistent and thus affect educated adults’ response accuracies. The term “educated adults” refers to people who possess a secondary education degree, that is, they have successfully completed at least 12 years of formal math instruction, and thus have in principle the knowledge and skills required to deal with the tasks in question. This goal is in line with Fischbein’s (1987) claim that intuitions are resistant to formal instruction. We hypothesized that such intuitions would indeed still influence educated adults’ reasoning, and therefore predicted that educated adults would give more erroneous responses to incongruent items than to congruent items.

As a second goal, we aimed at further establishing the intuitive nature of the reasoning about the effect of the operations, in particular the characteristic of immediacy (Fischbein, 1987). Based on the assumptions of dual-process theories and previous chronometric studies in this field, we expected that when educated adults provide a correct answer to an incongruent item, this will require more time than providing a correct answer in a congruent item, because the intuitive response has to be inhibited for a correct answer to be given.

4 Method

4.1 Participants

The participants of the study were 127 educated adults, namely students in the Faculty of Psychology and Educational Sciences, Katholieke Universiteit Leuven, Belgium (about 2/3 females between 18 and 28 years old). They participated in the experiment in return for course credit.

4.2 Materials

Participants took part in an experiment about rational number understanding. A first task in this experiment addressed the effect of operations and will be the focus of this brief report. Within this task, there were eight experimental items targeting addition and subtraction, and eight others targeting multiplication and division. The experimental items are presented in Table 1. Each item presented an operation with a known and an unknown quantity and made a statement about the outcome. Participants were asked to judge the correctness of the statement (True/False). Half of the items were congruent (e.g., “1 + 10y is always smaller than 1”); the other half were incongruent (e.g., “5 ÷ x can be bigger than 5”). For half of the congruent and incongruent items, the correct answer was “true” and for the other half, it was “false”. Eight additional items were used as buffers to counter the repeated use of the expressions “always” and “can be” in false and correct statements, respectively. In the buffer items the expression “always” was used in true statements and “can be” in false statements. For instance, “10y + 1 is always greater than 10y” is a true statement.

Table 1 Overview of experimental items by type (addition/subtraction, multiplication/division) and congruency (congruent, incongruent)
Full size table

4.3 Procedure

Participants were tested in groups of about 20 in a computer room, where they each worked individually through the test, which was programmed in E-prime v.1.0. The experiment started with the general explanation that the participants would have to decide about the truth of a series of statements, and specific instructions about the buttons corresponding to the options “true” and “false”. Then the items were presented in random order, preceded by a fixation cross during 300 ms. Items remained on the screen until a participant had entered his/her response, that is, the key indicating “true” or the key indicating “false”. The responses as well as the reaction times were registered.

5 Results

The data were analyzed using the Generalized Estimating Equations module (GEE) in SPSS that accounts for repeated measurements. The analysis of accuracies (a binary outcome) was done using a logistic regression approach. A linear regression approach was used to analyze reaction times. Before doing the linear regressions, outliers that took longer than the group mean reaction time plus and minus 3 SD were removed in order to normalize the distribution of reaction times. In line with our hypothesis that correct responses in incongruent items take longer than in congruent ones, we included only the reaction times for correct responses in our analysis. Congruency of the item (incongruent vs. incongruent) was the factor in the analysis of accuracy and of reaction times.

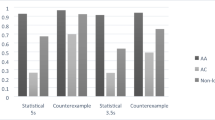
With respect to accuracy, the analysis showed a significant main effect of congruence on addition/subtraction items, Wald chi-square (127, 1) = 75.513, p < .001, and also in multiplication/division items, Wald chi-square (127, 1) = 38.483, p < .001. Table 2 presents the mean accuracy per block, for congruent and incongruent items. Performance was high in congruent items for both blocks, but considerably lower in incongruent items, indicating that participants made judgments in line with the expected intuitions.

Table 2 Mean accuracies per type (addition/subtraction, multiplication/division), for congruent and incongruent items
Full size table

With respect to reaction time for correct responses, the analysis showed a significant main effect of congruence in addition/subtraction items, Wald chi-square (127, 1) = 16.369, p < .001, as well as in multiplication/division items, Wald chi-square (127, 1) = 9.052, p < .01. Table 3 presents the mean reaction time per block, for congruent and incongruent items. In both blocks, correct responses took significantly longer for incongruent as compared to congruent items.

Table 3 Mean reaction time (in millisecond) per type (addition/subtraction, multiplication/division), for correct responses to congruent and incongruent items
Full size table

6 Discussion

In this study, we tested the hypothesis that educated adults, who have been exposed from grade 3 on to systematic instruction about non-natural numbers, are still affected by intuitions about the effect of operations that are valid for natural numbers, but not necessarily so when rational numbers are involved. To this end, we confronted participants with statements about the outcome of operations and measured their accuracy as well as their reaction time for correctly solved items. It is important to note that there were hardly any mistakes on the congruent items, and that accuracy in the incongruent items was rather high as well. This indicates that the tasks were well within the grasp of the participants. Nevertheless, the incongruent items, as predicted, elicited significantly more incorrect responses than the congruent ones, which is an indication that the participants were still affected by the intuitions about the effects of operations.

Moreover, by means of a reaction time method, we were able to show that even when adults provide a correct answer, they are still affected by these intuitions in the sense that they require more time to respond correctly to incongruent items—where the intuitive response has to be inhibited—than to congruent items—where the correct response is in line with the intuitive one. From the perspective of dual-process accounts of reasoning (Evans & Over, 1996; Kahneman, 2000), these findings indicate that, when dealing with these tasks, the response that came to participants’ mind first was the one in line with the assumed intuition, e.g., along the lines of “addition makes bigger”. For incongruent items, correct answers took significantly longer than for congruent items, indicating that participants had to override an initial intuitive response that was not in line with the correct answer.

Fischbein et al. (1985) claimed that there are primitive models of operations, which students are largely unaware of, that continue to impose constraints on their reasoning, even after they have been confronted in instruction with information disconfirming many aspects of these models. Our findings do not provide evidence regarding the specific features of these models—they do not, for instance, tell us if multiplication is conceptualized as repeated addition, or not. They do show, however, that expectations that are related to natural numbers and their “behavior” with respect to operations are difficult to overcome. Moreover, these findings indicate that these expectations have an intuitive basis: They may lead people to erroneous responses; but they may also affect people’s reasoning even in cases when they answer correctly. We acknowledge that it is possible that some participants had adopted a strategy that circumvents the problem of predicting the effect of the operations. More specifically, participants could substitute specific numbers for the variable and see what the outcome is. In that case, our assumption would be that natural numbers would come to their mind first as possible placeholders for the variable. This would lead to an incorrect answer in the incongruent items, unless they asked themselves what would happen if they tried a non-natural number (e.g., a negative number, or a positive number smaller than one). In other words, adopting this strategy would involve again an intuitive response stemming from S1 (the intuitive/heuristic system), and thus S2 (the analytic system) should intervene for the initial response to be inhibited. This particular strategy is also related to the more general, underlying issue of the prominence of natural-number-based reasoning that has, we claim, a strong intuitive character. However, further research, in particular with qualitative methods, is necessary in order to clarify how individual participants reach a decision with respect to the particular tasks, and—if they substitute numbers for the placeholders—what types of numbers they are inclined to use (e.g., natural numbers, negative whole numbers, and positive and negative fractions).

Fischbein (1987) conjectured that some intuitions are never extinguished, that they survive instruction, and that they may coexist with scientific accounts throughout a person’s life. Further research could test various aspects of rational number reasoning and the influence that natural number-based prior knowledge may have in this. Research could also compare between various ages and levels of expertise, such as secondary students, educated adults, and expert adults, such as mathematics graduates. It would be particularly interesting to see whether this latter group of experts is still affected by these intuitions. Qualitative data coming from individual interviews could shed some light on the successful individual’s strategies when dealing with counter-intuitive tasks, with a view to inform instruction. In this direction, we suggest that our study points to the importance of metacognitive training as a means of dealing with the effect of intuitions in mathematical reasoning. More specifically, we suggest that instruction that (a) takes into consideration that students hold intuitive ideas about various mathematical topics, (b) raises students’ awareness about the discrepancy between their intuitive ideas and the mathematically correct perspective, and (c) trains students to adopt a “stop and think” strategy with respect to such “risky” mathematical topics, has the potential to facilitate students to engage in analytical reasoning. These suggestions are in line with Fischbein’s (1990) plea for “developing ‘alarm devices’ which would stop the student from reacting automatically” (p. 47). A possible way to facilitate the development of such metacognitive skills is to ask students to contrast between various responses to counter-intuitive mathematical tasks and judge whether they are based on rational and mathematically sound analysis of the situation (for supporting evidence for this claim, see Amsel et al., 2008).

Finally, we note that the dual-process framework offers more methodological tools than we have taken advantage of in this study (Gillard et al., 2009a). These include restricting solution time, and increasing working memory load by means of a secondary task. Both measures are assumed to hinder the function of S2 (i.e., the analytic system) and are thus expected to result in an increase of errors in the incongruent items, but not in congruent items. Such measures could be used to further establish the intuitive nature of students’ reasoning in counter-intuitive mathematical tasks, such as the ones we used in the present study.

Another interesting question from a dual-process perspective is whether the individuals are aware of the conflict between their intuitions and the valid mathematical knowledge (Gillard et al., 2009b; De Neys, Moyens, & Vansteenwegen, 2010). Depending on the answer, there could be different explanations regarding errors. More specifically, errors could be explained to result from failure to detect the conflict, or from failure to discard the initial, compelling intuition. In this respect, quantitative data on people’s self-assessment of certitude of correctness, or qualitative data based on in-depth individual interviews could be useful. One could also expect individual differences in the way people deal with conflict (see, for example, Merenluoto & Lehtinen, 2004, for a theoretical model of the dynamics among the cognitive and motivational factors in dealing with conflict that predicts that there are people with low tolerance of ambiguity who may spot the conflict, but avoid dealing with it, returning to their initial response). Methods coming from neuroscientific research could also be valuable. For instance, De Neys, Moyens, and Vansteenwegen (2010) recently argued that basic measures of electrodermal activation can be used as biological indexes of conflict detection in reasoning. They monitored their participants’ skin conductance while they solved reasoning tasks that were either consistent with intuition, or not. As expected, they found increased skin conductance in the latter, which indicates that people had a sense of conflict while solving the counter-intuitive reasoning tasks. Such methods can be employed to address the issue of conflict detection in counter-intuitive mathematical tasks.