Embracing pivotal teaching moments: elementary teachers’ role in advancing high cognitive levels of mathematics discourse

Abstract

The study of pivotal teaching moments (PTMs) offers significant insights into mathematics classroom interactions. PTMs are student-generated instances within a lesson that provide opportunities for teachers to modify planned instruction (Stockero & Van Zoest, 2013). Given the importance of interactions and discourse in students’ mathematical growth and understanding, we examine them in the context of PTM episode triples. PTM episode triples consist of three main elements: (1) a PTM, (2) a teacher response to the PTM, and (3) the immediately ensuing student utterance. Analysis of data from nine elementary mathematics lessons shows that teacher responses that explicitly “pursued students’ thinking” elicited significantly higher cognitive levels of student discourse than teachers who "ignored or dismissed" PTMs or simply "acknowledged [PTMs] but continued as planned." While many researchers have focused on PTM episode “doubles” (combinations of student-generated interruptions and the teacher’s response), no studies to our knowledge have addressed PTM episode “triples” as we have. Implications of these findings prove helpful for identifying concrete ways that educators can increase the cognitive level of student discourse within their classrooms. Further, our integration and modification of existing theory and frameworks for analyzing PTM episode triples—incorporating the relationship between PTMs and teachers’ responses to them, on the one hand, and the cognitive level of the ensuing student utterance, on the other hand—are a unique contribution to the field and provide a method by which researchers and educators can study classroom practice.

Introduction

Teaching is a profession where uncertainty is an inherent certainty (Campbell, 2007). Educators constantly face unforeseen scenarios in their classrooms where students raise questions, make connections, or give answers outside those reasonably anticipated by the teacher. Such instances require teachers to act swiftly and make decisions that balance “a variety of interests that need to be satisfied” (Lampert, 1985, p. 190). A pivotal teaching moment (PTM) is an “instance in a classroom lesson in which a[] [student-generated] interruption in the flow of the lesson provides the teacher an opportunity to modify instruction in order to extend or change the nature of students' mathematical understanding” (p. 127). That is, a PTM is an utterance, authored by a student, that provides an opportunity to modify instruction and which if pursued by the teacher could further support student understanding (Stockero & Van Zoest, 2013).

In this study, we analyze a convenience sample of nine video-recorded third and fourth grade teachers’ self-selected lessons to answer the following research question: What is the relationship (if any) between the teacher response to PTMs and the cognitive level of student discourse of the student utterance elicited by the response, and/or the PTM type which prompted the response? By building on and extending past work (e.g., Stockero & Van Zoest, 2013; Weaver et al., 2005), to give us a framework for analyses to fill an identified research gap, we demonstrate that it is possible to code and analyze these types of classroom interactions. Further, our findings suggest that there are indeed such relationships that can be described. For instance, a dominant teacher response type in our data led to high cognitive levels of discourse of the ensuing student utterance. This finding is confirmatory empirical evidence of what may be only a previously assumed hypothesis (e.g., Chi et al., 1994). Interestingly, we find that the only PTMs ignored or dismissed by teachers in our study involved incorrect or contradictory statements by students.

Pivotal teaching moments and cognitive levels of discourse

PTMs are rooted in the concept of contingent situations in the mathematics classroom (Rowland et al., 2005). In addition to necessary content and curricular knowledge, “teaching also involves attending to students’ questions, anticipating some difficulties and dealing with unexpected ones, taking advantage of opportunities, making connections, and extending students’ horizons beyond the immediate tasks. In short, teaching involves dealing with unpredictable, contingent events in the classroom” (Rowland & Zazkis, 2013, p. 138). Stockero and Van Zoest (2013) define a PTM as an utterance authored by a student that provides an opportunity to modify instruction which if pursued by the teacher could further support student understanding.

Pivotal teaching moments

The notion of a PTM is derived from research on teacher noticing (e.g., van Es & Sherin, 2008) and the fourth element of Rowland et al. (2005) teacher knowledge quartet, known as the contingency. The contingency is “a teacher’s recognition of the value in students’ unexpected ideas and their ability to deviate from the planned lesson, when appropriate, in response to these ideas” (Stockero & Van Zoest, 2013, p. 127). Though it is a student utterance that is the PTM, the student utterance may or may not be a noticeable deviation from the planned instruction, but in some way provides a moment where the instructional plan could “pivot” and further develop student thinking. For example, Stockero and Van Zoest (2013) described a teacher who was explaining that slope and intercept of a linear equation can be found from the graph. A student reply asking if it was possible to have more than one y-intercept is a PTM. This particular student utterance provided an opportunity for the teacher to modify instruction. The student “pivoted” the lesson from a procedural focus—identifying slope and intercept on a graph—to conceptual—questioning the possibility of multiple y-intercepts.

Pivotal teaching moment episodes

One common classroom verbal interaction structure is a teacher initiation → student response → teacher feedback or evaluation sequence. In such interactions in mathematics classrooms, the teacher-initiated probe or prompt is often seeking a simple arithmetic computation or a “remember” or recall-type answer (Bloom et al., 1956), and the teacher is anticipating the responses. These types of student utterances might be characterized as having a low level of cognitive demand (e.g., Weaver et al., 2005). “The teacher, by evaluating what students say, assumes the right to control the talk. Also, as initiator of the sequence, the teacher maintains the right to call on students and allocate turns, in essence organizing and orchestrating the discussions” (Greenleaf & Freedman, 1993, p. 466). Though further discussion is beyond the scope of this paper, much research and work have been done to understand this classroom structure (e.g., Cazden, 1988; Mehan, 1979; Sinclair & Coulthard, 1975), especially in efforts to build teachers' capacity to initiate student responses that require high cognitive demand (e.g., Weaver et al., 2005).

PTMs create a somewhat inverted interaction structure. That is, our conceptualization of PTM episode triples follows a student initiation → teacher response → student response sequence. Recall, PTMs are unique from other interactions in the classroom in that they can “pivot” the planned lesson and they are not reasonably anticipated by the teacher. This student-generated “interruption in the flow of the lesson provides the teacher an opportunity to modify instruction in order to extend or change the nature of students' mathematical understanding” (Stockero & Van Zoest, 2013, p.127). One “modification” or impact of interest is the opportunity to support students’ use of high cognitive levels of discourse.

Mathematical thinking and discourse

While the relationship is not yet clearly articulated or agreed upon in the field, some researchers suggest that student engagement explaining mathematical thinking supports mathematical achievement (e.g., Stein & Lane, 1996). Cognitive processes, like thinking, reasoning, and problem-solving skills (Henningsen & Stein, 1997), are observed through students’ language. One measure of students’ mathematical thinking is through the cognitive levels of their discourse, that is, the levels of thinking or comprehension that students display through their speech. Higher cognitive levels of student discourse can be thought of as higher quality mathematical utterances, say of “justifying” or “generalizing” natures (levels 8 and 9, Weaver et al., 2005). These types of responses are in contrast to “lower quality” utterances, like those that give just a short (e.g., “recall”) answer to a direct question from the teacher or another student (levels 1 and 2, Weaver et al., 2005).

Student mathematical discourse, defined in our study as “the act of [students] articulating mathematical ideas or procedures” (Weaver et al., 2005, p. 3), has been identified as a key element in students’ cognitive development (e.g., Forman, 1996; Lampert & Cobb, 2003; Yackel et al., 1991). It is language on which the processes of teaching and learning mathematics depend. “Abstract mathematical ideas are brought into being through classroom talk or writing” (Barwell, 2008). The important role of discourse in students’ mathematical growth and understanding is reflected in standards and curricula generated from all over the world (e.g., Australian Curriculum, Assessment and Reporting Authority, 2015; National Council of Teachers of Mathematics, 2000, 2013; National Curriculum of England, 2014; National Governors Association Center and Council of Chief State School Officers, 2010).

Potential impact of teacher response to a PTM on student learning, discourse

Stockero and Van Zoest (2013) opined that PTMs to which the teacher responds “inactively” lack significant potential to impact student learning. Inactive responses lack any active pursuit of the PTM. They may be intentional or unintentional ignoring of the PTM (the latter when a teacher does not recognize or notice the PTM) or an explicit disregard of the PTM. “Active” responses are “productive” in that they have potential to positively impact student learning. “These [teacher response] decisions provide a starting point for helping to learn to use student thinking in ways that support the development of students’ mathematical understanding” (Stockero & Van Zoest, 2013, p. 144). Active responses may extend students’ mathematical thinking or emphasize the meaning of mathematics, for example.

In their exploratory study of PTMs and beginning secondary teachers, Stockero and Van Zoest (2013) found that the teacher response “decision to extend or make connections was the one most likely to have a positive impact on learning ([which they anticipated might do so] 83% of the time in [their] study), regardless of the PTM type that the decision was in response to” (p. 142). Stockero and Van Zoest (2013) “hypothesized that the decision-making process involved with PTMs may be more obvious with [beginning teachers] than with skilled teachers” (p. 129). Sun and Hanna (2013) applied Stockero and Van Zoest’s (2013) framework with professionally produced videos of secondary mathematics teachers with at least 5-year experience and found that PTMs could both be found and categorized with the existing framework. Sun and Hanna (2013) showed that while “skilled teachers may recognize a PTM and make the decision to act so quickly and smoothly that the interruption would not be easily observable by someone who was not intricately familiar with the teacher’s plan for the lesson” (Stockero & Van Zoest, 2013, p. 129), and thus coding for PTMs may be more difficult, it is indeed possible. Yet, their application did not account for anticipated or actual impact of the teacher response. Additional applications of Stockero and Van Zoest’s (2013) PTM and teacher response framework have been carried out (e.g., teaching with technology) (e.g., Cayton et al., 2017; Coskun et al., 2021; Hollebrands et al., 2013; Shaughnessy et al., 2020); yet, none examined actual impact on student discourse as we propose.

Study purpose

Understanding the relationship between teacher responses to PTMs and the resulting cognitive levels of student discourse uncovers particular combinations of interactions that encourage higher levels of mathematics discourse. That is, this study uncovers what cognitive levels of discourse students used to respond in the third element of the PTM episode triple, given the particular teacher response to PTMs and/or the PTM type. Such knowledge aids school mathematics teacher pedagogy: through such analysis, teachers would know how their actions affect conversations in the classroom and how to intentionally foster the goal of higher cognitive levels of discourse. “Continued research on Pivotal Teaching Moments is warranted as long as mathematics teacher educators are concerned with developing teachers’ abilities to take advantage of ‘teachable moments’ in the classroom” (Sun & Hanna, 2013, p. 1031).

Conceptual and theoretical framework

To move from anticipated impact of particular PTM episode doubles and consider actual impact—here, on the cognitive level of the ensuing student utterance—we marry a modification of Weaver et al. (2005) framework, for characterizing cognitive levels of discourse, with Stockero and Van Zoest’s (2013) framework for characterizing PTMs and teacher responses. This study is centered on the relationships between a teacher response to a PTM and the cognitive level of student discourse of the student utterance elicited by the response, and/or the PTM type which prompted the response—as connectors between the individual and collective properties of classroom mathematical discourse (that is, two paired relationships, between PTM episode triple elements 1 and 2 and elements 2 and 3). Stockero and Van Zoest’s (2013) framework allows us to distinguish basic types of student and teacher actions at the utterance level. Our modified Weaver et al. (2005) protocol is used to document the quality of students’ mathematical discourse based on the level of thinking displayed in specific types of remarks.

Pivotal teaching moments and teacher responses to PTMs: Stockero and Van Zoest (2013)

Pivotal teaching moment identification and types

Stockero and Van Zoest (2013) have defined five types of PTMs. In the example (Stockero & Van Zoest, 2013) from the classroom where a teacher was explaining that slope and intercept of a linear equation can be found from the graph, an Extending-type PTM was made by a student who asked if it was possible to have more than one y-intercept. Extending PTMs are a student comment or question that, while related to the mathematics at hand, deepens the content being addressed. Incorrect Mathematics-type PTMs are student utterances of incorrect mathematical thinking or a solution which may interfere with students’ mathematical understanding. Mathematical Contradiction differs from Incorrect Mathematics in that the initial student utterance provides an opposing answer in some way. This opposing answer may, or may not, be mathematically incorrect. We tease out the sometimes subtle differences of these two categories in our Results section. While Sense Making-type PTMs occur when students seek clarification of mathematical concepts, Mathematical Confusion PTM types are those utterances that make a lack of understanding of a specific mathematical process explicit.

Teacher response types

A teacher’s response to a PTM is categorized in one of five ways: (1) Acknowledges, but Continues as Planned, (2) Emphasizes Meaning of the Mathematics, (3) Extends Mathematics and/or Makes Connections, (4) Ignores or Dismisses, and (5) Pursues Student Thinking. Recall the example previously presented from Stockero and Van Zoest (2013). When the student asked if it was possible to have more than one y-intercept, the teacher could have “made a connection” by responding with a prompt to consider the definition of a function. The teacher might use the Pursues Student Thinking-type response by asking probing questions or use the Emphasizes Meaning of the Mathematics-type response by highlighting mathematical definitions or procedures. An Extends Mathematics and/or Makes Connections-type teacher response may “go beyond the topic that students are working on in the lesson to revisit and make connections to past learning or to foreshadow or lay a foundation for future learning” (Stockero & Van Zoest, 2013, p. 138).

An Ignores or Dismisses situation arises when the teacher does not address the student-initiated PTM at all, though the teacher may instead use the Acknowledges, but Continues as Planned type response, recognizing the student utterance explicitly but choosing not to address it further. This may sound like a “thank you”- or “interesting!”-type response from the teacher, or even a “we aren’t going to talk about that at this time”-type response. The PTM, when answered with these inactive (Stockero & Van Zoest, 2013) responses—Acknowledges, but Continues as Planned or Ignores or Dismisses—is not pursued. Only in the former teacher response type is the PTM utterance directly acknowledged. A code of “Acknowledges, but Continues as Planned” does not make a judgment from such a perspective that the teacher’s instructional plans were known and that there was no derivation. Simply, the code points to the lack of any active pursuit of the PTM. Table 1 is a list of each of the five PTM types and teacher response types, with a description and example; see Stockero and Van Zoest (2013, 2014) for additional examples.

Table 1 PTM and teacher response types, descriptions and examples,

Student responses, discourse in PTM episode triples

While particular PTM episode doubles (the PTM and teacher response) can be used to anticipate likely impact on student learning, as Stockero and Van Zoest (2013) have done, this is also a limitation of their model for our purposes. Recall, our particular interest in the current study is to continue to trace the PTM episode through the third element, assessing the quality of the discourse via the immediately ensuing student utterance.

Discourse is both individual and collective—it is constituted of utterances made by individuals, but can also be considered as a whole, as a connected body of responses among teacher and students. Each of the three components of a PTM episode triple—the initial student utterance, the teacher’s response, and the ensuing student response—can be examined individually, or in connection to the utterances that precede or follow it, but at the same time fit into a longer conversation which has its own properties. One might consider, for instance, the cognitive level of individual utterances in a conversation, or instead the overall cognitive level of discourse of the entire discussion. At both levels, there are several possible measures to use as indicators.

Analyzing the cognitive level of the student utterance which most closely follows a teacher move, across the span of an entire lesson, provides one measure of the impact of that teacher response on student discourse. The mean cognitive level of all student utterances following the given teacher move and prior to the next teacher move would give another such measure. Both ostensibly allow for analyses of our interaction structure of interest. In order to focus on trends in the relationships among the components of a PTM episode triple, this study uses the properties of individual contributions to discourse as markers which may lead to identifying emergent properties of the collective discourse in the lesson through future study and analyses. Note, in PTM episode triples, the “final” student response (element 3) needs not be made by the same student who initiated the PTM, and in fact, the teacher may not allow for a student response.

Although later student discourse (e.g., beyond PTM episode triple element 3) may be less clearly or reliably causally connected to a preceding teacher move, examining just the ensuing student utterance following a teacher’s response to a PTM may not completely capture the most highly valued response to the teacher’s question or comment. That is, in typical discourse, responses may often require some thought, and three or four children may respond to a teacher’s question or comment, or a 10-min discussion among students may result. Following more sustained discourse threads could capture more complexity, yet it goes beyond the scope and purpose of this study. Further, we note that few, if any, sustained interactions originating with a PTM (that is, interaction chains longer than the PTM episode triple as we envision it) existed in our data corpus.

Cognitive level of a student utterance: Weaver et al. (2005)

Weaver et al. (2005) Classroom Observation Protocol allows for the identification of nine types of mathematical discourse, each given a numerical value, and varying in cognitive levels that range representative of the “continuum of discourse in terms of increasing levels of cognitive demand” (Weaver et al., 2005, p. 3).

At level 1, Answering, a student gives a short answer to a direct question from the teacher or another student. Level 2, Stating or Sharing, occurs when a student makes a simple statement or assertion or shares their work with others and the statement or sharing does not involve an explanation of how or why. Explaining (level 3) is a student utterance that explains a mathematical idea or procedure by stating a description of what the student did or how the student solved a problem, but without providing any justification of the validity of the idea or procedure. Level 4 is Questioning—a student-posed question seeking clarification of mathematical idea or procedure.

In contrast to levels 1–4, those of “lower” quality discourse, levels 5–9 are considered “higher” quality discourse (Weaver et al., 2005). Challenging (level 5) is a student statement or question that challenges the validity of a mathematical idea or procedure. The utterance may include a counterexample and requires someone else to reevaluate the student’s thinking. Relating, level 6, is a student statement indicating a connection or relationship to some prior knowledge or experience, while Predicting or Conjecturing, level 7, is a student utterance that makes a prediction or conjecture based on an understanding of the mathematics behind a problem. For example, a student may recognize a pattern in a sequence of numbers, make a prediction about what might come next in the sequence, or state a hypothesized mathematical property observed in a problem.

At the final two levels are Justifying and Generalizing. Justifying, level 8, is when a student provides justification for the validity of a mathematical idea or procedure by providing an explanation of the thinking that led to the idea or procedure. The justification may be in defense of an idea challenged by the teacher or another student. Generalizing, level 9, is a student utterance that is evidence of a shift from a specific example to the general case.

Level 0 or no response

In addition to the nine levels of discourse outlined by Weaver et al. (2005) previously discussed, we found an outcome in discourse records not addressed by the protocol. Our additional level, level 0 or No Response, captures the instances where, for whatever reason, no student responded verbally. In these cases, the PTM episode would only include the PTM type and teacher response type elements without the addition of our code to allow a level 0 for the final element. Weaver et al. (2005) protocol does not include a level 0 because it was developed to analyze student discourse when it occurs, not in response to some other stimulus. Therefore, we adopt our modified version of Weaver et al. (2005) protocol for this study; we consider level 0 to be of lowest quality discourse, since no quality whatsoever can be determined.

“Lower” and “higher” quality discourse, cognitive levels

Answering and Stating or Sharing are of lowest cognitive demand and are thus considered lowest-quality discourse (levels 1 and 2). Justifying and Generalizing (levels 8 and 9) are of highest cognitive demand and are thus considered highest-quality discourse. “The order of the discourse types represents the continuum of discourse in terms of increasing levels of cognitive demand. That is, giving a short right or wrong answer to a direct question represents the lowest level of cognitive demand and justifying mathematical ideas and procedures and making generalizations represent the highest levels” (Weaver et al., 2005, p. 3).

Interrelating existing frameworks for analyzing PTM episode triples

Individually, our modified Weaver et al. (2005) and the Stockero and Van Zoest (2013) frameworks provide lenses through which to examine isolated elements of PTM episodes. However, a PTM, teacher response, and immediately ensuing student utterance level of discourse are interrelated in complex mathematics classroom interactions. We contend a teacher’s response to a PTM shapes the type of student utterance that follows. Thus, we combine the Stockero and Van Zoest (2013), and the modified Weaver et al. (2005) structures in order to identify trends in teacher actions and student discourse and help isolate the effects of particular teacher moves. The simultaneous use of these two frameworks offers the potential to uncover discourse-based connections which educators could leverage. While the trends identified in this study are limited to the specific lessons studied, as well as potentially to instructional context characteristics (e.g., third- and fourth-grade, teacher self-selected or designed lessons on a given topic), even in this limited scope, the relationships observed can be important descriptors of the tie between the individual and collective facets of classroom mathematical discourse.

Figure 1 illustrates our interrelated use of Stockero and van Zoest’s (2013) framework and our modified Weaver et al. (2005) framework for analyzing PTM episode triples. Element 1 is the PTM, with five possible categories, element 2 is the teacher response, also with five possible categories, and element 3 is the student response, with 10 total cognitive level of discourse categories.

Fig. 1

Illustration of PTM episode triple elements, frameworks for analyses

Methodology

This project deals with the descriptive analysis of discourse from a convenience sample of nine third and fourth grade mathematics lessons, which were videorecorded at public elementary schools in large urban and suburban school districts in the state of Texas. The lessons were self-selected and taught by certified elementary school mathematics teachers, all of whom had at least 4 years of teaching experience (range 4–28, median 12) and held mathematics instructional leadership positions on their campuses. Further, each teacher was enrolled in a multi-year professional development program on mathematics education and discourse moderation during the time that the lessons were recorded. Teachers used their own videos, including those in this study, to analyze various aspects of their classroom practice. The teachers neither learned about nor analyzed their videos for PTMs, and the teachers’ analyses are not considered in the present study. The second author was the professional developer.

The teachers were tasked to submit videos representative of their teaching practices from lessons of multiplication and division content. We note that some draw from multiplication and division content but also emphasize fractional understanding, the result of division (e.g., lessons D and G, see Appendix 1). We include all submitted lessons in analyses; the content and nature of the lessons may impact the interactions and thus the PTM episode triples. Yet, given the infancy of the work we propose, the content and teaching methodology are not yet considered as a mediator or moderator. We discuss this further in the Discussion section. Each lesson had a duration of 15:03 to 53:44 min (median 31.38 min) and was transcribed for analyses.

Analysis

Our analysis followed a seven-phase process. Phases 1–3 are guided by the work of Stockero and Van Zoest (2013), a process operationalized by others (e.g., Cayton et al., 2017; Hollebrands et al., 2013; Sun & Hanna, 2013).

Phase 1: PTM identification

The first and second author identified PTMs within each lesson, watching each of the nine videos in this study and reading their transcripts to identify PTMs. Decontextualized utterances, similar to the examples provided in Table 1 and the illustrations presented in the Results section, are especially difficult to understand as PTMs (and particular types of PTMs or teacher responses). Context allows for easier and more accurate coding. We had access to the teachers’ entire class transcript and the classroom video and supplemental documentation (e.g., lesson plan) and therefore a robust and contextualized data corpus. Each PTM identified represents the first element in a PTM episode triple. PTMs were identified regardless of whether a teacher followed up the initial student utterance (e.g., when students made mathematical comments that were incorrect, did not relate to the topic under discussion, or expressed a need to clarify mathematical concepts). That is, a teacher’s decision not to respond to a PTM utterance from a student, perhaps because s/he did not notice it, did not preclude the PTM from analyses.

Specifically, and guided by the work of Stockero and Van Zoest (2013), “the [first and second] authors marked on the transcripts the points in the dialogue at which PTMs occurred” (p. 131) using the definition: a student utterance that in some way provides a moment where the instructional plan could “pivot” and further develop student thinking. Those researchers coded the data corpus for PTMs independently to improve reliability; the process revealed more than 82% inter-rater reliability. Discrepancies (of which there were 15 total; less than 18% of the 84 PTMs found) were resolved through discussion using “a collaborative process of analyzing and discussing the results,” as Stockero and Van Zoest (2013, p. 131) suggest. This choice to “team code” (Miles et al., 2014), where “two researchers code the same data set and discuss their initial difficulties” (p. 84), was used intentionally to increase reliability.

Phase 2: PTM categorization

In phase 2 (again, using team coding, Miles et al., 2014), each identified PTM (phase 1, element 1 in the PTM episode triple) was coded independently by both the first and second authors with one of the following tags: (Mathematical) Confusion, (Mathematical) Contradiction, Extending, Incorrect (Mathematics), or Sense Making. Discrepancies in coding were found for 19 instances (less than 23%), for resolution, phase 5.

Phase 3: teacher response categorization

Each teacher response to the PTMs (element 2 in the PTM episode triple) was coded, using the same researcher process as outlined in phase 2, into the following categories: ACP (Acknowledges, but Continues as Planned), EMM (Emphasizes Meaning of the Mathematics), EM/MC (Extends Mathematics and/or Makes Connections), I/D ( Ignores or Dismisses), or PST (Pursues Student Thinking). Eighteen (about 21%) discrepancies had to be resolved.

Phase 4: student response categorization

In phase 4, each of the student responses (element 3 in the PTM episode triple) were coded using our modified Weaver et al. (2005) framework of ten cognitive levels of discourse. Codes were assigned independently by the first and second authors (i.e., team coding, Miles et al., 2014), revealing 11 (about 13%) discrepancies to be resolved.

Phase 5: coding comparison, discrepancy resolution, and final codes

Codes from phases 2–4 were compared across researchers (revealing the discrepancies, rates for each phase reported previously). On average, across phases 2–4, about 19% of all coding revealed discrepancies. In phase 5, a codebook was generated (following the recommendations of MacQueen et al, 1998) with the codes, descriptions of each, and data-based examples, which was operationalized for discussing and resolving discrepancies in coding. Final coding of all three PTM episode elements was thus established.

Phase 6: descriptive analysis

Using the final coding (phase 5), relationships between a PTM type and the type of response the teacher makes and between the teacher’s response and the immediately ensuing student utterance, were represented in data displays (see Miles et al., 2014) and described. Further, data from the corpus was identified as exemplar of particular findings, and anomalies or unique findings were addressed.

Phase 7: additional, statistical analysis

In addition to a descriptive analysis, we further examined the relationship between teacher responses to PTMs and the cognitive levels of student discourse of the immediately ensuing student utterances through statistical tools. When treating the Weaver et al. (2005) protocol as a ranking of discourse, the nonparametric Kruskal-Wallis test was used to test for differences between the mean cognitive levels of student discourse (PTM episode triple element 3) among teacher response types (PTM episode triple element 2) (not to be confused with teachers or a test for differences between the mean cognitive levels of student discourse among classes).

Following the Kruskal-Wallis test, Dunn’s test was employed to pinpoint which differences between two types’ mean discourse levels are statistically significant. Details of the Kruskal-Wallis and Dunn’s analyses can be found in Appendix 2. The authors also chose to investigate the effect of treating the discourse in the Weaver et al. (2005) protocol as numerical data and used the one-way ANOVA and Tukey-Kramer test which are appropriate for analyzing such data. In Weaver et al. (2005) initial work, their levels were not intended to be treated numerically, only categorically, but we chose to do so because of the indication of higher levels for discourse. This is essentially a first approximation to a ranking, though we know the levels might not be equidistant. We find that cognitive level of discourse can be treated as numerical or categorical and the results are the same (see next section), so there is essentially no issue treating as numerical.

A note on analyses of relationships between PTM episode triple elements

At this time, and under various constraints of the work (e.g., size of corpus), we would not be able to confidently find accumulation points in a three-way analysis between the PTM episode triple elements. However, this is work that we would like to do, and we believe that our findings (see Results) of the two-way analyses (between teacher responses to PTMs and the cognitive levels of student discourse of the student utterances elicited by the response, and/or the PTM types which prompt the response) warrant continued work to analyze triples. Thus, our work here focuses on linking PTM episode triple Elements 1 and 2 and Elements 2 and 3, as explained by our research question.

Results

PTM episodes

A total of 84 PTMs (and therefore PTM episode triples) were identified from the nine videos. The different numbers of PTMs present within each lesson may also affect our data. It was calculated that PTM occurrences in each lesson ranged from 1.36 to 9.75 PTMs per 15 min. The particular combinations of PTMs, teacher response types, and student discourse levels of immediately ensuing student utterances that occurred within the data set are illustrated in Table 2. For instance, there were 6 total Confusion-type PTMs; 2 of those were followed by the teacher response type ACP, and in both of those cases, the student cognitive level of discourse in the immediately ensuing response was level 1.

Table 2 Number of different combinations of PTMs, teacher response types, and cognitive levels of student discourse responses

PTM and teacher response combinations

Incorrect mathematics-type PTMs

The overwhelming majority (77%) of the PTMs involved some sort of mathematical error or contradiction made by students (Incorrect or Contradiction). The most commonly observed type was Incorrect; about 40% (34 of 84) of the PTMs were of this type. Teacher responses to Incorrect-type PTMs were somewhat evenly spread among I/D (24%), ACP (21%), EMM (26%), and PST (29%).

A teacher response of EMM to an Incorrect-type PTM is illustrated in the excerpt from lesson E (described in Appendix 1) as shown below:

T: “Our system of numbers is based on ten. What are the ten digits that we use to make up every number in…that we can possibly come up with? What are the ten digits?”

S: “Ones, tens, hundreds…”

T: “Those are places. Those are places. Digits are to numbers like letters are to words.”

The student incorrectly named place values instead of digits. In response to this thinking, the teacher emphasized the meaning of ones, tens, and hundreds by repeatedly saying that those are ‘places,’ then emphasized the meaning of the mathematical term ‘digit’ by making an analogy to letters and words.

Mathematical contradiction-type PTMs

The next most frequent PTM type observed was Contradiction. Approximately 37% (31 of 84) of the PTMs were of this type. Recall, Contradiction-type PTMs can be a specialized form of incorrect mathematics, that is, the contradiction can be made by a student utterance that is an incorrect answer or idea. Of course, not all Incorrect-type PTMs are contradictions and not all Contradiction-type PTMs are incorrect mathematics. The overall majority of teachers’ responses to Contradiction-type PTMs were nearly evenly split between pursuit of student thinking and dismissal: about 45% resulted in a teacher response of PST, 39% resulted in a teacher response of I/D, 10% in EMM, 3% in EM/MC, and 3% in ACP.

Multiple examples of Contradiction-type PTMs were seen in lesson D where students (who are in groups) are asked to share three tortillas equally among eight people and determine what fraction of a tortilla each person would get. In this excerpt, the teacher has come across a group that has figured out how to cut the tortillas evenly:

T: “What did you cut this one [model of a tortilla] into?”

S1: “Eighths.”

S2: “They’re all wholes.”

T: “Why do you call it a whole?”

Here, the teacher’s questioning PST to understand the Contradiction between student 1 and student 2.

Sense making-type PTMs

Following Contradiction type in frequency is the Sense Making-type PTM, constituting about 10% (8 of 84) of the PTMs in this data set. In this category, 63% of the teachers responded by PST and the remaining 37% by ACP.

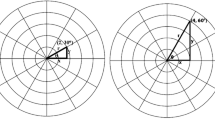
An example of a teacher responding to a Sense Making-type PTM with a PST-type response occurs in lesson G. In this lesson, students are given a model, divided into four unequal pieces and similar to the image in Fig. 2, and asked to decide whether the model represents one-third.

S: “If you look more carefully, you could have just erased the line.” Student refers to the line circled in Fig. 2.

T: Teacher erases the line circled in Fig. 2. “Okay, so what about now? Would that be equal?”

Fig. 2

Lesson G fraction model

Mathematical confusion-type PTMs

About 7% (6 of 84) of the PTMs were Confusion. Most (67%) of the teacher responses to these PTMs were of PST while close to 33% were of ACP.

An example of a Confusion-type PTM followed by PST response is seen in lesson D. Prior to the excerpt below, one student divided each of the three tortillas models into eighths in order to share them equally among eight people. This student claimed that each person would get three tortillas pieces (eighths) but another student did not understand why:

S: “But how would all of them get three because it would be like three, six, and nine. I can’t go by threes to get to eight.”

T: “Why are you counting by threes to get to eight?”

Through the teacher’s question following this Confusion, one can see that she seeks to understand what prompted the student to count by threes.

Extending-type PTMs

Lastly, the Extending-type PTM consisted of about 6% of the data. Within this category, 80% of teacher responses were PST while 20% were EM/MC. All Extending-type PTMs garnered active teacher responses.

An example of a teacher EM/MC in response to an Extending-type PTM is in lesson H. Students were learning the relationship between multiplying by two and doubling. The teacher calls out asking students to tell the “doubles.” In the midst of this, the following utterances are made:

S: “I just need to learn my seven’s.”

T: “When you’re multiplying by seven what are you doing?”

The comment that the student made certainly dealt with multiplication but went beyond what was being taught at the moment (multiplication by 2). For context, the student connected doubling to multiplication and beyond, thinking about multiplying by 3’s and 4’s and so forth, and was noting that he would not be able to carry out multiplication or repeated addition of 7’s and would “just need to learn [their] seven’s” to be able to do so. The question that the teacher asked in response to the PTM utterance shows her desire to know what concept the student relates with multiplication by 7, which we have explained.

In summary, our analyses show that teacher responses of I/D and EMM only followed instances of Incorrect or Contradiction-type PTMs, with a majority of the EMM responses following Incorrect-type PTMs. ACP responses occurred after all PTM types except for Extending. However, just over 50% of ACP followed Incorrect-type PTMs. Lastly, PST was well distributed across all PTM types, whereas EM/MC (which only happened a total of two times in the data corpus) occurred after Contradiction- or Extending-type PTMs.

Teacher response and following student utterance discourse level combinations

The frequency of student discourse type associated with each teacher response is shown in Fig. 3.

Fig. 3

Teacher response and associated student discourse

Level 1 discourse

Most of the I/D, ACP, and EMM teacher responses led to discourse of level 1. An example of an ACP response which led to discourse of level 1 is in lesson C. In this lesson, students were representing multiplication using arrays and highlighted the fact that they could represent 6 × 7 two different ways because they would yield the same amount.

T: “What property is that?”

S1: “Identity.”

T: “Not the identity…”

S2: “The product.”

In this example, the teacher acknowledges the incorrect mathematics of this PTM, saying “Not the identity…” However, by simply acknowledging that the response is not correct, students were led to continue answering.

Pursues student thinking-type teacher responses

An interesting shift in the pattern of these data emerged with the teacher response of PST. With this response type, there was a similar amount of discourse of cognitive level 8 (30%) and level 1 (32%). An example of a PST teacher response which resulted in discourse of level 8 can be seen in the continuation of a previous example from lesson D:

T: “What did you cut this one (model of a tortilla) into?”

S1: “Eighths.”

S2: “They’re all wholes.” (model shows each whole divided into eighths).

T: “Why do you call it a whole?”

S2: “Because it’s (the piece of tortilla which actually represents one-eighth) one of these (student is referring to a whole tortilla) but into pieces.”

As a result of the teacher PST response, the student gave a justification of why he believes his piece is a whole. Although this justification is mathematically imprecise, we consider it a justification because of the student’s intent. Through the video, it is clear that the student is trying to articulate the distinction between whole items and group sizes.

It was also with the PST teacher response type that we see occurrence of student cognitive level 0, meaning that after an instance where a teacher PST students did not further respond.

Teacher ignores or dismisses-type response and student discourse level 8

Worthy of note is that the sole instance of I/D leading to high-level student discourse (level 8) came from the teacher not intervening when students offered contradictory answers about what part of a fraction a tortilla piece represented.

Some students: “One fourth.”

Other students: “One third.”

Some students: “One fourth.”

Other students: “One third.” [they argue back and forth like this for 15 s]

S1: “It’s one third because there are three pieces.”

The teacher’s inactive response resulted in one of the students offering a justification for his answer in an attempt to convince others. This example occurred in lesson D, the lesson with by far the highest frequency of PTMs (0.65 per minute, more than twice that in all but one of the other lessons), which also included 7 of the 11 instances in which PST-type teacher response led to student justifications. This teacher frequently asked her students “why?” questions; justification was clearly one of the class norms.

Variations of teacher response types across lessons

A representative indicator of the variations across lessons is given in Table 3, which shows percentages of teacher response types observed in each lesson. Collectively, the teacher response types in the data show a trend of 44% PST, 24% I/D, 15% ACP, 14% EMM, and 2% EM/MC. Although two thirds of the data in Table 3 fall within about 10 percentage points of these means, certain teachers diverged significantly from this trend within their lessons. Examples include teacher A whose lesson showed 50% I/D, teacher E whose lesson showed 54% ACP, teacher H whose lesson showed 29% EMM response, and teacher I who displayed 66% PST. In addition, more than half of the teachers observed overwhelmingly (more than 50% of the time) used one specific type of response to PTMs. Teachers B, D, F, and I favored PST while teacher E favored ACP.

Table 3 Percentage of teacher response types by lesson

Statistical analysis

By treating the cognitive levels of discourse (Weaver et al., 2005) as ordinal rankings, the Kruskal-Wallis and Dunn’s method were used to test for differences in the cognitive level of student discourse in the third element of PTM triples among the five teacher responses to PTMs. The results of the Kruskal-Wallis test showed a chi-squared value of 12.746 and a p value of about 0.01. Therefore, we conclude the following: the difference in the mean rank of the cognitive level of student discourse in an utterance followed from each teacher response to a PTM is statistically significant. The unadjusted p values in Dunn’s test, as depicted in Table 4, show that a difference in cognitive level of discourse of a student response is seen between two pairs of teacher responses: (1) PST and I/D and (2) PST and ACP (an adjusted p value of 0.07 does not recognize the latter difference as statistically significant). The results of the unadjusted p values in Dunn’s test are identical to the one-way ANOVA and Tukey-Kramer test results obtained when treating the discourse levels as numerical data. Regardless of whether the discourse levels were considered as ordinal or numerical data, the Kruskal-Wallis and ANOVA test both showed that the cognitive levels of student discourse differed significantly across the five teacher response types.

Table 4 Dunn’s test results

Summary

Our results indicate that lower-quality discourse (levels 1–4 and 0) occurred after all teacher response types; however, teachers successfully elicited higher-quality discourse (levels 5–9) mostly after PST responses, with one instance each of higher-quality discourse after EMM and I/D. Although every PTM type showed at least one instance in which a teacher response led to higher-quality discourse, the majority—and the only category with more than one or two instances—followed a Contradiction-type PTM, and in most cases, a PST teacher response. It is important to note that although all PTM and teacher response types found in Stockero and Van Zoest’s (2013) study were found in this study, not all discourse level types were observed. Students were not found to display discourse levels 6, 7, or 9; this is consistent with results of Weaver et al. (2005).

Discussion

Relationship between elements of the PTM episode triple

We found a concentration of certain types of PTMs, teacher responses, and the immediately ensuing student utterance cognitive levels of discourse, thus confirming the relevance of the relationships identified in the results to the vast majority of PTM episodes analyzed. Most of the PTMs were Contradiction or Incorrect types, and many teacher responses involved either PST or I/D.

Dominant teacher response types

Although PST and I/D were the two most common teacher response types, their results were drastically different. The inactive response (Stockero & Van Zoest, 2013) of I/D typically led to the lowest cognitive level of student discourse in student responses (levels 1–2 and 0), while the active response of PST led to more justification (Level 8) than any other cognitive level of discourse. Furthermore, 81% of the student response discourse in the lessons was in the range of levels 0–4.

The results that were found hint to a possible connection between dominant PTM (accounting for 50% or more of the PTMs within the lesson) and teacher response types. Recall, in lessons A, C, E, H, and I, the dominant PTM type was that of Incorrect while in lessons D, F, and G, it was Contradiction. Although the leading PTM types within these lessons differed, in general the dominant teacher response (across all PTM types) was that of PST. Although every PTM type led at least once to a PST response, only Incorrect and Contradiction-type (the two types that may involve a mathematical error, accounting for 77% of observed PTMs) ever led to an I/D response. In fact, for most (6 out of 9) teachers in the study, I/D was, if not the most common response to an Incorrect or Contradiction-type PTM, within 1 PTM of being the most common (including ties). This suggests that in lessons where most PTMs involved some kind of mathematical error, those teachers tended, in general, to use PST as a dominant move (across all PTM types), but the responses of all teachers to error-related PTMs tended to be more hit-or-miss (either PST or I/D) than responses to other PTM types.

Empirical evidence for impact of pursues student thinking teacher response type

Teacher response type PST was a dominant response regardless of PTM types and led to the highest cognitive levels of discourse in the ensuing student utterance. Dunn’s test and the Tukey-Kramer test indicate a significant difference in the cognitive level of student discourse between the I/D versus PST and ACP versus PST responses (the adjusted p value for the latter comparison may limit the statistical significance of the difference). This reveals that when teachers pursued student thinking, they were more successful at eliciting higher cognitive level responses from students than when they ignored or merely acknowledged PTMs.

Limitations, accounting for variances in the data

Certain aspects of this study limit the extent to which we can generalize its results. For one, the small sample size keeps us from concluding that the concentrations of PTMs, teacher responses to PTMs, and the immediately ensuing student utterance’s cognitive level noted in this paper are indicative of the atmosphere in third and fourth grade mathematics classrooms. In order to bolster confidence in our results, there is a need to analyze more mathematics lessons from those specific grade levels (and on other topics). Secondly, the group of teachers observed in this study may also have affected the results that were found. This is because PTMs/responses are difficult to detect in the lessons of highly experienced teachers (Stockero & Van Zoest, 2013), and we may consider that many, if not all, of the teachers in this study are experienced. Minimally, they are committed, as they all were both active in a three to four-year professional development and held mathematics instructional leadership positions on their campuses. Thus, not all of the PTMs and responses that were present in each lesson may have been accounted for in the data. In addition, instances where teachers did not respond to a PTM were not discussed afterward with the teachers, to determine whether they recognized and deliberately I/D the PTM or simply failed to notice it (although in either case it would be classified as I/D).

The unequal distribution of PTMs and teacher response types within each lesson may limit our understanding of how teacher responses to PTMs could generally affect student discourse, and specifically the cognitive level of the ensuing student utterance, in elementary school classrooms. Also note, PTMs and teacher responses in this study were labeled using the Stockero and Van Zoest (2013) framework. However, since the framework was created in the context of high school classrooms and used primarily in secondary classroom contexts previously (e.g., Cayton et al., 2017; Hollebrands et al., 2013; Sun & Hanna, 2013), its use may serve as a potential limitation of this research project. However, recall that there were no PTMs or teacher response utterances in the data that could not be categorized with Stockero and Van Zoest’s (2013) framework. Therefore, we have demonstrated an application of this framework to elementary classrooms.

Variations in the data may also bear on generalizability, namely the content of the lessons. Given that the nature of tasks may vary quite significantly from day to day, the limitation to single lessons could rather restrict the range of PTMs likely to occur. It is quite possible that specific interaction patterns may have been different in different parts of a teaching sequence. In addition, as noted in developing our framework for analysis, we focused our analysis of teacher impact through the immediately ensuing student utterance, rather than on patterns in any extended student discourse that may have followed.

Connections to literature

Some results of this study resemble those of projects previously discussed. For instance, the prevalence of lower-quality discourse in the third and fourth grade classrooms aligns with the findings of Weaver et al. (2005), which also found a high proportion of discourse recorded in elementary classrooms to be of lower-quality (Weaver et al., 2005). Another conspicuous similarity that our research had with Weaver et al. (2005) was the lack of two specific discourse types: Predicting or Conjecturing (level 7) and Generalizing (level 9). While Weaver et al. (2005) observed that middle and high school students displayed these discourse types (even if only in a small number), students in elementary schools did not. The fact that this finding is confirmed in our results, while perhaps unsurprising, is of concern. If “conceptual understanding is critically important to begin developing in primary grades” (Georgius, 2014, p. 48), this phenomenon must be addressed. Further research which looks closely into what may be hindering these specific discourse types could identify what combination of instruction, curriculum, and cognitive development is keeping children from reaching these discourse levels.

The fact that PST appears in this study to be the most successful teacher response type in eliciting higher-quality discourse from students is supported by teaching practices such as Smith and Stein’s (2011) 5 Practices for Orchestrating Productive Mathematics Discussions. At their core, the five practices—anticipating likely student responses to cognitively demanding mathematical tasks, monitoring students’ responses to tasks, selecting particular students to present mathematical responses, sequencing student responses, and making connections between student responses—require educators to build on students’ mathematical ideas and show PST utterances as a foundation for providing students with the opportunity to discuss mathematics at high levels.

Conclusion

We demonstrate that it is possible to code and analyze PTM episode triple classroom interactions and element relationships, thus filling a gap in terms of tracing interactions and discourse by building on and extending past work to give us a framework to do just that. Overall, this project provides a distinctive view of PTMs, one that shows them as intricately woven with teacher responses and immediately ensuing student utterance discourse into the very fabric of a lesson. Teacher actions are the vital link between PTMs and the types of student responses displayed in the classroom. As depicted in this work, inactive teacher responses to PTMs can be detrimental to the quality of discourse present in elementary mathematics classrooms. To help students discuss mathematics more deeply, educators must draw on students’ original mathematical ideas through the act of pursuing student thinking.

We also envision this study to serve as the basis of a resource for future researchers investigating effective responses to PTMs and could be used in teacher professional development. For example, teacher professional development could include teachers’ collection of their teaching videos, which could be analyzed using the framework we provide here, to identify particular interactions in their own classrooms. That is, this study frames a way for teachers to see their own practice through the PTM lens to better understand the effects of their own instructional decisions. “By examining teaching practice through the lens of PTMs, pre-service and inservice teachers can learn to recognize and act on these moments with their own students, with the aim of increasing their abilities to positively impact students’ academic achievement” (Sun & Hanna, 2013, p. 1031). Although some limitations exist within this study, one thing remains clear: the role that a teacher plays in the face of PTMs should never be underestimated. Teacher actions hold consequences for student thinking and can be used to steer the nature of student discourse within individual classrooms.

Appendices

Appendix 1. Lesson descriptions

In Lesson A, third grade students (n = 19), in groups, model measurement division of 15 by 3 using manipulatives, to solve the following problem: Joel makes fifteen pancakes for his friends. He wants to serve three pancakes on each plate; how many plates will Joel need? Before solving, students are challenged to decide what type of division (measurement or partitive) the problem represents. In lesson B, third grade students (n = 22) skip count by 2s or 5s to multiply. The students, in groups, discuss the following using paper and markers: What are different ways you can find out how many legs are in a group of nine chickens? What are some different ways you can find out how many fingers will there be in seven mittens?

The fourth grade students (n = 4) in lesson C use counters to practice single digit multiplication. The fourth grade class in lesson D explores how to model partitive division of 3 by 8 through the use of tortillas as a visual model and contextualized through the prompt: “What fraction of a tortilla each person would get if eight people share three tortillas? In lesson E, fourth grade students (n = 22) use array and area models to multiply double digit numbers. In lesson F, a fourth grade (n = 17) whole class discussion considers the following problem: How much less would each friend pay if six friends shared the cost of a $36 item instead of four?

The objective in lesson G is to identify parts of a whole. Here, fourth grade students (n = 19) draw a model of fractions and discuss whether or not the model represents the given fraction. Fourth grade students (n = 6) in lesson H use counters to make a connection between multiplication and addition as they learn to multiply by 2. And in lesson I, fourth graders (n = 16) play a game in pairs to practice double by single digit multiplication. The students must manipulate digit cards to see who can get the largest product.

Appendix 2. Kruskal-Wallis and Dunn’s test description

The Kruskal-Wallis test is a rank-based test used to investigate whether significant differences exist between different groups of an independent variable on a continuous or ordinal dependent variable (Montgomery, 2013). In our case, the different types of teacher responses were the set of independent variables and the cognitive level of student discourse was the dependent variable. The null hypothesis for this test was that the mean ranks for all conditions being tested were equal.

Performing the Kruskal-Wallis test on our data began with a ranking of all discourse levels observed in the student response portion of the PTM episodes. These discourse levels were then replaced with their ranks and a test statistic was generated using the sum of the ranks in each teacher response group, the total number of observations, and the variance of the ranks (Montgomery, 2013). The Kruskal-Wallis test was performed using R programming language.

Following the Kruskal-Wallis test, we used Dunn’s test to further analyze the data. Dunn’s test examines all possible two-way comparisons within a set of data using rank sums in order to pinpoint which particular groups are statistically different. This test generates unadjusted and adjusted p values. Due to the increased risk of type I errors, errors of falsely rejecting a null hypothesis, that are possible when doing multiple comparisons, some researchers base their discovery of statistical significance using the adjusted p values. These adjusted values, however, may increase the likelihood of type II errors, errors associated with falsely accepting a null hypothesis. Since there is currently no consensus as to which p value should be used in drawing final conclusions from Dunn’s test, researchers must be careful of how they interpret the results of this test (Feise, 2002). In our study, Dunn’s test was performed in R programming language with p values adjusted using the Benjamini-Hochberg adjustment (Benjamini & Hochberg, 1995).