1 Introduction

Ultra-low interest rates and increased longevity have put retirement schemes and pension plans under pressure worldwide. In parallel, adequate elderly financial planning is a concern in aging societies. Recently in Europe, the EIOPA has finalized the PEPP regulation, “Pan-European Pension Plan” intending to increase consumer choices in elective pension plans—which are crucially lacking in some member states. Pensions are also gradually shifting from defined benefit (DB) to defined contribution (DC)—along with an increasing trend to move occupational pension to collective defined contribution (CDC) schemes.

In this context, longevity risk-sharing mechanisms are gaining traction in the retirement industry. “Tontine-like” schemes are being launched by pension institutions and insurance companies across the world—with some precursors located in Australia and already existing in various forms in France (Le Conservateur), US (CREF), Canada (VPLAs), and Japan.

For its members, modern tontines can offer longevity protection at a lower cost with increased flexibility. Individual Lifetime income solutions are generally limited and expensive. For instance, traditional life annuities and QLACFootnote 1 are impacted by low rates and longevity, while Variable Annuities such as GLIBsFootnote 2 are mainly distributed in US and are extremely expensive. Some non-lifetime decumulation schemes are flourishing in the Asset management industry—but generally do not protect the consumer against longevity. Decumulation—“the nastiest, hardest problem in finance”Footnote 3—indeed…

For administrators, the risk-sharing nature of the scheme leads to lower exposure to longevity trends and market risk. This translates into low capital requirements under risk-based capital requirements such as Solvency 2. With technology, one can envision that such schemes will require a low administrative burden and will in turn allow financial institutions to scale decumulation solutions and better address the needs of retirees with increased capacity.

Used primarily for fundraising purposes since the seventeenth century, some prejudice persists against tontines which are still associated with their controversial past and can be infamously referred to in popular cultureFootnote 4 as a morbid lottery among subscribers. “The winner takes it all” is more fiction than reality and it is probably more embezzlement, bankruptcy and abusive clauses that led to their demise in the early twentieth century as shown by [8, 9].

The regulatory framework for tontines is restricted—though not forbidden as commonly believed. In Australia and South Africa, some participating annuities and longevity pooling schemes have features equivalent to tontines. In France, the “Code des Assurances” stipulates special conditions to form tontines associations—Le Conservateur being an example—founded in 1844 and still present today in a niche, high net-worth, and trending market. In the US, the CREF from TIAA is still in force while Canada is discussing the re-introduction of VPLAs, “Variable Payment Life Annuities”—a scheme introduced by University of British Columbia (UBC). Also, “Tontine Trust” is an InsurTech that plans to bring a form of P2P tontines to the consumers.

Pooling longevity risk among insured is a common theme in pension research. Piggott et al. [12] proposed the Grouped Self Annuitization or Pooled Annuity fund. Goldsticker [7] discussed the possibility to use mutual funds to distribute Annuity like benefits. Stamos [19] further analyzed the Pooled Annuity Funds. Rotemberg [15] described a Continuously Liquidating Tontine (or Mutual Inheritance Fund) as an alternative for immediate annuities.

Open-ended tontine funds with an allocation mechanism based on all member demographics are proposed by [16, 17]. Qiao and Sherris [14] further developed the GSP—Grouped Self Pooled funds, while [2] studied the Actuarial Fairness and Solidarity in Pooled Annuity Funds. [10, 11] proposed further optimization to income tontines.

Forman and Sabin [13,14,5] have been also active in the study of Tontine Pensions and Survivors Funds, while [22] provided an overview of such schemes named “Modern Tontines”. More recently [1] proposed the “Tonuity”, an annuity and tontine hybrid.

2 Modern tontines approach

In this section, we revisit the ITA—Individual Tontine Account—a concept defined by [6]. The reason for selecting this formulation is that it is one of the most practical oriented with an acceptable bias of “actuarial fairness” for a large population.

The Modern Tontine is a generalization of a tontine—with a heterogenous population, an open subscription mechanism, variable account units and flexible outgoes scheme (selected at issue). Once subscribed, there is no withdrawal and proceedings are to be paid upon survival following the schedule selected at onboarding. As a standard annuity or tontine, there are no benefits paid upon death, and the proceedings of deceased members are to be allocated among the members still alive.

2.1 Term, payouts and contribution schedule

2.1.1 Contribution scheme

Since the Modern Tontine can be subscribed at any start of period,Footnote 5 the contribution scheme can be flexible: single, regular, and flexible payments. However, new money is subscribed at current existing conditions.

A particularity for regular contributions can be elaborated: as discussed below, a selection factor is proposed to be applied on the first 5–10 years for each new payment done (namely, it will reduce the Tontine Share amount to avoid the Term Dilemma effect and reverse moral hazard). We believe that this selection could be lifted for regular premium contributions, provided there is no payment lapse. This should create a fidelity advantage for the members who commit and maintain fixed contributions during the accumulation period.

2.1.2 Payout scheme

Similarly, the payout scheme is fully customizable: lump sum, life annuity, temporary annuity, or a hybrid of these—with various weights. The mathematics below will consider a “flow intensity” to apprehend this flexibility.

Practically, the “payout intensity” allows designs with increasing payouts for inflation and/or lump sum payments at some arbitrary dates.

2.2 Reversion or joint survival features

Common features in retirement schemes are the reversion benefit or joint survival life annuity.

A reversionary pension provides a reduced pension payout for the second life in case the first life death precedes the second, while the benefits are unchanged if the second life death happens before the first.

A joint survival annuity pays a given scheme while both lives are alive (the “joint life” status), and switches to another scheme when one life deceases—generally with lower payouts (common commercial proposed ratios range from 50 to 75%).

A generalization of the mathematical framework to encompass such options is proposed below.

2.3 Fund investment and allocation

2.3.1 Flexible allocation

The fund allocation itself is also customizable—where a typical unit-linked mechanism could allow full flexibility for the members to manage and plan their allocation as per their preferences. As shown experimentally by [6] the fund return volatility of individual members has only a second-order impact on the individual performances of the Tontine—provided that the fund size is large enough.

2.3.2 Other advanced features

Like 401 k funds or standard Asset Management services, the investment platform can provide additional services such as a wide fund selection, predefined investment strategies such as lifestyle re-allocation, automatic arbitrage, portfolio replication, robot-advisor to name a few.

2.4 Mechanism & actuarial fairness

2.4.1 Longevity credits

In a similar fashion to a standard Tontine, the Account Value of deceased members are re-allocated to survivors—the “longevity credits”. In theory, actuarial fairness is maximized using a continuous time frame where proceedings are immediately allocated upon death. This approach is currently unrealistic in practice, and most schemes use a yearly time-period to check survival and allocate proceedings.

2.4.2 Intuition

The cornerstone of the model is the allocation key to assign longevity credits to the survival population at each time step. This allocation key is based on the mortality probabilities of each member for the assessed period, weighed by the projected account value. This value is referred to below as the “Expected Survival Gain” for the whole member horizon or the “Tontine Share” for the specific period where the allocation is made.

Mathematically, this “Tontine Share” can be derived by ensuring that the “Expected Gain” is null. For a given member with a death probability \(q\) and an Account value \(AV\), the “Expected Gain” can be expressed as follow:

$$E\left[Gain\right]=0$$
$${Loss}_{Death}+{Gain}_{Surv}=0$$
$$-qAV+TontShare\left(1-q\right)=0$$
$$TontShare=\frac{q}{\left(1-q\right)}AV$$

The resulting formula is familiar: the \(\frac{q}{\left(1-q\right)}\) factor is the one found in the stepwise change in a recursive annuity reserve calculation (net of discount factor impact).

It is also notable that this amount is independent of the other member’s statuses. In theory, to be fully exact, the longevity credits depend on the whole pool demographics. However, as shown below, the bias induced can be negligible provided the fund is large enough and the Tontine Shares are sufficiently homogeneous.

2.4.3 Actuarial fairness

  • Age/Gender and other characteristics are supposedly embedded in the mortality table assumptions. The table selection challenges are apprehended in the Discussion section.

  • Different horizon and payment terms are embedded in the prospective view, the Tontine Share defined at a time step level and the allocation of mortality gains only up to the maximum common period of the considered cash flows.

  • The variation of Account Value among members is also reflected in the Tontine Share calculation. It is to be noted that large outliers will impact the volatility of longevity credits and thus reduce mutualization.

  • The Pool can welcome new entrants at the beginning of every recalculation period. An interpolation/generalization could be introduced for entrants in the middle—but this is not explored in this paper.

  • The personalized asset allocation results in different account value paths. The frequent recalculation of Tontine Share allows reflecting the impact of volatile results on the Tontine Share at each period start.

2.5 With bequest alternative

From a commercial perspective, offering only non-redeemable options without any benefit in case of death is a key limiting factor. Though not explored in this article, it is to be noted that it is technically possible to (1) bundle the Modern Tontine with a standard investment platform or (2) include death benefit insurance to protect heirs.

When the Modern Tontine is bundled with a standard investment account, the members retain the flexibility of top-ups and withdrawals along with the balance returned to the beneficiary in case of death. This fund could use the same fund management infrastructure—but, from an actuarial fairness perspective, this fund cannot benefit from the Modern Tontine additional longevity returns.

Some schemes also propose death benefit insurance inside the schemes. Technically, this option is meaningful for members only if the term insurance rate is lower than the expected longevity credits. However, in countries where the estate tax gap is large between a standard investment and an insured death benefit, this option could be beneficial in terms of tax optimization for the members compared to 1st option.

2.6 Value proposition: summary

Tables 1 and 2.

Table 1 Pros and cons of modern tontines from consumer and carrier perspective
Full size table
Table 2 Features comparison—modern tontine vs standard fund
Full size table

3 Mathematical framework: single period

3.1 Single time period framework

We denote:

  1. (1)

    Members participating in the tontine are noted n ϵ [0, N], index \(i\)

  2. (2)

    The timeFootnote 6 step considered is noted tc ϵ [0, ∞]

  3. (3)

    The attained age of member \(n\) at \({t}_{c}\) is noted \({x}_{n}\). Follows:

    1. (a)

      The survival probability at age \(t+{x}_{n}\): \({{}_{t}{}p}_{{x}_{n}}\).

    2. (b)

      The death probability at age \({x}_{n}\): \({q}_{{x}_{n}}\).

    3. (c)

      The death period in which the member die is noted \({T}_{n}\):

      1. (i)

        The indicator for the event “member survives”:1{Tn > tc}.

      2. (ii)

        The indicator for the event “member deceases”:1{Tn = tc}.

  4. (4)

    Account Value for member n at time \(t\):

    1. (a)

      “Beginning of period” \({AV}_{bop }^{t,n}\) (includes contribution).

    2. (b)

      “Middle of period” \({AV}_{mop }^{t, n}\) (includes financial return, before redemption from deceased members and longevity credit allocation).

    3. (c)

      “End of period” \({AV}_{eop }^{t,n}\) (after longevity credit allocation).

    For simplification, we will drop the time index in the single period calculation.

  5. (5)

    For this section, contribution {Ct}t ϵ [0, ∞] and benefits {Bt}t ϵ [0, ∞] are not required since we will focus solely on longevity credit allocation which is based on Account value accumulated on the period. Contribution and benefits will be introduced in 4.1.

  6. (6)

    Key tontine indicators for member \(n\) at time \({t}_{c}\):

    1. (a)

      Tontine Redeem amount is the forfeited account value for deceased members: \({R}_{{t}_{c}}^{n}\). The total accumulated redeem amount is noted \({R}_{{t}_{c}}^{\Sigma }\).

    2. (b)

      Tontine Share is the allocation key used to assign the longevity credits: \({S}_{{t}_{c}}^{n}\).

    3. (c)

      Longevity Credits are the redeemed amount allocated to survivors: \({L}_{{t}_{c}}^{n}\).

3.2 Longevity credits mechanism

Based on the above definition, the redeem amountFootnote 7 at time \({t}_{c}\) for member \(n\) is equal to the account value of deceased members:

$${R}_{{t}_{c}}^{n}={AV}_{mop }^{ {t}_{c},n} {1}_{\left\{{T}_{n}={t}_{c}\right\}}.$$

The tontine scheme redeem amount at time \({t}_{c}\) can be expressed as the sum of the account values of deceased members during the period:

$$R_{{t_{c} }}^{\sum } = \sum\limits_{{n \in \left[ {0,\,N} \right]}} {R_{{t_{c} }}^{n} } = \sum\limits_{{n \in \left[ {0,\,N} \right]}} {AV_{mop}^{{t_{c} ,\,n}} 1_{{\left\{ {T_{n} = T_{c} } \right\}}} }.$$

The Tontine Share for member \(n\) is the Fair Expected Survival Gain based on the member account value (after financial return) \({AV}_{mop }^{n}\):

$${{S}_{ {t}_{c} }^{n}}=\left(\frac{{q}_{{x}_{n}}}{1-{q}_{{x}_{n}}}\right){AV}_{mop }^{{t}_{c}, n}.$$

The Longevity Returns \({L}_{{t}_{c}}^{n}\) are expressed as the total redeem amount \({R}_{{t}_{c}}^{\Sigma }\) on the period \({t}_{c}\), allocated to survived members using the tontine share \({{S}_{ {t}_{c} }^{n}}\) as an allocation key:

$$\forall n\,{\text{where}}\left\{ {T_{n} > t_{c} } \right\}\quad L_{{t_{c} }}^{n} = R_{{t_{c} }}^{\sum } \frac{{S_{{t_{c} }}^{n} }}{{\sum\nolimits_{{i \in \left[ {0,\,N} \right]}} {S_{{t_{c} }}^{n} \;1_{{\left\{ {T_{n} > t_{c} } \right\}}} } }}.$$

To recoup with the notation defined in [6], we can define the “Group Gain” as:

$$\forall n\,{\text{where}}\left\{ {T_{n} > t_{c} } \right\}\quad G_{{t_{c} }} = \frac{{R_{{t_{c} }}^{\sum } }}{{\sum\nolimits_{{n \in \left[ {0,\,N} \right]}} {S_{{t_{c} }}^{n} \;1_{{\left\{ {T_{n} > t_{c} } \right\}}} } }}$$

and ensure:

$$\forall n\, {\text{where}} \left\{{T}_{n}>{t}_{c}\right\} {L}_{{t}_{c}}^{n}={S}_{ {t}_{c} }^{n}{\text{G}}_{{t}_{c}}.$$

3.3 Actuarial fairness and bias analysis

3.3.1 Consistency check

Thanks to the Tontine Share construction, it is easy to prove that the Expected Value of the total redeemed amounts on the period \({R}_{{t}_{c}}^{\Sigma }\) is equal to the Expected Value of all the tontine shares for survivors:

$$E\left[ {\sum\limits_{{n \in \left[ {0,\,N} \right]}} {S_{{t_{c} }}^{n} \;1_{{\left\{ {T_{n} > t_{c} } \right\}}} } } \right] = E\left[ {R_{{t_{c} }}^{\sum } } \right].$$

By noting:

$$E\left[ {R_{{t_{c} }}^{\sum } } \right] = E\left[ {\sum\limits_{{n \in \left[ {0,\,N} \right]}} {AV_{mop}^{{t_{c} ,n}} \;1_{{\left\{ {T_{n} = t_{c} } \right\}}} } } \right]$$

and developing the first term:

$$E\left[ {\sum\limits_{{n \in \left[ {0,\,N} \right]}} {S_{{t_{c} }}^{n} \;1_{{\left\{ {T_{n} > t_{c} } \right\}}} } } \right] = \sum\limits_{{n \in \left[ {0,\,N} \right]}} {\left( {1 - q_{{x_{n} }} } \right)} S_{{t_{c} }}^{n} =$$
$$\begin{gathered} \sum\limits_{{n \in \left[ {0,\,N} \right]}} {\left[ {\left( {1 - q_{{x_{n} }} } \right)\left( {\frac{{q_{{x_{n} }} }}{{1 - q_{{x_{n} }} }}} \right)AV_{mop}^{{t_{c} ,n}} } \right]} = \sum\limits_{{n \in \left[ {0,\,N} \right]}} {q_{{x_{n} }} AV_{mop}^{{t_{c} ,n}} } \hfill \\ = E\left[ {\sum\limits_{{n \in \left[ {0,\,N} \right]}} {AV_{mop}^{{t_{c} ,n}} \;1_{{\left\{ {T_{n} = t_{c} } \right\}}} } } \right] \hfill \\ \end{gathered}$$

we get the equality.Footnote 8 This is however not enough to prove that the allocation model works.

3.3.2 Model actuarial fairness: intuition

Having the allocation model work is equivalent to show that the longevity credits expected value are in line to the longevity credits for each individual member. In practice, this is not the case, as shown and discussed by [2, 18].

This bias exists since the total longevity credit of a given period depends on the individual member status (alive or not), creating a bias in the group gain.

A simple way to grasp the intuition is to create a fictive pool with 2 profiles:

  1. (1)

    A single member with a large Account Value and an extremely high death probability

  2. (2)

    Other members (5000) with relatively low Account Value and low death probabilities (Table 3)

Table 3 Illustration of Bias existing in an extremely non-homogenous population—assumptions
Full size table

With above calculation, the 1st member tontine share is \(\frac{5\%}{1-5\%}\times \text{500,000}=\text{26,316}\) while profile 2 members tontine share are \(\frac{0.2\%}{1-0.2\%}\times 1000=2.00\)

Let’s assume that the unique member with the 1st profile survives, while the 2nd profile members have a survival experience consistent with assumption, the pool becomes (Table 4).

Table 4 Illustration of Bias existing in an extremely non-homogenous population—results
Full size table

For the member with 1st profile, the allocated longevity credits in case of survival are much lower than the tontine share, despite having a mortality experience in line with assumption for the remaining members of the pool. The member theoretical longevity credits are thus very different from the actual longevity credits: (1–5%) × 26,316 = 25,000 versus 7242 × (1–5%) = 6880.26.

This example shows that the 1st member has a very low chance of getting Longevity Credits in line with his/her tontine share. On the other hand, profile 2 members can expect a large longevity credit allocation in the eventuality member 1 passes away. As shown below, this deviation is mainly due to the heterogeneity of the tontine share distribution.

3.3.3 Model actuarial fairness: bounds

The actuarial fairness of the scheme has been extensively studied in [18]. The difficulty of the characterization resides in the intercorrelation of the expected tontine return of an individual with other participants in the tontine. Intuitively, one can expect this dependence to reduce once the pool size increases—however—an exact analytical characterization depends on each member and is thus too complex. However, [18] proposed a lower bound result for the mean tontine return:

$$\forall n \in \left[ {0,\,N} \right]\quad E\left[ {L_{{t_{c} }}^{n} 1_{{\left\{ {T_{n} > t_{c} } \right\}}} } \right] \ge S_{{t_{c} }}^{n} \frac{{\left( {1 - \frac{{q_{{x_{n} }} AV_{mop}^{{t_{c} ,n}} }}{{\sum_{i} q_{{x_{i} }} AV_{mop}^{{t_{c} ,i}} }}} \right)}}{{\left( {1 + \frac{{q_{{x_{n} }} S_{{t_{c} }}^{n} }}{{\sum_{i} q_{{x_{i} }} AV_{mop}^{{t_{c} ,i}} }}} \right)}},$$

which can also be expressed as:

$$\forall n \in \left[ {0,\,N} \right]\quad E\left[ {L_{{t_{c} }}^{n} 1_{{\left\{ {T_{n} > t_{c} } \right\}}} } \right] \ge S_{{t_{c} }}^{n} \frac{{\left( {1 - q_{{x_{n} }} } \right)}}{{\left( {1 - q_{{x_{n} }} + \frac{{q_{{x_{n} }} AV_{mop}^{{t_{c} ,n}} }}{{\sum_{i \ne n} q_{{x_{i} }} AV_{mop}^{{t_{c} ,i}} }}} \right)}},$$
$$\forall n \in \left[ {0,\,N} \right]\quad E\left[ {L_{{t_{c} }}^{n} 1_{{\left\{ {T_{n} > t_{c} } \right\}}} } \right] \ge S_{{t_{c} }}^{n} \frac{{\sum_{i \ne n} q_{{x_{i} }} AV_{mop}^{{t_{c} ,i}} }}{{S_{{t_{c} }}^{n} + \sum_{i \ne n} q_{{x_{i} }} AV_{mop}^{{t_{c} ,i}} }}.$$

The demonstration is detailed in [18] and notably uses the Jensen inequality to un-meddle the expected value of a product of correlated variable (at the expense of losing the equality).

3.3.4 Individual bias error

Re-using above notations, we can define the error bias asFootnote 9

$${error}_{n}=1-\frac{E\left[{L}_{ {t}_{c}}^{ n} {1}_{\left\{{T}_{n}>{t}_{c}\right\}}\right]}{{S}_{{t}_{c}}^{n}}.$$

This bias represents the “loss” compared to the expected mean. It can be further written as:

$${error}_{n}=1-\frac{E\left[{L}_{ {t}_{c}}^{ n}{1}_{\left\{{T}_{n}>{t}_{c}\right\}}\right]}{{S}_{{t}_{c}}^{n}}\le 1-\frac{\left(1-{q}_{{x}_{n}}\right)}{1-{q}_{{x}_{n}}+{\frac{{q}_{{x}_{n}}{AV}_{mop }^{{t}_{c},n}}{\sum_{i\ne n}{{q}_{{x}_{i}}AV}_{mop }^{{t}_{c},i}}}}$$

or:

$${error}_{n}\le 1-\frac{\sum_{i\ne n}{q}_{{x}_{i}}{AV}_{mop }^{{t}_{c},i}}{{S}_{{t}_{c}}^{n}+\sum_{i\ne n}{q}_{{x}_{i}}{AV}_{mop }^{{t}_{c},i}}$$

and:

$${error}_{n}\le \frac{{S}_{{t}_{c}}^{n}}{{S}_{{t}_{c}}^{n}+\sum_{i\ne n}{{q}_{{x}_{i}}AV}_{mop }^{{t}_{c},i}}.$$

It is to be noted that the error bias tends towards 0 when N is large: \(\underset{N\to \infty }{\text{lim}}{{error}_{n}}\le 0,\)

which experimentally shows that the bias is highly linked to the “atomization” of the Tontine Share—or the heterogeneity of the qAV.

3.4 The term dilemma and possible moral hazard

3.4.1 Positive selection factor and moral hazard

The moral hazard in Annuities is a common subject in the actuarial field. Valdez et al. [21] showed that adverse selection can exist in Annuities and GSA (Group Self Annuitization)—although the effect is expected to be less severe in GSA than in traditional annuity. While we do not think it should be an issue for non-voluntary contribution (compulsory retirement funds, proceeds from a term life…)—we believe that there will be a positive selection effect for elective contribution.

3.4.2 The term dilemma: description

The Term dilemma arises from the fact that it is possible to break down a given investment in 2 sub-terms while keeping the same longevity credits. For instance, instead of investing for a lump sum target of 10 years, one could elect to invest in a 5-year term first, then reinvest 5 years later to reach the term of 10 years.

Of course, in the second case, the member would have an option not to follow its investment after the first 5 years (in case of health issues for instance), while the first choice locks the member for 10 years.

This raises an issue in terms of fairness and makes the Modern Tontine workable only if everybody elects to invest in the shortest period available—which is against the essence of the scheme.

4 Mathematical framework: prospective benchmarks

As shown above, the allocation of longevity credit is dependent on a single period only. The mathematic framework for a single period is therefore enough to proceed to the simulation of a tontine scheme.

However, it is useful to develop a prospective approach, especially to:

  1. (1)

    Manage all the possible contribution and decumulation schemes.

  2. (2)

    Introduce dependent lives options such as reversion and joint-life benefits.

  3. (3)

    Assess the outcomes of the modern tontine scheme:

    1. (a)

      Benchmark the overall scheme simulated outcome compared with the “expected” returns seen at member onboarding date.

    2. (b)

      Characterize numerically the long-term impact of the above bias a simulated path.

4.1 Notation

The previous notation will be reused, with the following conventions:

  1. (1)

    Single member Following calculations are done at a single member level, who is considered alive. For lighter notations, the member index n is not present.

  2. (2)

    Like 3.1.6, the Tontine Share for this single member at time \({t}\) is noted \({S}_{t}\).

  3. (3)

    Time period and periodicity for practical purposes, a discrete approach, and yearly stepsFootnote 10 have been selected. It will be noted t ∈ [0, ∞], secondary index \(k\).

  4. (4)

    Contributions {Ct}t ∈ [0, ∞] are assumed to be paid at beginning of the period (bop).

  5. (5)

    Benefits {Bt}t ∈ [0, ∞] are assumed to be paid at end of the period (eop).

  6. (6)

    In practice, this prospective view can be updated at each time step since the actual path of a tontine for a single member depends on realized longevity credits and actual financial returns. This is an interesting feature from a Key Information Disclosure perspective and to enhance members understanding of their account.

  7. (7)

    We introduce the expected financial return for each future time step \({r}_{t}\) and its associated cumulated discounting index (bop):

    $$v_{0} = 1,\quad \forall t \ge 1\,v_{t} = \prod\limits_{k < t} {\left( {1 + r_{k} } \right)}^{ - 1}.$$
  8. (8)

    The payout structure is represented by a “nominal intensity” \({b}_{t}^{*}\) and a “nominal benefit” \({B}_{t}\) derived from classic actuarial equalities (see 4.2). This which allows to tune the decumulation and use flexible schemes:

    $$\left\{ {b_{t}^{*} } \right\}_{{t \in \left[ {0,\,\infty } \right]}} \forall t \ge 0\quad B_{t} = cB\,b_{t}^{*}.$$

For instance, if the member selects inflation protected income deferred 5 years, \(inf\) being the annual revalorization factor, the payouts structure becomes:

$$\left\{ {b_{t}^{*} } \right\}_{{t \in \left[ {0,\,\infty } \right]}} = \left\{ {0,\,0,\,0,\,0,\,0,\,\left( {1 + \inf } \right),\,\left( {1 + \inf } \right)^{2} , \ldots ,\,\left( {1 + \inf } \right)^{t} , \ldots } \right\}_{{_{{t \in \left[ {0,\,\infty } \right]}} }}.$$

4.2 Actuarial flows

The approach is closely related to standard annuities mathematics, and the tontine is then based on the standard actuarial equality:

$$NPV\left(Contributions\right)=NPV\left(Benefits\right),$$

which can be expressed as:

$$\sum_{t\ge 0}{C}_{t}\times {{}_{t}{}p}_{x}{v}_{t}=nB\sum_{t\ge 0}{b}_{t}^{*}\times {{}_{t+1}{}p}_{x}{v}_{t+1}.$$

The nominal benefit is derived:

$$nB=\frac{\sum_{t\ge 0}{C}_{t}\times {{}_{t}{}p}_{x}{v}_{t}}{\sum_{t\ge 0}{b}_{t}^{*}\times {{}_{t+1}{}p}_{x}{v}_{t+1}}.$$

This allows expressing each benefit payment—assuming survival—as:

$${B}_{t}=nB {b}_{t}^{*}.$$

4.3 Account value and tontine share

For each time step, the member projected tontine share is similar as above:

$${S}_{t }=\left(\frac{{q}_{x+t}}{1-{q}_{x+t}}\right){AV}_{mop}^{t}.$$

The member projected Account Value is similar as above with:

  • Starting period AV: \({AV}_{bop}^{0}=0, \forall t\ge 1, { AV}_{bop}^{t}={ AV}_{eop}^{t-1}+{C}_{t}\).

  • Middle period AV: \({AV}_{mop}^{t}={AV}_{bop}^{t}\left(1+{r}_{t}\right)\).

  • End of period AV: \({AV}_{eop}^{t}={AV}_{mop}^{t}+{S}_{t }-{B}_{t}\).

4.4 Non-recursive expression

One can derive non-recursive expressions for expected Account Value, Financial Returns, and Tontine Share, by leveraging actuarial prospective and retrospective equalities. This is useful to optimize runtime via vector-based calculations.

4.4.1 Prospective

$${AV}_{mop}^{t}=\frac{ \sum_{k\ge t}{B}_{k}{\times {}_{k+1}{}^{ }p}_{x}{v}_{k+1}-\sum_{k>t}{C}_{k}\times {{}_{k}{}^{ }p}_{x}{v}_{k}}{{{}_{t}{}^{ }p}_{x}{v}_{t+1}}$$
$${S}_{t }=\frac{\sum_{k\ge t}{B}_{k}{\times {}_{k+1}{}^{ }p}_{x}{v}_{k+1}-\sum_{k>t}{C}_{k}\times {{}_{k}{}^{ }p}_{x}{v}_{k}}{{{}_{t+1}{}^{ }p}_{x}{v}_{t+1}}{q}_{x+t}$$
$${FinReturn}_{t }=\frac{\sum_{k\ge t}{B}_{k}{\times {}_{k+1}{}^{ }p}_{x}{v}_{k+1}-\sum_{k>t}{C}_{k}\times {{}_{k}{}^{ }p}_{x}{v}_{k}}{{{}_{t}{}^{ }p}_{x}{v}_{t+1}}{r}_{t}$$

4.4.2 Retrospective

$$\forall t\ge 1, {AV}_{mop}^{t}=\frac{\sum_{k\le t}{C}_{k}\times {{}_{k}{}^{ }p}_{x}{v}_{k}- \sum_{k<t}{B}_{k}{\times {}_{k+1}{}^{ }p}_{x}{v}_{k+1}}{{{}_{t}{}^{ }p}_{x}{v}_{t+1}}$$
$$\forall t\ge 1, {S}_{t }=\frac{\sum_{k>t}{C}_{k}\times {{}_{k}{}^{ }p}_{x}{v}_{k}- \sum_{k\ge t}{B}_{k}{\times {}_{k+1}{}^{ }p}_{x}{v}_{k+1}}{{{}_{t+1}{}^{ }p}_{x}{v}_{t+1}}{q}_{x+t}$$
$$\forall t\ge 1, {FinReturn}_{t }=\frac{\sum_{k>t}{C}_{k}\times {{}_{k}{}^{ }p}_{x}{v}_{k}- \sum_{k\ge t}{B}_{k}{\times {}_{k+1}{}^{ }p}_{x}{v}_{k+1}}{{{}_{t}{}^{ }p}_{x}{v}_{t+1}}{r}_{t}$$

4.4.3 Demonstration

We will focus on the first equality, the remaining statements being trivial once one is demonstrated.

For \({AV}_{mop}^{0}\), by noting that \(\sum_{k>0}{C}_{k}\times {{}_{k}{}^{ }p}_{x}{v}_{k}= \sum_{k\ge t}{B}_{k}{\times {}_{k+1}{}^{ }p}_{x}{v}_{k+1}-{C}_{0}\), we get:

$${AV}_{mop}^{0}=\frac{{C}_{0}}{1\times {v}_{1}}={C}_{0}\left(1+{r}_{0}\right).$$

Let’s assume the equality valid at \(t\) and prove it at \(t+1\). By definition:

$${AV}_{mop}^{t+1}=\left({C}_{t+1}+{AV}_{mop}^{t}+{S}_{t }-{B}_{t}\right)\left(1+{r}_{t+1}\right),$$
$${AV}_{mop}^{t+1}=\left({{C}_{t+1}+AV}_{mop}^{t}+\left(\frac{{q}_{x+t}}{1-{q}_{x+t}}\right){AV}_{mop}^{t}-{B}_{t}\right)\frac{{v}_{t+1}}{{v}_{t+2}},$$
$${AV}_{mop}^{t+1}=\frac{{{C}_{t+1}\times {}_{t+1}{}^{ }p}_{x}{v}_{t+1}}{{{}_{t+1}{}^{ }p}_{x}{v}_{t+2}}+\left(\frac{{AV}_{mop}^{t}}{1-{q}_{x+t}}-{B}_{t}\right)\frac{{{}_{t+1}{}^{ }p}_{x}{v}_{t+1}}{{{}_{t+1}{}^{ }p}_{x}{v}_{t+2}},$$
$${AV}_{mop}^{t+1}=\frac{{{C}_{t+1}\times {}_{t+1}{}^{ }p}_{x}{v}_{t+1}}{{{}_{t+1}{}^{ }p}_{x}{v}_{t+2}}+\frac{{AV}_{mop}^{t}}{{p}_{x+t}}\frac{{{}_{t+1}{}^{ }p}_{x}{v}_{t+1}}{{{}_{t+1}{}^{ }p}_{x}{v}_{t+2}}-{B}_{t}\frac{{{}_{t+1}{}^{ }p}_{x}{v}_{t+1}}{{{}_{t+1}{}^{ }p}_{x}{v}_{t+2}}.$$

By reinjecting the equality:

$$\frac{{AV}_{mop}^{t}}{{p}_{x+t}}\frac{{{}_{t+1}{}^{ }p}_{x}{v}_{t+1}}{{{}_{t+1}{}^{ }p}_{x}{v}_{t+2}}=\frac{\sum_{k\ge t}{B}_{k}{\times {}_{k+1}{}^{ }p}_{x}{v}_{k+1}-\sum_{k>t}{C}_{k}\times {{}_{k}{}^{ }p}_{x}{v}_{k} }{{{}_{t}{}^{ }p}_{x}{v}_{t+1}}\times \frac{1}{{p}_{x+t}}\times \frac{{{}_{t+1}{}^{ }p}_{x}{v}_{t+1}}{{{}_{t+1}{}^{ }p}_{x}{v}_{t+2}}$$
$$=\frac{\sum_{k\ge t}{B}_{k}\times {{p}_{x+t}\times {}_{k+1}{}^{ }p}_{x}{v}_{k+1}-\sum_{k>t}{C}_{k}\times {{}_{k}{}^{ }p}_{x}{v}_{k}}{{{}_{t+1}{}^{ }p}_{x}{v}_{t+2}}.$$

This gives:

$${AV}_{mop}^{t+1}=\frac{{{C}_{t+1}\times {}_{t+1}{}^{ }p}_{x}{v}_{t+1}}{{{}_{t+1}{}^{ }p}_{x}{v}_{t+2}}+\frac{\sum_{k\ge t}{B}_{k}{\times {}_{k+1}{}^{ }p}_{x}{v}_{k+1}-\sum_{k>t}{C}_{k}\times {{}_{k}{}^{ }p}_{x}{v}_{k}}{{{}_{t+1}{}^{ }p}_{x}{v}_{t+2}}-{B}_{t}\frac{{{}_{t+1}{}^{ }p}_{x}{v}_{t+1}}{{{}_{t+1}{}^{ }p}_{x}{v}_{t+2}}$$
$${AV}_{mop}^{t+1}=\frac{\sum_{k\ge t+1}{B}_{k}{\times {}_{k+1}{}^{ }p}_{x}{v}_{k+1}-\sum_{k>t+1}{C}_{k}\times {{}_{k}{}^{ }p}_{x}{v}_{k}}{{{}_{t+1}{}^{ }p}_{x}{v}_{t+2}}.$$

Which proves the result at \(t+1\).

4.5 Contributed values

A basic property useful for unit test and analysis purposes—is the decomposition of the account value among contributions, benefits, financial returns, and longevity credits:

$$\forall t,\, {AV}_{eop}^{t}=\sum_{k\le t}{C}_{t}+\sum_{k\le t}{S}_{t }+\sum_{k\le t}{FinReturn}_{t }-\sum_{k\le t}{B}_{t}.$$

This ensures that nothing is created or lost—and that the numerical dispersion is acceptable (if any).

4.6 Joint life and reversionary features

4.6.1 Joint life generalization via synthetic schemes

A rather straightforward method to generalize the Tontine Share calculation to joint life is to create a synthetic scheme that replicates the selected option payouts, as described by [13]. The idea is to express all possible joint life options as a sum of 3 basic components which are contingent on events that are easily manipulated from a probabilistic perspective: the 1st life survival, the 2nd life survival, and pure joint-life survival status (i.e., both are alive). For instance, let’s denote the nominal flows:

  • \(\left\{{b}_{t}^{*1}\right\}\) that are paid when the 1st life is alive.

  • \(\left\{{b}_{t}^{*2}\right\}\) when the second life is alive.

  • \(\left\{{b}_{t}^{*pj}\right\}\) when both the first and second life are alive.

The Reversion option can be expressed as two individual life payout schemes and a negative pure joint life payout scheme:

  • \(\left\{{b}_{t}^{*1}\right\}\) the initial payout scheme, which applies to the joint-life status and that will be maintained for the 1st life in case the 2nd life death precedes.

  • \(\left\{{b}_{t}^{*2}\right\}\) the reversion flows for the 2nd life in case the 1st life death precedes.

  • \(\left\{{b}_{t}^{*pj} \right\}= \left\{{b}_{t}^{*2}\right\}\), the synthetic pure joint payouts.

For instance, for a reversionary with 60% value:

$${\left\{{b}_{t}^{*1}=1\right\}}_{t\ge 0}, {\left\{{b}_{t}^{*2}=0.6\right\}}_{t\ge 0}, {\left\{{b}_{t}^{*pj}=-0.6\right\}}_{t\ge 0}.$$

The Joint Survival Life option can similarly be expressed as two individual life payout schemes and a negative pure joint-life payout scheme. By noting \(\left\{{F}_{t}^{joint}\right\}\) the amount to be paid when both lives are alive, one can write:

  • \(\left\{{b}_{t}^{*1}\right\}\) the payout for the 1st life in case the 2nd life death precedes.

  • \(\left\{{b}_{t}^{*2}\right\}\) the payout for the 2nd life in case the 1st life death precedes.

  • \(\left\{{b}_{t}^{*pj} \right\}= \left\{{b}_{t}^{*joint} \right\} - \left\{{b}_{t}^{*1} \right\}- \left\{{b}_{t}^{*2}\right\}\), the synthetic pure joint payouts.

For instance, for a joint status at 100% and 60% value in case only one survives:

$${\left\{{b}_{t}^{*1}=0.6\right\}}_{t\ge 0},\,{\left\{{b}_{t}^{*2}=0.6\right\}}_{t\ge 0},\,{\left\{{b}_{t}^{*pj}=-0.2\right\}}_{t\ge 0}.$$

4.6.2 Integration in the existing model

Once the target joint-life payout scheme has been broken down into the 3 basic components \(\left\{{b}_{t}^{*1}\right\}\), \(\left\{{b}_{t}^{*2}\right\}\), \(\left\{{b}_{t}^{*pj}\right\}\) the mathematics is common to all joint life options.

By re-using previous notations, and noting \({{}_{t}{}p}_{x}\), \({{}_{t}{}p}_{y}\) and \({{}_{t}{}p}_{xy}\) the actuarial probabilities for 1st life, 2nd life, and pure joint life status, one can get the nominal benefit equation:

$$\sum_{t\ge 0}{C}_{t}\times {{}_{t}{}^{ }p}_{x}{v}_{t}=nB\left[\sum_{t\ge 0}{b}_{t}^{*}\times {{}_{t+1}{}^{ }p}_{x}{v}_{t+1}+\sum_{t\ge 0}{b}_{t}^{*2}\times {{}_{t+1}{}^{ }p}_{y}{v}_{t+1}+\sum_{t\ge 0}{b}_{t}^{*pj}\times {{}_{t+1}{}^{ }p}_{xy}{v}_{t+1}\right].$$

4.6.3 Tontine share

The Tontine share calculation is then equivalent to the one done in the single life case—performed on each of the individual components using the appropriate decrements.

$${{TontShare}_{ {t}_{ } }^{ }}_{ }=\left(\frac{{q}_{{x}_{ }}^{ }}{1-{q}_{{x}_{ }}^{ }}\right){AV}_{mop }^{1}+\left(\frac{{q}_{{y}_{ }}^{ }}{1-{q}_{{y}_{ }}^{ }}\right){AV}_{mop }^{2}+\left(\frac{{q}_{{xy}_{ }}^{ }}{1-{q}_{{xy}_{ }}^{ }}\right){AV}_{mop }^{pj}$$

5 Modeling: conventions & hypothesis

5.1 Introduction

5.1.1 Approach

For the projection, assets and mortality are simulated stochastically. The longevity credits are allocated at each time step using the single period approach (Sect. 3) with the simulation outputs broadcasted at member level as an input (financial returns and deceased members). The prospective approach (Sect. 4) serves at each time step to re-adjust benefit payments based on updated account value and compare actual payments with expected payments at issue. These expected payments at issue are calculated based on mean expected returns used as input for fund simulations and the mortality table selected.

5.1.2 Conventions

Similar conventions as above will be used, namely:

  1. (1)

    Annual stepFootnote 11

  2. (2)

    Benefit payments are made at the end of the period.

  3. (3)

    Contributions are made at the beginning of the period.

  4. (4)

    Tontine Share are calculated after financial return.

  5. (5)

    3 funds projected: Low, Mid, and High volatility (with Low, Mid, and High returns).

  6. (6)

    Account values are as follow (for one given simulation, for member \(n\) and time \(t\)):

    • Starting period AV: \({AV}_{bop}^{0,n}=0, \forall t\ge 1, { AV}_{bop}^{t,n}={ AV}_{eop}^{t-1,n}+{C}_{t}^{n}\).

    • Middle period AV: \({AV}_{mop}^{t,n}={AV}_{bop}^{t,n}\left(1+{r}_{t}^{n}\right)\).

    • End of period AV: \({AV}_{eop}^{t,n}={AV}_{mop}^{t,n}+{S}_{t}^{n}-{B}_{t}^{n}\).

5.1.3 Mortality

In terms of mortality, we will use the latest Taiwan TSO 2011. This is purely an arbitrary choice for illustration purposes. The ins and out of mortality selection will be further discussed below.

We introduce a selection factor—arbitrary fixed to 40% in the first year increasing to 90% with an annual step of 5% (member presence).

5.2 Algorithm

The algorithm used can be summarized as follows:

Start period:

  • Add new members.

  • Collect contributions.

“Mid” period:

  • Add financial return for the step based on stochastic simulations.

  • Apply stochastic mortality.

  • Calculate redeemed amounts.

  • Calculate tontine shares.

End Period:

  • Remove deceased members from the pool.

  • Allocate longevity credits.

  • Adjust benefits based on the new account value.

  • Pay benefits.

5.3 Scenario generation

1000 scenarios, including both mortality and fund scenarios.

5.3.1 Random number generator

The Mersenne Twister pseudo-random number generator algorithm is being used.

5.3.2 Fund scenarios

For the matter of generating stochastic returns, a standard Black & Scholes framework with intercorrelated Brownian motions has been selected. Key parameters are described below (Tables 5 and 6).

Table 5 Return and volatility assumptions
Full size table
Table 6 Correlation assumptions
Full size table

5.3.3 Mortality scenarios

The mortality scenarios are derived from a random uniform distribution (between 0 and 1) applied to the survival function at the member subscription date.

5.4 Metrics used

To assess the model, the following indicators will be extracted from the simulation tool.

  • Mortality A/E ratio \(\text{this is the standard A}/\text{E}\) ratio for mortality, expressed by count or amount.

  • Tontine Share A/E ratio is the Tontine Gain compared to the Expected Tontine Share supposed to be accumulated. The Expected Tontine Share can either be the expected Share calculated at subscription (based on prospective indicators and average financial return) or the one calculated at beginning of each allocation step (path-dependent).

  • Survival Payouts A/E ratio same as previous but for the Survival Expected Payouts vs Actual Payouts. The Expected Amount can also be estimated at subscription or the start of each period (path-dependent).

6 Modeling: global

6.1 Model points

6.1.1 Distribution

  • 5000 new insured per year for 10 years, projected until run-off.

  • 40 to 70 years old entry age, Male & Female equal proportion.

  • Distributed contribution: Single Pay, 5, 10, 15 and 20 year pay.

  • Annuitization starts at 65 up to 100.

  • Asset Allocation: Random among the 3 funds (by default, we assume rebalancing of assets at each step with the target allocation).

6.2 Single simulation result

6.2.1 Fund overview over the years

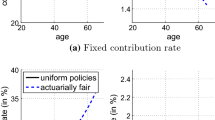
The above graphs show a single simulation of the fund over the year. The left column allows the apprehend the population size peak (reached around 10 years with little less than 50,000) and the extinction of the fund in 50 years. Maturities are staged depending on the annuity length selected by members. Finally, the death count is slightly skewed on the right compared with in force members count, logically increased by the population aging (Fig. 1).

Fig. 1
figure 1

Single simulation of a modern tontine fund: demographics and returns over the years

Full size image

Right graphs illustrate contribution and payout, and the investment and longevity credits compared with expected. The longevity credits increase with age—which is expected, but so does its deviation from benchmark. Interestingly, we can see the impact of financial return on longevity credits with the “initial benchmark”.

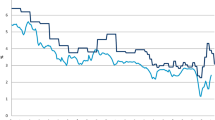
6.2.2 Actual vs expected longevity credits

Right side graphs show the correlation of A/E ratios on mortality with A/E ratios for the tontine share. On the last graph, the “Current benchmark” stays fairly closes to 1 in the middle years of the tontine. The deviation is higher at the start and the end of the scheme, due to population size and idiosyncratic bias. Initial benchmark shows the additional impact of financial return on A/E for tontine share. When recouping with the previous graph, we can observe the similar movements, reflecting the impact of Financial return (lower, higher, lower) (Fig. 2).

Fig. 2
figure 2

Single simulation of a modern tontine fund: actual vs expected returns

Full size image

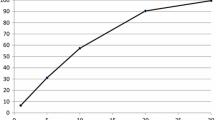
6.3 1000 simulations distribution analysis

As observed on a single simulation, the Tontine return follows a similar deviation at the start and end of the scheme, due to idiosyncratic mortality risk linked to small fund size. This shows the importance of having the largest pool possible to neutralize this volatile effect (Fig. 3).

Fig. 3
figure 3

1000 simulations distribution: actual vs expected dearh and returns (financial and tontine)

Full size image

7 Modeling: focused tests

7.1 Actuarial fairness bias

7.1.1 Simulation

To isolate the bias, here is the projection hypothesis used:

  • 500, 1000 and 5000 insured.

  • 40 to 70 years old entry age, Male & Female equal proportion.

  • Distributed contribution: Single Pay only.

  • Only 1 year projected, Lump Sum.

  • Asset Allocation: financial return forced to 0.

7.1.2 Results

The impact of fund size on bias is evident, with high deviation for 500 members. When considering 5000 members, the deviation is much smaller, showing the reduction impact of a larger population on the bias. The 2nd line of graphs shows a good fitting of the bias proxy in this particular case (Fig. 4).

Fig. 4
figure 4

Bias analysis: 1st row: observed (as a % of tontine share), 2nd row: estimated (as a % of tontine share), 3rd Line: observed (as % of AUM)

Full size image

7.2 Sensitivity analysis mortality & longevity deviations

7.2.1 Simulation

To isolate the bias, here is the projection hypothesis used:

  • 1000 and 5000 insured.

  • 40 to 70 years old entry age, Male only.

  • Distributed contribution: Single Pay only.

  • Only 1 year projected, Lump Sum.

  • Asset Allocation: financial return forced to 0.

  • Selection factors forced to 1.

Based on the above graphs (1st line), longevity credits are consistent with the mortality factor—the average mortality scenario. Of course, the returns in case of survival are limited for people at 40 years while they are indeed remarkably high for high ages (95). In the current low-rate environment, we could conclude that they are material after 65. Given this observation, low ages are not meaningful in terms of return for these solutions (minimum age of 40 with a long horizon), while higher ages could benefit from a payout schedule that neutralizes the exponential growth of the force of mortality (Fig. 5).

Fig. 5
figure 5

Deviation of longevity credits due to mortality fluctuation by age

Full size image

8 Discussion

8.1 Technical

8.1.1 Allocation bias

As shown, the model has an inherent bias, linked to the inter-dependency of individual longevity credits with pool returns. In practice, we observed that this bias is proportional to the ratio of the member tontine share divided by the total tontine share. Also, this bias was small compared to the overall returns and mortality idiosyncratic risk.

To manage this bias, the key is to limit the “atomization” of the Tontine Share—i.e., ensure that there is no member with an abnormally high share compared to the rest. The Tontine share depending both on the death probability and the account value—it seems logical to introduce limitations in terms of maximum contribution and minimum/maximum age. Along with enough member participation (5000 seems enough from our simulation), the bias becomes negligible.

8.1.2 Idiosyncratic mortality risk

The idiosyncratic is a significant source of volatility for the Modern Tontine longevity credits. The same measures described in the bias mitigation can be proposed: ensure a large pool size (5000 members and over seems ideal), limit the entry age (40 to 80), and limit the contribution size.

8.1.3 Financial risk

The scheme being designed on a “Unit-Linked” concept, the financial risk will be bear exclusively by the members. Various investment strategies—passive and active—could be proposed as a service to each member to mitigate this risk and match their preferences.

As a note, it should be reminded that a member would primarily bear the risk linked to its own asset allocation. The return of the other member of the pool will only impact the members’ longevity credits—and thus the overall investment only as a second-order factor.

8.1.4 Reverse moral hazard and term dilemma

Due to the non-refundable nature of the Tontine in case of death, one could expect a natural self-selection process on elective schemes—qualified as a “Reverse Moral Hazard”.

Additionally, as shown above, the Term dilemma is a significant drawback for elective plans—and should be carefully considered. A way to characterize it is to consider an “option” for the member to discontinue the Tontine pooling in case additional information about his/her health arises. The value of such “option” could be tentatively valued, assuming one could separate the “sudden” from the “foreseeable” causes of death at a given horizon. This separation of the mortality could allow using different decrements depending on the terms selected. In practice, this means applying selection factors calibrated on the “predictiveness” of the causes of death.

Practically, some mitigators to manage reverse moral hazard and term dilemma could be:

  • Propose Modern Tontines only for “compulsory” plans where payouts are preset and contribution not elective (government retirement plan).

  • Create “sub” Modern Tontines funds for each maturity Given the sensitivity of this scheme to Mortality idiosyncratic risk—this solution seems sub-efficient.

  • Introduce a selection factor for early years Like a Term Life with strict underwriting, one could imagine a selection factor to be applied on the mortality table selected for the first years of a member in the Modern Tontine. This will favor longer terms return-wise and should counterbalance the Term Dilemma benefits.

  • Increase minimum maturity Along with the selection factor introduction—allowing a minimum term between the first investment and the outgoes would allow to level the adverse selection risk. A minimum term of 5–10 years seems aligned with the purpose of a retirement plan.

8.1.5 The step length selection

The step at which the Tontine mechanism is triggered is an important consideration practically. From a purely theoretical standpoint, the “instantaneous” allocation is the most accurate. For modeling purposes, an annual step has been used. Some constraints arise: existing members need to prove their survival and new entrants would expect to join the pool as soon as possible. Given the importance of longevity credits in the scheme, we tend to prioritize the survival checks—especially when some actuarial interpolation techniques could be applied to the new joiners. The driver here to select the step would probably be the technology used for the survival checks.

8.2 Practical/commercial

8.2.1 Regulatory framework

Pan European Pension Plan (PEPP) shows the attention politics and regulators give to adequate elderly financial planning. Further work is however expected to fit the Modern Tontines in an existing framework.

8.2.2 No benefit upon death

Though not exclusive to Tontine—this is a limitation from the consumer perspective. Providing a with bequest alternative (and thus no longevity credits) could respond to this drawback. A reversion scheme could also be designed by generalizing the mathematics or using automatic transfer from the with-bequest to the tontine fund with appropriate time and weights.

8.2.3 Complexity of mechanism to be exposed

Exposing the mechanism to the consumer will be a limitation—especially given the possible volatility on returns and the “sharing” nature of the mortality proceeds. Illustration, transparency, and regular communication will be required.

8.2.4 Mortality table

The Tontine share—the cornerstone of the allocation model—is highly dependent on the mortality assumption retained. Choosing the mortality across different generations raises several questions: best estimate assessment, segmentation, and re-evaluation.

Best estimate selection it should be appropriate with the target population and available experience, either internal and/or external.

Segmentation Up to which level the segmentation of mortality assessment should be done is left open. The model shown used a standard Age/Gender segmentation as per the mortality table used for illustration. This question goes beyond the sole technical point and is ultimately an arbitrage between fairness, solidarity, and regulation.

Re-evaluation of assumptions Once size and experience are large enough; it should be possible to develop “internal” experience benchmarks. The question of whether and how to impact existing and new joiners are left open.

8.2.5 Selection factors

As discussed above—selection factors are expected to be a key mitigator for the “Term Dilemma” and “Reverse Moral Hazard” on elective schemes. From insurance lines in case of death, one can observe that the underwriting selection effect generally lasts around 5 years, and seldom lasts more than 10 years. Ideally, these factors could be further calibrated by entry age—especially if the expected mortality gap is wide from a member to another.

Several methods could be used to derive these factors, among them:

  • Calibration from experience on Annuity portfolios with similar features.

  • Approximation from other lines underwriting effect.

  • Mortality causes analyses and separation among “sudden” and “foreseeable”.

8.2.6 Regular survival checks

As the history of tontine has shown, fraud is a possibility that cannot be excluded. Survival checks can be time-consuming and would directly impact the operation of the pools, as discussed during the step selection. The technology used to realize this task will directly impact the administration efficiency and benefits for members.

9 Conclusion

“The Tontine is perhaps the most discredited financial instrument in history”.Footnote 12

Used primarily as a fund-raising vehicle, their history is indeed tainted with scandals, bankruptcies, and a popular belief of “indecency” toward gamble on human life.

However, in the current context—aging population, longevity improvements, and pension underfunding epidemic—Modern Tontines could become a viable retirement instrument and fill part of the increasing need for adequate elderly financial planning. By generalizing the tontine concept to a traditional annuity-like instrument, Modern Tontines can efficiently transform capital into fully funded lifetime income. Without the need for a carrier, they offer efficient decumulation schemes with individual longevity protection, attractive returns thanks to low fees, and high flexibility in terms of design. Technically, there are limitations since the financial and idiosyncratic longevity risks would be borne by the pool. However, as illustrated, the variability of outgoes can be mitigated provided certain conditions are met—while retaining the benefits of fully funded lifetime income vehicles.

Technically, the method presented contains an inherent fairness bias in the longevity credit allocation—linked to the atomization of the Tontine Share. We have observed mathematically and experimentally that this bias could be negligible with appropriate limits sets in terms of fund size, demographics, and contribution size. Similarly, the idiosyncratic mortality risk is a direct function of the pool size and its homogeneousness. With the financial risk being a consequence of the member choice and preferences in terms of allocation and strategy, the pool is left only with the global longevity risk—which shows much lower volatility at a member level compared to the idiosyncratic longevity risk.

Operationally, annuities can be subject to moral hazard and in extreme cases fraud. The “Term Dilemma” is a serious drawback of the model—which can however be mitigated by setting adequate minimum term limits and introducing some selection factors on the mortality to favor longer terms. The survival check will also be a key operational challenge and its implementation will dictate the robustness of the pool along with some of its characteristics. Aside from the tontine mechanism, Modern Tontines as presented here are close to standard asset management or unit-linked insurance activity—a well-known and developed activity. Finally, Modern Tontines implementation is tightly linked with the regulatory framework.