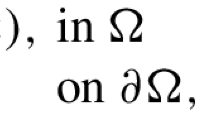Existence of solutions for some quasilinear elliptic system with weight and measure-valued right hand side

Abstract

Let $\Omega$ be an open bounded domain in $I\!\!R^{n},$ we prove the existence of a solution u for the nonlinear elliptic system

$$\begin{aligned} \text{(QES) } \left\{ \begin{array}{ll} -div\sigma \left( x,u\left( x\right) ,Du\left( x\right) \right) = \mu &{}\quad \text{ in } \Omega \\ u = 0 &{}\quad \text{ on } \partial \Omega , \end{array} \right. \end{aligned}$$

(0.1)

where $\mu$ is Radon measure on $\Omega$ with finite mass. In particular, we show that if the coercivity rate of $\sigma$ lies in the range $]\frac{s+1}{s},(\frac{s+1}{s})(2-\frac{1}{n})]$ with $s\in \left( \frac{n}{p}\,\ \infty \right) \cap \left( \frac{1}{p-1}\,\ \infty \right) ,$ then u is approximately differentiable and the equation holds with Du replaced by $\text{ apDu }$. The proof relies on an approximation of $\mu$ by smooth functions $f_{k}$ and a compactness result for the corresponding solutions $u_{k}.$ This follows from a detailed analysis of the Young measure $\{\delta _{u}(x)\otimes \vartheta (x)\}$ generated by the sequence ${(u_{k},Du_{k})}$, and the div-curl type inequality $\langle \vartheta (x),\sigma (x,u,\cdot )\rangle \le \overline{\sigma }(x)\langle \vartheta (x),\cdot \rangle$ for the weak limit $\overline{\sigma }$ of the sequence.

1 Introduction

We consider the existence and compactness questions for elliptic systems of the form

$$\begin{aligned} \text{(QES) } \left\{ \begin{array}{ll} -div\sigma \left( x,u\left( x\right) ,Du\left( x\right) \right) = \mu &{}\quad \text{ in } \Omega \\ u = 0 &{}\quad \text{ on } \partial \Omega , \end{array} \right. \end{aligned}$$

(1.1)

with measure-valued right hand side $\mu \in M(\Omega ,I\!\!R^{m})$ on an open, bounded domain $\Omega$ in $I\!\!R^{n},$ we denote by $M(\Omega ,I\!\!R^{m}),$ with $m\in I\!\!N^{*},$ the Banach space of vectors $\mu$ of bounded Radon measures

$$\begin{aligned} \mu = (\mu _{1},\ldots \mu _{m})\;\;\; with \;\;\; \mu _{i}\in M(\Omega )\;\;\;for \;\;i\;=\;1,\ldots ,m. \end{aligned}$$

With $M(\Omega )$ be a vector space of bounded Radon measures.

$\omega = \left\{ \omega _{ij} \mid 0\le i\le n, \, 1\le j\le m \right\}$ is a family of weight functions defined on $\Omega$ with $\omega _{ij}(x)>0$ for almost every $x \in \Omega$ and $\omega ^{*} =\{\omega ^{*}_{ij}=\omega _{ij}^{1-p'}, 0 \le i \le n, \; 1\le j \le m\}$, $(\frac{1}{p}+ \frac{1}{P'}= 1).$ In this paper we are interested in the solution u in the Sobolev space $W_{0}^{1,p}(\Omega ,\omega ,I\!\!R^{m}),$ and estimations in the weak Lebesgues spaces. We assume that $\sigma$ satisfies the following hypotheses $(H_{0})$–$(H_{3})$ explained below. We denote by $I\!\!M^{m \times n}$ the real vector space of $m\times n$ matrices equipped with the inner product $\displaystyle M:N = \sum \nolimits _{ij} M_{ij}N_{ij}.$ The Jacobian matrix of a function $u: \Omega \longrightarrow I\!\!R^{m}$ is denoted by

$$\begin{aligned} Du(x)=(D_{1}u(x),D_{2}u(x),\ldots ,D_{n}u(x))\; \text{ with } D_{i}=\partial /\partial x_{i}. \end{aligned}$$

Let $\omega = \left\{ \omega _{i j} \mid \, 0\le i\le n,\ 1\le j\le m \right\}$, and $\overline{\omega _{0}}= (\omega _{0j})$ for all $1\le j \le m$ the weight functions system defined in $\Omega$ satisfying the following integrability conditions

$$\begin{aligned}{} & {} \omega _{ij} \in L_{loc}^{1}(\Omega ),\ \ \ \omega _{ij}^{\frac{-1}{p-1}}\in L_{loc}^{1}(\Omega ) \end{aligned}$$

(1.2)

$$\begin{aligned}{} & {} \omega _{ij}^{-s} \in L^{1}(\Omega ) \end{aligned}$$

(1.3)

for some $s\in \left( \frac{n}{p}\,\ \infty \right) \cap \left( \frac{1}{p-1}\,\ \infty \right) .$ The space $W^{1,p}(\Omega ,\omega ,I\!\!R^{m})$ is the set of functions

$$\begin{aligned} \displaystyle \left\{ u= u(x) \mid u\in L^{p}(\Omega ,\overline{\omega _{0}},I\!\!R^{m}),\ D_{ij}u = \frac{\partial u^{i}}{\partial x_{j}} \in L^{p}(\Omega ,\omega _{ij},I\!\!R^{m}),\ 1\le i \le n,\ 1\le j \le m\}\right\} \end{aligned}$$

with

$$\begin{aligned} L^{p}(\Omega ,{\omega _{ij}},I\!\!R^{m})=\displaystyle \left\{ u= u(x) \mid \, \mid u\mid {\omega _{ij}}^{\frac{1}{p}} \in L^{p} (\Omega ,I\!\!R^{m})\right\} . \end{aligned}$$

The weighted space $W^{1,p}(\Omega ,\omega ,I\!\!R^{m})$ can be equipped by the norm

$$\begin{aligned} \displaystyle \left\| u\right\| _{1,p,\omega } =\displaystyle \left( \sum _{j=1}^{m} \int _{\Omega }|u_j|^{p} w_{0j}dx + \sum _{1 \le i \le n, 1 \le j \le m}\int _{\Omega }|D_{ij}u|^{p} \omega _{ij} dx\right) ^{\frac{1}{p}}. \end{aligned}$$

The norm $\Vert \cdot \Vert _{1,\omega ,p}$ is equivalent to the norm $\mid \mid \mid \cdot \mid \mid \mid$ on $W_0^{1,p}(\Omega ,\omega ,I\!\!R^{m}),$ defined by $\mid \mid \mid u \mid \mid \mid = \displaystyle (\sum \nolimits _{1 \le i \le n, 1 \le j \le m}\int _{\Omega }|D_{ij}u|^{p} \omega _{ij} dx)^{\frac{1}{p}}.$ The condition (1.2) implies $(W^{1,p}(\Omega ,\omega ,I\!\!R^{m}),\left\| \cdot \right\| _{1,p,\omega })$ is a Banach space and $C_{0}^{\infty }(\Omega ,I\!\!R^{m})$ subspace of $(W^{1,p}(\Omega ,\omega ,I\!\!R^{m}).$ The space $(W_{0}^{1,p}(\Omega ,\omega ,I\!\!R^{m})$ is the closure of $C_{0}^{\infty }(\Omega ,I\!\!R^{m})$ in $W^{1,p}(\Omega ,\omega ,I\!\!R^{m})$ for the norm $\left\| \cdot \right\| _{1,p,\omega }^{p}.$ The condition (1.3), implies

$$\begin{aligned} W^{1,p}(\Omega ,\omega ,I\!\!R^{m})\hookrightarrow W^{1,p_{s}}(\Omega ,I\!\!R^{m})\hookrightarrow L^{r}(\Omega ,I\!\!R^{m}), \end{aligned}$$

(1.4)

for all $1\le r\le p_{s}^{*}$ if $p\times s\le n(s+1),$ and $\forall r\ge 1$ if $p\times s> n(s+1)$ with $p_{s}=\frac{p\times s}{s+1}$ and $p_{s}^{*}=\frac{n\times p\times s}{n(s+1)-p\times s},$for proof see [1].

Our article deals with the existence of a weak solution of system declared at the top in each of the four cases located in the part of the hypotheses in $(H_{2})$ and in a Sobolev space with weights, but the article in [2] treats in a weightless Sobolev space.

2 Hypothesis

$(H_{0})$:

(Continuity) $\sigma :\Omega \times I\!\!R^{m}\times I\!\!M^{m\times n}\longrightarrow I\!\!M^{m\times n}$ is a Carathéodory function, i.e:

$x\longmapsto \sigma (x,u,p)$ is measurable for every (u, p) and $(u,p)\longmapsto \sigma (x,u,p)$ is continuous for almost every $x\in \Omega .$

$(H_{1})$:

(Coercivity and growth): There exist constants $c_{1},\,c_{2},\,\beta >0$ and $\lambda _{1}\in L^{p'}(\Omega )$, $\lambda _{2}\in L^{1}(\Omega ),$ $\lambda _{3}\in L^{(\frac{p}{\alpha })^{'}}(\Omega ),$ $0<\alpha <p,$ $1<q<\frac{p^{2}}{\alpha }$, $0<\theta <\frac{n(p_{s}-1)}{n-1},$ such that, for all $1\le r\le n$, and $1\le s\le m$

$$\begin{aligned} |\sigma _{rs}(x,u,F)|\le & {} \beta \omega _{rs}^{\frac{1}{p}}\left[ \lambda _{1}+c_{1}\sum _{j=1}^{m}\gamma _{j}^{\frac{1}{p'}}| u_{j}|^{\frac{q}{p'}}+c_{1}\sum _{i,j}\omega _{ij}^{\frac{1}{p'}}| F_{ij}|^{\theta }\right] \\ \sigma (x,u,F):F\ge & {} -\lambda _{2}-\sum _{j=1}^{m}\lambda _{3}\gamma _{j}^{\frac{\alpha }{p}}| u_{j}|^{\frac{q\alpha }{p}}+c_{2}\sum _{i,j}\omega _{ij}| F_{ij}|^{p}. \end{aligned}$$

$(H_{2})$:

(Monotonicity) $\sigma$ satisfies one of the following conditions:

a) For all $x\in \Omega ,\,u\in I\!\!R^{m}$ the function $F\longmapsto \sigma (x,u,F)$ is a $C^{1}$ and monotone function, which means $(\sigma (x,u,F)-\sigma (x,u,G)):(F-G)\ge 0,$ for all $x\in \Omega$, $u\in I\!\!R^{m}$, and $F,G\in I\!\!M^{m\times n}.$

b) There exist a function $W:\Omega \times I\!\!R^{m}\times I\!\!M^{m\times n}\rightarrow R$ such that

$\sigma (x,u,F)=\frac{\partial W}{\partial F}(x,u,F),$ and the function $F\longmapsto W(x,u,F)$ is a convex $C^1$ function.

c) $\sigma$ is strictly monotone, i.e. $\sigma$ is monotone, i.e., $(\sigma (x,u,F)-\sigma (x,u,G)):(F-G)\ge 0$ and $(\sigma (x,u,F)-\sigma (x,u,G)):(F-G)=0.$ implies $F=G.$

d) The function $F\longmapsto \sigma (x,u,F)$ is strictly p-quasi-monotone, i.e.,

$\int _{I\!\!M^{m\times n}}(\sigma (x,u,\lambda )-\sigma (x,u,\bar{\lambda })):(\lambda -\bar{\lambda })d\nu (\lambda )>0,$ for all homogeneous $W^{1,p}$-gradient Young measures $\nu$ with center of mass $\bar{\lambda }=\langle \nu ;\text{ Id }\rangle = \displaystyle \int _{I\!\!M^{m\times n}}\lambda d\nu (\lambda )$ which are not a single Dirac mass.

$(H_{3})$:

(structure conditions) i) (Angle condition) for all $x\in \Omega ,$ $u\in I\!\!R^{m}$ and $F\in I\!\!M^{m\times n}$ there holds

$\sigma (x,u,F):MF\ge 0$, for all matrices $M\in I\!\!M^{m\times m}$ of the form $M=\text{ Id }-a\otimes a$ with $\left| a\right| \le 1.$ ii) (The sign condition) for all $x\in \Omega ,$ $u\in I\!\!R^{m}$ and $F\in I\!\!M^{m\times n},$ we have $\sigma _{j}(x,u,F):F_{j}\ge 0,$ for all $1\le j\le m$ where $F_{j}$ and $\sigma _{j}$ are the columns j of the matrix F and $\sigma ,$ respectively.

$(H_{4})$:

(The Hardy-Type Inequality) There exist $c>0$, a weight function $\gamma =(\gamma _{j})_{1\le j\le m}$, and a parameter $1<q<\frac{p^{2}}{\alpha }$ ($H_{1}$), such that:

$$\begin{aligned} \left( \sum _{j=1}^{m}\int _{\Omega }\gamma _{j}\mid u_{j}\mid ^{q}dx\right) ^{\frac{1}{q}}\le c\left( \sum _{i,j}\int _{\Omega }\omega _{ij}\mid D_{ij}u\mid ^{p}dx\right) ^{\frac{1}{p}}. \end{aligned}$$

Remark 2.1

• 1. Assumption $(H_{0})$ ensures that $\sigma (x,u(x),U(x))$ is measurable on $\Omega$ for measurable function $u:\Omega \longrightarrow I\!\!R^{m}$ and $U:\Omega \longrightarrow I\!\!M^{m\times n}.$ A typical example for a function $\sigma$ satisfying $(H_{0})$ is $\sigma (x,u,p)=\xi (x,u,p)p$ with a real valued non-negative function $\xi .$

• 2. A serious technical obstacle is that for $p_{s}\in (1,2-1/n]$ solutions of the system (1.1) in general do not belong to the Sobolev space $W^{1,1}(\Omega ,\omega ,I\!\!R^{m})$ [2].

This fact has led to the use of normalized solutions in [2] and generalized entropy solutions in [3] for elliptic equations of the above type. We will use a notion of solution where the weak derivative Du is replaced by the approximate derivative $\text{ apDu }.$ Recall that a measurable function u is said to be approximately differentiable at $x\in \Omega$ if there exists a matrix $F_{x}\in I\!\!M^{m\times n}$ such that for all $\epsilon >0$, $\displaystyle \lim _{r\rightarrow 0}\frac{1}{r^{n}}\text{ meas } \left\{ {y\in B(x,r):\left| u(y)-u(x)-F_{x}(y-x)\right| >\epsilon r}\right\} =0.$ We write $\text{ apDu }(x)=F_{x}.$

Definition 2.1

A measurable function $u:\Omega \longrightarrow I\!\!R^{m}$ is called a solution of the system (1.1) if:

(i):

u is almost everywhere approximately differentiable.

(ii):

$\eta \circ u\in W^{1,1}(\Omega ,\omega ,I\!\!R^{m}),$ for all, $\eta \in C_{0}^{1}(I\!\!R^{m},I\!\!R^{m})$.

(iii):

$\sigma (x,u, \text{ apDu})\in L^{1}(\Omega ,I\!\!M^{m\times n});$

(iv):

The equation $-div\sigma (x,u(x),Du(x))=\mu$ holds in the sense of distributions. Moreover we say that u satisfies the boundary condition (1.2) if $\eta \circ u\in W_{0}^{1,1}(\Omega ,\omega ,I\!\!R^{m})$, for all, $\eta \in C^{1}(I\!\!R^{m},I\!\!R^{m})\cap L^{\infty }(I\!\!R^{m},I\!\!R^{m})$ with $\eta =\text{ Id }$ on B(0, r), for some $r>0,$ and $| D\eta (y)|\le c(1+| y|)^{-1},$ with $c<\infty .$

Remark 2.2

• 1. The conditions in Definition (2.1) (except (ii)) are the weakest possible in order to define the system (1.1) in the sense of distributions. Note that if u is approximately differentiable, then $\text{ apDu }$ is measurable, so $\sigma (\cdot , u,\text{ apDu})$ is measurable.

• 2. The assumption $\eta \circ u \in W^{1,1}(\Omega ,I\!\!R^{m})$ ensures minimal regularity of u. For example, if $\mu =0,$ and $\sigma (x,u,p)=\sigma (p)$ with $\sigma (0)=0,$ then piecewise constant functions u satisfy $\text{ apDu }=0$ a.e. but are not admissible solutions. The following theorem is the main result in this paper.

Theorem 2.1

Let $\Omega$ be a bounded, open set. We suppose that the hypotheses $(H_{0})$–$(H_{2})$–$(H_{3})$ and the coercivity condition in $(H_{1})$ are satisfied. Let $\mu$ denote a $I\!\!R^{m}$-valued Radon measure on $\Omega$ with finite mass. Then the system (1.1) has a solution u in the sense of Definition 2.1, which satisfies the weak Lebesgue space estimate

$$\begin{aligned} \Vert u\Vert _{L^{t^{*}_{p_{s},\infty }}(\Omega ,I\!\!R^{m})}^{*}+\Vert apDu\Vert ^{*}_{L^{t_{p_{s}, \infty }}(\Omega ,I\!\!M^{m\times n})}\le C, \end{aligned}$$

(2.1)

with the constant C depending on $|\Omega |,c,c_{2},\text{ and } \parallel \lambda _{3}\parallel _{L^{(\frac{p}{\alpha })^{,}}(\Omega )},$ with $t_{p_{s}}=\frac{n(p_{s}-1)}{n-1}$ and $t_{p_{s}}^{*}=\frac{n(p_{s}-1)}{n-p_{s}}$ is the Sobolev exponent of $t_{p_{s}}.$ If $c_{2}=0$ the right hand side of (1.2) reduces to $C(c_{1})\left\| \mu ^{\frac{1}{p-1}}\right\| _{M}.$

Remark 2.3

• 1. If $p_{s}>2-\frac{1}{n}$, then $t_{p_{s}}>1$ and $Du\in L^{1}(\Omega ,$ ${M}^{m\times n}).$

• 2. If $p> n$ one can replace the $L^{s,\infty }$-norm of u in (1.3) by the $C^{0,\beta }$-norm with $\beta =1-\frac{n}{p}$. For $p=q=n$ it is an open question whether $Du\in L^{n,\infty }.$ See Section 7 [4] for the (weaker) inclusion $u\in BMO_{loc}.$

• 3. The exponent in (1.2) are optimal as can be seen from the nonlinear Green’s function $G_{p}(x)=c\left| x\right| ^{\frac{-n}{s^{*}}}$ for the p-Laplace equation: $-div(\left| Du\right| ^{p-2}Du)=\delta _{0}$ in $I\!\!R^{m}$, $n\ge 3.$ In particular, $L^{s,\infty }$ cannot be replaced by $L^{s}$ where $L^{s,\infty }$, is a Laurent space.

• 4. The pointwise monotonicity condition can be replaced by a weaker integrated version, called quasi-monotonicity.

  The key point in the proof of the theorem, is the div-curl inequality for the Young measure $\left\{ \vartheta _{x}\right\} _{x\epsilon \Omega }$ generated by a sequence $Du_{k}$ of gradients of approximate solutions. Together with the identity. (1.4)

  $\text{ apDu }(x)=<\vartheta _{x},Id>.$ The div-curl inequality implies easily that $\sigma (\cdot ,u_{k},Du_{k})$ converges weakly in $L^{1}$ to $\sigma (\cdot ,u,\text{ apDu}).$ (1.4) is a consequence of general properties of young measures if $p>2-\frac{1}{n}$ since in this case $Du_{k}$ is bounded in $L^{s}$ for some $s>1.$ If $1<p\le 2-\frac{1}{n}$ one only has the weaker bounds.

3 Some preliminary lemmas

In this section, we will also use the Young measures, and Inequality div-curl for assume the convergence of subsequence $u_{k}\longrightarrow u$ in measure and for almost every subsequence, with u is approximately differentiable, and $\text{ apDu } = <\nu _{x},\text{ Id }>,$ $\nu _{x}$ is the Young measures generated by a sequence $Du_{k}.$

Lemma 3.1

Let $u_{k:}:\Omega \longrightarrow I\!\!R^{m}$ a sequence of measurable functions such that:

$$\begin{aligned} \sup _{k\in I\!\!N}\int _{\Omega }| u_{k}|^{s}dx<+\infty \ \text{ for } \text{ some } s>0. \end{aligned}$$

(3.1)

We suppose that for each $\alpha >0$ the sequence of truncated functions $\left\{ T_{\alpha }(u_{k})\right\} _{k\in I\!\!N}$ is precompact in $L^{1}(\Omega ,I\!\!R^{m}).$ Then there exists a measurable function u on $\Omega$ such that for a subsequence $u_{k}\longrightarrow u$ in measure.

Proof

Choose a subsequence of $\left\{ u_{k}\right\}$ (not relabeled) which generates a Young measure $\{\vartheta _{x}\}_{x\in \Omega }.$ By 3.1 and Theorem (Young, Tartar, Ball) the measure $\nu _{x}$ are probability measure for almost every a $x\in \Omega$ and $T_{\alpha }(u_{k})\longrightarrow v_{\alpha }=\langle \nu _{x};T_{\alpha }\rangle ,$ weakly in $L^{1}(\Omega ,I\!\!R^{m})$ and in fact strongly since $T_{\alpha }(u_{k})$ is precompact in $L^{1}.$ Consequently there exists a subsequence such that $T_{\alpha }(u_{k_{l}})\longrightarrow v_{\alpha }$ almost uniformly, i.e.

$$\begin{aligned} T_{\alpha }(u_{k_{l}})\longrightarrow v_{\alpha }\ \text{ uniformly } \text{ up } \text{ to } \text{ a } \text{ set } \text{ of } \text{ arbitrary } \text{ small } \text{ measure. } \end{aligned}$$

(3.2)

Let $M_{\alpha }=\left\{ x\in \Omega :| v_{\alpha }(x)\mid <\alpha \right\} .$ Then for each $\epsilon >0$ and $\delta >0$ there exists a set $E_{\epsilon }$ of measure meas$(E_{\epsilon })<\epsilon$ and an index $l_{0}(\epsilon ;\delta )$ such that: $| T_{\alpha }(u_{k_{l}})|<| v_{\alpha }(x)|+\delta$ for all $x\in M_{\alpha }{\setminus } E_{\epsilon }$ and all $l>l_{0}.$ It follows that $u_{k_{l}}(x)\longrightarrow v_{\alpha }(x)$ for almost every$x\in M_{\alpha }{\setminus } E_{\epsilon }$ consider first $x\in M_{\beta };\,\beta <\alpha$ and then the union over $\beta <\alpha )$. Since $\varepsilon >0$ was arbitrary it follows that $\nu _{x}=\delta _{v_{\alpha }}(x)$ for almost every $x\in M_{\alpha }$ In view of the Ball’s theorem it suffices to show that $\cup M_{\alpha }$ has full measure. Now clearly $M_{\alpha }\subset M_{\beta }$ for $\alpha <\beta$ since $T_{\beta }(u_{k_{l}})\longrightarrow T_{\beta }(v_{\alpha })\;=\; v_{\alpha }$ almost everywhere in $M_{\alpha }$ and therefore$v_{\alpha }\;=\;v_{\beta }$ on $M_{\alpha }.$ By (3.2) there exists for each $\epsilon >0$ a set $E_{\epsilon },$ and an index $l_{0}(\epsilon ,\alpha )$ such that meas $(E_{\epsilon })<\epsilon$ and $\mid u_{k_{l}}\mid \;\ge \;\mid T_{\alpha }(u_{k_{l}})\mid \;\ge \;\frac{\alpha }{2}$ on $(\Omega {\setminus } E_{\epsilon }){\setminus } M_{\alpha }$ for all $l\ge l_{0}.$ In view of (3.2) this implies meas $((\Omega {\setminus } E_{\epsilon }){\setminus } M_{\alpha })\le \frac{c}{\alpha ^{s}} \epsilon \longrightarrow 0$ we deduce meas$(\Omega {\setminus }\cup M_{\alpha })$ = $\lim _{\alpha \longrightarrow \infty }\text{ meas }(\Omega {{\setminus }} M_{\alpha })=0$ $\square$

Lemma 3.2

Let $\Omega$ be a domain in $I\!\!R^{n}$ with $|\Omega |<\infty$ and $u_{k}\in W^{1,1}(\Omega ,I\!\!R^{m}).$ Suppose that there exist $p>1$ and $s>0$ such that:

$$\begin{aligned} \sup _{k}\sum _{ i,j}\displaystyle \int _{| u_{k}|\le \alpha }\omega _{ij}| D_{ij}u_{k}|^{p}dx\le c(\alpha )<\infty ,\ \forall \alpha >0, \end{aligned}$$

(3.3)

and $\sup _{k\in I\!\!N}\displaystyle \int _{\Omega }| u_{k}|^{s}dx\le c<\infty .$ Then there exist a subsequence $u_{k_{j}}$ and a measurable function $u:\Omega \longrightarrow I\!\!R^{m}$ such that $u_{k_{j}}\longrightarrow u$ in measure. Moreover u is for almost every $x\in \Omega$ approximately differentiable, for all $\eta \in C_{0}^{1}(\Omega ,I\!\!R^{m})$ there holds $\eta \circ u\in W^{1,p}(\Omega ,\omega ,I\!\!R^{m}).$ if $u_{k}\in W_{0}^{1,1}(\Omega ,I\!\!R^{m})$ then $\eta \circ u\in W_{0}^{1,1}(\Omega ,I\!\!R^{m})\cap W^{1,p}(\Omega ,\omega ,I\!\!R^{m})$ provided that $\eta =\text{ Id }$ on B(0, r) for some $r>0.$

Proof

Choose

$$\begin{aligned} (u_{k})_{\alpha }=\left\{ \begin{array}{ll} u_{k} &{}\quad \text{ if } \quad |u_{k}|\le \alpha , \\ 0 &{}\quad \text{ if } \quad |u_{k}|>\alpha . \end{array} \right. \end{aligned}$$

For the hypotheses:

$$\begin{aligned} \displaystyle \sum _{i,j}\int _{\Omega }\omega _{ij}| D_{ij}(u_{k})_{\alpha }|^{p}dx=\sum _{i,j}\int _{| u_{k}|\le \alpha } \omega _{ij}| D_{ij}u_{k}|^{p}dx\le c(\alpha ) <\infty . \end{aligned}$$

Then, $(u_{k})_{\alpha }\in W_{0}^{1,1}(\Omega ,w,I\!\!R^{m})$ and for (1.4), $(H_{4})$ and $|D| u||\le | Du|$ we have

$$\begin{aligned} \int _{\Omega }| DT_{\alpha }(| u_{k}|)|^{p_{s}}dx= & {} \int _{| u_{k}|\le \alpha }| D| u_{k}|)|^{p_{s}}dx\\\le & {} \sum _{i,j } \int _{\Omega }\omega _{ij}| D_{ij}(u_{k})_{\alpha }|^{p}dx\\\le & {} c(\alpha ) <+\infty \end{aligned}$$

Hence by the compact Sobolev embedding $W_{s}^{1,p_{s}}(\Omega )\hookrightarrow \hookrightarrow L^{p_{s}}(\Omega ),$ we have $\{T_{\alpha }(| u_{k}|)\}$ is precompact in $L^{1}(\Omega ).$ And, if $\eta \in C_{0}^{\infty }\left( B(0,3\alpha ),I\!\!R^{m}\right)$ a symmetric radial such that $\eta = \text{ Id }$ on $B(0,2\alpha ),$ then by (1.2) and (3.3) $\displaystyle \sum \nolimits _{i,j}\int _{\Omega }\omega _{ij}| D_{ij}\left( \eta (u_{k})\right) |^{p}dx= \displaystyle \sum \nolimits _{ij}\int _{\mid u_{k}|\le \alpha }\omega _{ij}| D_{ij}(u_{k})|^{p}dx+\sum \nolimits _{i,j}\int _{\alpha<| u_{k}|\le 2\alpha }\omega _{ij}| D_{ij}(id)|^{p}dx+\sum \nolimits _{i,j}\int _{2\alpha<| u_{k}|\le 3\alpha }\omega _{ij}| D_{ij}\left( \eta (u_{k})\right) |^{p}dx\le c(\alpha )+c\sum \nolimits _{i,j}\parallel \omega _{ij}\parallel _{L_{loc}^{1}(\Omega )}+c<\infty .$ Then, by (1.4), $\eta (u_{k})$ is precompact in $L^{p_{s}}(\Omega ,I\!\!R^{m})$, and as in Lemma 8 [2], there exist a measurable function $u:\Omega \longrightarrow I\!\!R^{m}$ such that $u_{k}\longrightarrow u$ in measure, with $u(x)=<\vartheta _{x},\text{ Id }>$ for almost every $x\in \Omega$ and u is approximately differentiable because $\eta (u_{k})\rightharpoonup \eta (u)$ in $W^{1,P}(\Omega ,\omega ,I\!\!R^{m})$ and $apDu=ap(\eta \circ u)$. $\square$

Lemma 3.3

Let $u_{k}$ be as in Lemma (3.2) with $p>1.$ Then the Young measure $\vartheta _{x}$ generated by (a subsequence of) $Du_{k}$ has the following properties:

(a):

$\vartheta _{x}$ is a probability measure for almost every $x\in \Omega$.

(b):

$\vartheta _{x}$ has finite $p_{s}$-th- moment for almost every $x\displaystyle \in \Omega$, i.e., $\int _{M^{m\times n}}\mid \lambda \mid ^{p_{s}}d\vartheta _{x}(\lambda )$ is finite for almost every $x\in \Omega$.

(c):

$\vartheta _{x}$ satisfies $<\vartheta _{x},\text{ Id }>= \text{ apDu }(x)$ almost everywhere in $\Omega .$

(d):

$\vartheta _{x}$ is a homogeneous $W^{1,P_s}$-gradient young measure for almost every $x\in \Omega .$

Proof

Let $\widetilde{\vartheta _{x}}$ denote the Young measure generated by (a subsequence of) the sequence $\{u_{k},Du_{k}\}.$ By Lemma 3.2 we have:

$$\begin{aligned} \widetilde{\vartheta _{x}}=\delta _{u(x)}\otimes \vartheta _{x}. \end{aligned}$$

Let $\eta \in C_{0}^{\infty }(B(0,2\alpha ),\ I\!\!R^{m}),$ $\eta =Id$ on $B(0,\alpha ),$ and let $\vartheta ^{\eta }$ be the Young measure generated by

$$\begin{aligned} D(\eta \circ u_{k})=(D\eta )(u_{k})Du(x), \end{aligned}$$

then $\vartheta ^{\eta }$ is a probability measure, has finite p-th moment and

$$\begin{aligned} <\vartheta ^{\eta },Id>\,=(D(\eta \circ u))(x)=D\eta (u(x)) \text{ apDu }(x). \end{aligned}$$

It follows for $\varphi \in C_{0}^{\infty }(M^{m\times n}),$ that:

$$\begin{aligned} \varphi (D(\eta \circ u_{k}))\rightharpoonup \langle \vartheta ^{\eta },\varphi \rangle =\int _{M^{m\times n}}\varphi (\lambda )d\vartheta _{x}^{\eta }(\lambda ). \end{aligned}$$

Based on the proof (3.2), we have $\sum _{i,j}\int _{\Omega }|\omega _{ij} D_{ij}(\eta \circ u_{k})|^{p}dx<\infty ,$ and by (1.4)

$\sup _{k\in I\!\!N}\int _{\Omega }| D(\eta \circ u_{k})|^{p_{s}}dx<\infty ,$ and the (Ball’s Theorem, proof lemma 9 [2]) we conclude (a)-(b)-(c)- and (d). $\square$

4 Approximate solutions and a priori bounds

We introduce the following approximating problems

$$\begin{aligned}{} & {} -div\sigma (x,u_{k},Du_{k})=f_{k\,\,\,}in\,\Omega . \end{aligned}$$

(4.1)

$$\begin{aligned}{} & {} u_{k}=0\,\,\,on\,\partial \Omega . \end{aligned}$$

(4.2)

With $f_{k}\in W^{-1,p^{'}}(\Omega ,\omega ^{*},I\!\!R^{m})\cap L^{1}(\Omega ,I\!\!R^{m})$ and $f_{k}\rightharpoonup ^*\mu \;in\;M(\Omega ,I\!\!R^{m})$ such that $\parallel f_{k}\parallel _{L^{1}(\Omega ,I\!\!R^{m})}\le \parallel \mu \parallel _{M(\Omega ,I\!\!R^{m})}.$ By [5] and using the assumptions $(H_{0}),$ $(H_{1})$,$(H_{2})$ and $(H_{4}),$ the problem (4.1) and (4.2) has a solution $u_{k}$ $u_{k}\in W_{0}^{1,p}(\Omega ,\omega ,I\!\!R^{m})$ $u_{k}$ is the subsequence approximates solutions of (1.1). The results of Theorem (2.1) is the consequence of the following proposition

Proposition 4.1

Let, $f\in L^{1}(\Omega ,I\!\!R^{m})$ and $\sigma$ satisfies $(H_{0}),$ the coercivity of $(H_{1})$ and $(H_{3}).$ If $u\in W_{0}^{1,p}(\Omega ,\omega ,I\!\!R^{m})$ is a solution of

$$\begin{aligned} -div\sigma (x,u,Du)= f \quad in\,\Omega . \end{aligned}$$

(4.3)

in the sense of distributions. Then

$$\begin{aligned} u\in L^{t_{p_{s}}^{*},\infty }(\Omega ,I\!\!R^{m}),\quad Du\in L^{t_{p_{s}},\infty }(\Omega ,I\!\!R^{m}) \end{aligned}$$

and

$$\begin{aligned}{} & {} \parallel u\parallel _{L^{t_{p_{s}}^{*},\infty }(\Omega ,I\!\!R^{m})}^{*}+\parallel Du\parallel _{L^{t_{p_{s}},\infty }(\Omega ,M^{m\times n})}^{*}\\{} & {} \quad \le C\bigg (|\Omega |,\parallel \lambda _{1}\parallel _{L^{1}(\Omega )},\parallel \lambda _{3} \parallel _{L^{(\frac{p}{\alpha })^{'}}(\Omega )},\parallel f\parallel _{L^{1}(\Omega ,I\!\!R^{m})}\bigg ) \sum _{i,j}\int _{| u|\le \alpha }\omega _{ij}| D_{ij}u|^{p}dx\\{} & {} \quad \le M\alpha +L,\quad \forall \alpha >0, \end{aligned}$$

M and L are the constants depending on:

$$\begin{aligned} \parallel \lambda _{1}\parallel _{L^{1}(\Omega )},\parallel \lambda _{3}\parallel _{L^{(\frac{p}{\alpha })^{'}}(\Omega )}, \parallel f\parallel _{L^{1}(\Omega ,I\!\!R^{m})},c_{2}. \end{aligned}$$

Proof

We suppose the condition of l’angle in $(H_{3}).$ Let $\alpha >0.$ Testing $T_{\alpha }(u)$ in (4.3) and we use the coercivity condition in $(H_{1}),$ and Hölder inequality, we have

$$\begin{aligned}{} & {} c_{2}.\sum _{i,j}\int _{| u|\le \alpha }\omega _{ij} |D_{ij}u|^{p}dx\le \alpha \parallel f\parallel _{L^{1}(\Omega ,I\!\!R^{m})}+\parallel \lambda _{2}\parallel _{L^{1}(\Omega )}\nonumber \\{} & {} \quad +\,c\parallel \lambda _{3}\parallel _{L^{\left( \frac{p}{\alpha }\right) ^{'}}}\left( \sum _{j=1}^{m}\int _{| u|\le \alpha }\gamma _{j}\mid u_{j}\mid ^{q}dx\right) ^{\frac{\alpha }{p}} \end{aligned}$$

(4.4)

Choose:

$$\begin{aligned} (u)_{\alpha }= \left\{ \begin{array}{ll} u&{}\quad \text{ if } \quad | u|\le \alpha , \\ 0 &{}\quad \text{ if } \quad | u|>\alpha . \end{array} \right. \end{aligned}$$

Then $u\in W_{0}^{1,p}(\Omega ,\omega ,I\!\!R^{m})$ because $u\in W_{0}^{1,p}(\Omega ,\omega ,I\!\!R^{m})$ and by Hardy-Type inequality

$$\begin{aligned} \displaystyle \sum _{j}^{m}\int _{| u|\le \alpha }\gamma _{j} | u_{j}|^{q}dx= & {} \displaystyle \sum _{j}^{m}\int _{| u|\le \alpha }\gamma _{j}|(u_{\alpha })_{j}|^{q}dx\\\le & {} c\left( \displaystyle \sum _{i,j}\int _{\Omega }\omega _{ij} |D_{ij}u_{\alpha }|^{p}dx\right) ^{\frac{q}{p}}\\\le & {} c\left( \displaystyle \sum _{i;j}\int _{| u|\le \alpha }\omega _{ij}| D_{ij}u_{\alpha }|^{p}dx\right) ^{\frac{q}{p}} \end{aligned}$$

By (4.4)

$$\begin{aligned} c_{2}\left( \sum _{ij}\int _{|u|\le \alpha }\omega _{ij}|D_{ij}u|^{p}dx\right)\le & {} \alpha \parallel f\parallel _{L^{1}(\Omega ,I\!\!R^{m})}+\parallel \lambda _{2}\parallel _{L^{1}(\Omega )}\\{} & {} +\,c\parallel \lambda _{3}\parallel _{L^{\left( \frac{p}{\alpha }\right) ^{'}}}. \left( \sum _{i,j}\int _{| u|\le \alpha }\omega _{ij}| D_{ij}u|^{p}dx\right) ^{\frac{\alpha q}{p^{2}}} \end{aligned}$$

and $\frac{\alpha q}{p^{2}}<1.$ Then

$$\begin{aligned} \left( \sum _{ij}\int _{|u|\le \alpha }\omega _{ij}|D_{ij}u|^{p}dx\right) \le c\left( \alpha \parallel f\parallel _{L^{1}(\Omega ,I\!\!R^{m})} +\parallel \lambda _{2}\parallel _{L^{1}(\Omega )}\right) \le M\alpha +L, \end{aligned}$$

(4.5)

with $L=L\left( c,\parallel \lambda _{2}\parallel _{L^{1}(\Omega )}, c\parallel \lambda _{3}\parallel _{L^{\left( \frac{p}{\alpha }\right) ^{.}}}\right)$ and $M=M\left( c_{1},c_{2}\parallel \lambda _{3}\parallel ,{\parallel f\parallel _{L^{1}(\Omega ,I\!\!R^{m})}}\right) ,$ we choose $u^{\alpha }=\min (|u|,\alpha ),$ then by $|D|u||\le | Du|$

$$\begin{aligned}{} & {} \displaystyle \int _{\Omega }| Du^{\alpha }|^{p_{s}}dx=\displaystyle \int _{| u|\le \alpha }| D| u||^{p_{s}}dx+0\le \displaystyle \int _{| u|\le \alpha }| Du|^{p_{s}}dx= \displaystyle \int _{\Omega }| Du_{\alpha }|^{p_{s}}dx\\{} & {} \quad \le \left( \displaystyle \sum _{i,j}\int _{\Omega }\omega _{ij}| D_{ij}u_{\alpha }|^{p}dx\right) ^{\frac{p_{s}}{p}}=\left( \displaystyle \sum _{i,j} \int _{|u|\le \alpha }\omega _{ij}|D_{ij}u|^{p}dx\right) ^{\frac{p_{s}}{p}} \end{aligned}$$

And by (4.5), and $p_{s}\le p,$ we have:

$$\begin{aligned} \displaystyle \int _{\Omega }| Du^{\alpha }|^{p_{s}}dx\le c\left( \alpha \parallel f\parallel _{| L^{1} (\Omega ,I\!\!R^{m})}+\parallel \lambda _{1}\parallel _{L^{1}(\Omega )}\right) . \end{aligned}$$

(4.6)

By (1.4) and (4.6), we have

$$\begin{aligned} \displaystyle \int _{\Omega }|u^{\alpha }|^{p_{s}^{*}}dx\le c\left( \displaystyle \int _{\Omega }| Du^{\alpha }|^{p_{s}}dx\right) ^{\frac{p_{s}^{*}}{p}} \le c\left( \alpha \parallel f\parallel _{L^{1}(\Omega ;I\!\!R^{m})} +\parallel \lambda _{1}\parallel _{L^{1}(\Omega )}\right) ^{\frac{p_{s}^{*}}{p}} \end{aligned}$$

(4.7)

Then

$$\begin{aligned} \lambda _{| u|}(\alpha )= & {} \alpha ^{-p_{s}^{*}}\int _{| u|>\alpha }\alpha ^{p_{s}^{*}}dx \le \alpha ^{-p_{s}^{*}}\int _{| u|>\alpha }| u^{\alpha }|^{p_{s}^{*}}dx\nonumber \\\le & {} c\alpha ^{-p_{s}^{*}}\left( \alpha \parallel f\parallel _{L^{1}(\Omega ,I\!\!R^{m})} +\parallel \lambda _{2}\parallel _{L^{1}(\Omega )}\right) ^{\frac{p_{s}^{*}}{p}} \end{aligned}$$

(4.8)

and we continue in the same way as in a case that is non-degenerated [2] by replacing p by $p_{s}$ as well as

$$\begin{aligned} \Vert u\Vert ^{*}_{L^{{t^{*}_{p_{s}}},\infty }}(\Omega ,I\!\!R^{m})= & {} \sup _{\alpha>0}\alpha |\lambda _{| u|}(\alpha )|^{\frac{1}{t^{*}_{p_{s}}}}\\\le & {} |\Omega |+\sup _{\alpha >1}\alpha |\lambda _{|u|}(\alpha )|^{\frac{1}{t^{*}_{p_{s}}}}\\\le & {} |\Omega |+c(\parallel f\parallel _{L^{1}(\Omega ,I\!\!R^{m})}^{\frac{1}{p_{s}-1}},\parallel \lambda _{2}\parallel _{L^{1}(\Omega )}^{\frac{1}{p_{s}-1}}) \end{aligned}$$

i.e.

$$\begin{aligned} \Vert u\Vert ^{*}_{L^{t_{p_{s}}^{*},\infty }}(\Omega ,I\!\!R^{m}) \le c\left( |\Omega |,\parallel \lambda _{2}\parallel _{L^{1}(\Omega )},\parallel \lambda _{3} \parallel _{L^{\left( \frac{p}{\alpha }\right) _{(\Omega )}^{'};}}c_{2},\parallel f\parallel _{L^{1}(\Omega ,I\!\!R^{m})}\right) , \end{aligned}$$

(4.9)

on the other hen, by using $(p_{s}\le p)$ and thinks to (1.4), we obtain

$$\begin{aligned} \lambda _{| Du|}(s)\le & {} s^{-p_{s}}\displaystyle \int _{| u|\le \alpha }| Du|^{p_{s}}dx+\lambda _{| u|}(\alpha )\\= & {} s^{-p_{s}}\displaystyle \int _{| u|\le \alpha }| Du_{\alpha }|^{p_{s}}dx+\lambda _{| u|}(\alpha ) \\\le & {} s^{-p_{s}}\left( \displaystyle \sum _{i,j}\int _{| u|\le \alpha }\omega _{ij}| D_{ij}u_{\alpha }|^{p}dx\right) +\lambda _{| u|}(\alpha )\\\le & {} s^{-p_{s}}\left( \displaystyle \sum _{i,j}\int _{| u|\le \alpha }\omega _{ij}| D_{ij}u|^{p}dx\right) +\lambda _{| u|}(\alpha ) \end{aligned}$$

By (4.5) and (4.8):

$$\begin{aligned} \lambda _{| Du|}(s)\le c\left( \max \left( \frac{\alpha }{s^{p_{s}}}, \frac{1}{s^{p_{s}}}\right) +\max \left( \alpha ^{-p_{s}^{*}},\alpha ^{\frac{p_{s}^{*}}{p_{s}}-p_{s}^{*}}\right) \right) \end{aligned}$$

or $-t_{p_{s}}^{*}=\frac{p_{s}^{*}}{p_{s}}-p_{s}^{*},$ so as in [6]

$$\begin{aligned} \parallel Du\parallel _{L^{t_{p_{s}}, \infty }(\Omega , M^{m\times n})}^{*}\le c\left( |\Omega |, \parallel \lambda _{2}\parallel _{L^{1}(\Omega )}, \parallel \lambda _{3}\parallel _{L^{\left( \frac{p}{\alpha }\right) _{(\Omega )}^{'}}},c_{2},\parallel f\parallel _{L^{1}(\Omega ;I\!\!R^{m})}\right) . \end{aligned}$$

(4.10)

From (4.5), (4.9) and (4.10), we obtain the result of the proposition (4.1) in case i). ii)-Suppose the angle condition in ($H_{3}$), let $S_{\alpha }(y)=\left( T_{\alpha }(y_{1}); T_{\alpha }(y_{2});\ldots T_{\alpha }(y_{m})\right) ,$ $y\in I\!\!R^{m},$ the cubic truncation, we have $Ds_{\alpha }(y)=\text{ Id }$ if $| y|_{max}=\max _{1\le i\le m}| y_{i}|\le \alpha ,$ in the same way as in i)- by testing $S_{\alpha }(u)$ in (4.3). Then $\displaystyle \int _{\Omega }\sigma (x,u,Du):D(S_{\alpha }(u))dx = \displaystyle \int _{\Omega }f \cdot S_{\alpha }(u)dx$ or

and like $\displaystyle \sum \nolimits _{i=1}^{m}\sigma _{i}(x,u,Du):Du_{i}dx=\sigma (x,u,Du):Du.$ By the coercivity condition in $(H_{1})$ and the Hölder Inequality we obtain:

$$\begin{aligned} c_{2}\displaystyle \sum _{i,j}\int _{| u|\le \alpha }\omega _{ij}| D_{ij}u|^{p}dx\le&\,\sqrt{m}.\alpha \parallel f\parallel _{L^{1}(\Omega ;I\!\!R^{m})}+\parallel \lambda _{2}\parallel _{L^{1}(\Omega )}\\&+ c\parallel \lambda _{3}\parallel _{L^{\left( \frac{p}{\alpha }\right) _{(\Omega )}^{'}}} \left( \sum _{j=1}^{m}\int _{\mid u|\le \alpha }\gamma _{j}| u_{j}|^{q}dx\right) ^{\frac{q}{p}} \end{aligned}$$

and we continue in the same way as in i), this completes the proof of the Proposition (4.1) $\quad \square$

5 A div-curl inequality

The result of this section is the key ingredient for the proof that one can pass to the limit in the Eq. (4.1) for the solution $\{u_{k}\}_{k\in I\!\!N}$ of approximating problems. Since it is independent of the differential equation we state it a more general form using only the hypotheses (5.1)–(5.8) below:

$$\begin{aligned} \sigma ;\tau :\Omega \times I\!\!R^{m}\times M^{m\times n}\longrightarrow M^{m\times n}, \end{aligned}$$

(5.1)

is a Carathéodory function.

$$\begin{aligned} \sigma \text{ and } \tau \text{ satisfing } \text{ one } \text{ of } \text{ the } \text{ fellowing } \text{ conditions: } \end{aligned}$$

(5.2)

(i):

$\sigma (x,u,F):MF\ge 0$, $\tau (x,u,F):MF\ge 0$; $M=\text{ Id }-b\otimes b\in M^{m\times n},$ with $|b|\le 1.$

(ii):

$\sigma _{j}(x;u;F):F_{j}\ge 0$, and $\tau _{j}(x,u,F):F_{j}\ge 0;$ $1\le j\le m$, $\sigma _{j},$ $\tau _{j}$ and $F_{j}$ is the $j^{eme}$ columns of $\sigma , \ \tau ,\ F.$

$$\begin{aligned}{} & {} u_{k}\in W^{1;1}(\Omega ,I\!\!R^{m}) \text{ and } \text{ there } \text{ exists } \text{ an } s\ge 0 \text{ such } \text{ that } \int _{\Omega }\mid Du_{k}\mid ^{s}dx\le c \text{ uniformly } \text{ in } k\nonumber \\ \end{aligned}$$

(5.3)

$$\begin{aligned}{} & {} \text{ The } \text{ sequence } \sigma _{k}(x)=\sigma (x,u_{k},Du_{k}) \text{ is } \text{ equiintegrale. } \end{aligned}$$

(5.4)

$$\begin{aligned}{} & {} \text{ The } \text{ sequence } u_{k} \text{ converges } \text{ in } \text{ measure } \text{ to } \text{ some } \text{ function } u,\nonumber \\{} & {} \quad \text{ and } u \text{ is } \text{ almost } \text{ everywhere } \text{ approximately } \text{ differentiable. } \end{aligned}$$

(5.5)

$$\begin{aligned}{} & {} \text{ The } \text{ sequence } f_{k}=-div(\sigma _{k}+\tau _{k})-\mu \text{ is } \text{ bounded } \text{ in } L^{1}(\Omega ,I\!\!R^{m}). \end{aligned}$$

(5.6)

$$\begin{aligned}{} & {} D_{ij}u_{k}\in L_{loc}^{r}(\Omega ,\omega _{ij},M^{m\times n}) \text{ and } (\sigma _{k}+\tau _{k})\in L_{loc}^{r^{,}}(\Omega ,w^{*},M^{m\times n}), \text{ for } \text{ some } \nonumber \\{} & {} 1\le r\prec \infty \text{ and } (1\le i\le n,\ 1\le j\le m.) \end{aligned}$$

(5.7)

$$\begin{aligned}{} & {} \text{ The } \text{ sequence } \tau _{k}(x)=\tau [x](x,u,Du_{k}) \text{ converges } \text{ to } \text{ weakly } \text{ to } 0 \text{ in } L^{1}(\Omega ,M^{m\times n}). \end{aligned}$$

(5.8)

Lemma 5.1

Suppose (5.1)–(5.8). Then (after passage to a subsequence) the sequence $\sigma _{k}$ converges weakly in $L^{1}(\Omega ,M^{m\times n})$ and the weak limit $\overline{\sigma }$ is given by $\overline{\sigma }(x)= \langle \nu _{x};\sigma (x,u(x),\,.)\rangle .$ Moreover the following inequality holds:

$$\begin{aligned} \displaystyle \int _{M^{m\times n}},\sigma (x,u(x),\lambda ):\lambda d\nu _{x}(\lambda )\le \overline{\sigma }(x):apDu(x) \text{ for } \text{ a.e. } x\in \Omega . \end{aligned}$$

(5.9)

Proof

See [6] $\square$

6 Passage to the limit

Proposition 6.1

Suppose that the sequence $(u_{k})_{k\in I\!\!N}$ satisfies the hypotheses (5.1)–(5.7), $(H_{2})$ and that the Young measure $\nu$ generated by the sequence $(Du_{k})_{k\in I\!\!N}$ satisfies: a)-c) and d)- in Lemma (3.3). Then the sequence $(\sigma _{k})$ is weakly converge in $L^{1}(\Omega ,M^{m\times n}),$ with $\overline{\sigma }$ is the limit and $\overline{\sigma (x)}=\langle \nu _{x},u(x),\text{ apDu }(x)\rangle .$ If in $(H_{2})$ b)- c)-or d)-holds, $\sigma (x,u_{k},Du_{k})\rightarrow \sigma (x,u,\text{ apDu})$ strongly in $L^{1}(\Omega ,M^{m\times n}).$

In the cases (c) and (d) it follows addition that $Du_{k}\rightarrow apDu$ in measure.

Proof

See [6].

Proof of the Theorem 2.1

Case: $\theta =p-1$ For using the results of Proposition (6.1): we assume that (5.1)–(5.7) and the Young measure $\nu _{x}$ generated by the sequence $Du_{k}$ satisfies:(i), (ii) and (iii) in Lemma(3.3), for the approximate systems (4.1) and (4.2). By the proposition 6.1, with $u_{k}\in W_{0}^{1,p}(\Omega ,w,I\!\!R^{m}),$ we have: $\parallel \mu \parallel _{L^{t_{p_{s}}^{*},\infty }(\Omega ,I\!\!R^{m})}\le c\left( |\Omega |,\parallel \lambda _{2}\parallel _{L^{1}(\Omega )},\parallel \lambda _{3} \parallel _{L^{\left( \frac{p}{\alpha }\right) _{(\Omega )}^{'}}},c_{2}, \parallel \mu \parallel _{M(\Omega ,\omega ^{*},I\!\!R^{m})}\right)$ and

$$\begin{aligned} \sum _{i,j}\int _{| u_k|\le \alpha }\omega _{ij}| D_{ij}u_k|^{p}dx\le M\alpha +L<\infty . \end{aligned}$$

(6.1)

By $L^{t_{p_{s}}^{*},\imath \infty }(\Omega ,I\!\!R^{m})\hookrightarrow L^{p}(\Omega ,I\!\!R^{m})$ for all $1< p< t_{p_{s}}^{*},$ then

$$\begin{aligned} \parallel u_{k}\parallel _{L^{p}(\Omega ,I\!\!R^{m})}\le c<\infty . \end{aligned}$$

(6.2)

Now

• (5.1) is $(H_{0})$

• (5.2) is $(H_{3})$

• (5.3): $u_{k}\in W_{0}^{1,p}(\Omega ,\omega ,I\!\!R^{m})\hookrightarrow W_{0}^{1,p_{s}}(\Omega ,I\!\!R^{m})$ with $p_{s}>1,$ then $u_{k}\in W^{1,1}(\Omega ,I\!\!R^{m}).$ Moreover, by the proposition

  $$\begin{aligned} \parallel Du_{k}\parallel _{L^{t_{p_{s}},\infty }(\Omega ,I\!\!R^{m})} \le c\left( |\Omega |,\parallel \lambda _{2}\parallel _{L^{1}(\Omega )}, \parallel \lambda _{3}\parallel _{L^{\left( \frac{p}{\alpha }\right) _{(\Omega )}^{'}}},c_{2}, \parallel \mu \parallel _{M(\Omega ,\omega ^{*}, I\!\!R^{m})}\right) \end{aligned}$$

  hence

  $$\begin{aligned} \parallel Du_{k}\parallel _{L^{s}(\Omega ,M^{m\times n})}\le c>\infty ,\ \forall \ 1<s<t_{p_{s}} \end{aligned}$$

  with $\sup _{k\in I\!\!N}\displaystyle \int _{\Omega }| Du_{k}|^{s}dx<\infty .$

• (5.4): Let A a measurable in $\Omega$, by $(H_{1})$ and Hölder we have

  $$\begin{aligned} \displaystyle \int _{A} |\sigma (x,u_{k},Du_{k})|dx\le & {} c\left( \displaystyle \sum _{r,s}\int _{\Omega }\omega _{rs}dx\right) ^{\frac{1}{p}}.\left[ \parallel \lambda _{1}\parallel _{L^{p^{'}}(\Omega )}\right. \\{} & {} \left. +\,\left( \displaystyle \sum _{j=1}^{m}\int _{\Omega }\gamma _{j}|(u_{k})_{j}|^{q}dx\right) ^{\frac{1}{p^{'}}} +\left( \displaystyle \sum _{i;j}\int _{\Omega }\omega _{ij}| D_{ij}u_{k}|^{p}dx\right) ^{\frac{1}{p^{'}}}\right] , \end{aligned}$$

  and with (1.4) and (1.2):

  $$\begin{aligned} \displaystyle \int _{A}|\sigma (x,u_{k},Du_{k})| dx\le & {} c\left( \displaystyle \sum _{r,s}\parallel \omega _{rs}\parallel _{L_{loc}^{1}(\Omega )}^{\frac{1}{p}}\right) \\{} & {} \times \Bigg [\parallel \lambda _{1}\parallel _{L^{p'}(\Omega )}+\parallel u_{k} \parallel _{1,p,\omega }^{\frac{q}{pp'}}+\parallel u_{k}\parallel _{1,p,\omega }^{\frac{p}{p'}}\Bigg ] <\infty . \end{aligned}$$

• (5.5): By (6.1) and (6.2) and Lemma (3.2).

• (5.6): $\parallel f_{k}\parallel _{L^{1}(\Omega ,I\!\!R^{m})}\le \parallel \mu \parallel _{M(\Omega ,\omega ^{*},I\!\!R^{m})}$.

• (5.7): $\forall \varepsilon >0$ and $x_{0}\in \Omega$ $\displaystyle \int _{B(x_{0},\varepsilon )}|D_{ij}u_{k}|^{p}\omega _{ij}dx\le \parallel u_{k}\parallel _{1,p,\omega }^{p}<\infty$ and by $(H_{3})$ we implies

  $$\begin{aligned} \displaystyle \int _{B(x_{0},\varepsilon )}|\sigma _{rs}(x,u_{k},Du_{k})|^{p'}\omega _{rs}^{*}dx= & {} \displaystyle \int _{B(x_{0},\varepsilon )}|\sigma _{rs}(x,u_{k},Du_{k})|^{p'}\omega _{rs}^{1-p'}dx \\\le & {} c\displaystyle \int _{_{B(x_{0},\varepsilon )}}w^{1-p'+\frac{p'}{p}}\left[ |\lambda _{1}|^{p'} +\displaystyle \sum _{j=1}^{m}\gamma _{j}|(u_{k})_{j}|^{q}\right. \\{} & {} \left. + \displaystyle \sum _{i,j} \omega _{ij}|D_{ij}u_{k}|^{p}\right] dx\\\le & {} c\left( \parallel \lambda _{1}\parallel _{L^{p'}(\Omega )}^{p'} +\parallel u_{k}\parallel _{1,p,w}^{\frac{q}{p}}+\parallel u_{k}\parallel _{1,p,\omega }^{p}\right) <\infty . \end{aligned}$$

  Then, by the Proposition (6.1) $\sigma (x,u_{k},Du_{k})\longrightarrow \sigma (x,u,apDu)$ in $L^{1}(\Omega ,I\!\!M^{m\times n})$ and $\forall \varphi \in C_{0}^{\infty }(\Omega ,I\!\!R^{m}); \;D\varphi \in L^{\infty }(\Omega ,I\!\!M^{m\times n})$ hence

  $$\begin{aligned} \displaystyle \int _{\Omega }\sigma (x,u_{k},Du_{k}):D\varphi dx\longrightarrow \int _{\Omega }\sigma (x,u,apDu):D\varphi dx \end{aligned}$$

  i.e.

  $$\begin{aligned} -div\sigma (x,u_{k},apDu_{k})\longrightarrow -div\sigma (x,u,\text{ apDu}) \end{aligned}$$

  In the sense of distributions. On the other hand $f_{k}{\mathop {\longrightarrow \mu }\limits ^{*}}$ in $L^{1}(\Omega ,I\!\!R^{m}).$ Then $\displaystyle \int _{\Omega }f_{k}.\varphi dx\longrightarrow \displaystyle \int _{\Omega }\mu .\varphi dx\;\;\;\forall \varphi \in C_{0}^{\infty }(\Omega ,I\!\!R^{m})$ so $\mu$ is the solution in $W_{0}^{1,p}(\Omega ,\omega ,I\!\!R^{m})$ of the system:

  $$\begin{aligned}{} & {} -div\sigma (x,u,\text{ apDu})=\mu \;\;\;\text{ in }\;\; \Omega \\{} & {} u=0 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\text{ on }\;\; \partial \Omega \end{aligned}$$

  to show the estimation (2.1), we take the function $\eta$ in $C_{0}^{1}(B(0,2\alpha ),I\!\!R^{m}); \eta = \text{ Id }$ in $B(0,\alpha )$ and $| D\eta |\le c,$ then:

  $$\begin{aligned} \displaystyle \sum _{i,j}\int _{\Omega }\omega _{ij}| D_{ij}\eta (u_{k})|^{p}dx= & {} \displaystyle \sum _{i,j}\int _{\Omega }\omega _{ij}|(D_{ij}\eta )(u_{k})|^{p}|Du_{k}\Vert ^{p}dx\\\le & {} c^{p}.\displaystyle \sum _{ij}\int _{|u_{k}|\le \alpha }\omega _{ij}| D_{ij}u_{k})| dx\\{} & {} +\,c\displaystyle \sum _{i,j}\int _{|u_{k}|\le 2\alpha }\omega _{ij} D_{ij}u_{k}|^{p}dx\\\le & {} c.c(\alpha )+c.c(2\alpha )<\infty , \end{aligned}$$

  thanks to (6.1).

  Now, we have $\eta (u_{k})\longrightarrow \eta (u),$ for every $x\in \Omega$ because $\eta$ is $C^{\infty }.$ Then $\eta (u_{k})\rightharpoonup \eta (u),$ in $W_{0}^{1,p}(\Omega ,\omega ,I\!\!R^{m})$ and $\text{ apDu } = \text{ apD }(\eta \circ u)$ on $\left\{ |u|\prec \alpha \right\} .$ Hence,

  $$\begin{aligned} \displaystyle \sum _{i,j}\int _{\Omega }\omega _{ij}| D_{ij}(\eta \circ u)|^{p}dx\le & {} \liminf _{k\longrightarrow \infty }\int _{\Omega }w|D(\eta \circ u_{k})|^{p}dx \\\le & {} \liminf _{k\longrightarrow \infty }\displaystyle \sum _{ij}\int _{| u_{k}|\le 2\alpha }| D_{ij}\eta (u_{k})|^{p}| D_{ij}u_{k}| \omega _{ij}dx \\\le & {} \le c\liminf _{k\longrightarrow \infty }\int _{| u_{k}|\le 2\alpha }\omega _{ij}|D_{ij}u_{k})|^{p}dx \\\le & {} c.c(2\alpha )<\infty . \end{aligned}$$

  Then:

  $$\begin{aligned} \displaystyle \sum _{i,j}\int _{| u|\le \alpha }\omega _{ij}| apDu|^{p}dx=\displaystyle \sum _{i,j}\int _{| u_{k}|\le 2\alpha }\omega _{ij}| D(\eta \circ u)|^{p}dx<\infty , \end{aligned}$$

  in the same as in the proof of the Proposition (4.1) by replacing $u_{k}$ by u and $f_{k}$ by $\mu$, we obtain the estimation (2.1) and this completes the proof of the Theorem 2.1$\Box$

Case: $0<\theta <\frac{n(p_{s}-1)}{n-1}$ (the general case) The idea is to consider the regularized problems:

$$\begin{aligned}{} & {} -div\phi _{\varepsilon }(x,u_{\varepsilon },Du_{\varepsilon })=\mu \;\;\; \text{ in } \Omega , \end{aligned}$$

(6.3)

$$\begin{aligned}{} & {} u_{\varepsilon }= 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \text{ on } \partial \Omega \end{aligned}$$

(6.4)

with

$$\begin{aligned} \phi _{\varepsilon ,r,s}(x,u,F)=\sigma _{rs}(x,u,F)+\varepsilon \beta \left( \displaystyle \sum _{ij}\omega _{ij}^{\frac{1}{p'}}| F_{ij}|^{s-2}\right) \omega _{rs}^{\frac{1}{p}}F_{rs}, \end{aligned}$$

$\forall 1\le r\le n,\ \forall 1\le s\le m$ with $s>n+1,$ and $\varepsilon <\frac{1}{2},$ we have $p<s,$ then $s'<p',$ and

$(\frac{s}{\alpha })'<(\frac{p}{\alpha })'.$ Moreover $\exists c>0$ which doesn’t depend on p,  s,  such that $\omega _{rs}^{\frac{1}{p}}\le c\omega _{rs}^{\frac{1}{s}}$

$\forall \ 1\le r\le n$ and $1\le s\le m.$

By $(H_{1})$ for $\sigma ,$ we obtain

$$\begin{aligned} |\phi _{\varepsilon ,r,s}(x,u,F)|\le & {} \beta ^{'}.| \omega _{rs}|^{\frac{1}{p}}\left[ \lambda _{1}+\sum _{j=1}^{m}\gamma _{j}^{\frac{1}{p'}}| u_{j}|^{\frac{q}{p'}}+\sum _{i,j}\omega _{ij}^{\frac{1}{p'}}| F_{ij}|^{\theta }\right] \\{} & {} +\,\varepsilon \beta \omega _{rs}^{\frac{1}{p}}\left( \sum _{i,j}\omega _{ij}^{\frac{1}{p'}}| F_{ij}|^{s-1}\right) \left( \theta<\frac{n(p_{s}-1)}{n-1}<n(s-1)\right) \\\le & {} \le \beta '\omega _{rs}^{\frac{1}{p}}\left[ \lambda _{1}+\sum _{j=1}^{m}\gamma _{j}^{\frac{1}{p'}}| u_{j}|^{\frac{q}{p'}}+\sum _{i,j}\omega _{ij}^{\frac{1}{p'}}| F_{ij}|^{s-1}\right] . \end{aligned}$$

And $p<s,$ then $\frac{1}{p'}<\frac{1}{s'}$ and like $\omega _{rs}^{\frac{1}{p}}\le c\omega _{rs}^{\frac{1}{s}},$ then: $|\phi _{\varepsilon ,r,s}(x,u,F)|\le \beta '.| \omega _{rs}|^{\frac{1}{s}}\left[ \lambda _{1}+\displaystyle \sum _{j=1}^{m}\gamma _{j}^{\frac{1}{s'}}| u_{j}|^{\frac{q}{s'}}+\sum _{ij}\omega _{ij}^{\frac{1}{s'}}| F_{ij}|^{s-1}\right] ,$ and by $(H_{3}),$ we conclude that

$$\begin{aligned} \phi _{\varepsilon }(x,u,F):F=\sigma (x,u,F):F+\varepsilon \sum _{i,j,r,s} \omega _{ij}^{\frac{1}{p'}}\omega _{rs}^{\frac{1}{p}}| F_{ij}|^{s-2}F_{ij}.F_{rs} \end{aligned}$$

$\ge -\lambda _{2}-\sum _{j=1}^{m}\lambda _{3}\gamma _{j}^{\frac{q}{s}}.| u_{j}|^{\frac{q\alpha }{s}}+\varepsilon \sum _{ij}\omega _{ij}| F_{ij}|^{s}.$

On the other hand, $0<\alpha<p-1<s-1,$ $1<q<\frac{p^{2}}{\alpha }<\frac{s^{2}}{\alpha '},$ $\lambda _{1}\in L^{p'}(\Omega )\hookrightarrow L^{s'}(\Omega ),$ and $\lambda _{3}\in L^{(\frac{p}{\alpha })'}(\Omega )\hookrightarrow L^{(\frac{s}{\alpha })'}(\Omega )$ and as $\sigma _{\varepsilon }$ verifies the conditions of the structures (of l’angle and sign), the strict monotony, the s-quasi monotonous with regard to F is a $C^{1}$ monotony in relation with F or accepting a convex potential because: $F\longrightarrow \varepsilon \beta \left( \displaystyle \sum \nolimits _{ij}\omega _{ij}^{\frac{1}{p'}}| F_{ij}|^{s-2}\right) \omega _{rs}^{\frac{1}{p}}F_{rs}$ verify them as well, hence $\sigma _{\varepsilon }$ verifies the hypotheses $(H_{0})$–$(H_{5}),$ for the regularized Problems (6.3) and (6.4), thus for the previous case, $\theta =s-1$ of Theorem 2.1, there exists a solution, $u_{\varepsilon }\in W_{0}^{1,s}(\Omega ,\omega ,I\!\!R^{m})$ of the system (6.3) and (6.4). Now showing that the conditions: i), ii) and iii), of lemma (3.3), and the hypotheses (5.1)–(5.8) of the div-curl inequality are verified for $u_{\varepsilon }$ with order s in the place of p.

We suppose the condition of l’angle verifying that $\phi _{\varepsilon }$ by testing, $T_{\alpha }(u_{\varepsilon })$ $\alpha >0$ in (5.3) and (5.4), we get: $\displaystyle \int _{\Omega }\phi _{\varepsilon }(x,u_{\varepsilon },Du_{\varepsilon }):DT_{\alpha }(u_{\varepsilon })dx$= $\displaystyle \int _{\Omega }f.T_{\alpha }(u_{\varepsilon })dx,$ so

$$\begin{aligned}{} & {} \displaystyle \int _{|u_{\varepsilon }|\le \alpha }\sigma (x,u_{\varepsilon },Du_{\varepsilon }):Du_{\varepsilon }dx+ \displaystyle \int _{|u_{\varepsilon }|>\alpha }\frac{\alpha }{|u_{\varepsilon }|}\sigma _{\varepsilon }(x,u_{\varepsilon },Du_{\varepsilon }):\left( \text{ Id }-\frac{u_{\varepsilon }}{| u_{\varepsilon }|}\otimes \frac{u_{\varepsilon }}{| u_{\varepsilon }|}\right) Du_{\varepsilon }dx\\{} & {} \qquad +\,\varepsilon \beta \int _{| u_{\varepsilon }|\le \alpha }\displaystyle \sum _{i,j}\omega _{ij}^{\frac{1}{p'}}| D_{ij}u_{\varepsilon }|^{s-2}\displaystyle \sum _{r,s}\omega _{rs}^{\frac{1}{p}}| D_{rs}u_{\varepsilon }|^{2}dx\\{} & {} \qquad +\,\varepsilon \beta \int _{| u_{\varepsilon }|>\alpha }\sum _{ij}\omega _{ij}^{\frac{1}{p'}}| D_{ij}u_{\varepsilon }|^{s-2}\sum _{r,s}\omega _{rs}D_{rs}u_{\varepsilon }\left( Id-\frac{u_{\varepsilon }}{| u_{\varepsilon }|}\otimes \frac{u_{\varepsilon }}{| u_{\varepsilon }|}\right) \\{} & {} \quad \le \alpha .\parallel f\parallel _{L^{1}(\Omega ,I\!\!R^{m})}. \end{aligned}$$

since

$$\begin{aligned} \displaystyle \sum _{rs}| D_{rs}u_{\varepsilon }|^{s-2}D_{rs}u_{\varepsilon }\left( \text{ Id }-\frac{\alpha }{| u_{\varepsilon }|}\left( \frac{u_{\varepsilon }}{| u_{\varepsilon }|}\otimes \frac{u_{\varepsilon }}{| u_{\varepsilon }|}\right) \right) \ge 0 \end{aligned}$$

so

$$\begin{aligned} \displaystyle \int _{| u_{\varepsilon }|\le \alpha }\sigma (x,u_{\varepsilon },Du_{\varepsilon }):Du_{\varepsilon }dx\le \alpha \parallel f\parallel _{L^{1}(\Omega ,I\!\!R^{m})}. \end{aligned}$$

And by the coercivity condition of $\sigma$ in $(H_{1})$ and Hölder inequality, we get as in the proof of the Proposition 4.1

$$\begin{aligned} \displaystyle \sum _{ij}\int _{| u_{\varepsilon }|\le \alpha }\omega _{ij}|D_{ij}u_{\varepsilon }|^{p}dx\le M'\alpha +L', \end{aligned}$$

(6.5)

And the following a priori estimation:

$$\begin{aligned} \parallel u_{\varepsilon }\parallel _{L^{t_{p_{s};\infty }^{*}}(\Omega ,I\!\!R^{m})}^{*}+\parallel Du_{\varepsilon }\parallel _{L^{t_{p_{s},\infty }}(\Omega ,I\!\!R^{m\times n})}^{*}<c<\infty , \end{aligned}$$

(6.6)

and by the injection $L^{\beta ',\infty }\hookrightarrow L^{\alpha '},\forall 0<\alpha '<\beta ',$ then $\forall ,\;\;0<r<t_{p_{s}}^{*},$ $\forall 0<p<t_{p_{s}}$

$$\begin{aligned} \parallel u_{\varepsilon }\parallel _{L^{r}(\Omega ,I\!\!R^{m})}+\parallel Du_{\varepsilon }\parallel _{L^{p}(\Omega ,I\!\!M^{m\times n})}+\parallel Du_{\varepsilon }\parallel _{L^{t_{p_{s},\infty }}(\Omega ,I\!\!M^{m\times n})}^{*}<\infty . \end{aligned}$$

(6.7)

We suppose that the condition of the sign is verify.

As in the same way in the proof of the Proposition (4.1), we test $S_{\alpha }(u_{\varepsilon })$ in (6.3) and (6.4), we obtain (6.5) and (6.7).

Starting with verifying that i), ii) et iii) of lemma (3.3) and the hypotheses (5.1) and(5.7) for $\sigma _{\varepsilon }$. By (6.5)and(6.7), the points i), ii) et iii) are a direct consequence of Lemmas (3.2) and (3.3). On the other hand:

• (5.1): for $\sigma$ is $(H_{0})$ and $\tau _{rs}(x,u,F)=\varepsilon \beta \left( \sum _{i,j}\omega _{ij}^{\frac{1}{p'}}| F_{ij}|^{s-2}\right) .\omega _{rs}^{\frac{1}{p}}F_{rs}$ is a Carathéodory function, because $x\longmapsto \omega _{ij}(x),$ is measurable, so $\sigma _{\varepsilon }$ is a Cathéodory function.

• (5.2)

(i):

$\phi _{\varepsilon }(x,u,F):MF=\sigma (x,u,F):MF+\left( \displaystyle \sum \nolimits _{rs} (\varepsilon \sum \nolimits _{i,j}\omega _{ij}^{\frac{1}{p'}}| F_{ij}|^{s-2})\omega _{rs}^{\frac{1}{p}}F_{rs}\right) (MF)_{rs}\ge 0$, with $M= \text{ Id }-a\otimes a$ and $| a|\le 1.$

(ii):

$$\begin{aligned} \phi _{rs}(x,u,F) \cdot F_{j}= & {} \sigma _{j}(x,u,F):F_{j}+\tau _{j}(x,u,F) \cdot F_{j} \\= & {} \sigma _{j}(x,u,F):F_{j}+\displaystyle \sum _{l=1}^{m}\varepsilon \beta \left( \displaystyle \sum _{_{i,j}}\omega _{ij}^{\frac{1}{p'}}| F_{ij}|^{s-1}\right) \cdot w_{lj}^{\frac{1}{p}}| F_{lj}|^{2}\ge 0, \end{aligned}$$

$\forall 1\le j\le m.$

• (5, 3): $u_{\varepsilon }\in W_{0}^{1,s}(\Omega ,\omega ,I\!\!R^{m})\hookrightarrow W_{0}^{1,s_{s}}(\Omega ,I\!\!R^{m}),$ $s_{s}>1,$ so $u_{\varepsilon }\in W^{1,1}(\Omega ,I\!\!R^{m})$, and by (6.7) $\sup _{\varepsilon >0}\displaystyle \int _{\Omega }| Du_{\varepsilon }|^{p}dx<\infty ,$ $\forall ,$ $0<p<t_{p_{s}}.$

  (4.5): $\sigma (x,u_{\varepsilon },Du_{\varepsilon })$ is equi-integrable as previously $\forall \;\Omega '\subset \Omega ,$ measurable, we have:

  $$\begin{aligned}{} & {} \displaystyle \int _{\Omega '}\left| \sum _{i,j}(\omega _{ij}^{\frac{1}{p'}}\right| D_{ij}u_{\varepsilon }|^{s-2})\omega _{rs}^{\frac{1}{p}}D_{rs}u_{\varepsilon }|dx\\{} & {} \quad \le \left( \displaystyle \sum _{i,j}\int _{\Omega '}\omega _{ij}| D_{ij}u_{\varepsilon }|^{s-1}dx\right) \\{} & {} \quad \le c\displaystyle \sum _{ij}\int _{\Omega '}\omega _{ij}| D_{ij}u_{\varepsilon }|^{s}dx\le c\parallel u_{\varepsilon }\parallel _{1,s,w}^{s}. \end{aligned}$$

• (5.5): by (6.7) and the Lemma (3.2).

• (5.6): by (6.3), $-div(\sigma _{l}+\tau _{k})-\mu =0,$ with $\mu \in M(\Omega ,I\!\!R^{m})$ is bounded in $L^{1}(\Omega ,I\!\!R^{m}).$

• (5.7): $\forall \;\varepsilon >0$ and $x_{0}\in \Omega ,$ by the growth condition of $\sigma _{\varepsilon }$ and previously with s in the place of p, $\displaystyle \int _{B(x,{\varepsilon })}|\sigma _{\varepsilon }(x,u_{\varepsilon },Du_{\varepsilon })|^{s}\omega _{rs}^{*}dx<\infty$ and

• (5.8): $\displaystyle \int _{B(x,{\varepsilon })}| D_{ij}u_{\varepsilon }|^{s}\omega _{rs}dx<\parallel u_{\varepsilon }\parallel _{1,s,w}^{\varepsilon }<\infty .$

Testing that $u_{\varepsilon }$ in (6.3) and (6.4)

$$\begin{aligned}{} & {} \varepsilon \beta \displaystyle \int _{\Omega }\left( \displaystyle \sum _{ij}\omega _{ij}^{\frac{1}{p'}}| D_{ij}u_{\varepsilon }|^{s-2}\right) \left( \displaystyle \sum _{rs}\omega _{rs}^{\frac{1}{p}}|D_{rs} u_{\varepsilon }|^{2}\right) dx\nonumber \\{} & {} \quad \le \parallel u_{\varepsilon }\parallel _{L^{\infty }(\Omega ,I\!\!R^{m})}\parallel \mu \parallel _{M(\Omega ,\omega ^{*},I\!\!R^{m})} \end{aligned}$$

(6.8)

We have $W_{0}^{1,s}(\Omega ,w,I\!\!R^{m})\hookrightarrow W_{0}^{1,s_{s}}(\Omega ,I\!\!R^{m})\hookrightarrow L^{\infty }(\Omega ,I\!\!R^{m}).$ Then

$$\begin{aligned} \begin{aligned} \parallel u_{\varepsilon }\parallel _{L^{\infty }(\Omega ,I\!\!R^{m})}&\le c\left( \displaystyle \sum _{i,j}\int _{\Omega }\omega _{ij}| D_{ij}u_{\varepsilon }|^{s}dx\right) ^{\frac{1}{s}} \\&\le c\left( \displaystyle \sum _{i,j}\int _{\Omega }\omega _{ij}^{\frac{1}{p'}} |D_{ij}u_{\varepsilon }|^{s-2}\omega _{ij}^{\frac{1}{p}}| D_{ij}u_{\varepsilon }|^{2}dx\right) ^{\frac{1}{s}} \\&\le c\left( \displaystyle \int _{\Omega }\left( \sum _{i,j}\omega _{ij}^{\frac{1}{p'}} |D_{ij}u_{\varepsilon }|^{s-2}\right) \cdot \left( \displaystyle \sum _{r,s}\omega _{rs}^{\frac{1}{p}} | D_{rs}u_{\varepsilon }|^{2}dx\right) \right) ^{\frac{1}{s}}. \end{aligned} \end{aligned}$$

(6.9)

Thanks to (6.8) and (6.9), we have

$$\begin{aligned} \displaystyle \int _{\Omega }\sum _{ij}\omega _{ij}^{\frac{1}{p'}} | D_{ij}u_{\varepsilon }|^{s-2}\displaystyle \sum _{rs}\omega _{rs}^{\frac{1}{p}}| D_{rs}u_{\varepsilon }|^{2}dx \end{aligned}$$

$\ \ \ \le \frac{c\parallel \mu \parallel _{M(\Omega ,\omega ^{*},I\!\!R^{m})}}{\varepsilon }\left( \displaystyle \int _{\Omega }\left( \displaystyle \sum _{i,j}\omega _{ij}^{\frac{1}{p'}}| D_{ij}u_{\varepsilon }|^{s-2}\right) .\left( \displaystyle \sum _{rs}\omega _{rs}^{\frac{1}{p}}| D_{rs}u_{\varepsilon }|^{2}dx\right) \right)$ So:

$$\begin{aligned} \left( \displaystyle \int _{\Omega }\left( \sum _{i,j}\omega _{ij}^{\frac{1}{p'}}| D_{ij}u_{\varepsilon }|^{s-2}\right) \cdot \left( \displaystyle \sum _{r,s}\omega _{rs}^{\frac{1}{p}}| D_{rs}u_{\varepsilon }|^{2}dx\right) \right) ^{\frac{s-1}{s}}\le \frac{c\parallel \mu \parallel _{M}}{\varepsilon }, \end{aligned}$$

which mean that

$$\begin{aligned} \left( \int _{\Omega }(\displaystyle \sum _{i,j}\omega _{ij}^{\frac{1}{p'}}|D_{ij}u_{\varepsilon }|^{s-2}).(\displaystyle \sum _{r,s}\omega _{rs}^{\frac{1}{p}}| D_{rs}u_{\varepsilon }|^{2}dx\right) ^{\frac{1}{s}}\le \frac{c\parallel \mu \parallel _{M}}{\varepsilon }, \end{aligned}$$

(6.10)

and

$$\begin{aligned} \parallel u_{\varepsilon }\parallel _{L^{\infty }(\Omega ,I\!\!R^{m})}\le c\left( c\frac{\parallel \mu \parallel _{M}}{\varepsilon }\right) ^{\frac{1}{s-1}}. \end{aligned}$$

(6.11)

On the other hand and $\forall \, \; 1< p <\frac{s}{s-1},$ can write

$$\begin{aligned} \begin{aligned}&\parallel \epsilon \displaystyle \sum _{i,j}\omega _{ij}^{\frac{1}{p'}}| D_{ij}u_{\varepsilon }|^{s-2}\omega _{rs}^{\frac{1}{p}}| F_{rs}|\parallel _{L^{\frac{s}{s-1}}(\Omega ,I\!\!M^{m\times n})} \\&\quad \le \varepsilon ^{\frac{s}{s-1}}\left( \displaystyle \int _{\Omega }|\sum _{i,j}\omega _{ij}^{\frac{1}{p'}} D_{ij}u_{\varepsilon }|^{s-1}\omega _{rs}^{\frac{1}{p}}|^{\frac{s}{s-1}}dx\right) ^{\frac{s-1}{s}}\\&\quad \le c\varepsilon ^{\frac{s}{s-1}}\left( |\displaystyle \sum _{i,j}\int _{\Omega }\omega _{ij}^{\frac{1}{p'}}| D_{ij}u_{\varepsilon }|^{s-1}\omega _{rs}^{\frac{1}{p}}|^{\frac{s}{s-1}}dx\right) ^{\frac{s-1}{s}}\\&\quad \le c\varepsilon ^{\frac{s}{s-1}}\left( \displaystyle \sum _{i,j}\int _{\Omega }\omega _{ij} |D_{ij}u_{\varepsilon }|^{s-2}\displaystyle \sum _{r,s}\omega _{rs}^{\frac{s}{(s-1)p}} | D_{rs}u_{\varepsilon }|^{2}dx\right) <\infty . \end{aligned} \end{aligned}$$

thanks to (6.10). Now, since $u_{\varepsilon }\in W_{0}^{1,s}(\Omega ,\omega ,I\!\!R^{m})\hookrightarrow W_{0}^{1,s_{s}}(\Omega ,I\!\!R^{m})\,\hookrightarrow \,W_{0}^{1,p_{s}}(\Omega ,I\!\!R^{m}),$ so by testing $T_{\alpha }(u_{\varepsilon })$ in (6.3) and (6.4), we obtain as in the proof of the proposition (4.1)

$$\begin{aligned} \parallel Du_{\varepsilon }\parallel ^*_{L^{\frac{n(p_{s}-1)}{n-1},\infty }(\Omega ,I\!\!M^{m\times n})}\le c. \end{aligned}$$

(6.12)

By the Hölder inequality for the exponent a with a and $\xi$ are the solutions of systems:

$$\begin{aligned} \left\{ \begin{array}{rcl} a'\xi = \tau &{} > &{} \frac{n(p_{s}-1)}{n-1} \\ a\left( (s-1)\rho -\xi \right) &{} = &{} s \end{array} \right. \end{aligned}$$

a given system accepting the solution when $\rho <\frac{s}{s-1}.$ So

$$\begin{aligned}{} & {} \int _{\Omega } | \varepsilon \sum _{i,j}\omega _{ij}^{\frac{1}{p'}}|D_{ij}u_{\varepsilon }|^{s-1} \omega _{ij}^{\frac{1}{p}}|^{\rho }dx\\{} & {} \quad \le c\displaystyle \int _{\Omega }\varepsilon ^{\rho }\left( \displaystyle \sum _{i,j} \omega _{ij}^{\frac{\rho }{p'}}| D_{ij}u_{\varepsilon }|^{(s-1)\rho -\xi } \omega _{ij}^{\frac{\rho }{p}}| D_{ij}u_{\varepsilon }|^{\xi }\right) ^{\rho }dx\\{} & {} \quad \le c\varepsilon ^{\rho }\left( \displaystyle \sum _{i,j}\int _{\Omega }\omega _{ij}^{a\rho }| D_{ij}u_{\varepsilon }|^{a\left( (s-1)\rho -\xi \right) }dx\right) ^{\frac{1}{a}}. \left( \int _{\Omega }| Du_{\varepsilon }|^{a'\xi }dx\right) ^{\frac{1}{a'}}\\{} & {} \quad \le c\varepsilon ^{\rho }\left( \displaystyle \sum _{i,j}\int _{\Omega } \omega _{ij}^{\frac{1}{p'}}| D_{ij}u_{\varepsilon }|^{s-2} \displaystyle \sum _{r,s}\omega _{rs}^{\frac{1}{p}}| D_{rs}u_{\varepsilon }|^{2}\right) ^{\frac{1}{a}}. \parallel Du_{\varepsilon }\parallel _{L^{\tau }(\Omega ,I\!\!M^{m\times n})}^{\frac{\tau }{a}}. \end{aligned}$$

And by the injection: $L^{\frac{n(p_{s}-1)}{n-1}}\hookrightarrow L^{\tau }\qquad \forall \tau >\frac{n(p_{s}-1)}{n-1}$ and thanks to (6.10)–(6.12), we get:

$$\begin{aligned} \displaystyle \int _{\Omega }|\varepsilon \sum _{i,j}\omega _{ij}^{\frac{1}{p'}}|D_{ij}u_{\varepsilon }|^{s-1} \omega _{ij}^{\frac{1}{p}}|^{\rho }dx\le & {} c.\varepsilon ^{\rho }\left( \frac{c\parallel \mu \parallel _{M}}{\varepsilon }\right) ^{\frac{s}{(s-1)a}}.c^{\frac{\tau }{a}} \\\le & {} c.c^{\frac{\tau }{a}}\varepsilon ^{\frac{a\left( (s-1)\rho -s)\right) }{a(s-1)}}\\\le & {} c.c^{\frac{\tau }{a}}\varepsilon ^{\frac{a\xi }{a(s-1)}}\\\le & {} c.c^{\frac{\tau }{a}}.\varepsilon ^{\frac{\xi }{s-1}} \end{aligned}$$

with $\frac{\xi }{s-1}>0.$ Hence

$$\begin{aligned} \lim _{\varepsilon \longrightarrow }\parallel \varepsilon \displaystyle \sum _{i,j}\omega _{ij}^{\frac{1}{p'}}| D_{ij}u_{\varepsilon }|^{s-1}\omega _{rs}^{\frac{1}{p}}D_{rs}u_{\varepsilon }\parallel _{L^{p}(\Omega ,I\!\!M^{m\times n})}=0,\quad \forall \rho <\frac{s}{s-1}. \end{aligned}$$

In particular for $\rho =1$

$$\begin{aligned} \lim _{\varepsilon \longrightarrow }\int _{\Omega }|\varepsilon \sum _{i,j}\omega _{ij}^{\frac{1}{p'}}| D_{ij}u_{\varepsilon }|^{s-1}\omega _{rs}^{\frac{1}{p}}D_{rs}u_{\varepsilon }| dx=0, \end{aligned}$$

which mean that

$$\begin{aligned} \tau [\varepsilon ]\left( x,u_{\varepsilon },Du_{\varepsilon }\right) =\varepsilon \displaystyle \sum _{i,j}^{\frac{1}{p'}}|D_{ij}u_{\varepsilon }|^{s-2} \omega _{rs}^{\frac{1}{p}}D_{rs}u_{\varepsilon }\rightharpoonup 0 \end{aligned}$$

in $L^{1}(\Omega ,I\!\!M^{m\times n}).$

As well as by the Proposition 6.1,$div\sigma (x,u_{\varepsilon },Du_{\varepsilon })$ converges to $div\sigma (x,u,\text{ apD }u),$ in the sense of the distributions, and as

$$\begin{aligned} \tau [\varepsilon ]\left( x,u_{\varepsilon },Du_{\varepsilon }\right) =\varepsilon \sum _{i,j}\omega _{ij}^{\frac{1}{p'}}| D_{ij}u_{\varepsilon }|^{s-2} \omega _{rs}^{\frac{1}{p}}D_{rs}u_{\varepsilon }\rightharpoonup 0, \end{aligned}$$

in $L^{1}(\Omega ,I\!\!M^{m\times n}).$ Then $div\sigma _{\varepsilon }(x,u_{\varepsilon },Du_{\varepsilon })$ converge to $div\sigma (x,u,\text{ apD }u)$ in the sense of distributions, i-e: u is the solution of the system

$$\begin{aligned} \left\{ \begin{array}{ll} -div\sigma (x,u,\text{ apD }u) = \mu &{}\quad \text{ in } \Omega \\ u = 0 &{}\quad \text{ on } \partial \Omega . \end{array} \right. \end{aligned}$$

In the same way as in the case of $\theta =p-1$, we have

$$\begin{aligned} \displaystyle \int _{| u|\le \alpha }| apDu|^{s}dx<c(\alpha )<\infty \text{ and } p<s. \end{aligned}$$

So we conclude as in the proof of the Proposition 6.1, in order to get the estimation of Theorem (2.1). This completes the proof of the theorem. $\square$