1 Introduction

Bernstein introduced the most famous algebraic polynomials \({B}_n(f;x)\) in approximation theory in order to give a constructive proof of Weierstrass’s theorem which is given by

$$\begin{aligned} {B}_n(f;x)=\displaystyle \sum _{k=0}^np_{n,k}(x)f\left( \frac{k}{n}\right) , \quad \ x\in [0,1], \end{aligned}$$

where \(p_{n,k}(x)=\displaystyle {n\atopwithdelims ()k}x^k(1-x)^{n-k}\) and he proved that if \(f\in C[0,1]\) then \(B_n(f;x)\) converges uniformly to f(x) in [0, 1].

The Bernstein operators have been used in many branches of mathematics and computer science. Due to their useful structure, Bernstein polynomials and their generalizations have been intensively studied. Among others we refer the readers to (cf. [4, 13, 19, 26, 32, 35, 36]).

For \(f\in C(J)\) with \(J=[0,1],\) Chen et al. [15] introduced a vital generalization of the Bernstein operators depending on a non-negative real parameter \(\alpha \)\((0\le \alpha \le 1)\) as

$$\begin{aligned} T_n^{(\alpha )}(f;x)=\sum _{k=0}^{n}p_{n,k}^{(\alpha )}(x)f\left( \frac{k}{n}\right) , \quad x\in J \end{aligned}$$
(1.1)

where \(p_{n,k}^{(\alpha )}(x)=\left[ {n-2\atopwithdelims ()k}(1-\alpha )x+{n-2\atopwithdelims ()k-2}(1-\alpha )(1-x)+{n\atopwithdelims ()k}\alpha x(1-x)\right] x^{k-1}(1-x)^{n-k-1}\) and \(n\ge 2.\) They obtained a Voronovskaja type asymptotic formula, the rate of approximation in terms of modulus of smoothness and shape preserving properties for these operators. In the particular case, \(\alpha =1,\) these operators reduce to the well-known Bernstein operators. Kajla and Acar [28] introduced the Durrmeyer variant of the operators (1.1) and investigated the rate of approximation of these operators.

Gonska and Pǎltǎnea [21] presented genuine Bernstein–Durrmeyer type operators and obtained the simultaneous approximation for these operators. Gupta and Rassias [25] studied approximation behavior of Durrmeyer type of Lupaş operators based on Polya distribution. Goyal et al. [22] derived Baskakov–Szàsz type operators and studied quantitative convergence theorems for these operators. Gupta et al. [23] introduced a hybrid operators based on inverse Polya–Eggenberger distribution and studied the degree of approximation and uniform convergence. Acu and Gupta [8] introduced a summation-integral type operators involving two parameters and studied some direct results e.g. Voronovskaja type asymptotic formula, local approximation and weighted approximation of these operators. Very recently, Kajla and Goyal [31] considered the hybrid operators involving non-negative parameters and investigated their order of approximation. In the literature survey, several researchers have been studied the approximation properties of hybrid operators [cf. [1,2,3, 5,6,7, 9,10,12, 14, 20, 24, 27, 29, 30, 34]].

For \(f\in C(J),\) we construct the following Durrmeyer variant of the operators (1.1) depending on a parameter \(\rho >0\) as follows:

$$\begin{aligned} \mathcal {G}_{n,\rho }^{(\alpha )}(f;x)=\sum _{k=0}^{n}p_{n,k}^{(\alpha )}(x) \int _{0}^1 \mu _{n,\rho }(t)f(t) dt, \end{aligned}$$
(1.2)

where \(\mu _{n,\rho }(t)=\dfrac{t^{k\rho }(1-t)^{(n-k)\rho }}{B\left( k\rho +1,(n-k)\rho +1\right) }\) and \(B\left( k\rho +1,(n-k)\rho +1\right) \) is the beta function defined by \(B(e,f)=\int _0^1t^{e-1}(1-t)^{f-1}dt=\dfrac{\Gamma (e) \Gamma (f)}{\Gamma (e+f)},\)\(e,f>0\) and \(p_{n,k}^{(\alpha )}(x)\) is defined as above. It is seen that the operators \(\mathcal {G}_{n,\rho }^{(\alpha )}\) reproduce the constant functions.

The aim of this note is to find the approximation properties for the generalized Bernstein–Durrmeyer operators involving a nonnegative parameter of the operators defined in (1.2). We give a Voronovskaja type theorem, global approximation theorem by means of Ditzian–Totik modulus of smoothness, Lipschitz type space and a local approximation theorem with the help of second order modulus of continuity. Furthermore, we study the rate of approximation for absolutely continuous functions having a derivative equivalent to a function of bounded variation. Lastly, we illustrate the convergence of these operators for certain functions using Maple software.

2 Auxiliary results

Lemma 1

Let \(e_i(x)=x^i, i=\overline{0,4}.\) For the generalized Bernstein–Durrmeyer operators \(\mathcal {G}_{n,\rho }^{(\alpha )}(f;x),\) we have

  1. (i)
    $$\begin{aligned} \mathcal {G}_{n,\rho }^{(\alpha )}(e_0;x)=1; \end{aligned}$$
  2. (ii)
    $$\begin{aligned} \mathcal {G}_{n,\rho }^{(\alpha )}(e_1;x)=\dfrac{n\rho x+1}{n\rho +2}; \end{aligned}$$
  3. (iii)
    $$\begin{aligned} \mathcal {G}_{n,\rho }^{(\alpha )}(e_2;x)= & {} \dfrac{x^2\rho ^2\left( n^2+2(\alpha -1)-n\right) }{(n\rho +3)(n\rho +2)}+\dfrac{x\rho \left( n\rho ^2+3n\rho -2(\alpha -1)\rho ^2\right) }{(n\rho +3)(n\rho +2)}\\&+ \dfrac{2}{(n\rho +3)(n\rho +2)}; \end{aligned}$$
  4. (iv)
    $$\begin{aligned} \mathcal {G}_{n,\rho }^{(\alpha )}(e_3;x)= & {} \dfrac{x^3\rho ^3\left( n^3+6n\alpha -3n^2-4n-12(\alpha -1)\right) }{(n\rho +4)(n\rho +3)(n\rho +2)}\\&+\dfrac{3x^2\rho ^2\left( 6n^2+3n\rho +3n^2\rho -6n\alpha \rho -6n+6(\alpha -1)(2+3\rho )\right) }{(n\rho +4)(n\rho +3)(n\rho +2)}\\&+ \dfrac{x\rho \left( n\rho ^2+6n\rho +11n-6(\alpha -1)\rho (2+\rho )\right) }{(n\rho +4)(n\rho +3)(n\rho +2)}\\&+\dfrac{6}{(n\rho +4)(n\rho +3)(n\rho +2)}; \end{aligned}$$
  5. (v)
    $$\begin{aligned} \mathcal {G}_{n,\rho }^{(\alpha )}(e_4;x)= & {} \dfrac{x^4\rho ^4\left( n^4-6n^3+72(\alpha -1)-6n(10\alpha -9)+n^2(12\alpha -1)\right) }{(n\rho +5)(n\rho +4)(n\rho +3)(n\rho +2)}\\&+ \dfrac{x^3\rho ^3}{(n\rho +5)(n\rho +4)(n\rho +3)(n\rho +2)}\bigg [10n^3-30n^2+10n(6\alpha -4)\\&-7n^2\rho +6n^3\rho +6n(6\alpha -5)\rho +6n(10\alpha -9)\rho +n^2(12\alpha -1)\rho \\&-24(\alpha -1)(6\rho +5)\bigg ]+\dfrac{x^2\rho ^2}{(n\rho +5)(n\rho +4)(n\rho +3)(n\rho +2)}\\&\times \bigg [35n(n-1)-10n\rho +30n^2\rho -10n(6\alpha -4)\rho -n\rho ^2+7n^2\rho ^2\\&-6n(6\alpha -5)\rho ^2+2(\alpha -1) (43\rho ^2+90\rho +35)\bigg ]\\&+ \dfrac{x\rho \left( 35n\rho +50n+10n\rho ^2+n\rho ^3-2(\alpha -1)\rho (7\rho ^2+30\rho +35)\right) }{(n\rho +5)(n\rho +4)(n\rho +3)(n\rho +2)}\\&+\dfrac{24}{(n\rho +5)(n\rho +4)(n\rho +3)(n\rho +2)}. \end{aligned}$$

Lemma 2

For \(m=1,2,\) the \(m^{th}\) order central moments of \( \mathcal {G}_{n,\rho }^{(\alpha )}\) defined as \(\tau _{n,\rho ,m}^{(\alpha )}(x)=\mathcal {G}_{n,\rho }^{(\alpha )}((t-x)^m;x)\) we get

  1. (i)
    $$\begin{aligned} \tau _{n,\rho ,1}^{(\alpha )}(x)=\dfrac{1-2x}{(n\rho +2)}; \end{aligned}$$
  2. (ii)
    $$\begin{aligned} \tau _{n,\rho ,2}^{(\alpha )}(x)=\dfrac{x(1-x)\left( \rho (n+(n-2\alpha +2)\rho )-6\right) }{(n\rho +2)(n\rho +3)}+\dfrac{2}{(n\rho +2)(n\rho +3)}. \end{aligned}$$

Remark 1

For every \(x\in J,\) we have

$$\begin{aligned} \displaystyle \lim _{n\rightarrow \infty } n~\tau _{n,\rho ,1}^{(\alpha )}(x)= & {} \dfrac{1-2x}{\rho },\\ \displaystyle \lim _{n\rightarrow \infty }n ~\tau _{n,\rho ,2}^{(\alpha )}(x)= & {} \frac{x(1-x)(1+\rho )}{\rho },\\ \displaystyle \lim _{n\rightarrow \infty } n^2~\tau _{n,\rho ,4}^{(\alpha )}(x)= & {} \frac{3x^2(1-x)^2(1+\rho )^2}{\rho ^2}. \end{aligned}$$

Lemma 3

For \(n\in \mathbb {N}\), we obtain

$$\begin{aligned} \mathcal {G}_{n,\rho }^{(\alpha )}((t-x)^2;x)\le \frac{\mathcal {X}_{\rho }^{(\alpha )}~~ x(1-x)}{(1+n\rho )}, \end{aligned}$$

where \(\mathcal {X}_{\rho }^{(\alpha )}\) is a positive constant depending on \(\alpha \) and \(\rho .\)

3 Direct estimates

Theorem 1

Let \(f\in C(J).\) Then \(\displaystyle \lim _{n\rightarrow \infty }\mathcal {G}_{n,\rho }^{(\alpha )}(f;x)=f(x),\) uniformly on J.

Proof

In view of Lemma 1, \(\mathcal {G}_{n,\rho }^{(\alpha )}(1;x)=1,\)\(\mathcal {G}_{n,\rho }^{(\alpha )}(e_1;x)\rightarrow x,\)\(\mathcal {G}_{n,\rho }^{(\alpha )}(e_2;x)\rightarrow x^2\) as \(n\rightarrow \infty ,\) uniformly in J. Applying Bohman-Korovkin criterion, it follows that \(\mathcal {G}_{n,\rho }^{(\alpha )}(f;x)\rightarrow f(x)\) as \(n\rightarrow \infty ,\) uniformly on J. \(\square \)

3.1 Voronovskaja type theorem

In this section we prove Voronvoskaja type theorem for the operators \(\mathcal {G}_{n,\rho }^{(\alpha )}\).

Theorem 2

Let \(f\in C(J).\) If \(f''\) exists at a point \(x\in J,\) then we have

$$\begin{aligned} \displaystyle \lim _{n\rightarrow \infty }n\left[ \mathcal {G}_{n,\rho }^{(\alpha )}(f;x)-f(x)\right] =\displaystyle \dfrac{1-2x}{\rho }f'(x)+\frac{(1+\rho )x(1-x)}{2\rho }f^{\prime \prime }(x). \end{aligned}$$

Proof

By Taylor’s expansion of f, we get

$$\begin{aligned} f(t)=f(x)+f'(x)(t-x)+\frac{1}{2}f''(x)(t-x)^2+\varpi (t,x)(t-x)^2, \end{aligned}$$
(3.1)

where \(\displaystyle \lim _{t\rightarrow x}\varpi (t,x)=0\). By applying the linearity of the operator \(\mathcal {G}_{n,\rho }^{(\alpha )}\), we obtain

$$\begin{aligned} \mathcal {G}_{n,\rho }^{(\alpha )}(f;x)-f(x)&=\mathcal {G}_{n,\rho }^{(\alpha )}((t-x);x)f'(x)+\frac{1}{2}\mathcal {G}_{n,\rho }^{(\alpha )}((t-x)^2;x)f''(x)\\&\quad +\mathcal {G}_{n,\rho }^{(\alpha )}(\varpi (t,x)(t-x)^2;x). \end{aligned}$$

Now, applying Cauchy–Schwarz property, we can get

$$\begin{aligned} n\mathcal {G}_{n,\rho }^{(\alpha )}(\varpi (t,x)(t-x)^2;x)\le \sqrt{\mathcal {G}_{n,\rho }^{(\alpha )}(\varpi ^2(t,x);x)} \sqrt{n^2\mathcal {G}_{n,\rho }^{(\alpha )}((t-x)^4;x)}. \end{aligned}$$

From Theorem 1, we have \(\displaystyle \lim _{n\rightarrow \infty }\mathcal {G}_{n,\rho }^{(\alpha )}(\varpi ^2(t,x);x)\)= \(\varpi ^2(x,x)=0,\) since \(\varpi (t,x)\rightarrow 0\) as \(t\rightarrow x,\) and Remark 1 for every \(x\in J,\) we may write

$$\begin{aligned} \displaystyle \lim _{n\rightarrow \infty }n^2\mathcal {G}_{n,\rho }^{(\alpha )}\left( (t-x)^4;x\right)&=\frac{3x^2(1-x)^2(1+\rho )^2}{\rho ^2}. \end{aligned}$$
(3.2)

Hence,

$$\begin{aligned} n\mathcal {G}_{n,\rho }^{(\alpha )}(\varpi (t,x)(t-x)^2;x)=0. \end{aligned}$$

Applying Remark 1, we get

$$\begin{aligned} \displaystyle \lim _{n\rightarrow \infty }n\mathcal {G}_{n,\rho }^{(\alpha )}\left( t-x;x\right)&=\dfrac{1-2x}{\rho },\nonumber \\ \displaystyle \lim _{n\rightarrow \infty }n\mathcal {G}_{n,\rho }^{(\alpha )}\left( (t-x)^2;x\right)&=\frac{(1+\rho )x(1-x)}{\rho }. \end{aligned}$$
(3.3)

Collecting the results from above the theorem is completed. \(\square \)

3.2 Local approximation

We begin by recalling the following K-functional :

$$\begin{aligned} K_2(f,\delta )=\inf \{|| f-g||+\delta ||g''||:g\in W^2\}\,\,(\delta >0), \end{aligned}$$

where \(W^2=\{g:g''\in C(J)\}\) and ||.|| is the uniform norm on C(J). By [16], \(\exists \) a positive constant \(M>0\) such that

$$\begin{aligned} K_2(f,\delta )\le M\omega _2(f,\sqrt{\delta }), \end{aligned}$$
(3.4)

where the modulus of smoothness of second order for \(f\in C(J)\) is defined as

$$\begin{aligned} \omega _2(f,\sqrt{\delta })=\displaystyle \sup _{0<h\le \sqrt{\delta }}\displaystyle \sup _{x,x+2h\in J}|f(x+2h)-2f(x+h)+f(x)|. \end{aligned}$$

The modulus of continuity for \(f\in C(J)\) is defined by

$$\begin{aligned} \omega (f,\delta )=\displaystyle \sup _{0<h\le \delta }\sup _{x,x+h\in J}|f(x+h)-f(x)|. \end{aligned}$$

The Steklov mean is defined as

$$\begin{aligned} f_h(x)=\displaystyle \dfrac{4}{h^2}\int _0^{\frac{h}{2}}\int _0^{\frac{h}{2}} \left[ 2f(x+u+v)-f(x+2(u+v))\right] du~dv. \end{aligned}$$
(3.5)

The Steklov mean satisfies the following inequality:

  1. (a)

    \(\Vert f_h-f\Vert _{C(J)}\le \omega _2(f,h).\)

  2. (b)

    \(f'_h,f_h''\in C(J)\) and \(\Vert f'_h\Vert _{C(J)}\le \dfrac{5}{h}\omega (f,h),\quad \Vert f''_h\Vert _{C(J)}\le \dfrac{9}{h^2}\omega _2(f,h)\),

Theorem 3

Let \(f\in C(J)\). Then for each \(x\in J,\) we have

$$\begin{aligned} \left| \mathcal {G}_{n,\rho }^{(\alpha )}(f;x)-f(x)\right| \le 5 \omega \left( f,\sqrt{\tau _{n,\rho ,2}^{(\alpha )}(x)}\right) +\frac{13}{2} \omega _2\left( f,\sqrt{\tau _{n,\rho ,2}^{(\alpha )}(x)}\right) . \end{aligned}$$

Proof

For \(x\in J,\) and applying the Steklov mean \(f_h\) that is given by (3.5), we can write

$$\begin{aligned} \left| \mathcal {G}_{n,\rho }^{(\alpha )}(f;x)-f(x)\right| \le \mathcal {G}_{n,\rho }^{(\alpha )}\left( |f-f_h|;x\right) +|\mathcal {G}_{n,\rho }^{(\alpha )}\left( f_h-f_h(x);x\right) |+|f_h(x)-f(x)|. \end{aligned}$$
(3.6)

From (1.2), for each \(f\in C(J)\) we obtain

$$\begin{aligned} \left| \mathcal {G}_{n,\rho }^{(\alpha )}(f;x)\right| \le ||f||. \end{aligned}$$
(3.7)

By assumption (a) of the Steklov mean and (3.7), we get

$$\begin{aligned} \mathcal {G}_{n,\rho }^{(\alpha )}\left( |f-f_h|;x\right) \le \Vert \mathcal {G}_{n,\rho }^{(\alpha )}\left( f-f_h\right) \Vert \le \Vert f-f_h\Vert \le \omega _2(f,h). \end{aligned}$$

Applying Taylor’s expansion and Cauchy–Schwarz inequality, we have

$$\begin{aligned} \left| \mathcal {G}_{n,\rho }^{(\alpha )}\left( f_h-f_h(x);x\right) \right|&\le \Vert f_h'\Vert \sqrt{\mathcal {G}_{n,\rho }^{(\alpha )}\left( (t-x)^2;x\right) }+\dfrac{1}{2}\Vert f_h''\Vert \mathcal {G}_{n,\rho }^{(\alpha )}\left( (t-x)^2;x\right) . \end{aligned}$$

By Lemma 2 and property (b) of the Steklov mean, we get

$$\begin{aligned} \left| \mathcal {G}_{n,\rho }^{(\alpha )}\left( f_h-f_h(x);x\right) \right| \le \dfrac{5}{h}\omega (f,h) \sqrt{\tau _{n,\rho ,2}^{(\alpha )}(x)}+\dfrac{9}{2h^2}\omega _2(f,h)\tau _{n,\rho ,2}^{(\alpha )}(x). \end{aligned}$$

Finally, choosing \(h=\sqrt{\tau _{n,\rho ,2}^{(\alpha )}(x)}\), we obtain the desired result. \(\square \)

3.3 Global approximation

Now, we recall the definitions of the Ditzian–Totik first order modulus of continuity and the K-functional [17]. Let \( \phi (x) =\sqrt{x(1-x) }\) and \(f\in C(J).\) The first order modulus of smoothness is defined by

$$\begin{aligned} \omega _{\phi }(f,t)=\sup _{0<h\le t}\bigg \{\left| f\bigg (x+\frac{h\phi (x)}{2}\bigg )-f\bigg (x-\frac{h\phi (x)}{2}\bigg )\right| ,x\pm \frac{h\phi (x)}{2}\in J\bigg \} , \end{aligned}$$

and the corresponding K-functional is given by

$$\begin{aligned} \overline{K}_{\phi }(f,t)=\inf _{g\in W_{\phi }}\{||f-g||+t||\phi g^{\prime }|| +t^{2}|| g^{\prime }||\}\,\,(t>0), \end{aligned}$$

where \(W_{\phi }=\{g:g\in AC_{loc},||\phi g^{\prime }||<\infty ,||g^{\prime }||<\infty \}\) and ||.|| is the uniform norm on C(J). It is well known that (Theorem 3.1.2, [17]) \(\overline{K}_{\phi }(f,t)\sim \omega _{\phi }(f,t)\) which means that there exists a constant \(M>0\) such that

$$\begin{aligned} M^{-1}\omega _{\phi }(f,t)\le \overline{K}_{\phi }(f,t)\le M\omega _{\phi }(f,t). \end{aligned}$$
(3.8)

Now, we establish the order of approximation with the aid of the Ditzian–Totik modulus of the first and second order.

Theorem 4

Let f be in C(J) and \(\phi (x) =\sqrt{x(1-x)},\) then for each \(x\in [0,1),\) we get

$$\begin{aligned} |\mathcal {G}_{n,\rho }^{(\alpha )}(f;x)-f(x)|\le & {} C \omega _{\phi }\left( f,\sqrt{\frac{\mathcal {X}_{\rho }^{(\alpha )}}{(1+n\rho )}}\right) , \end{aligned}$$

where \(\mathcal {X}_{\rho }^{(\alpha )}\) is defined in Lemma 3 and \(C>0\) is a constant.

Proof

By using the relation \( g(t)=g(x)+\int _{x}^{t}g^{\prime }(u)du,\) we can write

$$\begin{aligned} \left| \mathcal {G}_{n,\rho }^{(\alpha )}(g;x)-g(x)\right|= & {} \left| \mathcal {G}_{n,\rho }^{(\alpha )}\bigg (\int _{x}^{t}g^{\prime }(u)du;x\bigg )\right| . \end{aligned}$$
(3.9)

For any \(x,t\in (0,1),\) we get

$$\begin{aligned} \bigg |\int _{x}^{t}g^{\prime }(u)du\bigg |\le ||\phi g'||\bigg |\int _{x}^t\frac{1}{\phi (u)}du\bigg |. \end{aligned}$$
(3.10)

Therefore,

$$\begin{aligned} \bigg |\int _{x}^t\frac{1}{\phi (u)}du\bigg |= & {} \bigg |\int _{x}^t\frac{1}{\sqrt{u(1-u)}}du\bigg | \le \bigg |\int _{x}^t\bigg (\frac{1}{\sqrt{u}}+\frac{1}{\sqrt{1-u}}\bigg )du\bigg |\nonumber \\\le & {} 2\bigg (\mid \sqrt{t}-\sqrt{x}\mid +\mid \sqrt{1-t}-\sqrt{1-x}\mid \bigg )\nonumber \\= & {} 2|t-x|\bigg (\frac{1}{\sqrt{t}+\sqrt{x}}+\frac{1}{\sqrt{1-t}+\sqrt{1-x}}\bigg )\nonumber \\< & {} 2|t-x|\bigg (\frac{1}{\sqrt{x}}+\frac{1}{\sqrt{1-x}}\bigg ) \le \frac{2\sqrt{2}~|t-x|}{\phi (x)}. \end{aligned}$$
(3.11)

Combining (3.9)–(3.11) and applying Cauchy–Schwarz inequality, we have

$$\begin{aligned} |\mathcal {G}_{n,\rho }^{(\alpha )}(g;x)-g(x)|< & {} 2\sqrt{2}||\phi g'||\phi ^{-1}(x)\mathcal {G}_{n,\rho }^{(\alpha )}(|t-x|;x)\\\le & {} 2\sqrt{2}||\phi g'||\phi ^{-1}(x)\bigg ( \mathcal {G}_{n,\rho }^{(\alpha )}((t-x)^2;x)\bigg )^{1/2}. \end{aligned}$$

From Lemma 3, we get

$$\begin{aligned} |\mathcal {G}_{n,\rho }^{(\alpha )}(g;x)-g(x)|< C\sqrt{\frac{\mathcal {X}_{\rho }^{(\alpha )}}{(1+n\rho )}}||\phi g'||. \end{aligned}$$
(3.12)

Applying Lemma 1 and (3.12), we get

$$\begin{aligned} \mid \mathcal {G}_{n,\rho }^{(\alpha )}(f)-f\mid\le & {} \mid \mathcal {G}_{n,\rho }^{(\alpha )}(f-g;x)\mid +|f-g|+\mid \mathcal {G}_{n,\rho }^{(\alpha )}(g;x)-g(x)\mid \nonumber \\\le & {} C\left( ||f-g||+\sqrt{\frac{\mathcal {X}_{\rho }^{(\alpha )}}{(1+n\rho )}}||\phi g'||\right) . \end{aligned}$$
(3.13)

Taking infimum on the right hand side of (3.13) over all \(g\in W_\phi ,\) we may write

$$\begin{aligned} |\mathcal {G}_{n,\rho }^{(\alpha )}(f;x)-f(x)|\le C \overline{K}_{\phi }\left( f;\sqrt{\frac{\mathcal {X}_{\rho }^{(\alpha )}}{(1+n\rho )}}\right) . \end{aligned}$$
(3.14)

Using \(\overline{K_\phi }(f,t)\sim \omega _\phi (f,t)\), we immediately arrive to the required relation. \(\square \)

[33] Let us consider the Lipschitz-type space with two parameters \(\kappa _1\ge 0, \kappa _2>0,\) we have

$$\begin{aligned} Lip_M^{(\kappa _1,\kappa _2)}(\sigma ):=\left\{ f\in C(J):|f(t)-f(x)|\le M\frac{|t-x|^{\sigma }}{(t+\kappa _1x^2+\kappa _2x)^{\frac{\sigma }{2}}};t\in J, x\in (0,1]\right\} , \end{aligned}$$

where \(0<\sigma \le 1.\)

Theorem 5

Let \(f\in Lip_M^{(\kappa _1,\kappa _2)}(\sigma )\). Then for all \(x\in (0,1],\) we have

$$\begin{aligned} \left| \mathcal {G}_{n,\rho }^{(\alpha )}(f;x)-f(x)\right| \le M\left( \frac{\tau _{n,\rho ,2}^{(\alpha )}(x)}{\kappa _1x^2+\kappa _2x}\right) ^{\sigma /2}. \end{aligned}$$

Proof

Let us prove the theorem for the case \(0<\sigma \le 1\), using Holder’s property with \(p=\frac{2}{\sigma }, q=\frac{2}{2-\sigma }.\)

$$\begin{aligned} \left| \mathcal {G}_{n,\rho }^{(\alpha )}(f;x)-f(x)\right|\le & {} \displaystyle \sum _{k=0}^{n}p_{n,k}^{(\alpha )}(x)\displaystyle \int _0^1\left| f(t)-f(x)\right| \mu _{n,\rho }(t)dt\\\le & {} \displaystyle \sum _{k=0}^{n}p_{n,k}^{(\alpha )}(x)\left( \displaystyle \int _0^1\left| f(t)-f(x)\right| ^{\frac{2}{\sigma }}\mu _{n,\rho }(t)dt\right) ^{\frac{\sigma }{2}}\\\le & {} \left\{ \displaystyle \sum _{k=0}^{n}p_{n,k}^{(\alpha )}(x)\displaystyle \int _0^1\left| f(t)-f(x)\right| ^{\frac{2}{\sigma }}\mu _{n,\rho }(t)dt\right\} ^{\frac{\sigma }{2}}\\&\times \left( \displaystyle \sum _{k=0}^{n}p_{n,k}^{(\alpha )}(x)\int _0^1\mu _{n,\rho }(t)dt\right) ^{\frac{2-\sigma }{2}}\\= & {} \left( \displaystyle \sum _{k=0}^{n}p_{n,k}^{(\alpha )}(x)\displaystyle \int _0^1\left| f(t)-f(x)\right| ^{\frac{2}{\sigma }}\mu _{n,\rho }(t)dt\right) ^{\frac{\sigma }{2}}\\\le & {} M \left( \displaystyle \sum _{k=0}^{n}p_{n,k}^{(\alpha )}(x)\displaystyle \int _0^1\frac{(t-x)^2}{(t+\kappa _1x^2+\kappa _2x)}\mu _{n,\rho }(t)dt\right) ^{\frac{\sigma }{2}}\\\le & {} \frac{M}{\left( \kappa _1x^2+\kappa _2x\right) ^{\frac{\sigma }{2}}}\left( \displaystyle \sum _{k=0}^{n}p_{n,k}^{(\alpha )}(x)\displaystyle \int _0^1(t-x)^2\mu _{n,\rho }(t)dt\right) ^{\frac{\sigma }{2}}\\= & {} \frac{M}{\left( \kappa _1x^2+\kappa _2x\right) ^{\frac{\sigma }{2}}}\mathcal {G}_{n,\rho }^{(\alpha )}((t-x)^2;x)^{\frac{\sigma }{2}}\\= & {} \frac{M}{\left( \kappa _1x^2+\kappa _2x\right) ^{\frac{\sigma }{2}}}(\tau _{n,\rho ,2}^{(\alpha )}(x))^{\frac{\sigma }{2}}. \end{aligned}$$

\(\square \)

Theorem 6

For \(f\in C^1(J)\) and \(x\in J,\) we have

$$\begin{aligned} \left| \mathcal {G}_{n,\rho }^{(\alpha )}(f;x)-f(x)\right| \le \left| \dfrac{1-2x}{(n\rho +2)}\right| |f'(x)|+2\sqrt{\tau _{n,\rho ,2}^{(\alpha )}(x)}\, \omega \left( f',\sqrt{\tau _{n,\rho ,2}^{(\alpha )}(x)}\right) . \end{aligned}$$
(3.15)

Proof

Let \(f\in C^1(J)\). For any \(t,x\in J,\) we have

$$\begin{aligned} f(t)-f(x)=f'(x)(t-x)+\int _{x}^t\left( f'(u)-f'(x)\right) du. \end{aligned}$$

Using \(\mathcal {G}_{n,\rho }^{(\alpha )}(\cdot ;x)\) on both sides of the above relation, we may write

$$\begin{aligned} \mathcal {G}_{n,\rho }^{(\alpha )}(f(t)-f(x);q_n,x)=f'(x)\mathcal {G}_{n,\rho }^{(\alpha )}(t-x;x)+ \mathcal {G}_{n,\rho }^{(\alpha )}\left( \int _{x}^t\left( f'(u)-f'(x)\right) du;x\right) \end{aligned}$$

Using the well-known inequality of modulus of continuity \(|f(t)-f(x)|\le \omega (f,\delta )\left( \frac{|t-x|}{\delta }+1\right) ,\delta >0,\) we obtain

$$\begin{aligned} \left| \int _{x}^t\left( f'(u)-f'(x)\right) du\right| \le \omega (f',\delta )\left( \frac{(t-x)^2}{\delta }+|t-x|\right) , \end{aligned}$$

it follows that

$$\begin{aligned} \left| \mathcal {G}_{n,\rho }^{(\alpha )}(f;x)-f(x)\right|\le & {} |f'(x)|~~~|\mathcal {G}_{n,\rho }^{(\alpha )}(t-x;x)|\\&+ \omega (f',\delta )\left\{ \frac{1}{\delta }\mathcal {G}_{n,\rho }^{(\alpha )}((t-x)^2;x) +\mathcal {G}_{n,\rho }^{(\alpha )}(|t-x|;x)\right\} . \end{aligned}$$

From Cauchy–Schwarz inequality, we have

$$\begin{aligned} \left| \mathcal {G}_{n,\rho }^{(\alpha )}(f;x)-f(x)\right|\le & {} |f'(x)|~~~|\mathcal {G}_{n,\rho }^{(\alpha )}(t-x;x)|\\&+ \omega (f',\delta )\left\{ \dfrac{1}{\delta }\sqrt{\mathcal {G}_{n,\rho }^{(\alpha )}((t-x)^2;x)}+1\right\} \sqrt{\mathcal {G}_{n,\rho }^{(\alpha )}((t-x)^2;x)}. \end{aligned}$$

Now, choosing \(\delta =\sqrt{\tau _{n,\rho ,2}^{(\alpha )}(x)},\) the required result follows. \(\square \)

3.4 Rate of convergence

Let \(DBV_{(J)}\) be the class of all absolutely continuous functions f defined on J, having on J a derivative \(f^{\prime }\) equivalent to a function of bounded variation on J. We observed that the functions f\(\in DBV_{(J)}\) possess a representation

$$\begin{aligned} f(x)=\int _{0}^xg(t)dt+f(0) \end{aligned}$$

where \(g\in BV_{(J)}\), i.e., g is a function of bounded variation on J.

The operators \(\mathcal {G}_{n,\rho }^{(\alpha )}(f;x)\) also admit the integral representation

$$\begin{aligned} \mathcal {G}_{n,\rho }^{(\alpha )}(f;x)=\int _{0}^{1}\mathcal {U}_{n,\rho }^{(\alpha )}(x,t) f(t) dt, \end{aligned}$$
(3.16)

where the kernel \(\mathcal {U}_{n,\rho }^{(\alpha )}(x,t)\) is given by

$$\begin{aligned} \mathcal {U}_{n,\rho }^{(\alpha )}(x,t)=\sum _{k=0}^{n}p_{n,k}^{(\alpha )}(x)\mu _{n,\rho }(t). \end{aligned}$$

Lemma 4

For a fixed \(x\in (0,1)\) and sufficiently large n, we have

  1. (i)

    \(\gamma _{n,\rho }^{(\alpha )}(x,y)=\displaystyle \int _{0}^{y}\mathcal {U}_{n,\rho }^{(\alpha )}(x,t)dt\le \dfrac{\mathcal {X}_{\rho }^{(\alpha )}}{(1+n\rho )}\frac{x(1-x)}{(x-y)^{2}}\,,\,\,0\le y<x,\)

  2. (ii)

    \(1-\gamma _{n,\rho }^{(\alpha )}(x,z)=\displaystyle \int _{z}^{1}\mathcal {U}_{n,\rho }^{(\alpha )}(x,t)dt\le \) \(\dfrac{\mathcal {X}_{\rho }^{(\alpha )}}{(1+n\rho )}\dfrac{x(1-x)}{(z-x)^{2}},\) \(x<z<1,\)

where \(\mathcal {X}_{\rho }^{(\alpha )}\) is defined in Lemma 3.

Proof

(i) From Lemma 3, we get

$$\begin{aligned} \gamma _{n,\rho }^{(\alpha )}(x,y)= & {} \int \limits _{0}^{y}\mathcal {U}_{n,\rho }^{(\alpha )}(x,t)dt\le \int _{0}^{y}\bigg (\frac{x-t}{x-y}\bigg )^{2}\mathcal {U}_{n,\rho }^{(\alpha )}(x,t)dt \\= & {} \mathcal {G}_{n,\rho }^{(\alpha )}((t-x)^{2};x)( x-y) ^{-2}\le \dfrac{\mathcal {X}_{\rho }^{(\alpha )}}{(1+n\rho )}\dfrac{x(1-x)}{(x-y)^{2}}. \end{aligned}$$

The proof of (ii) is similar hence the details are missing. \(\square \)

Theorem 7

Let f\(\in DBV(J).\) Then for every \(x\in (0,1)\) and sufficiently large n, we have

$$\begin{aligned} \left| \mathcal {G}_{n,\rho }^{(\alpha )}(f;x)-f(x)\right|\le & {} \frac{(1-2x)}{(n\rho +2)}\frac{| f^{\prime }(x+)+f^{\prime }(x-)|}{2}\\&+\sqrt{\frac{\mathcal {X}_{\rho }^{(\alpha )} x(1-x)}{(1+n\rho )}}\frac{|f^{\prime }(x+)-f^{\prime }(x-)|}{2}\\&+\frac{\mathcal {X}_{\rho }^{(\alpha )} (1-x)}{(1+n\rho )}\sum _{k=1}^{[\sqrt{n}] }\bigvee _{x-(x/k)}^{x}(f^{\prime }_{x}) + \frac{x}{\sqrt{n}}\bigvee _{x-(x/\sqrt{n})}^{x}(f^{\prime }_x)\\&+\frac{\mathcal {X}_{\rho }^{(\alpha )} x}{(1+n\rho )}\sum _{k=1}^{[\sqrt{n}] }\bigvee _{x}^{x+((1-x)/k)}(f^{\prime }_x) +\frac{(1-x)}{\sqrt{n}}\bigvee _{x}^{x+((1-x)/\sqrt{n})}(f^{\prime }_x), \end{aligned}$$

where \(\bigvee _{c}^{d}(f^{\prime }_{x}) \) denotes the total variation of \(f^{\prime }_{x} \) on [c, d] and \(f^{\prime }_{x}\) is defined by

$$\begin{aligned} f_{x}^{\prime }(t)=\left\{ \begin{array}{cc} f^{\prime }(t)-f^{\prime }(x-), &{} 0\le t<x \\ 0, &{} t=x \\ f^{\prime }(t)-f^{\prime }(x+) &{} x<t<1. \end{array} \right. \end{aligned}$$
(3.17)

Proof

Since \(\mathcal {G}_{n,\rho }^{(\alpha )}(1;x)=1,\) by using (3.16), for every \(x\in (0,1)\) we may write

$$\begin{aligned} \mathcal {G}_{n,\rho }^{(\alpha )}( f;x) -f(x)= & {} \int _{0}^{1}\mathcal {U}_{n,\rho }^{(\alpha )}(x,t)(f(t)-f(x)) dt \nonumber \\= & {} \int _{0}^{1}\mathcal {U}_{n,\rho }^{(\alpha )}(x,t)\left( \int _{x}^{t}f^{\prime }(u) du\right) dt. \end{aligned}$$
(3.18)

For any \(f\in DBV(J),\) by (3.17) we can write

$$\begin{aligned} f^{\prime }(u)= & {} f'_{x}(u)+\frac{1}{2}( f^{\prime }(x+)+f^{\prime }(x-)) +\frac{1}{2}( f^{\prime }(x+)-f^{\prime }(x-)) sgn(u-x) \nonumber \\&+\delta _{x}(u)\left[ f^{\prime }(u)-\frac{1}{2}( f^{\prime }(x+)+f^{\prime }(x-))\right] , \end{aligned}$$
(3.19)

where

$$\begin{aligned} \delta _{x}(u)=\left\{ \begin{array}{c} 1\,\,,\,\,u=x \\ 0\,\,,\,\,u\ne x. \end{array} \right. \end{aligned}$$

Obviously,

$$\begin{aligned} \int _{0}^{1}\bigg ( \int _{x}^{t}\bigg (f^{\prime }(u)-\frac{1}{2}(f^{\prime }(x+)+f^{\prime }(x-))\bigg )\delta _{x}(u)du\bigg ) \mathcal {U}_{n,\rho }^{(\alpha )}(x,t)dt=0. \end{aligned}$$

By (3.16) and simple calculations we find

$$\begin{aligned}&\int _{0}^{1}\bigg ( \int _{x}^{t}\frac{1}{2}( f^{\prime }(x+)+f^{\prime }(x-)) du\bigg ) \mathcal {U}_{n,\rho }^{(\alpha )}(x,t)dt\\&\quad =\frac{1}{2}(f^{\prime }(x+)+f^{\prime }(x-))\int _{0}^{1}( t-x) \mathcal {U}_{n,\rho }^{(\alpha )}(x,t)dt \\&\quad =\frac{1}{2}( f^{\prime }(x+)+f^{\prime }(x-)) \mathcal {G}_{n,\rho }^{(\alpha )}( (t-x);x) \end{aligned}$$

and

$$\begin{aligned}&\displaystyle \left| \int _{0}^{1}\mathcal {U}_{n,\rho }^{(\alpha )}(x,t)\bigg ( \int _{x}^{t}\frac{1}{2}(f^{\prime }(x+)-f^{\prime }(x-)) sgn(u-x)du\bigg ) dt\right| \\&\quad \le \frac{1}{2}\mid f^{\prime }(x+)-f^{\prime }(x-)\mid \int _{0}^{1}|t-x|\mathcal {U}_{n,\rho }^{(\alpha )}(x,t)dt \\&\quad \le \frac{1}{2}\mid f^{\prime }(x+)-f^{\prime }(x-)\mid \mathcal {G}_{n,\rho }^{(\alpha )}(|t-x|;x) \\&\quad \le \frac{1}{2}\mid f^{\prime }(x+)-f^{\prime }(x-)\mid \bigg (\mathcal {G}_{n,\rho }^{(\alpha )}((t-x) ^{2};x)\bigg ) ^{1/2}. \end{aligned}$$

By Lemmas 2 and 3, using (3.18)–(3.19) we find

$$\begin{aligned} | \mathcal {G}_{n,\rho }^{(\alpha )}(f;x)-f(x)|\le & {} \frac{1}{2}|f^{\prime }(x+)-f^{\prime }(x-)| \sqrt{\frac{\mathcal {X}_{\rho }^{(\alpha )} x(1-x)}{(1+n\rho )}}\nonumber \\&+\bigg |\int _{0}^{x}\left( \int _{x}^{t}f^{\prime }_{x}(u)du\right) \mathcal {U}_{n,\rho }^{(\alpha )}(x,t)dt\nonumber \\&+\int _{x}^{1}\left( \int _{x}^{t}f^{\prime }_{x}(u)du\right) \mathcal {U}_{n,\rho }^{(\alpha )}(x,t)dt\bigg |. \end{aligned}$$
(3.20)

Let

$$\begin{aligned} \mathcal {S}_{n,\rho }^{(\alpha )}(f'_x,x)= & {} \int _{0}^{x}\left( \int _{x}^{t}f'_{x}(u)du\right) \mathcal {U}_{n,\rho }^{(\alpha )}(x,t)dt,\\ \mathcal {T}_{n,\rho }^{(\alpha )}(f'_x,x)= & {} \int _{x}^{1}\left( \int _{x}^{t}f'_{x}(u)du\right) \mathcal {U}_{n,\rho }^{(\alpha )}(x,t)dt. \end{aligned}$$

To complete the proof, it is sufficient to determine the terms \(\mathcal {S}_{n,\rho }^{(\alpha )}(f'_x,x)\) and \(\mathcal {T}_{n,\rho }^{(\alpha )}(f'_x,x).\) Since \(\int _{c}^{d}d_{t}\gamma _{n,\rho }^{(\alpha )}(x,t)\le 1\) for all \([c,d]\subseteq J,\) applying the integration by parts and applying Lemma 4 with \(y=x-(x/\sqrt{n}),\) we have

$$\begin{aligned} |\mathcal {S}_{n,\rho }^{(\alpha )}(f'_x,x)|= & {} \bigg |\int _{0}^{x}\left( \int _{x}^{t}f'_{x}(u)du\right) d_{t}\gamma _{n,\rho }^{(\alpha )}(x,t)\bigg |\\= & {} \bigg |\int _{0}^{x}\gamma _{n,\rho }^{(\alpha )}(x,t)f'_{x}(t)dt\bigg |\\\le & {} \bigg (\int _{0}^{y}+\int _{y}^{x}\bigg ) |f'_{x}(t)|\,\,|\gamma _{n,\rho }^{(\alpha )}(x,t)| dt\\\le & {} \frac{\mathcal {X}_{\rho }^{(\alpha )} x(1-x)}{(1+n\rho )}\int _{0}^{y}\bigvee _{t}^{x}(f'_{x})(x-t)^{-2}dt+\int _{y}^{x}\bigvee _{t}^{x}(f'_{x}) dt\\\le & {} \frac{\mathcal {X}_{\rho }^{(\alpha )} x(1-x)}{(1+n\rho )}\int _{0}^{x-(x/\sqrt{n})}\bigvee _{t}^{x}(f^{\prime }_{x})( x-t)^{-2}dt+\frac{x}{\sqrt{n}}\bigvee _{x-(x/\sqrt{n})}^{x}(f'_{x}). \end{aligned}$$

By the substitution of \(u=x/(x-t),\) we have

$$\begin{aligned} \frac{\mathcal {X}_{\rho }^{(\alpha )} x(1-x)}{(1+n\rho )}\int _{0}^{x-(x/\sqrt{n})}(x-t)^{-2}\bigvee _{t}^{x}(f^{\prime }_{x}) dt= & {} \frac{\mathcal {X}_{\rho }^{(\alpha )} (1-x)}{(1+n\rho )}\int _{1}^{\sqrt{n}}\bigvee _{x-(x/u)}^{x}(f^{\prime }_{x}) du \\\le & {} \frac{\mathcal {X}_{\rho }^{(\alpha )} (1-x)}{(1+n\rho )}\sum _{k=1}^{[\sqrt{n}]}\int _{k}^{k+1}\bigvee _{x-(x/u)}^{x}(f^{\prime }_{x}) du \\\le & {} \frac{\mathcal {X}_{\rho }^{(\alpha )} (1-x)}{(1+n\rho )}\sum _{k=1}^{[\sqrt{n}] }\bigvee _{x-(x/k)}^{x}(f'_{x}) . \end{aligned}$$

Thus,

$$\begin{aligned} \left| \mathcal {S}_{n,\rho }^{(\alpha )}(f'_x,x)\right| \le \frac{\mathcal {X}_{\rho }^{(\alpha )} (1-x)}{(1+n\rho )}\sum _{k=1}^{[ \sqrt{n}] }\bigvee _{x-(x/k)}^{x}(f^{\prime }_{x}) +\frac{x}{\sqrt{n}} \bigvee _{x-(x/\sqrt{n})}^{x}(f^{\prime }_{x}). \end{aligned}$$
(3.21)

Using the integration by parts and Lemma 4 with \(z=x+((1-x)/\sqrt{n}),\) we can write

$$\begin{aligned} \left| \mathcal {T}_{n,\rho }^{(\alpha )}(f^{\prime }_x,x)\right|= & {} \bigg |\int _{x}^{1}\left( \int _{x}^{t}f'_{x}(u)du\right) \mathcal {U}_{n,\rho }^{(\alpha )}(x,t)dt\bigg |\\= & {} \bigg |\int _{x}^{z}\left( \int _{x}^{t}f'_{x}(u)du\right) d_{t}(1-\gamma _{n,\rho }^{(\alpha )}(x,t))\\&+\int _{z}^{1}\left( \int _{x}^{t}f'_{x}(u)du\right) d_{t}(1-\gamma _{n,\rho }^{(\alpha )}(x,t))\bigg |\\= & {} \bigg |\bigg [\int _{x}^tf'_{x}(u)(1-\gamma _{n,\rho }^{(\alpha )}(x,t))du\bigg ]_{x}^z-\int _{x}^z f'_{x}(t)(1-\gamma _{n,\rho }^{(\alpha )}(x,t))dt\\&+\int _{z}^{1}\left( \int _{x}^{t}f'_{x}(u)du\right) d_{t}(1-\gamma _{n,\rho }^{(\alpha )}(x,t))\bigg |\\= & {} \bigg |\int _{x}^zf'_{x}(u)du(1-\gamma _{n,\rho }^{(\alpha )}(x,z))-\int _{x}^z f'_{x}(t)(1-\gamma _{n,\rho }^{(\alpha )}(x,t))dt\\&+\bigg [\int _{x}^t f'_{x}(u)du(1-\gamma _{n,\rho }^{(\alpha )}(x,t))\bigg ]_{z}^1\\&-\int _{z}^1f'_{x}(t)(1-\gamma _{n,\rho }^{(\alpha )}(x,t))dt\bigg |\\= & {} \bigg | \int _{x}^z f'_{x}(t)(1-\gamma _{n,\rho }^{(\alpha )}(x,t))dt+\int _{z}^1f'_{x}(t)(1-\gamma _{n,\rho }^{(\alpha )}(x,t))dt\bigg |\\\le & {} \frac{\mathcal {X}_{\rho }^{(\alpha )} x(1-x)}{(1+n\rho )}\int _{z}^1 \bigvee _{x}^t(f'_{x})(t-x)^{-2}dt+\int _{x}^z\bigvee _{x}^t(f'_{x})dt\\= & {} \frac{\mathcal {X}_{\rho }^{(\alpha )} x(1-x)}{(1+n\rho )}\int _{x+((1-x)/\sqrt{n})}^1\bigvee _{x}^t(f'_{x})(t-x)^{-2}dt\\&+\frac{(1-x)}{\sqrt{n}}\bigvee _{x}^{x+(( 1-x) /\sqrt{n})}(f'_{x}). \end{aligned}$$

By the substitution of \(v=(1-x)/(t-x),\) we have

$$\begin{aligned} \left| \mathcal {T}_{n,\rho }^{(\alpha )}(f^{\prime }_x,x)\right|\le & {} \frac{\mathcal {X}_{\rho }^{(\alpha )} x(1-x)}{(1+n\rho )}\int _{1}^{\sqrt{n}}\bigvee _{x}^{x+((1-x)/v)}(f'_{x})(1-x)^{-1}dv\nonumber \\&+\frac{(1-x)}{\sqrt{n}}\bigvee _{x}^{x+(( 1-x) /\sqrt{n})}(f'_{x})\nonumber \\\le & {} \frac{\mathcal {X}_{\rho }^{(\alpha )} x}{(1+n\rho )}\sum _{k=1}^{[\sqrt{n}]}\int _{k}^{k+1}\bigvee _{x}^{x+((1-x)/v)}(f'_{x})dv+\frac{(1-x)}{\sqrt{n}}\bigvee _{x}^{x+(( 1-x) /\sqrt{n})}(f'_{x})\nonumber \\= & {} \frac{\mathcal {X}_{\rho }^{(\alpha )} x}{(1+n\rho )}\sum _{k=1}^{[ \sqrt{n}] }\bigvee _{x}^{x+((1-x)/k)}(f'_{x}) + \frac{(1-x)}{\sqrt{n}}\bigvee _{x}^{x+((1-x))/\sqrt{n}}(f'_{x}). \end{aligned}$$
(3.22)

Combining (3.20)–(3.22), we get the desired relation. \(\square \)

Fig. 1
figure 1

The convergence of \(\mathcal {G}_{20,4}^{(0.3)}(f;x)\) and \(D_{20}(f;x)\) to f(x)

Full size image
Fig. 2
figure 2

The convergence of \(\mathcal {G}_{n,\rho }^{(\alpha )}(f;x)\) to f(x)

Full size image

4 Numerical examples

Example 1

In Fig. 1, for \(n=20, \alpha =0.3, \rho =4,\) the comparison of convergence of \(\mathcal {G}_{20,4}^{(0.3)}(f;x)\) (blue) and the Bernstein–Durrmeyer \(D_n(f;x)\) [18] (red) operators to \(f(x)= x^2\sin \left( 2x/\pi \right) \)(yellow) is illustrated. It is observed that the \(\mathcal {G}_{20,4}^{(0.3)}(f;x)\) operators gives a better approximation to f(x) than Bernstein–Durrmeyer \(D_n(f;x)\) for \(n=20, \alpha =0.3, \rho =4.\)

Example 2

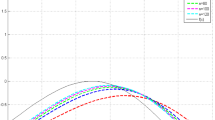
For \(n\in \{10,20,50\}\), \(\alpha =0.2\) and \(\rho =4,\) the convergence of the operators \(\mathcal {G}_{10,4}^{(0.2)}(f;x)\) (green), \(\mathcal {G}_{20,4}^{(0.2)}(f;x)\) (red) and \(\mathcal {G}_{50,4}^{(0.2)}(f;x)\) (blue) to \(f(x)=x^7+10x^5+x\) (yellow) is illustrated in Fig. 2. We observed that for the values of n increasing, the graph of \(\mathcal {G}_{n,\rho }^{(\alpha )}(f;x)\) goes to the graph of the function f(x).