Analysis of a Chebyshev-type spectral method for the Korteweg-de Vries equation in the real line

Abstract

Many problems in science and engineering involve nonlinear PDEs which are posed on the real line (${\mathbb {R}}$). Particular examples include a number of important nonlinear wave equations. A rigorous numerical analysis of such problems is especially challenging due to the spatial discretization of the nonlinear operators involved in the models. Classically, such problems have been treated using Fourier pseudo-spectral methods by truncating the spatial domain and imposing periodic boundary conditions. Unfortunately, in many cases this approach may not be appropriate to adequately capture the dynamics of the problem on the spatial domain. In this paper, we consider a Chebyshev-type pseudo-spectral method based on the algebraically mapped Chebyshev basis defined in ${\mathbb {R}}$. The approximation properties of this basis are naturally described on the scale of weighted Bessel potential spaces and lead to optimal error estimates for the method. Based on these estimates an efficient spectral scheme for solving the nonlinear Korteweg-de Vries equation globally in ${\mathbb {R}}$ is proposed. The numerical simulations presented in the paper confirm our theoretical results.

1 Introduction

Spectral/pseudo-spectral methods belong to a class of techniques that are widely used in applied mathematics and scientific computing to numerically solve PDEs, ODEs and eigenvalue problems that involve differential equations (for the list of applications see e.g. the bibliography in [5, 6]). In any such method, the numerical solution is expressed as a linear combination of a specific set of “basis functions” which are defined globally in the spatial domain of the equation. The coefficients in the sum may be chosen in a number of ways. In particular, one can use either collocation, Galerkin or Tau approach, see [5, 6] and references therein. If the computational basis is chosen appropriately, spectral methods are computationally more efficient than finite difference/finite-element schemes.

For a large class of PDEs posed in the real line, it was found that the algebraically mapped Chebyshev basis has a great potential both in terms of the numerical accuracy and the computational efficiency, see e.g. [5, 6] and discussion therein. Applications of the algebraically mapped Chebyshev spectral approximations are numerous, ranging from the classical linear equations of mathematical physics to much more computationally challenging nonlinear models that involve nonlocal operators, see e.g. [7] where the fractional KdV-Burgers equation is treated.

Recently, it was shown in [10] that spectral schemes based on algebraically mapped Chebyshev functions yield very efficient numerical algorithms when applied to the nonlinear Schrödinger equation. In this paper, we demonstrate that the approximation results of [10] can be used to construct very accurate and fast computational schemes in the context of many other nonlinear wave equations posed in the real line.

As a particular instance, we develop a Chebyshev-type pseudo-spectral scheme for the classical Korteweg-de Vries equation

$$\begin{aligned} u_t+\nu u_x+\delta uu_x+ \sigma u_{xxx} = f,\;\; u(0) = u_0,\;\; \nu ,\delta ,\sigma \in {\mathbb {R}}, \;\; \delta \ne 0, \;\; \sigma >0. \end{aligned}$$

(1)

When the source is trivial ($f=0$), the problem (1) is Hamiltonian (i.e. $u_t={\mathcal {J}}\nabla {\mathcal {H}}(u)$), with

$$\begin{aligned} {\mathcal {H}}(u) = \tfrac{1}{2}\int _{\mathbb {R}} \left( \nu u^2 + \tfrac{\delta }{3} u^3 - \sigma u_x^2\right) dx, \end{aligned}$$

(2)

the first order skew-symmetric automorphism of the Hilbert scale ${H^{\alpha }({\mathbb {R}})}_{\alpha \in {\mathbb {R}}}$ reads ${\mathcal {J}} = -\partial _x$ and the associated duality pairing is given by the standard $L^2({\mathbb {R}})$ inner product $\langle u,v\rangle$. In this case the Eq. (1) is completely integrable, the exact solutions are obtained via the inverse scattering transform, see [1] and references therein. In the general situation ($f\ne 0$), the initial value problem (1) is well posed, provided the input data $(u_0,f)$ is sufficiently regular. In particular, $u\in C([0,T], H^{\alpha }({\mathbb {R}}))$ and $\partial _t^ku\in C([0, T], H^{\alpha -3k}({\mathbb {R}}))$, $0\le k\le \lfloor \tfrac{\alpha }{3}\rfloor$, provided $u_0\in H^{\alpha }({\mathbb {R}})$ and $f\in C([0,T], H^{\alpha }({\mathbb {R}}))$ and $\partial _t^kf\in C([0, T], H^{\alpha -3k}({\mathbb {R}}))$, $0\le k\le \lfloor \tfrac{\alpha }{3}\rfloor$, see e.g. [3, 4].

The paper is organized as follows: Sect. 2 is introductory and contains auxiliary results used throughout the paper. The Chebyshev-type pseudo-spectral scheme is presented in Sect. 3. Here, we provide a comprehensive stability and convergence analyses. In particular, we derive explicit error estimates for the pseudo-spectral approximation in finite time intervals. Efficient practical implementation as well as numerical simulations are presented in Sect. 4. Section 5, concludes the paper.

2 Preliminaries

A comprehensive study of the algebraically mapped Chebyshev basis is found in [10]. For the readers convenience, below we fix the notation and list the key results that are pertinent for the numerical analysis presented in Sect. 3.

2.1 The algebraically mapped Chebyshev basis

The algebraically mapped Chebyshev basis reads

$$\begin{aligned} \ TB_n(x) = \tfrac{\sqrt{\ell }}{\sqrt{\ell ^2 + x^2}}T_n \left( \tfrac{x}{\sqrt{\ell ^2 + x^2}} \right) , \quad n>0, \quad \ell >0, \end{aligned}$$

(3)

where $T_n(x) = \cos (n\arccos x)$, $x\in [-1,1]$, $n\ge 0$, are the Chebyshev polynomials of the first kind. Parameter $\ell >0$ is used in practical simulations to tune up the convergence speed.

The system $\{TB_n(x)\}_{n\ge 0}$ provides a complete orthogonal basis in $L^2({\mathbb {R}})$. Furthermore,

$$\begin{aligned} \langle TB_n, TB_m \rangle = \int _{{\mathbb {R}}} TB_n(x) TB_m(x) dx= \delta _{nm}\kappa _n,\;\;\kappa _n = \left\{ \begin{array}{ll} \pi ,&{} \quad \text {if}~ {n=0},\\ \frac{\pi }{2},&{}\quad \text {if}~ {n>0} , \end{array} \right. \end{aligned}$$

(4)

and any function $f\in L^2({\mathbb {R}})$ can be represented by its convergent (in the sense of $L^2$) Chebyshev-Fourier series

$$\begin{aligned} f(x) = \sum _{n\ge 0} \frac{f_n}{\kappa _n} TB_n(x),\;\; f_n = \langle TB_n, f\rangle . \end{aligned}$$

(5)

In connection with the system $\{TB_n(x)\}_{n\ge 0}$, we set ${\mathbb {P}}_N = {{\mathrm{span}}}\{TB_n\}_{n=0}^{N}$ and introduce two operators: the orthogonal projector ${\mathcal {P}}_N: L^2 ({\mathbb {R}}) \rightarrow {\mathbb {P}}_N$ and the interpolant ${\mathcal {I}}_N: L^2 ({\mathbb {R}}) \rightarrow {\mathbb {P}}_N$. The latter is uniquely determined by

$$\begin{aligned} {\mathcal {I}}_N[f](x_{k,N}) = f(x_{k,N}),\quad x_{k,N} = \ell \cot \tfrac{(2k+1)\pi }{2(N+1)}, \quad 0\le k\le N, \end{aligned}$$

(6)

and acts as the identity in the finite dimensional space ${\mathbb {P}}_N$, see [10].

2.2 Scale of weighted Bessel potential spaces in ${\mathbb {R}}$

The approximation properties of $\{TB_n(x)\}_{n\ge 0}$ are naturally described on the scale of weighted Bessel potential spaces $H^{\alpha }_{\beta }({\mathbb {R}})$, $\alpha ,\beta \in {\mathbb {R}}$. These are Hilbert spaces whose inner products and induced norm are defined in terms of power weights $w_\alpha (\cdot ) = (\ell + \cdot ^2)^{\frac{\alpha }{2}}$ and Fourier multipliers $J^{\alpha ,\ell }[\cdot ] = {\mathcal {F}}^{-1}w_{-\alpha }(\xi ){\mathcal {F}}[\cdot ]$¹ associated with the symbol $w_{-\alpha }(\cdot )$:

$$\begin{aligned} \langle f, g \rangle _{H^{\alpha }_\beta } = \int _{{\mathbb {R}}} w_\beta ^2 J^{-\alpha ,\ell }[f]\overline{J^{-\alpha ,\ell }[g]}dx, \quad \Vert f\Vert ^2_{H^{\alpha }_\beta } = \langle f, f \rangle _{H^{\alpha }_\beta }, \quad \alpha ,\beta \in {\mathbb {R}}, \end{aligned}$$

see [10] for an equivalent definition. For trivial weights ($\beta =0$), the spaces coincide with the standard Hilbert scale of Sobolev spaces [2], in this case we omit the subscript $\beta$ and write $H^{\alpha }({\mathbb {R}})$. Finally, we mention that

$$\begin{aligned} \Vert fg\Vert _{H^{\alpha }_\beta } \le c_{\alpha ,\beta }\Vert f\Vert _{H^{\alpha }_\beta } \Vert g\Vert _{H^{\alpha }_\beta }, \end{aligned}$$

(7)

provided that $\alpha >\tfrac{1}{2}$ and $\beta \ge 0$, see [10] for the details.

2.3 Approximation and interpolation errors

The following estimates, reported in [10], are crucial in the analysis presented in Section 3.

Theorem 1

If $0<\alpha$, $\tfrac{1}{2}<\gamma$ and $\max \{\alpha ,\gamma \}<\beta$. Then

$$\begin{aligned}&\Vert ({\mathcal {I}}-{\mathcal {P}}_N)[f]\Vert _{H^{\alpha }} \le c(\ell N)^{-(\beta -\alpha )}\Vert f\Vert _{H^{\beta }_{2\beta }},\end{aligned}$$

(8a)

$$\begin{aligned}&\Vert ({\mathcal {I}}-{\mathcal {I}}_N)[f]\Vert _{H^{\alpha }} \le c'(\ell N)^{\frac{1}{2}-(\beta -\alpha -\gamma )} \Vert f\Vert _{H^{\beta }_{2\beta }}, \end{aligned}$$

(8b)

where $c,c'>0$ do not depend on N or f.

We remark that in contrast with the orthogonal projector ${\mathcal {P}}_N$, the interpolation operator ${\mathcal {I}}_N$ is bounded only as map from $H^\gamma ({\mathbb {R}})$ to $L^2({\mathbb {R}})$, whith $\gamma >\tfrac{1}{2}$. This yields a slight reduction of the convergence rate in the estimate (8b) as compared to (8a).

3 Application to the Korteweg-de Vries equation

3.1 The numerical scheme

To semi-discretize (1) in space, we employ the Galerkin scheme. That is for a fixed $N>0$, we replace (1) with the following problem: find ${\hat{u}}\in C([0,T], {\mathbb {P}}_N)\cap C^{(1)}((0,T), {\mathbb {P}}_N)$ so that

$$\begin{aligned} \left\{ \begin{array}{ll} \bigl \langle {\hat{u}}_t + \nu {\hat{u}}_x + \delta {\hat{u}}{\hat{u}}_x + \sigma {\hat{u}}_{xxx}, \phi \bigr \rangle = \langle {\hat{f}}, \phi \rangle ,&{}\quad \text {for all}\;\; \phi \in {\mathbb {P}}_N,\\ {\hat{u}}(0) = {\hat{u}}_0 := {\mathcal {I}}_N[u_0], &{}\quad {\hat{f}}:={\mathcal {I}}_N[f]. \end{array} \right. \end{aligned}$$

(9)

Problem (9) represents a coupled system of $N+1$ ordinary differential equations (ODEs) for the unknown discrete spectral coefficients ${\hat{u}}_n(t)$. In the sequel of this section, we show that the numerical solution ${\hat{u}}$ converges to the exact one in finite time intervals.

3.2 Stability analysis

We show that the numerical scheme (9) depends continuously on the input data $({\hat{u}}_0, f)$.

Lemma 1

(Stability) Let ${\hat{u}}_1$, ${\hat{u}}_2$ satisfy (9) equipped with the data $({\hat{u}}_{01},{\hat{f}}_1)$ and $({\hat{u}}_{02},{\hat{f}}_2)$, respectively. Then

$$\begin{aligned} \Vert {\hat{u}}_1 - {\hat{u}}_2\Vert \le c\Bigl (\Vert {\hat{u}}_{01}-{\hat{u}}_{02}\Vert +\Vert {\hat{f}}_1-{\hat{f}}_2\Vert _{L^2((0,T)\times {\mathbb {R}})}\Bigr ),\quad t\in [0, T], \end{aligned}$$

(10)

where $c>0$ depends on T and $\Vert {\hat{u}}_{2}\Vert _{C([0,T],H^{2})}$ only.

Proof

Straightforward calculations imply that the error ${\hat{e}} = {\hat{u}}_1-{\hat{u}}_2$ satisfies

$$\begin{aligned} \left\{ \begin{array}{l} \langle {\hat{e}}_t+\nu {\hat{e}}_x+\delta {\hat{e}}{\hat{e}}_x+\sigma {\hat{e}}_{xxx}, \phi \rangle = \langle {\hat{g}},\phi \rangle , \quad \text {for all}\; \phi \in {\mathbb {P}}_N,\\ {\hat{e}}_0 = {\hat{u}}_{01} - {\hat{u}}_{02}, \end{array} \right. \end{aligned}$$

(11)

where

$$\begin{aligned} {\hat{g}} = {\hat{f}}_1-{\hat{f}}_2+E[{\hat{e}},{\hat{u}}_2],\quad E[{\hat{e}},{\hat{u}}_2] = -\delta ({\hat{e}}{\hat{u}}_{2})_x. \end{aligned}$$

We let $\phi =2{\hat{e}}$ in the equation above to obtain

$$\begin{aligned} \tfrac{d}{dt}\Vert {\hat{e}}\Vert ^2 = 2\langle {\hat{f}}_1-{\hat{f}}_2, e\rangle + 2\langle E[{\hat{e}},{\hat{u}}_2], e\rangle . \end{aligned}$$

To estimate the last term, we observe that

$$\begin{aligned} -2\langle E[{\hat{e}},{\hat{u}}_{2}], e\rangle = 2\delta \langle {\hat{e}}, ({\hat{e}}{\hat{u}}_2)_x\rangle = \delta \langle {\hat{e}}^2,{\hat{u}}_{2x}\rangle . \end{aligned}$$

Elementary interpolation inequality $\Vert u\Vert _{\infty }\le \sqrt{2}\Vert u\Vert ^{1/2}\cdot \Vert u_x\Vert ^{1/2}$ implies

$$\begin{aligned} |2\langle E[{\hat{e}},{\hat{u}}_2], {\hat{e}}\rangle | \le \sqrt{2}\delta \Vert {\hat{e}}\Vert ^2 \Vert {\hat{u}}_{2x}\Vert ^{1/2}\cdot \Vert {\hat{u}}_{2xx}\Vert ^{1/2} \le \sqrt{2}\delta \Vert {\hat{u}}_2\Vert _{H^{2}} \Vert {\hat{e}}\Vert ^2. \end{aligned}$$

Consequently

$$\begin{aligned} \tfrac{d}{dt}\Vert e\Vert ^2 \le \bigl (1+\sqrt{2}\delta \Vert {\hat{u}}_2\Vert _{H^{2}}\bigr )\Vert e\Vert ^2+ \Vert {\hat{f}}_1-{\hat{f}}_2]\Vert ^2. \end{aligned}$$

Hence, by Gronwall’s inequality

$$\begin{aligned} \Vert {\hat{e}}\Vert ^2 \le e^{t\bigl (1+\sqrt{2}\delta \Vert {\hat{u}}_2\Vert _{C([0,T],H^{2})}\bigr )}\left( \Vert {\hat{e}}_0\Vert ^2 + \int _0^t \Vert {\hat{f}}_1-{\hat{f}}_2\Vert ^2d\tau \right) . \end{aligned}$$

The last estimate shows that (10) holds with $c = e^{T\bigl (1+\sqrt{2}\delta \Vert {\hat{u}}_2\Vert _{C([0,T],H^{2})}\bigr )}$ that is completely controlled by T and $C([0,T],H^{2}({\mathbb {R}}))$ norm of ${\hat{u}}_2$. $\square$

Lemma 1 implies in particular that numerical solutions ${\hat{u}}$ remain $L^2({\mathbb {R}})$-bounded in bounded time intervals. Indeed, letting $({\hat{u}}_{01}, f_1) = ({\hat{u}},{\hat{f}})$ and $({\hat{u}}_{02}, {\hat{f}}_2) = (0,0)$ in (10), we infer

$$\begin{aligned} \Vert {\hat{u}}\Vert \le c \bigl (\Vert {\hat{u}}_0\Vert + \Vert {\mathcal {I}}_N[f]\Vert _{L^2((0,T)\times {\mathbb {R}})}\bigr ), \end{aligned}$$

(12)

with $c>0$ that depends on T only. Furthermore, if in addition $f=0$, then $\langle E[{\hat{e}},{\hat{u}}_2], {\hat{e}}\rangle = 0$ and the $L^2$-norm of the numerical solution is conserved, i.e. $\tfrac{d}{dt}\Vert u\Vert ^2 = 0$.

3.3 Consistency and convergence

For the exact solution u of (1), we let ${\bar{u}} = {\mathcal {P}}_N[u]$. Upon substitution into (9), we infer

$$\begin{aligned} \left\{ \begin{array}{l} \bigl \langle {\bar{u}}_t + \nu {\bar{u}}_x + \delta {\bar{u}}{\bar{u}}_x +\sigma {\bar{u}}_{xxx}, \phi \bigr \rangle = \langle {\hat{f}} + {\bar{d}}, \phi \rangle ,\;\;\text {for all}\;\; \phi \in {\mathbb {P}}_N,\\ {\bar{u}}(0) = {\bar{u}}_0= {\mathcal {P}}_N[u_0],\quad {\bar{d}} = ({\mathcal {P}}_N-{\mathcal {I}}_N)[f] + \delta {\mathcal {P}}_N[{\bar{u}}{\bar{u}}_x - uu_x]. \end{array} \right. \end{aligned}$$

(13)

The following result shows that the defect ${\bar{d}}$ is small provided u is sufficiently regular.

Lemma 2

(Consistency) Assume $\gamma >\frac{1}{2}$ and $\beta >1$. Then

$$\begin{aligned} \Vert {\bar{d}}\Vert _{L^2((0,T)\times {\mathbb {R}})} \le c(\ell N)^{\frac{1}{2}+\gamma -\beta } \left( \Vert f\Vert _{L^2((0,T), H^{\beta }_{2\beta }({\mathbb {R}}))} + \Vert u\Vert _{L^4((0,T), H^{\beta }_{2\beta }({\mathbb {R}}))}^2\right) , \end{aligned}$$

(14)

where $c>0$ does not depend on N, u or f.

Proof

We write ${\bar{d}} = {\bar{d}}_1+\delta {\bar{d}}_2$, where ${\bar{d}}_1 = ({\mathcal {P}}_N-{\mathcal {I}}_N)[f]$ and ${\bar{d}}_2 = {\mathcal {P}}_N[{\bar{u}}{\bar{u}}_x - uu_x]$. For ${\bar{d}}_1$ we employ Theorem 1 to obtain

$$\begin{aligned} \Vert {\bar{d}}_1\Vert&= \Vert {\mathcal {P}}_N({\mathcal {I}}-{\mathcal {I}}_N)[f]\Vert \le \Vert ({\mathcal {I}}-{\mathcal {I}}_N)[f]\Vert \\&\le c(\ell N)^{\tfrac{1}{2}-(\beta -\gamma )} \Vert f\Vert _{H^{\beta }_{2\beta }}, \end{aligned}$$

with some uniform constant $c>0$. To bound ${\bar{d}}_2$, we recall that $\Vert u\Vert _\infty \le \sqrt{2}\Vert u\Vert _{H^{1}}$ and then apply (8a). This gives

$$\begin{aligned} \Vert {\bar{d}}_2\Vert&= \Vert u_x(I-{\mathcal {P}}_N)[u] + u(I-{\mathcal {P}}_N)[u]_x\Vert \\&\le \Vert u_x\Vert \Vert (I-{\mathcal {P}}_N)[u]\Vert _\infty + \Vert u\Vert _\infty \Vert (I-{\mathcal {P}}_N)[u]\Vert _{H^{1}}\\&\le c''\Vert u\Vert _{H^{1}}\Vert (I-{\mathcal {P}}_N)[u]\Vert _{H^{1}} \le c''' (\ell N)^{1-\beta }\Vert u\Vert _{H^{\beta }_{2\beta }}^2, \end{aligned}$$

with $c'',c'''>0$ that do not depend on N or u. Adding these estimates together and integrating over interval [0, T], we arrive at (14). $\square$

Lemmas 1 and 2, combined together, yield convergence.

Theorem 2

Assume $\beta \ge 2$ and $\gamma >\tfrac{1}{2}$. Then

$$\begin{aligned} \Vert u-{\hat{u}}\Vert _{L^2((0,T)\times {\mathbb {R}})}\le & {} c(\ell N)^{\frac{1}{2}+\gamma -\beta } \left( \phantom {\left. +\Vert f\Vert _{L^2((0,T), H^{\beta }_{2\beta }({\mathbb {R}}))} + \Vert u\Vert _{L^4((0,T), H^{\beta }_{2\beta }({\mathbb {R}}))}^2\right) }\Vert u_0\Vert _{H^{\beta }_{2\beta }}\right. \nonumber \\&\left. +\Vert f\Vert _{L^2((0,T), H^{\beta }_{2\beta }({\mathbb {R}}))} + \Vert u\Vert _{L^4((0,T), H^{\beta }_{2\beta }({\mathbb {R}}))}^2\right) , \end{aligned}$$

(15)

where $c>0$ depends on T and $\Vert u\Vert _{C([0,T],H^{2})}$ only.

Proof

From Theorem 1 it follows immediately that

$$\begin{aligned} \Vert u-{\bar{u}}\Vert _{L^2((0,T)\times {\mathbb {R}})} = \Vert ({\mathcal {I}}-{\mathcal {P}}_N)[u]\Vert _{L^2((0,T)\times {\mathbb {R}})} \le c(\ell N)^{-\beta }\Vert u\Vert _{L^2((0,T), H^{\beta }_{2\beta }({\mathbb {R}}))}, \end{aligned}$$

where $c>0$ does not depend on N or u. Both the numerical solution ${\hat{u}}$ and the spectral projection ${\bar{u}}$ satisfy (9) with the input data $({\hat{u}}_0, {\hat{f}})$ and $({\bar{u}}_0, {\hat{f}}+{\bar{d}})$, respectively. By virtue of Lemma 1,

$$\begin{aligned} \Vert {\hat{u}}-{\bar{u}}\Vert _{L^2((0,T)\times {\mathbb {R}})} \le c' \Bigl (\Vert {\hat{u}}_0 - {\bar{u}}_0\Vert + \Vert {\bar{d}}\Vert _{L^2((0,T)\times {\mathbb {R}})}\Bigr ), \end{aligned}$$

where $c'>0$ depends on T and $\Vert {\mathcal {P}}_N[u]\Vert _{C([0,T],H^{2})}$ only. While from Theorem 1, we deduce

$$\begin{aligned} \Vert {\hat{u}}_0 - {\bar{u}}_0\Vert = \Vert {\mathcal {P}}_N({\mathcal {I}} - {\mathcal {I}}_N)[u_0]\Vert \le c''(\ell N)^{\frac{1}{2}+\gamma - \beta }\Vert u_0\Vert _{H^{\beta }_{2\beta }}, \end{aligned}$$

with $c''>0$ independent on N and $u_0$. Hence, Lemma 2, combined with the triangle inequality $\Vert u-{\hat{u}}\Vert \le \Vert u-{\bar{u}}\Vert +\Vert {\hat{u}}-{\bar{u}}\Vert$, yields (14). $\square$

Theorem 2 shows that scheme (9) converges spectrally, provided the exact solution is smooth and decay sufficiently fast at infinity.

4 Numerical simulations

4.1 Practical implementation

The numerical scheme (9) leads to the semi-linear system of ODEs of the form

$$\begin{aligned} {\dot{Y}} = -(\nu A + \sigma B)Y - \delta CF(Y) = G(Y), \end{aligned}$$

(16)

where $A, B, C\in {\mathbb {R}}^{(n+1)\times (n+1)}$, are realizations of the discrete differentiation operators

$$\begin{aligned} {\mathcal {A}}_N = {\mathcal {P}}_N\partial _x{\mathcal {P}}_N,\quad {\mathcal {B}}_N = {\mathcal {P}}_N\partial _{xxx}{\mathcal {P}}_N,\quad {\mathcal {C}}_N = \tfrac{1}{2}{\mathcal {P}}_N \partial _x\tfrac{\sqrt{\ell }}{\sqrt{\ell ^2+x^2}}, \end{aligned}$$

F(Y) is the nonlinearity and the neutral symbol Y represents either the vector of pseudo-spectral coefficients

$$\begin{aligned} {\hat{U}} = ({\hat{u}}_n, 0\le n\le N)^T, \end{aligned}$$

or the vector

$$\begin{aligned} U = ({\hat{u}}(x_{k,N}), 0\le k\le N), \end{aligned}$$

containing values of ${\hat{u}}$ at Gauss–Chebyshev nodes. The particular structure of A, B, C and G depends on whether (9) is integrated in Fourier or physical space. For instance, matrix A is dense in physical, while $A_{ij} = 0$ for $i+j$ even in Fourier space. Moreover, in the latter case it can be written as a sum of two Toeplitz and two Hankel matrices. Similarly, the nonlinearity is given explicitly by

$$\begin{aligned} F(Y) = \tfrac{1}{\sqrt{\ell }}\left( \left[ \ell ^2+x_{k,2N}^2\right] ^{\frac{1}{2}}{\hat{u}}(x_{k,2N})^2, 0\le k\le 2N\right) , \end{aligned}$$

in physical space (note 2N instead of N), while its representation in Fourier space involves two discrete convolutions.

The exact solutions to ODE (16) are not known. In practice, it is integrated using an appropriate time-stepping algorithm. There are two important practical issues that arise in this connection. First of all, straightforward computation of the vector field G(Y) would require ${\mathcal {O}}(N^2)$ operations and, hence, is not numerically feasible for large values of N. Secondly, the semi-discretization (9) is stiff and, despite the fact that it does not preserve symplecticity of the continuous flow, (9) remains $\rho$-reversible (i.e. $\rho \circ G = - G\circ \rho$) under the reflection map $\rho [u](x) = u(-x)$. A reasonable time-stepping algorithm must be able to cope with stiffness and at the same time preserve the $\rho$-reversible of the exact flow. Both issues are briefly addressed below.

Computing the vector field  Direct calculations show that

$$\begin{aligned} \langle TB_m, \partial _x TB_n\rangle&= \tfrac{n}{2\ell }\bigl [\tfrac{1}{1-(n-m-1)^2} - \tfrac{1}{1-(n-m+1)^2}\bigr ]\\&\quad +\tfrac{n}{2\ell }\left[ \tfrac{1}{1-(n+m-1)^2} + \tfrac{1}{1-(n+m+1)^2}\right] \\&\quad -\tfrac{1}{2\ell }\left[ \tfrac{1}{1-(n-m-1)^2} + \tfrac{1}{1-(n-m+1)^2}\right] \\&\quad -\tfrac{1}{2\ell }\left[ \tfrac{1}{1-(n+m-1)^2} + \tfrac{1}{1-(n+m+1)^2}\right] , \quad 0\le n,m\le N, \end{aligned}$$

when $n+m$ is odd and is zero otherwise. It follows that in terms of Chebyshev-Fourier modes, $Y = {\hat{U}}$, the action ${\mathcal {A}}_N[{\hat{u}}]$ is realized as the matrix-vector product with $A\in {\mathbb {R}}^{(n+1)\times (n+1)}$ that is made up of two Toeplitz and two Hankel matrices. For such matrices, multiplication can be written in the form of discrete convolutions, as a consequence, the product AY requires only ${\mathcal {O}}(N\log _2 N)$ floating point operations. The same observation applies to the product BY. Indeed, ${\mathcal {B}}_N[{\hat{u}}] = ({\mathcal {P}}_N {\mathcal {A}}_{N+4} \partial _{xx})[{\hat{u}}]$, while (see [10])

$$\begin{aligned} \partial _{xx} TB_0(x)&= \tfrac{1}{(4\ell )^2}\bigl [-6TB_4(x)+8TB_2(x)-2TB_0(x) \bigr ],\\ \partial _{xx} TB_2(x)&= \tfrac{1}{(4\ell )^2}\bigl [-15TB_6(x)+36TB_4(x)-25TB_2(x)+4TB_0(x) \bigr ],\\ \partial _{xx} TB_n(x)&= \tfrac{1}{(4\ell )^2}\bigl [-(n-1)(n-3)TB_{n-4}(x) + 4(n-1)^2TB_{n-2}(x)\\&\quad -(6n^2+2)TB_n(x) + 4(n+1)^2TB_{n+2}(x)\\&\quad - (n+1)(n+3)TB_{n+4}(x)\bigl ],\quad n = 1, 3,4,\ldots . \end{aligned}$$

As a consequence, computing $\partial _{xx}{\hat{u}}$ requires ${\mathcal {O}}(N)$ operations and the overall complexity of the product BY is again ${\mathcal {O}}(N\log _2 N)$.

The nonlinearity F(Y) can be evaluated either in physical or in Fourier space. The first approach involves transformation of the physical data U into its Chebyshev-Fourier counterpart ${\hat{U}}$. As shown in [10], computational complexity of both operations is $O(N\log _2 N)$. On another hand, one can employ the elementary identity

$$\begin{aligned} \tfrac{2}{\sqrt{\ell }}\left[ \ell ^2+x_{k,2N}^2\right] ^{\frac{1}{2}}TB_m(x) TB_n(x) = TB_{|m-n|}(x) + TB_{m+n}(x) \end{aligned}$$

to write ${\hat{u}}^2$ as a sum of two discrete convolutions involving components of ${\hat{U}}$. This yields an alternative algorithm with the same complexity of ${\mathcal {O}}(N\log _2 N)$. Finally, we note that

$$\begin{aligned} \Bigl \langle \partial _x TB_0, \tfrac{\sqrt{\ell }}{\sqrt{\ell ^2+x^2}} TB_n\Bigr \rangle&= \tfrac{\pi }{8\ell ^{\frac{3}{2}}}\bigl [-(n-2)\delta _{0,n-3}+2n\delta _{0,n-1}],\quad n\ge 0, \\ \Bigl \langle \partial _x TB_m, \tfrac{\sqrt{\ell }}{\sqrt{\ell ^2+x^2}} TB_0\Bigr \rangle&= \tfrac{\pi }{4\ell ^{\frac{3}{2}}}\bigl [\delta _{1,m-2} - \delta _{m,1}],\quad m\ge 1,\\ \Bigl \langle \partial _x TB_m, \tfrac{\sqrt{\ell }}{\sqrt{\ell ^2+x^2}} TB_n\Bigr \rangle&= \tfrac{\pi }{16\ell ^{\frac{3}{2}}}\bigl [ \delta _{m,n+3}(m-1) - \delta _{m,n+1}(3m-1)\\&\quad + \delta _{m,n-1}(3m+1) - \delta _{m,n+3}(m+1) \bigr ],\quad m \ge 1, \;\; n\ge 1, \end{aligned}$$

i.e. C is four diagonal in Fourier space, computing the matrix-vector product with matrix C requires ${\mathcal {O}}(N)$ operations, and the total cost of evaluating G(Y) is ${\mathcal {O}}(N\log _2 N)$.

Time stepping  As mentioned earlier, the semi-discrete problem (16) is stiff and hence cannot be integrated using an explicit ODE solver. Furthermore, its flow is $\rho$-reversible. To cope with the stiffness and to preserve the structure of the flow, we are forced to use symmetric time-stepping schemes, see e.g. discussion in [8]. In our simulations, we employ the implicit midpoint rule

$$\begin{aligned} Y(\tau ) = \varPhi _\tau Y(0) = \left( I + \tfrac{\tau }{2} D\right) ^{-1}\Bigl [ (I - \tfrac{\tau }{2} D)Y(0) - \tau \delta CF\left( \tfrac{1}{2}(Y(0)+Y(\tau )\right) \Bigr ], \end{aligned}$$

(17)

where $D = \nu A + \sigma B$. The time-discrete map $\varPhi _\tau$ is unconditionally stable, symmetric, $\rho$-reversible and has classical order of convergence $p=2$. To lift its order, we observe that semi-discretization (9) preserves hyperbolicity of (1),² and hence the symmetric composition technique applies, see e.g. [8] and references therein. In our simulations, we employ

$$\begin{aligned} {\hat{\varPhi }}_\tau = \varPhi _{\gamma _1 \tau }\circ \cdots \circ \varPhi _{\gamma _m\tau }, \end{aligned}$$

(18)

with the composition coefficients $\gamma _i$, $1\le i\le 35$, given in [9], this yields time-stepping scheme of classical order $p=10$.

4.2 Numerical simulations

Below, we present several numerical simulations demonstrating the computational efficiency of the algorithm (9). To begin, we integrate (1) numerically with $f=0$. In this settings, (1) is completely integrable, the closed form solutions are constructed via the inverse scattering transform, see e.g. [1]. For instance, the no reflection scenario with $\nu =0$, $\delta = -6$, $\sigma =1$, yields the so called J-solitons

$$\begin{aligned} u(x,t)= & {} - 2\partial _{xx} \ln \det (I + A(x,t)),\nonumber \\ A(x,t)= & {} \left( b_ie^{\lambda ^3_i t} \tfrac{e^{-\lambda _ix-\lambda _j x}}{\lambda _i+\lambda _j}, 1\le i,j\le J\right) ,\nonumber \\ \lambda _i= & {} \tfrac{1}{2}\sqrt{v_i}\quad b_i = 2\lambda _ie^{2\phi _i\lambda _i},\quad 1\le i\le J, \end{aligned}$$

(19)

where $v_i$ and $\phi _i$ control the velocity and phase of the traveling waves.

Fig. 1

The numerical solution of problem (1) (top to bottom): $-{\hat{u}}$, $|u-{\hat{u}}|$, with $N=2^7$. The right diagram: $\Vert u-{\hat{u}}\Vert _{L^2({\mathbb {R}})}$ (blue), $\Vert u-{\hat{u}}\Vert _{L^\infty ({\mathbb {R}})}$ (teal), $\max _t \bigl |\Vert {\hat{u}}(t)\Vert _{L^2({\mathbb {R}})} - \Vert {\hat{u}}_0\Vert _{L^2({\mathbb {R}})}\bigr |$ (red) and $\max _t \bigl |\hat{{\mathcal {H}}}({\hat{u}}(t)) - \hat{{\mathcal {H}}}({\hat{u}})(0)\bigr |$ (orange)

Example 1

In our first numerical example, we integrate (1) in the time interval [0, 4], with $\nu =0$, $\delta = -6$, $\sigma =1$ and initial data $u_0$, obtained from (19) with $J=1$, $v_1 = 2$ and $\phi _1 = -2$. The exact solution u is a single traveling wave moving in the positive x-direction. Directly from (19), it follows that u is analytic in a strip containing the x axis and decays exponentially fast as $x\rightarrow \pm \infty$. The situation is ideal and, in view of Theorem 2, we expect spectral convergence.

The results of simulations, with $2^4\le N\le 2^7$ and $\ell =4$, (see right diagram in Fig. 1) confirm that this is indeed the case. Both, $L^2({\mathbb {R}})$ and $L^\infty ({\mathbb {R}})$ (blue and teal lines, respectively) errors decrease geometrically as N increases. The same observation applies to the Hamiltonian ${\mathcal {H}}(u)$ (orange line), it is not preserved but the variation $\max _t |{\mathcal {H}}({\hat{u}}(t)) - {\mathcal {H}}({\hat{u}}(0))|$ decreases geometrically as N increases.

According to the remark that follows immediately after Lemma 1, the quantity $\Vert {\hat{u}}(t)\Vert _{L^2({\mathbb {R}})}$ is conserved along exact trajectories of (9). This is confirmed by our simulations, the $L^2$ norm of the numerical solution remains almost independent on the discretization parameter N (the magnitude of fluctuations remains with in the range $[10^{-13}, 10^{-12}]$).

Fig. 2

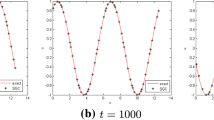
The numerical solution of problem (1) (top to bottom): $-{\hat{u}}$, $|u-{\hat{u}}|$, with $N=2^7$. The right diagram: $\Vert u-{\hat{u}}\Vert _{L^2({\mathbb {R}})}$ (blue), $\Vert u-{\hat{u}}\Vert _{L^\infty ({\mathbb {R}})}$ (teal), $\max _t \bigl |\Vert {\hat{u}}(t)\Vert _{L^2({\mathbb {R}})} - \Vert {\hat{u}}_0\Vert _{L^2({\mathbb {R}})}\bigr |$ (red) and $\max _t \bigl |\hat{{\mathcal {H}}}({\hat{u}}(t)) - \hat{{\mathcal {H}}}({\hat{u}})(0)\bigr |$ (orange)

Example 2

Here, we integrate (1) in the time interval [0, 4], with $\nu =0$, $\delta = -6$, $\sigma =1$ and initial data $u_0$, obtained from (19) with $J=2$, $v_1 = 2$, $v_2=1$ and $\phi _1 = -2$, $\phi _2 = 0$. The scenario models elastic collision of two traveling waves ( the collision happens at $t=2$). As in Example 1, the exact solution is analytic in a strip containing the real axis and decays to zero exponentially at $\pm \infty$.

The results of simulations, with $2^4\le N\le 2^8$ and $\ell =4$ are presented in Fig. 2. As in Example 1, we see that both, $L^2({\mathbb {R}})$ and $L^\infty ({\mathbb {R}})$ (blue and teal lines, respectively) errors as well as variation in the Hamiltonian $\max _t |{\mathcal {H}}({\hat{u}}(t)) - {\mathcal {H}}({\hat{u}}(0))|$ (orange line) decrease geometrically. As before, the scheme preserves the $L^2$ norm of the solution.

Fig. 3

The numerical solution of problem (1) (top to bottom): $-{\hat{u}}$, $|u-{\hat{u}}|$, with $N=2^7$. The right diagram: $\Vert u-{\hat{u}}\Vert _{L^2({\mathbb {R}})}$ (blue), $\Vert u-{\hat{u}}\Vert _{L^\infty ({\mathbb {R}})}$ (teal), $\max _t \bigl |\Vert {\hat{u}}(t)\Vert _{L^2({\mathbb {R}})} - \Vert {\hat{u}}_0\Vert _{L^2({\mathbb {R}})}\bigr |$ (red) and $\max _t \bigl |\hat{{\mathcal {H}}}({\hat{u}}(t)) - \hat{{\mathcal {H}}}({\hat{u}})(0)\bigr |$ (orange)

Example 3

As another example, we take $\nu =0$, $\delta = -6$, $\sigma =1$, $J=3$, $v_1 = \tfrac{3}{2}$, $v_2=1$, $v_3 = \tfrac{1}{2}$ and $\phi _1 = -3$, $\phi _2 = -2$ and $\phi _3 = -1$. The resulting 3-soliton solution represents three traveling waves colliding at $t=2$.

For $2^4\le N\le 2^8$ and $\ell =4$ the output data are displayed in Fig. 3. Both $L^2({\mathbb {R}})$ and $L^\infty ({\mathbb {R}})$ (blue and teal lines, respectively) errors and the deviation $\max _t |{\mathcal {H}}({\hat{u}}(t)) - {\mathcal {H}}({\hat{u}}(0))|$ (orange line) demonstrate the same qualitative behavior as in all our previous simulations. The convergence is geometric (the error curves are concave). However, the absolute accuracy drops. The reason is—as the time increases, the waves enter a region with relatively few grid points, where solutions cannot be resolved accurately. The situation can be improved by taking larger values for N.

Fig. 4

The numerical solution of problem (1) (top to bottom): $-{\hat{u}}$, $|u-{\hat{u}}|$, with $N=2^7$. The right diagram: $\Vert u-{\hat{u}}\Vert _{L^2({\mathbb {R}})}$ (blue), $\Vert u-{\hat{u}}\Vert _{L^\infty ({\mathbb {R}})}$ (teal)

Example 4

In our last example we demonstrate accuracy of (9) in the presence of nontrivial source. We set $\nu =\delta =\sigma =1$ and choose the f so that the exact solution is given by $u= e^{-x^2}$. The history of simulations, recorded in Fig. 4, confirms excellent numerical properties of our spectral scheme, provided that the source term is regular and decreases sufficiently fast at infinity.

5 Conclusions

The main focus of this paper was to demonstrate efficiency of the Chebyshev-type spectral schemes in context of nonlinear wave equations posed in unbounded spatial domains. In this regard, we presented a numerical scheme, based on $\{TB_n(x)\}_{n\ge 0}$, which was applied to the nonlinear Korteweg-de Vries equation. Rigorous theoretical analysis, presented in Sections 3-4, indicates that the resulting numerical scheme (9) is stable, admits efficient practical implementation and converges rapidly, provided exact solutions are smooth. The theoretical conclusions are supported by the numerical simulations, presented in Section 4.