1 Introduction

The Hermitian and skew-Hermitian splitting (HSS) iteration method [12] has been firstly presented by Bai et al. to solve the linear system

$$\begin{aligned} Ax=b, \end{aligned}$$
(1)

where \(A \in \mathbb {C}^{q\times q}\) is a large and sparse non-Hermitian positive definite (HPD) matrix and \(x,b\in \mathbb {C}^q\). The proposed method has been widely used in solving various problems such as convection-diffusion equation [12], saddle-point problem [10, 15], continuous Sylvester equation [7], image restoration problem [3]. Many works have also been done to improve the HSS method such as modified HSS (MHSS) [8], accelerated HSS (AHSS) [9], generalized HSS (GHSS) [14] and preconditioned HSS (PHSS) [13, 26]. Besides the proposed methods, the Krylov subspace methods are widely used to solve the linear systems in the literature [24]. Due to the structure of system (1), choosing the most practical and effective method can be difficult [23]. In this study, we use the generalized minimum residual (GMRES) algorithm which is arguably the most popular choice [25].

In practice, from the ill-conditioning of system (1), the Krylov subspace methods converge slowly or sometimes diverge. Thus, the Krylov subspace methods are often applied to solve the proposed linear systems in conjunction with a suitable preconditioner. The effect of the preconditioned method is to increase the rate of convergence of the Krylov subspace methods such as GMRES method. Several preconditioning techniques have been presented to improve the performance and reliability of Krylov subspace methods [20]. In the last decade, several extensions of the HSS iteration method have been widely applied as preconditioners to accelerate a Krylov subspace method. Convergence and the preconditioning properties of the HSS method have been investigated by Benzi and Golub [16]. Convergence properties of the PHSS methods for non-Hermitian positive semidefinite matrices have also been investigated in [11]. Applications of the HSS iteration method as a preconditioner for Krylov subspace method in solving singular, non-Hermitian and positive semidefinite systems have been presented in [6]. The MHSS-preconditioned GMRES [8] has been applied to solve a class of complex symmetric linear systems. Cao et al. presented the relaxed HSS (RGHSS) to accelerate the convergence of GMRES method for solving saddle point problems [18].

The polynomial preconditioners have been successfully presented for solving linear systems and performing parallel computing, see [1, 2, 17]. To design the proposed proconditioners, similar to the usual techniques, the coefficient matrix A is split as \(A=M-N\), where M is a nonsingular matrix. Suppose that \(G=M^{-1}N\) and \(\rho (G)\) is the spectral radius of G. If \(\rho (G)<1\), from Neumann series, then a preconditioner based on approximating inverse can be given as follows [17],

$$\begin{aligned} P(m)=M\left( I+G+G^2+\cdots +G^{m-1}\right) ^{-1}, \end{aligned}$$
(2)

which also called polynomial preconditioner. From Eq. (2), the proconditioned matrix can be given as:

$$\begin{aligned} P(m)^{-1}A=\left( I+G+G^2+\cdots +G^{m-1}\right) M^{-1}A=I-G^{m}. \end{aligned}$$
(3)

Furthermore, since the coefficient matrix A can be split by iterative matrix \(G^m\) as follows,

$$\begin{aligned} A=P(m)-P(m)G^m=P(m)-N(m), \end{aligned}$$
(4)

the matrix P(m) is also called the m-step preconditioner. Indeed, the linear system \(P(m) v=r\), which is mainly encountered in the preconditioned Krylov subspace iteration methods, can be effectively solved by the following m-step iteration method with \(v^{(0)}=0\) as the initial guess,

$$\begin{aligned} Mv^{(j)}=Nv^{(j-1)}+r, \quad j=1,\ldots ,m. \end{aligned}$$
(5)

Huang in [22] presented an m-step HSS (HSS(m)) polynomial preconditioner for the Krylov subspace iteration methods to solve linear system (1). To do so, the matrices M and G in (2) have been extracted from the HSS iteration method to construct an m-step polynomial preconditioner.

Recently, the two-parameter GHSS (TGHSS) iteration method has been presented to solve the non-Hermitian positive definite linear systems [4]. In this study, we use the idea of polynomial preconditioning technique and the TGHSS method to present a new m-step preconditioning matrix. Convergence of method and spectral properties of the preconditioned matrix are also investigated. Throughout the paper, for a matrix \(A \in {\mathbb {C}}^{q\times q}\), the symbols \(\rho (A)\) and \(\sigma (A)\) stand for the spectral radius and the spectrum of A, respectively. For a matrix \(X\in {\mathbb {R}}^{q \times q}\) whose eigenvalues are real, its smallest eigenvalues is denoted by \(\lambda _q(X)\).

This paper is organized as follows. A brief description of the m-step HSS preconditioner is given in Sect. 2. In Sect. 3, the TGHSS method is introduced and the m-step TGHSS preconditioner is presented to use in Krylov subspace methods such as GMRES. Section 4 is devoted to the implementation issues of the proposed preconditioner. Three numerical examples are given in Sect. 5. Finally, in Sect. 6 we present some concluding remarks.

2 A brief description of the m-step HSS preconditioning technique

The HSS iteration method has been presented based on the splitting of the coefficient matrix A into Hermitian part \(H=(A+A^*)/2\) and skew-Hermitian part \(S=(A-A^*)/2\). Indeed, the proposed method has been introduced using the shifted matrices \(\alpha I+H\) and \(\alpha I+S\) to solve non-Hermitian positive definite linear systems as follows:

$$\begin{aligned} \left\{ \begin{array}{l} (H+\alpha I)x^{(k+\frac{1}{2})}=(\alpha I-S)x^{(k)}+b, \\ (S+\alpha I)x^{(k+1)}= (\alpha I-H)x^{(k+\frac{1}{2})}+b, \end{array} \right. \quad k=0,1,\ldots , \end{aligned}$$
(6)

where \(\alpha \) is positive parameter and I is the identity matrix of order q. It is shown that the HSS iteration (6) is convergent for all \(\alpha >0\) [12]. It is easy to see that the iteration (6) can be written as:

$$\begin{aligned} x^{(k+1)}=G_{\alpha }x^{(k)}+M_{\alpha }^{-1}b, \quad k=0,1,\ldots , \end{aligned}$$

where

$$\begin{aligned} \begin{array}{l} M_{\alpha }=\frac{1}{2\alpha }(\alpha I + H)(\alpha I + S), \\ G_{\alpha }=(\alpha I + S)^{-1}(\alpha I - H)(\alpha I + H)^{-1}(\alpha I - S). \end{array} \end{aligned}$$
(7)

In the m-step HSS preconditioning method, the preconditioner matrix (2) has been constructed with the matrices \(G_{\alpha }\) and \(M_{\alpha }\) which have been extracted from the HSS iteration method. Huang has shown that the spectral distribution of preconditioned matrix becomes increasingly clustered as m gets larger [22].

3 The m-step TGHSS preconditioning method

In this section, the TGHSS iteration method is briefly introduced, then the m-step TGHSS preconditioner is constructed to accelerate the Krylov subspace methods such as GMRES.

It has been mentioned that the matrix A naturally possesses a Hermitian/skew-Hermitian splitting as \(A=H+S\). In the TGHSS iteration method, the Hermitian part is also split as \(H=T+K\) where T and K are positive semidefinite matrices. To implement the proposed method, two following splittings of A are given

$$\begin{aligned} A = (\alpha I+T) - (\alpha I - S-K) \quad \text { and } \quad A = (\beta I + S + K) - (\beta I- T), \end{aligned}$$
(8)

where \(\alpha \) and \(\beta \) are positive parameters. These shifted matrices lead to the following TGHSS iteration method [4]:

$$\begin{aligned} \left\{ \begin{array}{l} (\alpha I+T)x^{(k+\frac{1}{2})}=(\alpha I-S-K)x^{(k)}+b, \\ (\beta I+S+K)x^{(k+1)}= (\beta I-T)x^{(k+\frac{1}{2})}+b, \end{array} \right. \quad k=0,1,\ldots , \end{aligned}$$
(9)

After eliminating \(x^{(k+\frac{1}{2})}\) from Eq. (9), the following stationary method is obtained:

$$\begin{aligned} x^{(k+1)}=G_{\alpha ,\beta }x^{(k)}+M_{\alpha ,\beta }^{-1}b, \quad k=0,1,\ldots , \end{aligned}$$

where

$$\begin{aligned} \begin{array}{l} M_{\alpha , \beta }=\frac{1}{\alpha +\beta }(\alpha I + T)(\beta I + S + K),\\ G_{\alpha , \beta }=I-M_{\alpha ,\beta }^{-1}A=(\beta I+S+K)^{-1}(\beta I-T)(\alpha I+T)^{-1}(\alpha I-S-K). \end{array} \end{aligned}$$
(10)

The convergence properties of the TGHSS method is briefly introduced in the following theorem which has been completely investigated in [4].

Theorem 1

Let \(A = (T + K) + S = H + S\), where T and K are Hermitian positive semidefinite matrices and S is a skew-Hermitian matrix. Let \(\alpha \) and \(\beta \) be two nonnegative numbers with \((\alpha ,\beta )\ne 0\). Alternating iteration (9) converges to the unique solution of (1) if one of the following conditions holds:

  1. (i)

    T is positive definite, K is positive semidefinite matrix and

    $$\begin{aligned} \alpha<\beta \le \alpha +2\lambda _q(T) \quad \text { or } \; \alpha \le \beta <\alpha +2\lambda _q(T). \end{aligned}$$
  2. (ii)

    T is positive semidefinite, K is positive definite matrix and

    $$\begin{aligned} \beta \le \alpha< \beta +\frac{1}{2}\lambda _q(K) \quad \text { or } \; \beta <\alpha \le \beta +\frac{1}{2}\lambda _q(K). \end{aligned}$$
  3. (iii)

    T is positive definite, K is positive definite matrix and

    $$\begin{aligned} \alpha< & {} \beta +\frac{1}{2}\lambda _q(K)\le \alpha +2\lambda _q(T)+\frac{1}{2}\lambda _q(K) \\ \text {or } \quad \alpha\le & {} \beta +\frac{1}{2}\lambda _q(K)<\alpha +2\lambda _q(T)+\frac{1}{2}\lambda _q(K). \end{aligned}$$

    Furthermore, the spectral radius \(\rho (G_{\alpha ,\beta })\) of the iteration matrix is bounded by

    $$\begin{aligned} \sigma (\alpha ,\beta )= \max _{\lambda \in \sigma (T)} \frac{|\beta -\lambda |}{\alpha +\lambda }. \end{aligned}$$

From Theorem 1, if all assumptions are fulfilled, small values of the \(\sigma (\alpha ,\beta )\) lead to small values of the spectral radius of the iteration matrix.

Now, we use the presented matrices \(G_{\alpha ,\beta }\) and \(M_{\alpha , \beta }\) in (10) to construct the preconditioner matrix in Eq. (2). Indeed, substitution of the proposed matrices in Eq. (2) leads to the following m-step TGHSS preconditioning matrix

$$\begin{aligned} P_{\alpha ,\beta }(m)=M_{\alpha ,\beta }\left( I+G_{\alpha ,\beta }+G_{\alpha ,\beta }^2+\cdots +G_{\alpha ,\beta }^{m-1}\right) ^{-1}, \end{aligned}$$
(11)

where

$$\begin{aligned} G_{\alpha ,\beta }^k=\left[ (\beta I+S+K)^{-1}(\beta I-T)(\alpha I+T)^{-1}(\alpha I-S-K)\right] ^k. \end{aligned}$$

The preconditioning matrix \(P_{\alpha ,\beta }(m)\) in (11) can be applied to solve the linear system (1) using preconditioned Krylov subspace iteration methods such as GMRES. From (3), the preconditioned matrix is also given by

$$\begin{aligned} P_{\alpha ,\beta }(m)^{-1}A= I-G_{\alpha ,\beta }^m. \end{aligned}$$

Now, since spectral radius of \(G_{\alpha ,\beta }\) can be less than one, the following theorem is stated to summarize the properties of preconditioned matrix.

Theorem 2

Let the assumptions of Theorem 1 be fulfilled. Moreover, let \(P_{\alpha ,\beta }(m)\) be the matrix defined as in (11). Then,

  1. (i)

    \(\rho (G_{\alpha ,\beta }^m) \le \sigma {(\alpha ,\beta )}^m < 1\);

  2. (ii)

    the eigenvalues of the preconditioned matrix \(P_{\alpha ,\beta }(m)^{-1} A\) are enclosed in a circle centered at (1, 0) with radius \(\rho (G_{\alpha ,\beta }^m)\).

From Theorem 2, it can be easily seen that the eigenvalues of the preconditioned matrix \(P_{\alpha ,\beta }(m)^{-1} A\) are more clustered by increasing m. Note that larger values of m increase the computational costs and hence choosing the best value of m is a key issue. However, finding the proposed value is a critical task and hence we experimentally determine the optimal values of m which preserve the efficiency of the method. In the sequel, to make the notation more concise, the m-step TGHSS preconditioning matrix and the preconditioned GMRES method are denoted as TGHSS(m) and TGHSS(m)-GMRES, respectively.

4 Implementation issues

In applying the preconditioner \(P_{\alpha ,\beta }(m)\) within a Krylov subspace method like GMRES, we need to compute a vector of the form \(z=P_{\alpha ,\beta }(m)^{-1}y\) for a given vector y. To compute the vector z we may solve the system \(P_{\alpha ,\beta }(m)z=y\) for z. To do so, we first solve the system \(M_{\alpha ,\beta }w=y\) for w and then compute \(z=(I+G_{\alpha ,\beta }+G_{\alpha ,\beta }^2+\cdots +G_{\alpha ,\beta }^{m-1})w\). It is worth noting that the computation of z can be done by the using the Horner’s well-known rule. Summarising the above discussion yields the following scheme for computing the vector z.

  1. 1.

    Solve \(M_{\alpha ,\beta } w =y\) for w

  2. 2.

    \(z:=w+Gw\)

  3. 3.

    For \(k=1,2,\ldots ,m-2\)

  4. 4.

    \(z:=w+Gz\)

  5. 5.

    End For

In step (1) to solve the system and in step (4) to compute the vector Gz we need to solve two systems with the coefficient matrices \(\alpha I+T\) and \(\beta I + S+K\). The first one can be solve exactly by the Cholesky method or inexactly by the conjugate gradient (CG) method, and the second one may be solved exactly by the LU factorization or inexactly by the GMRES method.

5 Numerical examples

In this section, the TGHSS(m)-GMRES method is applied to solve non-Hermitian positive definite linear systems presented in three examples. Furthermore, the numerical results of the proposed method are compared with HSS(m)-GMRES method. In all examples, the vector of all ones is the right-hand side vector b. In addition, the initial guess is set to be the zero vector and the iteration is terminated whenever

$$\begin{aligned} \frac{\Vert r^{(k)}\Vert _2}{\Vert r^{(0)}\Vert _2}\le 10^{-6}, \end{aligned}$$

where \(r^{(k)}=b-Ax^{(k)}\). We consider the following splitting for the matrices T and K to implement the TGHSS(m)-GMRES method

$$\begin{aligned} T=H-\lambda _{\min }(H)I, \quad K=\lambda _{min}(H), \end{aligned}$$

where \(\lambda _{\min }(H)\) is the minimum eigenvalue of Hermitian matrix H. In general it is difficult to compute the optimal parameter in the HSS method and it is problem-based. Bai et al. have presented the optimal parameters in the HSS method for certain two-by-two block matrices [10]. The quasi-optimal parameters in the HSS-like methods for saddle-point problems has been given in [5]. Haung has presented a practical formula to approximate the optimal parameters in the HSS iteration methods [21]. In all examples, the optimal value of unknown parameter for the HSS(m) preconditioner is approximated by the proposed method in [21]. Note that TGHSS(m) preconditioner contains two parameters and computing the optimal parameters is a very complicated task. Hence, the unknown values in the TGHSS(m) preconditioner are approximated experimentally. All the computations have been implemented in Matlab 8.1 software on a PC with Core i7, 2.67 GHz CPU and 4.00 GB RAM.

Example 1

In this example, we consider the linear system (1) with the coefficient matrix

$$\begin{aligned} A=\left( \begin{array}{cc} B &{} \quad E \\ -E^T &{} \quad C \end{array} \right) , \end{aligned}$$

where B and C are arbitrary symmetric positive definite matrices of size \(n^2 \times n^2\) and \(n \times n\), respectively, and E is any matrix of size \(n^2 \times n\). Note that the matrices B, E and C are randomly generated to implement the HSS(m)-GMRES and TGHSS(m)-GMRES methods. The experimental results show that iteration counts are very stable for any random matrices, and hence we present the numerical results for fixed matrices B, C, and E. The iteration numbers (Its.), CPU time (in seconds), upper bound of the iteration matrix and the spectral radius of the GMRES method with the m-step HSS preconditioners, GMRES method with the m-step HSS preconditioners, and GMRES without using a preconditioner are given in Tables 1, 2, 3 for \(n=8,16,32\). As the numerical results show, the new preconditioner is reliable and more effective than the m-step HSS preconditioner. For more investigation the eigenvalues distribution of the matrices A and \(P_{\alpha ,\beta }(m)^{-1}A\) with \((\alpha ,\beta )=(6.2,5.3)\) are shown for \(n=32\) and \(m=1,\ldots ,5\) in Fig. 1. As we see the eigenvalues of \(P_{\alpha ,\beta }(m)^{-1}A\) are more clustered than the matrix A.

Table 1 Numerical results for \(n = 8\) in Example 1
Full size table
Table 2 Numerical results for \(n = 16\) in Example 1
Full size table
Table 3 Numerical results for \(n = 32\) in Example 1
Full size table
Fig. 1
figure 1

Spectral distributions of coefficient matrix A and TGHSS(m)-preconditioned matrices \(P_{\alpha ,\beta }(m)^{-1} A\) for \((\alpha ,\beta )=(6.2,5.3)\) and \(n = 32\) in Example 1

Full size image

Example 2

The coefficient matrix A used for this example is obtained from discretization of the two-dimensional convection-diffusion equation [12]

$$\begin{aligned} -\left( u_{xx}+u_{yy}\right) +\delta \left( u_x+u_y \right) =f(x,y), \quad (x,y)\in \Omega , \end{aligned}$$

with the homogeneous Dirichlet boundary conditions, where \(\delta \) is a constant and \(\Omega =[0,1] \times [0,1]\). The proposed equation is descritized with five-point stencil and centered finite differences on a uniform grid with \(n \times n\) interior nodes which leading to a non-Hermitian positive definite linear system. The coefficient matrix A of the proposed linear system is given by

$$\begin{aligned} A=T\otimes I+I \otimes T, \end{aligned}$$

where

$$\begin{aligned} T=\text {tridiag}(-1-r, 2, -1+r), \quad r=(\delta h)/2, \end{aligned}$$

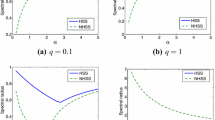
with r as the mesh Reynolds number and \(h=1/(n+1)\) as the step size. The value of \(\delta \) is set to be 1000 and the HSS(m) and TGHSS(m) preconditioners are used in GMRES for \(n=16,32\). The computational results are reported in Tables 4, 5. As the numerical results show the spectral radius of the iteration matrices and iteration numbers of various methods are decreased by increasing m. Furthermore, the running time of TGHSS(m) preconditioner is smaller than the HSS(m) and original method even for larger values of m which shows the effectiveness of the new method. Similar to the previous example, spectral distributions of coefficient matrix A and preconditioned matrices \(P_{\alpha ,\beta }(m)^{-1} A\), \(m=1,2,3,5,10\), are shown in Fig. 2. It can be seen that the spectra of the preconditioned matrices becomes more clustered with increasing m.

Table 4 Numerical results for \(n = 16\) in Example 2
Full size table
Table 5 Numerical results for \(n = 32\) in Example2
Full size table
Fig. 2
figure 2

Spectral distributions of coefficient matrix A and TGHSS(m)-preconditioned matrices \(P_{\alpha ,\beta }(m)^{-1} A\) for \((\alpha ,\beta )=(7.1,4.6)\) and \(n = 32\) in Example 2

Full size image

Example 3

In this example, we consider the linear system (1) with the following coefficient matrix which has been used in [19]

$$\begin{aligned} A=\left( \begin{array}{cc} D &{} \quad T \\ -T^T &{} \quad \mu I \end{array} \right) , \end{aligned}$$

where D is an \(n\times n\) real positive diagonal matrix and T is an \(n\times n\) real Toeplitz matrix which is defined as follows:

$$\begin{aligned} T_{i,j}=\frac{1}{\sqrt{2\pi }}\sigma e^{-|i-j|^2/(2\sigma ^2)}, \quad i,j=1,\ldots ,n. \end{aligned}$$

The HSS(m) preconditioner and TGHSS(m) preconditioner have been applied to solve the proposed linear system with \(\mu =0.01\) and \(\sigma =2\). A comparison of the proposed preconditioners has been done for \(n=16,32\) and the results are reported in Tables 6, 7. As the numerical results show, our new preconditioner is more effective than the HSS(m) preconditioner. However, the numerical experiments showed that the computational time (CPU time) is increasing with increasing the value of m. Hence, \(m=2\) can be considered as an optimal selection for this example.

Table 6 Numerical results for \(n = 16\) in Example 3
Full size table
Table 7 Numerical results for \(n = 32\) in Example 3
Full size table

6 Conclusion

In this paper, a new m-step preconditioner is presented based on the two-parameter generalized Hermitian and skew-Hermitian splitting (TGHSS) iteration method to solve non-Hermitian positive definite linear systems. The proposed preconditioner is used for Krylov subspace iteration methods such as GMRES to solve three known numerical examples. The computational results show that the new preconditioner is more effective than the recently proposed HSS(m) preconditioner.