Abstract
Our main concern in this paper is to study mixed regular-singular control problems, where the control variable has two components, the first being absolutely continuous and the second singular. The coefficients of the state process, as well as the running and final costs are random functions, so as the state process is no longer a Markov process. Our main result is to derive necessary conditions for optimality, also known as the Pontriagin stochastic maximum principle by using Malliavin calculus techniques. The adjoint process, which plays a key role in the stochastic maximum principle, is given by means of the Malliavin derivatives of the optimal state process.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper, we consider optimal mixed stochastic regular-singular control problems, where the state process satisfies the following stochastic differential equation:
The control is a pair \(\left( u_{t},\xi _{t}\right) \) such that \(u_{t}\) stands for the regular, called also the absolutely continuous part and \(\xi _{t}\) is the singular part.
The expected cost has the form
A major approach to deal with stochastic control problems is to derive optimality necessary conditions satisfied by some optimal control, known as the stochastic maximum principle. The first fundamental result on this subject was obtained by Kushner [24], for classical regular or absolutely continuous controls. Since then, a huge literature has been produced on this subject, among them, in particular, those by Benssoussan [10], Bismut [11], Haussmann [21] and Peng [30]. One can refer to the excellent book by Yong and Zhou [31] for a complete account on the subject and the references therein.
In this paper, we study general regular-singular stochastic control problems, in which the controller has only partial information. The control has two components, the first one is a classical regular control and the second one is a singular control. We consider systems driven by random coefficients and the running and the final costs are allowed to be random. It is clear that for such systems the dynamic programming does not hold, as the state process is no longer a Markov process. Our goal is to obtain necessary conditions for optimality satisfied by some optimal control.
We use Malliavin calculus techniques [27], to express the adjoint process in an explicit form. Our result extends those by Baghery and Oksendal [2], Meyer-Brandis et al. [25] and Øksendal and Sulem [29], to mixed regular-singular control problems. See also [26] for the mean field control problems. Note that in the stochastic maximum principle, a serious drawback is the computation at least numerically of the adjoint process. This process is given by a conditional expectation and satisfies a linear backward stochastic differential equation (BSDE). Numerical and Monte Carlo methods have been developed recently to deal with BSDEs by using Malliavin calculus, see [12, 13, 16, 19]. This could be seen as a step forward to solve numerically stochastic control problems by using these methods.
Stochastic control problems of singular type, have been studied extensively in the literature, as they model numerous situations in different areas, see [18, 28, 29]. A typical example in mathematical finance is the so called portfolio optimization problem, under transaction costs [17, 20]. These problems were studied through dynamic programming principle, see [22], where it was shown in particular that, the value function is continuous and is the unique viscosity solution of the HJB variational inequality. In particular the value function satisfies a variational inequality, which gives rise to a free boundary problem, and the optimal state process is a diffusion reflected at the free boundary. Bather and Chernoff [8] were the first to study such a problem. Benĕs et al. [9] solved a one dimensional example by observing that the value function in their example satisfies the so called the principle of smooth fit. Davis and Norman [17] solved the two dimensional problem, arising in portfolio selection models, under transaction costs. The case of diffusions with jumps has been studied in Øksendal and Sulem [28].
The first maximum principle for singular stochastic control problems was derived by Cadenillas and Haussmann [14], for systems with linear dynamics, convex cost criterion and convex state constraints. An extension to non linear systems has been developed via convex perturbations method for both absolutely continuous and singular components by Bahlali and Chala [3]. The second order stochastic maximum principle for nonlinear SDEs with a controlled diffusion matrix was obtained by Bahlali and Mezerdi [7], extending the Peng maximum principle [30] to singular control problems. Similar techniques have been used by Anderson [1] and Bahlali et al. [6], to study the stochastic maximum principle for relaxed-singular controls. The case of systems with non smooth coefficients has been treated by Bahlali et al. [4], where the classical derivatives are replaced by the generalized ones in the definition of adjoint processes. See also the recent paper by \(\varnothing \)ksendal and Sulem [29], where Malliavin calculus techniques have been used to define the adjoint process. The relationship between the stochastic maximum principle and dynamic programming has been investigated in [5, 15]. See also [28] for some worked examples.
2 Introduction to Malliavin calculus
In this section, we give some properties of the Malliavin derivatives, which will be useful for the definition of the adjoint process. The detailed proofs can be found in Nualart [27].
Let \(\left( B_{t}\right) \) be a \(d\)-dimensional Brownian motion, defined on a probability space \(\left( \Omega ,\mathcal {F},P\right) \) and let \(\left( \mathcal {F}_{t}\right) \) be its natural filtration. The following theorem gives the Wiener chaos expansion of a square integrable random variable, see [27] page 13.
Theorem 2.1
Any square integrable random variable \(F\in L^{2}\left( \Omega ,\mathcal {F} _{T},P\right) \) can be expanded into a series of multiple stochastic integrals:
for a unique sequence of symmetric deterministic functions \(f_{n}\in L^{2}\left( \lambda ^{n}\right) ,\) where \(\lambda \) is the Lebesgue measure on \(\left[ 0,T\right] \) and
(the \(n\)-times iterated integral of \(f_{n}\) with respect to \(B)\) for \(n=1,2,\ldots \) and \(I_{0}\left( f_{0}\right) =f_{0}\) when \(f_{0}\) is a constant.)
Moreover, we have the isometry
Definition 2.2
(Malliavin derivative \(D_{t}\)). Let \(F\in L^{2}\left( P\right) \) be \(\mathcal {F}_{T}-\)measurable.
-
(i)
We say that \(F\in \mathbb {D}_{1,2}\) if
$$\begin{aligned} \left\| F\right\| _{\mathbb {D}_{1,2}}^{2}:=\sum \limits _{n=1}^{\infty }nn!\left\| f_{n}\right\| _{L^{2}\left( \lambda ^{n}\right) } ^{2}<\infty . \end{aligned}$$(2.3) -
(ii)
For any \(F\in \mathbb {D}_{1,2}\), we define the Malliavin derivative \(D_{t}F\) of \(F\) at time \(t\), as the expansion
$$\begin{aligned} D_{t}F:=\sum \limits _{n=1}^{\infty }nI_{n-1}\left( f_{n}\left( .,t\right) \right) , \end{aligned}$$(2.4)
where \(I_{n-1}\left( f_{n}\left( .,t\right) \right) \) is the \(\left( n-1\right) -\)fold iterated integral of \(f_{n}\left( t_{1},\ldots ,t_{n-1} ,t\right) \) with respect to the first \(n-1\) variables \(t_{1},\ldots ,t_{n-1}\) and \(t_{n}=t\) is left as parameter.
Note that \(\left\| D_{.}F\right\| _{L^{2}\left( P\times \lambda \right) }=\left\| F\right\| _{\mathbb {D}_{1,2}}^{2}<\infty \), thus the derivative \(D_{t}F\) is well-defined as an element of \(L^{2}\left( P\times \lambda \right) .\)
Example
Let \(F=\int \limits _{0}^{T}f\left( s\right) dB_{s}\), where \(f\in L^{2}\left( \left[ 0,T\right] \right) \), then:
-
1.
\(D_{t}F=f\left( t\right) ,\)
-
2.
\(D_{t}\left( F^{n}\right) =nF^{n-1}D_{t}F=nF^{n-1}f\left( t\right) .\)
Now, we shall give a few rules that will be needed in this paper
-
Integration by parts and duality formula
Suppose that \(\left( u_{t}\right) \) is \(\mathcal {F}_{t}-\)adapted with \(E\left( \int \limits _{0}^{T}u_{t}^{2}dt\right) <+\infty \) and let \(F\in \mathbb {D}_{1,2}.\) Then
-
Clark-Ocone representation formula (see [27], Proposition 1.3.14 page 46).
Let \(F\in \mathbb {D}_{1,2},\) then
-
A generalized Clark-Ocone formula (see [27], Theorem 6.3.1, page 337).
Suppose that
where \(\theta =\left\{ \theta _{t},t\in \left[ 0,T\right] \right\} \) is an adapted and measurable process such that
Suppose that \(E\left( Z_{T}\right) =1\), where the process \(Z_{t}\) is given by
By the Girsanov theorem \(\tilde{B}=\left\{ \tilde{B}_{t},t\in \left[ 0,T\right] \right\} \) is a Brownian motion under the probability \(Q\) on \(\mathcal {F}_{T},\) with density\(\dfrac{dQ}{dP}=Z_{T}.\) Let \(F\) be an \(\mathcal {F}_{T}\)-measurable random variable such that \(F\in \mathbb {D}_{1,2}\) and let \(\theta \in L^{1,2}.\) Assume that
-
(i)
$$\begin{aligned} E\left( Z_{T}^{2}F^{2}\right) +E\left( Z_{T}^{2}\int \limits _{0}^{T}\left( D_{t}F\right) ^{2}dt\right) <\infty , \end{aligned}$$
-
(ii)
$$\begin{aligned} E\left( Z_{T}^{2}F^{2}\int \limits _{0}^{T}\left( \theta _{t}+\int \limits _{t}^{T}D_{t}\theta _{s}dB_{s}+\int \limits _{t}^{T}\theta _{s}D_{t} \theta _{s}ds\right) ^{2}dt\right) <\infty . \end{aligned}$$
Then
See also [23] for applications to finance.
3 Formulation of the problem
Suppose the state process \(x_{t}=x_{t}^{\left( u,\xi \right) }\); \(t\ge 0\), satisfies the following stochastic differential equation:
Here \(\left( B_{t}\right) \) is \(1\)-dimensional Brownian motion, defined on a filtered probability space \(\left( \Omega ,\mathcal {F},\left( \mathcal {F} _{t}\right) _{t\ge 0},P\right) ,\) satisfying the usual conditions. Assume that \(\left( \mathcal {F}_{t}\right) \) is the natural filtration of \(\left( B_{t}\right) \). The coefficients
are given \(\mathcal {F}_{t}-\)predictable processes.
Suppose in addition that we are given a subfiltration \(\mathcal {E}_{t} \subset \mathcal {F}_{t},\) \(t\in \left[ 0,T\right] \), representing the information available to the controller at time t and satisfying the usual conditions.
-
Let \(T\) be a strictly positive real number and consider the following sets.
-
\(\mathcal {U}_{1}^{\mathcal {E}}\) is the class of measurable, \(\mathcal {E}_{t}\)-adapted processes \(u:\left[ 0,T\right] \times \Omega \rightarrow U,\) where \(U\) is some Borel subset of \(\mathbb {R}^{k}.\)
-
\(\mathcal {U}_{2}^{\mathcal {E}}\) is the class of measurable, \(\mathcal {E}_{t}\)-adapted processes \(\xi :\left[ 0,T\right] \times \Omega \rightarrow \) \([0,\infty )\) such that \(\xi \) is nondecreasing, right-continuous with left hand limits and \(\xi _{0}=0.\)
Definition 3.1
An admissible control is an \(\mathcal {E}_{t}\)-adapted process \(\left( u,\xi \right) \in \mathcal {U}_{1}^{\mathcal {E}} \times \mathcal {U} _{2}^{\mathcal {E}}\) such that
We denote by \(\mathcal {A}_{\mathcal {E}}\) the set of all admissible controls.
The expected reward to be maximized has the form
where
are given \(\mathcal {F}_{t}\)-adapted processes.
The goal of the controller is to maximize the functional \(J\left( u,\xi \right) \) over \(\mathcal {A}_{\mathcal {E}}\). An admissible control \(\left( \hat{u},\hat{\xi }\right) \in \mathcal {A}_{\mathcal {E}}\) is optimal if:
Our objective is to derive necessary conditions satisfied by \(\left( \hat{u},\hat{\xi }\right) \).
Note that since we allow \(b\), \(\sigma \), \(h\), \(f\) and \(g\) to be random coefficients and also because our controls must be \(\mathcal {E}_{t}\)-adapted, this problem is no longer of Markovian type and hence cannot be solved by dynamic programming. Our attention will be focused on the stochastic maximum principle, for which an explicit form for the adjoint process is obtained. Malliavin calculus techniques will be used to get an explicit form of the adjoint process.
Assumptions The following assumptions will be in force throughout this paper.
\((\) H \(_{\mathbf {1}})\) \(b,\) \(\sigma \), \(g,\) \(f\) are adapted processes such that there exists a positive constant \(C\) satisfying:
\((\) H \(_{\mathbf {2}})\) \(b,\) \(\sigma \), \(g,\) \(f\) are continuously differentiable with respect to \(x\in \mathbb {R}\) and \(u\in U\) for each \(t\in \left[ 0,T\right] ,\) and a.s. \(\omega \in \Omega ,\) with bounded derivatives.
\((\) H \(_{\mathbf {3}})\) \(\lambda \), \(h\) are bounded continuous processes.
\((\) H \(_{\mathbf {4}})\)For all bounded \(\mathcal {F}_{t}-\)measurable random variables \(\alpha =\alpha \left( \omega \right) \) the process \(v_{s}^{\alpha }=\alpha \left( \omega \right) 1_{\left( t,r\right] }\left( s\right) ;\) \(s\in \left[ 0,T\right] \) belongs to \(\mathcal {U}_{1} ^{\varepsilon }.\)
\((\) H \(_{\mathbf {5}})\)For \(u\), \(v\) \(\in \) \(\mathcal {U}_{1}^{\mathcal {E} }\) with \(v\) bounded, there exists \(\delta >0\) such that
Under the above assumptions, for every \(\left( u,\xi \right) \in \mathcal {A}_{\mathcal {E}}\), Eq. (3.1) admits a unique strong solution given by
and the reward functional \(J\) is well defined from \(\mathcal {A}_{\mathcal {E}}\) into \( \mathbb {R} \).
We list some notations which will be used throughout this paper.
Notations For \(\xi \in U_{2}^{\mathcal {E}},\) let  denotes the set of \({\mathcal {E}}_{t}\)-adapted processes \(\eta \) of finite variation such that there exists \(\delta >0\) such that \(\xi \)
\(+\,\theta \eta \)
\(\in U_{2}^{\mathcal {E}},\) for all \(\theta \in [0,\delta ].\) For all \(u\in {\mathcal {U}}_{1}^{\mathcal {E}}\) and \(0\le t\le s\le T,\) we denote the following processes
denotes the set of \({\mathcal {E}}_{t}\)-adapted processes \(\eta \) of finite variation such that there exists \(\delta >0\) such that \(\xi \)
\(+\,\theta \eta \)
\(\in U_{2}^{\mathcal {E}},\) for all \(\theta \in [0,\delta ].\) For all \(u\in {\mathcal {U}}_{1}^{\mathcal {E}}\) and \(0\le t\le s\le T,\) we denote the following processes
We define the usual Hamiltonian of the control problem (3.1)–(3.2) by:
where
4 The stochastic maximum principle
The purpose of the stochastic maximum principle is to find necessary conditions for optimality satisfied by an optimal control. Suppose that \(\left( \hat{u},\hat{\xi }\right) \in \mathcal {A}_{\mathcal {E}}\) is an optimal control and let \(\hat{x}_{t}\) denotes the optimal trajectory, that is, the solution of (3.1) corresponding to \(\left( \hat{u},\hat{\xi }\right) .\) As it is well known the stochastic maximum principle is based on the computation of the derivative of the reward functional with respect to some perturbation parameter. Let us define the perturbed controls as follows.
-
\(u^{\theta }=\hat{u}+\theta v,\) where \(v\) is some bounded \(\mathcal {E} _{t}-\)adapted process. We know by (H \(_{\mathbf {5}}\)) that there exists \(\delta >0\) such that \(u^{\theta }=\hat{u}+\theta v\in \mathcal {U} _{1}^{\mathcal {E}}\) for all \(\theta \in \left[ -\delta ,\delta \right] \)
-
\(\xi ^{\theta }=\) \(\hat{\xi }\) \(+\,\theta \eta ,\) where
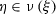 the set of \(\mathcal {E}_{t}-\)adapted processes of finite variation, for which there exists \(\delta =\delta (\hat{\xi })>0\) such that \(\hat{\xi }\)
\(+\,\theta \eta \)
\(\in \mathcal {U}_{2}^{\mathcal {E}}.\)
the set of \(\mathcal {E}_{t}-\)adapted processes of finite variation, for which there exists \(\delta =\delta (\hat{\xi })>0\) such that \(\hat{\xi }\)
\(+\,\theta \eta \)
\(\in \mathcal {U}_{2}^{\mathcal {E}}.\)
Since \(\left( \hat{u},\hat{\xi }\right) \) is an optimal control it holds that:
-
(1)
\( \begin{array}{l} \lim \limits _{\theta \rightarrow 0^{+}}\frac{1}{\theta }\left( J\left( \hat{u},\xi ^{\theta }\right) -J\left( \hat{u},\hat{\xi }\right) \right) \le 0 \end{array} \), where \(\xi ^{\theta }=\) \(\hat{\xi }\) \(+\,\theta \eta \), and
-
(2)
\( \begin{array}{l} \lim \limits _{\theta \rightarrow 0}\frac{1}{\theta }\left( J\left( u^{\theta },\hat{\xi }\right) -J\left( \hat{u},\hat{\xi }\right) \right) \le 0 \end{array},\) where \(u^{\theta }=\hat{u}+\theta v\).
We use the two limits to obtain the variational inequalities. To achieve this goal, we need the following technical Lemmas.
We define the derivative process \(\mathcal {Y}\left( t\right) \) by
Since that \(\mathcal {Y}\left( 0\right) =0\), then
where we use the abbreviated notation:
\(\dfrac{\partial b}{\partial x}\left( t\right) =\dfrac{\partial b}{\partial x}\left( t,\hat{x}_{t},\hat{u}_{t},\omega \right) ,\) \(\dfrac{\partial \sigma }{\partial x}\left( t\right) =\dfrac{\partial \sigma }{\partial x}\left( t,\hat{x}_{t},\hat{u}_{t},\omega \right) \).
Lemma 4.1
The solution of Eq. (4.2) is given by
where \(Z\left( t\right) \) is the solution of the homogeneous version of (4.2), i.e.
Proof
We set \(\mathcal {Y}\left( t\right) =Z\left( t\right) A_{t}\) where
By using Itô’s formula for semimartingales, we get
This completes the proof. \(\square \)
In the sequel, we use the abbreviated notation:
Lemma 4.2
Let \(\left( \hat{u},\hat{\xi }\right) \) be an optimal control. Then
where
Proof
We have
We have from (4.2)
Since \(\mathcal {Y}\left( 0\right) =0\), we have by the duality formulae for the Malliavin derivatives,
by using Fubini theorem
changing the notation \(s\rightarrow t\) , this becomes
Similarly we get
Combining (4.10) and (4.11) and using the notations (3.5) and (3.7), we obtain
where
and
We set
then by using Lemma 4.1 it follows that
Hence by using Fubini’s theorem we get by changing the notation \(s\rightarrow t\)
Finaly
This completes the proof. \(\square \)
We define the derivative process \(Y\left( t\right) \) by
then \(Y\left( t\right) \) satisfies the following equation
Lemma 4.3
The following identity holds
Proof
We have
where \(Y\left( t\right) =Y^{v}\left( t\right) \) is the solution of the linear equation
By the duality formula we get
Using similar arguments and Fubini’s theorem it follows that,
Changing the notation \(s\rightarrow t,\) we get
Using the notation
and combining (4.17) and (4.18), we get
which completes the proof. \(\square \)
Now, we are ready to state the main result of this paper. Note that the following theorem extends in particular [25] Theorem 3.4 and [29] Theorem 2.4 to mixed regular-singular control problems.
Theorem 4.4
(The stochastic maximum principle) Let \(\left( \hat{u},\hat{\xi }\right) \in \mathcal {A}_{\mathcal {E}}\) be an optimal control maximizing the reward \(J\) over \(\mathcal {A}_{\mathcal {E}}\) and \(\hat{x}_{t}\) denotes the optimal trajectory, then for a.e. \(t\in \left[ 0,T\right] \) we have:
-
i)
\(E\left[ V_{\left( \hat{u},\hat{\xi }\right) }(t)/\mathcal {E}_{t}\right] \le 0,\) and \(E\left[ V_{\left( \hat{u},\hat{\xi }\right) }(t)/\mathcal {E} _{t}\right] d\hat{\xi }_{t}=0\) where
$$\begin{aligned} V_{\left( \hat{u},\hat{\xi }\right) }(t)=\lambda \left( t\right) \hat{p}\left( t\right) +h\left( t\right) , \end{aligned}$$ -
ii)
\(E\left[ \dfrac{\partial H}{\partial u}\left( t,\hat{x}_{t},\hat{u} _{t}\right) /\mathcal {E}_{t}\right] =0,\) where
$$\begin{aligned} H\left( t,\hat{x}_{t},\hat{u}_{t},\hat{p}\left( t\right) ,\hat{q}\left( t\right) \right) =f\left( t,\hat{x}_{t},\hat{u}_{t}\right) +\hat{p}\left( t\right) b\left( t,\hat{x}_{t},\hat{u}_{t}\right) +\hat{q}\left( t\right) \sigma \left( t,\hat{x}_{t},\hat{u}_{t}\right) , \end{aligned}$$
is the usual Hamiltonian.
Proof
First, we start to prove \((i)\). By Lemma \(4.2\) we have
for all \(\eta \in \mathcal {U}_{2}^{\mathcal {E}}.\) In particular, this holds if we choose \(\eta \) such that \(d\eta \left( t\right) =a\left( t\right) dt,\) where \(a\left( t\right) \ge 0\) is continuous and \(\mathcal {E}_{t}-\)adapted, then
Since this holds for all such \(\mathcal {E}_{t}-\)adapted processes, we deduce that
Then, choosing \(\eta _{t}=-\hat{\xi }_{t}\) we get
Next, choosing \(\eta _{t}=\hat{\xi }_{t}\) we get
Hence
which combined with (4.20) gives
Now let us prove \((ii)\).
We have
Then by Lemma 4.3 we get
Now we apply the above to \(v=v_{\alpha }\in \mathcal {U}_{1}^{\mathcal {E}}\) of the form \(v_{\alpha }\left( s\right) =\alpha 1_{\left[ t,t+h\right] }\left( s\right) ,\) for some \(t,h\in \left( 0,T\right) \), \(t+h\le T,\) where \(\alpha =\alpha \left( \omega \right) \) is bounded and \(\mathcal {E}_{t} \)-measurable. Then \(\ Y^{v_{\alpha }}\left( s\right) =0\) for \(\ 0\le s\le t\), hence (4.21) becomes
where
and
Note that by (4.14), with \(Y\left( s\right) =Y^{v_{\alpha }}\left( s\right) \), \(s\ge t+h\) the process \(Y\left( s\right) \) satisfies the following dynamics
for \(s\ge t+h\) with initial condition \(Y\left( t+h\right) \) at time \(t+h.\) An application of Itô’s formula yields
where, for \(s\ge t\),
Note that \(G\left( t,s\right) \) does not depend on \(h,\) but \(Y\left( s\right) \) does. We have by (3.7)
Differentiating with respect to \(h\) at \(h=0\) we get
Using the fact that \(Y\left( t\right) =0,\) we see that
Therefore, using (4.24) and the fact that \(Y\left( t\right) =0\) it holds that,
By (4.16)
Therefore, by the duality formulae\(,\) \(\left. \dfrac{d}{dh}A_{1}\right| _{h=0}=\Lambda _{1}+\Lambda _{2},\) where
\(F\left( t,s\right) =\frac{\partial H_{0}}{\partial x}\left( s\right) G\left( t,s\right) ,\) and
Using the fact that \(Y\left( t\right) =0\), we see that
We conclude that
Moreover, we see directly that
Therefore, differentiating (4.26) with respect to \(h\) at \(h=0,\) gives the inequality
We can reformulate this by using the notation (3.9) and (3.10)
Using the definition of the Hamiltonian (3.11) the last inequality can be rewritten
Since this holds for all bounded \(\ \mathcal {E}_{t}\)-measurable random variable \(\alpha \), we conclude that
This completes the proof. \(\square \)
References
Anderson, D.: The relaxed general maximum principle for singular optimal control of diffusions. Syst. Control Lett. 58, 76–82 (2009)
Baghery, F., Oksendal, B.: A maximum principle for stochastic control with partial information. Stoch Anal. Appl. 25, 493–514 (2007)
Bahlali, S., Chala, A.: The stochastic maximum principle in optimal control of singular diffusions with nonlinear coefficients. Rand. Oper. Stoch. Equ. 13, 1–10 (2005)
Bahlali, K., Chighoub, F., Djehiche, B., Mezerdi, B.: Optimality necessary conditions in singular stochastic control problems with non smooth data. J. Math. Anal. Appl. 355, 479–494 (2009)
Bahlali, K., Chighoub, F., Mezerdi, B.: On the relationship between the maximum principle and dynamic programming in singular stochastic control. Stoch. Int. J. Prob. Stoch. Proc 84(2–3), 233–249 (2012)
Bahlali, S., Djehiche, B., Mezerdi, B.: The relaxed maximum principle in singular control of diffusions. SIAM J. Control Optim. 46, 427–444 (2007)
Bahlali, S., Mezerdi, B.: A general stochastic maximum principle for singular control problems. Electron. J. Prob. 10, 988–1004 (2005)
Bather, J.A., Chernoff, H.: Sequential decision in the control of a spaceship, (finite fuel). J. Appl. Prob. 49, 584–604 (1967)
Benĕs, V.E., Shepp, L.A., Witsenhausen, H.S.: Some solvable stochastic control problems. Stoch. Stoch. Rep. 4, 39–83 (1980)
Bensoussan, A.: Lectures on stochastic control. Lect. Notes in Math., vol. 972, pp. 1–62. Springer, Berlin (1983)
Bismut, J.M.: An introductory approach to duality in optimal stochastic control. SIAM Rev. 20(1), 62–78 (1978)
Bouchard, B., Ekeland, I., Touzi, N.: On the Malliavin approach to Monte Carlo approximation of conditional expectations. Finance Stoch. 8, 45–71 (2004)
Bouchard, B., Touzi, N.: Discrete-time approximation and Monte Carlo simulation of backward stochastic differential equations. Stoch. Proc. Appl. 111, 175–206 (2004)
Cadenillas, A., Haussmann, U.G.: The stochastic maximum principle for a singular control problem. Stoch. Stoch. Rep. 49, 211–237 (1994)
Chighoub, F., Mezerdi, B.: The relationship between the stochastic maximum principle and the dynamic programming in singular control of jump diffusions. Int. J. Stoch. Anal. p. 17 (2014) (Article ID 201491)
Crisan, D., Manolarakis, K., Touzi, N.: On the Monte Carlo simulation of backward SDES: an improvement on the Malliavin weights. Stoch. Proc. Appl. 120(7), 1133–1158 (2010)
Davis, M.H.A., Norman, A.: Portfolio selection with transaction costs. Math. Oper. Res. 15, 676–713 (1990)
Fleming, W.H., Soner, H.M.: Controlled Markov processes and viscosity solutions. Springer, Berlin (1993)
Fourni, E., Lasry, J.M., Lebuchoux, J., Lions, P.L.: Applications of Malliavin calculus to Monte-Carlo methods in finance. II. Finance Stoch. 5, 201–236 (2001)
Framstad, N.C., Øksendal, B., Sulem, A.: Optimal consumption and portfolio in a jump diffusion market with proportional transaction costs. J. Math. Econ. 35, 233–257 (2001)
Haussmann, U.G.: General necessary conditions for optimal control of stochastic systems. Math. Prog. Study 6, 34–48 (1976)
Haussmann, U.G., Suo, W.: Singular optimal stochastic controls II: dynamic programming. SIAM J. Control Optim. 33, 937–959 (1995)
Karatzas, I., Ocone, D.: A generalized Clark representation formula, with application to optimal portfolios. Stoch. Stoch. Rep. 34, 187–220 (1991)
Kushner, N.J.: Necessary conditions for continuous parameter stochastic optimization problems. SIAM J. Control Optim. 10, 550–565 (1972)
Meyer-Brandis, T., Øksendal, B., Zhou, X.Y.: A stochastic maximum principle via Malliavin calculus. University of Oslo (2008) (Eprint)
Meyer-Brandis, T., Øksendal, B., Zhou, X.Y.: A mean-field stochastic maximum principle via Malliavin calculus. Stochastics 84(5–6), 643–666 (2012)
Nualart, D.: Malliavin Calculus and related topics, 2nd edn. Springer, Berlin (2006)
Øksendal, B., Sulem, A.: Applied stochastic control of jumps diffusions. Springer, Universitext (2005)
Øksendal, B., Sulem, A.: Singular stochastic control and optimal stopping with partial information of Itô-Lévy processes. SIAM J. Control Optim. 50(4), 2254–2287 (2012)
Peng, S.: A general stochastic maximum principle for optimal control problems. SIAM J. Control Optim. 28, 966–979 (1990)
Yong, J., Zhou, X.Y.: Stochastic controls. Hamiltonian systems and HJB equations. Springer, Berlin (1999)
Author information
Authors and Affiliations
Corresponding author
Additional information
Partially supported by French-Algerian Cooperation Program, PHC Tassili 13 MDU 887.
Rights and permissions
About this article
Cite this article
Mezerdi, B., Yakhlef, S. A stochastic maximum principle for mixed regular-singular control problems via Malliavin calculus. Afr. Mat. 27, 409–426 (2016). https://doi.org/10.1007/s13370-015-0351-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13370-015-0351-6
Keywords
- Singular control
- Optimal control
- Stochastic maximum principle
- Malliavin derivative
- Partial information
- Necessary optimality conditions
- Adjoint process



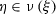 the set of
the set of