Natural convection from a vertical plate immersed in a power-law fluid saturated non-Darcy porous medium with viscous dissipation and Soret effects

Abstract

In this work, we study the viscous dissipation and thermal-diffusion effects on natural convection from a vertical plate embedded in a fluid saturated non-Darcy porous medium. The non-Newtonian behaviour of fluid is characterized by the generalized power-law model. The governing partial differential equations are transformed into a system of ordinary differential equations using a local non-similarity solution and the resulting boundary value problem is solved using a novel successive linearisation method (SLM). The accuracy of the SLM has been established by comparing the results with the shooting technique. The effects of physical parameters on heat and mass transfer coefficients for the convective motion of the power-law liquid are presented both qualitatively and quantitatively. The results show that the Nusselt number is reduced by viscous dissipation and enhanced by the Soret number but the Sherwood number increases with viscous dissipation and decreases with the Soret number. An increasing viscosity enhances heat and mass transfer coefficients in both cases of aiding buoyancy and opposing buoyancy.

1 Introduction

Recent decades have seen a spike in the number of studies devoted to the study of natural convection in fluid flows through porous media. This is an interesting and important subject in the area of heat transfer with wide applications in various fields such as geophysics, aerodynamic extrusion of polymer sheets, food processing and the manufacture of plastic films. The problem of natural convection and heat transfer in porous media have been carried out on vertical, inclined and horizontal surfaces by, among others, Chamkha and Khaled [4] who investigated the heat and mass transfer through mixed convection from a vertical plate embedded in a porous medium.

The problem of natural convection in a non-Newtonian fluid over a vertical surface in porous media was studied by Chen and Chen [5]. This was extended to a horizontal cylinder and a sphere in Chen and Chen [6]. Ching [9] studied heat and mass transfer from a vertical plate with variable wall heat and mass fluxes in a porous medium saturated with a non-Newtonian power-law fluid. El-Hakiem [16] investigated the problem of mixed convective heat transfer from a horizontal surface with variable wall heat flux. The horizontal surface was embedded in a porous medium saturated with an Ostwald-de-Waele type non-Newtonian fluid. Grosan et al. [17] investigated free convection from a vertical flat plate saturated with a power-low Newtonian fluid. Nakayama et al. [36] discussed the problem of natural convection over a non-isothermal body of arbitrary shape embedded in a porous medium filled with a non-Newtonian fluid. Similarity and integral solutions were obtained by Nakayama and Koyama [34, 35] for free convection along a vertical plate which was immersed in a thermally stratified, fluid-saturated porous medium with variable wall temperature. Review of the extensive work in this area is available in books by Nield and Bejan [39], Ingham and Pop [21], Pop and Igham [41].

The effect of Soret and/or Dufour numbers on heat and mass transfer in porous medium with variable properties has been investigated by many researchers. Tsai and Huang [47] obtained the solutions for heat and mass transfer coefficients for natural convection along a vertical surface with variable heat fluxes embedded in a porous medium. Thermal-diffusion (Soret) and diffusion-thermo (Dufour) effects were assumed to be significant. The effect of Soret and Dufour on free convection from a vertical plate with variable wall heat and mass fluxes in a porous medium saturated with a non-Newtonian power law fluid was investigated by Ching [7]. Partha et al. [40] studied the Soret and Dufour effects in a non-Darcy porous medium. Narayana and Murthy [37, 38] investigated the Soret and Dufour effects on free convection from a horizontal flat plate in doubly stratified Darcy porous media. Cheng [10] investigated the effect of Soret and Dufour on heat and mass transfer from a vertical cone in a porous medium with a constant wall temperature and concentration. Cheng [11] investigated the effect of Soret and Dufour on free convection boundary layer flow over a vertical cylinder in a porous medium with constant wall temperature and concentration. Khelifa et al. [2] used a power law model to characterize the non-Newtonian fluid behavior for natural convection in a porous cavity filled with a binary solution. Hajmohammadi and Nourazar [18] studied the insertion of a thin gas layer in micro cylindrical Couette flows involving power-law liquids. The effects of a thin gas layer exerts on the hydrodynamic aspects of power law liquid in a radial Couette flow between two cylinders has been investigated by Hajmohammadi et al. [19].

The semi analytical methods have been used and applied successfully to find exact and approximate solutions of linear and non-linear differential equations. The efficiency of ADM and DTM has been considered by Hajmohammadi and Nourazar [20] for solving a characteristic value problem. They showed that DTM handles the solution very conveniently and accurately. The conjugate forced convection heat transfer from a good conducting plate with temperature-dependent thermal conductivity was studied by Hajmohammadi et al. [20]. They concluded that in case of the conjugate heat transfer, the temperature distribution of the plate is flatter than the one in the nonconjugate case. The variational iteration method (VIM) has been applied on Green’s functions and fixed point iterations perspective by Khuri and Sayfy [24].

This study aims to investigate the viscous dissipation and the Soret effect on natural convection from a vertical plate immersed in a non-Darcy porous medium saturated with a non-Newtonian power-law fluid. The viscosity variation is modelled using Reynolds’ law [29, 42], which assumes that the viscosity decreases exponentially with temperature. Here we have considered viscous dissipation non-Newtonian fluid when the flow is laminar because the viscosity is high. The governing equations were solved using a novel successive linearisation method (see Awad et al. [1], Makukula et al. [27], Motsa and Sibanda [31] and Motsa et al. [32, 33]). Makukula et al. [25] solved the classical von Karman equations governing the boundary layer flow induced by a rotating disk using the spectral homotopy analysis method and successive linearisation method (SLM). They showed that the SLM gives better accuracy at lower orders than the spectral homotopy analysis method. Other studies such as [26, 28, 43] used the SLM to solve different boundary value problems and showed by comparison with numerical techniques that the successive linearisation method is accurate, gives rapid convergence and is thus superior to some existing semi-analytical methods such as the Adomian decomposition method, the Laplace transform decomposition technique, the variational iteration method and the homotopy perturbation method. The SLM method can be used in place of traditional numerical methods such as finite differences, Runge–Kutta and shooting methods in solving non-linear boundary value problems.

2 Mathematical formulation

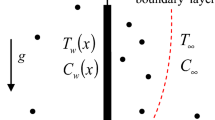
Consider two-dimensional steady boundary layer flow over a vertical plate embedded in a non-Darcy porous medium saturated with a non-Newtonian power-law fluid with variable viscosity. The $x$-coordinate is measured along the plate from its leading edge and the $y$-coordinate normal to the plate. The plate is maintained at a constant temperature $T_w$ and concentration $C_w$. The ambient fluid temperature is $T_\infty$ and the concentration is $C_\infty$. The governing equations of continuity, momentum, energy and concentration under the Boussinesq approximations may be written as (see [44])

$$\begin{aligned}&\displaystyle \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y}=0, \end{aligned}$$

(1)

$$\begin{aligned}&\displaystyle \frac{\partial u^n}{\partial y}+\frac{\partial }{\partial y}\left( \frac{\rho _\infty bK^*}{\mu }u^2\right) = \frac{\partial }{\partial y}\left( \frac{\rho _\infty K^*\mathrm {g}}{\mu }\left[ \beta _T(T-T_\infty )+\beta _C(C-C_\infty )\right] \right) \end{aligned}$$

(2)

$$\begin{aligned}&\displaystyle u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} = \alpha \frac{\partial ^2 T}{\partial y^2} + \frac{\mu }{\rho _\infty K^*c_p} u \left( u^n+\frac{b\rho _\infty K^*}{\mu }u^2\right) \end{aligned}$$

(3)

$$\begin{aligned}&\displaystyle u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}=D\frac{\partial ^2 C}{\partial y^2}+D_1\frac{\partial ^2 T}{\partial y^2}, \end{aligned}$$

(4)

where $u$ and $v$ are the velocity components along the $x$ and $y$-directions respectively, $n$ is the power-law index such that $n < 1$ describes a pseudoplastic, $n = 1$ represents a Newtonian fluid and $n> 1$ is dilatant fluid, $T$ and $C$ are the fluid temperature and the concentration respectively, $\rho _\infty$ is the reference density, $g$ is the acceleration due to gravity, $\alpha$ is the effective thermal diffusivity, $D$ is the effective solutal diffusivity, $\beta _T$ and $\beta _C$ are the thermal and concentration expansion coefficients, respectively, $c_p$ is the specific heat at constant pressure, $D_1$ quantifies the contribution to the mass flux due to temperature gradient, $b$ is the empirical constant associated with the Forchheimer porous inertia term, $\mu$ is the consistency index of power law fluid and $K^*$ is the modified permeability of the flow of the non-Newtonian power-law fluid. The modified permeability $K^*$ is defined (see Christopher and Middleman [12] and Dharmadhikari and Kale [13]) as;

$$\begin{aligned} K^*=\frac{1}{c_t}\left( \frac{n\varphi }{3n+1}\right) ^n\left( \frac{50K}{3\varphi }\right) ^{\frac{n+1}{2}} \text {with} \quad K=\frac{\varphi ^3d^2}{150(1-\varphi )^2} \end{aligned}$$

where $\varphi$ is the porosity of the medium, $d$ is the particle size and the constant $c_t$ is given by

$$\begin{aligned} c_t = \left\{ \begin{array}{ll} \frac{25}{12}&{}\quad \text {Christopher and Middleman [12]}\\ \frac{3}{2}\left( \frac{8n}{9n+3}\right) ^n\left( \frac{10n-3}{6n+1}\right) \left( \frac{75}{16}\right) ^{3(10n-3)/(10n+11)}&{}\quad \text {Dharmadhikari and Kale [13]} \end{array} \right. \end{aligned}$$

For $n=1$, $c_t=\frac{25}{12}$.

The boundary conditions are

$$\begin{aligned} \left. \begin{array}{ll} v=0,\quad T=T_w,\quad C=C_w\quad \text {at} \quad y=0, \\ u\rightarrow 0, \quad T\rightarrow T_\infty ,\quad C\rightarrow C_\infty \quad \text {as} \quad y\rightarrow \infty . \end{array} \right\} \end{aligned}$$

(5)

The system of non-similar partial differential equations can be simplified by using the stream function $\psi$ where

$$\begin{aligned} u=\frac{\partial \psi }{\partial y} \quad \text {and} \quad v=-\frac{\partial \psi }{\partial x}, \end{aligned}$$

(6)

together with the following transformations

$$\begin{aligned} \eta =\frac{y}{x}Ra_x^{1/2}\quad \psi (\varepsilon ,\eta )=\alpha Ra_x^{1/2}f(\varepsilon ,\eta ) \quad \theta (\varepsilon ,\eta )=\frac{T\!-\!T_\infty }{T_w\!-\!T_\infty } \quad \text {and}\quad \phi (\varepsilon ,\eta )=\frac{C-C_\infty }{C_w-C_\infty } \end{aligned}$$

(7)

where $Ra_x = \left( \frac{x}{\alpha }\right) \big [\frac{\rho _\infty K^*\mathrm g \beta _T (T_w-T_\infty )}{\mu _\infty }\big ]^{1/n}$ is the local Rayleigh number and $\varepsilon =\frac{g\beta _T x}{c_p}$ is the viscous dissipation parameter. The variation of viscosity with the dimensionless temperature is written in the form (see [15, 29])

$$\begin{aligned} \mu (\theta )=\mu _\infty e^{-\gamma \theta }, \end{aligned}$$

(8)

where $\gamma$ is a non-dimensional viscosity parameter that depends on the nature of the fluid, and $\mu _\infty$ is the ambient viscosity of the fluid. Using (7), the momentum, energy and concentration Eqs. (2)–(4) reduce to the following system of equations;

$$\begin{aligned}&\displaystyle nf'^{n-1}f''+Gre^{\gamma \theta }\left( 2f'f''+\gamma \theta 'f'^2\right) =e^{\gamma \theta }\left[ \theta '(\gamma \theta +1)+\Lambda (\gamma \theta '\phi +\phi ')\right] , \end{aligned}$$

(9)

$$\begin{aligned}&\displaystyle \theta ''+\frac{1}{2}f\theta '+\varepsilon e^{-\gamma \theta }f' \left( f'^n+Gre^{\gamma \theta }f'^2\right) =\varepsilon \left( f'\frac{\partial \theta }{\partial \varepsilon }-\theta '\frac{\partial f}{\partial \varepsilon }\right) ,\end{aligned}$$

(10)

$$\begin{aligned}&\displaystyle Le^{-1}\phi ''+\frac{1}{2}f\phi '+Sr\theta ''=\varepsilon \left( f'\frac{\partial \phi }{\partial \varepsilon }-\phi '\frac{\partial f}{\partial \varepsilon }\right) . \end{aligned}$$

(11)

The transformed boundary conditions are

$$\begin{aligned} \left. \begin{array}{cc} f(\varepsilon ,\eta ) + 2\varepsilon \frac{\partial f(\varepsilon ,\eta )}{\partial \varepsilon }=0, \quad \theta (\varepsilon ,\eta )=1, \quad \phi (\varepsilon ,\eta )=1 \quad \text {at} \quad \eta =0\\ f'(\varepsilon ,\eta )\rightarrow 0,\qquad \qquad \quad \quad \theta (\varepsilon ,\eta ) \rightarrow 0,\quad \phi (\varepsilon ,\eta ) \rightarrow 0 \quad \text {as} \quad \eta \rightarrow \infty \end{array}\right\} . \end{aligned}$$

(12)

where $Gr^* =b \left( \frac{K^{*2}\rho _\infty ^2[g\beta _T(T_w-T_\infty )]^{2-n}}{\mu _\infty ^2}\right) ^{1/n}$ is the modified Grashof number, $Le = \frac{\alpha }{D}$ is the Lewis number, $Sr=\frac{D_1(T_w-T_\infty )}{\alpha (C_w-C_\infty )}$ is the Soret number and $\Lambda =\frac{\beta _C(C_w-C_\infty )}{\beta _T(T_w-T_\infty )}$ is the buoyancy term (where $\Lambda > 0$ represents aiding buoyancy and $\Lambda < 0$ represents opposing buoyancy). The primes in Eqs.  (9)–(11) represent differentiation with respect to the variable $\eta$.

Integrating Eq. (9) once and using the boundary conditions (12) gives

$$\begin{aligned} f'^n+Gre^{\gamma \theta }f'^2=(\theta +\Lambda \phi )e^{\gamma \theta }. \end{aligned}$$

(13)

Substituting (13) in (9) and (10) we obtain

$$\begin{aligned}&\displaystyle \left( nf'^{n-1}+2Gr^* e^{\gamma \theta }f'\right) f''=\left( \theta '+\Lambda \phi '\right) e^{\gamma \theta } + \gamma \theta 'f'^n,\end{aligned}$$

(14)

$$\begin{aligned}&\displaystyle \theta ''+\frac{1}{2}f\theta '+\varepsilon f'(\theta +\Lambda \phi ) =\varepsilon \left( f'\frac{\partial \theta }{\partial \varepsilon }-\theta '\frac{\partial f}{\partial \varepsilon }\right) . \end{aligned}$$

(15)

The skin friction, heat and mass transfer coefficients can be respectively obtained from

$$\begin{aligned} \left. \begin{array}{l} \frac{Re_x^2}{2PrRa_x^{3/2}}C_f=f''(\varepsilon ,0)\\ Nu_x/Ra_x^{1/2}=-\theta '(\varepsilon ,0) \\ Sh_x/Ra_x^{1/2}=-\phi '(\varepsilon ,0) \end{array}\right\} . \end{aligned}$$

(16)

3 Method of solution

Equations (11), (14) and (15) are solved subject to the boundary conditions (12). We first apply a local similarity and local non-similarity method (see [30, 45]) and for the first level of truncation, we neglect the terms multiplied by $\varepsilon \frac{\partial }{\partial \varepsilon }$. This is particularly appropriate when $\varepsilon \ll 1$. Thus the system of equations obtained is given by:

$$\begin{aligned}&\displaystyle \left( nf'^{n-1}+2Gr^* e^{\gamma \theta }f'\right) f''=\left( \theta '+\Lambda \phi '\right) e^{\gamma \theta } + \gamma \theta 'f'^n,\end{aligned}$$

(17)

$$\begin{aligned}&\displaystyle \theta ''+\frac{1}{2}f\theta '+\varepsilon f'(\theta +\Lambda \phi ) =0,\end{aligned}$$

(18)

$$\begin{aligned}&\displaystyle Le^{-1}\phi ''+\frac{1}{2}f\phi '+Sr\theta ''=0. \end{aligned}$$

(19)

The corresponding boundary conditions are

$$\begin{aligned} \left. \begin{array}{cc} f(\varepsilon ,\eta )=0, \quad \theta (\varepsilon ,\eta )=1, \quad \phi (\varepsilon ,\eta )=1 \quad \text {at} \quad \eta =0,\\ f'(\varepsilon ,\eta )\rightarrow 0,\quad \theta (\varepsilon ,\eta ) \rightarrow 0,\quad \phi (\varepsilon ,\eta ) \rightarrow 0 \quad \text {as} \quad \eta \rightarrow \infty , \end{array}\right\} \end{aligned}$$

(20)

For the second level of truncations, we introduce the following auxiliary variables $g = \frac{\partial f}{\partial \varepsilon }$, $h = \frac{\partial \theta }{\partial \varepsilon }$ and $k = \frac{\partial \phi }{\partial \varepsilon }$ and recover the neglected terms at the first level of truncation. Thus, the governing equations at the second level are given by

$$\begin{aligned}&\displaystyle \left( nf'^{n-1}+2Gr^* e^{\gamma \theta }f'\right) f''=\left( \theta '+\Lambda \phi '\right) e^{\gamma \theta } + \gamma \theta 'f'^n,\end{aligned}$$

(21)

$$\begin{aligned}&\displaystyle \theta ''+\frac{1}{2}f\theta '+\varepsilon f'(\theta +\Lambda \phi ) =\varepsilon (f' h-\theta 'g),\end{aligned}$$

(22)

$$\begin{aligned}&\displaystyle Le^{-1}\phi ''+\frac{1}{2}f\phi '+Sr\theta ''=\varepsilon (f' k-\phi 'g), \end{aligned}$$

(23)

and the corresponding boundary conditions are

$$\begin{aligned} \left. \begin{array}{cc} f(\varepsilon ,\eta ) + 2\varepsilon \frac{\partial f(\varepsilon ,\eta )}{\partial \varepsilon }=0, \quad \theta (\varepsilon ,\eta )=1, \quad \phi (\varepsilon ,\eta )=1 \quad \text {at} \quad \eta =0,\\ f'(\varepsilon ,\eta )\rightarrow 0,\qquad \qquad \quad \quad \theta (\varepsilon ,\eta ) \rightarrow 0,\quad \phi (\varepsilon ,\eta ) \rightarrow 0 \quad \text {as} \quad \eta \rightarrow \infty , \end{array}\right\} . \end{aligned}$$

(24)

The third level can be obtained by differentiating Eqs.  (21)–(23) with respect to $\varepsilon$ and neglecting the terms $\frac{\partial g}{\partial \varepsilon }$, $\frac{\partial h}{\partial \varepsilon }$ and $\frac{\partial k}{\partial \varepsilon }$ to get the set of equations

$$\begin{aligned}&\left( nf'^{n-1}+2Gr^* e^{\gamma \theta }f'\right) g''+\left[ n(n-1)f'^{n-2}g'+2Gr^* e^{\gamma \theta }(g'+\gamma hf')\right] f''\nonumber \\&\qquad \qquad -\left[ \gamma h(\theta '+\Lambda \phi ')+h'+\Lambda k'\right] e^{\gamma \theta }-\gamma \left( n\theta 'g'f'^{n-1}+f'^nh'\right) =0,\end{aligned}$$

(25)

$$\begin{aligned}&h''+\frac{1}{2}(fh'+3g\theta ')-f'h+\varepsilon f'(h+\Lambda k)+(\theta +\Lambda \phi )(\varepsilon g'+f')+\varepsilon (h' g-g'h)=0,\nonumber \\ \end{aligned}$$

(26)

$$\begin{aligned}&Le^{-1}k''+\frac{1}{2}(fk'+3g\phi ')-f'k+Srh''+\varepsilon (k' g-g'k)=0. \end{aligned}$$

(27)

The corresponding boundary conditions are

$$\begin{aligned} \left. \begin{array}{cc} g(\varepsilon ,\eta )=0, \quad h(\varepsilon ,\eta )=0,\quad k(\varepsilon ,\eta )=0 \quad \text {at} \quad \eta =0\\ g'(\varepsilon ,\eta )\rightarrow 0, \quad h(\varepsilon ,\eta ) \rightarrow 0, \quad k(\varepsilon ,\eta ) \rightarrow 0 \quad \text {as} \quad \eta \rightarrow \infty \end{array} \right\} . \end{aligned}$$

(28)

The set of differential Eqs. (21)–(23) and (25)–(27) together with the boundary conditions (24) and (28) were solved by means of the successive linearisation method (SLM). The SLM algorithm starts with the assumption that the variables $f(\eta ),\theta (\eta ),\phi (\eta ), g(\eta ),h(\eta )$ and $k(\eta )$ can be expressed as

$$\begin{aligned} \left. \begin{array}{cc} f(\eta )=f_i(\eta )+\sum _{m=0}^{i-1}F_m(\eta ),\;\; \theta (\eta )=\theta _i(\eta )+\sum _{m=0}^{i-1}\Theta _m(\eta ),\;\; \phi (\eta )=\phi _i(\eta )+\sum _{m=0}^{i-1}\Phi _m(\eta )\\ g(\eta )=g_i(\eta )+\sum _{m=0}^{i-1}G_m(\eta ),\;\; h(\eta )=h_i(\eta )+\sum _{m=0}^{i-1}H_m(\eta ),\;\; k(\eta )=k_i(\eta )+\sum _{m=0}^{i-1}K_m(\eta ) \end{array} \right\} . \end{aligned}$$

(29)

where $f_i,\theta _i,\phi _i,g_i,h_i$ and $k_i$ are unknown functions and $F_m,\Theta _m,\Phi _m,G_m,H_m$ and $K_m$, $(m\ge 1)$ are successive approximations which are obtained by recursively solving the linear part of the equation system that results from substituting firstly Eq. (29) in Eqs.  (21)–(23) and (25)–(27). The main assumption of the SLM is that $f_i,\theta _i,\phi _i,g_i,h_i$ and $k_i$ become increasingly smaller when $i$ becomes large, that is

$$\begin{aligned} \lim _{i\rightarrow \infty }f_i=\lim _{i\rightarrow \infty }\theta _i=\lim _{i\rightarrow \infty }\phi _i=\lim _{i\rightarrow \infty }g_i=\lim _{i\rightarrow \infty }h_i=\lim _{i\rightarrow \infty }k_i=0. \end{aligned}$$

(30)

The initial guesses $F_0(\eta ),\Theta _0(\eta ),\Phi _0(\eta ),G_0(\eta ),H_0(\eta )$ and $K_0(\eta )$ which are chosen to satisfy the boundary conditions (24) and (28) which are taken to be

$$\begin{aligned}&F_0(\eta )=1-e^{-\eta }, \quad \Theta _0(\eta )=e^{-\eta },\quad \Phi _0(\eta )=e^{-\eta } \quad G_0(\eta )=1-e^{-\eta },\quad H_0(\eta )=\eta e^{-\eta },\nonumber \\&K_0(\eta )=\eta e^{-\eta }. \end{aligned}$$

(31)

Thus, starting from the initial guesses, the subsequent solutions $F_i,\Theta _i,\Phi _i,G_i,H_i$ and $K_i$ $(i\ge 1)$ are obtained by successively solving the linearised form of the equations which are obtained by substituting Eq. (29) in the governing Eqs. (21)–(23) and (25)–(27). The linearised equations to be solved are

$$\begin{aligned}&a_{1,i-1}F_i''+a_{2,i-1}F_i'+a_{3,i-1}\Theta '_i+a_{4,i-1}\Theta _i+a_{5,i-1}\Phi '_i=r_{1,i-1},\end{aligned}$$

(32)

$$\begin{aligned}&b_{1,i-1}\Theta _i''+b_{2,i-1}\Theta '_i+b_{3,i-1}\Theta _i+b_{4,i-1}F'_i+b_{5,i-1}F_i+b_{6,i-1}\Phi _i\nonumber \\&\quad +\,b_{7,i-1}G_i+b_{8,i-1}H_i=r_{2,i-1},\end{aligned}$$

(33)

$$\begin{aligned}&c_{1,i-1}\Phi _i''+c_{2,i-1}\Phi _i'+c_{3,i-1}F_i'+c_{4,i-1}F_i+c_{5,i-1}\Theta _i''+c_{6,i-1}G_i\nonumber \\&\quad +\,c_{7,i-1}K_i=r_{3,i-1}, \end{aligned}$$

(34)

$$\begin{aligned}&d_{1,i-1}G_i''+d_{2,i-1}G_i'+d_{3,i-1}F''_i+d_{4,i-1}F_i'+d_{6,i-1}\Theta _i'+d_{7,i-1}\Theta _i+d_{8,i-1}\Phi _i\nonumber \\&\quad +\,b_{9,i-1}H'_i+b_{10,i-1}H_i+b_{11,i-1}K'_i=r_{4,i-1},\end{aligned}$$

(35)

$$\begin{aligned}&e_{1,i-1}H_i''+e_{2,i-1}H_i'+e_{3,i-1}H_i+e_{4,i-1}F_i'+e_{6,i-1}F_i+e_{7,i-1}\Theta '_i+e_{8,i-1}\Theta _i\nonumber \\&\quad +\,e_{9,i-1}\Phi _i+e_{10,i-1}G'_i+e_{11,i-1}G_i+e_{11,i-1}K_i=r_{5,i-1},\end{aligned}$$

(36)

$$\begin{aligned}&q_{1,i-1}K_i''+q_{2,i-1}K_i'+q_{3,i-1}K_i+q_{4,i-1}F_i'+q_{6,i-1}F_i+q_{7,i-1}\Phi '_i+q_{8,i-1}G'_i\nonumber \\&\quad +\,q_{9,i-1}G_i+q_{10,i-1}H''_i=r_{6,i-1} \end{aligned}$$

(37)

subject to the boundary conditions

$$\begin{aligned} \left. \begin{array}{cc} F_i(0)=F_i'(\infty )=\Theta _i(0)=\Theta _i(\infty )=\Phi _i(0)=\Phi _i(\infty )\\ G_i(0)=G'_i(\infty )=H_i(0)=H_i(\infty )=K_i(0)=K_i(\infty )=0 \end{array} \right\} . \end{aligned}$$

(38)

where the coefficients parameters $a_{k,i-1},b_{k,i-1},c_{k,i-1},d_{k,i-1},e_{k,i-1},q_{k,i-1}$ and $r_{k,i-1}$ depend on $F_0(\eta )$, $\Theta _0(\eta )$, $\Phi _0(\eta )$, $G_0(\eta )$, $H_0(\eta )$ and $K_0(\eta )$ and on their derivatives.

The solution for $F_i$, $\Theta _i$,$\Phi _i$, $G_i$, $H_i$ and $K_i$ for $i\ge 1$ has been found by iteratively solving Eqs.  (32)–(38) and finally after $M$ iterations the solutions $f(\eta )$, $\theta (\eta )$, $g(\eta )$ and $h(\eta )$ can be written as

$$\begin{aligned} \left. \begin{array}{cc} f(\eta )\approx \sum _{m=0}^MF_m(\eta ), \theta (\eta )\approx \sum _{m=0}^M\Theta _m(\eta ), \phi (\eta )\approx \sum _{m=0}^M\Phi _m(\eta )\\ g(\eta )\approx \sum _{m=0}^MG_m(\eta ), h(\eta )\approx \sum _{m=0}^MH_m(\eta ), k(\eta )\approx \sum _{m=0}^MK_m(\eta ) \end{array} \right\} . \end{aligned}$$

(39)

where $M$ is termed the order of SLM approximations. Now we apply the Chebyshev spectral collocation method (see [3, 14, 46]) to Eqs. (32)–(38). We apply the mapping

$$\begin{aligned} \frac{\eta }{L}=\frac{\xi +1}{2},\quad -1\le \xi \le 1, \end{aligned}$$

(40)

to transform the domain $[0,\infty )$ to $[-1,1]$ where $L$ is used to invoke the boundary condition at infinity. We discretize the domain $[-1,1]$ using the Gauss-Lobatto collocation points defined by

$$\begin{aligned} \xi =\cos \frac{\pi j}{N},\quad j=0,1,2,\ldots ,N, \end{aligned}$$

(41)

where $N$ is the number of collocation points. The functions $F_i$, $\Theta _i$, $G_i$ and $H_i$ for $i\ge 1$ are approximated at the collocation points as follows

$$\begin{aligned} \left. \begin{array}{l} F_i(\xi )\approx \sum ^N_{k=0}F_i(\xi _k)T_k(\xi _j), \Theta _i(\xi )\approx \sum ^N_{k=0}\Theta _i(\xi _k)T_k(\xi _j), \Phi _i(\xi )\approx \sum ^N_{k=0}\Phi _i(\xi _k)T_k(\xi _j)\\ G_i(\xi )\approx \sum ^N_{k=0}G_i(\xi _k)T_k(\xi _j), H_i(\xi )\approx \sum ^N_{k=0}H_i(\xi _k)T_k(\xi _j), K_i(\xi )\approx \sum ^N_{k=0}K_i(\xi _k)T_k(\xi _j) \end{array}\right\} \quad j=0,1,\ldots ,N, \end{aligned}$$

(42)

where $T_k$ is the $k\text {th}$ Chebyshev polynomial given by

$$\begin{aligned} T_k(\xi )=\cos \left[ k\cos ^{-1}(\xi )\right] . \end{aligned}$$

(43)

The derivatives of the variables at the collocation points are

$$\begin{aligned} \left. \begin{array}{l} \frac{d^rF_i}{d\eta ^r}=\sum ^N_{k=0}\mathcal {D}^r_{kj}F_i(\xi _k), \frac{d^r\Theta _i}{d\eta ^r}=\sum ^N_{k=0}\mathcal {D}^r_{kj}\Theta _i(\xi _k), \frac{d^r\Phi _i}{d\eta ^r}=\sum ^N_{k=0}\mathcal {D}^r_{kj}\Phi _i(\xi _k)\\ \frac{d^rG_i}{d\eta ^r}=\sum ^N_{k=0}\mathcal {D}^r_{kj}G_i(\xi _k), \frac{d^rH_i}{d\eta ^r}=\sum ^N_{k=0}\mathcal {D}^r_{kj}H_i(\xi _k), \frac{d^rK_i}{d\eta ^r}=\sum ^N_{k=0}\mathcal {D}^r_{kj}K_i(\xi _k) \end{array}\right\} \quad j=0,1,\ldots ,N, \end{aligned}$$

(44)

where $r$ is the order of differentiation and $\mathcal {D}$ is the Chebyshev spectral differentiation matrix whose entries are defined as [3, 14, 46]

$$\begin{aligned} \left. \begin{array}{ccl} \mathcal {D}_{00} &{} = &{} \frac{2N^2 + 1}{6}, \\ \mathcal {D}_{jk} &{} = &{} \frac{c_{j}}{c_{k}}\frac{(-1)^{j+k}}{ \xi _{j} - \xi _{k}}, \quad j \ne k ; \quad j , k = 0, 1, \ldots , N, \\ \mathcal {D}_{kk} &{} = &{} - \frac{\xi _{k}}{2(1-\xi _{k}^2)}, \quad k = 1, 2, \ldots , N - 1, \\ \mathcal {D}_{NN} &{} = &{} - \frac{2N^2 + 1}{6}. \end{array}\right\} \end{aligned}$$

(45)

After applying the Chebyshev spectral method to (32)–(37) we get the matrix system of equations

$$\begin{aligned} \mathbf A _{i-1}\mathbf X _{i}=\mathbf R _{i-1}. \end{aligned}$$

(46)

subject to

$$\begin{aligned} \left. \begin{array}{l} F_i(\xi _N)=\sum ^N_{k=0}\mathbf D _{0k}F_i(\xi _k)=0,\qquad \Theta _i(\xi _N)=\Theta _i(\xi _0)=0,\qquad \Phi _i(\xi _N)=\Phi _i(\xi _0)=0\\ G_i(\xi _N)=\sum ^N_{k=0}\mathbf D _{0k}G_i(\xi _k)=0,\qquad H_i(\xi _N)=H_i(\xi _0)=0,\qquad K_i(\xi _N)=K_i(\xi _0)=0 \end{array}\right\} \end{aligned}$$

(47)

In Eq. (46), $\mathbf A _{i-1}$ is a $(6N+6)\times (6N+6)$ square matrix and $\mathbf X _i$ and $\mathbf R _{i-1}$ are $(6N+6)\times 1$ column vectors and $\mathbf D =\frac{2}{L}\mathcal {D}$. Finally the solution is obtained as

$$\begin{aligned} \mathbf X _{i}=\mathbf A _{i-1}^{-1}\mathbf R _{i-1}. \end{aligned}$$

(48)

4 Results and discussion

The governing nonlinear differential equations were solved by means of the successive linearisation method. The value of $L$ was suitably chosen so that the boundary conditions at the outer edge of the boundary layer are satisfied. The results obtained are accurate up to the $5$th decimal place. In order to assess the accuracy of the solutions, we made a comparison with the shooting technique. The comparison is given in Tables 1 and 2 for aiding and opposing buoyancy respectively. The results are in good agreement pointing to the accuracy of the SLM solutions. In addition, a comparison between the present results and Cheng [8] for various buoyancy and Lewis numbers $Le$ is given in Table 3. The comparison shows that the present results are in excellent agreement with the similarity solutions reported by Cheng [8]. The effect of the physical parameters on the temperature, concentration, heat and mass transfer coefficients are shown in Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12.

Table 1 A comparison of $f'(\eta )$, $\theta (\eta )$ and $\phi (\eta )$ using the SLM and the shooting method for different values of $n$ with $Gr^*=1$, $\gamma =1$, $Sr=0.1$, $Le=1$, $\varepsilon =0.2$ and $\Lambda =0.1$

Table 2 A comparison of $f'(\eta )$, $\theta (\eta )$ and $\phi (\eta )$ using the SLM and shooting method for different values of $n$ with $Gr^*=1$, $\gamma =1$, $Sr=0.1$, $Le=1$, $\varepsilon =0.2$ and $\Lambda =-0.1$

Table 3 Comparison of the local Nusselt and Sherwood numbers between the current results and Cheng [8] for various values of $\Lambda$ and $Le$ when $n=1$, $Gr^*=0$, $\gamma =0$, $Sr=0$, and $\varepsilon =0$

Fig. 1

Variation of $f'(\eta )$ against $\eta$ varying $S_r$ and $n$ when $\gamma =1, Gr^*=1, \varepsilon =0.2, Le=1$ and $\Lambda =0.1$

Fig. 2

Variation of a $\theta (\eta )$ and b $\phi (\eta )$ against $\eta$ varying $\varepsilon$ and $n$ when $\gamma =1, Gr^*=1, Sr=0.1, Le=1$ and $\Lambda =0.1$

Fig. 3

Variation of a $\theta (\eta )$ and b $\phi (\eta )$ against $\eta$ varying $Sr$ and $n$ when $\gamma =1, Gr^*=1, \varepsilon =0.2, Le=1$ and $\Lambda =0.1$

Fig. 4

Variation of a skin friction b heat transfer and c mass transfer coefficients against $\varepsilon$ varying $Sr$ and $n$ when $\gamma =1,Gr^*=1,Le=1$ and $\Lambda =0.1$

Fig. 5

Variation of a heat transfer and b mass transfer coefficients against $Sr$ varying $\varepsilon$ and $n$ when $\gamma =0.5, Gr^*=1, Le=1$ and $\Lambda =0.1$

Fig. 6

Variation of a heat transfer and b mass transfer coefficients against $\gamma$ varying $\varepsilon$ and $n$ when $Sr=0.1, Gr^*=1, Le=1$ and $\Lambda =0.1$

Fig. 7

Variation of $f'(\eta )$ against $\eta$ varying $S_r$ and $n$ when $\gamma =1, Gr^*=1, \varepsilon =0.2, Le=1$ and $\Lambda =-0.1$

Fig. 8

Variation of a $\theta (\eta )$ and b $\phi (\eta )$ against $\eta$ varying $\varepsilon$ and $n$ when $\gamma =1, Gr^*=1, Sr=0.1, Le=1$ and $\Lambda =-0.1$

Fig. 9

Variation of a $\theta (\eta )$ and b $\phi (\eta )$ against $\eta$ varying $Sr$ and $n$ when $\gamma =1,Gr^*=1,\varepsilon =0.2,Le=1$ and $\Lambda =-0.1$

Fig. 10

Variation of a skin friction b heat transfer and c mass transfer coefficients against $\varepsilon$ varying $Sr$ and $n$ when $\gamma =0.1,Gr^*=1,Le=1$ and $\Lambda =-0.1$

Fig. 11

Variation of a heat transfer and b mass transfer coefficients against $Sr$ varying $\varepsilon$ and $n$ when $\gamma =0.5,Gr^*=1,Le=1$ and $\Lambda =-0.2$

Fig. 12

Variation of a heat transfer and b mass transfer coefficients against $\gamma$ varying $\varepsilon$ and $n$ when $Sr=0.1,Gr^*=1,Le=1$ and $\Lambda =-0.1$

4.1 Aiding buoyancy

Figure 1 shows the variation of the non-dimensional velocity profile $f'(\eta )$ for $n=0.5$, $n=1$ and $n=1.5$ for two different values of Soret number $S_r$ and for fixed values of $\gamma$, $GR^*$, $\varepsilon$, $Le$ and $\Lambda$. We observe that the velocity increases with increased in Soret number for all indices $n$.

Figure 2a shows the variation of the non-dimensional temperature distribution $\theta (\eta )$ for $n=0.5$, $n=1$ and $n=1.5$ for two different values of viscous dissipation $\varepsilon$ and for fixed values of $\gamma$, $GR^*$, $Sr$, $Le$ and $\Lambda$. We observe that the thermal boundary layer thickens with increased in viscous dissipation for all indices $n$. The effects of $n$ and $\varepsilon$ on the concentration profile $\phi (\eta )$ is shown in Fig. 2b. It is noted that increasing the viscous dissipation and power law index $n$ reduces the concentration boundary layer thickness.

The effect of Soret parameter on temperature and concentration profiles is shown in Fig. 3 for the aiding buoyancy case. It is clear that the Soret parameter reduces the thermal boundary layer thickness while increasing the concentration boundary layer thickness.

The effect of the viscous dissipation parameter $\varepsilon$ and the Soret number $Sr$ on the skin friction, Nusselt and Sherwood numbers are shown in Fig. 4 for $n<1$, $n=1$ and $n>1$. Increasing both the viscous dissipation and the power-law index reduced the heat transfer coefficient while enhancing the skin friction and mass transfer coefficients. Consequently, heat transfer is much more pronounced in a pseudoplastic as compared to both a Newtonian and a dilatant fluid. The opposite is however true in the case of mass transfer. The variation of the Nusselt and Sherwood numbers as a function of $Sr$ is given in Fig. 5 for different values of $n$ and viscous dissipation parameter $\varepsilon$. Increasing the Soret number increases the heat transfer rate for pseudoplastics, Newtonian and dilatant fluids while reducing the mass transfer rate.

Figure 6 shows the variation of the Nusselt and Sherwood numbers with the viscosity parameter $\gamma$. Increasing the viscosity parameter increases the rates of heat and mass transfer for all values of $\varepsilon$ and power low index $n$. Similar results were obtained by Jayanthi et al. [22] and Kairi et al. [23].

4.2 Opposing buoyancy

Figure 7 shows the variation of the non-dimensional velocity profile $f'(\eta )$ for $n=0.5$, $n=1$ and $n=1.5$ for two different values of Soret number $S_r$ and for fixed values of $\gamma$, $GR^*$, $\varepsilon$, $Le$ and $\Lambda$. We observe that the velocity decreases with increased in Soret number for indices $n$.

Figure 8 shows the temperature and concentration distributions when $n=0.5$, $n=1$ and $n=1.5$ for $\varepsilon =0$ and $0.2$. Increasing $\varepsilon$ reduces the thermal and concentration boundary layer thickness profiles for all values of $n$.

In the opposing buoyancy case, the effect of the Soret parameter on the temperature and concentration distributions in Fig.  9a, b for different values of the power-law index $n$ and $\varepsilon$. Both thermal and concentration boundary layer thicknesses decrease with increases in $Sr$ for all $n$. We note here that the effect of the Soret number on the concentration profiles in the case of opposing buoyancy is opposite to that of aiding buoyancy. In Fig. 10, the variation of $f''(\varepsilon ,0)$, $Nu_x/Ra_x^{1/2}$ and $Sh_x/Ra_x^{1/2}$ as a function of $\varepsilon$ are shown for different types of power-law fluids and two values of $Sr$ while the other parameters are fixed. We note that, as in the case of aiding buoyancy, an increase in both $\varepsilon$ and $n$ reduces $Nu_x/Ra_x^{1/2}$ while $f''(\varepsilon ,0)$ and $Sh_x/Ra_x^{1/2}$ increases with the Soret effect. The variation of the Nusselt and Sherwood numbers as a functions of $Sr$ is displayed in Fig. 11 for different values of $n$ and $\varepsilon$. We observed that both Nusselt and Sherwood numbers increased with the Soret number.

Increasing the viscosity parameter $\gamma$ enhances the rates of heat and mass transfer for all types of power-law fluids $n$ as shown in Fig. 12. This is also in line with the findings by Jayanthi et al. [22] and Kairi et al. [23].

5 Conclusions

In this paper, viscous dissipation and the Soret effects on natural convection from a vertical plate immersed in a non-Darcy porous medium saturated with a non-Newtonian power-law fluid has been studied. The governing equations are transformed into ordinary differential equations and solved using the successive linearisation method. Qualitative results were presented showing the effects of various physical parameters on the fluid properties and the rates of heat and mass transfer. Velocity and temperature profiles are significantly effected by viscous dissipation, Soret number and variable viscosity parameters. The Nusselt number is reduced by viscous dissipation and enhanced by the Soret number for both the aiding and opposing buoyancy cases. The Sherwood number increases with viscous dissipation for both the aiding and opposing buoyancy cases and decreases with the Soret number in the case of aiding buoyancy. Increasing viscosity enhances heat and mass transfer coefficients in both cases of aiding buoyancy and opposing buoyancy. Heat transfer is much pronounced in the case of a pseudoplastic as compared to both a Newtonian and a dilatant fluids. Mass transfer is however greater in the case of Newtonian and dilatant fluids than for pseudoplastics.