1 Introduction

Electrical peak load forecasting plays a vital role in ensuring the reliability, safety, and economic efficiency of power system operations and planning. It provides valuable reference values and guidance for integrating renewable energy sources, such as wind and solar power, into the smart grid [1,2,3,4]. The research literature has proposed numerous models for electrical peak load forecasting, which can be categorized into two major groups: (1) classic stage, and (2) advanced stage. The classic stage category includes well-known forecasting methods such as Regression [5, 6], Stochastic time series [7, 8], and Exponential Smoothing [9, 10]. In the advanced stage group, researchers have reported the effectiveness of Fuzzy logic [11, 12], Artificial neural network [13,14,15], Support Vector Machines [16, 17], Hybrid Techniques [18,19,20], and Ensemble Learning [21, 22]. In this context, ensemble learning is a machine learning technique that combines predictions from two or more models to increase the accuracy and reliability of the final results. By leveraging the collective predictions of multiple models, ensemble learning can achieve higher accuracy and more reliable predictions compared to individual models. Recently, there has been extensive research on the application of ensemble learning using decision tree-based machine learning algorithms in load forecasting, resulting in remarkable outcomes. Notably, this paper will consider models such as GBDT, XGBoost, LightGBM, and CatBoost, which have demonstrated promising performance in this field [23,24,25,26,27,28,29,30].

Since peak load is a time series, it is common to utilize the Sliding Window procedure when applying ensemble algorithms. This procedure helps partition the data into input and target sets, enabling the training and forecasting processes for the load profile to be performed using ensemble algorithm models [28, 31, 32]. Another aspect examined in this study is the periodicity of peak load. For example, the load characteristics of a specific Monday may exhibit similarities to those of the previous Monday. When using only the Sliding Window procedure in data processing, the cyclic nature of the load data may inadvertently be overlooked. Therefore, in this study, the author recommends a novel approach that involves incorporating the input data Differencing Operator to account for the cyclical characteristics of the load data. More specifically, the analysis will focus on the series Zt = Yt–Yt-d as an alternative to using the original data Yt, where d represents the differencing order. The Differencing Operator, integrated with the Sliding Window procedure, will be employed in combination with ensemble learning algorithms. The proposed method's effectiveness will be assessed through the evaluation of forecast errors and program execution time. The GBDT, XGBoost, LightGBM, and CatBoost algorithms will be sequentially investigated. Each algorithm will consider a large number of hyperparameter combinations. Furthermore, this study will utilize peak load data from two Australian states, New South Wales and Queensland, enhancing the reliability of the research results.

This paper is organized as follows: In Sect. 2, a brief introduction to ensemble algorithms is presented; Sect. 3 proposes a new approach through the combination of the Sliding Window procedure with the Differencing Operator; Sect. 4 conducts empirical assessments on real datasets from two states of Australia; and finally, Sect. 5 presents the conclusions.

2 Review of Ensemble Algorithm

Ensemble learning is a technique that enhances predictive performance by combining multiple models, surpassing the performance of individual models used in isolation. There are three main classes of ensemble learning: bagging, stacking, and boosting [33]. Bagging is an ensemble learning algorithm that creates a diverse group of ensemble members by training models on different subsets of the training dataset. On the other hand, stacking involves training different types of models on the training data to generate predictions, which are then combined using another model. Boosting is an ensemble algorithm that leverages the mistakes made by previous predictors to improve future predictions. Boosting algorithms have gained significant attention in recent years and will also be employed in this paper. Notably, boosting algorithms come in various forms, including GBDT (Gradient Boosting Decision Trees), XGBoost (Extreme Gradient Boosting), LightGBM (Light Gradient Boosting Machine), and CatBoost (Categorical Boosting) [34,35,36].

2.1 Ensemble Algorithms

GBDT algorithm was first introduced by Friedman in 2001, presenting a novel approach that combines Gradient Boosting and Decision Trees in machine learning [37, 38]. In Gradient Boosting, multiple weak learners are connected sequentially, with each learner aiming to minimize the error of the previous learner. Gradient Boosting utilizes gradient descent to construct new weak learners along the direction of the current model's loss function. The Decision Tree plays a crucial role as the main component of GBDT and serves as a weak learner within the Gradient Boosting process. The integration of Gradient Boosting and Decision Trees in GBDT leads to enhanced effectiveness in learning and optimization.

XGBoost is a scalable, end-to-end tree boosting method developed by Chen and Guestrin in 2016 [39]. It is an improved algorithm based on the GBDT model, which uses second-order Taylor expansion on the loss function and incorporates regular terms into the objective function to achieve the optimal solution. This approach helps control the decline of the objective function and the complexity of a model, resulting in better convergence, prevention of overfitting, and ultimately providing higher forecasting accuracy. Additionally, XGBoost processes the data and stores the results before training, enabling their reuse in subsequent iterations to reduce computational complexity and facilitate parallel execution, thereby increasing efficiency.

LightGBM is a novel gradient boosting framework developed by Microsoft Research Asia in 2017 [40]. It is an enhanced version of GBDT that incorporates two key techniques: Gradient-based One-Side Sampling (GOSS) and Exclusive Feature Bundling (EFB). The core concept behind GOSS is that larger gradients contribute more to the information gain. The GOSS algorithm identifies samples with high gradients and randomly selects a subset from samples with small gradients. This approach effectively utilizes the samples during the training process, optimizing their impact on the model. On the other hand, EFB focuses on reducing the number of features by merging mutually exclusive ones. EFB consists of two algorithms: one for exclusive feature bundling, which combines related features, and another for merging feature bundles and assigning a value to the resulting bundle.

CatBoost is a new gradient descent algorithm that was presented by Prokhorenkova et al. in 2018 [41]. It is highly effective in predicting categorical features and is based on the utilization of binary decision trees as base predictors. This algorithm incorporates several techniques including permutation methods, one-hot-max-size encoding, greedy methods for new tree splits, and target-based statistics. These techniques are applied as follows: The dataset is randomly permuted into subsets, the labels are converted to integer numbers, and the categorical values are transformed into numerical representations. This combination of techniques enhances the effectiveness of CatBoost in handling categorical data and improves its predictive capabilities.

2.2 Hyperparameters

One concern when using hybrid learning techniques is the hyperparameters of the model, which affect the performance and accuracy of an ensemble model. Hyperparameters are parameters that are set prior to training a machine learning model, unlike model parameters which are learned from data during training. There are many hyperparameters for ensemble algorithms, which can be classified into many groups such as Accuracy, Speed, and Overfitting. In this research, each model of GBDT, XGBoost, LightGBM, and CatBoost will be performed and evaluated in combination with different values of typical hyperparameters to increase the reliability of the results [42, 43]. These key hyperparameters that will be considered in this paper include:

  • The learning rate (lr), which determines the step size at each iteration with respect to the loss gradient function.

  • The maximum depth (md), which is an integer that controls the maximum distance between the root node and a leaf node.

  • The number of estimators (ne), which is the number of trees used in the model.

3 Proposed Method

3.1 Sliding Window Procedure

Time series data refers to a collection of observations on the values that a variable takes at different points in time, following a uniform time–frequency. It can be represented by the equation:

$$y_{1} , \, y_{2} , \, \ldots , \, y_{m} , \, \ldots , \, y_{M}$$
(1)

where m ranges from 1 to M, representing the number of observation values.

To incorporate time series data into an ensemble algorithm, the Sliding Window procedure has been utilized to extract both time series data and production data features. The Sliding Window procedure is illustrated in Fig. 1, where a window size of 7 has been employed [32].

Fig. 1
figure 1

The process of the Sliding Window procedure

Full size image

When working with a time series dataset of length M, the Sliding Window procedure is applied using a window size denoted as N. Subsequently, the dataset is divided into training and testing subsets, where the number of testing instances is denoted as H. The steps for constructing the dataset using the sliding window procedure are detailed in Table 1.

Table 1 The Sliding Window procedure process
Full size table

The training dataset is composed of an input sequence Xtrain = {y1, …, yN; y2, …., yN+1; ….; yM-H-N, …, yM-H-1} and an output sequence Ytrain = {yN+1, …yM-H}. On the other hand, the testing dataset includes an input sequence Xtest = {yM-H+1-N, …, yM-H; yM-H+2-N, …., yM-H+1; ….; YM-N, …, yM-1} and an output sequence Ytest = {yM-H+1, …yM}. Following the Sliding Window procedure mentioned earlier, the data is structured into input and output components. The training data is represented as (Xtrain, Ytrain), while the testing data is represented as (Xtest, Ytest). These training and testing datasets serve as the foundation for applying machine learning algorithm in time series forecasting.

3.2 Differencing Operator

The repetitive nature of time series refers to the regular or periodic patterns that occur in the data over time. These patterns can occur at regular intervals, such as hourly, daily, weekly, monthly, or yearly for electric load patterns. To address the repetitive nature and make time series data more amenable to analysis, the Differencing Operator is often applied. The Differencing Operator involves computing the difference between consecutive observations in the time series by subtracting the previous value from the current value. This captures the changes or fluctuations in the data, as shown by the equation below:

$$y\left( t \right) \, = \, y\left( t \right) \, {-} \, y\left( {t - d} \right)$$
(2)

where d is the order of differencing.

The algorithm flowchart of the Differencing Operator is shown in Fig. 2. By applying differencing, the operator helps remove the trend and seasonality from the data, making it stationary. This process allows for better modeling and prediction of the time series.

Fig. 2
figure 2

The flow chart of the Differencing Operator

Full size image

3.3 The Integration of Differencing Operator into the Sliding Window Procedures

Based on the presentation above, the Differencing Operator has the potential to significantly impact the forecast of time series data. Therefore, in this study, the author proposes the utilization of the Differencing Operator integrated into the Sliding Window Procedure for ensemble learning algorithms in the case of peak load forecasting, as illustrated in Fig. 3. Figure 3 depicts the training and testing process of the ensemble learning algorithm. First, ensemble algorithms are trained using {Xtrain, Ytrain} as input and output variables, which generates a regression model called \({{\varvec{m}}{\varvec{d}}{\varvec{l}}}_{{\varvec{i}}}^{(\boldsymbol{ }{\varvec{d}})}\). Secondly, this trained regression model, \({{\varvec{m}}{\varvec{d}}{\varvec{l}}}_{{\varvec{i}}}^{(\boldsymbol{ }{\varvec{d}})}\), produces the output variable \(\widehat{Y}\) corresponding to Xtest in the testing process. The error rate (such as MAPE) between the predict value \(\widehat{Y}\) and real value Ytest values is used to evaluate the effectiveness of the ensemble algorithms.

Fig. 3
figure 3

The training and testing process of the ensemble learning algorithm

Full size image

The pseudocode for the training process is shown in Fig. 4. The input data for this process is assigned to training data, The output of the training stage is a trained model, \({{\varvec{m}}{\varvec{d}}{\varvec{l}}}_{{\varvec{i}}}^{({\varvec{d}})}\), where subscript i represents one case of the combination of hyperparameters, and superscript (d) refers to the differencing order d. The training process is performed as follows:

  • The original data is differenced according to the order d, as defined in Eq. (2).

  • Transforming data into input-target pairs: The input Xtrain and output Ytrain for the training process are established using the Sliding Window procedure discussed earlier in Sect. 3.1.

  • Defining the ensemble model: The ensemble algorithms, namely GBDT, XGBoost, LightGBM, and CatBoost models, are defined within the Python environment for this research. The corresponding libraries used are sklearn, xgboost, lightgbm, and catboost.

  • The model training is conducted using the input-target data (Xtrain and Ytrain), which correspond to the defined model from the previous step.

Fig. 4
figure 4

The pseudocode of training stage

Full size image

The pseudocode for the testing process is presented in Fig. 5. During the testing process, the input consists of the testing data, the trained model\({{\varvec{m}}{\varvec{d}}{\varvec{l}}}_{{\varvec{i}}}^{({\varvec{d}})}\), and the training data used to invert the Differencing Operator. The testing process follows these main steps:

  • Obtaining rolling data and differencing offset: The training data is used to obtain the rolling data and determine the differencing offset.

  • Obtaining the input Xtest: The input Xtest is obtained from the rolling data, using the Sliding Window procedure.

  • Obtaining the first predicted value \({\widehat{\text{y}}}_{1}\): Using the model \({{\varvec{m}}{\varvec{d}}{\varvec{l}}}_{{\varvec{i}}}^{(\boldsymbol{ }{\varvec{d}})}\) and the Xtest, the initial predicted value \({\widehat{\text{y}}}_{1}\) is caculated. It is then adjusted by the differencing offset.

  • Updating the rolling data and repeating the process: The rolling data is updated with the actual observation, and the process is repeated for the remaining predicted values \({\widehat{\text{y}}}_{i}\), i = 2, …h.

Fig. 5
figure 5

The pseudocode of testing stage

Full size image

The output of the testing process is the error rate, which is calculated based on the real values [yn-h+1, yn-h+2, …,yn] and the predicted values [\({\widehat{\text{y}}}_{1}, {\widehat{\text{y}}}_{2}, \dots , {\widehat{y}}_{n}\)]. In this paper, the mean absolute percentage error (MAPE) is calculated to evaluate forecasting accuracy. The MAPE error rate is expressed by the following formula [44, 45]:

$$\text{MAPE}=\frac{1}{h} \sum_{i=1}^{h}\left|\frac{{y}_{n-h+i}-{\widehat{y}}_{i}}{{y}_{n-h+i}}\right|$$
(3)

Note:

To evaluate the effectiveness of the Differencing Operator based on the Sliding Window Procedure for ensemble algorithms, it is necessary to analyze the performance of these algorithms according to the differencing order d. This is the reason why there is a superscript (d) in the model \({\mathbf{m}\mathbf{d}\mathbf{l}}_{{\varvec{i}}}^{({\varvec{d}})}\), and the error rate \({\mathbf{M}\mathbf{A}\mathbf{P}\mathbf{E}}_{{\varvec{i}}}^{({\varvec{d}})}\) in Figs. 3, 4, and 5as presented above.

Additionally, to enhance the reliability of the results, it is suggested to combine different values of hyperparameters for each ensemble algorithm. That explains why there is the input Hi = {lra, mdb, nec} in the training process, as well as the subscript (i) in the variable \({\mathbf{m}\mathbf{d}\mathbf{l}}_{{\varvec{i}}}^{({\varvec{d}})}\) and the error rate \({\mathbf{M}\mathbf{A}\mathbf{P}\mathbf{E}}_{{\varvec{i}}}^{({\varvec{d}})}\).

Thus, based on the procedure outlined in Fig. 3 and the integrated pseudocode in Figs. 4 and 5, the error rate of each ensemble model can be determined by considering specific values of differencing order (d). This allows for the evaluation of the effectiveness of integrating Differencing Operator into the Sliding Window Procedures based on ensemble algorithms.

4 Experimental Study

4.1 Experimental setup

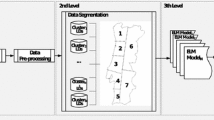
In this study, the author recommends utilizing the daily peak load data of New South Wales (NSW) and Queensland (QL), Australia, for both training and testing. Figure 6 depicts the peak load graph of these two states from March 4, 2012 to May 31, 2014, along with their corresponding characteristics listed in Table 2. The training phase utilizes data from March 4, 2012 to May 3, 2014, while the testing phase encompasses the period from May 4, 2014 to May 31, 2014, covering a duration of 28 days.

Fig. 6
figure 6

The daily peak load of New South Wales and Queensland

Full size image
Table 2 The descriptive statistics of data
Full size table

To enhance the reliability of the proposed method, it is crucial to explore multiple cases for each ensemble algorithm. In this study, the author suggests simultaneously investigating different combinations of significant common hyperparameters for the GBD, XGBoost, LightBoost, and CatBoost models. These hyperparameters include the learning rate (lr), maximum depth (md), and number of estimators (ne), as discussed in Sects. 2 and 3. The range and the number of survey participants for these hyperparameters are presented in Table 3 below. The total number of combinations for the lr, md, and ne hyperparameters is 2000 cases.

Table 3 The ranges for hyperparameters
Full size table

In the present work, the focus is on forecasting daily peak loads. For this purpose, several differencing values are proposed, including d = 0 (no differencing), d = 1 (first differencing), d = 7 (weekly seasonal differencing), and d = 28 (monthly seasonal differencing). Additionally, for the experimental application of the proposed algorithm to peak load data, three window sizes have been established:

  • Window size = 1, which uses the data taken from the previous day for forecasting.

  • Window size = 7, which uses the data taken from the previous week.

  • Window size = 28, which considers a typical month's data, specifically, from four preceding weeks.

After executing the program and analyzing the results from the mentioned window sizes, the obtained outcomes were quite similar across the board. However, the window size of 7 proved to be the most effective one. Notably, this finding is helpful for the paper focus that is devoted to clarifying the impact of the Differencing Operator. As a result, the window size of 7 was chosen for further study in this research.

The experiments were implemented using the Scikit-learn, math, Matplotlib, and other libraries, as well as the XGBoost, LightGBM, and CatBoost libraries in the Python environment on the Google Colab platform. The runtime type in Colab is TPU with high RAM.

4.2 Evaluation of Error Rates

Figure 7 displays a boxplot of the error rate (MAPE) between the predicted value (\(\widehat{Y}\)) and the actual value (Ytest) for different values of differencing order d (0, 1, 7, 28). The result corresponds to the GBDT, XGBoost, LightBoost, and CatBoost models for the New South Wales and Queensland data cases.

Fig. 7
figure 7

The error rates for differencing orders of 0, 1, 7, and 28: (a) New South Wales, (b) Queensland

Full size image

Table 4 presents statistics for each set of differencing order d (d = 0, 1, 7, 28) shown in Fig. 7. For each set, five statistical values are provided, including minimum, 25th percentile, 50th percentile, 75th percentile, and maximum. For example, in the upper-left subfigure of Fig. 7 (GBDT model, New South Wales data), a differencing order d = 0 yields statistical values of 5.84 (minimum), 6.54 (25th percentile), 6.68 (50th percentile), 6.79 (75th percentile), and 7.47 (maximum). Similarly, for the last subfigure on the bottom right (CatBoost model, Queensland data), a differencing order d = 28 gives statistic values of 3.21 (minimum), 3.51 (25th percentile), 3.59 (50th percentile), 3.68 (75th percentile), and 4.32 (maximum).

Table 4 The descriptive statistics of error rate
Full size table

An in-depth analysis of Figs. 7 and Table 4 reveals that the application of the Differencing Operator to the input data (d = 1, 7, 28) leads to significantly better results, with a drastic reduction in prediction error compared to using the original data (d = 0). Specifically, when examining the GBDT model and New South Wales data, Fig. 7 and Table 4 show that using the original data yields excessively high forecast error values (minimum: 5.84, 25th percentile: 6.54, 50th percentile: 6.68, 75th percentile: 6.79, maximum: 7.47), whereas cases with d = 1 (minimum: 2.45, 25th percentile: 3.11, 50th percentile: 3.30, 75th percentile: 3.49, maximum: 4.01), d = 7 (minimum: 2.82, 25th percentile: 3.13, 50th percentile: 3.23, 75th percentile: 3.36, maximum: 4.11), and d = 28 (minimum: 4.47, 25th percentile: 4.92, 50th percentile: 5.23, 75th percentile: 5.43, maximum: 6.31) demonstrate significantly improved results. Similar trends are observed in all other cases. Moreover, a comparison of the error values across different Differencing Operator cases (d = 1, 7, 28) highlights that the most optimal results are achieved when d = 7.

To accurately evaluate the impact of the Differencing Operator, the next step focuses on calculating the ratio of the error rate between the differencing cases (d = 1, 7, 28) and the original data case (d = 0). Figure 8 displays a boxplot of the error rate ratio for the GBDT, XGBoost, LightGBM, and CatBoost models applied to the New South Wales and Queensland data. The statistical values for each column in Fig. 8 are summarized in Table 5.

Fig. 8
figure 8

The error ratio between differencing order d of 1, 7, 28 and 0: (a) New South Wales, (b) Queensland

Full size image
Table 5 The descriptive statistics of error rate
Full size table

The results in Figs. 8 and Table 5 clearly demonstrate the fluctuation range of the error rate ratio for both the New South Wales and Queensland data. For the New South Wales data, the ratio of the error rate ranges from 0.36 to 0.68 for the minimum statistic, 0.46 to 0.75 for the 25th percentile, 0.48 to 0.78 for the median (50th percentile), 0.50 to 0.81 for the 75th percentile, and 0.59 to 0.93 for the maximum statistic. Similarly, for the Queensland data, the ratio ranges from 0.51 to 0.73 for the minimum statistic, 0.58 to 0.85 for the 25th percentile, 0.60 to 0.88 for the median, 0.62 to 0.92 for the 75th percentile, and 0.80 to 1.16 for the maximum statistic.

For the New South Wales data, all error ratios of the Differencing Operator (d = 1, 7, 28) to the original data (d = 0) are less than 1. However, in the Queensland dataset, there are instances where the ratio 28/0 (d = 28/d = 0) exceeds 1, as detailed in Tables 6 below. Table 6 reveals 10 instances in the GBDT model, 12 instances in the XGBoost model, 5 instances in the LightGBM model, and 14 instances in the CatBoost model where the ratios are greater than 1. Considering the total of 2000 combinations of hyperparameters (lr, md, and ne) for each model, the number of cases where the ratio exceeds 1 is exceptionally small. This indicates that the utilization of the Differencing Operator (d = 1, 7, 28) can effectively enhance the precision of the forecasting process for ensemble algorithms. The data analysis also demonstrates that the differencing order of 7 may result in the smallest error ratio compared to the differencing orders of 1 or 28 for most values of the min, 25th, 50th, 75th, and max statistics.

Table 6 The list of ratios 28/0 greater than 1 for the Queensland data
Full size table

In conclusion, the results confirm that the utilization of the Differencing Operator (d = 1, 7, 28) has a positive impact on reducing errors and improving the accuracy of the forecasting process for ensemble algorithms. The analysis also suggests that a differencing order of 7 tends to yield the smallest error ratio compared to orders of 1 or 28 for various statistical values.

4.3 Evaluation of Execution Time

Figure 9 illustrates a boxplot representing the execution time for different differencing orders (d = 0, 1, 7, 28) corresponding to the GBDT, XGBoost, LightGBM, and CatBoost models applied to the New South Wales and Queensland data cases. Table 7 presents the statistical values for each set of differencing orders (d = 0, 1, 7, 28) as shown in Fig. 9.

Fig. 9
figure 9

The execution time for differencing orders of 0, 1, 7, and 28: (a) New South Wales, (b) Queensland

Full size image
Table 7 The descriptive statistics of execution time
Full size table

A detailed analysis of Fig. 9 and Table 7 reveals that the application of the Differencing Operator (d = 1, 7, 28) does not significantly increase the execution time of the program compared to the case where the original data (d = 0) is used. For example, let's consider the GBDT network with the New South Wales dataset. The results presented in Fig. 9 and Table 7 show that the execution time statistic values for the original data case (d = 0) are as follows: minimum: 0.12 s, 25th percentile: 0.55 s, 50th percentile: 0.95 s, 75th percentile: 1.57 s, and maximum: 3.14 s. These values remain largely unchanged when compared to the cases of d = 1 (minimum: 0.14, 25th percentile: 0.58, 50th percentile: 0.99, 75th percentile: 1.62, and maximum: 3.19), d = 7 (minimum: 0.14, 25th percentile: 0.57, 50th percentile: 0.98, 75th percentile: 1.59, and maximum: 3.15), and d = 28 (minimum: 0.13, 25th percentile: 0.55, 50th percentile: 0.94, 75th percentile: 1.53, and maximum: 3.13). And all other cases have similar results.

In addition, Fig. 10 presents a boxplot illustrating the execution time ratios between the Differencing Operator (d = 1, 7, 28) and the original data case (d = 0). The corresponding statistical values for each column in Fig. 10 are summarized in Table 8. For instance, in the 50th percentile statistical case (median values), the error ratio of the execution time with the Differencing Operator to that with the original data ranges from [0.99 to 1.20] for all New South Wales data cases. Similarly, for the Queensland data, the ratio fluctuates within the range of [0.99–1.18]. These findings indicate that there is no significant difference in the execution time when considering differencing orders of 1, 7, or 28 for the GBDT, XGBoost, LightGBM, and CatBoost models, respectively. Figures 10 and Table 8 consistently demonstrate that the execution time remains largely unchanged when the Differencing Operator is applied.

Fig. 10
figure 10

The time ratio between differencing order of 1, 7, 28 and 0: (a) New South Wales, (b) Queensland

Full size image
Table 8 The descriptive statistics of time ratio
Full size table

5 Conclusion

In this study, the author suggests the combination of the input data Differencing Operator with the Sliding Window procedure for ensemble learning algorithms. The objective was to assess the error rate and execution time for the GBDT, XGBoost, LightGBM, and CatBoost models in the forecasting process. Extensive exploration of hyperparameter combinations, such as learning rate, max depth, and number of estimations, was conducted to evaluate the effectiveness of the proposed approach. The results clearly demonstrated that implementing the input data difference approach (d = 1, 7, 28) led to a significant reduction in prediction error. Furthermore, it was observed that the execution time only experienced a slight increase when employing the data partitioning approach. In conclusion, the integration of the Differencing Operator into the Sliding Window Procedure for ensemble learning presents a promising solution to address technical challenges, particularly in the domain of peak load forecasting. This result lays the foundation for the author to further develop the proposed algorithm toward various machine learning models, particularly deep learning models. Additionally, it enables the extension of the algorithm’s application in diverse types of time series data, such as financial and weather data. Moreover, exploring its effectiveness in real-time data processing or under different operational conditions presents an important challenge.