1 Introduction

Heat transfer through porous media is a subject of considerable interest and importance in various engineering and industrial applications [1,2,3,4]. The ability to control and enhance heat transfer in such systems is crucial for optimizing thermal management processes. Effective heat transfer through porous media and fluid dynamics enables efficient temperature regulation, which is essential for various industrial applications, such as cooling of electronic devices, heat exchangers, and thermal energy storage systems. Moreover, understanding and optimizing heat transfer mechanisms in porous media and fluid dynamics can lead to improved system performance, reduced energy consumption, and increased overall efficiency. By harnessing the principles of heat transfer and fluid dynamics, engineers can design and develop innovative solutions for thermal management, leading to breakthroughs in fields like aerospace, automotive, and renewable energy.

Porous media have been used in a wide range of applications, including material, aerospace, biological, and medical engineering, including fiber composites, packed beds, granular materials and foam [5]. A porous medium is described as any material with a solid matrix and connecting voids with occupied transport fluids [6]. By extending the heat transfer surface, the porous medium causes an increase in heat transfer. Additionally, the existence of ligaments [7] in comparison to the absence of a porous medium, increases the amount of heat transfer surface in an identical volume. Pressure, temperature, porosity, and packing structure are all factors that affect the thermal characteristics of porous media in addition to the inherent thermal properties and volume fraction of the different components [8]. The other contributing elements, which are specifically related to sediments, are mineralogy, gradation and packing structure; and physical inter-particle interaction between granules [9,10,11,12,13]. Heat transfer research on various types of fluids that contain metallic, nonmetallic, and CNT nanoparticles has sometimes focused on the fluid’s thermal conductivities [14,15,16,17]. Philip et al. [18] noticed a considerable increase in thermal conductivity of a nanofluid with magnetite particles with 6.7 nm on average in diameter when a magnetic field is applied. Another research [15] findings imply that well-dispersed nanoparticle-containing nanofluids do not significantly improve thermal conductivity, and it may have useful applications for creating a new class of thermally controllable nanofluids. Philip et al. [16] also describe a magnetically polarizable nanofluid with controllable thermal characteristics in detail by varying the nanofluids’ linear aggregation length from nano to micron scales. Besides, Wensel et al. [17] summarized their research and found that the thermal conductivity of heat transfer nanofluids including carbon nanotubes and metal oxide particles increases by 10% at very low percentage loadings of roughly 0.02 weight percent of each.

One of the techniques used to model the heat transfer variables is to use mono-domain ferromagnetic particles that are suspended in an inert carrier fluid to form ferrofluids. The particles, which are typically in the range of 10 nm in diameter, include surfactant coatings that have been adsorbed on them to maintain a stable suspension conditions [19]. Magnetic field is used in several areas containing nanofluids [20,21,22,23,24,25,26,27].

Other studies on the thermal conductivity of nanofluids, including ferrofluids [28] have been conducted, and the effects of various parameters such as nanoparticle and base fluid type have been investigated [29,30,31,32,33,34]. These findings show that the thermal conductivity of the base fluid is significantly increased due to the addition of nanoparticles. Pastoriza-Gallego et al. [35] conducted experimental research using synthesized magnetic nanoparticles (Fe3O4) and commercial (α-Fe2O3) to determine the thermal conductivity as a function of temperature and concentration and found that the improvement in thermal conductivity rises roughly linearly with concentration, peaking at 11% and 15% for magnetite and hematite nanofluids. As a result, ferrofluids, like ordinary nanofluids, can be utilized as working fluids of heat exchangers in a variety of industrial applications [36]. Ferrofluids have also been studied with and without an external magnetic field for forced convection heat transfer [37,38,39].

Recently, a few research studies have been conducted using a two-equation energy model to model the behavior of ferromagnetic fluid as the working fluid [40, 41]. There are still many configurations in which the interplay between magnetic and gravitational convection in porous media with thermal non-equilibrium needs to be addressed. These include the cases when the geometry and boundary conditions of the flow, as well as the location of the magnets, are not simple and conventional. In this context, the primary focus of this research is to assess the impact of key parameters on combined natural-magnetic heat transfer within the porous triple enclosure. These parameters include the magnetic and thermal Rayleigh numbers, the dimensionless convection coefficient at the two-phase interface, porosity coefficient, and Darcy number. By investigating these parameters, we aim to gain insights into how the magnetic field influences heat transfer and understand the interactions between the ferrofluid, solid matrix, and porous medium. In particular, the present study aims to answer the following questions: How does the presence of permanent magnets at the cavity top affect the convective behavior of ferrofluid within a porous enclosure? What is the influence of the porosity characteristics of the porous medium on the intensity of convection within the enclosure? How does thermal non-equilibrium between solid and liquid phases affect heat transfer within the porous cavity and what insights can it provide toward using one-equation models? What general implications do these findings have for heat transfer optimization within porous cavities and for the design of heat control devices?

2 Model Formulation and Problem Definition

In the present research, the natural convection of ferrofluid flowing through a Porous separated triple enclosure in the presence of permanent magnetic field is numerically studied. Two magnets are located in two separate parts of triple enclosure. Two energy non-equilibrium models were applied to model thermal transport through the porous media.

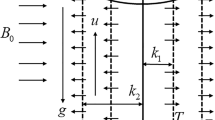
Figure 1 depicts the problem geometry and configuration. The lower and side walls of the porous separated triple enclosure are, respectively, receiving and repelling thermal energy at constant dimensional temperatures Th, and Tc. This temperature difference creates buoyancy forces due to density changes. The second external force acting on the ferrofluid particles is caused by the permanent magnetic field created by the two magnets. The details of the amount of force exerted by the permanent magnetic field on the ferrofluid particles are explained in the following sections. The two magnets are located at certain positions with coordinates (Sx1, Sy1), (Sx2, Sy2), while the remaining space of triple cavity is filled by porous material. The magnet walls, as well as the upper wall of the cavity, are adiabatic.

Fig. 1
figure 1

An schematic overview of a computational cross section and location of magnets

Full size image

The porous material is filled by a Newtonian ferrofluid. There are two mechanisms governing heat transfer through the porous material: conduction heat transfer via the solid matrix and natural-magnetic heat transfer via ferrofluid. As previously mentioned, these two mechanisms are modeled using the non-equilibrium two energy equations.

In brief, the governing equations include five equations: continuity equation, two-dimensional momentum equations, energy equation through ferrofluid and finally energy equation through the solid matrix, which are coupled:

$$ \frac{{\partial u^{ * } }}{{\partial x^{ * } }} + \frac{{\partial v^{ * } }}{{\partial y^{ * } }} = 0 $$
(1)
$$ \frac{{\rho_{ff} }}{{\varphi^{2} }}\left( {u^{ * } \frac{{\partial u^{ * } }}{{\partial x^{ * } }} + v^{ * } \frac{{\partial u^{ * } }}{{\partial y^{ * } }}} \right) = - \frac{{\partial p^{ * } }}{{\partial x^{ * } }} + \frac{{\mu_{ff} }}{\varphi }\left( {2\frac{{\partial^{2} u^{ * } }}{{\partial x^{*2} }} + \frac{\partial }{{\partial y^{ * } }}\left( {\frac{{\partial u^{ * } }}{{\partial y^{ * } }} + \frac{{\partial v^{ * } }}{{\partial x^{ * } }}} \right)} \right) - \frac{{\mu_{ff} u^{ * } }}{K} + ke_{{x^{*} }} $$
(2)
$$ \frac{{\rho_{ff} }}{{\varphi^{2} }}\left( {u^{ * } \frac{{\partial v^{ * } }}{{\partial x^{ * } }} + v^{ * } \frac{{\partial v^{ * } }}{{\partial y^{ * } }}} \right) = - \frac{{\partial p^{ * } }}{{\partial y^{ * } }} + \frac{{\mu_{ff} }}{\varphi }\left( {2\frac{{\partial^{2} v^{ * } }}{{\partial y^{2*} }} + \frac{\partial }{{\partial x^{ * } }}\left( {\frac{{\partial u^{ * } }}{{\partial y^{ * } }} + \frac{{\partial v^{ * } }}{{\partial x^{ * } }}} \right)} \right) - \frac{{\mu_{ff} v^{ * } }}{K} + ke_{{y^{ * } }} + \rho_{ff} g\beta_{ff} (T_{ff}^{ * } - T_{ff,c}^{ * } ) $$
(3)

By using the thermal non-equilibrium model in the porous medium, it is possible to consider the energy transfer through two phases of the porous medium separately, where these two media exchange heat at the contact points and surfaces.

Heat transfer in the porous medium includes two phases, solid and fluid, both of which participate in heat transfer through the porous medium. In the one- energy equation model, only average characteristics of these two mediums are considered, and the quality of heat transfer and thermal resistance at the interface of the two phases are not considered. In the two-energy equation model, the effect of the heat transfer coefficient on the interface of two phases is considered, and in fact, the contribution of heat transfer in the two phases is considered separately.

The energy equation in the ferrofluid phase that fills the holes of the porous medium is presented as follows:

$$ \frac{1}{\varphi }\left( {u^{ * } \frac{{\partial T_{ff}^{ * } }}{{\partial x^{ * } }} + v^{ * } \frac{{\partial T_{ff}^{ * } }}{{\partial y^{ * } }}} \right) = \alpha_{ff} \left( {\frac{{\partial^{2} T_{ff}^{ * } }}{{\partial x^{*2} }} + \frac{{\partial^{2} T_{ff}^{ * } }}{{\partial y^{*2} }}} \right) + \frac{{h_{ff - s} \left( {T_{p}^{ * } - T_{ff}^{ * } } \right)}}{{\varphi \left( {\rho c_{p} } \right)_{ff} }} - \mu_{0} T_{ff}^{ * } \left( {\frac{{\partial M^{*} }}{{\partial T^{ * } }}} \right)_{H} \left\{ {u\frac{{\partial H^{*} }}{\partial x} + v\frac{{\partial H^{*} }}{\partial y}} \right\} $$
(4)

In this equation, the term hff-s represents the interfacial heat transfer coefficient between the solid and liquid phases, which can change based on the properties of the two materials involved. This parameter also illustrates the degree of thermal equilibrium between two phases, such that thermal equilibrium is prevailing for high values of hff-s. It should be noted that the two-equation model applied in the present study provides a more accurate description of the interaction between the base fluid and the suspended particles, and can indicate the limitations in the one-equation model, which is only valid for high values of hff-s.

The energy equation related to the solid phase of the porous medium is also derived as follows [28, 42]:

$$ \left( {1 - \varphi } \right)k_{p} \left( {\frac{{\partial^{2} T_{p}^{ * } }}{{\partial x^{*2} }} + \frac{{\partial^{2} T_{p}^{ * } }}{{\partial y^{*2} }}} \right) + h_{ff - s} \left( {T^{ * }_{ff} - T^{ * }_{p} } \right) = 0 $$
(5)

The Kelvin force vector (\({\text{ke}}\)) on a magnetic fluid that is exposed to a permanent magnetic field is calculated using two parts, the magnetic intensity,\({\text{H}}^{ * }\), and the magnetization,\({\text{M}}^{ * }\):

Components of Kelvin force vector, \(\left( {{\text{ke}}_{{x^{ * } }} ,{\text{ke}}_{{y^{ * } }} } \right)\), can be calculated using the following relation:

$$ {\text{ke}} = (ke_{x} ,ke_{y} ) = \mu_{0} ({\text{M}}^{ * } {.}\nabla ){\text{H}}^{ * } $$
(6)

Magnetocaloric heating is the last term at right hand of energy equation which shows the energy production arises from presence of permanent magnetic field.

Here, two variables related to permanent magnetic field including the magnetization \(M^{ * }\) and the magnetic intensity \(H^{ * }\) should be calculated to model the phenomenon.

The Langevin function [43,44,45] (Ashouri et al., 2010; Ashouri & Behshad Shafii, 2017; Odenbach & Thurm, 2002) presents a correlation for the magnetization of the ferrofluid:

$$ M^{*} = M_{s}^{*} \left( {\coth \left( {\frac{{\mu_{0} M_{s}^{*} H^{*} }}{{NB_{c} T_{ff}^{{}} }}} \right) - \frac{{NB_{c} T_{ff}^{{}} }}{{\mu_{0} M_{s}^{*} H^{*} }}} \right) $$
(7)

The Langevin function is conventionally used to model the magnetization of the ferrofluid as a function of its temperature due to the permanent magnet, leading to the Kelvin forces presented in Eq. (6).

In a situation where the computational domain can be assumed to be free of ferromagnetic materials, the magnetic permeability can be assumed to be constant and based on this, for two-dimensional magnet with square cross section, the strength of the magnetic field can be presented independently in two dimensions of Cartesian coordinates as follows:

$$ \begin{aligned} H_{x}^{ * } = \frac{{B_{r} }}{{4\pi \mu_{0} }}\left\{ {\ln \left[ {1 + \frac{{(x^{ * } - s_{xi}^{ * } + {{h^{ * } } \mathord{\left/ {\vphantom {{h^{ * } } 2}} \right. \kern-0pt} 2})^{2} }}{{(y^{ * } - s_{yi}^{ * } - {{h^{ * } } \mathord{\left/ {\vphantom {{h^{ * } } 2}} \right. \kern-0pt} 2})^{2} }}} \right] - \ln \left[ {1 + \frac{{(x^{ * } - s_{xi}^{ * } - {{h^{ * } } \mathord{\left/ {\vphantom {{h^{ * } } 2}} \right. \kern-0pt} 2})^{2} }}{{(y^{ * } - s_{yi}^{ * } - {{h^{ * } } \mathord{\left/ {\vphantom {{h^{ * } } 2}} \right. \kern-0pt} 2})^{2} }}} \right]} \right.\hfill \\ \left. {\quad + \ln \left[ {1 + \frac{{(x^{ * } - s_{xi}^{ * } - {{h^{ * } } \mathord{\left/ {\vphantom {{h^{ * } } 2}} \right. \kern-0pt} 2})^{2} }}{{(y^{ * } - s_{yi}^{ * } + {{h^{ * } } \mathord{\left/ {\vphantom {{h^{ * } } 2}} \right. \kern-0pt} 2})^{2} }}} \right] - \ln \left[ {1 + \frac{{(x^{ * } - s_{xi}^{ * } + {{h^{ * } } \mathord{\left/ {\vphantom {{h^{ * } } 2}} \right. \kern-0pt} 2})^{2} }}{{(y^{ * } - s_{yi}^{ * } + {{h^{ * } } \mathord{\left/ {\vphantom {{h^{ * } } 2}} \right. \kern-0pt} 2})^{2} }}} \right]} \right\}\hfill \\ \end{aligned} $$
$$ \begin{aligned} H_{y}^{ * } & = \frac{{B_{r} }}{{2\pi \mu_{0} }}\left\{ {\arctan \left[ {\frac{{x^{ * } - s_{xi}^{ * } + {{h^{ * } } \mathord{\left/ {\vphantom {{h^{ * } } 2}} \right. \kern-0pt} 2}}}{{y^{ * } - s_{yi}^{ * } - {{h^{ * } } \mathord{\left/ {\vphantom {{h^{ * } } 2}} \right. \kern-0pt} 2}}}} \right] - \arctan \left[ {\frac{{x^{ * } - s_{xi}^{ * } - {{h^{ * } } \mathord{\left/ {\vphantom {{h^{ * } } 2}} \right. \kern-0pt} 2}}}{{y^{ * } - s_{yi}^{ * } - {{h^{ * } } \mathord{\left/ {\vphantom {{h^{ * } } 2}} \right. \kern-0pt} 2}}}} \right]} \right. \\ & \quad + \left. {\arctan \left[ {\frac{{x^{ * } - s_{xi}^{ * } - {{h^{ * } } \mathord{\left/ {\vphantom {{h^{ * } } 2}} \right. \kern-0pt} 2}}}{{y^{ * } - s_{yi}^{ * } + {{h^{ * } } \mathord{\left/ {\vphantom {{h^{ * } } 2}} \right. \kern-0pt} 2}}}} \right] - \arctan \left[ {\frac{{x^{ * } - s_{xi}^{ * } + {{h^{ * } } \mathord{\left/ {\vphantom {{h^{ * } } 2}} \right. \kern-0pt} 2}}}{{y^{ * } - s_{yi}^{ * } + {{h^{ * } } \mathord{\left/ {\vphantom {{h^{ * } } 2}} \right. \kern-0pt} 2}}}} \right]} \right\} \\ \end{aligned} $$
(8)

The subscript i refers to the number of the magnet (magnet#1 and magnet#2).

By performing a series of operations and simplifications on dimensional equations (Eq. (1)-(5)), they can be converted into the final dimensionless form:

Dimensionless form of Eq. (1):

$$ \frac{\partial u}{{\partial x}} + \frac{\partial v}{{\partial y}} = 0 $$
(9)

Dimensionless form of Eq. (2):

$$ \begin{aligned} \frac{1}{{\varphi^{2} }}\left( {u\frac{\partial u}{{\partial x}} + v\frac{\partial u}{{\partial y}}} \right) & = - \frac{\partial p}{{\partial x}} + \frac{2\Pr }{\varphi }\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{\Pr }{\varphi }\frac{\partial }{\partial y}\left( {\frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}}} \right) \\ & \quad - \frac{\Pr }{{Da}}\,u + \Pr {\text{Ra}}_{m} \frac{M}{H}\left( {H_{x} \frac{{\partial H_{x} }}{\partial x} + H_{y} \frac{{\partial H_{y} }}{\partial x}} \right) \\ \end{aligned} $$
(10)

Dimensionless form of Eq. (3):

$$ \begin{aligned} \frac{1}{{\varphi^{2} }}\left( {u\frac{\partial v}{{\partial x}} + v\frac{\partial v}{{\partial y}}} \right) = & - \frac{\partial p}{{\partial y}} + \frac{\Pr }{\varphi }\frac{\partial }{\partial x}\left( {\frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}}} \right) + \frac{2\Pr }{\varphi }\frac{\partial }{\partial y}\left( {\frac{\partial v}{{\partial y}}} \right) \\ & \quad - \frac{\Pr }{{Da}}\,v + \Pr {\text{Ra}}_{m} \frac{M}{H}\left( {H_{x} \frac{{\partial H_{x} }}{\partial Y} + H_{y} \frac{{\partial H_{y} }}{\partial y}} \right) + \Pr {\text{Ra}}T \\ \end{aligned} $$
(11)

Dimensionless form of Eq. (4):

$$ \begin{aligned} u\frac{{\partial \theta_{ff} }}{\partial x} + v\frac{{\partial \theta_{ff} }}{\partial y} & = \varphi \left( {\frac{{\partial^{2} \theta_{ff} }}{{\partial x^{2} }} + \frac{{\partial^{2} \theta_{ff} }}{{\partial y^{2} }}} \right) - \varphi {\text{Ma}}\,{(}\theta_{ff} + \varepsilon_{T} )\left( {\frac{\partial M}{{\partial \theta_{ff} }}} \right)_{H} \\ & \quad \left\{ {u\frac{\partial H}{{\partial x}} + v\frac{\partial H}{{\partial y}}} \right\} + H_{ff - s} \left( {\theta_{p} - \theta_{ff} } \right) \\ \end{aligned} $$
(12)

Dimensionless form of Eq. (5):

$$ \left( {\frac{{\partial^{2} \theta_{p} }}{{\partial x^{2} }} + \frac{{\partial^{2} \theta_{p} }}{{\partial y^{2} }}} \right) + H_{ff - s} k_{r} \left( {\theta_{ff} - \theta_{p} } \right) = 0 $$
(13)

Finally, this is the final form of the characteristic equations that have been solved in order to model the problem. Here, dimensionless variables \(H_{ff - s} = \frac{{h_{ff - s} w^{2} }}{{k_{ff} }}\), \(y = \frac{{y^{ * } }}{{w^{ * } }}\), \(x = \frac{{x^{ * } }}{{w^{ * } }}\), \(\alpha_{ff} = \frac{{k_{ff} }}{{(\rho C_{p} )_{ff} }}\), \(u = \frac{{u^{ * } w^{ * } }}{{\alpha_{ff} }}\), \(v = \frac{{v^{ * } w^{ * } }}{{\alpha_{ff} }}\),\(H_{x} = \frac{{H_{x}^{*} \mu_{0} }}{{B_{r} }}\), \(H_{y} = \frac{{H_{y}^{*} \mu_{0} }}{{B_{r} }}\), \(H = \frac{{H^{*} \mu_{0} }}{{B_{r} }}\), \(M = \frac{{M^{*} }}{{M_{s} }}\), \(p = \frac{{p^{ * } w^{ * 2} }}{{\rho_{ff} \alpha_{ff}^{2} }}\), \(\theta_{ff} = \frac{{T_{ff}^{ * } - T^{ * }_{ff,c} }}{{T^{ * }_{ff,h} - T^{ * }_{ff,c} }}\), \(\theta_{p} = \frac{{T_{p}^{ * } - T^{ * }_{p,c} }}{{T^{ * }_{p,h} - T^{ * }_{p,c} }}\) are used to derive the final equations.

Key dimensionless and meaningful parameters which appear in the non-dimensional form of the governing equations are Darcy number \(\left( {{\text{Da}} = \frac{K}{{w^{{*^{2} }} }}} \right)\),, thermal conductivity ratio of porous medium to fluid \(\left( {k_{r} = \frac{{k_{ff} }}{{k_{s} \left( {1 - \varphi } \right)}}} \right)\), temperature number \(\left( {\varepsilon_{T} = \frac{{T_{ff,c}^{*} }}{{T_{ff,h}^{*} - T_{ff,c}^{*} }}} \right)\), thermomagnetic number \(\left( {{\text{Ma}} = \frac{{B_{r} M_{s} }}{{\rho C_{p} (T_{ff,h}^{*} - T_{ff,c}^{*} )}}} \right)\), nondimensional magnetization (M*), Prandtl number \(\left( {\Pr = \frac{\mu }{\rho \alpha }} \right)\), magnetic Rayleigh \(\left( {{\text{Ra}}_{m} = \frac{{B_{r} M_{s} w^{{*^{2} }} }}{\eta \alpha }} \right)\), thermal Rayleigh \(\left( {{\text{Ra}}_{T} = \frac{{\rho g\beta (T_{ff,h}^{*} - T_{ff,c}^{*} )w^{{*^{3} }} }}{\mu \alpha }} \right)\).

The dimensionless magnetization is calculated as follows.

$$ M = \coth \left( {\beta H} \right) - \frac{1}{\beta H},\,\beta = \frac{{\beta_{c} }}{{1 + T_{ff} T_{pp} }},\,\beta_{c} = \frac{{B_{r} M_{s} }}{{Nk_{B} T_{ff,c} }},\,T_{pp} = \frac{{T_{ff,h} - T_{ff,c} }}{{T_{ff,c} }} $$
(14)

The non-dimensional form of the magnetic intensity vector is derived as the following forms [43, 46]:

$$ {\text{H}} = (H_{x} ,H_{y} ) $$
$$ \begin{aligned} H_{x} & = \frac{{B_{r} }}{{4\pi \mu_{0} }}\left\{ {\ln \left[ {1 + \frac{{(x - s_{xi}^{{}} + {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2})^{2} }}{{(y - s_{yi}^{{}} - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2})^{2} }}} \right] - \ln \left[ {1 + \frac{{(x - s_{xi}^{{}} - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2})^{2} }}{{(y - s_{yi}^{{}} - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2})^{2} }}} \right]} \right. \\ & \quad \left. { + \ln \left[ {1 + \frac{{(x - s_{xi}^{{}} - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2})^{2} }}{{(y - s_{yi}^{{}} + {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2})^{2} }}} \right] - \ln \left[ {1 + \frac{{(x - s_{xi}^{{}} + {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2})^{2} }}{{(y - s_{yi}^{{}} + {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2})^{2} }}} \right]} \right\} \\ \end{aligned} $$
$$ H_{y} = \frac{{B_{r} }}{{2\pi \mu_{0} }}\left\{ \begin{gathered} \arctan \left[ {\frac{{x - s_{xi} + {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2}}}{{y - s_{yi} - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2}}}} \right] - \arctan \left[ {\frac{{x - s_{xi} - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2}}}{{y - s_{yi} - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2}}}} \right] \hfill \\ + \arctan \left[ {\frac{{x - s_{xi} - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2}}}{{y - s_{yi} + {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2}}}} \right] - \arctan \left[ {\frac{{x - s_{xi} + {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2}}}{{y - s_{yi} + {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2}}}} \right] \hfill \\ \end{gathered} \right\},\,h = {{h^{ * } } \mathord{\left/ {\vphantom {{h^{ * } } w}} \right. \kern-0pt} w} $$
(15)

At the end, the dimensionless boundary conditions can be presented to put imposed conditions on the boundary of computational domain:

On the bottom wall

$$ \theta_{p} = 1, \, \theta_{ff} = 1, \, u = v = 0 \, \left\{ \begin{gathered} y = 0.1, \, 0.45 \le x \le 0.55 \hfill \\ y = 0, \, \left\{ \begin{gathered} {0} \le x \le 0.45 \hfill \\ 0.55 \le x \le 1 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right. $$
$$ \theta_{p} = 1, \, \theta_{ff} = 1, \, u = v = 0 \, x = 0.45, \, 0 \le y \le 0.1 \, $$
$$ \theta_{p} = 1, \, \theta_{ff} = 1, \, u = v = 0 \, x = 0.55, \, 0 \le y \le 0.1 \, $$

On the side walls

$$ \theta_{p} = 0, \, \theta_{ff} = 0, \, u = v = 0 \, x = 0, \, 0 \le y \le 1 $$
$$ \theta_{p} = 0, \, \theta_{ff} = 0, \, u = v = 0 \, x = 1, \, 0 \le y \le 1 $$

On the upper wall

$$ \frac{{\partial \theta_{p} }}{\partial y} = 0, \, \frac{{\partial \theta_{ff} }}{\partial y} = 0, \, u = v = 0 \, \, \left\{ \begin{gathered} y = 0.9, \, 0.45 \le x \le 0.55 \hfill \\ y = 1, \, \left\{ \begin{gathered} {0} \le x \le 0.45 \hfill \\ 0.55 \le x \le 1 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right. $$
$$ \frac{{\partial \theta_{p} }}{\partial y} = 0, \, \frac{{\partial \theta_{ff} }}{\partial y} = 0, \, u = v = 0 \, \left\{ \begin{gathered} x = 0.45, \, 0.9 \le y \le 1 \hfill \\ x = 0.55, \, 0.9 \le y \le 1 \hfill \\ \end{gathered} \right. $$
(16)

The local Nusselt number has been evaluated over the bottom boundary as depicted by redline in Fig. 1 using the following formula:

$$ Nu_{ff}^{*} = - \varphi \left( {\frac{{\partial \theta_{ff} }}{\partial n}} \right) $$
$$ Nu_{p}^{*} = - \frac{1}{{k_{r} }}\left( {\frac{{\partial \theta_{p} }}{\partial n}} \right) $$
(17)

n is normal direction on the hot bottom wall (θ = 1).

the average value can be calculated by integration of local Nusselt number over the bottom boundary:

$$ \begin{aligned} Nu_{{ff}} & = - \varphi \left(\frac{1}{{0.45}}\int\nolimits_{0}^{{0.45}} {\frac{{\partial \theta _{{ff}} }}{{\partial y_{{y = 0}} }}} dx + \frac{1}{{0.1}}\int_{{0.45}}^{{0.55}} {\left. {\frac{{\partial \theta _{{ff}} }}{{\partial y}}} \right|_{{y = 0.1}} dx} \right.\\ & \quad \left. + \frac{1}{{0.45}}\int_{{0.55}}^{1} {\left. {\frac{{\partial \theta _{{ff}} }}{{\partial y}}} \right|_{{y = 0}} dx} \right. \\ & \quad \left. { + \frac{1}{{0.45}}\int_{{0.55}}^{1} {\left. {\frac{{\partial \theta _{{ff}} }}{{\partial x}}} \right|_{{x = 0.45}} dy} + \frac{1}{{0.45}}\int_{{0.55}}^{1} {\left. {\frac{{\partial \theta _{{ff}} }}{{\partial x}}} \right|_{{x = 0.55}} dy} } \right) \\ \end{aligned} $$
$$ \begin{aligned} Nu_{s} & = - \frac{1}{{k_{r} }}\left( \frac{1}{0.45}\int\nolimits_{0}^{0.45} {\left. {\frac{{\partial \theta_{p} }}{\partial y}} \right|_{y = 0} dx + \frac{1}{0.1}} \int\nolimits_{0.45}^{0.55} {\left. {\frac{{\partial \theta_{p} }}{\partial y}} \right|_{y = 0.1} dx}\right. \\& \quad \left.+ \frac{1}{0.45}\int\nolimits_{0.55}^{1} {\left. {\frac{{\partial \theta_{p} }}{\partial y}} \right|_{y = 0} dx} \right. \\ & \quad \left. { + \frac{1}{0.45}\int\nolimits_{0.55}^{1} {\left. {\frac{{\partial \theta_{p} }}{\partial x}} \right|_{x = 0.45} dy} + \frac{1}{0.45}\int\nolimits_{0.55}^{1} {\left. {\frac{{\partial \theta_{p} }}{\partial x}} \right|_{x = 0.55} dy} } \right) \\ \end{aligned} $$
(18)

3 Numerical Solution Process

In order to solve the characteristic partial differential equations, the finite difference method, which is one of the most common and reliable methods of computational fluid dynamics, has been used. As mentioned above, the computational domain is divided into a network of discrete points and nodes. Then the differential equations are written and solved for each node.

an approximate solution is obtained over each subdomain from divided the computational domain. After that, a general solution can be obtained through integration of partial solutions was achieved in order to ensure continuity at the boundaries. The reader can refer to reference [47, 48] for more details.

Producing an optimal network that does not affect the results and at the same time does not increase the computational cost is one of the important stages of numerical calculations. In this study, several networks with different number of elements have been investigated. As Table 1 shows, with the increase in the number of network nodes and the fact that the network cells are smaller, there has been no significant change in the results. Therefore, the network with the number of 15,200 nodes has been used which are finer near solid boundaries as a computing grid in the current study.

Table 1 Grid independent study at Ra = 1e5, Ram = 1e7, Pr = 5, Da = 1e-4
Full size table

In order to certify the correctness of the numerical solution, the outcomes have been compared with the published research works done by Baytas & Pop [49] and Ashouri & Shafii [44]. Table 2 shows the validation of the average Nusselt number derived from the numerical study and the study done by Baytas & Pop [49]. Also, another comparison with data performed by Ashouri & Shafii [44] has been presented in Table 3. There is a very good agreement between the present results with both of different sources.

Table 2 Comparison between the average Nusselt numbers of both porous media phases with data extracted from Baytas and Pop work (Baytas & Pop, 2002) for Ra = 1e3
Full size table
Table 3 Validation of average Nusselt number for present work with data extracted by Ashouri and Shafii [44] at thifrent magnet size and magnetic Rayleigh number
Full size table

4 Results and Discussion

Two-Energy equation form has been applied to model heat transfer inside a porous separated triple enclosure exposed to permanent magnetic field. The impact of key parameters including magnetic (Ram = 0 − 1e7) and thermal Rayleigh (Ra = 1e3 − 1e6) numbers, dimensionless convection coefficient at two-phase interface (Hff-s = 50–5000), Porosity coefficient (ε = 0.4–0.9) and Darcy number (Da = 1e-5 − 1e-3), on combined natural-magnetic heat transfer is analyzed.

4.1 Analysis

The flow streamlines as well as the isotherms for the solid matrix and the ferrofluid are depicted in Fig. 2 for different values of Darcy number Da and porosity φ. First, for Da = 1e-5 and φ = 0.4, one recirculation zone appears in each part of the cavity, in the counterclockwise direction in the left part, and the clockwise direction in the right one. The isothermal contours reveal that the heat transfer in the solid matrix is dominated by conduction, and that there is mostly a thermal equilibrium between the solid matrix and the ferrofluid, as their isotherms are adjacent.

Fig. 2
figure 2

Variation of streamlines inside porous media pores (left side) and isothermal lines of both ferrofluid (solid blue lines) and solid matrix (dash orange lines) phases (right side) respect to porosity coefficient (φ) and Darcy number (Da) for Ra = 1e3 and 1e6

Full size image

Increasing Da to 1e-3 strongly intensifies the ferrofluid circulations as can be seen from the values of the stream function. The recirculation zone that was initially observed for Da = 1e-5 in each half is split into two vortices. In the left half, there is a counterclockwise vortex resulting from the natural convection due to the temperature difference between the hot and cold walls, and another clockwise vortex resulting from the temperature difference between the hot ferrofluid and the colder one present in the middle partition. A symmetrical behavior is observed in the right half of the enclosure, but the vortices are moving in the opposite direction compared to the left half. The intensification of the flow is due to the raise of the permeability for higher Da, as there is more ease for the ferrofluid to move in the porous medium when Da is increased. This also affects the isotherms of the ferrofluid, which tend to be disturbed in the middle of the cavity due to the enhanced mixing of the flow. The non-equilibrium between the ferrofluid and solid parts of the porous medium is more apparent here, as the stronger flow of the ferrofluid tend to increase the discrepancy between the two parts and enhance the interfacial heat transfer. Comparing the first and third rows of Fig. 2 indicates that raising φ from 0.4 to 0.9 while keeping Da = 1e-5 has a limited effect on the flow patterns and the isothermal contours. Therefore, even if the porosity is increased, the flow circulation remains inhibited by the low permeability and, consequently, the porosity impact becomes negligible.

Fig. 3 shows the 3D bar variation of average Nusselt number for the solid matrix Nuavg,s and for the ferrofluid Nuavg,ff as functions of Da and φ, for two values of magnetic Rayleigh number Ram = 0 and Ram = 1e7. For Ram = 0, in the absence of magnetic effects, it can be seen that increasing Da raises Nuavg-ff for all the values of φ.

Fig. 3
figure 3figure 3

3D Bar variation of average Nusselt number for ferrofluid phase (left side) and for solid matrix (right side) respect to Da and ε at Ra = 5e5

Full size image

This is due to the fact that the ferrofluid circulation is more facilitated for higher permeability, which leads to more mixing and enhanced heat transfer. Similarly, for a fixed Da, increasing the porosity φ also leads to higher values of Nuavg-ff. The effect of φ on Nuavg-ff is more apparent for high Da. For indication, around 100% increase in Nuavg-ff is observed when φ is increased from 0.4 to 0.9 for Da = 1e-3. Regarding the solid matrix, a small change is observed in the variation of Nuavg-ss with Da when Hff-s = 50. On the other hand, increasing Hff-s to 5000 reduces Nuavg-ff and raises Nuavg-ss, and also enhances the impact of Da on the variation of Nuavg-s. Namely, a 25% rise on average is seen in Nuavg-s is found when Hff-s is raised from 50 to 5000 for Da = 1e-5. Moreover, around 41% increase in Nuavg-s is observed when Da is raised from 1e-5 to 1e-3 for Havg-s = 5000, while almost no change was seen in Nuavg-ss when Da was varied for Hff-s = 50. Similar observations to the aforementioned ones are found for Ram = 1e7.

Figure 4 illustrates the isothermal contours and the flow patterns in the enclosure for different values of Ram and of the heat transfer at the pore coefficient Hff-s, for two values of thermal Rayleigh number Ra = 1e3 and Ra = 1e6. The cases Ram = 0 correspond to the absence of magnetic effects and, thus, only natural convective effects are present. In these cases, a large recirculation zone appears in each half of the enclosure, in the counterclockwise direction on the left and the clockwise direction on the right. In fact, as the ferrofluid at the bottom of the enclosure absorbs heat, it undergoes an increase in temperature, causing a decrease in its density due to the thermal expansion (Eq. 3). This decrease in density makes the heated ferrofluid less dense than the surrounding cooler ferrofluid. As a result, it tends to rise upward due to buoyancy forces, forming convective cells within the enclosure [50,51,52]. Conversely, the cooler ferrofluid at the top of the enclosure, being denser, tends to sink toward the bottom wall. This movement completes the convective flow loop, with heated ferrofluid rising and cooler ferrofluid sinking, thereby establishing a continuous circulation pattern. Therefore, the observed convective flow in the ferrofluid can be attributed to the buoyancy effects resulting from the density differences induced by heating at the bottom wall. A smaller vortex is observed in each half, in a direction opposite to the large recirculation zone, due to the temperature difference between the ferrofluid in each half and the ferrofluid in the middle partition. For Ra = 1e3, the flow circulation intensity is low as the convective effects are relatively weak. For this reason, the heat transfer is dominated by conduction in both the ferrofluid and the solid matrix. Also, a thermal equilibrium is observed between the ferrofluid and the solid, even when Hff-s is changed for 50–5000, as the isotherms of the two phases are almost adjacent through the cavity. In both cases, the weak convective effects and the low flow intensity reduce the impact of the ferrofluid circulation and the resulting interfacial heat transfer with the solid matrix. On the other hand, for Ra = 1e5, the flow patterns remain similar, but the flow intensity is considerably enhanced, due to the increase of the relative importance of the buoyancy effects with respect to the viscous resistance. In addition, the effect of Hff-s is more apparent. As can be seen, setting Hff-s to be equal to 50 clearly disturbs the thermal equilibrium which is present when Hff-s = 5000.

Fig. 4
figure 4figure 4

Variation of streamlines inside porous media pores (left side) and isothermal lines of both ferrofluid (solid blue lines) and solid matrix (dash orange lines) phases (right side) respect to magnetic Rayleigh numberand convection coeffiecent at pores interface for Ra = 1e3 and 1e6 at ε = 0.5, Da = 1e-2, Mnf = 100, Ra = 5e5

Full size image

In the zones away from the hot and cold walls, where the convective effects are most dominant, the ferrofluid isotherms clearly deviate from the solid matrix ones for Hff-s = 50. As for the effect of Ram, its importance lies in the thermomagnetic convection that may occur due to the magnetic field resulting from the magnets. In fact, both magnetic and buoyancy-driven convection occurs due to the temperature gradient in the fluid. The latter occurs when the hotter fluid has a lower density than the colder one, it moves upward and gets replaced by the colder one. The magnetic convection, on the other hand, is related to the magnetization of the fluid. The cold ferrofluid, which has a higher magnetization, is attracted toward the region with higher magnetic ferrofluid intensity that it located near the magnets. Conversely, the hot ferrofluid moves to replace the cold ferrofluid that moved, and magnetic convection takes place. Based on the position of the magnets, the magnetic convection can either help or inhibit the gravitational natural convection. In the case being studied here, as the magnets are located at the top, the cold ferrofluid tends to move upward, such that the magnetic convection and the gravitational one are in opposite direction. For this reason, raising Ram tends to diminish the gravitational convection effects. For Ra = 1e3, the thermomagnetic convection completely dominates the already weak gravitational convection. The large recirculation zones shift their direction to become clockwise in the left half and counterclockwise in the right one. On the other hand, for Ra = 1e6, the gravitational convection remains dominant when Ram is raised from 0 to 1e7, but the intensity of circulation is weakened by the gravitational convection. For both values of Ra, and for Ram = 1e7, a thermal equilibrium between the ferrofluid and the solid matrix is observed, because the interfacial coefficient Hff-s is set at the high value of 5000.

The variations of Nuavg, s and Nuavg, ff as functions of Hff-s are plotted in Fig. 5 for various values of Ram. First, it is seen for Ra = 1e3 that both values of Nu increase with Ram and are maximum for Ram = 1E7. This is due to the fact that the magnetic convection is the dominant mode of heat transfer in this case, and the effects of this convection are more important for higher Ram. However, for the values considered here, the effect of Ram is very small, as only an increase of 0.5% and 0.9% are observed, respectively, in Nuavg, ff and Nuavg, s when Ram is raised from 0 to 1e7.

Fig. 5
figure 5

Variation of average Nusselt number for ferrofluid phase (left side) and solid matrix (right side) respect to convection coefficiemnt at pores interface (Hff-s) at different magnetic and thermal Rayleigh number

Full size image

The effect of Ram on the values of Nuavg is also small for Ra = 1e6, but in this case, raising Ram tends to reduce Nuavg. As discussed previously, the gravitational convection is dominant here, and the magnetic convection is acting in the opposite direction, such that raising the effects of the latter by increasing Ram diminishes the overall convective heat transfer. It is also observed that in all the cases, raising Hff-s increases Nuavg-s and reduces Nuavg-ff. Indeed, the ferrofluid undergoes convective heat transfer as well as an interfacial heat transfer with solid matrix. Raising the H enhances the heat transmission from the solid to the ferrofluid. Consequently, the temperature gradient in the solid increases, such that Nuavg, s rises, while the opposite occurs for Nuavg, ff. This aspect is more apparent when the flow intensity and convective effects are important, i.e., for Ra = 1e6. Namely, an average of 20% reduction in Nuavg-ff is found when Hff-s is raised from 0 to 5000, for Ra = 1e6.

4.2 Discussion

The results of the numerical simulation clearly indicate that the presence of a permanent magnet effectively alters the flow and thermal behavior of the ferrofluid, an observation that is in line with the different previous studies that considered this phenomenon (e.g., [20, 21, 23, 37, 44],). Locating the magnet upward led to a magnetic convection that opposed the buoyancy-driven one, leading to inhibited convective effects when Ram is increased. It should be noted here that this aspect is only related to the interplay between the buoyancy-driven and magnetic convections, and is fully dependent on the boundary conditions leading to these mechanisms [53]. In other words, if, in the present study, the bottom wall was cooled with respect to the side walls instead of being heated, moving the magnets upwards would lead to the opposite effect. Also, differentially heating the side walls and adding a single magnet in the middle of the cavity would also deliver higher heat transfer, as reported by Ashouri & Shafii [44]. So overall, selecting a magnet location should take into account the geometrical and boundary conditions of the system. The impact of the magnet is more apparent when the free convective effects are weak. The convection intensifies when the porosity of the porous medium is raised, due to the ease at which the fluid can circulate. The thermal non-equilibrium between the solid and liquid phases in the porous cavity also affects the results. The impact of fluid-solid interface behavior in the porous medium has been initially reported by Baytas & Pop [49], who found that the thermal non-equilibrium model is more representative of the heat transfer at the solid matrix level. In the present study, a higher coefficient can reduce the heat transfer in the fluid phase. This means that the thermal equilibrium assumption can provide an inaccurate representation of the real behavior inside the porous cavity when the convective effects are important. On the other hand, for low Rayleigh numbers, the thermal equilibrium assumption can still efficiently capture the thermal response of the ferrofluid in the enclosure, as discussed by Izadi et al. [28].

These results can provide many implications for real-world applications, mainly for the optimization of heat transfer, by identifying optimal configurations and operating conditions for enhancing or limiting heat transfer within the porous cavity. This can be particularly important for thermal management systems, like electronic cooling, where managing heat dissipation is crucial to prevent overheating and ensure optimal performance. Moreover, the insights gained from the simulation can inform the design and optimization of magnetic heat transfer devices, such as magnetic refrigeration systems or magnetic fluid-based heat exchangers. In addition, the outcomes related to the porosity and impact of magnetic forces the development of materials for applications in energy storage, thermal insulation, and heat dissipation, where heat transfer can be controlled by external magnets. Nonetheless, several aspects still need to be considered. Mainly, the numerical simulation results should be rigorously validated and verified through experiments, as real-world conditions may introduce some uncertainties that need to be considered in the simulation models. In addition, the simulation assumes an idealized behavior in which the fluid is homogeneous. But the stability and thermal properties of ferrofluids under varying magnetic fields and temperature gradients need to be carefully evaluated, because such aspects can affect the long-term performance and reliability of heat transfer systems.

5 Summary and Conclusion

In the present work, the combined natural-magnetic convection in a porous triple enclosure. Two permanent magnets are placed symmetrically near the top of the enclosure. The bottom wall is heated, the side walls are cold, and the top wall is adiabatic. The difference in temperature leads to a change in density, which results in the buoyancy-driven free convection. Simultaneously, a change in the magnetization of the ferromagnetic ferrofluid with temperature occurs, which leads to the thermomagnetic convection. The behavior of the ferrofluid is governed by the interplay between the natural and magnetic convections. The influence of various parameters such that the gravitational and magnetic Rayleigh number (Ra and Ram, respectively), the interfacial heat transfer coefficient Hff-s between the solid matrix and the ferrofluid, as well as the porosity φ and Darcy number Da, on the flow and thermal characteristics of the ferrofluid was assessed. A summary of the main findings of the study is as follows:

  • For the triple enclosure considered, when the natural convection is strong (high Ra), the magnetic convection inhibits the free convection, as the flow direction resulting from each mode of convection is opposite to the other. This results in lower values of solid and ferrofluid Nusselt numbers when Ram is raised.

  • When the natural convection is weak (low Ra), the magnetic convection dominates the flow and heat transfer, and augmenting Ram raises both Nusselt numbers.

  • It was observed that increasing Hff-s leads to higher average Nusselt number in the solid matrix and lower one in the ferrofluid, due to the enhanced heat transfer between the two phases.

  • Regarding the porous media properties, it was found that the Nusselt number in the liquid increases with both Da and ε, and that the effect of the porosity on the heat transfer in the ferrofluid is more apparent for high Da.

These findings can provide many insights for heat transfer optimization, in thermal management systems for instance. They can also be useful for the development of magnetic heat transfer devices, like magnetic fluid-based heat exchangers. However, designing and performing experiments that can replicate the same conditions of the simulations would be beneficial to fully validate the results and address other aspects like the stability of ferrofluids under real-world conditions. In addition, in this work, fixing the position of the two magnets at the top lead to a resistance to the free convection by the magnetic one. Evaluating the impact of the magnets’ position, as well as other geometrical configurations for the cavity, can be the subject of future studies.