Application of Auxetic Core to Improve Dynamic Response of Sandwich Panels Under Low-Velocity Impact

Abstract

Using high-order shear and normal deformation theory (HSNDT), this study analyzes the dynamic response and time history of the impact force of the sandwich plate with the auxetic core under low-velocity impact. The impact was modeled using a two-degree-of-freedom mass and spring model, and the Hertz linearized model was utilized to derive the contact force's time history. The rectangular sandwich panel has simple supported boundary conditions and consists of three layers: two aluminum top face sheets and one auxetic core layer with a negative Poisson's ratio. Using the energy technique, the system's governing equations are derived. The equilibrium equations were solved by the analytic approach of the Navier method in the space domain and the numerical method of Newmark in the time domain. The use of HSNDT distinguishes this article from others on similar topics, and the flexibility of the thick core in the thickness direction is considered. The Effects of different geometric and material properties have been investigated, and the results have been compared with those of other similar papers and studies for validation. The data indicate that the greater the degree of inclination of the cell, the longer the impact period and the lower the peak impact force. Moreover, the larger angle of the auxetic cell reduces the deflection at the impact site. In terms of minimizing deflection, the auxetic honeycomb sandwich panel is 25% superior to the non-auxetic honeycomb panel.

1 Introduction

Due to the extensive usage of sandwich panels in the production of various structures, it is crucial to understand their mechanical characteristics. In the majority of instances, sandwich panel face sheets can bear in-plane normal (bending) stresses, while the core can withstand shear and transverse normal stresses. The core is the most crucial component of sandwich construction. The core material should have qualities such as low density to reduce the weight of the structure, a high vertical Young’s modulus to avoid excessive deformation along the thickness, and a quick decrease in bending stiffness [1]. Sandwich panels are susceptible to impact damage due to the lack of a reinforcing component in the thickness direction. Typically, sandwich panels are subject to impacts from exterior components such as bird and stone strikes. Low-velocity impact damage is crucial in aerospace applications because, although it is undetectable during standard inspections, it may reduce the compressive strength of sandwich panels by 30 to 40 percent [2]. The impact often causes warping, cracking of the matrix, and breaking of the fibers in the tops, as well as core failure and separation of the top from the core [3].

The law of impact, which links the equations of motion of the impacting objects, describes the connection between the indentation and the collision force [4]. Hertz [5] conducted the first study on the subject of the law of static impact; he examined the issue of the impact between two homogeneous isotropic elastic masses. Sveklo's impact law is another considered impact law. This impact rule is also known as the Hertz–Sveklo theory due to the many similarities between Sveklo's method for the issue of contact loading of non-isotropic substances and Hertz's theory in many respects (Mittal & Khalili [6]). The low-velocity impact reactions and crashworthiness of various aluminum foam-core sandwich constructions were examined by Huo et al. [7]. Guo et al. [8] have carried out thorough examinations on sandwich structures subjected to different impact loads.

There are several mathematical approaches for simulating impact, including the energy balance model and the mass and spring model. Lal [9] introduced a mass and spring design with two degrees of freedom, where the second degree of freedom added to the preceding design is the impactor’s stiffness. He analyzed the sheet's bending, shearing, and collision stiffnesses. Khalili [10] examined the orthotropic sheet subjected to impact stress. He employed the Hertz–Sveklo hypothesis for the impact, assuming that the sheet was infinitely big. He also used classical sheet theory and Fourier transformations to get the dynamic response of the sheet analytically. Malekzadeh et al. [11, 12] employed innovative mass-spring-damper vibration designs with three degrees of freedom to calculate and derive the dynamic response of a sandwich sheet by considering transverse flexibility and structural damping. Bagheri et al. [13, 14] conducted a study where they examined the response of sandwich structures with a polypropylene core reinforced with nanoparticles to low-velocity impacts. The investigation involved both experimental and numerical methods.

Due to their exceptional mechanical qualities, which include low mass, high specific stiffness or strength, outstanding energy absorption capacity, and other multifunctional qualities, lightweight metallic cellular materials (MCMs) have been used in many technical applications to date [15, 16]. Materials having a negative Poisson ratio have drawn the attention of academics in recent years as one of these novel situations. This indicates that, owing to axial stress, their transverse length increases [17]. Lakes [18] transformed a regular material into an auxetic for the first time by employing heating, cooling, condensation, and regeneration time. Based on the huge deviation theory, Wan et al. [19] provided a theoretical technique for calculating Poisson's ratio of honeycomb networks. Zhang et al. [20] examined the influence of auxetic honeycomb cell microstructure on in-plane stochastic behavior and energy absorption using the finite element technique. Huang et al. [21] introduced a novel design for the auxetic honeycomb, including a hexagonal component and a thin plate. Prawoto [22] has explored the mechanical characteristics and applications of auxetic materials. Qin et al. [23] conducted an investigation into novel failure modes when dynamically compressing metal honeycomb-like hierarchical structures featuring perforated walls.

The impact response of sandwich panels has been analyzed using a variety of methods. The first-order shear deformation theory (FSDT) and the higher-order shear deformation theory (HSDT) disregard the transverse flexibility of the core and the interaction between the processes and the flexible core [24, 25]. Zhang et al. [26] conducted an investigation into the effects of a large mass at low velocity on sandwich beams consisting entirely of an affixed metal foam core and fiber-metal laminate face sheets. Frostig et al. [27] provided a high-order theory (HSAPT) for a sandwich beam with a flexible transverse core based on the laws of change. The longitudinal and lateral changes of the core were determined using the fundamental equations of the isotropic material and compatibility criteria in the common face, as well as nonlinear expressions for the thickness coordinates. By updating Frostig's higher-order theory of sandwich plates, Malekzadeh et al. [28] developed a revised and enhanced higher-order theory of sandwich plates. In this theory, the contribution of the plane forces of the top and lower surfaces of the sandwich sheet and the equivalent consumption factor of the sandwich sheet was estimated, and for the study of vibrations, the damping of the system was also explored. Zhang et al. [29] investigated the effects of a large mass on constrained square sandwich plates (SSP) composed of fiber-metal laminate (FML) face sheets and a metal foam core subjected to low-velocity impact. Additionally, they examined the response of fully clamped multilayer sandwich beams with metal foam cores under low-velocity impact conditions. They employed analytical, experimental, and numerical techniques in their investigation [30].

Yang et al. [31] studied the vertical impact resistance of a sandwich panel with an auxetic core. In their study, a sandwich panel with an aluminum foam core and an auxetic honeycomb was investigated numerically (using a finite element method) and then experimentally (an impact test). Allen et al. [32] did an experimental study on open-cell auxetic foam and regular PU foam subjected to quasi-static and low-velocity impacts. Chang et al. [33] studied experimentally and statistically the impact resistance of sandwich panels with an aluminum shell and an auxetic internal honeycomb core and determined that the auxetic internal honeycomb is more resistant than other forms of auxetic honeycomb. Beharic et al. [34] investigated the amount of energy absorbed by different sandwich panels with auxetic honeycomb cores, including mesh, interior, and truss, during a drop weight impact test. Hou et al. [35] performed an experimental study on the impact resistance of auxetic and non-auxetic composites subjected to low-velocity loads. Multiscale modeling and nonlinear impact analysis of sandwich panels with graphene-reinforced composite faceplates and functionally graded (FG) three-dimensional auxetic lattice cores were reported by Li et al. [36]. Plastic failure modes were measured by Qin et al. [37], who conducted experiments on sandwich plates that were entirely fastened and subjected to low-velocity impact from a drop hammer featuring a hemispherical muzzle.

For the analytical solution of sandwich panels, there are several theories, including first-order and higher-order shear deformation theories, the zigzag theory, the layered theory, and the sinusoidal theory, among others [38,39,40]. Excellent research on sandwich panels under load. Nevertheless, fewer of these investigations have viewed the core as auxetic.

As mentioned, numerous studies have been conducted in the area of low-velocity impacts of sandwich panels with auxetic cores, but fewer of these researches are parametric studies and analytical. In this article, an effort will be made to determine the dynamic response of a low-velocity impact on a sandwich panel with an auxetic core using high-order shear and normal deformation theory (HSNDT) with transverse flexibility along the panel's thickness. The impact force history is computed using two degrees of freedom of the mass and spring model and the linearized Hertz model.

2 Modeling the System and Getting its Governing Equations

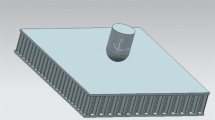
The schematic of the rectangular sandwich panel under investigation is shown in Fig. 1. Cartesian coordinates (x, y, and z) are used to indicate spatial coordinates and displacement components of object points, as seen in this diagram. The proposed sandwich panel is a rectangular sheet with dimensions a and b and a uniform thickness of h and two isotropic surfaces and a soft and flexible auxetic central core. In the dynamic analysis of the sheet, modest displacements are considered, and the linear elastic range is assumed for the analysis. The layers and the central core are integrally linked, and the strain functions are continuous at the connecting surfaces of the layers. The coordinate system is defined so that the x–y plane coincides with the plane in the center. The thickness of the top layer, the middle layer, and the bottom layer are $h_{t}$, $h_{c}$, and $h_{b}$, respectively.

Fig. 1

Schematic of an internal auxetic honeycomb sandwich panel

2.1 Auxetic Core

As shown in Fig. 1, the core employed in this sandwich panel is a sort of concave or inward honeycomb auxetic core. Figure 2 depicts the schematic of a core unit cell of the internal auxetic honeycomb and geometric parameters.

Fig. 2

Schematic representation of the unit cell core of an internal auxetic honeycomb [41]

As shown in the figure, $l_{1}$ and $l_{2}$ are the lengths of the cellular's straight and sloping walls, $t_{1}$ and $t_{2}$ are their thicknesses, and $\theta$ is the cellular's inclined angle.

The equivalent elastic properties of the core layer are determined from the bending and tensile deformations of the core cells using the following formulas [42]:

$$E_{1}^{(2)} = E_{s} \frac{{\eta_{3}^{3} (\eta_{1} - \sin \theta )}}{{\cos^{3} \theta [1 + (\tan^{2} \theta + \eta_{1} \sec^{2} \theta )\eta_{3}^{2} ]}}$$

(1)

$$E_{2}^{(2)} = E_{s} \frac{{\eta_{3}^{3} }}{{\cos \theta (\eta_{1} - \sin \theta )(\tan^{2} \theta + \eta_{3}^{2} )}}$$

(2)

$$G_{12}^{(2)} = E_{s} \frac{{\eta_{3}^{3} }}{{\eta_{1} (1 - 2\eta_{1} )\cos \theta }}$$

(3)

$$G_{23}^{(2)} = G_{s} \frac{{\eta_{3} \cos \theta }}{{\eta_{1} - \sin \theta }}$$

(4)

$$G_{31}^{(2)} = \cos \frac{{\eta_{3} }}{2\cos \theta }\left[ {\frac{{\eta_{1} - \sin \theta }}{{1 + 2\eta_{1} }} + \frac{{\eta_{1} + 2\sin^{2} \theta }}{{2(\eta_{1} - \sin \theta )}}} \right]$$

(5)

$$\nu_{12}^{(2)} = - \frac{{\sin \theta (1 - \eta_{3}^{2} )(\eta_{1} - \sin \theta )}}{{\cos^{2} \theta \left[ {1 + (\tan^{2} \theta + \sec^{2} \theta \eta_{1} )\eta_{3}^{2} } \right]}}$$

(6)

$$\nu_{21}^{(2)} = - \frac{{\sin \theta (1 - \eta_{3}^{2} )}}{{(\tan^{2} \theta + \eta_{3}^{2} )(\eta_{1} - \sin \theta )}}$$

(7)

$$\rho^{(2)} = \rho_{s} \frac{{\eta_{3} (\eta_{1} + 2)}}{{2\cos \theta (\eta_{1} - \sin \theta )}}$$

(8)

where $\eta_{1} = \frac{{l_{2} }}{{l_{1} }}$, $\eta_{2} = \frac{{t_{2} }}{{t_{1} }}$, and $\eta_{3} = \frac{{t_{1} }}{{l_{1} }}$. In the above relations, superscript 2 indicates that the material properties are related to the second layer (core). In addition, the values of $E_{s}$, $\rho_{s}$, and $G_{s}$ correspond to the coefficients of elastic modulus, shear modulus, and density of material that makes up the core.

2.2 HSNDT Displacement Field

To obtain the sandwich panel’s equations of motion, Hamilton's principle and HSNDT are used, in which deflection in the direction of the constant thickness is not considered and flexibility of the core in the direction of thickness is considered. So, based on the sandwich panel's characteristics, HSNDT is a more realistic theory than the other classical theories. This theory divides deflection into three phases: bending, shearing, and thickness stretching. This theory has five unknown general variables, compared to six or more in other shear and normal deformation theories. According to this theory, the displacement field is supposed to be as follows [43]:

$$\begin{gathered} u(x,y,z,t) = u_{0} (x,y,t) - z\frac{{\partial w_{b} }}{\partial x} - f(z)\frac{{\partial w_{s} }}{\partial x} \hfill \\ v(x,y,z,t) = v_{0} (x,y,t) - z\frac{{\partial w_{b} }}{\partial y} - f(z)\frac{{\partial w_{s} }}{\partial y} \hfill \\ w(x,y,z,t) = w_{b} (x,y,t) + w_{s} (x,y,t) + g(z)\varphi (x,y,t) \hfill \\ \end{gathered}$$

(9)

In the preceding relationship, $u_{0}$ and $v_{0}$ represent mid-plane displacement along x and y axis, respectively. Also, $w_{b}$, $w_{s}$ and $\varphi$ are transverse deflection due to bending, shearing, and deformation along the thickness, respectively.

And:

$$\begin{gathered} f(z) = z - h\sinh \left( \frac{z}{h} \right) + z\cosh \left( \frac{1}{2} \right) \hfill \\ g(z) = \cosh \left( \frac{z}{h} \right) - \cosh \left( \frac{1}{2} \right) \hfill \\ \end{gathered}$$

(10)

Sandwich plate strain–displacement relations are given as the following equations:

$$\left\{ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{y} } \\ {\gamma_{xy} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\varepsilon_{x}^{0} } \\ {\varepsilon_{y}^{0} } \\ {\gamma_{xy}^{0} } \\ \end{array} } \right\} + z\left\{ {\begin{array}{*{20}c} {k_{x}^{b} } \\ {k_{y}^{b} } \\ {k_{xy}^{b} } \\ \end{array} } \right\} + f\left\{ {\begin{array}{*{20}c} {k_{x}^{s} } \\ {k_{y}^{s} } \\ {k_{xy}^{s} } \\ \end{array} } \right\}{, }\left\{ {\begin{array}{*{20}c} {\gamma_{yz} } \\ {\gamma_{xz} } \\ \end{array} } \right\} = g\left\{ {\begin{array}{*{20}c} {\gamma_{yz}^{0} } \\ {\gamma_{xz}^{0} } \\ \end{array} } \right\}{, }\varepsilon_{z} = g^{\prime}\varepsilon_{z}^{0}$$

(11)

where:

$$\begin{aligned} \left\{ {\begin{array}{*{20}c} {\varepsilon_{x}^{0} } \\ {\varepsilon_{y}^{0} } \\ {\gamma_{xy}^{0} } \\ \end{array} } \right\} &= \left\{ {\begin{array}{*{20}c} {\frac{{\partial u_{0} }}{\partial x}} \\ {\frac{{\partial v_{0} }}{\partial x}} \\ {\frac{{\partial u_{0} }}{\partial y} + \frac{{\partial v_{0} }}{\partial x}} \\ \end{array} } \right\}, \, \left\{ {\begin{array}{*{20}c} {k_{x}^{b} } \\ {k_{y}^{b} } \\ {k_{xy}^{b} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} { - \frac{{\partial^{2} w_{b} }}{{\partial x^{2} }}} \\ { - \frac{{\partial^{2} w_{b} }}{{\partial y^{2} }}} \\ { - 2\frac{{\partial^{2} w_{b} }}{\partial x\partial y}} \\ \end{array} } \right\}, \, \left\{ {\begin{array}{*{20}c} {k_{x}^{s} } \\ {k_{y}^{s} } \\ {k_{xy}^{s} } \\ \end{array} } \right\}\\ & = \left\{ {\begin{array}{*{20}c} { - \frac{{\partial^{2} w_{s} }}{{\partial x^{2} }}} \\ { - \frac{{\partial^{2} w_{s} }}{{\partial y^{2} }}} \\ { - 2\frac{{\partial^{2} w_{s} }}{\partial x\partial y}} \\ \end{array} } \right\}, \hfill \\ \left\{ {\begin{array}{*{20}c} {\gamma_{yz}^{0} } \\ {\gamma_{xz}^{0} } \\ \end{array} } \right\} &= \left\{ {\begin{array}{*{20}c} {\frac{{\partial w_{s} }}{\partial y} + \frac{\partial \varphi }{{\partial y}}} \\ {\frac{{\partial w_{s} }}{\partial x} + \frac{\partial \varphi }{{\partial y}}} \\ \end{array} } \right\}, \, \varepsilon_{z}^{0} = \varphi \hfill \\ \end{aligned}$$

(12)

The constitutive relations for the orthotropic state are as follows [6]:

$$\left\{ {\begin{array}{*{20}c} {\sigma_{x} } \\ {\sigma_{y} } \\ {\sigma_{z} } \\ {\tau_{yz} } \\ {\tau_{xz} } \\ {\tau_{xy} } \\ \end{array} } \right\}^{(k)} = \left[ {\begin{array}{*{20}c} {C_{11}^{(k)} } & {C_{12}^{(k)} } & {C_{13}^{(k)} } & 0 & 0 & 0 \\ {C_{12}^{(k)} } & {C_{22}^{(k)} } & {C_{23}^{(k)} } & 0 & 0 & 0 \\ {C_{13}^{(k)} } & {C_{23}^{(k)} } & {C_{33}^{(k)} } & 0 & 0 & 0 \\ 0 & 0 & 0 & {C_{44}^{(k)} } & 0 & 0 \\ 0 & 0 & 0 & 0 & {C_{55}^{(k)} } & 0 \\ 0 & 0 & 0 & 0 & 0 & {C_{66}^{(k)} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{y} } \\ {\varepsilon_{z} } \\ {\gamma_{yz} } \\ {\gamma_{xz} } \\ {\gamma_{xy} } \\ \end{array} } \right\}$$

(13)

where in the above relation, $\,\sigma_{ij} , \, \varepsilon_{ij}^{{}} \,$ and $C_{ij} \,$ are the stress, strain, and three-dimensional elastic constants, respectively. Moreover, index k (= 1,3) subscript represents the first to the third layer. The following equations provide the three-dimensional constants of elasticity:

$$\begin{gathered} C_{11}^{(k)} = C_{22}^{(k)} = C_{33}^{(k)} = \frac{{(1 - \nu^{(k)} )}}{{\nu^{(k)} }}\lambda^{(k)} , \, C_{12}^{(k)} = C_{13}^{(k)} = C_{23}^{(k)} = \lambda^{(k)} \hfill \\ C_{44}^{(k)} = C_{55}^{(k)} = C_{66}^{(k)} = G^{(k)} = \mu^{(k)} = \frac{{E^{(k)} }}{{2(1 + \nu^{(k)} )}} \hfill \\ C_{11}^{(2)} = \frac{{E_{1}^{(2)} }}{{1 - \nu_{12}^{(2)} \nu_{21}^{(2)} }}, \, C_{22}^{(2)} = \frac{{E_{2}^{(2)} }}{{1 - \nu_{12}^{(2)} \nu_{21}^{(2)} }} \hfill \\ C_{66}^{(2)} = G_{12}^{(2)} , \, C_{44}^{(2)} = G_{23}^{(2)} , \, C_{55}^{(2)} = G_{13}^{(2)} , \, C_{12}^{(2)} = C_{21}^{(2)} \hfill \\ \end{gathered}$$

(14)

where in the aforementioned relationship, the parameters are:

$$\lambda^{(k)} = \frac{{\nu E^{(k)} }}{{(1 - 2\nu^{(k)} )(1 + \nu^{(k)} )}}, \, \mu^{(k)} = G^{(k)} = \frac{E}{2(1 + \nu )}$$

(15)

2.3 Governing Equations

Hamilton's principle for obtain the equations of motion is as follows [44]:

$$\int_{0}^{t} {(\delta U + \delta K - \delta T)} dt = 0$$

(16)

where $\delta U$, $\delta K$, and $\delta T$ indicate variations in strain energy, potential energy, and kinetic energy, respectively.

Variations of the strain energy is computed as follows:

$$\begin{aligned} \delta U &= \int_{v} {\left[ {\sigma _{x} \delta \varepsilon _{x} + \sigma _{y} \delta \varepsilon _{y} + \sigma _{z} \delta \varepsilon _{z} + \tau _{{xy}} \delta \gamma _{{xy}} + \tau _{{yz}} \delta \gamma _{{yz}} + \tau _{{xz}} \delta \gamma _{{xz}} } \right]dV} \\ &= \int_{A} {[N_{x} \delta \varepsilon _{x}^{0} + N_{y} \delta \varepsilon _{y}^{0} + N_{z} \delta \varepsilon _{z}^{0} + N_{{xy}} \delta \gamma _{{xy}}^{0} + M_{x}^{b} \delta k_{x}^{b} + M_{y}^{b} \delta k_{y}^{b} + M_{{xy}}^{b} \delta k_{{xy}}^{b} } \\ & \quad + M_{x}^{s} \delta k_{x}^{s} + M_{y}^{s} \delta k_{y}^{s} + M_{{xy}}^{s} \delta k_{{xy}}^{s} + S_{{yz}}^{s} \delta \gamma _{{yz}} + S_{{xz}}^{s} \delta \gamma _{{xz}} ]dA \\ \end{aligned}$$

(17)

where stress resultants N, M, and S in the aforementioned relationship are as follows:

$$\begin{gathered} \left\{ {\begin{array}{*{20}c} {N_{x} } & {N_{y} } & {N_{xy} } \\ {M_{x}^{b} } & {M_{y}^{b} } & {M_{xy}^{b} } \\ {M_{x}^{s} } & {M_{y}^{s} } & {M_{xy}^{s} } \\ \end{array} } \right\} = \sum\limits_{n = 1}^{3} {\int_{{h_{n} }}^{{h_{n + 1} }} {(\sigma_{x} ,\sigma_{y} ,\tau_{xy} )^{(n)} \left\{ {\begin{array}{*{20}c} 1 \\ z \\ f \\ \end{array} } \right\}dz} } \hfill \\ N_{z} = \sum\limits_{n = 1}^{3} {\int_{{h_{n} }}^{{h_{n + 1} }} {(\sigma_{z} )^{(n)} g^{\prime}dz} } \hfill \\ \left( {S_{xz}^{s} ,S_{yz}^{s} } \right) = \sum\limits_{n = 1}^{3} {\int_{{h_{n} }}^{{h_{n + 1} }} {(\tau_{xz} ,\tau_{yz} )^{(n)} gdz} } \hfill \\ \end{gathered}$$

(18)

In the above relations, the parameters h_n+1 and h_n are the locations of the top and bottom layers of the nth layer in z direction.

Variations of potential energy of applied loads are expressed in the following format:

$$\delta k = - \int_{A} {q\delta \left( {w_{b} + w_{s} + w_{st} } \right)dA}$$

(19)

In the aforementioned connection, q represents the concentrated transverse load.

Variations of the plate's kinetic energy may be expressed as follows:

$$\begin{aligned} \delta T & = \int_{V} {\left[ {\dot{u}\delta \dot{u} + \dot{v}\delta \dot{v} + \dot{w}\delta \dot{w}} \right]\rho dV} \\ &= \int_{A} {\{ I_{0} \left( {\dot{u}_{0} \delta \dot{u}_{0} + \dot{v}_{0} \delta \dot{v}_{0} + \left( {\dot{w}_{b} + \dot{w}_{s} } \right)\left( {\delta \dot{w}_{b} + \delta \dot{w}_{s} } \right)} \right)} \\ &\quad - I_{1} \left( {\dot{u}_{0} \frac{{\partial \delta \dot{w}_{b} }}{\partial x} + \frac{{\partial \dot{w}_{b} }}{\partial x}\delta \dot{u}_{0} + \dot{v}_{0} \frac{{\partial \delta \dot{w}_{b} }}{\partial y} + \frac{{\partial \dot{w}_{b} }}{\partial y}\delta \dot{v}_{0} } \right) \\ &\quad - J_{1} \left( {\dot{u}_{0} \frac{{\partial \delta \dot{w}_{s} }}{\partial x} + \frac{{\partial \dot{w}_{s} }}{\partial x}\delta \dot{u}_{0} + \dot{v}_{0} \frac{{\partial \delta \dot{w}_{s} }}{\partial y} + \frac{{\partial \dot{w}_{s} }}{\partial y}\delta \dot{v}_{0} } \right) \\ &\quad + I_{2} \left( {\frac{{\partial \dot{w}_{b} }}{\partial x}\frac{{\partial \delta \dot{w}_{b} }}{\partial x} + \frac{{\partial \dot{w}_{b} }}{\partial y}\frac{{\partial \delta \dot{w}_{b} }}{\partial y}} \right) + K_{2} \left( {\frac{{\partial \dot{w}_{s} }}{\partial x}\frac{{\partial \delta \dot{w}_{s} }}{\partial x} + \frac{{\partial \dot{w}_{s} }}{\partial y}\frac{{\partial \delta \dot{w}_{s} }}{\partial y}} \right) \\ &\quad + J_{2} \left( {\frac{{\partial \dot{w}_{b} }}{\partial x}\frac{{\partial \delta \dot{w}_{s} }}{\partial x} + \frac{{\partial \dot{w}_{s} }}{\partial x}\frac{{\partial \delta \dot{w}_{b} }}{\partial x} + \frac{{\partial \dot{w}_{b} }}{\partial y}\frac{{\partial \delta \dot{w}_{s} }}{\partial y} + \frac{{\partial \dot{w}_{s} }}{\partial y}\frac{{\partial \delta \dot{w}_{b} }}{\partial y}} \right) \\ &\quad + J_{1}^{s} \left( {\left( {\dot{w}_{b} + \dot{w}_{s} } \right)\delta \dot{\varphi } + \dot{\varphi }\delta \left( {\dot{w}_{b} + \dot{w}_{s} } \right)} \right) + K_{2}^{s} \dot{\varphi }\delta \dot{\varphi }\} dA \\ \end{aligned}$$

(20)

In the above relations, $\rho$ represents the plate's density, and:

$$(I_{0} ,I_{1} ,J_{1} ,J_{1}^{s} ,I_{2} ,J_{2} ,K_{2} ,K_{2}^{s} ) = \sum\limits_{n = 1}^{3} {\int_{{h_{n} }}^{{h_{n + 1} }} {(1,} } z,f,g,z^{2} ,zf,f^{2} ,g^{2} )\rho dz$$

(21)

After some mathematical efforts and some simplifications, final definition of five equations of motion is as follow:

$$\begin{aligned} \delta u_{0} :A_{11} d_{11} u_{0} + A_{66} d_{22} u_{0} + (A_{12} + A_{66} )d_{12} v_{0} - B_{11} d_{111} w_{b} - (B_{12} + 2B_{66} )d_{122} w_{b} \hfill \\ - (B_{12}^{s} + 2B_{66}^{s} )d_{122} w_{s} - B_{11}^{s} d_{111} w_{s} + Ld_{1} \varphi = I_{0} \ddot{u}_{0} - I_{1} d_{1} \ddot{w}_{b} - J_{1} d_{1} \ddot{w}_{s} \hfill \\ \end{aligned}$$

(22)

$$\begin{aligned} \delta v_{0} :A_{22} d_{22} v_{0} + A_{66} d_{11} v_{0} + (A_{12} + A_{66} )d_{12} u_{0} - B_{22} d_{222} w_{b} - (B_{12} + 2B_{66} )d_{112} w_{b} \hfill \\ - (B_{12}^{s} + 2B_{66}^{s} )d_{112} w_{s} - B_{22}^{s} d_{222} w_{s} + Ld_{2} \varphi = I_{0} \ddot{v}_{0} - I_{1} d_{2} \ddot{w}_{b} - J_{1} d_{2} \ddot{w}_{s} \hfill \\ \end{aligned}$$

(23)

$$\begin{aligned} \delta w_{b} :B_{11} d_{111} u_{0} + (B_{12} + 2B_{66} )d_{122} u_{0} + (B_{12} + 2B_{66} )d_{112} v_{0} + B_{22} d_{222} v_{0} \hfill \\ - D_{11} d_{1111} w_{b} - 2(D_{12} + 2D_{66} )d_{1122} w_{b} - D_{22} d_{2222} w_{b} - D_{11}^{s} d_{1111} w_{s} \hfill \\ - 2(D_{12}^{s} + 2D_{66}^{s} )d_{1122} w_{s} - D_{22}^{s} d_{2222} w_{s} + L^{s} (d_{11} \varphi + d_{22} \varphi ) + q = I_{0} (\ddot{w}_{b} + \ddot{w}_{s} ) \hfill \\ + I_{1} (d_{1} \ddot{u}_{0} + d_{2} \ddot{v}_{0} ) - I_{2} (d_{11} \ddot{w}_{b} + d_{22} \ddot{w}_{b} ) - J_{2} (d_{11} \ddot{w}_{s} + d_{22} \ddot{w}_{s} ) + J_{1}^{s} \ddot{\varphi } \hfill \\ \end{aligned}$$

(24)

$$\begin{aligned} \delta w_{s} :B_{11}^{s} d_{111} u_{0} + (B_{12}^{s} + 2B_{66}^{s} )d_{122} u_{0} + (B_{12}^{s} + 2B_{66}^{s} )d_{112} v_{0} + B_{22}^{s} d_{222} v_{0} \hfill \\ - D_{11}^{s} d_{1111} w_{b} - 2(D_{12}^{s} + 2D_{66}^{s} )d_{1122} w_{b} - D_{22}^{s} d_{2222} w_{b} - H_{11}^{s} d_{1111} w_{s} \hfill \\ - 2(H_{12}^{s} + 2H_{66}^{s} )d_{1122} w_{s} - H_{22}^{s} d_{2222} w_{s} + A_{44}^{s} d_{11} w_{s} + A_{55}^{s} d_{22} w_{s} \hfill \\ + R(d_{11} \varphi + d_{22} \varphi ) + A_{44}^{s} d_{11} \varphi + A_{55}^{s} d_{22} \varphi + q = I_{0} (\ddot{w}_{b} + \ddot{w}_{s} ) \hfill \\ + J_{1} (d_{1} \ddot{u}_{0} + d_{2} \ddot{v}_{0} ) - J_{2} (d_{11} \ddot{w}_{b} + d_{22} \ddot{w}_{b} ) - K_{2} (d_{11} \ddot{w}_{s} + d_{22} \ddot{w}_{s} ) + J_{1}^{s} \ddot{\varphi } \hfill \\ \end{aligned}$$

(25)

$$\begin{aligned} \delta \varphi :L(d_{1} u_{0} + d_{2} v_{0} ) - L^{s} (d_{11} w_{b} + d_{22} w_{b} ) + (R - A_{44}^{s} )d_{11} w_{s} + (R - A_{55}^{s} )d_{22} w_{s} \hfill \\ + R^{s} \varphi - A_{44}^{s} d_{11} \varphi - A_{55}^{s} d_{22} \varphi = J_{1}^{s} (\ddot{w}_{b} + \ddot{w}_{s} ) + K_{2}^{s} \ddot{\varphi } \hfill \\ \end{aligned}$$

(26)

In the above relationships, $d_{ij}$, $d_{ijl}$, and $d_{ijlm}$ are differential operators with the following definitions:

$$d_{ij} = \frac{{\partial^{2} }}{{\partial x_{i} \partial x_{j} }}, \, d_{ijl} = \frac{{\partial^{3} }}{{\partial x_{i} \partial x_{j} \partial x_{l} }}, \, d_{ijlm} = \frac{{\partial^{4} }}{{\partial x_{i} \partial x_{j} \partial x_{l} \partial x_{m} }}, \, (i,j,l,m = 1,2)$$

(27)

In addition:

$$\left\{ {\begin{array}{*{20}c} L \\ {L^{s} } \\ R \\ {R^{s} } \\ \end{array} } \right\} = \sum\limits_{n = 1}^{3} {\int_{{h_{n} }}^{{h_{n + 1} }} {\lambda \left\{ {\begin{array}{*{20}c} 1 \\ z \\ f \\ {g^{\prime}\frac{1 - \nu }{\nu }} \\ \end{array} } \right\}} } g^{\prime}dz$$

(28)

In the equations of motion (21)-(26), the stiffness matrices are derived as follows:

$$\begin{aligned} \left\{ {\begin{array}{*{20}c} {A_{11} } & {B_{11} } & {D_{11} } & {B_{11}^{s} } & {D_{11}^{s} } & {H_{11}^{s} } \\ {A_{12} } & {B_{12} } & {D_{12} } & {B_{12}^{s} } & {D_{12}^{s} } & {H_{12}^{s} } \\ {A_{66} } & {B_{66} } & {D_{66} } & {B_{66}^{s} } & {D_{66}^{s} } & {H_{66}^{s} } \\ \end{array} } \right\} = \sum\limits_{n = 1}^{3} {\int_{{h_{n} }}^{{h_{n + 1} }} {\lambda (} } 1,z,z^{2} ,f,zf,f^{2} )\left\{ {\begin{array}{*{20}c} {\frac{1 - \nu }{\nu }} \\ 1 \\ {\frac{1 - 2\nu }{{2\nu }}} \\ \end{array} } \right\}dz \hfill \\ (A_{22} ,B_{22} ,D_{22} ,B_{22}^{s} ,D_{22}^{s} ,H_{22}^{s} ) = (A_{11} ,B_{11} ,D_{11} ,B_{11}^{s} ,D_{11}^{s} ,H_{11}^{s} ) \hfill \\ A_{44}^{s} = A_{55}^{s} = \sum\limits_{n = 1}^{3} {\int_{{h_{n} }}^{{h_{n + 1} }} {\mu \left( g \right)^{2} dz} } \hfill \\ \end{aligned}$$

(29)

2.4 Exact Solution

In the present study, the boundary conditions of the sandwich plate at the lateral edges are simple supports, and Navier's technique may be employed in the space domain to discretize the differential equations of system. In order to satisfy the boundary conditions, the displacement field variables are addressed in the following double Fourier sinusoidal series form [24]:

$$\left\{ {\begin{array}{*{20}c} {u_{0} } \\ {v_{0} } \\ {w_{b} } \\ {w_{s} } \\ \varphi \\ \end{array} } \right\} = \sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 1}^{\infty } {\left\{ {\begin{array}{*{20}c} {u(t)\cos (\alpha x)\sin (\beta y)} \\ {v(t)\sin (\alpha x)\cos (\beta y)} \\ {w_{b} (t)\sin (\alpha x)\sin (\beta y)} \\ {w_{s} (t)\sin (\alpha x)\sin (\beta y)} \\ {\varphi (t)\sin (\alpha x)\sin (\beta y)} \\ \end{array} } \right\}} }$$

(30)

In the following connection, $u(t)$, $v(t)$, $w_{b} (t)$, $w_{s} (t)$, and $\varphi (t)$ indicate the time parameters of the dynamic response and:

$$\alpha = m\pi /a \, \beta = n\pi /b$$

(31)

where parameters a and b are the sheet’s length and width. Moreover, the transverse load q is expanded as follows in the double Fourier sinusoidal series:

$$q(x,y,t) = \sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 1}^{\infty } {q_{mn} \sin (\alpha x)\sin (\beta y)} }$$

(32)

The term $q_{mn}$, which is considered to represent a concentrated load, will be discussed in the section on impact modeling.

By substituting Eqs. (30) into the equations of motion (22)-(26), the following differential equations are obtained from which we may determine the dynamic reaction of the sheet:

$$\left[ M \right]\left\{ {\ddot{\chi }} \right\} + \left[ K \right]\left\{ \chi \right\} = \left\{ Q \right\}$$

(33)

$\left[ M \right]$ and $\left[ K \right]$ are the mass and stiffness matrices of the system, respectively, and $\left\{ Q \right\}$ represents the impact force. The analytical solution to the above problem is obtained through the Newmark time integral solution method. The values of $a_{ij}$ and $m_{ij}$ are given in the appendix.

In addition, eigen-frequency associated with the (m,n)th mode is obtained from solution of following eigen-value problem:

$$\begin{aligned} &\left( {\left[ {\begin{array}{*{20}c} {a_{11} } & {a_{12} } & {a_{13} } & {a_{14} } & {a_{15} } \\ {a_{12} } & {a_{22} } & {a_{23} } & {a_{24} } & {a_{25} } \\ {a_{13} } & {a_{23} } & {a_{33} } & {a_{34} } & {a_{35} } \\ {a_{14} } & {a_{24} } & {a_{34} } & {a_{44} } & {a_{45} } \\ {a_{15} } & {a_{25} } & {a_{35} } & {a_{45} } & {a_{55} } \\ \end{array} } \right] - \omega^{2} \left[ {\begin{array}{*{20}c} {m_{11} } & 0 & {m_{13} } & {m_{14} } & 0 \\ 0 & {m_{22} } & {m_{23} } & {m_{24} } & 0 \\ {m_{13} } & {m_{23} } & {m_{33} } & {m_{34} } & {m_{35} } \\ {m_{14} } & {m_{24} } & {m_{34} } & {m_{44} } & {m_{45} } \\ 0 & 0 & {m_{35} } & {m_{45} } & {m_{55} } \\ \end{array} } \right]} \right)\\ &\quad \left\{ {\begin{array}{*{20}c} {U_{mn} } \\ {V_{mn} } \\ {W_{bmn} } \\ {W_{smn} } \\ {\Phi_{mn} } \\ \end{array} } \right\} = 0 \end{aligned}$$

(34)

where $U_{mn}$, $V_{mn}$, $W_{bmn}$, $W_{smn}$, and $\Phi_{mn}$ are arbitrary parameters associated with (m,n)th eigen-vector mode.

3 Impact Modeling:

Two degrees of freedom of mass and spring model is used to calculate the impact force and the transverse deflection of the sheet at the point of impact [12, 45]. This vibration method is used when the boundary conditions are only applied to the surfaces, the surfaces and the middle core of the sheet are in the elastic area at the moment of impact, and the middle core of the sheet is not crushed. Figure 3 depicts the two-degree-of-freedom system under consideration.

Fig. 3

Two-degree-of-freedom mass and spring configuration [12]

In Fig. 3, $M_{eff}^{p}$ represents the effective mass of the sandwich panel, $m_{I}$ represents the projectile mass, $K_{c}^{*}$ indicates the linearized contact stiffness, and $K_{g}^{{}}$ indicates the sandwich panel's equivalent stiffness.

The impactor is assumed to impact the middle of the sandwich sheet with an initial velocity of $V_{0}$. By using Newton's second law, the following equations of motion may be derived for two-degree-of-freedom system:

$$\left\{ {\begin{array}{*{20}c} {m_{I} \ddot{\Delta }_{1} + K_{c}^{*} (\Delta_{1} - \Delta_{2} ) = 0} \\ {M_{eff}^{p} \ddot{\Delta }_{2} + K_{c}^{*} (\Delta_{2} - \Delta_{1} ) + K_{g} \Delta_{2} = 0} \\ \end{array} } \right.$$

(35)

The effective mass of the panel for the simple support mode is equal to one-fourth of the sandwich panel's overall mass [12]. The relationship (36) describes the vertical displacement of the impacting mass and the effective mass of the sandwich panel.

$$\begin{gathered} \Delta_{1} = A_{1} \sin (\omega t + \varphi ) \hfill \\ \Delta_{2} = A_{2} \sin (\omega t + \varphi ) \hfill \\ \end{gathered}$$

(36)

The equivalent stiffness at the impact point may be derived from the static analysis using the higher-order theory of sandwich sheets [12] and, in the special case when the impact occurs in the center of the surface, from the following relationship [11]:

$$K_{g} = M_{tot} \omega_{11}^{2}$$

(37)

where ω₁₁ is the frequency of the first mode of vibration, which is found using equation)34(. The following equation will be used to get the value of the contact stiffness for the enhanced Hertz contact law.

$$K_{c} = \frac{4}{3}ER^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}}$$

(38)

In the preceding relationship, $E$ and $R$ represent the plate’s elasticity coefficient and radius of curvature, as follows:

$$\frac{1}{R} = \frac{1}{{R_{1} }} + \frac{1}{{R_{2} }}{ , }\frac{1}{E} = \frac{{1 - \nu_{eff}^{2} }}{{E_{eff} }} + \frac{{1 - \nu_{imp}^{2} }}{{E_{imp} }}$$

(39)

In the above connection, $R_{1}$ and $R_{2}$ represent the curvature of the impactor and the plate, respectively, while $E_{imp}$, $\nu_{imp}^{{}}$, $E_{eff}$, and $\nu_{eff}^{{}}$ represent the effective elasticity and Poisson coefficients for the impactor and the plate, respectively. Moreover:

$$\begin{gathered} E_{eff} = \frac{h}{{\frac{{h_{t} }}{{E_{33t} }} + \frac{{h_{b} }}{{E_{33b} }} + \frac{{h_{c} }}{{E_{33c} }}}} \hfill \\ \nu_{eff} = \nu_{13t} \left( {\frac{{h_{t} }}{h}} \right) + \nu_{13b} \left( {\frac{{h_{b} }}{h}} \right) + \nu_{13c} \left( {\frac{{h_{c} }}{h}} \right) \hfill \\ \end{gathered}$$

(40)

By linearizing the relationship (38) about the maximum impact force and the maximum relative shape change between the impactor and the target, the following relationship can be expressed [11]:

$$K_{c}^{ * } = K_{c}^{\frac{1}{n}} \, F_{\max }^{{\frac{n - 1}{n}}}$$

(41)

where $K_{c}^{{}}$ represents the enhanced Hertz contact stiffness and is determined by Eq. (38). The value of n is often 1.5. The maximum contact force may be determined using the concept of energy conservation by equating the initial kinetic energy of the impactor with the work done or the strain energy stored in the springs:

$$\frac{{F_{\max }^{2} }}{{2K_{g} }} + \frac{{F_{\max }^{{1 + \frac{1}{n}}} }}{{(n + 1)K_{c}^{\frac{1}{n}} }} = \frac{1}{2}m_{I} V_{0}^{2}$$

(42)

By replacing the Eqs. (36) in the formula (35), and by sorting and converting to the matrix multiplication mode, it is obtained:

$$\left[ {\begin{array}{*{20}c} { - m_{I} \omega^{2} + K_{c}^{*} } & { - K_{c}^{*} } \\ { - K_{c}^{*} } & { - M_{eff}^{p} \omega^{2} + K_{c}^{*} + K_{g} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {A_{1} } \\ {A_{2} } \\ \end{array} } \right] = 0$$

(43)

To solve the given system of equations, the determinants of the matrix of coefficients must be made equal to zero, resulting in:

$$(m_{I} M_{eff}^{p} )\omega^{4} + ( - m_{I} K_{c}^{*} - m_{I} K_{g} - K_{c}^{*} M_{eff}^{p} )\omega^{2} + K_{c}^{*} K_{g} = 0$$

(44)

By solving the preceding equation, we get two values for $\omega_{n1}$ and $\omega_{n2}$. We represent the values of elements of Eigen-vector $A_{1}$ associated with $\omega_{n1}$ as $A_{1}^{(1)} ,A_{2}^{(1)}$ and elements of Eigen-vector $A_{2}$ associated with $\omega_{n2}$ as $A_{1}^{(2)} ,A_{2}^{(2)}$. The ratios of $r_{1} = \frac{{A_{2}^{(1)} }}{{A_{1}^{(1)} }}$ and $r_{2} = \frac{{A_{2}^{(2)} }}{{A_{1}^{(2)} }}$ may be found given the values of $\omega_{n1}$ and $\omega_{n2}$ using the following relations:

$$r_{1} = \frac{{A_{2}^{(1)} }}{{A_{1}^{(1)} }} = \frac{{ - m_{I} \omega_{n1}^{2} + K_{c}^{ * } }}{{K_{c}^{ * } }} = \frac{{K_{c}^{ * } }}{{ - M_{eff}^{p} \omega_{n1}^{2} + K_{c}^{*} + K_{g} }}$$

(45)

$$r_{2} = \frac{{A_{2}^{(2)} }}{{A_{1}^{(2)} }} = \frac{{ - m_{I} \omega_{n2}^{2} + K_{c}^{ * } }}{{K_{c}^{ * } }} = \frac{{K_{c}^{ * } }}{{ - M_{eff}^{p} \omega_{n2}^{2} + K_{c}^{*} + K_{g} }}$$

(46)

The natural states of oscillatory motion associated with $\omega_{n1}^{2}$ and $\omega_{n2}^{2}$ may be described as relations (47), based on the ratios derived from relations (45) and (46).

$$\vec{\varphi }^{(1)} = \left\{ {\begin{array}{*{20}c} {A_{1}^{(1)} } \\ {A_{2}^{(1)} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {A_{1}^{(1)} } \\ {r_{1} A_{1}^{(1)} } \\ \end{array} } \right\} \, \vec{\varphi }^{(2)} = \left\{ {\begin{array}{*{20}c} {A_{1}^{(2)} } \\ {A_{2}^{(2)} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {A_{1}^{(2)} } \\ {r_{2} A_{1}^{(2)} } \\ \end{array} } \right\}$$

(47)

The system's overall motion at time t may be described as follows:

$$\left\{ {\begin{array}{*{20}c} {\Delta_{1} } \\ {\Delta_{2} } \\ \end{array} } \right\} = C_{1} \vec{\varphi }^{(1)} \sin (\omega_{n1} t + \psi_{1} ) + C_{2} \vec{\varphi }^{(2)} \sin (\omega_{n2} t + \psi_{2} )$$

(48)

The unknown coefficients $C_{1}$, $C_{2}$, $\psi_{1}$, and $\psi_{2}$ may be found by applying the initial conditions listed below:

$$\left\{ {\begin{array}{*{20}c} {\Delta_{1} (t = 0) = 0} \\ {\Delta_{2} (t = 0) = 0} \\ \end{array} } \right\}{ , }\left\{ {\begin{array}{*{20}c} {\dot{\Delta }_{1} (t = 0) = V_{0} } \\ {\dot{\Delta }_{2} (t = 0) = 0} \\ \end{array} } \right\}$$

(49)

We have, by applying the initial conditions:

$$\begin{gathered} \psi_{1} = \psi_{2} = 0 \hfill \\ C_{1} = \frac{{V_{0} r_{2} }}{{\omega_{n1} (r_{2} - r_{1} )}} \, C_{2} = - \frac{{r_{1} \omega_{n1} }}{{r_{2} \omega_{n2} }}C_{1} \hfill \\ \end{gathered}$$

(50)

The contact force function may be determined by knowing the unknowns in Eq. (48):

$$F(t) = K_{c}^{ * } (\Delta_{1} - \Delta_{2} )$$

(51)

Applying the aforementioned relationship, the contact force history may be calculated. To compute the history of the sheet’s deflection, we model the contact force function as a concentrated load at the sheet's center:

$$q_{mn} = \frac{4F(t)}{{ab}}\sin \frac{{m\pi x_{0} }}{a}\sin \frac{{n\pi y_{0} }}{b}$$

(52)

According to the equation presented, $x_{0} = \frac{a}{2}$ and $y_{0} = \frac{b}{2}$. Now, we insert Eq. (52) into Eq. (32) and solve Eq. (34) using Newmark's time integral to get the deflection history in the center of the sheet.

4 Discussion and Results

In this section, the numerical findings' analysis is described. Before reviewing new results, we will confirm all the offered approaches, including the natural frequency of free vibration of the sandwich sheet, the two-degree-of-freedom mass and spring model, and the sheet's deflection based on the supplied theory. Lastly, we will compare the effects of the auxetic and non-auxetic cores on the impact response and investigate the parameters that influence the history of deflection and contact force of the sandwich sheet with the auxetic core.

The geometric specifications used for the sandwich panel with the auxetic core and aluminum face sheets are listed in Table 1. The physical properties of the aluminum top face sheets, the auxetic core, and the non-auxetic core are listed in Table 2 and 3. In addition, the specifications of the steel impactor with a steel spherical head are listed in Table 4.

Table 1 Geometric characteristics of sandwich panel with auxetic core

Table 2 Physical characteristics of aluminum sheet surfaces

Table 3 Physical properties of the auxetic and non-auxetic cores at various tilt angles [46]

Table 4 Characteristics of the steel impactor with the steel spherical head

4.1 Verification

4.1.1 Natural Frequency

To confirm the results, we first compare the fundamental frequency obtained from the HSNDT with those obtained from the study by Yuan et al. [47] for sandwich sheets with aluminum tops and honeycomb cores using finite element analysis. The material and geometric properties of the sandwich sheet used for the research by Yuan et al. are reported in Table 5, 6, 7 and the results of the two methods are listed in Table 8.

Table 5 Geometric characteristics of the sandwich sheet with honeycomb core [47]

Table 6 Material characteristics of the sandwich sheet tops with honeycomb core [47]

Table 7 Material properties of the honeycomb core [47]

Table 8 Comparison between the fundamental frequency of the aluminum sandwich sheet with honeycomb core [47]

As Table 8 shows, the natural frequency found by the current method is very close to the natural frequency found by Yuan et al. [47]., which proves that the current method is accurate for finding the sheet’s natural frequency.

4.1.2 Force's Time History and Impact Site’s Deflection

To validate the accuracy of the two-degree-of-freedom mass and spring model, the force history of a steel ball hitting the center of a square steel sheet at a low speed with simple boundary conditions on all four sides is compared to the force history obtained by [48]. Material and geometric properties of the steel sheet are shown in Table 9; the steel ball has a radius of curvature of 10 mm and an initial velocity of 1 m/s.

Table 9 Material and geometrical characteristics of square steel sheet [48]

According to Fig. 4, the results of the current approach in the mass and spring model and the theory utilized to derive the time history of the impact force agree well with the results acquired from the reference.

Fig. 4

A comparison of the temporal evolution of the impact force exerted on the simply supported plate by the steel sphere [48]

In Fig. 5, time history of the plate's deflection obtained by current research and those obtained by Shariayat et al. [49] are compared. The material and geometric properties of the sheet are shown in Table 10, and the steel ball has a radius of curvature of 10 mm and an initial velocity of 1 m/s. As can be observed, the outcome of this study is in excellent accord with that of Shariayat et al.

Fig. 5

A comparison between the present study by Shariayat et al. [49] regarding the time history of deflection due to low-velocity impact

Table 10 Material and geometrical features of rectangular steel sheet [49]

4.2 Effects of the Auxetic Core

As known, the auxetic materials are characterized by negative Poisson’s ratio. So, they have different behavior in bending compared to normal materials. To show this, we expose a monolayer auxetic core with simple support conditions to a static distributed load as shown and compare it with a normal regular honeycomb monolayer. The geometric characteristics of the single-layer sheet can be found in Table 11, and the material specifications of the auxetic and honeycomb core can be found in Table 3. Figure 6 displays the amount of displacement along the x-axis for the auxetic single layer and the ordinary honeycomb due to bending. As seen in the diagram, in contrast to the honeycomb core, the bending displacement of the auxetic core is inversed.

Table 11 Geometric properties of auxetic and honeycomb single-layer materials

Fig. 6

Displacement in the x direction owing to the extensive load in the single layer of a normal and b auxetic honeycombs

4.3 Numerical Results

In this section, the new numerical results analysis is described. This section's objective is to examine the influence of various factors on the time histories of dynamic deflection and impact force in the ideal sandwich plate with auxetic core.

Figure 7 illustrates the time evolution of sandwich panel force for three different angles of inclination of the auxetic honeycomb cell. Evidently, the internal angle of the core has a major influence on the time history of the impact force. The smaller the angle of the auxetic cell, based on Eqs. (2), the transverse stiffer the auxetic core becomes. This enhancement of the core stiffness increases the ability to resist deformation of the struts. Consequently, when a sandwich panel experiences an impact force, a core with a larger angle of the auxetic cell will exhibit increased stiffness, thereby reducing deflection at the point of impact. As a result, the greater the cell's degree of inclination, the longer the duration of impact and the lower the maximum impact force. In addition, Fig. 8 shows the effect of the angle of inclination of the auxetic honeycomb cell on the time history of the impact site's deflection. As can be observed, the larger angle of the auxetic cell causes a smaller deflection of the impact site. This is because raising the cellular slope of the auxetic core improves the elasticity coefficient, thereby increasing the sandwich panel's stiffness and decreasing its deflection. Figure 8 indicates that the core with an internal angle of $\theta = 60^{^\circ }$ is more effective in reducing the deflection amplitude.

Fig. 7

Time history of impact force on the sandwich plate with different auxetic core internal angles

Fig. 8

Time history of the sandwich plate impact site deflection in auxetic cores with different internal angles

Figures 9 and 10 compare the time histories of the impact force and impact site deflection for sandwich panels with auxetic and non-auxetic honeycomb cores, respectively. As shown in Fig. 9, the sandwich panel of the auxetic honeycomb has a longer collision time and a lower maximum contact force than the honeycomb panel with a positive Poisson ratio. Figure 10 demonstrates that the auxetic core deflects less than the non-auxetic core. The auxetic honeycomb core demonstrates a negative Poisson's ratio, which implies that it expands sideways when subjected to longitudinal stretching. This distinctive characteristic enables the core to efficiently absorb and distribute impact energy. In the event of a collision, the auxetic core undergoes controlled deformation, leading to an extended duration of the collision. Additionally, the expansion of the core aids in decreasing the maximum contact force by dispersing it across a wider surface area, thereby minimizing the occurrence of localized stress concentrations and potential damage.

Fig. 9

Time history of the impact force of the sandwich panel with the auxetic honeycomb core at a $45^{^\circ }$ tilt angle and the non-auxetic honeycomb core at a $- 30^{^\circ }$ tilt angle

Fig. 10

History of the impact site deflection of the sandwich panel with the auxetic honeycomb core at a $45^{^\circ }$ tilt angle and the non-auxetic honeycomb core at a $- 30^{^\circ }$ tilt angle

In the following, we will continue with the material properties of auxetic honeycomb sandwich panel with $30^{0}$ inclined angle.

Figure 11 illustrates time history of the impact force at various impact velocity. It can be observed, as the impactor's velocity rises, so does the maximum impact force, but the duration of the impact reduces. These phenomena are a result of the impactor's increased kinetic energy. A combination of an increase in the maximum impact force and a reduction in impact duration allows for a higher quantity of the impactor's kinetic energy to transfer to the sandwich sheet with a shorter duration, which causes a shock to the structure.

Fig. 11

Time history of impact force of the sandwich panel with the auxetic core for different speeds

Figure 12 depicts the time history of the deflection of the impact site for low-velocity impacts at various velocities. According to this graphic, as the impactor's velocity rises, so does the amount of deflection at the point of impact. The impact force is proportional to the rate of momentum change, which depends on the mass and velocity of the object causing the impact. When the velocity increases, both the rate of momentum change and the applied force increases correspondingly. The greater force exerted on the target material leads to a more pronounced deflection response.

Fig. 12

Time history of deflection at the impact site of the sandwich panel with the auxetic core for different speeds

Figures 13 and 14 illustrate the influence of the impacting mass on the time history of the impact force and the deflection of the impact site, respectively. The solution is found for various ratio of the impactor mass to the overall mass of the sheet; it is assumed that the total mass of the sheet to be around 0.256 kg. As seen from Fig. 13, when the mass of the impactor increases, both the maximum impact force and the duration of the impact increase. An increase in the impacting mass increases the kinetic energy, which in turn raises the maximum force of the impact, resulting in an extension of the impact’s duration. Also, Fig. 14 shows that as the impactor's mass goes up, so does its kinetic energy and, as a result, does the deflection at the impact site. This makes the duration of the impact longer.

Fig. 13

Time history of the impact force of the sandwich panel with the auxetic core for different ratios of the impact mass to the total mass of the sheet

Fig. 14

Time history of deflection at the impact site of the sandwich panel with the auxetic core for different ratios of the impact mass to the total mass of the sheet

Figure 15 depicts the time evolution of the impact force on the sandwich panel of the auxetic honeycomb for various ratios of the core thickness to the overall thickness. It is evident that the thicker core causes to the lighter mass of the sheet, reduces stiffness of the sheet, increases the maximum contact force and minimizes contact duration. In addition, Fig. 16 illustrates the time history of the deflection under low-velocity impact force for various ratios of core thickness to total thickness (h_c/h). According to this diagram, it is evident that the greater the core thickness, the greater the range of lateral displacements under the same load. Since the sandwich plate's overall thickness is constant, when the ratio of core thickness to total thickness (h_c/h) increases, the face sheet thickness decreases. This leads to a decrease in the flexural stiffness of the sandwich plate, an increase in the maximum deflection at the collision site, and a subsequent reduction in the collision duration.

Fig. 15

Time history of the impact force of the sandwich panel with the auxetic core for different ratios of the core thickness to the total thickness

Fig. 16

Time history of deflection at the impact site of the sandwich panel with the auxetic core for different ratios of the core thickness to the total thickness

5 Conclusion

In the current research, the time history of the impact force and the history of the impact site's deflection caused by a low-velocity impact on a sandwich panel with the auxetic core were investigated. The effect of auxetic core and other geometrical parameters on the dynamic response of the sheet and the time history of impact force was explored. The low-velocity impact was modeled using the two-degree-of-freedom spring and mass model. Using Hamilton's principle, the equations governing the dynamic response of the system were derived. In order to solve partial differential governing equations taking into account the boundary conditions of simple supports, the analytical approach of Navier was utilized in the space domain and the numerical solution of Newmark was used in the time domain. The outcomes of this investigation are briefly discussed in the following section:

The results obtained from the two-degree-of-freedom mass and spring model and the high-order shear and normal deformation theory used in this study to determine the dynamic response and time history of the impact force are in excellent agreement with those of prior studies.

The auxetic honeycomb sandwich panel outperforms the non-auxetic honeycomb sandwich panel by 9.5% in minimizing deflection.

When the impactor's velocity rises, the maximum impact force increases, the impact duration reduces, and the impact point's deflection increases.

An increase in the impactor's mass increases the kinetic energy and, thus, the maximum force; this, in turn, increases the collision's duration and the deflection of the impact site.

The greater the thickness of the core, the greater the maximum contact force and the shorter the duration of the impact. Due to the lighter mass of the sheet, the equivalent stiffness of the sheet decreases, causing an increase in the maximum contact force, a decrease in the duration of the impact, and an increase in the deflection of the impact site.

The greater the angle of tilt of the auxetic core cell, the longer the duration of the impact, and the smaller the maximum time history of the contact force and deflection of the impact site; thus, the auxetic core with an angle of $60^{0}$ has 54.73 percent less deflection than the core with an angle of $30^{0}$.

Appendix

The following terms apply to the matrix terms of Eq. (33).

$$\begin{aligned} a_{11} = - (A_{11} \alpha^{2} + A_{66} \beta^{2} ), \, a_{12} = - \alpha \mu (A_{12} + A_{66} ) \hfill \\ a_{13} = \alpha [B_{11} \alpha^{2} + (B_{12} + 2B_{66} )\beta^{2} ], \, a_{14} = \alpha [B_{11}^{s} \alpha^{2} + (B_{12}^{s} + 2B_{66}^{s} )\beta^{2} ] \hfill \\ a_{15} = L\alpha , \, a_{22} = - (A_{66} \alpha^{2} + A_{22} \beta^{2} ) \hfill \\ a_{23} = \beta [(B_{12} + 2B_{66} )\alpha^{2} + B_{22} \beta^{2} ], \, a_{24} = \beta [(B_{12}^{s} + 2B_{66}^{s} )\alpha^{2} + B_{22}^{s} \beta^{2} ] \hfill \\ a_{25} = L\beta , \, a_{33} = - \left( {D_{11} \alpha^{4} + 2(D_{12} + 2D_{66} )\alpha^{2} \beta^{2} + D_{22} \beta^{4} } \right) \hfill \\ a_{34} = - \left( {D_{11}^{s} \alpha^{4} + 2(D_{12}^{s} + 2D_{66}^{s} )\alpha^{2} \beta^{2} + D_{22}^{s} \beta^{4} } \right) \hfill \\ a_{35} = - L^{s} (\alpha^{2} + \beta^{2} ), \, a_{44} = - \left( {H_{11}^{s} \alpha^{4} + 2(H_{12}^{s} + 2H_{66}^{s} )\alpha^{2} \beta^{2} + H_{22}^{s} \beta^{4} } \right) + A_{55}^{s} \alpha^{2} + A_{44}^{s} \beta^{2} ) \hfill \\ a_{45} = - [A_{55}^{s} \alpha^{2} + A_{44}^{s} \beta^{2} + R(\alpha^{2} + \beta^{2} )], \, a_{55} = - (A_{44}^{s} \alpha^{2} + A_{55}^{s} \beta^{2} + R^{s} ) \hfill \\ m_{11} = m_{12} = - I_{0} ,m_{13} = \alpha I_{1} ,m_{14} = \alpha J_{1} ,m_{23} = \beta I_{1} ,m_{24} = \beta J_{1} \hfill \\ \end{aligned}$$