1 Introduction

Non-renewable energy resources containing conventional fossil fuels are likely to deplete with time. Renewable energy resources are now considered a primary source of energy. The most important feature of renewable energy is that it does not release any harmful pollutants when harnessed. To overcome the environmental pollutants by burning fossil fuels to attain energy, SPV (solar photovoltaic) modules lead to the advantage of a clean and green environment. In general, SPVC in renewable energy systems are not a consistent source of energy as the power obtained from them varies with ambient conditions. In South Asia, SPV modules are a much better source of energy as it enjoys the highest average solar hours per year in the region's major cities, so a large amount of energy could be harnessed. Moreover, SPV modules are associated with less maintenance cost and possess an industrial standard life span of about 25 to 30 years. Additionally, solar cell prices are decreasing day by day as well [1].

Compared with a standalone PV system, a grid-tied inverter system allows for more savings, better efficiency rates, and lower equipment and installation costs [2, 3]. The combination of the SPV array in a hybrid combination has the advantage to connect with the grid alongside other renewable energy resources. Hybrid solar systems generally contain a battery storage package and have the disadvantages of the high cost of battery banks, complex installation requirements, larger space requirements, higher installation costs, and longer payback time [4]. A standalone solar system for the application of water pumping systems with batteries as energy storing devices is presented in [5]. Dynamic modeling of solar water pumping with two types of energy storage systems such as electric energy using a battery bank and stored water in a large water tank is presented in [6]. The battery bank connected with the solar system is typically comprised of lead-acid or Li-ion types batteries. Several electrical and thermal hazards are associated with Li-ion batteries and generate hazardous waste at the end of their lifespan. Lead-acid battery material is toxic and hazardous to the environment. Installation of a battery bank with a solar system also increases capital costs and requires additional maintenance [7].

Where grid supply is available, a grid-connected solar system is preferred over battery connected system. Few researchers proposed a standalone solar pump system that does not have grid-connected and power quality improvement features [8,9,10,11]. The hybrid wind energy conversion system (WECS), SPV, and battery storage are reported in [12]. This system has a high initial cost and requires substantial maintenance. Self-excited generators are also used, but they require a capacitor for their reactive power compensation.

Solar radiation reaches the earth's surface with parameter variations such as time of day, weather, geographic location, and local landscape. Sun intensity (temperature change), the orientation of installed solar panels, weather change, and solar shedding are the key factors that affect SPVC efficiency [13]. The characteristics curve of the SPV array shows that its maximum operating point changes with the change in the parameters. The current and power drawn from the SPVC can be changed by changing the output voltage of the cells as given in Fig. 1 [14].

Fig. 1
figure 1

I–V and PV characteristics curves of SPV for varying temperature [14]

Full size image

The new technique of nonlinear integral backstepping controller to track standalone solar system maximum power point (MPP) has been proposed in [14]. The key objective of this research is to extend the work in [14] to achieve the optimum operation of the SPV system and power factor improvement based on the MPPT control strategy under uniform solar irradiance and temperature within a specific time interval. MPPT is an algorithm that is included in charge controllers to extract maximum available power from SPV modules. In [15], an ideal buck-boost DC-DC converter, MPPT, and resistive load are used in the interface between solar and load. The duty cycle is set in such a way that it operates on its peak voltage to draw maximum current from solar. Several techniques for MPPT have been developed and a comprehensive review is presented in [16]. Due to the simple structure and less expensive, offline MPPT strategies, such as the short-circuit current (SCC) strategy [17] and open-circuit voltage (OCV) strategy [18], have been frequently employed in the SPV systems. These strategies have the disadvantage of failure under varying meteorological conditions and are incapable of operating under partial shading conditions [19]. Due to the varying irradiance and temperature uncertainty of SPV modules, the fuzzy logic control-based intelligent MPPT method is implemented in [20], which is better as compared with conventional SPV algorithms systems. A simple and efficient off-grid SPV water pumping system is presented in [21]. The offered system is based on a DC-DC boost converter, a three-phase DC-AC inverter, and a three-phase induction motor (IM) coupled to the centrifugal pump. An improved fractional open-circuit voltage control method is proposed that is associated with MPPT and closed-loop scalar control.

Online MPPT techniques include the number of variants of three basic algorithms; perturb and observe (P&O), incremental conductance (INC), and extremum seeking control (ESC) methods reported in the literature [22,23,24]. These techniques usually try to find the maxima of  SPV power and voltage to obtain the MPP. This process takes time and the algorithm always keeps on searching until maximum power has been reached. This produces oscillations in voltages; hence, the overall efficiency of the system is reduced [25]. The combination of both offline and online MPPT techniques to estimate the duty cycle of the converter to achieve maximum power point is called the hybrid control technique and is presented in [26]. In the offline phase, temperature and radiation intensity are the inputs of the system to estimate the approximate maximum power based on analytical equations of the SPVC. In the online phase, the P&O method is utilized for fine-tuning and tracking maximum power point. Improved INC technique by updating the duty cycle of the boost converter with LC resonance has been reported in [27].

Many nonlinear controllers can be implemented to track MPP, as the inherent nonlinear nature of SPVC [28]. A nonlinear controller is more robust and stable so it can track MPP better than any other linear controller. To reduce the steady-state error of the PVC system, the new technique of nonlinear backstepping controller to track MPP with integral action has been proposed in [14]. grid-connected and standalone MPPT-based nonlinear control problems are solved in [29, 30].

The PF is an important parameter when dealing with inductive loads. Improving the PF can reduce power losses, improve system voltages, maximize current-carrying capacity, and lower electric bills. The use of inductive loads i.e., induction motor drives and power converters, is the main cause of PF distortion in the distribution system. Unbalancing operation and voltage distortion due to inductive loads also deteriorate power quality [31].

In a grid-tied SPV system, a diode bridge rectifier (DBR) with a DC link capacitor is used to convert source AC voltage into DC. The inductive load is lagging and nonlinear so it reduces the PF [32]. For PFC, a boost converter is used after the DBR output voltage which maintains the DC link voltage across the capacitor [33]. DC-DC boost converter for PF improvement is reported in [34, 35]. The PI controller is used for PFC in this research. PFC circuit maintains the DC desired value to 400 V and also makes the input current should follow the input voltage waveform for power factor improvement. However, the proposed controller in this literature is complex with a high computational burden. The grid-connected hybrid solar system is reported in [36]. The DC-DC boost converter is utilized, and the closed loop current control technique with PI controller is implemented for PFC. For MPPT, an incremental conductance-based maximum power point tracking control is implemented.

The nonlinear backstepping technique has also been implemented for MPPT in this research and compared with the conventional P&O technique. Due to the nonlinear nature of the solar, the proposed nonlinear IBS controller is more robust in tracking MPPT and also produces fewer variations in MPP voltage. Till now, the nonlinear control method is not implemented for PFC using the IBS technique. In this research, nonlinear backstepping controller with integral action has been designed for PFC using a boost converter. By applying the nonlinear technique, PF has been improved as compared with the PI controller. Due to the nonlinear load, the proposed controller is more robust and also reduces total harmonic distortion (THD) in output current when compared with the PI controller.

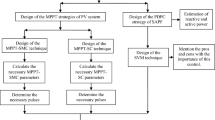
The main system configuration and modes for power control for nonlinear backstepping with an integral action controller using a boost converter have been presented for MPPT and PFC in Sect. 2. Control methodology is described in Sect. 3. Mathematical modeling of the non-inverting boost converter is described in Sect. 4. An integral backstepping controller for MPPT is presented in Sect. 5. The proposed integral backstepping controller for PFC is designed in Sect. 6. MATLAB/Simulink simulation results of MPPT by varying temperature & irradiations, comparison with P&O, PF and THD improvements are given in Sect. 7.

2 Detailed System Configuration and Description

The complete system description for this research is presented in Fig. 2. In the proposed control scheme, an intelligent hybrid system is designed to connect the grid and SPV simultaneously to share power for the nonlinear load. Two boost converters and one voltage source inverter (VSI) have been used where VSI is used to provide an AC output voltage. DC boost converter connected with grid side is used to increase the DC output voltage to the desired level and also for PFC of the main AC supply. A boost converter at SPV is used for MPPT and LC filter after DBR is used for removing high switching ripples in AC mains.

Fig. 2
figure 2

Proposed control scheme

Full size image

2.1 Modes for Power Control

Smart power sharing has been implemented between two sources: SPV and grid. Priority is given to the SPV and whatever high power is available from it. If the required output power is larger than the power obtained from SPV, in this situation grid compensates for that remaining power. Two boost converters, one for PFC and one for MPPT, have been implemented. In both, a nonlinear backstepping technique with integral action has been implemented. The function of the system is divided into three modes.

  • Mode 1 Standalone SPV mode: In this mode, power is delivered in the daytime only by SPV standalone. A boost converter is used for MPPT which also maintains the D.C bus voltage. MPPT and D.C bus voltage are controlled by a nonlinear IBS controller.

  • Mode II Standalone grid mode: In this mode, only the grid delivers power to the system at night when power from solar is not available. A.C input is rectified by DBR and D.C link capacitors connected to the DBR. The output current is distorted and not maintained according to IEEE standards. So, a PFC boost converter is used, which maintains the A.C input current sinusoidal.

  • Mode III Shared mode: In this mode, power is available from both grid and SPV. The priority is to extract maximum power from the SPV source while taking less power from the grid supply. In this mode, PFC remains in function by keeping the THD within limits.

2.2 Backstepping Control Concept

The backstepping control method is a recursive design technique to asymptotically stabilize a controller with the choice of a Lyapunov function control. The controller links with the design of a feedback controller and assures global asymptotic stability of the strict feedback systems. To overcome the limitations of the feedback linearization technique, active backstepping control method is a practical tool in the control literature. The generalized backstepping control technique is given in Fig. 3 [37, 38].

$$\left\{ {\begin{array}{*{20}c} {\dot{x} = f\left( x \right) + g\left( x \right)T} \\ {\dot{T} = u} \\ \end{array} } \right.$$
(1)
Fig. 3
figure 3

Initial system of of backstepping controller

Full size image

A nonlinear IBS controller is used for MPPT and PFC boost converters as given in Fig. 4, which provides the duty cycle for both converters. It tracks the MPPT successfully and also maintains a power factor nearly equal to unity and reduces the THD of the system. In Fig. 4, the SW1 is used for boost converter 1, which is connected after a rectifier for PFC to maintain 400 V at the DC bus. SW2 is used for boost converter 2, which is connected after SPV for MPPT. SW3 is used to disconnect the grid with solar for intelligent power-sharing purposes and ON when Pin < Pload to connect the grid to the load.

Fig. 4
figure 4

Non-inverting boost converter for MPPT & PFC

Full size image

3 Control Methodology

The conventional method for MPPT and the proposed methodology is fairly different. A linear regression plane of the SPV module is utilized in the proposed system. It gives a reference voltage for MPP by sensing the temperature and irradiation on the SPV module. The regression plane uses a relationship between V_mpp, temperature, and irradiation to provide reference peak voltage. The nonlinear controller tracks this reference voltage and provides output signal \(u\) by mathematical modeling of a boost converter. This \(u\) generates the pulse width modulation (PWM) duty ratio and provides the signal to the converter.

The flow chart given by the researcher [14] proposed the non-inverting buck-boost converter with its modeling. The proposed research used the modeling of a non-inverting boost converter shown in Fig. 5. The regression plane generates the reference voltage (V_ref) and compared it with the SPV voltage V_ref. Their difference generates an error signal and is fed to the IBS controller. The controller generates an input PWM signal by controlling the width of the signal. This PWM drives the converter and tracks the reference voltage. Changes in temperature and/or irradiation generate a new reference voltage which results in the generation of a new signal \(u\) for the PWM to track this reference voltage.

Fig. 5
figure 5

Integral backstepping algorithm for boost converter [14]

Full size image

4 Reference Voltage Generation by Regression Plane

Changes in the temperature and irradiation parameters result in a modified characteristics curve of the SPVC, consequently by modifying the MPP. By varying the temperature in increments from 25 °C to 50 °C and keeping the irradiance level constant at 1000 W/m2, several MPPs have been observed. By keeping the temperature constant at 25 °C and varying the irradiation from 200 W/m2 to 1400 W/m2, several more points have been observed. By using the linear regression method, a three-dimensional regression plane has been generated which provides the peak power voltage on any radiation and temperature with the following equation [15]

$$V\_mpp = 332 - 1.34*T - 0.00964*I\quad {\text{where}}\quad \, T = {\text{temperature }}\& \, I = {\text{ irradiation}}$$

5 Modeling of Non-Inverting Boost Converter

A non-inverting DC-DC boost converter is used to step up the output voltage and the circuit configuration of the converter as shown in Fig. 6.

Fig. 6
figure 6

Non-inverting boost converter with solar

Full size image

The model of the boost converter is derived assuming ideal switches and diodes. Similarly, for an ideal converter, the resistance of the inductor and capacitor is assumed to be zero and all switches are considered in continuous current mode (CCM). Both boost converters have the same model and consist of two modes of operation.

In Mode 1, the switch is closed/turned on and the diode is reverse biased, i.e., not conducting. The equations are computed by Kirchhoff’s current and voltage law.

In Mode 2, the switch is opened/turned off and the diode is forward biased. Then, capacitor C2 is connected with an inductor which charges the capacitor. The state variables of the given circuits are defined as \(V_{{C_{1} }} = X_{1} , I_{L} = X_{2} \& V_{{C_{2} }} = X_{3}\)

$$I_{s} = I_{c1} + { }I_{L}$$
(2)
$$V_{C1} = V_{L}$$
(3)
$$I_{{C_{2} }} = - I_{R}$$
(4)

For Mode 2, when the switch is opened/turned OFF and a diode is in conduction mode, then applying Kirchhoff's voltage and current law the equations have the form

$$I_{s} = I_{c1} + { }I_{L}$$
(5)
$$V_{L} = V_{C1} - { }V_{C2}$$
(6)
$$I_{C2} = I_{L} - I_{R}$$
(7)

Applying the capacitor charge balance equation and inductor’s voltage balance equation, we can write

$$\dot{V}_{C1} = \frac{{I_{s} }}{{C_{1} }} - \frac{{I_{L} }}{{C_{1} }}$$
(8)
$$\dot{I}_{L} = \frac{{V_{C1} }}{L} - \frac{{V_{C2} }}{L}\left( {1 - u} \right)$$
(9)
$$\dot{V}_{C2} = \frac{{I_{L} }}{{C_{2} }}\left( {1 - u} \right) - \frac{{V_{C2} }}{{RC_{2} }}$$
(10)

Apply the average model on the above equation on one switch period.

Assume that

$$\left| {X_{1} X_{2} X_{3} } \right| = \left[ {\left\langle {V_{C1} } \right\rangle \left\langle {I_{L} } \right\rangle \left\langle {V_{C2} } \right\rangle } \right]$$

The equations become

$$\dot{X}_{1} = \frac{{I_{s} }}{{C_{1} }} - \frac{{X_{2} }}{{C_{1} }}$$
(11)
$$\dot{X}_{2} = \frac{{X_{1} }}{L} - \frac{{X_{3} }}{L}\left( {1 - u} \right)$$
(12)
$$\dot{X}_{3} = \frac{{X_{2} }}{{C_{2} }}\left( {1 - u} \right) - \frac{{X_{3} }}{{RC_{2} }}$$
(13)

The average state-space model is used to track the reference voltage, and Eq. (13) is used to track the reference voltage for MMPT and PFC. The parameters of the SPV array are given in Table 1.

Table 1 Parameters and values for SPV array
Full size table

6 Modeling of Integral Backstepping Controller for MPPT

A nonlinear backstepping controller is modified by introducing integral action in MPPT to track the generated reference voltage for the SPV array. The designed controller provides the input \(u\), which determines the duty cycle for converter switching. The reference MPP generated in Sect. 3 is termed X1ref since it is the first state of the converter modeling. The modified modeling of the IBS controller for MPPT is given below.

For MPPT, \(V_{mpp}\) of the solar is the reference voltage and it is traced by Eq. (13). Assume that \(\in_{1}\) is the error between a reference voltage and actual voltage

$$\in_{1} = X_{3} - X_{{3{\text{ref}}}}$$
(14)
$$\dot{ \in }_{1} = \dot{X}_{3} - \dot{X}_{{3{\text{ref}}}}$$
(15)

We have to converge the error \(\dot{ \in }_{1}\) to zero by taking the time derivative of Eq. (14), and putting the value of \(\dot{X}_{3}\) we have

$$\dot{ \in }_{1} = \dot{X}_{3} - \dot{X}_{{3{\text{ref}}}} = \left( {{\raise0.7ex\hbox{${X_{2} }$} \!\mathord{\left/ {\vphantom {{X_{2} } {C_{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${C_{2} }$}}} \right)\left( {1 - u} \right) - {\raise0.7ex\hbox{${X_{3} }$} \!\mathord{\left/ {\vphantom {{X_{3} } {RC_{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${RC_{2} }$}} - \dot{X}_{{3{\text{ref}}}}$$
(16)

Adding integral action S to error

$$e_{1} = \in_{1} + S$$
(17)
$$S = \mathop \smallint \limits_{0}^{t} \left( {X_{1} - X_{{1{\text{ref}}}} } \right)dt$$
(18)

For checking the convergence of \(\in_{1}\) to 0, let \(V_{1}\) be the Lyapunov function candidate

$$V_{1} = \frac{1}{2}\left( { \in_{1} } \right)^{2} + \frac{K}{2}S^{2}$$
(19)

where K is the positive definite real number. To check the asymptotic stability, a derivative of the Lyapunov function should be negative definite. By taking the derivative of Eq. (19), we get

$$\dot{V}_{1} = \dot{ \in }_{1} \in_{1} + KS\dot{S}$$
(20)

By putting the value of \(\dot{ \in }_{1}\) from Eq. (16) into Eq. (20), we get

$$\begin{aligned}\dot{V}_{1} &= \in_{1} \left( {\left( {{\raise0.7ex\hbox{${X_{2} }$} \!\mathord{\left/ {\vphantom {{X_{2} } {C_{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${C_{2} }$}}} \right)\left( {1 - u} \right) - {\raise0.7ex\hbox{${X_{3} }$} \!\mathord{\left/ {\vphantom {{X_{3} } {RC_{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${RC_{2} }$}} - \dot{X}_{{1{\text{ref}}}} } \right) \\ & \quad + KS\left( {X_{1} - \dot{X}_{{1{\text{ref}}}} } \right) \end{aligned}$$
(21)

Simplify

$$\dot{V}_{1} = \in_{1} \left( {\left( {{\raise0.7ex\hbox{${X_{2} }$} \!\mathord{\left/ {\vphantom {{X_{2} } {C_{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${C_{2} }$}}} \right)\left( {1 - u} \right) - {\raise0.7ex\hbox{${X_{3} }$} \!\mathord{\left/ {\vphantom {{X_{3} } {{\text{RC}}_{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{\text{RC}}_{2} }$}} + KS - \dot{X}_{{1{\text{ref}}}} } \right)$$
(22)

For making \(\dot{V}_{1}\) negative definite, let

$$\left( {\left( {{\raise0.7ex\hbox{${X_{2} }$} \!\mathord{\left/ {\vphantom {{X_{2} } {C_{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${C_{2} }$}}} \right)\left( {1 - u} \right) - {\raise0.7ex\hbox{${X_{3} }$} \!\mathord{\left/ {\vphantom {{X_{3} } {{\text{RC}}_{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{\text{RC}}_{2} }$}} + KS - \dot{X}_{{1{\text{ref}}}} } \right) = - K_{1} \in_{1}$$
(23)
$$\dot{V}_{1} = - K_{1} \left( { \in_{1} } \right)^{2}$$
(24)

Rewriting Eq. (23) for \({X}_{2},\) we get

$$\frac{{C_{2} }}{{\left( {1 - u} \right)}}\left( { - K_{1} \in_{1} + \left( {{\raise0.7ex\hbox{${X_{3} }$} \!\mathord{\left/ {\vphantom {{X_{3} } {C_{2} R}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${C_{2} R}$}}} \right) - {\text{KS}} + \dot{X}_{{1{\text{ref}}}} } \right) = X_{2}$$
(25)

Let Eq. (25) be the desired reference for the inductor's current

$$X_{2} = {\text{Reference}} = \beta$$

Now introduce the error in \(X_{2}\) to track \(\beta\)

$$X_{2} = \in_{2} + \beta$$
(26)
$$\dot{ \in }_{1} = \left( {{\raise0.7ex\hbox{${X_{2} }$} \!\mathord{\left/ {\vphantom {{X_{2} } {C_{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${C_{2} }$}}} \right)\left( {1 - u} \right) - {\raise0.7ex\hbox{${X_{3} }$} \!\mathord{\left/ {\vphantom {{X_{3} } {RC_{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${RC_{2} }$}} - \dot{X}_{1ref}$$

Putting Eq. (26) into Eq. (16)

$$\dot{ \in }_{1} = \frac{{ \in_{2} + \beta }}{{C_{2} }}\left( {1 - u} \right) - {\raise0.7ex\hbox{${X_{3} }$} \!\mathord{\left/ {\vphantom {{X_{3} } {RC_{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${RC_{2} }$}} - \dot{X}_{{1{\text{ref}}}}$$
(27)
$$\beta = \frac{{C_{2} }}{{\left( {1 - u} \right)}}\left( { - K_{1} \in_{1} + \left( {{\raise0.7ex\hbox{${X_{3} }$} \!\mathord{\left/ {\vphantom {{X_{3} } {C_{2} R}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${C_{2} R}$}}} \right) - KS + \dot{X}_{{1{\text{ref}}}} } \right)$$
$$\dot{ \in }_{1} = \frac{{ \in_{2} \left( {1 - u} \right)}}{{C_{2} }} + \frac{{\beta \left( {1 - u} \right)}}{{C_{2} }} - {\raise0.7ex\hbox{${X_{3} }$} \!\mathord{\left/ {\vphantom {{X_{3} } {RC_{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${RC_{2} }$}} - \dot{X}_{{1{\text{ref}}}}$$
$$\begin{aligned} \dot{ \in }_{1} &= \frac{{ \in_{2} \left( {1 - u} \right)}}{{C_{2} }} + \left( { - K_{1} \in_{1} + \left( {{\raise0.7ex\hbox{${X_{3} }$} \!\mathord{\left/ {\vphantom {{X_{3} } {C_{2} R}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${C_{2} R}$}}} \right) - KS + \dot{X}_{{1{\text{ref}}}} } \right) \\ & \quad - \frac{{X_{3} }}{{RC_{2} }} - \dot{X}_{{1{\text{ref}}}} \end{aligned}$$

By putting the value of \(\beta\) in Eq. (27), we get

$$\dot{ \in }_{1} = \frac{{ \in_{2} \left( {1 - u} \right)}}{{C_{2} }} - K_{1} \in_{1} - KS$$
(28)

So, Eq. (20) becomes

$$\dot{V}_{1} = \in_{1} \dot{ \in }_{1} + KS\dot{S}$$
(29)

Simplify and assume

$$\dot{V}_{1} = - K_{1} \left( { \in_{1} } \right)^{2} + \frac{{ \in_{1} \in_{2} \left( {1 - u} \right)}}{{C_{2} }}$$
(30)

In the above equation, the first term is negative definite, now for the second term.

$$\in_{2} = X_{2} - \beta$$
(31)

By taking the derivative of Eq. (31) and simplifying

$$\dot{ \in }_{2} = \dot{X}_{2} - \dot{\beta }$$
(32)
$$\beta = \frac{{C_{2} }}{{\left( {1 - u} \right)}}\left( { - K_{1} \in_{1} + {\raise0.7ex\hbox{${X_{3} }$} \!\mathord{\left/ {\vphantom {{X_{3} } {{\text{RC}}_{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{\text{RC}}_{2} }$}} - KS + \dot{X}_{{1{\text{ref}}}} } \right)$$

Taking the derivative of the above equation

$$\begin{aligned} \dot{\beta } &= \frac{{C_{2} }}{{\left( {1 - u} \right)}}\Bigg( - K_{1} \frac{{ \in_{2} \left( {1 - u} \right)}}{{C_{2} }} - \left( {K_{1} } \right)^{2} \in_{1} - K_{1} {\text{KS}} \\ & \quad + {\raise0.7ex\hbox{${X_{3} }$} \!\mathord{\left/ {\vphantom {{X_{3} } {RC_{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${RC_{2} }$}} - K\dot{S} + \ddot{X}_{{1{\text{ref}}}} \Bigg) + \frac{{\beta \dot{u}}}{1 - u} \end{aligned}$$

Simplifying for \(\dot{\beta }\) we have

$$\dot{\beta } = - K_{1} \in_{2} - \frac{{\left( {K_{1} } \right)^{2} \in_{1} C_{2} }}{1 - u} - \frac{{K_{1} {\text{KSC}}_{2} }}{{\left( {1 - u} \right)}} + \frac{{X_{3} }}{{R\left( {1 - u} \right)}} - \frac{{K\dot{S}C_{2} }}{{\left( {1 - u} \right)}} + \frac{{\ddot{X}_{1ref} C_{2} }}{{\left( {1 - u} \right)}} + \frac{{\beta \dot{u}}}{1 - u}$$
(33)

Now insert the value of \(\dot{\beta }\) in Eq. (32)

To converge both errors \(\in_{1}\) and \(\in_{2}\) to 0, a new Lyapunov function \(V_{c}\) is introduced and its derivative should be negative definite

$$V_{c} = V_{1} + \frac{1}{2}\left( { \in_{2} } \right)^{2}$$
(34)

Taking the derivative of Eq. (34)

$$\dot{V}_{c} = \dot{V}_{1} + \in_{2} \dot{ \in }_{2}$$
(35)
$$\dot{V}_{1} = \frac{{ \in_{1} \in_{2} \left( {1 - u} \right)}}{{C_{2} }} - K_{1} \left( { \in_{1} } \right)^{2} - K \in_{1} S + KS\dot{S}$$

Putting the value of \(\dot{V}_{1}\) in Eq. (35), we get

$$\dot{V}_{c} = \frac{{ \in_{1} \in_{2} \left( {1 - u} \right)}}{{C_{2} }} - K_{1} \left( { \in_{1} } \right)^{2} + \in_{2} \dot{ \in }_{2}$$
(36)
$$\dot{V}_{c} = - K_{1} \left( { \in_{1} } \right)^{2} + \in_{2} \left( {\frac{{ \in_{1} \left( {1 - u} \right)}}{{C_{2} }} + \dot{ \in }_{2} } \right)$$
(37)

For \(\dot{V}_{1}\) to be negative definite, let

$$\frac{{ \in_{1} \left( {1 - u} \right)}}{{C_{2} }} + \dot{ \in }_{2} = - K_{2} \in_{2}$$
(38)
$$\dot{V}_{c} = - K_{1} \left( { \in_{1} } \right)^{2} - K_{2} \left( { \in_{2} } \right)^{2}$$
(39)
$$- K_{2} \in_{2} = \dot{X}_{2} - \dot{\beta } + \mathop {\frac{{ \in_{1} \left( {1 - u} \right)}}{{C_{2} }}}\limits^{.}$$
(40)

\(\dot{u} = \frac{{ - K_{2} \in_{2} \left( {1 - u} \right)}}{\beta } - \left( {\frac{{\dot{X}_{1} }}{L} - \frac{{X_{3} }}{L}\left( {1 - u} \right)} \right)\frac{{\dot{X}_{2} }}{\beta }\left( {1 - u} \right) - \frac{{K_{1} \in_{2} \left( {1 - u} \right)}}{\beta } + \frac{{\left( {K_{1} } \right)^{2} \in_{1} C_{2} }}{\beta } - \frac{{K_{1} KSC_{2} }}{\beta } - \frac{{X_{3} }}{R\beta } + \frac{{K\dot{S}C_{2} }}{\beta } - \frac{{\ddot{X}_{1ref} C_{2} }}{\beta }\) Now the value of \(u\) is between 0 and 1 and \(\beta\) ≠ 0. This value of \(u\) is used for controlling the duty cycle of the switches. \(\dot{u}\) in above equation shows the asymptotic stability of the controller; a derivative of the Lyapunov function is negative definite which ensures the convergence of the error \(\in_{1}\) equal to 0.

7 Proposed Control Topology for PFC

Without the incorporation of PFC in modes II and III, the power quality of A.C supply remains low. The boost PFC converter control is generally accomplished by a current loop and voltage loop. The current loop has the objective of making the converter input current follow the sinusoidal waveform of the input voltage, providing a high power factor to the converter and low THD to the current drawn from the electric system. The objective of the voltage loop is to regulate the output voltage of the converter.

The boost PFC converter is designed to raise the utility ac input voltage to a dc desired value (400 V) and to make the input current waveform follow the input voltage waveform. The main advantages of this control system are that the converter operates in continuous current mode (CCM) at high power and provides low input current THD and high converter PF for the entire output power range. The proposed PFC technique used a boost converter in continuous current mode. In CCM, both output capacitor and inductor are in continuous conduction mode throughout the period. IBS controller is used for PFC which maintains the sinusoidal shape of the current and tries to maintain both current and voltage in phase.

7.1 Modeling of Integral Backstepping Controller for PFC

IBS controller has been designed for PFC by applying the IBS technique on the boost converter. The duty cycle equation for the PWM of the boost converter is derived. The converter should have to maintain the 400 V at DC bus to track the reference voltage for PFC and to track Eq. (13) is used.

Assuming that \(\in_{1}\) is the error between the reference voltage and actual voltage

$$\begin{gathered} \in_{1} = X_{3} - X_{{3{\text{ref}}}} \hfill \\ \dot{ \in }_{1} = \dot{X}_{3} - \dot{X}_{{{\text{3ref}}}} \hfill \\ \end{gathered}$$
(41)

We have to converge the error \(\dot{ \in }_{1}\) to zero by taking the time derivative of Eq. (41) and putting the value of \(\dot{X}_{3}\) we have

$$\dot{ \in }_{1} = \dot{X}_{3} - \dot{X}_{{{\text{3ref}}}} = \left( {{\raise0.7ex\hbox{${X_{2} }$} \!\mathord{\left/ {\vphantom {{X_{2} } {C_{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${C_{2} }$}}} \right)\left( {1 - u} \right) - {\raise0.7ex\hbox{${X_{3} }$} \!\mathord{\left/ {\vphantom {{X_{3} } {RC_{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${RC_{2} }$}} - \dot{X}_{{3{\text{ref}}}}$$
(42)

Adding integral action S to error

$$e_{1} = \in_{1} + S$$
(43)
$$S = \mathop \smallint \limits_{0}^{t} \left( {X_{3} - X_{{3{\text{ref}}}} } \right)dt$$
(44)

For checking the convergence of \(\in_{1}\) to 0, let \(V_{1}\) be the Lyapunov function candidate

$$V_{1} = \frac{1}{2}\left( { \in_{1} } \right)^{2} + \frac{K}{2}S^{2}$$
(45)

where K is the positive definite real number. To check the asymptotic stability, the derivative of the Lyapunov function should be negative definite. By taking the derivative of Eq. (45), we get

$$\dot{V}_{1} = \dot{ \in }_{1} \in_{1} + KS\dot{S}$$
(46)

By putting the value of \(\dot{ \in }_{1}\) from Eq. (42) into Eq. (46), we get

$$\begin{aligned} \dot{V}_{1} &= \in_{1} \left( {\left( {{\raise0.7ex\hbox{${X_{2} }$} \!\mathord{\left/ {\vphantom {{X_{2} } {C_{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${C_{2} }$}}} \right)\left( {1 - u} \right) - {\raise0.7ex\hbox{${X_{3} }$} \!\mathord{\left/ {\vphantom {{X_{3} } {{\text{RC}}_{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{\text{RC}}_{2} }$}} - \dot{X}_{{3{\text{ref}}}} } \right) \\ & \quad + KS\left( {X_{3} - X_{{3{\text{ref}}}} } \right) \end{aligned}$$
(47)

Simplify

$$\dot{V}_{1} = \in_{1} \left( {\left( {{\raise0.7ex\hbox{${X_{2} }$} \!\mathord{\left/ {\vphantom {{X_{2} } {C_{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${C_{2} }$}}} \right)\left( {1 - u} \right) - {\raise0.7ex\hbox{${X_{3} }$} \!\mathord{\left/ {\vphantom {{X_{3} } {{\text{RC}}_{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{\text{RC}}_{2} }$}} + KS - \dot{X}_{{3{\text{ref}}}} } \right)$$
(48)

We have to make \(\dot{V}_{1}\) negative definite; for this, let

$$\left( {\left( {{\raise0.7ex\hbox{${X_{2} }$} \!\mathord{\left/ {\vphantom {{X_{2} } {C_{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${C_{2} }$}}} \right)\left( {1 - u} \right) - {\raise0.7ex\hbox{${X_{3} }$} \!\mathord{\left/ {\vphantom {{X_{3} } {{\text{RC}}_{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{\text{RC}}_{2} }$}} + KS - \dot{X}_{{3{\text{ref}}}} } \right) = - K_{1} \in_{1}$$
(49)
$$\dot{V}_{1} = - K_{1} \left( { \in_{1} } \right)^{2}$$
(50)

Rewriting Eq. (49) for \({\text{X}}_{2}\), we get

$$\frac{{C_{2} }}{{\left( {1 - u} \right)}}\left( { - K_{1} \in_{1} + \left( {{\raise0.7ex\hbox{${X_{3} }$} \!\mathord{\left/ {\vphantom {{X_{3} } {C_{2} R}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${C_{2} R}$}}} \right) - KS + \dot{X}_{3ref} } \right) = X_{2}$$
(51)

Let Eq. (51) be the desired reference for the inductor's current

$$X_{2} = {\text{Reference}} = \beta$$

Now introduce another error in \(X_{2}\) to track \(\beta\)

$$\in_{2} = X_{2} - \beta$$
$$X_{2} = \in_{2} + \beta$$
(52)
$$\dot{ \in }_{1} = \left( {{\raise0.7ex\hbox{${X_{2} }$} \!\mathord{\left/ {\vphantom {{X_{2} } {C_{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${C_{2} }$}}} \right)\left( {1 - u} \right) - {\raise0.7ex\hbox{${X_{3} }$} \!\mathord{\left/ {\vphantom {{X_{3} } {{\text{RC}}_{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{\text{RC}}_{2} }$}} - \dot{X}_{{3{\text{ref}}}}$$

Putting Eq. (52) into Eq. (42),

$$\dot{ \in }_{1} = \frac{{ \in_{2} + \beta }}{{C_{2} }}\left( {1 - u} \right) - {\raise0.7ex\hbox{${X_{3} }$} \!\mathord{\left/ {\vphantom {{X_{3} } {{\text{RC}}_{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{\text{RC}}_{2} }$}} - \dot{X}_{{3{\text{ref}}}}$$
(53)

From Eq. (51),

$$\beta = \frac{{C_{2} }}{{\left( {1 - u} \right)}}\left( { - K_{1} \in_{1} + \left( {{\raise0.7ex\hbox{${X_{3} }$} \!\mathord{\left/ {\vphantom {{X_{3} } {C_{2} R}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${C_{2} R}$}}} \right) - {\text{KS}} + \dot{X}_{{3{\text{ref}}}} } \right)$$
(54)
$$\dot{ \in }_{1} = \frac{{ \in_{2} \left( {1 - u} \right)}}{{C_{2} }} + \frac{{\beta \left( {1 - u} \right)}}{{C_{2} }} - {\raise0.7ex\hbox{${X_{3} }$} \!\mathord{\left/ {\vphantom {{X_{3} } {{\text{RC}}_{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{\text{RC}}_{2} }$}} - \dot{X}_{{{\text{3ref}}}}$$
$$\begin{aligned} \dot{ \in }_{1} &= \frac{{ \in_{2} \left( {1 - u} \right)}}{{C_{2} }} + \left( { - K_{1} \in_{1} + \left( {{\raise0.7ex\hbox{${X_{3} }$} \!\mathord{\left/ {\vphantom {{X_{3} } {C_{2} R}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${C_{2} R}$}}} \right) - {\text{KS}} + \dot{X}_{3ref} } \right) \\ & \quad - \frac{{X_{3} }}{{{\text{RC}}_{2} }} - \dot{X}_{{3{\text{ref}}}} \end{aligned}$$

By putting the value of \(\beta\) in Eq. (53), after simplification

$$\dot{ \in }_{1} = \frac{{ \in_{2} \left( {1 - u} \right)}}{{C_{2} }} - K_{1} \in_{1} - {\text{KS}}$$
(55)

So, Eq. (46) become

$$\dot{V}_{1} = \in_{1} \dot{ \in }_{1} + KS\dot{S}$$
(56)

Simplify and assume

$$\dot{V}_{1} = - K_{1} \left( { \in_{1} } \right)^{2} + \frac{{ \in_{1} \in_{2} \left( {1 - u} \right)}}{{C_{2} }}$$
(57)

In the above equation, the first term is negative definite, but we are not sure about the second term.

$$\in_{2} = X_{2} - \beta$$
(58)

By taking the derivative of the above equation on and simplifying

$$\dot{ \in }_{2} = \dot{X}_{2} - \dot{\beta }$$
(59)

Taking the derivative of Eq. (54), we get

$$\dot{\beta } = \frac{{C_{2} }}{{\left( {1 - u} \right)}}\left( { - K_{1} \dot{ \in }_{1} + {\raise0.7ex\hbox{${X_{3} }$} \!\mathord{\left/ {\vphantom {{X_{3} } {RC_{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${RC_{2} }$}} - K\dot{S} + \ddot{X}_{3ref} } \right) + \frac{{\beta \dot{u}}}{1 - u}$$
$$\begin{aligned} \dot{\beta } &= \frac{{C_{2} }}{{\left( {1 - u} \right)}}\Bigg( - K_{1} \left( {\frac{{ \in_{2} \left( {1 - u} \right)}}{{C_{2} }} - K_{1} \in_{1} - KS} \right) \\ & \quad + {\raise0.7ex\hbox{${X_{3} }$} \!\mathord{\left/ {\vphantom {{X_{3} } {RC_{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${RC_{2} }$}} - K\dot{S} + \ddot{X}_{3ref} \Bigg) + \frac{{\beta \dot{u}}}{1 - u} \end{aligned}$$
$$\begin{aligned} \dot{\beta } &= \frac{{C_{2} }}{{\left( {1 - u} \right)}}\Bigg( - K_{1} \frac{{ \in_{2} \left( {1 - u} \right)}}{{C_{2} }} - \left( {K_{1} } \right)^{2} \in_{1} - K_{1} KS \\ & \quad + {\raise0.7ex\hbox{${X_{3} }$} \!\mathord{\left/ {\vphantom {{X_{3} } {RC_{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${RC_{2} }$}} - K\dot{S} + \ddot{X}_{3ref} \Bigg) + \frac{{\beta \dot{u}}}{1 - u} \end{aligned}$$

Simplifying for \(\dot{\beta }\), we have

$$\dot{\beta } = - K_{1} \in_{2} - \frac{{\left( {K_{1} } \right)^{2} \in_{1} C_{2} }}{1 - u} - \frac{{K_{1} KSC_{2} }}{{\left( {1 - u} \right)}} + \frac{{X_{3} }}{{R\left( {1 - u} \right)}} - \frac{{K\dot{S}C_{2} }}{{\left( {1 - u} \right)}} + \frac{{\ddot{X}_{3ref} C_{2} }}{{\left( {1 - u} \right)}} + \frac{{\beta \dot{u}}}{1 - u}$$
(60)

Now insert the value of \(\dot{\beta }\) in Eq. (59).

To converge both errors \(\in_{1}\) and \(\in_{2}\) to 0, a new Lyapunov function \(V_{c}\) is introduced and its time derivative should be negative definite for system stability.

$$V_{c} = V_{1} + \frac{1}{2}\left( { \in_{2} } \right)^{2}$$
(61)

Taking the derivative of the above equation

$$\dot{V}_{c} = \dot{V}_{1} + \in_{2} \dot{ \in }_{2}$$
(62)
$$\dot{V}_{1} = \frac{{ \in_{1} \in_{2} \left( {1 - u} \right)}}{{C_{2} }} - K_{1} \left( { \in_{1} } \right)^{2} - K \in_{1} S + KS\dot{S}$$

Putting the value of \(\dot{V}_{1}\) in Eq. (61), we get

$$\dot{V}_{c} = \frac{{ \in_{1} \in_{2} \left( {1 - u} \right)}}{{C_{2} }} - K_{1} \left( { \in_{1} } \right)^{2} + \in_{2} \dot{ \in }_{2}$$
(63)
$$\dot{V}_{c} = - K_{1} \left( { \in_{1} } \right)^{2} + \in_{2} \left( {\frac{{ \in_{1} \left( {1 - u} \right)}}{{C_{2} }} + \dot{ \in }_{2} } \right)$$
(64)

For \(\dot{V}_{1}\) to be negative and definite, let

$$\frac{{ \in_{1} \left( {1 - u} \right)}}{{C_{2} }} + \dot{ \in }_{2} = - K_{2} \in_{2}$$
(65)

So \(\dot{V}_{c}\) becomes

$$\dot{V}_{c} = - K_{1} \left( { \in_{1} } \right)^{2} - K_{2} \left( { \in_{2} } \right)^{2}$$
(66)
$$- K_{2} \in_{2} = \dot{X}_{2} - \dot{\beta } + \mathop {\frac{{ \in_{1} \left( {1 - u} \right)}}{{C_{2} }}}\limits^{.}$$
(67)

Now putting the values in Eq. (65), the final equation is

$$\begin{aligned} \dot{u} &= \frac{{ - K_{2} \in_{2} \left( {1 - u} \right)}}{\beta } - \left( {\frac{{\dot{X}_{1} }}{L}\left( {1 - 2u} \right) + \frac{{X_{3} }}{L}\left( {1 - u} \right)} \right)\\ & \quad \frac{{\left( {1 - u} \right)}}{\beta } - \frac{{K_{1} \in_{2} \left( {1 - u} \right)}}{\beta }+ \frac{{\left( {K_{1} } \right)^{2} \in_{1} C_{2} }}{\beta } \\ & \quad - \frac{{K_{1} KSC_{2} }}{\beta } - \frac{{X_{3} }}{R\beta } + \frac{{K\dot{S}C_{2} }}{\beta } - \frac{{\ddot{X}_{3ref} C_{2} }}{\beta } \end{aligned}$$

Now the value of \(u\) is between 0 and 1 and \(\beta\)≠0. This value of \(u\) is used for controlling the duty cycle of the switch. \(\dot{u}\) in the equation shows the asymptotic stability of the controller; a derivative of Lyapunov function is negative definite which ensures the convergence of the error \({\in }_{1}\) equal to 0.

8 Simulations Results

MATLAB/Simulink is used for the verification of the proposed controller. Simulation results are separated into four sections. Results of the IBS controller on SPV for MPPT by varying temperature and irradiations are discussed in Sect. 7.1. In Sect. 7.2, a comparison is presented between conventional MPPT and P&O with the proposed controller by varying temperature and irradiation. Results of the IBS controller for PFC with grid-connected and the comparison of PI controller and IBS controller for PFC are presented in Sect. 7.3. Parameters of the integral backstepping controller are given in Table 2.

Table 2 Parameters and values for MPPT controller & PFC controller
Full size table

8.1 MPPT by Varying Irradiation and Temperature

8.1.1 Case 1: Test Under Varying Irradiation

The regression plane generates the reference voltage for MPPT, and the controller successfully tracks the reference voltage shown in Fig. 7 with a 4% overshoot and approximately zero steady-state error. The test results of power generated by the SPV array with change in irradiation are shown in Fig. 8a–e, which consists of irradiance, temperature, power, voltage, and duty cycle graphs. To test the proposed controller under rapidly varying conditions, irradiation for testing the SPV array varies from 200 \({\text{W}}/{\text{m}}^{2}\) to 600 \({\text{W}}/{\text{m}}^{2}\) at time 0.05 s with a constant temperature of 25 ℃. There is an abrupt change from 600 \({\text{W}}/{\text{m}}^{2}\) to 1000 \({\text{W}}/{\text{m}}^{2}\) at 0.1 s. It shows that MPP is achieved in 2 ms with no ripples while power is being transmitted to the load.

Fig. 7
figure 7

MPP voltage using IBS under varying irradiation

Full size image
Fig. 8
figure 8

MPPT simulation under varying irradiation

Full size image

8.1.2 Case 2: Test Under Varying Temperature

In this test, the simulation is carried out by keeping the irradiation of the SPV array constant at 1000 W/m2 and under varying temperatures. Initially, the temperature is kept constant at 25 °C till 0.5 s and the temperature change occurs from 25 °C to 50 °C from 0.5 s onwards. Due to the temperature change, the regression plane generates the new reference voltage also successfully tracked by the controller with a small overshoot of 2% and again steady-state error is approximately zero as shown in Fig. 9. The test results of power generated by the SPV array with temperature variations are shown in Fig. 10a–e, which consists of irradiance, temperature, power, voltage, and duty cycle graphs. By increasing the temperature, power generated by the solar cells decreases, but the controller successfully tracks the MPP with negotiable ripples at the output.

Fig. 9
figure 9

MPP voltage using IBS under varying temperature

Full size image
Fig. 10
figure 10

MPPT simulations under varying temperature

Full size image

8.2 Comparison with P&O

Conventional P&O technique for MPPT is applied on the same SPV system, and simulations are performed. The P&O technique is tested under the same variations in input parameters and compared with the proposed controller. The results are shown in Fig. 11 for comparison of the SPV voltage. It shows that the conventional MPPT output produces voltage fluctuation and takes more time to reach the MPP voltage. The difference between the MPP voltage of IBS and P&O under varying irradiation and varying temperatures is shown in Figs. 12 and 13. It has been observed that the proposed controller is more robust compared to P&O which not only tracks the setpoint voltage but also acquires MPPT robustly. The power comparison results of P&O and the proposed controller are shown in Figs. 14 and 15. It is observed from the graphs that the power generated by the proposed controller reaches the maximum power more quickly than the P&O. The P&O technique takes more time and the proposed controller is more robust.

Fig. 11
figure 11

MPP voltage comparison between P&O and IBS under varying irradiation & temperature

Full size image
Fig. 12
figure 12

Difference between MPP voltage of IBS and P&O under varying irradiation

Full size image
Fig. 13
figure 13

Difference in MPP voltage by IBS and P&O under varying temperature

Full size image
Fig. 14
figure 14

Comparison between powers generated by IBS and P&O under varying irradiation

Full size image
Fig. 15
figure 15

difference in power generated by P&O and IBS

Full size image

8.3 Power Factor Improvement in Grid-Connected System

The proposed controller is compared with the PI controller for power factor improvement by using a boost converter with IBS. Parameters of the boost converter are given above in Table 2. Figure 16a, b shows the output current and the DC link voltage of the PFC boost converter. It has been observed that the proposed controller successfully tracks the reference voltage within 1 ms. Figure 17 shows the voltage and current relationship for the IBS controller. Figure 18a shows the power factor of the proposed controller. The power factor of the system has been improved to 99.26%. Figure 18b shows the power factor achieved using the PI controller is 97%. Furthermore, the proposed controller is more robust and produces less fluctuation in power factor compared to the PI controller. Figure 19a, b shows the THD of both PI and IBS controllers. THD has also been reduced by the proposed controller. THD is 1.28% by using the integral backstepping controller while it is 12.11% using the PI controller.

Fig. 16
figure 16

a Output current of the PFC boost converter, b DC bus (link) voltage

Full size image
Fig. 17
figure 17

IBS voltage and current relationship

Full size image
Fig. 18
figure 18

a Power factor using IBS technique. b Power factor using PI

Full size image
Fig. 19
figure 19

a THD using a PI controller. b IBS technique

Full size image

The proposed controller performed well in comparison with all of them, and it completely removes the steady state error as well. Although the controller is exceptional in its performance, it is completely dependent on the authenticity of the regression plane. Since the PV arrays are subjected to wear and tear in the real world, maintenance of the regression plane is necessary for the controller’s optimal performance. The reference generation under partial shading may require the integration of other techniques such as particle swarm optimization (PSO) and ant colony optimization (ACO) to successfully generate maximum power.

The designed hybrid solar inverters used mostly conventional techniques of PFC and MPPT which is less efficient than the proposed controller. These techniques can be replaced by the proposed IBS controller easily for making the system more efficient. These techniques can easily be implemented on any 32-bit microcontroller.

9 Conclusion

The integral backstepping controller improves the system's robustness in case of modeling uncertainties and external disturbance, therefore improving steady-state control accuracy. In this work, the IBS technique has been applied for PFC and MPPT using the boost converter. The performance of the proposed controller and its comparison with the conventional controller has been simulated in MATLAB Simulink. The simulation results show that the proposed controller for PFC has reduced the THD in output current from 12 to 1% and the power factor has been improved with error reduction from 3 to 1%. The proposed controller is also implemented for MPPT where the simulation result shows that the controller successfully tracks the MPP voltage. The proposed controller is more robust and reduces voltage variation with approximately 0.2% steady-state error in comparison with the P&O technique. Also, simulation results for PFC show that the IBS technique is more robust than the PI controller. It reduces THD and improves the power factor of the system to 0.99 which improves the efficiency of the system. For future work, regression plane under partial shading needs other optimization techniques such as PSO and ACO integrated into the system for better performance in terms of power.