1 Introduction

Image-guided surgery (IGS) offers interventional surgeries with better precision and excellent results due to integrating imaging scanners in the surgical workflow. Classical IGS, on the other hand, is often based on previously obtained images, but intra-operative imaging offers "a real-time treatment" by providing a feedback channel for necessary adjustment. Many excellent guiding modalities were used to provide real-time, volumetric, multi-parametric imaging with good soft tissue contrast, etc. [1, 2].

Robot-assisted minimally invasive surgery (MIS) provides substantial benefits over manual procedures in treatments demanding great precision and accuracy [3]. Significant efforts have been made to develop percutaneous needle therapies that use imaging modalities, including magnetic resonance imaging (MRI), Computed tomography (CT), and ultrasound [1, 4].

Currently, the combination of robotics and neuroimaging (CT and MRI) has expanded surgical options, enabling physicians to reach deeper targets, such as in the human brainstem [5, 6].

The advancement in neuroimaging accuracy, navigational capabilities, flexibility, and speed of robots was game-changing in executing autonomous surgical operations, such as accessing a target in the brain [7]. Furthermore, the robot manipulator may perform a variety of duties in addition to serving as a simple alternative for frame-based or frameless stereotactic equipment [5, 8].

Stereotactic neurosurgery is a surgical treatment that uses the brain's three-dimensional scan (image) to guide the insertion of probes or needles for therapeutic or diagnostic applications. Following registration from images acquired using a CT or MRI scanner, these probes are normally positioned and inserted manually utilizing a stereotactic frame. Recently, research has focused on the use of a robot to aid in the performance of stereotactic operations with the patient inside the scanner bore [9].

Extending on prior research and integrating robotic probe alignment with robotic in-bore manipulation offers the potential to simplify and improve stereotactic treatments [9].

The well-known Neuromate robot, designed for stereotactic neurosurgery, was presented in [10]. The robot is a passive aid that moves to a predetermined location near the target area. The surgical tool is manually placed by a neurosurgeon when the robot has reached the preset place. Cardinale et al. [10] used in vivo procedure and reported the robot frame-based technique localization error to be 0.86 ± 0.54 mm at the entrance point and 2.04 ± 1.31 mm at the target point in 91 SEEG operations.

Rosa (Medtech Surgical, Inc, Montpellier, France) is made up of a 6-DoF revolute joint set on a movable platform and a pre-surgical planning workstation unified with an imaging scanner. It is capable of determining the most efficient path to the goal. Its flexibility allows it to undertake a wide range of neurosurgical operations. Studies by [11] examined the robot registration with phantom and actual clinical use using multiple image paradigms and found that the robot obtained an accuracy of 1.22 mm using a frameless registration using CT and reference imaging.

Renaissance system was developed as a frameless and markerless technology to solve the head immobilization associated with stereotaxic frames. It consists of a 6-DoF miniature (5 × 8 × 8 cm) parallel robot of weight 250 g. It serves as tool guidance. However, the clinician drills and inserts probes or other tools on his own. The surface registration error of the robot was estimated to be around 1 mm, whereas the target registration error was roughly 1.7 mm [12,13,14]. A study conducted by Joskowicz et al. [15] on a phantom revealed a target registration error of 0.65 mm.

Some of the neurosurgery robots served as frameless stereotaxic navigation devices by combining the notions of intraoperative microscopy and neuronavigation in IGS. The prominent MKM systems incorporate a microscope attached to a 6-DoF robotic arm. Researchers in [16] recounted a mean biopsy localization error of 4.5 mm using adhesive markers and 3.3 mm using bone screws.

However, neurosurgical diagnostic and therapy robotization are moving very slowly. Clinics mainly employ frame-based procedures or entirely depend on traditional frame systems. This paved the way for modifying and using industrial robots with less cost and high accuracy for neurosurgical use. Various robotic neuronavigation devices based on industrial manipulators have been created and used in clinical practice [17, 18]. For example, Wang et al. invented Remebot and obtained approval from the Chinese Food and Drug Administration (CFDA) in 2015, and it is now used for biopsy procedures and other therapies [19].

All the aforementioned robotic systems dedicated to neurosurgery have one or more major hitch: the overall cost remains relatively high. The Neuromate system, for example, has a yearly maintenance cost close to a new set of industrial manipulators. As a result, hospitals must strike a balance between overall cost and annual benefits. Secondly, some are bulky like Neuromate or have to be fixed on the skull like Renaissance. Thirdly, they do not possess a remote center motion which is very import and, some are just passive aids. Furthermore, despite the success of industrial manipulators in theater rooms, they still possess hitches of bulkiness that occupy a lot of space, need modification or use of an additional tool holder, cannot be placed on the scanner bed on particular intervention, and many more.

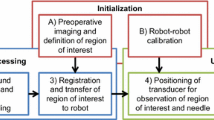
This study presented the mechanical design and evaluation of a 6-DoF CT-compatible stereotactic neurosurgery robot to allow future contributions in this field of stereotactic operations guided by feedback from live CT imaging. Before we employ the manipulator in a healthcare context, we limit the likelihood of failure through proper design characteristics [20].

The kinematic design works almost similar to a Leksell frame, a robust sliding mode control design for accurate positioning of the End-effector (EE), a thorough assessment of the robot's accuracy and repeatability based on the designed control method, and an evaluation of the robot's EE needle driver rotation and insertion accuracy.

The novelty of this work is as follows:

  • A hybrid architecture was used to give the robot rigidity, excellent accuracy, and enhanced dexterity by combining open and closed-chain design.

  • A novel RCM design that differs from traditional parallelogram connections is used to save space.

  • The robot can be attached to a scanner table using a particular device to give the surgeon a better view.

  • A sliding mode observer was designed to limit the use of many sensors that may cause interference and complicate the control scheme.

This work was done in preparation for pre-clinical phantom trials, which we conducted to evacuate a hematoma.

2 Materials and Methods

The manipulator is built with a 6-DoF of open and close chain structures to add rigidity, precision, repeatability, and increased reach. The newly adopted RCM design is shown in Fig. 1. The robot is meant to bring multiple tools to the pathology [21] and offer adequate space for the surgeon to see the surgical site to provide complete neurosurgical capabilities. The robot is divided into three modules, each having its function:

  • The first 3-DOF module (tz, Ry, Rx) is used to set the robot's RCM point at a target position and orientation.

  • RCM orientation module of 1-DOF aligns the needle or probe's axis into the burr hole.

  • An insertion/drilling module of 2-DOF (tx, Rx) that enables in-bore tools manipulation with the help of the RCM module to orient and target directional treatment.

Fig. 1
figure 1

RCM Mechanism diagram

Full size image

The first module uses a prismatic and two rotary joints driven by stepper motors (harmonic type) with a translational motion range of ± 300 mm in the sagittal plane, and the two rotary motion axes range of 0°—360° in transverse and frontal planes, as shown in Table 1. This significantly covered the prefrontal cortex to the visual cortex of the brain. Using this compact design, we may position the EE. in any configuration enclosed within a sphere. The primary building material for this module is aluminum 6061 for the shell and alloy steel for the rotating gears (see Fig. 2). The large ring gear hosted the RCM module and, with the remaining joints, placed the probe in an accurate position. The transmission ratio between the large and smaller ring gear is 48:120.

Table 1 Joint range specifications with motion range measured from home position
Full size table
Fig. 2
figure 2

Schematic diagram of the positioning and orienting mechanism

Full size image

Figure 2 shows an assembly of the RCM with an insertion mechanism and other links. The RCM mechanism uses two circular arc tracks whose center axes are parallel. The mechanism is actuated by a prismatic joint attached firmly to the insertion module and fixed to the large ring gear. The insertion/bone drilling device chassis is bolted on the front, and rear circular arc slide blocks move on circular arc tracks to ensure that the whole module always rotates around the RCM point when the prismatic joint is powered, which pushes the chassis along the circular arc rail. Furthermore, the aluminum 6061 is used to construct the entire module, except for the slide blocks and their circular arc tracks.

The insertion module is placed on the chassis with its end (tool) axis parallel to the axis of the large ring gear and perpendicular to the circular arc center axis, as shown in Fig. 2. This ensures that the whole insertion module always rotates around this point to provide the feed direction vector to meet the requirements of bone drilling and probe insertion at different angles and directions. A lead screw and nut assembly drive the prismatic joint probe insertion along a linear rail, with a D.C. motor attached to the table of the lead screw nut rotating the probe assembly. Following the draping of the robot, the surgeon sterilizes and attaches the probe assembly, a cannula, and a depth stop.

A fiducial frame is installed at the tip of joint 1 (base) to allow the robot to register to the CT scanner's coordinate frame. Attachment slots for reflecting optical tracking markers were also provided for bench-top accuracy assessment. These two reference frames are orthogonal to one another and have known spatial offsets.

The system is managed via a workstation connected to the robot controller. The manipulator control software depicted in Fig. 3 is installed on the workstation and used to operate the robot directly or communicate with a navigation system like 3D Slicer through OpenIGTLink [1].

Fig. 3
figure 3

Robot System architecture control

Full size image

2.1 Kinematics

Afore directing the surgical tool or needle to attain the planned path, the spatial relationships among the tool-tip, the patient, and the designed robot have to be defined [22, 23]. On the patient's skull and the insertion unit, pairs of optical passive tool markers are attached. For ease of reference, the passive tool marker installed on the patient's head is referred to as the patient reference frame, and the one mounted on the insertion module is referred to as the robot reference frame.

When using the robotic system for the first time in a surgical operation, it must be calibrated. Once the calibration is accomplished, there is no need to do one more for future use until the location of the Optical tracking system (OTS) is modified [24]. As shown in Fig. 4, a fixed transformation should be determined during the calibration.

Fig. 4
figure 4

Robotic elements’ kinematic relationships

Full size image

From Fig. 4, the transformation \({}_{TCP}^{Ins\_mod} T\) connects the insertion module reference frame and the coordinate frame of the tool center point (TCP), \({}_{Ins\_mod}^{OTS} T\) signifies the transformation among the OTS reference frame and the frame of the insertion module, \({}_{Base}^{OTS} T\) indicates the transformation between the OTS reference frame and the base frame of the robot, \({}_{Patient}^{OTS} T\) connects the OTS reference frame and the coordinate frame of the patient.

The beginning of TCP corresponds to the tool tip, with the coordinate frame assigned with the Z-axis along the tool shaft. The position vector \({}_{TCP}^{Ins\_mod} P\) is firstly obtained by compiling the measured distance and orientation of the coordinate frame \({}_{TCP}^{OTS} P\) and \({}_{Ins\_mod}^{OTS} P\) position vectors from reference frame OTS. The \({}_{TCP}^{Ins\_mod} P\) is calculated as follows:

$${}_{TCP}^{Ins\_mod} P = {}_{Ins\_mod}^{OTS} R^{T} \left( {{}_{TCP}^{OTS} P - {}_{Ins\_mod}^{OTS} P} \right)$$
(1)

where \({}_{Ins\_mod}^{OTS} R\) signifies the rotation among the OTS reference frame and the frame of the insertion module.

The transformation matrix \({}_{TCP}^{Ins\_mod} T\) is computed utilizing the values of these pair points, and the robot is then coded to follow a trajectory by modifying the joint configuration. The position vector \({}_{TCP}^{OTS} P\) and \({}_{Ins\_mod}^{OTS} P\) is updated with the information from reference frame measurement data. The following equation is used to calculate \({}_{Base}^{OTS} T\):

$${}_{Base}^{OTS} P\; = \;{}_{TCP}^{OTS} P\; - \;{}_{Base}^{OTS} R {}_{TCP}^{Base} P.$$
(2)

The rotation matrix \({}_{TCP}^{Base} R\) and the position vector \({}_{TCP}^{Base} P\) formed the transformation matrix \({}_{TCP}^{Base} T\) which constitute the forward kinematics of the robot. Based on the calculated parameters, the kinematic relation associating the tool-tip and the robot base is gotten:

$${}_{TCP}^{Base} T\; = \;{ }{}_{OTS}^{Base} T {}_{Ins\_mod}^{OTS} T {}_{TCP}^{Ins\_mod} T.$$
(3)

2.2 Control Design

A permanent magnet stepper motor (PMSM) is being designed to deliver a precise positioning control without employing sensors [25,26,27]. PMSM is very reliable with low friction and long life due to bearing in the motor [25, 28, 29]. Furthermore, there are no uses for contact brush, and little effort is needed to dissipate heat due to no rotor winding. As stated above, a PMSM is used with the designed robot.

To control PMSM, we have to explore its nonlinear property, which in [30] introduced differentially flat system theory, which provides a new method of controlling nonlinear dynamic systems. For this, a nonlinear system is differentially flat if its input and state can be obtainable by the output (flat) and its derivatives [31]. Once a system is flat, it indicates that its nonlinear structure can be described and that it can be used to design control schemes.

Moreover, a flat system also does not need the full definition of the external variables to the system to define it [30]. There is no systematic technique to identify the flat output, even though the flat output frequently has definite meanings. This theory has been effectively used for Cycab robots, hovercraft systems, aircraft guidance control, active car suspension, and other applications [32].

2.3 Modeling of Stepper Motor

Throughout this paper, we dealt with bipolar PMSM with no saliency; thus, the stepper motor runs unpredictably in actual applications (parameter discrepancy, load torque perturbation). When we consider the unknowns, the following equations provide the mathematical model for a PMSM.

Considering the parameter variations and load torque perturbation, DQ transformation provides the set of equations for the PMSM as [33];

$$\left\{\begin{array}{l}\frac{{di}_{d}}{dt}=\frac{1}{L}({\left({\delta }_{1}L+1\right)v}_{d}+{(\delta }_{2}L-{R)i}_{d}+N\omega L{i}_{q}) \\ \frac{{di}_{q}}{dt}=\frac{1}{L}({\left({\delta }_{1}L+1\right)v}_{q}+{{(\delta }_{2}L-R)i}_{q}-\left({\delta }_{3}L+{K}_{\infty }\right)\omega -N\omega {i}_{d}) \\ \frac{d\omega }{dt}=\frac{1}{J}(\left({\delta }_{4}J+{K}_{\infty }\right){i}_{q}+-\beta \omega -{\tau }_{L}) \\ \frac{d\theta }{dt}=\omega \end{array}\right.$$
(4)

where \({i}_{d}\), \({i}_{q}\), \({v}_{d}\), \({v}_{q}\) denote direct current, quadrature current, direct voltage, and quadrature voltage. Furthermore, \(N\) denotes the number of rotor teeth, \(J\) is the rotor, and load inertia, \(\beta\) is the viscous friction coefficient, \(R\), and \(L\) are the resistance and inductance of each phase winding, \({K}_{\infty }\) is the motor torque (back-emf) constant, and \({\tau }_{L}\) the load torque.

2.4 The Control Objective

The primary control goal is to maintain a particular position reference path \({\theta }_{r}(t)\). The flat output, \({i}_{d}\), will furthermore be limited to follow a reference trajectory \({i}_{dr}(t)\). The flatness attribute is used to simplify off-line path planning. Once the reference paths \({\theta }_{r}\) and \({i}_{dr}\) have been specified, the trajectories of all the reference parameters \({w}_{r}, {i}_{qr}, {v}_{dr}, and {v}_{qr}\) that fulfill the motor dynamics may be obtained without integrating the differential equations. Indeed, one gets;

$$\left\{\begin{array}{l}{w}_{r}=\frac{{d\theta }_{r}}{dt} \\ {i}_{qr}=\frac{1}{{K}_{\infty }}\left(J\frac{{d}^{2}{\theta }_{r}}{{dt}^{2}}+\beta \frac{{d\theta }_{r}}{dt}\right) \\ {v}_{dr}=L\frac{{di}_{dr}}{dt}+R{i}_{dr}-\frac{NL}{{K}_{\infty }}\frac{{d\theta }_{r}}{dt}\left(J\frac{{d}^{2}{\theta }_{r}}{{dt}^{2}}+\beta \frac{{d\theta }_{r}}{dt}\right) \\ {v}_{qr}=\frac{JL}{{K}_{\infty }}\frac{{{d}^{3}\theta }_{dr}}{{dt}^{3}}+\frac{1}{{K}_{\infty }}\left(L\beta +RJ\right)\frac{{d}^{2}{\theta }_{r}}{{dt}^{2}}+\left(\frac{R\beta }{{K}_{\infty }}+{K}_{\infty }+NL{i}_{dr}\right)\frac{{d\theta }_{r}}{dt}\end{array}\right.$$
(5)

The PMSM tracking error vector is \(e={\left[{e}_{1},{e}_{2},{e}_{3},{e}_{4}\right]}^{T}={\left[{{i}_{d}-i}_{dr, } {{i}_{q}-i}_{qr, } {w-w}_{r, } {\theta -\theta }_{r, }\right]}^{T}\), which its dynamics are given in Eq. (6);

$$\left\{\begin{array}{l}\dot{{e}_{1}}=\left(\frac{1}{L}+{\delta }_{1}\right)\overline{{v }_{d}}-\frac{R}{L}{e}_{1}+N\left({e}_{3}{e}_{2}+{e}_{3}{i}_{qr}+{e}_{2}{w}_{r}\right)\\ +{\delta }_{1}{v}_{dr}-{\delta }_{2}\left({e}_{1}+{i}_{dr}\right) \\ \dot{{e}_{2}}=\left(\frac{1}{L}+{\delta }_{2}\right)\overline{{v }_{q}}-\frac{R}{L}{e}_{2}-N\left({e}_{3}{e}_{1}+{e}_{3}{i}_{dr}+{e}_{1}{w}_{r}\right)\\ -\frac{{K}_{\infty }}{L}{e}_{3}+{\delta }_{1}{v}_{qr}-{\delta }_{2}\left({e}_{2}+{i}_{qr}\right)-{\delta }_{3}\left({e}_{3}+{w}_{r}\right)\\ \dot{{e}_{3}}=\frac{{K}_{\infty }}{J}{e}_{2}-\frac{\beta }{J}{e}_{3}-\frac{1}{J}{\tau }_{L}+{\delta }_{4}\left({e}_{2}+{i}_{qr}\right) \\ -{\delta }_{5}\left({e}_{3}+{w}_{r}\right)-{\delta }_{5}{\tau }_{L} \\ \dot{{e}_{4}}={e}_{3}\end{array}\right.$$
(6)

With voltage difference of \(\overline{{v }_{d}}={v}_{d}-{v}_{dr} and {v}_{q}-{v}_{qr}\). It should be noted that the flat outputs are coupled to the control inputs through Eq. (6);

$$\left\{\begin{array}{l}\dot{{e}_{1}}=\left(\frac{1}{L}+{\delta }_{1}\right)\overline{{v }_{d}}+{\varpi }_{1}\left(e\right)+{\varrho }_{1}\left(e\right) \\ {e}_{4}^{(3)}=\left(\frac{{K}_{\infty }}{JL}+\frac{{\delta }_{4}}{L}+\frac{{{K}_{\infty }\delta }_{1}}{J}+{\delta }_{1}{\delta }_{4}\right)\overline{{v }_{q}}+{\varpi }_{2}(e)+{\varrho }_{2}(e)\end{array}\right.$$
(7)

where the variables

$$\left\{\begin{array}{l}{\varpi }_{1}\left(e\right)=-\frac{R}{L}{e}_{1}+N\left({e}_{3}{e}_{2}+{e}_{3}{i}_{qr}+{e}_{2}{w}_{r}\right) \\ {\varpi }_{2}\left(e\right)=-\frac{{K}_{\infty }}{JL} \left({Re}_{2}+NL\left({e}_{3}{e}_{1}+{e}_{3}{i}_{dr}+{e}_{1}{w}_{r}\right)+{K}_{\infty }{e}_{3}\right)-\frac{\beta }{{J}^{2}}\left({K}_{\infty }{e}_{2}-\beta {e}_{3}\right) \\ \\ {\varrho }_{1}\left(e\right)={\delta }_{1}{v}_{dr}-{\delta }_{2}\left({e}_{1}+{i}_{dr}\right) \\ {\varrho }_{2}\left(e\right)={-\delta }_{4}\left(\frac{R}{L}{e}_{2}+N\left({e}_{3}{e}_{1}+{e}_{3}{i}_{dr}+{e}_{1}{w}_{r}\right)+\frac{{K}_{\infty }}{L}{e}_{3}\right) \\ { -\delta }_{4}\frac{{di}_{qr}}{dt}-{\delta }_{4}\left(\frac{{K}_{\infty }}{J}{e}_{2}-\frac{\beta }{J}{e}_{3}-\frac{1}{J}{\tau }_{L}+\frac{{dw}_{r}}{dt}\right) \\ -\left(\frac{\beta }{J}+{\delta }_{5}\right)\left({\delta }_{4}\left({e}_{2}+{i}_{qr}\right)-{\delta }_{5}\left({e}_{3}+{w}_{r}\right)-{\delta }_{6}{\tau }_{L}\right) \\ -\left(\frac{{K}_{\infty }}{J}+{\delta }_{4}\right)\left({\delta }_{3}\left({e}_{3}+{w}_{r}\right)+{\delta }_{2}\left({e}_{2}+{i}_{qr}\right)-{\delta }_{1}{v}_{dr}\right) \\ -{\delta }_{4}{\dot{\tau }}_{L}+\frac{\beta }{{J}^{2}}{\tau }_{L}-\frac{1}{J}{\dot{\tau }}_{L}\end{array}\right.$$
(8)

Defining the parameter uncertainties as \(\xi_{1} , \xi_{2} , \xi_{3} , \xi_{4}\); one obtained Eq. (9) as follows:

$$\left\{ {\begin{array}{*{20}l} {\mathop {e_{1} }\limits^{ \cdot } \; = \;\left( {1 + \xi_{1} } \right)u_{1} + \xi_{2} \left( e \right) } \\ {e_{4}^{\left( 3 \right)} \; = \;\left( {1 + \xi_{3} } \right)u_{2} + \xi_{4} \left( e \right)} \\ \end{array} } \right.$$
(9)

here

$$\left\{ {\begin{array}{*{20}l} {\begin{array}{*{20}l} {\xi_{1} = L\delta_{1} } \\ {\xi_{2} \left( e \right) = \varrho_{1} \left( e \right) - \xi_{1} \varpi_{1} \left( e \right) } \\ {\xi_{3} \left( e \right) = \frac{J}{{K_{\infty } }}\delta_{4} + \xi_{1} + \frac{J}{{K_{\infty } }}\delta_{1} \delta_{4} } \\ \end{array} } \\ { \xi_{4} \left( e \right) = \varrho_{2} \left( e \right) - \xi_{3} \varpi_{2} \left( e \right) } \\ \end{array} } \right.$$
(10)

Assumption: It is assumed that the parameter uncertainties \(\xi_{1} , \xi_{2} , \xi_{3} , \xi_{4}\) are bound by a positive constant \(\gamma \in \left( {0,1} \right)\) and a predefined positive function \(b\left( x \right)\) of nonlinear: nevertheless, this is not always true on \(\xi_{4} \left( e \right)\) since it is continuous on a compact set.

$$\left\{ {\begin{array}{*{20}c} {\left| {\xi_{1} \left( e \right),\xi_{3} \left( e \right)} \right|\; \le \;1 - \gamma } \\ {\left| {\xi_{2} \left( e \right),\xi_{4} \left( e \right)} \right|\; \le \;b\left( x \right)} \\ \end{array} } \right.$$
(11)

Hence, the control aims to stabilize Eq. (8) despite the uncertainties, given the control inputs of \(\overline{{v_{d} }} and \overline{{v_{q} }}\). With \(\overline{{v_{d} }} = L\left( {u_{1} - \varpi_{1} \left( e \right)} \right) and \overline{{v_{q} }} = \frac{JL}{{K_{\infty } }}\left( {u_{2} - \varpi_{2} \left( e \right)} \right)\).

Thus, this considerably simplifies the construction of a state feedback controller and spontaneously implies a sliding mode technique. Moreover, this strategy may make linearizing state feedback (known to be susceptible to external disturbance and uncertainty) more robust [34]. Additionally, the canonical forms often derived for constructing sliding mode control laws create zero dynamics [35], which is required for closed-loop stability.

2.5 Controller Design

In the instance of the PMSM, the task of importance is to produce an SM on a suitably chosen sliding manifold \(\zeta^{2}\) and confine the system trajectories to progress on it in a finite time. The sliding manifold is characterized by the vanishing of a related sliding variable \(S :R^{ + } \times R^{n} \to R\), as well as its subsequent time derivatives up to a specific degree, i.e., the nth-order sliding set.

$$\zeta^{2} \; = \;\left\{ {x \varepsilon R^{n} :S = \dot{S} = 0} \right\} .$$
(12)

2.6 Position Tracking

Suppose that load torque is acted on the motor, and all state variables are given for control. Two SMC laws are devised to meet the control target. We define the first sliding variable as:

$$s_{1} \left( t \right)\; = \;\delta_{1} \; = \;\mathop e\limits^{ \cdot \cdot }_{4} \; + \;K_{d} \dot{e}_{4} \; + \;\lambda \left( {\left| {e_{4} } \right|^{\alpha } sign\left( {e_{4} } \right)} \right).$$
(13)

With \(\lambda , K_{d} , > 0, \lambda {\textit{is chosen appropriately and}} \alpha\; is\break {\textit{strictly}}\; \ge 1\).The system has a relative degree of 2, about \(s_{1} \left( t \right)\), and its time derivatives are as follows:

$$\dot{s}_{1} \left( t \right)\; = \;\dddot e_{4} + K_{p} \mathop e\limits^{ \cdot \cdot }_{4} + \alpha \lambda \left| {e_{4} } \right|^{\alpha - 1} sign\left( \delta \right).$$
(14)

Since Eq. (14) is in third order, the finite-time stabilization of \(e_{4}^{\left( 3 \right)}\) requires a third-order SM controller.

$$\dot{S}_{1} \left( t \right)\; = \;\left( {\left( {1 + \xi_{3} } \right)u_{2} + \xi_{4} \left( e \right)} \right)\; + \;K_{d} \mathop e\limits^{ \cdot \cdot }_{4} \; + \;\alpha \lambda \left| {e_{4} } \right|^{\alpha - 1} sign\left( \delta \right).$$
(15)

As a result, the system trajectories formed on the manifold \(\zeta = 0\) in a finite time and stayed despite uncertainties. The equivalent control, \(u_{2}\), is achieved in SM by writing \(\zeta =\dot{\zeta }=\ddot{\zeta }=0\).

$$\left. {u_{2} \left( {1 + \xi_{3} } \right)\; = \; - \xi_{4} \left( e \right)\; - \;K_{d} \mathop e\limits^{ \cdot \cdot }_{4} \; - \;\alpha \lambda \left| {e_{4} } \right|^{\alpha - 1} sign\left( \delta \right)} \right\}.$$
(16)

Further simplification yields;

$$\frac{{\overline{{v_{q} }} K_{\infty } }}{JL} = - \varpi_{2} - K_{d\delta } - K_{d} \dot{e}_{3} - \alpha \lambda \left| {e_{4} } \right|^{\alpha - 1} sign\left( \delta \right)$$
(17a)

where the tracking error states and uncertainties are given as follows:

$$K_{d\delta } = K_{d} \left( {\frac{{K_{\infty } \xi_{3} \left( e \right)\overline{{v_{q} }} }}{JL} + \varrho_{2} \left( e \right)} \right),.$$
(17b)

It is worth noting that the demonstration of asymptotic stability and continuity relies on the availability of a nonempty compact set that is strictly positively constant to the closed-loop vector field [29, 36, 37]. The designed controller is similar to a sampled twisting algorithm with a slight modification of the function tracking error state \(\dot{e}_{3}\) and uncertainties states \(K_{d\delta }\). If all the parameter uncertainties in \(K_{d\delta }\) meet (11), and the variables \(K_{d}\) are selected appropriately, the control law established in (17a) is stable irrespective of uncertainty.

2.7 Direct Current (D.C.) Tracking

There are several types of nth-order SM algorithms in the literature, like sampled twisting and super twisting algorithms [36]. A super twisting algorithm suitable for the first-order system to evade chattering is used for D.C. tracking. The control law consists of two continuous parts that, once again, are independent of the sliding variable's first-time derivative. The discontinuity is only visible in the time difference of the control input:

$${\text{w}}_{s} \; \triangleq \;{\text{w}}_{st} \left( S \right)\; = \;v_{1} + v_{2}$$
(18a)
$$with \left\{ {\begin{array}{*{20}c} {\dot{v}_{1} = - \mu sign\left( S \right), } \\ {v_{2} = - \rho \left| S \right|^{1/2} sign\left( S \right), } \\ \end{array} \mu ,\alpha > 0} \right.$$

here

$$\mu \; > \;\frac{{C_{0} }}{{k_{m} }}\; and \rho \; \ge \;\frac{{4C_{0} \left( {K_{m} \mu + C_{0} } \right)}}{{k_{m}^{2} \left( {k_{m} \mu - C_{0} } \right)}}.$$
(18b)

Subject to sufficient conditions of control gains given by [38], one can get the convergence in a finite time of Eq. (9).

Let us define the second sliding variable as

$$S_{2} \left( t \right) = \delta_{2} = e_{1} .$$
(19)

The equivalent control, \(u_{1}\), is achieved in SM by writing \(\zeta =\dot{\zeta }=\ddot{\zeta }=0\).

$$\dot{S}_{2} \left( t \right) = \mathop {e_{1} }\limits^{ \cdot } = \left( {\frac{1}{L} + \delta_{1} } \right)\overline{{v_{d} }} + \varpi_{1} \left( e \right) + \varrho_{1} \left( e \right).$$
(20)

Further simplification yields;

$$\frac{{\overline{{v_{d} }} }}{L}\; = \; - \;\varpi_{1} \left( e \right)\; + \;\varpi_{\delta \delta }$$
(21)

where \(\varpi_{\delta \delta } = - \varrho_{1} \left( e \right) - \delta_{1} \overline{{v_{d} }}\).

The algorithms in (17) are used to design the controller with \(- \varpi_{\delta \delta } = {\text{w}}_{st} \left( S \right)\), Eq. (19) becomes;

$$\frac{{\overline{{v_{d} }} }}{L}\; = \; - \varpi_{1} \left( e \right)\; + \;{\text{w}}_{st} \left( {\delta_{2} } \right).$$
(22)

2.8 Position, Velocity, and Load Torque Observer

As control design depends on both measured \(\left( {i_{d} and \theta } \right)\) and non-measurable \(\left( {\dot{\theta } and \mathop \theta \limits^{ \cdot \cdot } } \right)\) variables, the velocity, and acceleration must be estimated in order to execute this controller. We consider part of Eq. (4) to design an observer based on the second-order SM control, with the unknown terms being replaced with an output injection. The dynamics of the observer is given as;

$$\frac{{d\hat{\omega }}}{dt}\; = \;\frac{1}{J} \left( {K_{\infty } i_{q} - \beta \hat{\omega }} \right)\; - \;\chi_{1} \left( {\theta - \hat{\theta }} \right).$$
(23)

The observer estimation error is \(\varepsilon_{\omega } = \omega - \hat{\omega } and \varepsilon_{\theta } = \theta - \hat{\theta }\) and its dynamic is expressed as;

$$\mathop \varepsilon \limits^{ \cdot \cdot }_{\theta } \; = \;\delta_{4} \left( {e_{2} + i_{qr} } \right)\; - \;\frac{\beta }{J}\varepsilon_{\omega } \; - \;\delta_{5} \left( {e_{3} + \omega_{r} } \right)\; - \;\tau_{L} \left( {\frac{1}{J} + \delta_{6} } \right)\; + \;\chi_{1} .$$
(24)

By considering \(\varepsilon_{\theta } = 0\) as a sliding manifold and defining \(\chi_{1}\) to be (25a), subject to sufficient conditions of (24b)

$${\text{w}}_{s} \triangleq {\text{w}}_{te} \left( {S,{\Delta }_{s} } \right) = \left\{ {\begin{array}{*{20}c} { - \lambda_{M} sign\left( S \right), if S{\Delta }_{s} > 0} \\ { - \lambda_{m} sign\left( S \right), if S{\Delta }_{s} \le 0} \\ \end{array} } \right..$$
(25a)
$$\left\{ {\begin{array}{*{20}c} {\lambda_{m} > \left| {\delta_{4} \left( {e_{2} + i_{qr} } \right) - \delta_{5} \left( {e_{3} + \omega_{r} } \right) - \tau_{L} \left( {\delta_{6} } \right)} \right| } \\ {\lambda_{M} > \lambda_{m} + 2\left| {\delta_{4} \left( {e_{2} + i_{qr} } \right) - \delta_{5} \left( {e_{3} + \omega_{r} } \right) - \tau_{L} \left( {\delta_{6} } \right)} \right|} \\ \end{array} } \right..$$
(25b)

One got

$$\mathop \varepsilon \limits^{ \cdot \cdot }_{\theta } \; = \; - \;\frac{\beta }{J}\varepsilon_{\omega } \; - \;\frac{1}{J}\tau_{L} \; + \;{\text{w}}_{te} \left( {S,{\Delta }_{s} } \right).$$
(26)

Its shown in [39] that \(\frac{\beta }{J}\varepsilon_{\omega }\) is a linear additive stabilizing component. With the equivalent control technique, one obtained the equivalent dynamics as:

$$\chi_{eq} - \frac{1}{J}\tau_{L} = 0.$$
(27)

Subsequently, at a finite time, the estimation of the load torque is obtained as;

$$\hat{\tau }_{L} = J\chi_{eq} .$$
(28)

2.9 Closed-Loop Stability

A nonlinear system does not work with separation law. This is true because the observer and controller cannot be designed disjointedly. Therefore, we need to analyze the stability of the joined observer–controller based on the speed observer. Considering the tracking error vector and its dynamics given in Eq. (7) and Eq. (23): i.e., \(e={\left[{e}_{1},{e}_{4}, {\ddot{\varepsilon }}_{\theta }\right]}^{T}\). The control laws are established on the observer output \(\widehat{\omega }\), hence \(\overline{{v }_{d}} and \overline{{v }_{q}}\) changed to;

$$\left\{\begin{array}{l}\frac{\overline{{v }_{d}}}{L}={-\varpi }_{1}^{^{\prime}}\left(e\right)+{\mathrm{w}}_{st}\left({\delta }_{2}\right) \\ \frac{{{K}_{\infty }K}_{d}\overline{{v }_{q}}}{JL}=-{\varpi }_{2}^{^{\prime}}\left(e\right)-{K}_{d\delta }-{K}_{d}{\dot{e}}_{3}-\alpha \lambda {\left|{e}_{4}\right|}^{\alpha -1}sign\left({e}_{4}\right)\\ \end{array}\right.$$
(29)

where

$$\left\{\begin{array}{l}{\varpi }_{1}^{^{\prime}}\left(e\right)=-\frac{R}{L}{e}_{1}+N\left(\mathrm{\rm E}{e}_{2}+\mathrm{\rm E}{i}_{qr}+{e}_{2}{w}_{r}\right) \\ {\varpi }_{2}^{^{\prime}}\left(e\right)=-\frac{{K}_{\infty }}{JL} \left({Re}_{2}+NL\left(\mathrm{\rm E}{e}_{1}+\mathrm{\rm E}{i}_{dr}+{e}_{1}{w}_{r}\right)+{K}_{\infty }\mathrm{\rm E}\right)\\ \\ {\rm E}=\widehat{\omega }-{\omega }_{r}={e}_{3}-{\varepsilon }_{\omega } \end{array}\right.-\frac{\beta }{{J}^{2}}\left({K}_{\infty }{e}_{2}-\beta \mathrm{\rm E}\right)$$
(30)

The second-order SM speed observer always provides observation errors that converge in a finite time to zero. Thereupon, \(\widehat{\omega }\) converges in a finite time to \(\omega\) for any control law [34]. Subsequent to this transitory time, the control law functions as described in (17a) and (22), satisfying the control aims. Moreover, to show that the system remains bounded during the transient convergence, we substituted (30) into tracking error vector dynamics in Eq. (7).

$$\left\{\begin{array}{l}\dot{{e}_{1}}=N\left({i}_{qr}+{e}_{2}\right){\varepsilon }_{\omega }+{\mathrm{w}}_{st}\left(S\right)+{\xi }_{2}^{^{\prime}}\left(e\right) \\ {e}_{4}^{\left(3\right)}=\frac{-{K}_{\infty }{\varepsilon }_{\omega }}{JL}\left(NL\left({e}_{1}+{i}_{dr}\right)+{K}_{\infty }\right)-\frac{{\varepsilon }_{\omega }}{{J}^{2}}{\beta }^{2} \\ -\frac{\left(1+{\xi }_{3}\left(e\right)\right)}{{K}_{d}}\left({K}_{d\delta }+{K}_{p}{\dot{e}}_{3}+{K}_{p\delta }+\alpha \lambda {\left|{e}_{4}\right|}^{\alpha -1}sign\left(\delta \right)\right)\\ +{\varrho }_{2}\left(e\right)-\frac{{\varpi }_{2}^{^{\prime}}\left(e\right)}{{K}_{\infty }}\left({\xi }_{1}{K}_{\infty }+J{\delta }_{4}({\xi }_{1}+1\right))\end{array}\right.$$
(31)

where \({\xi }_{2}^{\mathrm{^{\prime}}}\left(e\right)={\varrho }_{1}(e)-{\xi }_{1}({\varpi }_{1}^{\mathrm{^{\prime}}}\left(e\right)-{\mathrm{w}}_{st}\left(S\right))\)

Expressing \(X={\left[{e}_{1},{e}_{2},{e}_{3},{e}_{4}, {\ddot{\varepsilon }}_{\theta }, {\varepsilon }_{\theta }\right]}^{T}\), The system can be denoted as \(\dot{X}=f\left(X\right)+h\), in which both \(f\left(X\right) and h\) are given below.

$$f\left(X\right)=\left\{\begin{array}{l}N\left({i}_{q}\right){\varepsilon }_{\omega } \\ \left(\frac{-{K}_{\infty }{\varepsilon }_{\omega }}{JL}\left(NL{i}_{d}+{K}_{\infty }\right)-\frac{{\varepsilon }_{\omega }}{{J}^{2}}{\beta }^{2}\right)\\ \frac{1}{J}\left({{K}_{\infty }e}_{2}-\beta {e}_{3}\right)+{\delta }_{4}{i}_{q}-{\delta }_{5}w\\ {e}_{3} \\ -\frac{\beta }{J}{\varepsilon }_{\omega } \\ {\varepsilon }_{\omega }\end{array}\right.$$
$$h=\left\{\begin{array}{l}{\mathrm{w}}_{st}\left(S\right)+{\xi }_{2}^{^{\prime}}\left(e\right) \\ \left(\genfrac{}{}{0pt}{}{-\left(1+{\xi }_{3}\left(e\right)\right)\left({K}_{d\delta }+\alpha \lambda {\left|{e}_{4}\right|}^{\alpha -1}sign\left(\delta \right)\right)}{\begin{array}{c}+{\varrho }_{2}\left(e\right)-\frac{{\varpi }_{2}^{^{\prime}}\left(e\right)}{{K}_{\infty }}\left({\xi }_{1}{K}_{\infty }+J{\delta }_{4}({\xi }_{1}+1\right))\\ -{K}_{d}{\dot{e}}_{3}\left(1+{\xi }_{3}\left(e\right)\right)\end{array}}\right)\\ -\frac{1}{J}{\tau }_{L}-{\delta }_{5}{\tau }_{L} \\ 0 \\ -\frac{1}{J}{\tau }_{L}+{\mathrm{w}}_{te}\left(S,{\Delta }_{s}\right) \\ 0\end{array}\right.$$

With the practical supposition that the \(i_{d}\) and \(i_{q}\) are peaked \(\left( {\left| {i_{d} } \right| \le i_{dmax} and \left| {i_{q} } \right| \le i_{qmax} } \right)\), and considering h is a bounded quantity such that \(h \le \overline{h}\), one may write

$$\dot{X} \le CX + \overline{h}$$
(32)

where \(C > 0\). Integrating (32) yields

$$X\left( t \right) \le X\left( 0 \right) + \mathop \smallint \limits_{0}^{t} (CX\left( \tau \right) + \overline{h})d\tau$$
(33)

Using the Gronwell Lemma, Eq. (33) gives;

$$X\left( t \right) \le X\left( 0 \right){\text{exp}}\left( {Ct} \right) + \frac{{\overline{h}}}{C}{\text{exp}}\left( {Ct - 1} \right)$$
(34)

Equation (34) infers that Eq. (6) is bounded in a finite time using Eq. (29).

2.10 Implementation of the Controllers

We experimented with one motor to verify the designed controller and then implement the control algorithm on the whole robot. The objective of the control is to bring the motor to a position of 1.8° (0.0314 rad) from the initial position (0°) fast enough with the least error. To have good dynamics without discontinuity during the motion or maybe torque undulations, the initial and final velocity and acceleration are zero, while the reference position is chosen to be quintic trajectory, as shown in Fig. 5A. Similarly, Table 2 defines the characteristics and nominal values of the PMSM used with the states and inputs. The input voltages va and vb of the motor coil supplied by the dSPACE card were set to turn the rotor one step clockwise. This may be accomplished by applying phase voltages in A + and B + as indicated in Fig. 5B.

Fig. 5
figure 5

A Reference trajectories, B Reference voltages

Full size image
Table 2 PMSM parameters used for the experiment
Full size table

3 Experimental Results

All of the accompanying experimental findings were obtained using the following parameters: \(K_{d} = J, \alpha = 1.2, \lambda = 10, \rho = 70, \mu = 5, \lambda_{M} = 100, \lambda_{m} = 10, K_{d\delta } = 0.01.\) Any lump of disturbances that appeared in the equations is assumed to be bounded with except which has already been stated (Fig. 6). Figure 7 shows currents in winding a and b with velocity and motor position before and after applying controllers. These results were obtained under the application of load torque and disturbances.

Fig. 6
figure 6

States response without and with close-Loop control using applied input of 12 V

Full size image
Fig. 7
figure 7

Close-Loop Control of estimated position and velocity with estimated errors

Full size image

Similarly, estimated control signals and their errors are provided in Fig. 8.

Fig. 8
figure 8

Desired and actual trajectories evaluation using an E.M. sensor

Full size image

3.1 Robot Performance Validations

Experimentation with the robotic system is carried out to validate the application of the brain biopsy and the practicality of the control algorithm.

3.1.1 Positioning Accuracy Assessment

Accuracy and repeatability were evaluated based on the ISO 9283 standard for operating industrial robots [9]. A passive tool is constructed from plastic and incorporated with NDI passive spheres, and the assembly is mounted to the drill bit tip to calculate and analyze the position and orientation accuracy of the robot. The 3D coordinates of every point designated in the experimental setup were measured using a positional tracking device (Polaris, NDI Medical, Canada). Four sets of tests are carried out. Knowing the home position and orientation of the robot, an arbitrary end position, and the orientation of the robot's tool pose are obtained in the first test sets. Rotation and insertion accuracy was conducted in the second test. The desired logged and actual data are processed and presented in both cases.

The first test is conducted using a sphere trajectory selected to be on a plane diagonally dividing the maximum workspace and in accordance with the ISO standard, as illustrated in Fig. 9. The robot is maneuvered along the trajectory to the goal. We choose five points along the path to verify the position and orientation accuracy, i.e., P1, P2, P3, P4, P1, and P5. The position in which the robot stops is tagged as the real position. The robot traces the same path 30 times to measure its repeatability. The desired and logged actual data for the traces are compared with the mean and Standard deviation (STD) for each target point provided in the tables below.

Fig. 9
figure 9

Tests for localizing a-holes on the phantom model

Full size image

The EE. Position error considering only the goal point through which the EE. Passed during the 30 traces is given in Table 3. The mean position errors have maximum and minimum absolute values of 1.6401 mm and 0.3306 mm, respectively. Moreover, the EE. Orientation data are presented in Table 4. The mean orientation error is 0.99° and 0.13°, respectively.

Table 3 Position accuracy test results (unit in mm)
Full size table
Table 4 Orientation accuracy test results (unit in deg)
Full size table

The second test was carried out to verify the robot's rotation and insertion accuracy using a phantom constructed from plastic with a cylinder shape. Four locations of 100 mm depth were modeled as the target, which is a typical depth of stereotactic target under the human skull. The four markers used were directly placed above the testing hole. The coordinates of the measured targets were recorded with the robot coordinate system. A phantom needle (created with a wire of diameter of 2.5 mm) was employed. Attached to the needle is an electromagnetic (E.M.) sensor (trakStar 3D E.M. tracking unit), as illustrated in Fig. 10. The robot's needle driver rotation and insertion accuracy are independently presented in Tables 5 and 6.

Fig. 10
figure 10

CT scan images feedback from the debulking experiment. Image (A1) shows the preoperative scan, image (A2, A3, and A4) shows the Intraoperative scan of each of the three phases, where (B1) illustrates the remainder of the hematoma

Full size image
Table 5 Needle driver rotation accuracy (unit in deg)
Full size table
Table 6 Needle driver insertion accuracy (unit in mm)
Full size table

3.2 Ex Vivo Experiments

We used a brain phantom composed of KnoxTM gelatin, 5% by weight in the experiment. This concentration was found to have mechanical characteristics that were similar to mouse brain tissue, especially when it comes to the shear modulus [40]. We used the phantom to evacuate a blood clot of volume 52.39 mLas.

A CT image of the phantom was obtained in the Xoran XCAT CT scanner, and the position of the bleeding about the tip of the needle was determined using 3D Slicer segmentation. We use a layer-by-layer route planning technique that breaks down the tip trajectory planning problem into several 2D tasks in Matlab.

We start by separating the hemorrhage volume from the images and thereafter segment it into two-dimensional layers at 90° to the needle's axis [41]. A spiral tip and circle trajectory with a maximum spiral pitch and radius of 2 mm is produced for each layer surface, beginning at the midpoint of the layer and spiraling outward, taking on the form of the hemorrhagic border as it reaches the margins. After reaching the end of the first layer, the robot switches to the beginning of the next layer and spirals outward. We keep the layer spacing and spiral speed at 1 mm and 1 mm/s. After completing a few layers, the size and shapes of the hematoma keep on changing, giving rise to multiple image acquisition and path replanning to avoid healthy tissue damage.

Figure 6 depicts the experimental configuration with CT. The original volume of the clot was 52.39 mL. The process was executed in 3 phase iterations, with a CT image volume obtained at the beginning of each phase.

The preoperative and postoperative CT scan of each phase in Fig. 11 demonstrates that the anticipated hematoma volume was cleared with minor discernible injury to adjacent brain tissue with 87% aspiration achieved. Gomco Model 300 AC tabletop aspirator was employed to suck the cleared clot at each phase.

Fig. 11
figure 11

The preoperative CT scan with remaining hematoma overlaid in brown

Full size image

Figure 12 depicts the 87 percent aspiration accomplished by comparing the start and end volumes of the hematoma (final volume 6.81 mL).

Fig. 12
figure 12

The preoperative CT scan with remaining hematoma overlaid in brown

Full size image

4 Discussion

The experimental results given in this research show that intraoperative imaging can be advantageous for hematoma aspiration because it allows for tissue deformation to be seen and compensated for motion planning. If preoperative images were used alone, surgeons would be left with only experience and need to be careful. This usually results in treating only the hematoma's core and allows a considerable margin of safety to compensate for tissue distortion. Though this may still result in clinical benefit, how much clot needs to be removed for therapeutic efficacy to begin is lost. However, an estimate shows that as little as 25% removal may be clinically effective. Occasionally, a force has to be exerted in clearing the hematoma.

Aspirations in each phase took about 47, 43, and 67 min excluding image acquisition and motion planning. This is comparable to the time taken by the surgeon (20–40 min) to resect a hematoma after the hemorrhage surface has been reached. The backdrop of intraoperative is the patient's constant exposure to more radiation as a result of more scans. Because an ICH is a life-or-death scenario with a 40% mortality rate, this may be judged reasonable to undergo [31].

The future work will optimize the whole procedure and determine the average time taken from the beginning to the end of the procedure. A more realizable phantom will be constructed in the future, and use and the robot will be tested in vivo.

4.1 Conclusions

A semi-autonomous stereotactic robotic system was developed and used with an OTS to improve the hematoma and biopsy procedures. The robot is meant to insert the probe, treat and manage aspiration procedures, sample collection, and other diagnoses. The calibration technique was established and conducted since the robot location and insertion depth were controlled by an OTS. An SM control strategy was designed and validated for optimal performance of the robot motions while navigating. The designed controller demonstrated that the approach was good enough under perturbation. Following that, the usefulness of the robotic system was validated using ex-vivo trials with a CT scanner.