Impact of Inclined Lorentz Force and Schmidt Number on Chemically Reactive Newtonian Fluid Flow on a Stretchable Surface When Stefan Blowing and Thermal Radiation are Significant

Abstract

The influence of inclined magnetic field and heat and mass transfer of a hydromagnetic fluid on stretching/shrinking sheet with Stefan blowing effects and radiation has been investigated. The elementary viscous equations for momentum, heat and mass transfer, which are highly nonlinear partial differential equations, are mapped into highly nonlinear ordinary differential equations with the help of similarity transformation. The subsequent highly nonlinear differential equation is solved analytically. The exact solution of heat and mass transfer appearances is found in terms of the incomplete gamma function. The species and temperature boundary conditions are assumed to be a linear function of the distance from the origin. Further, the impact of various parameters, such as Chandrasekhar number, thermal radiation, inclined Lorentz force and mass transpiration on velocity and temperature summaries, are conferred in detail.

1 Introduction

In many engineering applications, Newtonian fluid flow due to stretching/shrinking sheet involves the extrusion of plastic sheets and drawing operation of plastic sheets among many things [1,2,3]. For the processes, for example, drying and purifying methods, where boundaries are perforated, Stefan blowing (wall injection) has significant applications. Stephan problem provides the idea of blowing effect, which is the major implementation of mass transfer of species. The product quality is greatly influenced by heat and mass flow between stretching sheet and flow [4].

A novel work on the boundary-layer flow over a continuously stretching sheet was done by Sakiadis [5]. The work becomes the inspiration for many researchers and motivated them to investigate stretching sheet problems in detail. Exact analytical solution for Navier–Stokes was investigated by Crane [6] and Fang et al. [7]. Banks [8] presented a similarity solution for stretching sheet using numerical and analytical techniques. Magyari and Keller [9] analytically evaluated the two-dimensional flow induced by stretching of permeable wall, and the exact solutions have been derived. Homotopy analysis methods were employed to obtain exact analytic solutions [10].

Carragher and Crane [11] theoretically investigated the thermal transport for a continuously stretching plate and obtained the rate of heat transfer for moderate and large Prandtl number (Pr). Grubka and Bobba [12] employed power-law distribution for temperature in thermal transport in a linearly stretching sheet. Two parameters, namely temperature parameter and Prandtl number, are used to demonstrate the heat transfer behaviour. Dutta et al. [13] analytically investigated flow over a continuously stretching sheet for temperature distribution. Uniform heat flux was given to a stretching sheet, and velocity of sheet directly depends on the slit distance. It was found that temperature decreases with an increase in Prandtl number.

Other similar work includes [14,15,16]. Weidman et al. [17] and Ishak et al. [18] explored a similar boundary flow over a moving surface and found dual solutions. The impact of Blasius flow and Sakiadis flow has been investigated for thermal radiation on a viscous boundary layer [19]. A slips model is used to investigate hydromagnetics flow and thermal transfer over expanding or stretching and shrinking surface [20]. Andersson [21,22,23,24] reported work related to chemical reaction for stretching plate. Pal and Mondal [25] approved a numerical examination to study the impact of Soret and Dufour, radiation and species on hydromagnetics flow due to stretching/shrinking surface in a porous medium. Khan [26] numerically reported the impact of homogeneous–heterogeneous reactions on the stretching sheet in non-Newtonian fluid and found that velocity of viscoelastic fluid is decreased with an increase in viscoelastic parameters, λ. Bhattacharyya et al. [27] examined the flow of MHD due to a stretching sheet with suction and blowing and reported a reduction in velocity and surge in concentration was observed with an increment in magnetic parameter.

Other studies involve transport of species (or mass transfer and Lorentz forces) [28,29,30, 44]. Spalding [31] investigated the mass or species transfer in viscous flow over a flat plate, vertical plate and sphere using the Karman–Pohlhausen–Kroujiline method. Recently, Mahabaleshwar et al. [32,33,34,35,36,37,38,39] and Khan et al. [40,41,42,43] have investigated analytical examination to impact of different fluids with numerous parameters MHD/porous media flow.

For the objective of the research, we consider the effect of radiation and MHD on Newtonian flow and chemical reaction over a stretching/shrinking sheet with Stefan blowing effects. By means of similarity transformation, the flow equations are mapped from PDEs to ODEs and solved analytically. The exact analytic solution of heat and mass transfer characteristics is obtained in terms of the incomplete gamma function.

2 Mathematical Formulation and Physical Modelled Equations

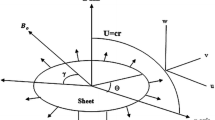
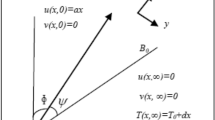
Laminar, steady two-dimensional motion in the Cartesian coordinate xy-plane on the stretching/shrinking sheet under the effect of inclined MHD, Stefan blowing and radiation has been investigated. The heat and mass impacts are investigated once thermal conductivity varies as a linear function of temperature and concentration. The laminar boundary flow is examined in the presence of radiation and MHD. A steady magnetic field at an angle $\tau$ to the positive direction of the y-axis has been applied. Magnetic Reynolds number is considered to be very small (see Mahabaleshwar 2007, 2008). Further, the concentration and temperature distribution at the sheet and $y \to \infty$ are assumed to be constants as $C_{w}$,$T_{w}$, $T_{\infty }$ and $C_{\infty }$, respectively.

The familiar Prandtl equations for two-dimensional flow, heat and mass equations under the boundary-layer approximations are stated as follows:

$$ \frac{\partial u}{{\partial x}} + \frac{{\partial {\text{v}}}}{\partial y} = 0, $$

(1)

$$ \rho \left( {u\frac{\partial u}{{\partial x}} + {\text{v}}\frac{\partial u}{{\partial y}}} \right) = - \frac{\partial p}{{\partial x}} + \mu \left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }}} \right) - \sigma B_{0}^{2} \sin^{2} \left( \tau \right)u, $$

(2)

$$ \rho \left( {u\frac{{\partial {\text{v}}}}{\partial x} + {\text{v}}\frac{{\partial {\text{v}}}}{\partial y}} \right) = - \frac{\partial p}{{\partial y}} + \mu \left( {\frac{{\partial^{2} {\text{v}}}}{{\partial x^{2} }} + \frac{{\partial^{2} {\text{v}}}}{{\partial y^{2} }}} \right), $$

(3)

$$ u\frac{\partial C}{{\partial x}} + {\text{v}}\frac{\partial C}{{\partial y}} = D\left( {\frac{{\partial^{2} C}}{{\partial x^{2} }} + \frac{{\partial^{2} C}}{{\partial y^{2} }}} \right), $$

(4)

$$ \rho C_{P} \left( {u\frac{\partial T}{{\partial x}} + {\text{v}}\frac{\partial T}{{\partial y}}} \right) = \kappa \left( {\frac{{\partial^{2} T}}{{\partial x^{2} }} + \frac{{\partial^{2} T}}{{\partial y^{2} }}} \right) - \frac{{\partial q_{r} }}{\partial y}, $$

(5)

where u and v are the velocity components in the x- and y-direction, respectively, p the pressure, C and $C_{\infty }$ the concentrations of species and concentration at infinity, respectively, T and $T_{\infty }$ the temperature and temperature at infinity, respectively, and $\rho \,,\,\mu \,,\,\sigma \,,\,D\,,\,C_{P} \,$ and $\kappa$ are the density, dynamic viscosity, electrical conductivity, mass diffusivity coefficient, constant pressure specific heat capacity and thermal conductivity, respectively.

Imposed conditions for these nonlinear governing equations are:

$$ \begin{gathered} y\, = \,0\,\,\,\,\,\,\,\,\,u = U_{w} \left( x \right) = \lambda ax\,\,\,,\,\,\,{\text{v}} = {\text{v}}_{w} \,\,\,,\,\,T = T_{w} \,\,\,,\,\,C = C_{w} \hfill \\ {\text{as}}\,\,y \to \infty \,\,\,\,\,u \to 0\,\,\,,\,\,\,T \to T_{\infty \,} \,\,\,\,,\,\,C \to C_{\infty } . \hfill \\ \end{gathered} $$

(6)

$u = U_{w} (x) = \lambda ax$ gives the velocity distribution of sheet. In given expression represents the coordinates along the direction in which sheet is stretching or shrinking, and $\lambda$ is the constant (λ > 0 means stretching, λ < 0 means shrinking and $\lambda = 0$ means surface is permeable).

The Rosseland approach for radiative heat flux is assumed by $q_{r}$ (see Mahabaleshwar el al. 2020),

$$ q_{r} = - \frac{{4\sigma^{*} }}{{3k^{*} }}\frac{{\partial T^{4} }}{\partial y}\,. $$

(7)

The Taylor-series expansion for the fourth power of temperature can be presented as:

$$ T^{4} = T_{\infty }^{4} + 4T_{\infty }^{3} \left( {T - T_{\infty } } \right) + 6T_{\infty }^{2} \left( {T - T_{\infty } } \right)^{2} + .... $$

(8)

In Eq. (8), neglecting the quadratic terms onwards

$$ T^{4} \cong - 3T_{\infty }^{4} + 4T_{\infty }^{3} T. $$

(9)

Substituting equation (7) into (9), one can obtain:

$$ \frac{{\partial q_{r} }}{\partial y} = - \frac{{16\sigma^{*} T_{\infty }^{3} }}{{3k^{*} }}\frac{{\partial^{2} T}}{{\partial y^{2} }}. $$

(10)

Equation (5) is converted into the subsequent equation (10)

$$ u\frac{\partial T}{{\partial x}} + {\text{v}}\frac{\partial T}{{\partial y}} = \left( {\alpha + \frac{{16\sigma^{*} T_{\infty }^{3} }}{{3\rho C_{P} k^{*} }}} \right)\frac{{\partial^{2} T}}{{\partial y^{2} }}. $$

(11)

Equations (1)–(5) by using dimensionless variables are given by

$$ \begin{aligned} \psi & = \left( {\sqrt {a\nu } } \right)xf\left( \eta \right),\,\eta = y\sqrt {\frac{a}{\nu }} , \\ u & = axf_{\eta } \left( \eta \right),\,v = - \sqrt {a\nu } f\left( \eta \right),\,\theta \left( \eta \right) = \frac{{T - T_{\infty } }}{{T_{w} - T_{\infty } }},\phi \left( \eta \right) = \frac{{C - C_{\infty } }}{{C_{w} - C_{\infty } }}. \\ \end{aligned} $$

(12)

The physical stream function $\psi$ is defined as follows:

$$ u = \frac{\partial \psi }{{\partial y}},\,\,v = - \frac{\partial \psi }{{\partial x}}. $$

(13)

Equation (13) satisfies the conservation of mass. Substituting Eq. (12a)–(12b) into Eq. (2) is transformed into:

$$ \frac{{\partial^{3} \psi }}{{\partial y^{3} }} + \frac{{\partial \left( {\psi ,\frac{\partial \psi }{{\partial y}}} \right)}}{{\partial \left( {x,y} \right)}} - \frac{{\sigma B_{0}^{2} }}{\rho }\sin^{{2}} \left( \tau \right)\frac{\partial \psi }{{\partial y}} = 0. $$

(14)

In Eq. (14), the second term specifies the Jacobian.

Substituting Eqs. (14) and (10) into Eq. (12b), the following transformed equation with constant coefficient is derived.

The similarity transformation $\psi \left( {x,y} \right) = \left( {\sqrt {a\nu } } \right)xf\left( \eta \right)$ is presented in Eqs. (2)–(5), which is given in the following equations:

$$ f_{\eta \eta \eta } + ff_{\eta \eta } - f_{\eta }^{2} - Q\sin^{2} \left( \tau \right)f_{\eta } = 0, $$

(15)

$$ \phi_{\eta \eta } + Sc\left( {f\phi_{\eta } } \right) = 0, $$

(16)

$$ \left( {1 + N_{R} } \right)\theta_{\eta \eta } + \Pr \left( {f\theta_{\eta } } \right) = 0. $$

(17)

In these problems, the pressure gradient is negligible.

The appropriate boundary conditions for Eqs. (15) to (17) are given by:

$$ \begin{gathered} f\left( 0 \right) = \Lambda \left( {\phi_{\eta } } \right)_{\eta = 0} ,\,\,f_{\eta } \left( 0 \right) = \lambda ,\,\,\theta \left( 0 \right) = \phi \left( 0 \right) = 1 \hfill \\ f_{\eta } \left( \infty \right) \to 0,\,\theta \left( \infty \right) = \phi \left( \infty \right) \to 0 \hfill \\ \end{gathered} $$

(18)

where $Q = \frac{{\sigma B_{0}^{2} }}{a\rho }$ is the Chandrasekhar number ($\sqrt Q$ is called Hartmann number), $\lambda$ represents stretching/shrinking parameter, λ > 0 for the stretching sheet, λ < 0 for the shrinking sheet and $\lambda = 0$ for the fixed surface, $\Lambda$ represents the Stefan blowing due to mass transpiration (suction/injection) and Stefan blowing velocity is given by ${\text{v}}_{w} = - \left( {\sqrt {a\rho } } \right)\Lambda \phi_{\eta } \left( 0 \right)$, $Sc = \frac{\nu }{D}$ represents the Schmidt number, $\Pr = \frac{\nu }{\alpha }$ represents the Prandtl number and $N_{R} = \frac{{16\sigma^{*} T_{\infty }^{3} }}{{3k^{*} K}}$ represents the thermal radiation (Fig. 1).

3 Methodology for Velocity

The nature of solution in the exact analytical solutions of equations (15) is given by,

$$ f\left( \eta \right) = \beta - \frac{1}{\beta }\left\{ {Q\sin^{2} \left( \tau \right) + \lambda Exp\left( { - \beta \eta } \right)} \right\} $$

(19)

and

$$ f_{\eta } \left( \eta \right) = \lambda Exp\left( { - \beta \eta } \right) $$

(20)

provided that β > 0.

Note that

• i) The classical Crane (1970) flow is recovered from Eq. (15) for $Q = 0\,\,,\,\,\lambda = 1\,$ and $\tau = 90^{0}$.

• ii) The classical Pavlov (1970) flow is recovered from Eq. (15) for $V_{C} = 0\,\,,\,\lambda = 1\,\,$ and $\tau = 90^{0}$.

• iii) The Mahabaleshwar et al. (2016) flow is recovered from Eq. (15) for $\lambda = 1$ and $\tau = 90^{0}$.

• iv) The Fang and Zing (2014) flow is recovered from Eq. (15) for $Q = 0\,\,,\,\,\lambda = 1\,$ and $\tau = 90^{0}$.

4 Methodology for Concentration and Temperature

Substituting Eq. (19) into Eqs. (16) and (17), the mass and temperature equations are transformed, using the relationship $\xi = \frac{Sc}{{\beta^{2} }}\exp \left( { - \beta \eta } \right)$ and $\zeta = \frac{\Pr }{{\beta^{2} }}{\text{exp}}\left( { - \beta \eta } \right)$, and are converted to:

$$ \xi \phi_{\xi \xi } + \left\{ {1 - Sc\left( {1 - \frac{1}{{\beta^{2} }}Q{\text{sin}}^{2} \tau } \right) + \xi \lambda } \right\}\phi_{\xi } = 0 $$

(21)

$$ \left( {1 + N_{R} } \right)\zeta \theta_{\zeta \zeta } + \left\{ {1 + N_{R} - \Pr \left( {1 - \frac{1}{{\beta^{2} }}Q{\text{sin}}^{2} \tau } \right) + \zeta \lambda } \right\}\theta_{\zeta } = 0 $$

(22)

subject to the corresponding boundary conditions

$$ \phi \left( {\frac{Sc}{{\beta^{2} }}} \right) = \theta \left( {\frac{\Pr }{{\beta^{2} }}} \right) = 1,\,\phi (0) = \theta (0) = 0. $$

(23)

The final solutions, after further transformations of Eqs. (21) and (22) into incomplete gamma function (Abramowitz and Stegun), are given by

$$ \phi \left( \xi \right) = \frac{{\Gamma \left[ {Sc\left( {1 - \frac{1}{{\beta^{2} }}Q{\text{sin}}^{2} \tau } \right)\,,\,0} \right] - \Gamma \left[ {Sc\left( {1 - \frac{1}{{\beta^{2} }}Q{\text{sin}}^{2} \tau } \right),\,\lambda \xi } \right]}}{{\Gamma \left[ {Sc\left( {1 - \frac{1}{{\beta^{2} }}Q{\text{sin}}^{2} \tau } \right)\,,\,0} \right] - \Gamma \left[ {Sc\left( {1 - \frac{1}{{\beta^{2} }}Q{\text{sin}}^{2} \tau } \right)\,,\,\lambda \frac{Sc}{{\beta^{2} }}} \right]}}, $$

(24)

$$ \theta \left( \zeta \right) = \frac{{\Gamma \left[ {\frac{{\Pr \left( {1 - \frac{1}{{\beta^{2} }}Q{\text{sin}}^{2} \tau } \right)}}{{1 + N_{R} }}\,,\,0} \right] - \Gamma \left[ {\frac{{\Pr \left( {1 - \frac{1}{{\beta^{2} }}Q{\text{sin}}^{2} \tau } \right)}}{{1 + N_{R} }}\,,\,\frac{\lambda }{{1 + N_{R} }}\zeta } \right]}}{{\Gamma \left[ {\frac{{\Pr \left( {1 - \frac{1}{{\beta^{2} }}Q{\text{sin}}^{2} \tau } \right)}}{{1 + N_{R} }}\,,\,0} \right] - \Gamma \left[ {\frac{{\Pr \left( {1 - \frac{1}{{\beta^{2} }}Q{\text{sin}}^{2} \tau } \right)}}{{1 + N_{R} }}\,,\,\frac{\lambda }{{1 + N_{R} }}\frac{\Pr }{{\beta^{2} }}} \right]}}, $$

(25)

where $\Gamma$ denotes the incomplete gamma function.

Substituting Eq. (23) into the final solutions of Eqs. (21) and (22) in terms of $\eta$, one can obtain:

$$ \phi \left( \eta \right) = \frac{{\Gamma \left[ {Sc\left( {1 - \frac{1}{{\beta^{2} }}Q{\text{sin}}^{2} \tau } \right),0} \right] - \Gamma \left[ {Sc\left( {1 - \frac{1}{{\beta^{2} }}Q{\text{sin}}^{2} \tau } \right),\frac{Sc}{{\beta^{2} }}\lambda \,\exp \left( { - \beta \eta } \right)} \right]}}{{\Gamma \left[ {Sc\left( {1 - \frac{1}{{\beta^{2} }}Q{\text{sin}}^{2} \tau } \right),\,0} \right] - \Gamma \left[ {Sc\left( {1 - \frac{1}{{\beta^{2} }}Q{\text{sin}}^{2} \tau } \right),\lambda \frac{Sc}{{\beta^{2} }}} \right]}}, $$

(26)

$$ \theta \left( \eta \right) = \frac{{\Gamma \left[ {\frac{{\Pr \left( {1 - \frac{1}{{\beta^{2} }}Q{\text{sin}}^{2} \tau } \right)}}{{1 + N_{R} }}\,,\,0} \right] - \Gamma \left[ {\frac{{\Pr \left( {1 - \frac{1}{{\beta^{2} }}Q{\text{sin}}^{2} \tau } \right)}}{{1 + N_{R} }}\,,\,\frac{\lambda }{{1 + N_{R} }}\frac{\Pr }{{\beta^{2} }}\exp \left( { - \beta \eta } \right)} \right]}}{{\Gamma \left[ {\frac{{\Pr \left( {1 - \frac{1}{{\beta^{2} }}Q{\text{sin}}^{2} \tau } \right)}}{{1 + N_{R} }}\,,\,0} \right] - \Gamma \left[ {\frac{{\Pr \left( {1 - \frac{1}{{\beta^{2} }}Q{\text{sin}}^{2} \tau } \right)}}{{1 + N_{R} }}\,,\,\frac{\lambda }{{1 + N_{R} }}\frac{\Pr }{{\beta^{2} }}} \right]}}. $$

(27)

The first derivatives of concentration and temperature with respect to Blasius similarity variable are as follows:

$$ \phi_{\eta } \left( \eta \right) = - \frac{{\beta \exp \left[ { - \,\frac{Sc}{{\beta^{2} }}\lambda \,\exp \left( { - \beta \eta } \right)} \right]\left( {\frac{Sc}{{\beta^{2} }}\lambda \,\exp \left( { - \beta \eta } \right)} \right)^{{Sc\left( {1 - \frac{1}{{\beta^{2} }}Q{\text{sin}}^{2} \tau } \right)}} }}{{\Gamma \left[ {Sc\left( {1 - \frac{1}{{\beta^{2} }}Q{\text{sin}}^{2} \tau } \right),0} \right] - \Gamma \left[ {Sc\left( {1 - \frac{1}{{\beta^{2} }}Q{\text{sin}}^{2} \tau } \right),\lambda \frac{Sc}{{\beta^{2} }}} \right]}}, $$

(28)

$$ \theta_{\eta } \left( \eta \right) = - \frac{{\beta \exp \left[ { - \,\frac{\Pr }{{\beta^{2} }}\frac{\lambda }{{1 + N_{R} }}\,\exp \left( { - \beta \eta } \right)} \right]\left( {\frac{\Pr }{{\beta^{2} }}\frac{\lambda }{{1 + N_{R} }}\exp \left( { - \beta \eta } \right)} \right)^{{\frac{{\Pr \left( {1 - \frac{1}{{\beta^{2} }}Q{\text{sin}}^{2} \tau } \right)}}{{1 + N_{R} }}}} }}{{\Gamma \left[ {\frac{{\Pr \left( {1 - \frac{1}{{\beta^{2} }}Q{\text{sin}}^{2} \tau } \right)}}{{1 + N_{R} }}\,,\,0} \right] - \Gamma \left[ {\frac{{\Pr \left( {1 - \frac{1}{{\beta^{2} }}Q{\text{sin}}^{2} \tau } \right)}}{{1 + N_{R} }}\,,\,\frac{\lambda }{{1 + N_{R} }}\frac{\Pr }{{\beta^{2} }}} \right]}}. $$

(29)

The dimensionless concentration and temperature gradients at the sheet are given by

$$ \left( {\phi_{\eta } \left( \eta \right)} \right)_{\eta = 0} = - \frac{{\beta \exp \left[ { - \,\frac{Sc}{{\beta^{2} }}\lambda \,} \right]\left( {\frac{Sc}{{\beta^{2} }}\lambda \,} \right)^{{Sc\left( {1 - \frac{1}{{\beta^{2} }}Q{\text{sin}}^{2} \tau } \right)}} }}{{\Gamma \left[ {Sc\left( {1 - \frac{1}{{\beta^{2} }}Q{\text{sin}}^{2} \tau } \right)\,,\,0} \right] - \Gamma \left[ {Sc\left( {1 - \frac{1}{{\beta^{2} }}Q{\text{sin}}^{2} \tau } \right)\,,\,\lambda \frac{Sc}{{\beta^{2} }}} \right]}}, $$

(30)

$$ \left( {\theta_{\eta } \left( \eta \right)} \right)_{\eta = 0} = - \frac{{\beta \exp \left[ { - \,\frac{\Pr }{{\beta^{2} }}\frac{\lambda }{{1 + N_{R} }}\,} \right]\left( {\frac{\Pr }{{\beta^{2} }}\frac{\lambda }{{1 + N_{R} }}} \right)^{{\frac{{\Pr \left( {1 - \frac{1}{{\beta^{2} }}Q{\text{sin}}^{2} \tau } \right)}}{{1 + N_{R} }}}} }}{{\Gamma \left[ {\frac{{\Pr \left( {1 - \frac{1}{{\beta^{2} }}Q{\text{sin}}^{2} \tau } \right)}}{{1 + N_{R} }}\,,\,0} \right] - \Gamma \left[ {\frac{{\Pr \left( {1 - \frac{1}{{\beta^{2} }}Q{\text{sin}}^{2} \tau } \right)}}{{1 + N_{R} }}\,,\,\frac{\lambda }{{1 + N_{R} }}\frac{\Pr }{{\beta^{2} }}} \right]}}. $$

(31)

Using Eq. (19), where β > 0 represents the root of the equation, solve unknown $\beta$ and satisfy the equation

$$ f\left( 0 \right) = \Lambda \left( {\phi_{\eta } \left( \eta \right)} \right)_{\eta = 0} $$

(32)

$$ 1 - \frac{1}{{\beta^{2} }}\left( {\lambda + Q\sin^{2} \tau } \right) = - \Lambda \frac{{\exp \left( { - \frac{Sc}{{\beta^{2} }}\lambda } \right)\left( {\frac{Sc}{{\beta^{2} }}\lambda } \right)^{{Sc\left( {1 - \frac{1}{{\beta^{2} }}Q{\text{sin}}^{2} \tau } \right)}} }}{{\Gamma \left[ {Sc\left( {1 - \frac{1}{{\beta^{2} }}Q{\text{sin}}^{2} \tau } \right),0} \right] - \Gamma \left[ {Sc\left( {1 - \frac{1}{{\beta^{2} }}Q{\text{sin}}^{2} \tau } \right),\frac{Sc}{{\beta^{2} }}\lambda } \right]}}. $$

(33)

Closed-form solutions of Fang and Zing (2014) flow are recovered from Eq. (34) for $Q = 0\,\,,\,\,\lambda = 1\,$ and $\tau = 90^{0}$.

5 Results and Discussion

The analysis is facilitated in part by systematic mapping of the equations for the velocity, temperature and concentrations, leading to a set of nonlinear ODEs. By employing proper similarity variables, exact analytical solutions for momentum, temperature and concentration profiles are obtained. One has therefore now understood the physics involved in these interesting dynamics, thanks to the various plots that are generated herein that elaborate on the problem.

Figure 2 represents the influence of Stefan blowing parameters (Λ) on transverse velocity when the stretching boundary (λ) is greater than zero. The Schmidt No. (Sc) is taken unity, while the magnetic field inclination (τ) is 90°. As the Stefan blowing parameter (Λ) is varied between 100, 5, 1 and 0.1, the transverse velocity (η) is increased. It is noted that when the constant magnetic parameter (Q) is 0, the transverse velocity $f\left( \eta \right)$ is lower than that when the constant magnetic parameter (Q) is taken as 5. It is also to note that when Q is 0, all the transverse velocity values thus obtained are less than zero. Initially, the transverse velocity increases when the Blasius similarity variable is increased but becomes constant after some value.

Fig. 1

Pictographic representation of stretching/shrinking boundary

Fig. 2

Influence of Stefan blowing parameter (Λ) on transverse velocity

Figure 3 represents the effect of Sc on transverse velocity when the stretching boundary (λ) is greater than zero. The inclined parameter of the magnetic field (τ) is 90°, and the Stefan blowing parameter is 15. Here, the Schmidt number (Sc) is decreased from 3, 2.5, 1 to 0.1. It is seen that when Q is 0 the transverse velocity $f\left( \eta \right)$ is below − 4 ranging between − 4 and − 7 and when Q is 1 the transverse velocity ranges between − 2 and − 4. Similarly, like Fig. 2, the transverse velocity $f\left( \eta \right)$ increases initially when the Blasius similarity variable (η) is increased but finally becomes a constant line.

Fig. 3

influence of Schmidt number on transverse velocity

Figure 4 represents the influence of Stefan blowing parameters on transverse velocity when the shrinking boundary (λ) is less than zero. The Schmidt number (Sc) is taken as 1, and the ‘Q’ value has been kept constant at 5. The inclined parameter of the magnetic field (τ) is 90°. As the Stefan blowing parameter (Λ) is varied between 100, 5, 1 and 0.1, the transverse velocity $f\left( \eta \right)$ is decreased initially. The transverse velocity $f\left( \eta \right)$ ranges from 3 to 2 and becomes constant eventually.

Fig. 4

Influence of Stefan blowing parameter on transverse velocity

Figure 5 represents the effect of Sc transverse velocity when the stretching boundary (λ) is less than zero. The Stefan blowing parameter (Λ) is kept fixed at 15, and the inclined parameter of the magnetic field (τ) is 90°. The constant magnetic parameter (Q) is taken as 5. Now, the Schmidt No. (Sc) is decreased from 5, 2, 1 to 0.1 and so does the corresponding values of transverse velocity $f\left( \eta \right)$. It is observed that there are no significant changes in the transverse velocity $f\left( \eta \right)$ at higher values of the Blasius similarity variable ($\eta$).

Fig. 5

Influence of Schmidt number on transverse velocity

Figure 6 represents the influence of Sc on Stefan blowing parameters when the stretching boundary (λ) is greater than zero. Two sets of curves are obtained with constant magnetic parameter (Q) being taken as 0 and 1. The inclined parameter of the magnetic field (τ) is 90°. The Schmidt No. (Sc) is increased from 0.1, 1, 10 to 100 and so the corresponding values of β change. When β is less than 0.5, it is seen that the Stefan blowing parameter (Λ) is infinite. And when the Stefan blowing parameter (Λ) is 0, the β value is found to be infinite.

Fig. 6

Influence of Schmidt number on Stefan blowing parameter

Figure 7 represents the effect of Schmidt number (Sc) on Stefan blowing parameters (Λ) when the stretching boundary (λ) is less than zero. For inclined parameter of the magnetic field (τ) of 90° and constant magnetic parameter (Q) of 2, the curves for these Schmidt numbers (Scs) 0.1, 1, 10 and 100 are obtained. These obtained curves are somewhat similar in nature for inclined parameter of the magnetic field (τ) of 45° and constant magnetic parameter (Q) of 5.

Fig. 7

Influence of Schmidt on blowing parameter

Figure 8 represents the effect of Schmidt number (Sc) on Stefan blowing parameters (Λ) and studying the changes in super-linear stretching (λ). The inclined parameter of the magnetic field (τ) is 90°. The β value is kept constant at 1. The Schmidt No. (Sc) is decreased from 4, 3, 2 to 1, and the plot obtained seems to be an exponentially increasing graph. As the Schmidt No. (Sc) value decreases, so the rate of increase decreases in the curve plot of (Λ) vs (λ). It is to note that for constant magnetic parameter (Q) value 1, the curves of super-linear stretching (λ) start from 0, while for constant magnetic parameter (Q) value 1, the curves of super-linear stretching (λ) start from 1. Both the sets of curves are somewhat similar.

Fig. 8

Influence of Schmidt number on Stefan blowing parameter

Figure 9 represents the effect of Sc on Stefan blowing parameters (Λ) by plotting a graph of Stefan blowing parameter (Λ) vs Chandrasekhar number (Q) when the stretching boundary (λ) is greater than zero with β value kept constant at 1. The Schmidt No. (Sc) is increased from 0.1, 1, 10 to 100, and the plot on Chandrasekhar number (Q) obtained seems to be an exponentially increasing graph. Two sets of curves are obtained with one value ($\lambda = 1$) and another ($\lambda = 2$).

Fig. 9

Influence of Schmidt number on Stefan blowing parameter

Figure 10 represents the impact of Prandtl number (Pr) on heat transfer flux at the wall ($- \theta_{\eta } \left( 0 \right)$) with the stretching boundary (λ) greater than 0. The inclined parameter of the magnetic field (τ) is 90°. The β value is varied between 0.2, 0.3, 0.4, 0.5 and 0.6. There are two sets of curves, one set with constant magnetic parameter (Q) and radiation parameter (N_R) values 0 and 1, respectively, and the other set with (Q) and (N_R) values 0 and 2, respectively. Both of the sets of curves follow a similar pattern. When the Prandtl number (Pr) is increased, the thermal flux at the wall $- \theta_{\eta } \left( 0 \right)$ value initially increases, reaches a peak value and then decreases. It is to note that when the β value increases, the peak point of the graph also increases.

Fig. 10

Influence of $\beta$ on heat transfer flux at wall

Figure 11 represents the influence of β on wall concentration gradient ($- \phi_{\eta } \left( 0 \right)$) with respect to Schmidt number (Sc) with the stretching boundary (λ) greater than 0. The inclined parameter of the magnetic field (τ) is 90°. The β value is varied between 0.2, 0.3, 0.4, 0.5 and 0.6. There are two sets of curves, one with constant magnetic parameter (Q) value 0 and the other set with (Q) value 1. When the Sc is increased, the wall concentration gradient ($- \phi_{\eta } \left( 0 \right)$) value initially increases, reaches a peak value and then decreases. It is to note that when the β value increases, the peak point of the graph also increases.

Fig. 11

Influence of $\beta$ on wall concentration gradient

Figure 12 represents the impact of Pr on heat transfer flux at wall ($- \theta_{\eta } \left( 0 \right)$) with respect to β with the stretching boundary (λ) greater than 0. The inclined parameter of the magnetic field (τ) is 90°. The Pr value is varied between 0.6, 0.5, 0.4, 0.3 and 0.2. There are two sets of curves, one set with constant magnetic parameter (Q) and radiation parameter (N_R) values 0 and 0, respectively, and the other set with (Q) and (N_R) values 1 and 2, respectively. The major portion of the graph follows a linearity (when β greater than 1) and keeps on increasing with a constant rate of increase. When (Q) and (N_R) values are 0 and 0, respectively, the curves are steeper when compared with the other set of data.

Fig. 12

Influence of Prandtl number (Pr) on heat transfer flux at wall

Figure 13 represents the impact of Pr on heat transfer flux at wall ($- \theta_{\eta } \left( 0 \right)$) with respect to β with the stretching boundary (λ) greater than 0. The inclined parameter of the magnetic field (τ) is 90°. The Pr value is varied between 0.6, 0.5, 0.4, 0.3 and 0.2. There are two sets of curves, one set with constant magnetic parameter (Q) and radiation parameter (N_R) values 0 and 0, respectively, and the other set with (Q) and (N_R) values 2 and 2, respectively. When (Q) and (N_R) values are 0 and 0, respectively, the curves plot indicates an infinite value of heat transfer flux at wall ($- \theta_{\eta } \left( 0 \right)$) with a β around 0 to 1, while these plots drastically change orientation and become linear when the β value crosses 2. When (Q) and (N_R) values are 2 and 2, respectively, the curves simply follow a linear pattern after β value crosses 1.

Fig. 13

Influence of Prandtl number (Pr) on heat transfer flux at wall

Figure 14 represents the influence of Sc on wall concentration gradient with the stretching boundary (λ) greater than 0. The inclined parameter of the magnetic field (τ) is 90°. The Sc value is varied between 0.6, 0.5, 0.4, 0.3 and 0.2. There are two sets of curves, one with constant magnetic parameter (Q) value 0 and the other set with (Q) value 1. When (Q) value is 0, the curves follow a linear pattern after β value crosses 1. And when (Q) value is 1, the linearity is followed after β value crosses 1.5.

Fig. 14

Influence of Schmidt number on wall concentration gradient

Figure 15 represents the influence of Schmidt number on wall concentration gradient ($- \phi_{\eta } \left( 0 \right)$) with respect to β with the stretching boundary (λ) less than 0. The inclined parameter of the magnetic field (τ) is 90°. The Sc value is varied between 0.6, 0.5, 0.4, 0.3 and 0.2. There are two sets of curves, one with constant magnetic parameter (Q) value 0 and the other set with (Q) value 1. When (Q) value is 0, at $\beta = 0$, for all values of Sc, the wall concentration gradient ($- \phi_{\eta } \left( 0 \right)$) value is infinite, while, for (Q) value 5 at $\beta = 0$, for all values of Sc, the wall concentration gradient ($- \phi_{\eta } \left( 0 \right)$) value is 0. It is to note that, for all taken Scs, below $\beta = 0$, the wall concentration gradient ($- \phi_{\eta } \left( 0 \right)$) value is either 0 or negative for both the (Q) values, while when β is greater than 0 the wall concentration gradient ($- \phi_{\eta } \left( 0 \right)$) value is either 0 or positive.

Fig. 15

Influence of Schmidt number on wall concentration gradient

Figure 16 represents the influence of Stefan blowing parameter on axial velocity $f_{\eta } \left( \eta \right)$ with similarity variable (η) with the stretching boundary (λ) greater than 0. The inclined parameter of the magnetic field (τ) is 90°. The Schmidt No. (Sc) value is kept constant at 1. The Stefan blowing parameter (Λ) is varied between 0.1, 1, 5 and 100. It is noted that the axial velocity $f_{\eta } \left( \eta \right)$ decreases with an increase in a value of similarity variable (η). For (Q) value 0, the axial velocity $f_{\eta } \left( \eta \right)$ becomes zero after similarity variable (η) value 6, while for (Q) value 5, the axial velocity $f_{\eta } \left( \eta \right)$ becomes zero after similarity variable (η) value 8.

Fig. 16

Influence of Stefan blowing parameter on axial velocity

Figure 17 represents the influence of Stefan blowing parameter on concentration $\phi \left( \eta \right)$ with respect to similarity variable (η) with the stretching boundary (λ) greater than 0. The inclined parameter of the magnetic field (τ) is 90°. The Schmidt No. (Sc) value is kept constant at 1. The Stefan blowing parameter (Λ) is varied between 0.1, 1, 5 and 100. For both the (Q) values, the plot bears resemblance with reverse sigmoid function.

Fig. 17

Influence of Stefan blowing parameter on concentration

Figure 18 represents the influence of Prandtl number (Pr) on temperature $\phi \left( \eta \right)$ with respect to similarity variable (η) with the stretching boundary (λ) greater than 0. The inclined parameter of the magnetic field (τ) is 90°. The Schmidt No. (Sc) value is kept constant at 2. The Stefan blowing parameter (Λ) is also kept constant at 5. The Pr value is varied between 4, 3, 2 and 1. There are two sets of curves, one set with constant magnetic parameter (Q) and radiation parameter (N_R) values 0 and 0, respectively, and the other set with (Q) and (N_R) values 4 and 0.1, respectively. In both the results, the plots are somewhat similar with minimalistic difference. There is a slight similarity in this plot with reverse sigmoid function.

Fig. 18

Influence of Prandtl number (Pr) on temperature

Figure 19 represents the influence of Stefan blowing parameter on temperature $\phi \left( \eta \right)$ with respect to similarity variable (η) with the stretching boundary (λ) greater than 0. The inclined parameter of the magnetic field (τ) is 90°. The Schmidt No. (Sc) value is kept constant at 2. The Prandtl number (Pr) is also kept constant at 1. The Stefan blowing parameter (Λ) value is varied between 0.1, 1, 5 and 10. There are two sets of curves, one set with constant magnetic parameter (Q) and radiation parameter (N_R) values 0 and 0, respectively, and the other set with (Q) and (N_R) values 5 and 0.1, respectively. In both the results, the plots are somewhat similar with minimalistic difference. Here, again a slight similarity in this plot with reverse sigmoid function is noted.

Fig. 19

Influence of Stefan blowing parameter on temperature

Figure 20 represents the influence of Schmidt number (Sc) on temperature $\phi \left( \eta \right)$ with respect to similarity variable (η) with the stretching boundary (λ) greater than 0. The inclined parameter of the magnetic field (τ) is 90°. The Stefan blowing parameter (Λ) value is kept constant at 2. The Prandtl number (Pr) is also kept constant at 1. The Schmidt No. (Sc) value is varied between 0.1, 1, 5 and 10. There are two sets of curves, one set with constant magnetic parameter (Q) and radiation parameter (N_R) values 0 and 0, respectively, and the other set with (Q) and (N_R) values 5 and 1, respectively. In both the results, the plots are somewhat similar with minimalistic difference. Here, again a slight similarity in this plot with reverse sigmoid function is noted. Addition, we mention in Table 1 for different physical parameters of β.

Fig. 20

Influence of Schmidt number on temperature

Table 1 Expression for β for various physical parameters

6 Concluding Remarks

The Newtonian fluid flow heat and mass transfer of an incompressible MHD Newtonian fluid over a stretching/shrinking sheet exists for different parameters such as the Stefan blowing parameter, the Chandrasekhar number, inclined angle, the Prandtl number, the wall temperature parameter and the radiation parameter. The exact analytic solution of heat and mass transfer characteristics is obtained in terms of the incomplete gamma function. The main conclusion derived from the present investigation can be drawn as follows:

• The temperature increases as the Chandrasekhar number (Q) parameter increases, but it decreases as the Prandtl number (Pr) increases.

• Radiation number increases the thermal boundary-layer thickness.

• Increasing radiation parameter heat diffusion is favoured and the temperature increases through the laminar boundary layer.

• Physical/chemical conditions are better suited for effective cooling of the boundary-layer flows.

The present results, industrial application, Newtonian fluid flow due to stretching/shrinking sheet involves the extrusion of plastic sheets, drawing operation of plastic sheets.