1 Introduction

Because of the sensitivity of vibration signals, time–frequency analysis of mechanical vibration signals has become a successful technique [1]. The discontinuity of hob teeth causes inevitable vibration in hobbing. Therefore, vibration analysis is an effective approach to evaluate hob wear status and diagnose hob faults. However, during the acquisition process, vibration signals are easily contaminated by noise, which interferes with the extraction of signal features [2,3,4]. Thus, denoising is necessary for signal feature extraction.

Mechanical vibration signals are non-stationary [5]. For such signals, traditional wavelet-based methods have achieved good results [6,7,8]. However, the selection of wavelet base function has an important impact on wavelet-based methods [9]. After wavelet-based methods, Huang [10] proposed a new signal decomposition method: empirical mode decomposition (EMD). Lots of researchers have explored its application in practice [11,12,13]. But EMD has the problem of mode mixing. To suppress mode mixing, Wu and Huang [14] improved EMD and proposed ensemble empirical mode decomposition (EEMD). EEMD has been widely used in noise removing and feature recognition, such as in literatures [15,16,17]. Nevertheless, EMD and EEMD are both empirical algorithms and lack a complete mathematical theory [18]. In 2014, Dragomiretskiy et al. [19] proposed variational mode decomposition (VMD) with the rigorous mathematical theory. VMD is an adaptive, quasi-orthogonal and completely non-recursive decomposition method for non-stationary signal. It transforms signal decomposition into a variational solution problem and decomposes a signal into a series of modes with limited bandwidth and centre frequency [20,21,22]. Previous studies have already indicated that VMD has better decomposition effect and stronger robustness than EMD and EEMD [20, 23]. In recent years, the application of VMD in signal denoising and signal feature extraction has become a research hotspot. In these studies, researchers mainly focus on two core issues. (1) Determination of the mode number K. K is the most important parameter of VMD. (2) Selection and processing of modes after VMD decomposition. In literature [24], VMD and wavelet threshold were combined for denoising and baseline drift removal of MEMS hydrophone signals. K was determined to be 7 according to a priori test. Correlation coefficients between all modes and the original signal were calculated. Then, the modes were selected and processed to obtain the denoised signal according to the correlation coefficients. In literature [25], K was fixed at 12 according to a priori test. After VMD decomposition, the soft thresholding method was used to denoise surface electromyography signals. In literatures [26,27,28], K was determined according to the centre frequency observation method or the researcher's experience. Both methods were empirical. In literature [29], K was set to be the same as the number of components of EMD. In addition, in literatures [24, 30, 31], the correlation coefficient, as a classical method, was applied to the selection of modes after VMD decomposition. Through the above review of the literatures related to VMD, we can find that: (1) most of the existing studies determine K by the empirical method or the priori test method. However, the empirical method will make the determination of K interfered with human factors. The priori test method has limitations and is not necessarily applicable to other types of signals. For literature [29], there is no evidence that the number of EMD components is suitable for VMD. (2) Like the applications of EMD and EEMD, many researchers apply the correlation coefficient method to VMD to select modes. But the criteria for judging the correlation based on the correlation coefficient are different, which makes the selection result subjective.

In this paper, grey relational analysis (GRA) is applied to VMD for the first time to solve the determination of K and the selection of modes. GRA is one of the core contents of the grey theory which is proposed by Deng [32, 33]. GRA distinguishes the correlation between sequences according to the geometric shape of the data sequence [34]. Through GRA, the factor sequences that are strongly associated with the target sequence can be selected from all factor sequences. In the field of mechanical engineering, GRA was mostly used to optimize the production process. In literature [35], the application of GRA realized the optimal selection of surface inclination angle and tool’s overhang to minimize the vibrations and cutting forces during precise ball end milling of hardened steel. Literature [36] used GRA to solve the complex correlation between multiple parameters and then optimized the cutting speed, feed speed and cutting depth of milling. In literature [37], GRA was used to optimize the key parameters of electrochemical machining. In literature [38], researchers used GRA to evaluate the risk of lathe machining. In addition, GRA was also widely applied to other fields, such as energy efficiency assessment [39,40,41], structural optimization design [42, 43] and image denoising [34]. From the above reviews, it can be found that there is no research on applying GRA to signal processing.

In this paper, GRA and VMD are combined and named GVMD. The original signal is first decomposed multiple times by VMD with different K. Then, the modes obtained by each decomposition are reconstructed to obtain multiple reconstructed signals corresponding to the different K. GRA is used to analyze the correlation between these reconstructed signals and the original signal. The K corresponding to the reconstructed signal that has the strongest correlation with the original signal is considered to be the optimal K. After VMD decomposition, GRA is used again to select noise-dominant modes. These noise-dominant modes are processed by the soft thresholding method and then reconstructed with other modes to obtain the denoised signal. Finally, signal features can be accurately extracted from the denoised signal.

The rest of the paper is organized as follows. Section 2 briefly introduces the principles of VMD and GRA. Section 3 describes the steps of the proposed method GVMD. Then, simulation signals are used to verify the effectiveness. Section 4 analyzes the application of GVMD in engineering, including hob wear features extraction and hob broken tooth features extraction. Finally, conclusions are given in Sect. 5.

2 Theoretical Basis of VMD and Grey Relational Analysis

2.1 VMD

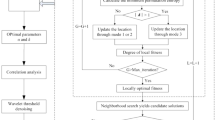
VMD is an adaptive signal decomposition method. It decomposes a signal into a specific number of modes \(u_{k}\) by constructing and solving a variational problem. Each mode is compact around a centre frequency \(\omega _{k}\). The detailed description of VMD can be found in [19]. Only the main concepts of VMD are given here. The flowchart of VMD is shown as in Fig. 1.

  1. (1)

    To determine \(u_{k}\) and \(\omega _{k}\), a constrained variational problem is first constructed as shown in Eq. (1).

    $$\begin{gathered} \mathop {\min }\limits_{{\left\{ {u_{k} } \right\},\left\{ {\omega _{k} } \right\}}} \left\{ {\sum\limits_{{k = 1}}^{K} {\left\| {\partial _{t} \left[ {\left( {\delta \left( t \right) + \frac{j}{{\pi t}}} \right)*u_{k} \left( t \right)} \right]e^{{ - j\omega _{k} t}} } \right\|_{2}^{2} } } \right\} \hfill \\ s.t.~~\sum\limits_{{k = 1}}^{K} {u_{k} } = f \hfill \\ \end{gathered} $$
    (1)

    where \(\left\{ {u_{k} } \right\}\) is the \(k\) th mode. \(\left\{ {\omega _{k} } \right\}\) is the \(k\) th centre frequency. \(\partial _{t}\) is the partial derivative of \(t\). \(\delta \left( t \right)\) is the unit impulse function. \(*\) represents convolution. \(f\) is the original signal.

  2. (2)

    The introduction of the quadratic penalty term \(\alpha\) and Largrangian multipliers \(\lambda\) makes Eq. (1) an unconstrained variational problem shown as Eq. (2).

    $$ \begin{aligned} & L\left( {\left\{ {u_{k} } \right\},\left\{ {\omega _{k} } \right\},\lambda } \right)\\ & \quad = \alpha \sum\limits_{{k = 1}}^{K} {\left\| {\partial _{t} \left[ {\left( {\delta \left( t \right) + \frac{j}{{\pi t}}} \right)*u_{k} \left( t \right)} \right]e^{{ - j\omega _{k} t}} } \right\|_{2}^{2} } \\ &\qquad+ \left\| {f\left( t \right) - \sum\limits_{{k = 1}}^{K} {u_{k} } \left( t \right)} \right\|_{2}^{2} + \lambda \left( t \right),f\left( t \right) - \sum\limits_{{k = 1}}^{K} {u_{k} } \left( t \right)\end{aligned} $$
    (2)
  3. (3)

    Initialize \(\left\{ {\hat{u}_{k}^{1} } \right\}\), \(\left\{ {\omega _{k}^{1} } \right\}\), \(\hat{\lambda }^{1}\), and \(n = 0\). Then, \(u_{k}\) and \(\omega _{k}\) are updated, respectively, by Eqs. (3) and (4).

    $$\hat{u}_{k}^{{n + 1}} \left( \omega \right) = \frac{{\hat{f}\left( \omega \right) - \sum\nolimits_{{i \ne k}} {\hat{u}_{i} \left( \omega \right)} + \frac{{\hat{\lambda }\left( \omega \right)}}{2}}}{{1 + 2\alpha \left( {\omega - \omega _{k} } \right)^{2} }} $$
    (3)
    $$ \omega _{k}^{{n + 1}} = \frac{{\mathop \smallint \nolimits_{0}^{\infty } \omega \left| {\hat{u}_{k} \left( \omega \right)} \right|^{2} d\omega }}{{\mathop \smallint \nolimits_{0}^{\infty } \left| {\hat{u}_{k} \left( \omega \right)} \right|^{2} d\omega }} $$
    (4)
  4. (4)

    The Largrangian multiplier \(\hat{\lambda }\) is also renewed by Eq. (5) after the update of modes and centre frequencies.

    $$ \hat{\lambda }^{{n + 1}} \left( \omega \right) = \hat{\lambda }^{n} \left( \omega \right) + \tau \left( {\hat{f}\left( \omega \right) - \mathop \sum \limits_{{k = 1}}^{K} \hat{u}_{k}^{{n + 1}} \left( \omega \right)} \right) $$
    (5)

    where \(\tau \) is the tolerance parameter of noise.

  5. (5)

    Iteration is stopped and K modes are finally obtained until the Eq. (6) is satisfied.

    $$ \mathop \sum \limits_{{k = 1}}^{K} \left\| {\hat{u}_{k}^{{n + 1}} - \hat{u}_{k}^{n} } \right\|_{2}^{2} /\left\| {\hat{u}_{k}^{n} } \right\|_{2}^{2} < \varepsilon $$
    (6)
Fig. 1
figure 1

The flowchart of VMD

Full size image

where \(\varepsilon\) is the given discriminant accuracy.

2.2 Grey Relational Analysis

GRA is used to analyze the correlation between different sequences. In practical applications, grey relational degree is calculated as the typical parameter of GRA. By comparing grey relational degrees, the degree of influence of different factor sequences on the target sequence can be evaluated. The following is the process of GRA. Figure 2 shows the flowchart of GRA.

  1. (1)

    Represent the sequence to be calculated as \({s}_{i}\).

    $$ {s}_{i} = \left( {s_{i} \left( 1 \right),s_{i} \left( 2 \right), \cdots ,s_{i} \left( n \right), \cdots ,s_{i} \left( {\text{N}} \right)} \right) $$
    (7)

    when \(i = 0\),\(~{s}_{0}\) represents the target sequence; \(i = 1,2, \cdots\), \({s}_{i}\) represents factor sequences. \(n\) represents the element in the sequence, \(n = 1,2, \cdots ,{\text{N}}\).

  2. (2)

    Original sequences are subjected to polarity unification and averaging to make sequences comparable. Corresponding sequences obtained are marked as \({s}_{i} ^{{\left( 0 \right)}}\) and \({s}_{i} ^{{\left( 1 \right)}}\).

    $$ s_{i} ^{{\left( 0 \right)}} \left( n \right) = {\text{~}}s_{i} \left( n \right) + \left| {{\text{min}}\left( {s_{i} \left( n \right)} \right)} \right| $$
    (8)
    $$ s_{i} ^{{\left( 1 \right)}} \left( n \right) = \frac{{s_{i} ^{{\left( 0 \right)}} \left( n \right)}}{{\frac{1}{{\text{N}}}\mathop \sum \nolimits_{{n = 1}}^{{\text{N}}} s_{i} ^{{\left( 0 \right)}} \left( n \right)}} $$
    (9)

    where \({{s}_{i}}^{\left(0\right)}\left(n\right)\) and \({{s}_{i}}^{\left(1\right)}\left(n\right)\) are the \(n\) th element in the sequences \({{\boldsymbol{s}}_{i}}^{(0)}\) and \({{\boldsymbol{s}}_{i}}^{(1)}\).

  3. (3)

    Calculate grey relational coefficient sequence \({\gamma }_{i}\) between the target sequence and factor sequences.

    $$ \gamma _{i} \left( n \right) = \frac{{\mathop {\min }\limits_{i} \mathop {\min }\limits_{n} \left| {s_{0} ^{{\left( 1 \right)}} \left( n \right) - s_{i} ^{{\left( 1 \right)}} \left( n \right)} \right| + \rho \mathop {\max }\limits_{i} \mathop {\max }\limits_{n} \left| {s_{0} ^{{\left( 1 \right)}} \left( n \right) - s_{i} ^{{\left( 1 \right)}} \left( n \right)} \right|}}{{\left| {s_{0} ^{{\left( 1 \right)}} \left( n \right) - s_{i} ^{{\left( 1 \right)}} \left( n \right)} \right| + \rho \mathop {\max }\limits_{i} \mathop {\max }\limits_{n} \left| {s_{0} ^{{\left( 1 \right)}} \left( n \right) - s_{i} ^{{\left( 1 \right)}} \left( n \right)} \right|}} $$
    (10)

    where \({\gamma }_{i}\) is the grey relational coefficient sequence between the \(i\) th factor sequence and the target sequence, \(i = 1,2, \cdots\). \(\gamma _{i} \left( n \right)\) is the \(n\) th element in the sequence \({\gamma }_{i}\). \(\rho\) represents the resolution coefficient, usually \(\rho = 0.5\).

  4. (4)

    Finally, calculate grey relational degrees between the target sequence and factor sequences.

    $$ \xi _{i} = \frac{1}{{\text{N}}}\mathop \sum \limits_{{n = 1}}^{{\text{N}}} \omega \gamma _{i} \left( n \right) $$
    (11)
Fig. 2
figure 2

The flowchart of GRA

Full size image

in Eq. (11) \(i=\mathrm{1,2},\cdots \), \({\xi }_{i}\) represents the grey relational degree between the \(i\) th factor sequence and the target sequence, \({\xi }_{i}\in [\mathrm{0,1}]\). \(\omega \) represents the weight coefficient, usually \(\omega =1\).

3 Proposed Method GVMD

A signal containing noise is decomposed to obtain several modes. These modes can be divided into two categories: noise-dominant modes and signal-dominant modes. Noise-dominant modes should be selected and processed first. Then, the processed noise-dominant modes and signal-dominant modes are reconstructed to obtain the denoised signal. In this paper, GVMD is proposed to solve two key problems in the process of signal denoising. (1) Determination of the mode number K in VMD. (2) Selection of noise-dominant modes.

In this and subsequent sections, the performance of GVMD will be compared with other methods. These methods include (1) VMD-AllST [25]: after VMD decomposition, all modes are processed by soft thresholding method. (2) VMD-CorST [24]: after VMD decomposition, the modes are selected by correlation coefficient method and then processed by soft thresholding method. (3) EEMD-AllST [17]: after EEMD decomposition, all modes are processed by soft thresholding method. (4) Wavelet-ST: classical wavelet soft thresholding method.

3.1 Determination of the Mode Number K in VMD

The mode number K is the most important parameter in VMD, which greatly affects the performance of VMD. Too few modes will lead to incomplete signal decomposition, while too many modes will cause additional modes to be introduced into the decomposition result. The main steps of GVMD to determine K are as follows.

  1. (1)

    Since the mode number of EMD is self-adaptive, the original signal is first decomposed by EMD to obtain the mode number \({\mathrm{K}}^{\mathrm{\text{'}}}\).

  2. (2)

    \([{\mathrm{K}}^{\mathrm{\text{'}}}-3,{\mathrm{K}}^{\mathrm{\text{'}}}+3]\) is taken as the range of the mode number K for VMD. The original signal is decomposed multiple times with different K.

  3. (3)

    The modes of each decomposition are reconstructed to obtain the reconstructed signal, respectively.

  4. (4)

    Grey relational degrees are calculated between the original signal and the reconstructed signals by GRA, respectively. The K corresponding to the largest grey relational degree is selected as the optimal K.

It should be noted that other parameters in VMD except K are generally set according to reference [19].

A simulation signal is used to verify the determination method of K. In rotating machinery, the pure vibration signal mainly contains periodic impulse components and harmonic components. The periodic impulse component has the feature of short duration in time domain and wide bandwidth in frequency domain, while the harmonic component has the feature of long duration in time domain and narrow bandwidth in frequency domain [21]. Therefore, in the frequency domain, the periodic impulse component appears as a frequency group, while the harmonic component appears as a single frequency.

$$ \left\{ {\begin{array}{*{20}c} {s_{1} = 3e^{{ - \theta t}} \sin \left( {2\pi f_{{n1}} t} \right) + 3e^{{ - \theta t}} \sin \left( {2\pi f_{{n2}} t} \right) + 3e^{{ - \theta t}} \sin \left( {2\pi f_{{n3}} t} \right)} \\ {s_{2} = \sin \left( {2\pi f_{r} t} \right) + 1} \\ {s_{3} = 0.3\sin \left( {2\pi f_{1} t} \right) + 0.3\sin \left( {2\pi f_{2} t} \right) + 0.3\sin \left( {2\pi f_{3} t} \right) + 0.3\sin \left( {2\pi f_{4} t} \right)} \\ {s = s_{1} \times s_{2} + s_{3} } \\ \end{array} } \right. $$
(12)

In Eq. (12), \(s_{1}\) represents three periodic impulse components; \({{\theta }} = 100\) is the decay factor; \(f_{{n1}} = 250~{\text{Hz}}\), \(f_{{n2}} = 350~{\text{Hz}}\),\({\text{~}}f_{{n3}} = 450~{\text{Hz}}\) are resonant frequencies. \(s_{2}\) represents the rotation component; \(f_{r} = 20~{\text{Hz}}\) is the rotation frequency. \(s_{3}\) represents four harmonic components; their frequencies are \(f_{1} = 50~{\text{Hz}}\), \(f_{2} = 100~{\text{Hz}}\), \(f_{3} = 150~{\text{Hz}}\), \(f_{4} = 200~{\text{Hz}}\). \(s\) represents the combined signal. \(s_{1} \times s_{2}\) represents modulation.

The EMD mode number is \({{K^{\prime}}} = 8\). Therefore, the range of the mode number K in VMD is [5, 11]. The grey relational degree of each VMD decomposition is calculated according to the above steps, as shown in Table 1. It can be seen that \({\text{K}} = 7\) corresponds to the maximum grey relational degree. Finally, it can be determined that the simulation signal \(s\) should be divided into 7 modes. These 7 modes in time domain and in frequency domain are shown in Fig. 3. As a comparison, Fig. 4 displays the VMD decomposition when \({\text{K}} = {\text{K}}^{{\text{'}}}\), which refers to reference [29]. Generally speaking, if there is no over-decomposition or under-decomposition, the decomposition result can be considered to be ideal. Over-decomposition means that a frequency component is decomposed into two modes. On the contrary, under-decomposition means that two frequency components appear in the same mode. In Fig. 3, each mode contains only one frequency component and all frequency components in the simulation signal can be accurately obtained. But there is over-decomposition in Fig. 4. \({f}_{n2}\)- frequency group is decomposed into mode \({u}_{6}\) and mode \({u}_{7}\). The results confirm the effectiveness of using GVMD to determine K.

Table 1 Grey relational degree of each VMD decomposition
Full size table
Fig. 3
figure 3

K determined by proposed method

Full size image
Fig. 4
figure 4

K equal to EMD mode number

Full size image

3.2 Selection of Noise-Dominant Modes

After decomposing the original signal into K modes, GVMD is used to identify the noise-dominant modes. The highest frequency mode is considered as the mode with the most noise, i.e. the Kth mode \({u}_{\mathrm{K}}\) [17, 44]. Therefore, grey relational degrees between \({u}_{\mathrm{K}}\) and other modes can be calculated. The stronger the correlation with \({u}_{\mathrm{K}}\) means the higher the noise level of the mode. The main steps of GVMD to select noise-dominant modes are as follows.

  1. (1)

    Calculate grey relational degrees between the last mode \({u}_{\mathrm{K}}\) and other modes.

  2. (2)

    \({u}_{\begin{array}{c}K\\ \end{array}}\) and the modes with grey relational degrees greater than their average are selected as noise-dominant modes. The remaining modes are considered to be signal-dominant modes.

  3. (3)

    The noise-dominant modes are processed by soft thresholding method to remove noise components while retaining useful information, as shown in Eq. (13).

  4. (4)

    The processed noise-dominant modes and the signal-dominant modes are reconstructed to gain the denoised signal. Then, signal features can be extracted.

    $$ \overline{{u_{{nd}} }} \left( t \right) = \left\{ {\begin{array}{*{20}c} {sign\left( {u_{{nd}} \left( t \right)} \right)\left( {\left| {u_{{nd}} \left( t \right)} \right| - T} \right)~\left| {u_{{nd}} \left( t \right)} \right| \ge T} \\ {0~~~~~~~~~~~~~~~~~~~~~~~\left| {u_{{nd}} \left( t \right)} \right| < T} \\ \end{array} } \right. $$
    (13)

where \(u_{{nd}} \left( t \right)\) and \(\overline{{u_{{nd}} }} \left( t \right)\) represent the noise-dominant mode and processed noise-dominant mode, respectively. \(sign\left( \cdot \right)\) represents the symbolic function. \(T\) is the thresholding value, \(T = \sigma \sqrt {2\ln N}\), \(\sigma = median\left( {\left| {u_{{nd}} \left( t \right)} \right|} \right)/0.6725\), \(N\) is the length of \(u_{{nd}} \left( t \right)\).

Noise is added to the simulation signal constructed in Sect. 3.1 to obtain the noisy simulation signal. The noise level of the signal is quantitatively evaluated by signal-to-noise ratio (\(SNR\)). The higher \(SNR\) means the lower noise level of the signal. \(SNR_{{in}}\) represents \(SNR\) of the input signal and \(SNR_{{out}}\) represents \(SNR\) the output signal, i.e. the denoised signal. Their calculation methods are shown as Eqs. (14) and (15).

$$ {\text{SNR}}_{{{\text{in}}}} = 10\log \left\{ {\frac{{\mathop \sum \nolimits_{{i = 1}}^{N} x_{p} \left( i \right)^{2} }}{{\mathop \sum \nolimits_{{i = 1}}^{N} \left( {x_{n} \left( i \right) - x_{p} \left( i \right)} \right)^{2} }}} \right\} $$
(14)
$$ {\text{SNR}}_{{{\text{out}}}} = 10\log \left\{ {\frac{{\mathop \sum \nolimits_{{i = 1}}^{N} x_{p} \left( i \right)^{2} }}{{\mathop \sum \nolimits_{{i = 1}}^{N} \left( {x_{d} \left( i \right) - x_{p} \left( i \right)} \right)^{2} }}} \right\} $$
(15)

where \(x_{p}\) represents the pure signal. \(x_{n}\) represents the noisy signal. \({x}_{d}\) represents the denoised signal.

\({SNR}_{in}\) is set to 0 dB in this case. Through GVMD, K = 10 is determined. The grey relational degrees of modes are calculated as shown in Table 2. \({u}_{6}\), \({u}_{7}\),\({u}_{8}\),\({u}_{9}\),\({u}_{10}\) are selected as noise-dominant modes. The performance of GVMD is compared with the competitive methods. Figure 5 shows the pure signal, the noisy signal and the denoised signals in the time domain. GVMD achieves the highest \({SNR}_{out}\), reaching 4.1143 dB. Because the other four methods cause the loss of the pure signal. The \({SNR}_{out}\) of these four methods are lower than that of GVMD. Furthermore, the signals in the frequency domain are displayed in Fig. 6. The frequency domain distribution conforms to the conclusions obtained from the time domain waveforms. While removing noise components, GVMD completely retains the frequency components of the pure signal. But the competitive methods cause the loss of some frequency components.

Table 2 Grey relational degrees of modes
Full size table
Fig. 5
figure 5

Simulation signal in time domain

Full size image
Fig. 6
figure 6

Simulation signal in frequency domain

Full size image

4 Engineering Application Analysis

In this study, two kinds of experiments were carried out to collect vibration signals: hob wear experiment and hob broken tooth experiment.

The focus of this paper is to denoise the collected vibration signals and extract effective features. Next, the proposed method GVMD will be applied to the collected vibration signals. Its performance will be compared with the competitive methods. Evaluation indicators for these methods include: signal waveforms, \(SNR\), and frequency components.

It should be pointed out that because pure components of the real signal cannot be obtained, \(SNR\) of the real signal is an estimated value, unlike the simulation signal. However, this estimate of \(SNR\) is still significant to compare the denoising effect of different methods on the real signal [3]. Equation (16) gives the calculation of \(SNR\) of the real signal.

$$ {\text{SNR}} = 10\log \left\{ {\frac{{\mathop \sum \nolimits_{{i = 1}}^{N} x\left( i \right)^{2} }}{{\mathop \sum \nolimits_{{i = 1}}^{N} \left( {x\left( i \right) - \hat{x}\left( i \right)} \right)^{2} }}} \right\} $$
(16)

where \(x\left( i \right)\) is the original signal. \(\hat{x}\left( i \right)\) is the denoised signal.

4.1 Hob Wear Features Extraction

To evaluate the hob wear status, vibration signals of the entire life cycle of the hob in actual production were collected. A total of 3692 workpieces were machined in this life cycle. The scene of the hob wear experiment is shown in Fig. 7. The experimental equipment mainly included a dry-cutting hobbing machine, an acceleration sensor and a data recorder. Tables 3 and 4, respectively, list equipment models and experimental conditions.

Fig. 7
figure 7

Hob wear experiment

Full size image
Table 3 The model of the equipment
Full size table
Table 4 Experimental conditions
Full size table

Three samples are selected for analysis from the front, middle and back segments of the 3692 sets of data, which are marked as Sample-F, Sample-M, Sample-B. According to GVMD, the mode number K and noise-dominant modes of the three samples can be determined, which are listed in Table 5. The noise-dominant modes are processed according to Eq. (13) and then reconstructed with other modes to obtain the denoised signal. The original signal and denoised signals are shown in Fig. 8. Comparing the denoising results, it is obvious that time-domain waveforms of GVMD are the closest to original signals. Moreover, these waveforms of GVMD are smoother than original signals. GVMD ensures the integrity of the original signal components as much as possible while reducing noise. The highest \(SNR\) achieved by GVMD in the three sample signals strongly proves this point. In comparison, the performance of other methods is significantly worse than GVMD. VMD-CorST and Wavelet-ST cause loss of original signal components. This phenomenon is particularly serious in VMD-AllST and EEMD-AllST. The waveforms of VMD-AllST and EEMD-AllST are very sparse and have small amplitude. Accurate denoising results and comparative analysis must be further explored in the frequency domain.

Table 5 Mode number K and noise-dominant modes in hob wear experiment
Full size table
Fig. 8
figure 8figure 8

Denoised signal waveforms in hob wear experiment: a Sample-F b Sample-M c Sample-B

Full size image

In this experiment, the rotation speed of the hob spindle is 680 r/min, so the rotation frequency is 11.3 Hz. When the hob meshes with the gear, a periodic cutting force acts on the hob along the axis direction. This will generate the meshing frequency (\({f}_{m}\)), which is determined by the rotation speed of the hob spindle and the number of hob heads. Furthermore, the existence of hob grooves causes intermittent cutting of the hob, so a periodic cutting force acts on the hob along the tangential direction. This will generate the hobbing frequency (\({f}_{h}\)), which is determined by the rotation speed of the hob spindle and the number of hob grooves. \({f}_{m}\) and \({f}_{h}\) can be calculated by Eqs. (17) and (18), respectively.

$$ f_{m} = \frac{{n \times z_{h} }}{{60}} $$
(17)
$$ f_{h} = \frac{{n \times z_{g} }}{{60}} $$
(18)

where \(n\) is the rotation speed of the hob spindle. \({z}_{h}\) is the number of hob heads. \({z}_{g}\) is the number of hob grooves. From the data in Table 4, it can be calculated that \({f}_{m}=22.7\) Hz, \({f}_{h}=158.7\) Hz.

In hobbing, the amplitude of the rotation frequency is much smaller than that of \({f}_{m}\) and \({f}_{h}\). In the frequency domain analysis of this section and the next section, the rotation frequency will not be marked. \({f}_{m}\) and \({f}_{h}\) are frequencies specific to hobbing. Therefore, \({f}_{m}\) and \({f}_{h}\) as well as their harmonics (\( 2f_{m} ,3f_{m} , \ldots ;2f_{h} ,3f_{h} , \ldots \)) will be analyzed as the feature frequencies of the hob. Other frequencies that have nothing to do with the rotation frequency, \({f}_{m}\) and \({f}_{h}\) are considered noise frequencies.

Figure 9 shows the envelope spectra of the three sample signals before and after denoising. It can be observed that in envelope spectra of original signals, feature frequencies and noise frequencies are mixed together. Feature frequencies cannot be effectively extracted. According to Fig. 9, performance of different methods is evaluated as follows. (1) After denoising by GVMD, noise frequencies in envelope spectra of the three sample signals have been removed and feature frequencies have been effectively retained. In addition, modulation sidebands are more obvious, indicating that there are steady-type faults in the hob spindle. (2) VMD-AllST and EEMD-AllST over-process the original signals, resulting in lower frequency amplitude than that of the other methods. Thus, feature frequencies cannot be obtained obviously. (3) In VMD-CorST, \({f}_{m}\)-related frequencies are extracted. But \({f}_{h}\)-related frequencies are not easily obtained. (4) For Sample-F and Sample-B, \({f}_{m}\)-related frequencies and \({f}_{h}\)-related frequencies can be obtained in Wavelet-ST. But for Sample-M, \({f}_{m}\)-related frequencies are not obvious. Overall, the frequency amplitude of Wavelet-ST is smaller than that of GVMD.

Fig. 9
figure 9figure 9

Denoised signal envelope spectra in hob wear experiment: a Sample-F b Sample-M c Sample-B

Full size image

4.2 Hob Broken Tooth Features Extraction

A broken tooth hob was used for machining experiment. The equipment of this experiment mainly included: a broken hob, a dry-cutting hobbing machine, an acceleration sensor and a data recorder, as shown in Fig. 10. The important parameters of the hob and sampling frequency are shown in Table 6. Vibration signals were collected under three different working conditions. Table 7 shows the details of the working conditions.

Fig. 10
figure 10

Hob broken tooth experiment

Full size image
Table 6 Parameters of the hob and sampling frequency
Full size table
Table 7 Three different working conditions
Full size table

Next, the mode number K and noise-dominant modes under the three working conditions are calculated according to GVMD, which are listed in Table 8. Figure 11 displays denoised signal waveforms by different methods. Obviously, the denoising effect of VMD-AllST and EEMD-AllST is very poor. These two methods seriously over-process the original signals, causing the loss of a large amount of original signal components. Moreover, these two methods significantly reduce the amplitude of the signals. These factors cause the \(SNR\) of VMD-AllST and EEMD-AllST to be much lower than that of other methods. VMD-CorST causes the loss of a part of original signal components. In condition 1 and condition 2, the \(SNR\) of VMD-CorST is acceptable. But in condition 3, the \(SNR\) is not good. GVMD and Wavelet-ST are the two most effective methods. But overall, the time-domain waveform of GVMD is smoother than that of Wavelet-ST. Moreover, the \(SNR\) of GVMD is also higher than that of Wavelet-ST in all three conditions. Furthermore, envelope spectra of various methods will be further analyzed.

Table 8 Mode number K and noise-dominant modes in hob broken tooth experiment
Full size table
Fig. 11
figure 11figure 11

Denoised signal waveforms in hob broken tooth experiment: a Condition 1 b Condition 2 c Condition 3

Full size image

The feature frequency of the broken teeth hob needs to be determined first. The absence of hob teeth results in a change in the frequency of the cutting force, which produces the feature frequency of the broken teeth hob (\(f_{b}\)). The calculation of \(f_{b}\) is shown in Eq. (19).

$$ f_{b} = \frac{{n \times (z_{g} - z_{b} )}}{{60}} $$
(19)

where \(n\) is the rotation speed of the hob. \({z}_{g}\) is the number of hob grooves. \({z}_{b}\) is the number of broken teeth, \({z}_{b}=1\) in this experiment. \({f}_{b}\) and its harmonics (\(2{f}_{b}\),\(3{f}_{b}\),\(\cdots \)) should be extracted as feature frequencies in envelope spectra. According to the Sect. 4.1, there is no doubt that the meshing frequency (\({f}_{m}\)) and its harmonics (\(2{f}_{m}\),\(3{f}_{m}\),\(\cdots \)) should also be retained in envelope spectra as feature frequencies. Table 9 gives calculation results of \({f}_{m}\) and \({f}_{b}\) under the three working conditions.

Table 9 Calculation results of \(f_{r}\) and \(f_{b}\) under the three working conditions
Full size table

Envelope spectra before and after denoising under the three working conditions are shown in Fig. 12. In envelope spectra of original signals, feature frequencies and noise frequencies coexist. After comparing and analyzing the effects of different methods, we summarize as follows. (1) VMD-AllST and EEMD-AllST seriously over-process original signals, causing their frequency amplitude to be much lower than that of other methods. The feature frequencies are buried in other frequencies. (2) In VMD-CorST, \({f}_{m}\)-related frequencies are extracted. By comparison, \({f}_{b}\)-related frequencies are less obvious. (3) In Wavelet-ST, the feature frequencies are effectively extracted. But noise frequencies are not completely removed. (4) Overall, the performance of GVMD is better than other methods. Not only noise frequencies are completely removed, but feature frequencies are also effectively extracted.

Fig. 12
figure 12figure 12

Denoised signal envelope spectra in hob broken tooth experiment: a Condition 1 b Condition 2 c Condition 3

Full size image

5 Conclusion

In engineering, the feature extraction of the vibration signal is susceptible to noise interference. This paper proposes a method combining GRA and VMD, named GVMD, to solve this problem. GRA is used to determine the mode number K which is an important parameter in VMD. K can be adaptively determined by GRA, which overcomes shortcomings of traditional methods that are easily affected by human factors. After VMD decomposition, GRA is used to analyze the correlation between the highest frequency mode and other modes to identify noise-dominant modes and signal-dominant modes. Finally, noise-dominant modes are processed and reconstructed with other modes to obtain the denoised signal.

The performance of GVMD has been evaluated and compared with other methods (VMD-AllST, VMD-CorST, Wavelet-ST, EEMD-AllST). In the analysis of simulation signals, GVMD determines the mode number K effectively. Compared with other methods, GVMD completely retains the frequency components of the signal while removing noise. Furthermore, the feature extraction results of hob vibration signals are analyzed. VMD-AllST and EEMD-AllST are prone to over-process original signals. VMD-CorST can only obtain part of the signal features. Wavelet-ST can effectively extract signal features in some cases, but cannot completely remove noise. In contrast, GVMD achieves the best results. GVMD can completely remove noise and effectively extract signal features.