1 Introduction

Artificial neural network (ANN) can prove to be a very effective statistical tool for handling variety of situations such as (1) absence of mathematical relations for complicated physics, (2) fast and time-effective approach to get the result, (3) use of noisy data (obtained from analytical/numerical/experimental method). One of the very powerful types of neural network, used to solve a wide range of practical problems, is the radial basis network. Radial basis network offers various advantages over perceptron types such as simple to use and better capability to handle noisy data for medium-sized data set [1, 2]. Because of these advantages, radial basis network has been employed by numerous researchers in a wide spectrum of problems of engineering and industrial applications.

Stochastic optimization methods [3, 4] are very powerful optimization methods with capability to handle optimization problems with local minimum traps. Most commonly used stochastic optimization methods (SOMs) are: genetic algorithm (GA) [5], global search algorithm (GSA) [6], multiple starting point algorithm (MSPA) [7], simulated annealing algorithm (SAA) [8], and pattern search algorithm (PSA) [9].

For design and optimization of various systems, inverse engineering has emerged as a new field in this regard [10, 11]. In the inverse engineering problems, independent variables are computed from the knowledge of dependent variables. Or, we can say that from the end product, we have to trace back the governing equations of the system. Inverse engineering proves to be very effective in situation such as [12] measurement of properties is a costly affair or not possible due to inaccessibility of location (re-entry of vehicles), or chances of perturbation of flow pattern due to intrusion of measuring probes. In the field of inverse engineering, ANN-based optimization techniques play a key role in the final analysis.

In the present study, implementation of radial basis neural network (RBNN) has been demonstrated by choosing a problem of engineering applications involving flow and heat transfer of a non-Newtonian third-grade fluid. A variety of engineering equipment such as mixer, heat exchanger and pumps handles different kinds of fluids such as slurry [13], polymers [14], medicines [15], and pastes [16] in industries like mining applications, polymer processing, etc. Flow of fluid through these equipments is not governed by a simple linear stress–strain rate model of Newtonian fluids. Instead, in many cases, a nonlinear stress–strain rate relation is better-suited to describe the intricacies associated with the flow of these substances, classified as non-Newtonian fluids.

A non-Newtonian fluid exhibits strange behavior such as shear thinning/thickening and elastic nature, which are not displayed by Newtonian fluids. But a mathematical modeling of problems involving non-Newtonian fluid is a formidable task. Over the years, several mathematical models such as power law model, visco-elastic model, visco-plastic model, and Rivlin–Erickson model of grade three (also known as third-grade fluids) are put forward by the researchers to describe the non-Newtonian fluids. Third-grade fluid model has been employed by numerous researchers for modeling the flow of polymer, slurry, lubricants. In the present study, flow and heat transfer of a non-Newtonian third-grade fluid has been chosen as a test case for the demonstration of implementation process of RBNN.

Flow of a non-Newtonian third-grade fluid through rectangular parallel plates, subjected to uniform heat fluxes, is considered. First, governing equations of the problem are solved by employing LSM [17]. Even though LSM approach is comparatively simple to apply, yet it takes significant time to find the solution for small alterations such as new type of boundary conditions, changes in thermo-physical properties of fluid and changes in geometry. One pair of velocity profile and temperature profile is computed for one value of third-grade fluid parameter (A). This process is repeated multiple times to generate 26 pairs for 26 different values of ‘A’. This constituted the first part of the problem.

In the second part, RBNN is explored to solve the energy equation, as well as to retrieve the value of A, corresponding to a given velocity profile. So, the present approach intends to two problems simultaneously: (a) to solve the direct problem to find the temperature profile and (b) to apply the inverse method to find TGF parameter ‘A’. To apply RBNN in the problem, one important parameter is required, called spread. Five different SOMs are used, one by one to compute the value of spread (required for RBNN). The data (velocity profile: as input, temperature profile & A: as target) generated by LSM are used to train RBNN. This leads to the development of stochastic optimization method-assisted radial basis neural network (SOMARBNN).

Once the SOMARBNNs are developed, a new velocity profile (not part of training data) is fed as input, and temperature profile along with A is obtained as output. The advantage of this approach is that only few cases need to be solved with any of the means: analytically, numerically or experimentally to generate data. Once sufficient data are generated to train SOMARBNNs, and then, various alterations can be solved by using SOMARBNNs. One case (i.e., producing temperature profile and A corresponding to any velocity profile) is shown in the present work, but the approach can be extended to solve any engineering problem. Present work reports first time use of SOMARBNNs, applied to non-Newtonian fluid flow problem.

Table 1 shows the latest literature available for application of ANN/RBNN on non-Newtonian fluids. It is observed from Table 1 that large number of work is done on non-Newtonian fluids by employing ANN, but optimization of RBNN by different stochastic optimization methods, and comparative assessment of the final result is not available in open literature. The present work intends to find a best solution to optimize RBNN for application in non-Newtonian fluids. The performance of different SOMARBNNs is compared and analyzed under various noises in the input data. PSAARBNN is found to be the most suitable in terms of accuracy, CPU time consumption, and capability to handle noisy data set. (Table 1 to be inserted here).

Table 1 Research available in open literature about use of ANN in fluid flows
Full size table

The advantages of present approach are: (i) the main attribute in RBNN is easily obtained, which otherwise requires lots of technical knowledge of neural networks, (ii) solving any inverse engineering problem becomes easy (iii), if few cases of any engineering problem are solved either experimentally, numerically or analytically, large number of other cases with various levels of alterations can be solved within very short time.

2 Formulation

2.1 First Part: Generation of Data for RBNN

Two parallel plates subject to uniform heat fluxes (q1 and q2) are arranged to make channel with the following dimensions: distance H, length L and width W. An incompressible non-Newtonian fluid flow through the parallel plates under the steady-state condition and is shown schematically in Fig. 1. The flow is assumed to be laminar and fully developed (thermally and hydro-dynamically). The dimension of the channel along the x* axis is large as compared to the dimension in other two axes, i.e., L >  > H W. The equations governing the flow can be presented as: (Fig. 1 to be inserted here).

Fig. 1
figure 1

Schematic of the non-Newtonian fluid flow under uniform heat flux

Full size image

Equation of continuity

$$\nabla\cdot V^{*} = 0$$
(1)

Equation of momentum conservation

$$\rho \frac{DV}{{Dt}}^{*} = \nabla\cdot \tau + f$$
(2)

It is to be noted that body forces are neglected in Eq. (2).

For modeling a non-Newtonian fluid flow, the nonlinear relationship between stress and the strain rate can be expressed by the third-grade fluid model as [17]:

$$\tau = - pI + \mu A_{1} + \alpha_{1} A_{2} + \alpha_{2} A_{1}^{2} + \beta_{1} A_{3} + \beta_{2} \left( {A_{1} A_{2} + A_{2} A_{1} } \right) + \beta_{3} \left( {trA_{1}^{2} } \right)A_{1}$$
(3)
$$A_{1} = (gradV^{*} ) + (gradV^{*} )^{Transpose}$$
(4)
$$\begin{gathered} A_{n} = \frac{{dA_{n - 1} }}{dt} + A_{n - 1} (gradV^{*} ) + (gradV^{*} )^{Transpose} A_{n - 1} , \hfill \\ n = 1,2,3 \hfill \\ \end{gathered}$$
(5)

Equation of energy conservation

$$\rho c_{p} \frac{{dT^{*} }}{dt} = \tau :grad(V^{*} ) - \nabla\cdot( - k_{th} \nabla T^{*} )$$
(6)

With the help of assumption of hydro-dynamically fully developed flow, the only velocity component that remains nonzero is the axial one, with dependency only on y*. Thus, the velocity vector becomes:

$$v^{*} = \left[ {u^{*} \left( {y^{*} } \right), \, 0,0} \right]$$
(7)

With the help of Eq. (7), the momentum conservation equation given by Eq. (2) simplifies to:

$$\frac{{\partial p^{*} }}{{\partial x^{*} }} = \mu \frac{{d^{2} u^{*} }}{{dy^{*2} }} + 2(\beta_{2} + \beta_{3} )\frac{d}{{dy^{*} }}\left( {\frac{{du^{*} }}{{dy^{*} }}} \right)^{3}$$
(8)
$$\frac{{\partial p^{*} }}{{\partial y^{*} }} = \left( {2\alpha_{1} + \alpha_{2} } \right)\frac{d}{{dy^{*} }}\left( {\frac{{du^{*} }}{{dy^{*} }}} \right)^{2}$$
(9)
$$\frac{{\partial p^{*} }}{{\partial z^{*} }} = 0$$
(10)

Similarly, by using Eq. (7), energy conservation equation given by Eq. (6) simplifies to:

$$\rho c_{p} u^{*} \frac{{\partial T^{*} }}{{\partial x^{*} }} = k_{th} \left( {\frac{{\partial^{2} T^{*} }}{{\partial x^{*2} }} + \frac{{\partial^{2} T^{*} }}{{\partial y^{*2} }}} \right) + \mu \left( {\frac{{du^{*} }}{{dy^{*} }}} \right)^{2} + 2(\beta_{2} + \beta_{3} )\left( {\frac{{du^{*} }}{{dy^{*} }}} \right)^{4}$$
(11)

The effect of third-grade fluid parameter A on energy equation is represented by the third term in the right-hand side of Eq. (11). Because of the assumption of thermally developed conditions, the temperature profile becomes independent of x* and depends only upon y*. The non-dimensional temperature can be defined as follows:

$$\theta = \frac{{T^{*} - T_{{w_{l} }}^{*} }}{{T_{m}^{*} - T_{{w_{l} }}^{*} }}$$

For constant wall heat flux condition, the following important relations can be deduced:

$$\frac{{\partial T^{*} }}{{\partial x^{*} }} = \frac{{dT_{m}^{*} }}{{dx^{*} }} = const.,\frac{{\partial^{2} T^{*} }}{{\partial x^{*2} }} = 0$$
(12)

Thus, substitution of Eq. (12) into Eq. (11) gives the following form of energy equation

$$\rho c_{p} u^{*} \frac{{\partial T^{*} }}{{\partial x^{*} }} = k_{th} \left( {\frac{{\partial^{2} T^{*} }}{{\partial y^{*2} }}} \right) + \mu \left( {\frac{{du^{*} }}{{dy^{*} }}} \right)^{2} + 2(\beta_{2} + \beta_{3} )\left( {\frac{{du^{*} }}{{dy^{*} }}} \right)^{4}$$
(13)

Boundary conditions: (a) constant and uniform heat fluxes on both the plates, (b) at the plate–fluid interface, no-slip conditions prevail. Thus, the following expressions can be written

$$u*\left( { - h} \right) = 0, \, u*\left( h \right) = 0$$
(14)
$$k_{th} \left( {\frac{{\partial T^{*} }}{{\partial y^{*} }}} \right)_{ - h} = \, \mp q_{1} ,k_{th} \left( {\frac{{\partial T^{*} }}{{\partial y^{*} }}} \right)_{h} = \, \pm q_{2}$$
(15)

To make the analysis independent of requirement of knowledge of plate surface temperature, the temperature is non-dimensionalized in the following way:

$$\theta = \frac{{T^{*} - T_{{w_{l} }}^{*} }}{{q_{1} h/k_{th} }}$$
(16)

Further, the fluid velocity at any location, and distance (along y* direction) are non-dimensionalized as:

$$u = \frac{{u^{*} }}{{u_{0} }},\,y = \frac{{y^{*} }}{h}$$
(17)

With the help of non-dimensional terms defined in Eqs. (16) and (17), conservation equations of momentum and energy can be expressed in the non-dimensional form as:

$$\frac{{d^{2} u}}{{dy^{2} }} + 6A\left( {\frac{du}{{dy}}} \right)^{2} \frac{{d^{2} u}}{{dy^{2} }} = N$$
(18)
$$\beta u = \frac{{d^{2} \theta }}{{dy^{2} }} + Br\left( {\frac{du}{{dy}}} \right)^{2} + 2ABr\left( {\frac{du}{{dy}}} \right)^{4}$$
(19)
$$A = \frac{{\beta_{2} + \beta_{3} }}{\mu }\left( {\frac{{u_{0} }}{h}} \right)^{2} ,\,Br = \frac{{\mu u_{0}^{2} }}{{q_{1} h}},\,\,u_{0} = \frac{1}{N}\frac{{dp^{*} }}{{dx^{*} }}\frac{{h^{2} }}{\mu },\,\beta = \frac{{\rho c_{p} u_{0} }}{{q_{1} }}\frac{{dT^{*} }}{{dx^{*} }}$$
(20)

In Eq. (20), \(u_{0}\) is the average velocity of fluid flow.

Equation (14) can now be presented in the non-dimensional form as:

$$u\left( { - 1} \right) = 0,u\left( 1 \right) = 0$$
(21)

Further, the boundary condition for energy equation becomes:

$$\theta ( - 1) = 0$$
(22)
$$\frac{d\theta }{{dx}}( - 1) = \mp 1$$
(23)
$$\frac{d\theta }{{dx}}(1) = \pm \frac{{q_{2} }}{{q_{1} }} = q$$
(24)

Solution of the governing equations subjected to the boundary conditions is obtained by LSM, and the methodology of LSM application is explained in the next section.

2.1.1 Solution

2.1.1.1 Least Square Method (LSM)

Starting with any arbitrary function v(y), and operating this with a differential operator D to get a function say g(y), it can be presented in the mathematical form as:

$$Dv(y) = g(y)$$
(25)

Also, a group of linear base functions who satisfy the boundary conditions can be arranged linearly to the function v to be \(\stackrel{\sim }{\mathrm{v}}\). This can be expressed as:

$$v \cong \tilde{v} = \sum\limits_{i = 1}^{n} {c_{i} \phi_{i} }$$
(26)

Thus, with the help of Eqs. (25) and (26), we can define the residue as:

$$R(y) = D\{ \tilde{v}(y)\} - g(y) \ne 0$$
(27)

The residue need not be zero at every point, but their average quantity will reduce to zero.

$$\int\limits_{x} {R(y)w_{i} (y)dy = 0,\,i = 0,2,3..n}$$
(28)

In Eq. (28), as per LSM method, the weights are taken to be equal to residual:

$$S = \int\limits_{y} {R(y)R(y)dy = \int\limits_{y} {R^{2} dy} }$$
(29)

Now, S can be minimized as:

$$\frac{\partial S}{{\partial c_{i} }} = 2\int\limits_{x} {R(y)\frac{\partial R}{{\partial c_{i} }}dy = 0}$$
(30)

Equation (30) gives equal number of algebraic relations and unknown constants, which can easily be computed.

2.1.1.2 Solution Methodology by Using LSM

A group of base functions, which satisfy the boundary conditions, are used to approximate the velocity field:

$$u(y) = c_{1} (1 - y^{2} ) + c_{2} (1 - y^{4} )$$
(31)

By using the definition of velocity field in Eq. (31), the residues are obtained from Eq. (18):

$$R(y) = a_{0} + a_{2} y^{2} + a_{4} y^{4} + a_{6} y^{6} + a_{8} y^{8}$$
(32)
$$a_{0} = - 2c_{1} - N,\,a_{2} = - 12c_{2} - 48c_{1}^{3} ,\,a_{4} = - 480Ac_{1}^{2} c_{2} ,\,a_{6} =\,6A(32 + 12.16)c_{1} c_{2}^{2} ,\,a_{8} = - 72.16Ac_{2}^{3}$$
(33)

With the help of Eq. (27) describing the LSM technique, the following relations are obtained from Eq. (30):

$$\int\limits_{ - 1}^{1} {R\frac{\partial R}{{\partial c_{1} }}dy = 0}$$
(34)
$$\int\limits_{ - 1}^{1} {R\frac{\partial R}{{\partial c_{2} }}dy = 0}$$
(35)

Now, Eq. (34) and Eq. (35) are solved for the values of the constants c1 and c2, by using practically possible values of Ha, N, H and A. The energy equation of Eq. (19) can be expressed in terms of base function by using the definition of velocity field given by Eq. (31):

$$\frac{{d^{2} \theta }}{{dy^{2} }} = b_{0} + b_{2} y^{2} + b_{4} y^{4} + b_{6} y^{6} + b_{8} y^{8} + b_{10} y^{10} + b_{12} y^{12}$$
(36)
$$\begin{gathered} b_{0} = \beta (c_{1} + c_{2} ),b_{2} = - \beta c_{1} - 4Brc_{1}^{2} ,b_{4} = - \beta c_{2} - 16Brc_{1} c_{2} - 32ABrc_{1}^{4} ,b_{6} = - 16Brc_{2}^{2} - 256ABrc_{1}^{3} c_{2} , \hfill \\ b_{8} = - 2ABr(128 + 1616)c_{1}^{2} c_{2}^{2} ,b_{10} = - 1024ABrc_{1} c_{2}^{3} ,b_{12} = - 32.16ABrc_{2}^{4} \hfill \\ \end{gathered}$$
(37)

The temperature field is obtained by integration of Eq. (36) as:

$$\theta =\,b_{0} \frac{{y^{2} }}{2} + b_{2} \frac{{y^{4} }}{12} + b_{4} \frac{{y^{6} }}{30} + b_{6} \frac{{y^{8} }}{56} + b_{8} \frac{{y^{10} }}{90} + b_{10} \frac{{y^{12} }}{11.12} + b_{12} \frac{{y^{14} }}{13.14} + r_{3} y + r_{4}$$
(38)

Substitution of boundary conditions from Eq. (22) to Eq. (24) gives the value of the constants r3 and r4 in Eq. (38) as:

$$\theta_{m} = \frac{{T_{m}^{*} - T_{1}^{*} }}{{q_{1} \frac{h}{k}}} = \frac{{\int\nolimits_{ - 1}^{1} {\theta udy} }}{{\int\nolimits_{ - 1}^{1} {udy} }}$$
(39)

Following definitions are used for Nusselt number:

(i) Nusselt number for the bottom plate:

$$\frac{hlw(4h)}{{k_{th} }} = \frac{{4\left. {\frac{d\theta }{{dy}}} \right|_{y = - 1} }}{{\frac{{T_{m}^{*} - T_{1}^{*} }}{{(q_{1} h/k_{th} )}}}}$$
(40)
$$Nu = - \frac{4}{{\theta_{m} }}$$
(41)

(ii) Nusselt number for the top plate: Nuupper = Nu q2/q1.

2.1.2 Validation of First Part

Once the governing equations are solved by using LSM, the first part of the problem is over. In the second part, data generated by the LSM are used for the development of SOMARBNNs. Before proceeding to the second part of the problem, the validation of the first part is presented in Figs. 2 and 3. Figure 2 shows that the velocity profile obtained from the LSM is compared with the data available in the literature [28]. Further, the temperature and the velocity profiles from LSM are compared with the result of analytical solution, for the Newtonian fluid, and are shown in Fig. 3. (Figs. 2 and 3 to be inserted here).

Fig. 2
figure 2

Validation of the first part by comparing the velocity by LSM with exact solution [28]

Full size image
Fig. 3
figure 3

Validation of the first part with exact solution for Newtonian fluid [28]. a Comparison of velocity profiles. b Comparison of non-dimensional temperature profiles

Full size image

2.2 Second Part: Designing of RBNN with the Help of SOMs

After completion of the first part of the problem, the second part of the problem is solved. In the second part, five different SOMs are used to design a RBNN. All the SOMs are implemented in the present work, without taking the results from any other work. A brief description of different SOMs is presented below:

2.2.1 Genetic Algorithm

GA is a mathematical tool to search global minimum and is inspired from nature’s process of evolution [29]. It mathematically mimics different processes of evolution such as selection, crossover, and mutation. The flowchart of GA is shown in Fig. 4. First of all, a group of probable solutions are generated, called population of first generation. Then, depending upon the value of fitness value from each individual, selection and mutation are carried out to generate children, also called next generation. In this way, good individuals are generated for few generations till only few good individuals remain. These good individuals correspond to the best solution. (Fig. 4 to be inserted here).

Fig. 4
figure 4

Flowchart of processes in GA

Full size image

2.2.2 Global Search Algorithm

GSA finds starting points for gradient-based local nonlinear programming (NLP) solvers [30]. Scatter search method OptQuest is employed by GSA to find the starting point for the gradient search algorithm. Global optimization along with powerful local search makes GSA very effective optimization tool. The scatter search is advanced than GA in terms of generating new generation in a deterministic means rather than the random means.

2.2.3 Multiple Starting Point Algorithm

MSPA uses local optimization routine but starts with various different points to solve any optimization problem [31]. The global solution is said to be obtained if best solution is picked. Chances of getting the global minimum increases with the increase in the number of starting points or repeating the program from different sets of starting points. The algorithm gives a set of good solutions, and any of them can be picked depending upon the required stability of the solution parameters.

2.2.4 Simulated Annealing Algorithm

SAA is very commonly used stochastic optimization method to solve unconstrained and bound-constrained problems [32]. It is inspired from the metallurgical process called annealing, where it mimics the physical process of heating a material and then slowly lowering the temperature to decrease defects in crystal structure, thus minimizing the system energy.

In each iteration, a new point is generated in a random way. A probability scale, proportional to the temperature, is used to locate the position of the new point, i.e., the extent of the search. The SAA accepts all the points, which give lower values for objective function. The algorithm also accepts few points with certain probabilities, which give higher values of objective function. This means of accepting the points with higher objective function helps the SAA to overcome the local minima and explore global minima.

2.2.5 Pattern Search Algorithm

PSA is computationally efficient algorithm yet very simple and easy to implement [33]. The flowchart of the steps involved in implementation of PSA is shown in Fig. 5. It starts with a single point \(Xn_{o}\); then, a mesh is generated around this point. The objective function for all the mesh points is computed and compared with the objective function for point \(Xn_{o}\).

Fig. 5
figure 5

Flowchart of pattern search algorithm (PSA)

Full size image

If the objective function for any of these mesh points is less than that for the initial point, then that mesh point is designated as new \(Xn_{1}\), and it is called successful poll. Then, a new mesh is generated around the point \(Xn_{1}\) with twice the size, and the whole process is repeated, whereas if the algorithm encounters unsuccessful poll, i.e., all the mesh point gives higher value of objective function than the central point, then a new mesh is generated with half the size. In this way, the algorithm proceeds until it achieves the required accuracy for the objective function or any other stopping criterion is met. (Fig. 5 to be inserted here).

2.2.6 Radial Basis Neural Network

A radial basis neural network (RBNN) function is one of the most commonly used neural networks, apart from perceptron network. In RBNN, the final input to the radbas transfer function is a distance between a weight vector and an input vector and multiplied by a bias. The transfer function calculates a neuron’s output as an = exp ( − nn2). When the distance is 0, the function gives it maximum value an = 1, and the function decreases with the increase in distance. The sensitivity of neuron is decided by the bias bn. The output of radbas for different inputs is shown in Fig. 6. The radial basis neuron is shown in Fig. 7. (Figs. 6 and 7 to be inserted here).

Fig. 6
figure 6

Radbas activation function

Full size image
Fig. 7
figure 7

Radial basis neuron

Full size image

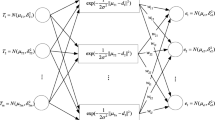
The network based on the radial basis function is illustrated in Fig. 8. One radial basis layer of sn1 nodes constitutes the hidden layer, and the output linear layer consists of sn2 nodes. With the help of input vector V and a weight matrix IWn1, a distance vector of size sn1 is generated. After scaling of the distances by bias vector bn1, the radial basis transfer function converts it into hidden layer output vector an1. The output layer in RBNN works similar to perceptron output layer with a linear transfer function to produce output vector an2 of size sn2. The coefficients IWn1, LWn2, bn1 and bn2, are computed automatically in MATLAB software. (Fig. 8 to be inserted here).

Fig. 8
figure 8

Architecture of RBNN

Full size image

One neuron is added at a time in the hidden layer, until the sum-squared error reaches the prescribed value or the prescribed maximum number of neurons is achieved. Thus, number of neurons in the hidden layer is automatically generated.

2.2.7 Stochastic Optimization Methods Assisted RBNN

RBNN is very simple to use, with only one parameter ‘spread’ is required from user to construct the model. Spread helps to decide the width of an area in the input space to which each neuron in the hidden layer responds. The accuracy and time consumption of the RBNN model depend on the value of spread. Proper selection of the value for spread is very vital for the performance of RBNN model and at the same time it is very difficult, as lot of experience is required to come to a final value. But in the present work, a novel approach of using stochastic optimization method for selecting suitable value for spread is proposed. Different stochastic optimization methods such as GA, GSA, MSPA, SAA, and PSA are used, and the results are compared and analyzed on the basis of accuracy and time consumption.

Flowchart of the stochastic optimization method-assisted RBNN (SOMARBNN) is shown in Fig. 9. First of all, the first part of the problem is used to generate multiple pairs of the velocity- and the temperature- profile for different values of A. This gives the data in the form of input (velocity profile) and target (temperature profile and A), to be used in the SOMARBNN for training purpose. Anyone SOM is selected to guess the value for spread, and by using this spread, RBNN is used. The RBNN returns mean-squared error (mse), which acts as objective function (OF) for the selected SOM. Once SOM gets lowest mse, it finalizes the guessed value of ‘spread’ for RBNN. Thus, this ‘spread’ is used in RBNN, and output is produced corresponding to any given input. (Fig. 9 to be inserted here).

Fig. 9
figure 9

Flowchart to use SOM-assisted RBNN for generating temperature profile along with A

Full size image

These steps are repeated for all the SOMs, and comparison of the result is done to select most suitable SOMARBNN. The analysis is also done with different levels (0.0, 0.1, 0.2, 0.5, 1.0, and 2.0) of perturbation in the input data. In all the SOMARBNNs, number of neurons in the hidden layer are 14, and it is automatically decided.

3 Results and Discussions

In the quest for generating an efficient and robust RBNN, different SOMs are explored to decide the values of spread. The SOMARBNNs are used to get the temperature profile and the value of A corresponding to any velocity profile (not part of initial data). With the help of mse, measured as the difference between the true value (computed by LSM) and the corresponding network output, the convergence of RBNN is monitored [34] and is given by Eq. (42) as:

$$OF = mse = \frac{1}{Rn + 1}\left( {\left( {A - A_{ret} } \right)^{2} + \sum\limits_{i = 1}^{Rn} {\left( {\theta_{i} - \tilde{\theta }_{i} } \right)}^{2} } \right)$$
(42)

where \(Rn\) is number of observation points (= 201), \(A\) and \(\theta\) is true value of TGF parameter and temperature (obtained from LSM), respectively. RBNN-generated TGF parameter and temperature are represented by \(A_{ret}\) and \(\tilde{\theta }\), respectively. The mse calculated in the last iteration of RBNN is allocated to the objective function OF, to be used in SOMs. The accuracy of retrieval of A is measured by using the following error function [34]:

$$error = \left| {\frac{{A - A_{ret} }}{A}} \right| \times 100$$
(43)

where \(A_{ret}\) is retrieved value of TGF parameter, and \(A\) is true value of TGF parameter.

Results of different SOMARBNNs are presented in Table 2. For no noise in the input data, all the SOMARBNNs retrieve the value of A with zero error. Under the total time column, CPU time consumption by different SOMARBNNs is listed. RBNNs assisted by MSPA and PSA take minimum time of 10 s. During the training stage of the SOMARBNNs, the performance of the RBNN is displayed under the column, fitness value (mse). Low value of fitness value indicates higher accuracy in the output (temperature profile and A) of SOMARBNNs. Value of spread for RBNN, as given by SOMs, is listed under the column ‘spread’. Once spread is given by the SOMs, RBNN runs very fast and takes 2–3 s for almost all the cases and is displayed under the column RBNN time.

Table 2 Results of different SOMARBNNs in retrieval of third-grade fluid parameter (Aret) for A = 0.75
Full size table

It is observed from Table 2 that the fitness value increases with the increase in noise level. Generation of spread by different SMOs is on the basis OF, with no observable trend. Error in the retrieved value of A, increases with the increase in the noise. Detailed interpretation and plots for different SOMARBNNs are discussed below: (Table 2 to be inserted here).

3.1 Performance Evaluation of GAARBNN

Figure 10 shows the error in the temperature profile generated by GAARBNN for different levels of noise in the input data. It is observed that for all the cases the error in the output is in the order of 10–4, which is highly accurate. Also, the error in the temperature profile generated by GAARBNN is proportional to the noise in the input data (Fig. 10 to be inserted here).

Fig. 10
figure 10

Enlarged view of error in the temperature generated by GAARBNN for different levels of noise in the input data

Full size image

In Fig. 11, a detailed performance evaluation of GAARBNN is presented. Temperature profile generated by LSM, along with the error in the temperature profile generated by GAARBNN, for different levels of noise in the input data, is shown in Fig. 11a. Robustness of the GAARBNN is evident from the observation that the error in the output is very less even for high-level noise (2.0%) in the input data. Figure 11b shows the performance of the GAARBNN during the training stage, for different levels of noise in the input data.

Fig. 11
figure 11

Performance evaluation of GAARBNN for different levels of noise in the input data a Comparison of error in the generated output, b Convergence of GAARBNN during training stage, c CPU time consumption, d error in the retrieval of A

Full size image

It is observed that the mse decreases continuously with the increase in iteration (epoch). CPU time consumption by GAARBNN for different cases is shown in Fig. 11c. For all the cases, time consumption is approximately the same. Error in the retrieved value of A for different cases is shown in Fig. 11d. For high noise (2.0%) case, the error in retrieval is more than 1%, whereas for all the other cases the error is less than 1%. This indicates that the GAARBNN is capable of giving accurate results, even under the situations where the input data are noisy. (Fig. 11 to be inserted here).

3.2 Performance Evaluation of GSAARBNN

Error in the temperature profile obtained from GSAARBNN for different levels of noise in the input data is compared in Fig. 12. For all the cases, the order of error is 10–3, which is poor as compared to GAARBNN. For high level of noise in the input data, the error in temperature profile is high. Figure 13 shows the results of GSAARBNN for different cases of noise in the input data. Figure 13a shows that along the whole height (distance along y*) the error in the result is very less. (Fig. 12 to be inserted here).

Fig. 12
figure 12

Enlarged view of error in the temperature generated by GSAARBNN for different levels of noise in the input data

Full size image
Fig. 13
figure 13

Performance evaluation of GSAARBNN for different levels of noise in the input data: a Comparison of error in the generated output, b convergence of GSAARBNN during training stage, c CPU time consumption, d error in retrieval of A

Full size image

Convergence of GSAARBNN during the training stage is shown in Fig. 13b. For no noise case, the rate of convergence is faster than other cases. All the cases converge very fast during 12th iteration. CPU time consumption by GSAARBNN for all the cases is shown in Fig. 13c. Time consumption for no noise case is very less, as compared to noisy cases. The error in the retrieved value of A from GSAARBNN for all the cases is shown in Fig. 13d. Except for high noise (2.0%) case, for all the cases the error in the retrieved value is less than 0.5. (Fig. 13 to be inserted here).

3.3 Performance Evaluation of MSPAARBNN

An enlarged view of the comparison of the error in the temperature profile generated by MSPAARBNN for different levels of noise in the input data is shown in Fig. 14. It is observed that for all the cases, the error is in the order of 10–4, which indicates high accuracy in results. Also, the errors for low noise level are less and high for high noise levels. Detailed performance evaluation of MSPAARBNN is presented in Fig. 15. Figure 15a shows the error in temperature profile generated by MSPAARBNN along the y* axis and compared against the LSM solution. It is observed that for all the cases the output is very accurate. (Fig. 14 to be inserted here).

Fig. 14
figure 14

Enlarged view of error in the temperature generated by MSPAARBNN for different levels of noise in the input data

Full size image
Fig. 15
figure 15

Performance evaluation of MSPAARBNN for different levels of noise in the input data: a Comparison of error in the generated output, b convergence of MSPAARBNN during training stage c CPU time consumption d error in retrieval of A

Full size image

Plots of iteration verses mse are plotted for different noise cases in Fig. 15b. For all the cases, accuracy improves significantly after iteration 12. CPU time consumption by MSPAARBNN for different cases is compared in Fig. 15c. Drastic difference in time consumption is observed between no noise and noisy cases. Error in the retrieved value of A is shown in Fig. 15d. Up to 1.0% noise, the error in result is found to be less than 0.6%, whereas for high level of noise (2.0%), the error in the result is more than 1.4%. (Fig. 15 to be inserted here).

3.4 Performance Evaluation of SAAARBNN

Enlarged view of the comparison of the error in the temperature profile generated by SAAARBNN for different levels of noise in the input data is shown in Fig. 16. Error in all the cases is of the order of 10–3, which is not so good as compared to some of the other SOMARBNNs. The error increases with the increase in noise in the input data. Detailed performance evaluation of SAAARBNN is presented in Fig. 17. Figure 17a shows the error in the temperature profile produced by SAAARBNN for different noise levels in the input data. It is observed that temperature along the y* axis, as produced by SAAARBNN, is having very less error for all the cases. (Fig. 16 to be inserted here).

Fig. 16
figure 16

Enlarged view of error in the temperature generated by SAAARBNN for different levels of noise in the input data

Full size image
Fig. 17
figure 17

Performance of SAAARBNN for different levels of noise in the input data: a error in the output generated, b convergence during the training stage c, consumption of CPU time, d error in retrieval of A

Full size image

Convergence of SAAARBNN is shown in Fig. 17b, and the mse falls continuously with the increase in iteration. Also, after iteration 12, the mse falls very rapidly. CPU time consumption by SAAARBNN is shown in Fig. 17c, and it is observed that CPU time is approximately independent of noise in the input data. Error in the retrieved value of A is shown in Fig. 17d. Error in the output, in all the cases except high noise (2.0%), is less than 0.4%. (Fig. 17 to be inserted here).

3.5 Performance Evaluation of PSAARBNN

Enlarged view of the comparison of the error in the temperature profile generated by PSAARBNN for different levels of noise in the input data is shown in Fig. 18. Maximum error out of all the cases is of the order of 10–3. The error increases with the increase in noise in the input data. Detailed performance evaluation of PSAARBNN is presented in Fig. 19. Figure 19a shows the error in the temperature profile produced by PSAARBNN for different noise levels in the input data. It is observed that the temperature along the y* axis, as produced by PSAARBNN is having very less error for all the cases. (Fig. 18 to be inserted here).

Fig. 18
figure 18

Enlarged view of error in the temperature generated by PSAARBNN for different levels of noise in the input data

Full size image
Fig. 19
figure 19

Performance evaluation of PSAARBNN for different levels of noise in the input data: a comparison of the output generated, b convergence of PSAARBNN during training stage, c CPU time consumption, d error in the retrieval of A

Full size image

Convergence of PSAARBNN is shown in Fig. 19b, and the mse falls continuously with the increase in iteration. Further, after iteration 12, the convergence speeds up rapidly. CPU time consumption by PSAARBNN is shown in Fig. 19c, and it is observed that the CPU time is approximately independent of noise levels in the input data. The error in the retrieved value of A is shown in Fig. 19d, for all the cases of noise levels in the input data. The error in the output is less than 0.05% for all the cases except for high noise (2.0%) (Fig. 19 to be inserted here).

3.6 Performance Evaluation of different SOMARBNN

Comparison of error in the temperature profile generated by different SOMARBNNs is shown in Fig. 20. Figure 20a shows error in the output temperature for the case of no noise in the input data. Output from RBNN, assisted by PSA and MSPA, has a maximum error, at the center of channel height. Similarly, Fig. 20b shows the error in the output temperature for the case of high noise (2.0%) in the input data. The error in the output from the RBNN assisted by PSA and GSA is higher than, by other SOMs. (Fig. 20 to be inserted here).

Fig. 20
figure 20

Comparison of error in the output of different SOMARBNNs a Noise in the input data is 0.0% b Noise in the input data is 2.0%

Full size image

Convergence comparison of different SOMARBNNs is shown in Fig. 21, for different cases of noise in the input data. Figure 21a and b shows the convergence for the case of no noise and high noise (2.0%) in the input data, respectively. All the SOMARBNNs converge slowly up to 12 iteration and then speed up to finally converge within 14 iterations. PSAARBNN gives lowest mse for both the cases of noise in the input data, thus indicating higher accuracy in the output (Fig. 21 to be inserted here).

Fig. 21
figure 21

Convergence comparison of different SOMARBNNs a noise in the input data is 0.0% and b noise in the input data is 2.0%

Full size image

Figure 22 shows the performance evaluation of different SOMARBNNs in the retrieval of A, for different cases of noise in the input data. Figure 22a compares the CPU time consumed by different SOMARBNNs for giving the value of spread for a RBNN, in case of no noise in the input data. GSA is found to take maximum time to achieve the target. Error in the retrieved value of A by different SOMARBNNs under no noise is shown in Fig. 22b. Through this graph also, GSAARBNN is found to be least suitable due to low accuracy. However, for all other SOMARBNNs, the error in the output is less than 0.1%.

Fig. 22
figure 22

Comparison of different SOMARBNNs in retrieval of A for different levels of noise in the input data a CPU time consumption for 0.0% noise, b error in retrieval of A for 0.1% noise, c CPU time consumption for 2.0% noise, d error in retrieval of A for 2.0% noise

Full size image

CPU time requirement by different SOMARBNNs is shown in Fig. 22c, for the case of high noise (2.0%) in the input data. PSA is found to take minimum time even in case of high noise. Figure 22d shows the error in the retrieved value of A by different SOMARBNNs under various level of noise in the input data. RBNN assisted by PSA is most accurate, while GSA gives poorest accuracy. All the runs were taken on 2.4 GHz processor with 8 GB RAM (Fig. 22 to be inserted here).

4 Conclusions

Implementation of radial basis neural network (RBNN) is demonstrated by choosing a test case of non-Newtonian third-grade fluid flow with heat transfer, through two parallel plates. First part of the problem involves solving the governing equations subjected to the prescribed boundary conditions, by employing LSM. Pairs of velocity profile and temperature profile along with A, are prepared for the second part of the problem.

In the second part, RBNN is designed with the help of the following SOMs: GA, GSA, MSPA, SAA, and PSA. The data generated in the first part are then fed to train SOMARBNNs. After successful training of the SOMARBNNs, a velocity profile is used as input, and outputs obtained are: (i) temperature profile (ii) A. Performance of different SOMARBNNs under varying noise levels in the input data is analyzed and evaluated in terms of CPU time consumption and error in the result.

Overall, all the SOMARBNNs are able to generate highly accurate temperature and value of A, corresponding to any velocity field, for different noise levels in the input data. GSAARBNN is found to be performing worst than other SOMARBNNs. PSAARBNN is found to be better than other SOMARBNNs in terms of CPU time consumption, accuracy, and ability to handle noisy input data.