An Exact Elasticity Solution for Monoclinic Functionally Graded Beams

Abstract

In this study, an elasticity solution is presented for monoclinic functionally graded beams subject to a transverse pressure distributed sinusoidally. Monoclinic material properties are assumed to vary exponentially throughout the thickness of the beam’s layers. An analytical formulation based on the classical Euler–Bernoulli beam theory is also derived for comparison purposes of simply supported monoclinic functionally graded beams. In benchmark examples, the numerical results of normal stresses, transverse shear stress, as well as axial and vertical displacements are presented. The effect of material grading, fiber angle, and beam length to thickness ratio on the stress and displacement distributions is comprehensively investigated. The proposed elasticity-based analytical solution and presented numerical results can be used for verification or comparison purposes of numerical procedures.

1 Introduction

Functionally Graded Materials (FGMs) as a relatively new class of nonhomogeneous composite materials have superior advantages compared to conventional laminates regarding their mechanical performance and minimized stress concentrations [1]. These advantages lead them to be preferred in numerous application fields such as electronics, aerospace, biomedicine, civil and mechanical engineering, etc. Due to their critical role in structural systems, FGM structures have to be analyzed in great accuracy and detail [2]. In addition, the accurate determination of elastic parameters and fracture properties of nonhomogeneous composites [3, 4] contributes greatly to the reliability of the structural analysis. Although numerical formulations such as finite element procedures are crucial for general design purposes of structural systems, e.g. nonlinear analyses [5, 6], nonstandard geometries [7], multi-field problems [8], exact and analytical solution procedures are essentially required for verification purposes. Hence, the exact solutions of FGM structures have attracted great attention from researchers and engineers recently [9,10,11,12,13,14,15,16,17,18,19]. Sankar [20] investigated the stress fields and displacements of FG beams subjected to transverse loadings by using the exact solutions of the plane elasticity equations. Venkataraman and Sankar [21] presented the stress and displacement fields of a sandwich beam having a FG core regarding the elasticity analysis. Ding et al. [22] studied the plane stress problem of anisotropic FG beams by adopting a unified formulation. Lü et al. [23] presented elasticity solutions for the bending and thermal deformations of bi-directional FG beams. Ying et al. [24] evaluated the bending characteristics and natural frequencies of orthotropic FG beams resting on a Winkler–Pasternak elastic foundation using 2D elasticity solutions. Wang and Liu [25] investigated the elasticity solutions for the stresses and displacements of orthotropic FG curved beams under uniform loads based on the Airy stress function method. Nie et al. [26] solved the plane stress problem of orthotropic FG beams for various boundary conditions using the displacement function approach. Daouadji et al. [27] studied the displacement and stress fields of cantilever FG beams under distributed loads. Xu et al. [28] calculated the stress and displacement fields of simply supported FG beams with variable thickness using the 2D elasticity theory. Alibeigloo [29] investigated the temperature, displacement, and stress fields of a simply supported sandwich panel with a FG core under thermo-mechanical and mechanical loads using the elasticity theory. Alibeigloo and Liew [30] studied the natural frequencies of a simply supported sandwich panel with a FG core using an exact 3D free vibration solution. Arefi [31] obtained the stresses of a FG curved beam subjected to pure bending analytically. Zafarmand and Kadkhodayan [32] analyzed the static and dynamic behaviors of multi-directional FG plates using the 3D elasticity theory. Chu et al. [33] investigated the mechanical behavior of FG beams subjected to uniaxial tension and bending using the 2D theory of elasticity. Demirbas [34] discussed the transient thermal residual stresses of FG plates using the 3D theory of elasticity. Benguediab [35] presented an elasticity solution for the displacements, strains and stresses of a cantilever FG beam under uniform loads. He et al. [36] presented the displacements and stresses of FG beams having different moduli in tension and compression under uniformly distributed loads analytically. Bhaskar and Ravindran [37] derived a 3D elasticity solution for the displacements and stresses of simply supported plates with dissimilar orthotropic stiffness coefficient variations. In the very recent studies, Yang et al. [38] derived a two-dimensional elasticity solution for time-dependent behavior of FG beams bonded by viscoelastic interlayers. Wu et al. [39] examined the time-dependent mechanical behavior of multilayer FG beams with viscoelastic interlayer analytically. Li et al. [40] investigated the vibrational characteristics of simply supported beams with varying thickness based on the two-dimensional elasticity theory. Ravindran and Bhaskar [41] tackled the elasticity solution of sandwich plates with composite stiffeners having in-plane grading. Huang and Ouyang [42] studied the bending of bidirectional FG Timoshenko beams analytically.

In recent decades, thin-walled structures, particularly involving material anisotropy, became very popular due to their various advanced engineering applications, e.g. modern devices, aircrafts, and piezoelectric sensors [43]. In addition, as a result of the miniaturization needed with the developing technology, recent years witnessed an increasing number of studies on the size-dependent analysis of composite structures [44]. Alam and Mishra [45] employed a two-step perturbation method to investigate the nonlinear vibration of FG beams interacting with a nonlinear compliant substrate based on nonlocal strain gradient theory. Alam et al. [46] obtained a closed-form solution of the critical external pressure exerted on a shallow spherical shell based on nonlocal strain gradient theory. Zhang et al. [47] presented an exact solution for bending of FG curved Timoshenko nano-beams. Zhang et al. [48] discussed the bending of curved Timoshenko microbeams analytically based on Eringen’s two-phase local/nonlocal integral model. Isotropic or orthotropic material structures have been comprehensively investigated in the literature, but the fact remains that materials of general anisotropy and monoclinic configurations gain more importance by researchers in the recent times. Tovstik and Tovstik [49] derived the two-dimensional equilibrium equations of a thin elastic inhomogeneous plate of general anisotropy by an asymptotic approach. Morozov et al. [50] obtained the equations reflecting second-order accuracy for a monoclinic material multilayered plate of nonuniform thickness. Schneider and Kienzler [51] introduced a second-order consistent plate theory having a monoclinic material configuration and examined various theories originating from the presented theory through a pseudo-reduction technique. Belyaev et al. [52] treated bending and vibration formulation of generally anisotropic plates based on an asymptotic approach. Çömez and Yilmaz [53] and Yilmaz et al. [54] investigated the frictional contact problem of a monoclinic half plane and a monoclinic coating half plane using the elasticity theory and integral transform technique. Çömez [55] studied the frictional contact problem of a FG monoclinic layer using the linear elasticity theory. The purpose of this study is to introduce the elasticity solution of the FG monoclinic beam which has not been addressed before. The considered beam is subjected to a sinusoidally varying transverse loading and material properties of it are assumed to vary exponentially through the thickness of the beam’s layers. In addition to the presented elasticity solution, an analytical solution based on Euler- Bernoulli beam theory is derived for the same problem. A comprehensive investigation of the FG monoclinic beam is conducted through numerical analyses. Stress and displacement component distributions and variations are examined regarding fiber angle, stiffness ratio, and length to thickness ratio of the beam, deeply.

2 Elasticity Analysis for FG Orthotropic Beam

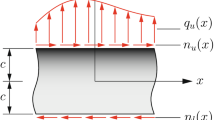
Figure 1 shows a functionally graded monoclinic beam of thickness $h$ and length $L$. The beam is assumed to be in a state of plane strain normal on the $xz$ plane, and the width in the y-direction is taken as unity. While the upper surface of the beam is free of tractions, the bottom surface of the beam is subjected to a symmetrically distributed sinusoidal pressure:

$$ p(x) = p_{0} \sin \beta {\kern 1pt} x $$

(1)

where

$$ \beta {\kern 1pt} = \frac{\pi }{L} $$

(2)

Fig. 1

Geometry of an FG monoclinic beam subjected to a symmetric transverse loading

The differential equations of equilibrium stated by elasticity theory are.

$$ \frac{{\partial \sigma_{x} }}{\partial x} + \frac{{\partial \tau_{xz} }}{\partial z} = 0, $$

(3a)

$$ \frac{{\partial \tau_{xy} }}{\partial x} + \frac{{\partial \tau_{yz} }}{\partial z} = 0, $$

(3b)

$$ \frac{{\partial \tau_{xz} }}{\partial x} + \frac{{\partial \sigma_{z} }}{\partial z} = 0 $$

(3c)

Assuming that the beam is FG monoclinic, the Hooke’s law can be written as follows:

$$ \left\{ {\begin{array}{*{20}c} {\sigma_{x} } \\ {\sigma_{y} } \\ {\sigma_{z} } \\ {\tau_{yz} } \\ {\tau_{zx} } \\ {\tau_{xy} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {\overline{C}_{11} (z)} & {\overline{C}_{12} (z)} & {\overline{C}_{13} (z)} & 0 & 0 & {\overline{C}_{16} (z)} \\ {} & {\overline{C}_{22} (z)} & {\overline{C}_{23} (z)} & 0 & 0 & {\overline{C}_{26} (z)} \\ {} & {} & {\overline{C}_{33} (z)} & 0 & 0 & {\overline{C}_{36} (z)} \\ {} & {} & {} & {\overline{C}_{44} (z)} & {\overline{C}_{45} (z)} & 0 \\ {} & {sym} & {} & {} & {\overline{C}_{55} (z)} & 0 \\ {} & {} & {} & {} & {} & {\overline{C}_{66} (z)} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\partial u/\partial x} \\ 0 \\ {\partial w/\partial z} \\ {\partial v/\partial z} \\ {\partial u/\partial z + \partial w/\partial x} \\ {\partial v/\partial x} \\ \end{array} } \right\} $$

(4)

where $u$, $v$ and $w$ are the x-, y- and z- components of the displacement vector.

It is assumed that Poisson’s ratios are constant and the coefficients of the stiffness matrix are functionally graded in the thickness direction according to the definitions

$$ \overline{C}_{ij} (z) = \overline{C}_{ij}^{0} e^{\gamma z} ,\quad \gamma h = {\text{Log}}(\Gamma ),\quad \Gamma = \overline{C}_{ij}^{h} /\overline{C}_{ij}^{0} $$

(5)

where $\gamma$ is the inhomogeneity parameter and $\Gamma$ is the stiffness ratio of the beam top surface to the bottom surface. Note that, primes “$^{0}$” and “$^{h}$” denote the bottom and top surfaces of the beam, respectively.

$\overline{C}_{ij}$ are the transformed stiffness coefficients in the global axes $x$, $y$ and $z$ and given as a function of the fiber orientation angle $\theta$ as follows (see Fig. 2):

$$ \overline{C}_{11} = C_{11} \cos^{4} \theta + 2(C_{12} + 2C_{66} )\cos^{2} \theta \sin^{2} \theta + C_{22} \sin^{4} \theta $$

(6a)

$$ \overline{C}_{12} = (C_{11} + C_{22} - 4C_{66} )\cos^{2} \theta \sin^{2} \theta + C_{12} (\cos^{4} \theta + \sin^{4} \theta ) $$

(6b)

$$ \overline{C}_{13} = C_{13} \cos^{2} \theta + C_{23} \sin^{2} \theta $$

(6c)

$$ \overline{C}_{16} = \cos \theta \sin \theta (\cos^{2} \theta (C_{11} - C_{12} - 2C_{66} ) + \sin^{2} \theta (C_{12} - C_{22} + 2C_{66} )) $$

(6d)

$$ \overline{C}_{22} = C_{11} \sin^{4} \theta + 2(C_{12} + 2C_{66} )\cos^{2} \theta \sin^{2} \theta + C_{22} \cos^{4} \theta $$

(6e)

$$ \overline{C}_{23} = C_{23} \cos^{2} \theta + C_{13} \sin^{2} \theta $$

(6f)

$$ \overline{C}_{33} = C_{33} $$

(6g)

$$ \overline{C}_{36} = (C_{13} - C_{23} )\cos \theta \sin \theta $$

(6h)

$$ \overline{C}_{44} = C_{44} \cos^{2} \theta + C_{55} \sin^{2} \theta $$

(6i)

$$ \overline{C}_{45} = (C_{55} - C_{44} )\cos \theta \sin \theta $$

(6j)

$$ \overline{C}_{55} = C_{55} \cos^{2} \theta + C_{44} \sin^{2} \theta $$

(6k)

$$ \overline{C}_{66} = (C_{11} - 2C_{12} - 2C_{22} )\cos^{2} \theta \sin^{2} \theta + C_{66} (\sin^{2} \theta - \cos^{2} \theta )^{2} $$

(6l)

where $C_{ij}$ are the stiffness coefficients of the beam in the parallel and perpendicular directions to the fiber and they are functions of the elastic material properties of the beam as follows:

$$ C_{ij} = \left[ \begin{gathered} \frac{{E_{11} ( - 1 + \nu_{23} \nu_{32} )}}{\Delta }\quad - \frac{{E_{11} (\nu_{21} + \nu_{23} \nu_{31} )}}{\Delta }\quad - \frac{{E_{11} (\nu_{31} + \nu_{21} \nu_{32} )}}{\Delta }\;\quad 0\quad \quad 0\quad \quad 0 \hfill \\ - \frac{{E_{22} (\nu_{12} + \nu_{13} \nu_{32} )}}{\Delta }\quad \frac{{E_{22} ( - 1 + \nu_{13} \nu_{31} )}}{\Delta }\quad - \frac{{E_{22} (\nu_{32} + \nu_{12} \nu_{31} )}}{\Delta }\quad \;0\quad \quad 0\quad \quad 0 \hfill \\ - \frac{{E_{33} (\nu_{13} + \nu_{12} \nu_{23} )}}{\Delta }\quad \frac{{E_{33} (\nu_{13} \nu_{21} + \nu_{23} )}}{\Delta }\quad - \frac{{E_{33} ( - 1 + \nu_{12} \nu_{21} )}}{\Delta }\quad \;0\quad \quad 0\quad \quad 0 \hfill \\ \quad \quad \quad \;\,0\quad \quad \quad \quad \quad \quad \;\;\;0\quad \quad \quad \quad \quad \quad \quad \;\;0\quad \quad \quad \quad G_{23} \quad \;\,0\quad \quad 0 \hfill \\ \quad \quad \quad \;\;0\quad \quad \quad \quad \quad \quad \;\;\;0\quad \quad \quad \quad \quad \quad \quad \;\;0\quad \quad \quad \quad \;0\quad \;\;G_{13} \quad \;\;0 \hfill \\ \quad \quad \quad \;\,0\quad \quad \quad \quad \quad \quad \;\;\;0\quad \quad \quad \quad \quad \quad \quad \;\;0\quad \quad \quad \quad \;\,0\quad \;\;\,0\quad \,\,\,\,G_{12} \hfill \\ \end{gathered} \right] $$

(7)

where

$$ \Delta = - 1 + \nu_{12} (\nu_{21} + \nu_{23} \nu_{31} ) + \nu_{23} \nu_{32} + \nu_{13} (\nu_{31} + \nu_{21} \nu_{32} ) $$

(8a)

Fig. 2

Variation of the material properties with the fiber angle

Note that the following relation exists between the Poisson’s ratios

$$ \nu_{21} = \nu_{12} \frac{{E_{22} }}{{E_{11} }},\quad \nu_{31} = \nu_{13} \frac{{E_{33} }}{{E_{11} }},\quad \nu_{32} = \nu_{23} \frac{{E_{33} }}{{E_{22} }} $$

(8b)

By substituting Eq. (4) into Eqs. (3), the following system of partial differential equations in terms of $u(x,z)$,$v(x,z)$, and $w(x,z)$ is obtained:

$$ \begin{aligned} & \overline{C}_{11}^{0} \frac{{\partial^{2} u}}{{\partial x^{2} }} + \overline{C}_{55}^{0} \frac{{\partial^{2} u}}{{\partial z^{2} }} + \overline{C}_{16}^{0} \frac{{\partial^{2} v}}{{\partial x^{2} }} + \overline{C}_{45}^{0} \frac{{\partial^{2} v}}{{\partial z^{2} }} + (\overline{C}_{13}^{0} + \overline{C}_{55}^{0} )\frac{{\partial^{2} w}}{\partial x\partial z} \\ & \quad + \gamma \left(\overline{C}_{55}^{0} \frac{\partial u}{{\partial z}} + \overline{C}_{45}^{0} \frac{\partial v}{{\partial z}} + \overline{C}_{55}^{0} \frac{\partial w}{{\partial x}}\right) = 0 \\ \end{aligned} $$

(9a)

$$ \begin{aligned} & \overline{C}_{16}^{0} \frac{{\partial^{2} u}}{{\partial x^{2} }} + \overline{C}_{45}^{0} \frac{{\partial^{2} u}}{{\partial z^{2} }} + \overline{C}_{66}^{0} \frac{{\partial^{2} v}}{{\partial x^{2} }} + \overline{C}_{44}^{0} \frac{{\partial^{2} v}}{{\partial z^{2} }} + (\overline{C}_{36}^{0} + \overline{C}_{45}^{0} )\frac{{\partial^{2} w}}{\partial x\partial z} \\ & \quad + \gamma \left( {\overline{C}_{45}^{0} \frac{\partial u}{{\partial z}} + \overline{C}_{44}^{0} \frac{\partial v}{{\partial z}} + \overline{C}_{45}^{0} \frac{\partial w}{{\partial x}}} \right) = 0 \\ \end{aligned} $$

(9b)

$$ \begin{aligned} & (\overline{C}_{13}^{0} + \overline{C}_{55}^{0} )\frac{{\partial^{2} u}}{\partial x\partial z} + (\overline{C}_{36}^{0} + \overline{C}_{45}^{0} )\frac{{\partial^{2} v}}{\partial x\partial z} + \overline{C}_{55}^{0} \frac{{\partial^{2} w}}{{\partial x^{2} }} + \overline{C}_{33}^{0} \frac{{\partial^{2} w}}{{\partial z^{2} }} \\ & \quad + \gamma \left( {\overline{C}_{13}^{0} \frac{\partial u}{{\partial x}} + \overline{C}_{36}^{0} \frac{\partial v}{{\partial x}} + \overline{C}_{33}^{0} \frac{\partial w}{{\partial z}}} \right) = 0 \\ \end{aligned} $$

(9c)

The solutions are assumed in a form such that they satisfy the boundary conditions on the left and right end faces of the simply supported beam [20],

$$ u(x,z) = \;\tilde{u}(z)\cos (\beta x)\quad v(x,z) = \;\tilde{v}(z)\cos (\beta x)\quad w(x,z) = \;\tilde{w}(z)\sin (\beta x) $$

(10)

By substituting Eqs. (10) into Eqs. (9), the following ordinary differential equation system can be obtained:

$$ \begin{aligned} & \overline{C}_{11}^{0} \xi^{2} \tilde{u} + \overline{C}_{16}^{0} \beta^{2} \tilde{v} - \beta (\overline{C}_{13}^{0} + \overline{C}_{55}^{0} )\frac{{d\tilde{w}}}{dz} - \overline{C}_{55}^{0} \frac{{d^{2} \tilde{u}}}{{dz^{2} }} - \overline{C}_{45}^{0} \frac{{d^{2} \tilde{v}}}{{dz^{2} }} \\ & \quad + - \gamma \left( {\overline{C}_{55}^{0} \frac{{d\tilde{u}}}{dz} + \overline{C}_{45}^{0} \frac{{d\tilde{v}}}{dz} + \beta \overline{C}_{55}^{0} \tilde{w}} \right) = 0 \\ \end{aligned} $$

(11a)

$$ \begin{aligned} & \overline{C}_{16}^{0} \beta^{2} \tilde{u} + \overline{C}_{66}^{0} \beta^{2} \tilde{v} - \beta (\overline{C}_{36}^{0} + \overline{C}_{45}^{0} )\frac{{d\tilde{w}}}{dz} - \overline{C}_{45}^{0} \frac{{d^{2} \tilde{u}}}{{dz^{2} }} - \overline{C}_{44}^{0} \frac{{d^{2} \tilde{v}}}{{dz^{2} }} \\ & \quad + - \gamma \left(\overline{C}_{45}^{0} \frac{{d\tilde{u}}}{dz} + \overline{C}_{44}^{0} \frac{{d\tilde{v}}}{dz} + \beta \overline{C}_{45}^{0} \tilde{w}\right) = 0 \\ \end{aligned} $$

(11b)

$$ \begin{aligned} & \overline{C}_{55}^{0} \beta^{2} \tilde{w} + \beta (\overline{C}_{13}^{0} + \overline{C}_{55}^{0} )\frac{{d\tilde{u}}}{dz} + \beta (\overline{C}_{36}^{0} + \overline{C}_{45}^{0} )\frac{{d\tilde{v}}}{dz} - \overline{C}_{33}^{0} \frac{{d^{2} \tilde{w}}}{{dz^{2} }} \\ & \quad + \gamma \left(\beta \overline{C}_{13}^{0} \tilde{u} + \beta \overline{C}_{36}^{0} \tilde{v} - \overline{C}_{33}^{0} \frac{{d\tilde{w}}}{dz}\right) = 0 \\ \end{aligned} $$

(11c)

The solutions of Eqs. (11) can be obtained as:

$$ \tilde{u} = \sum\limits_{j = 1}^{6} {A_{j} } e^{{s_{j} z}} ,\quad \tilde{v} = \sum\limits_{j = 1}^{6} {m_{j} A_{j} } e^{{s_{j} z}} ,\quad \tilde{w} = \sum\limits_{j = 1}^{6} {k_{j} A_{j} } e^{{s_{j} z}} $$

(12)

where $s_{j}$ $(j = 1,...,6)$ satisfies the following characteristic equation:

$$ s^{6} + L_{1} s^{5} + L_{2} s^{4} + L_{3} s^{3} + L_{4} s^{2} + L_{5} s + L_{6} = 0 $$

(13)

The expressions of the $m_{j}$, $k_{j}$ and $L_{j}$ $(j = 1, \ldots 6)$ are given in Appendix A .

After substituting Eqs. (12) into Eqs. (11), stress components for the FG monoclinic beam can be obtained as follows: [53]:

$$ \sigma_{x} (x,z) = \sum\limits_{j = 1}^{6} {A_{j} } T_{xj} (\beta )e^{{(\gamma + s_{j} )z}} {\text{sin}}(\beta x), $$

(14a)

$$ \sigma_{y} (x,z) = \sum\limits_{j = 1}^{6} {A_{j} } T_{yj} (\beta )e^{{(\gamma + s_{j} {\kern 1pt} )z}} {\text{sin}}(\beta x) $$

(14b)

$$ \sigma_{z} (x,z) = \sum\limits_{j = 1}^{6} {A_{j} } T_{zj} (\beta )\,e^{{(\gamma + s_{j} {\kern 1pt} )z}} {\text{sin}}(\beta x), $$

(14c)

$$ \tau_{yz} (x,z) = \sum\limits_{j = 1}^{6} {A_{j} } T_{yzj} (\beta )e^{{(\gamma + s_{j} {\kern 1pt} )z}} \cos (\beta x) $$

(14d)

$$ \tau_{xz} (x,z) = \sum\limits_{j = 1}^{6} {A_{j} } T_{xzj} (\beta )e^{{(\gamma + s_{j} {\kern 1pt} )z}} \cos (\beta x), $$

(14e)

$$ \tau_{xy} (x,z) = \sum\limits_{j = 1}^{6} {A_{j} } T_{xyj} (\beta )e^{{(\gamma + s_{j} {\kern 1pt} )z}} {\text{sin}}(\beta x) $$

(14f)

where

$$ T_{xj} (\beta ) = \overline{C}_{13}^{0} m_{j} s_{j} - (\overline{C}_{11}^{0} + \overline{C}_{16}^{0} k_{j} )\beta , $$

(15a)

$$ T_{yj} (\beta ) = \overline{C}_{23}^{0} m_{j} s_{j} - (\overline{C}_{22}^{0} + \overline{C}_{26}^{0} k_{j} )\beta $$

(15b)

$$ T_{zj} (\beta ) = \overline{C}_{33}^{0} m_{j} s_{j} - (\overline{C}_{33}^{0} + \overline{C}_{36}^{0} k_{j} )\beta , $$

(15c)

$$ T_{yzj} (\beta ) = \overline{C}_{44}^{0} k_{j} s_{j} + \overline{C}_{45}^{0} (s_{j} + m_{j} \beta ) $$

(15d)

$$ T_{xzj} (\beta ) = \overline{C}_{45}^{0} k_{j} s_{j} + \overline{C}_{55}^{0} (s_{j} + m_{j} \beta ), $$

(15e)

$$ T_{xyj} (\beta ) = \overline{C}_{36}^{0} m_{j} s_{j} - (\overline{C}_{16}^{0} + \overline{C}_{66}^{0} k_{j} )\beta $$

(15f)

where $A_{j}$$(j = 1, \ldots ,6)$ are the unknowns that will be determined from the boundary conditions on the top and bottom surfaces of the beam.

As the bottom surface is free of tangential tractions and the top surface is free of all tractions, the boundary conditions of the problem can be written as follows:

$$ \sigma_{z} (x,0) = - p_{0} \sin \beta {\kern 1pt} x, $$

(16a)

$$ \tau_{xz} (x,0) = 0, $$

(16b)

$$ \tau_{yz} (x,0) = 0 $$

(16c)

$$ \sigma_{z} (x,h) = 0, $$

(16d)

$$ \tau_{xz} (x,h) = 0, $$

(16e)

$$ \tau_{yz} (x,h) = 0 $$

(16f)

Using the boundary conditions given by (16), the following algebraic equations for $A_{j}$ can be obtained

$$ \left[ {\begin{array}{*{20}c} {T_{z1} } & {T_{z2} } & {T_{z3} } & {T_{z4} } & {T_{z5} } & {T_{z6} } \\ {T_{xz1} } & {T_{xz2} } & {T_{xz3} } & {T_{xz4} } & {T_{xz5} } & {T_{xz6} } \\ {T_{yz1} } & {T_{yz2} } & {T_{yz3} } & {T_{yz4} } & {T_{yz5} } & {T_{yz6} } \\ {T_{z1} e^{{s_{1} {\kern 1pt} z}} } & {T_{z2} e^{{s_{2} {\kern 1pt} z}} } & {T_{z3} e^{{s_{3} {\kern 1pt} z}} } & {T_{z4} e^{{s_{4} {\kern 1pt} z}} } & {T_{z5} e^{{s_{5} {\kern 1pt} z}} } & {T_{z6} e^{{s_{6} {\kern 1pt} z}} } \\ {T_{xz1} e^{{s_{1} {\kern 1pt} z}} } & {T_{xz2} e^{{s_{2} {\kern 1pt} z}} } & {T_{xz3} e^{{s_{3} {\kern 1pt} z}} } & {T_{xz4} e^{{s_{4} {\kern 1pt} z}} } & {T_{xz5} e^{{s_{5} {\kern 1pt} z}} } & {T_{xz6} e^{{s_{6} {\kern 1pt} z}} } \\ {T_{yz1} e^{{s_{1} {\kern 1pt} z}} } & {T_{yz2} e^{{s_{2} {\kern 1pt} z}} } & {T_{yz3} e^{{s_{3} {\kern 1pt} z}} } & {T_{yz4} e^{{s_{4} {\kern 1pt} z}} } & {T_{yz5} e^{{s_{5} {\kern 1pt} z}} } & {T_{yz6} e^{{s_{6} {\kern 1pt} z}} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {A_{1} } \\ {A_{2} } \\ {A_{3} } \\ {A_{4} } \\ {A_{5} } \\ {A_{6} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} { - p_{0} } \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{array} } \right\} $$

(17)

After unknowns $A_{j}$ computed from Eq. (17), the stresses and the displacements at any point of the layer can be obtained.

3 Euler–Bernoulli Beam Theory Solution of FG Monoclinic Beam

In the classical Euler–Bernoulli beam theory, it is assumed that the plane sections remain plane and normal to the beam axis after the beam deforms. Further, if it is assumed that the vertical displacements are independent of $z$, the following can be written

$$ \overline{w}(x,z) = \overline{w}(x) $$

(18a)

$$ \overline{u}(x,z) = \overline{u}_{0} (x) - z\frac{{{\text{d}}\overline{w}}}{{{\text{d}}x}} $$

(18b)

where $\overline{u}_{0} (x)$ denotes the displacements of points on the bottom surface of the beam. Assuming that the out of plane normal stress $\overline{\sigma }_{y} (x,z)$ is negligible, the constitutive equations can be written as follows:

$$ \overline{\sigma }_{x} (x,z) = \overline{C}_{11}^{0} e^{\gamma z} \frac{{d\overline{u}}}{dx}, $$

(19a)

$$ \overline{\tau }_{xy} (x,z) = \overline{C}_{55}^{0} e^{\gamma z} \left( {\frac{{d\overline{u}}}{dz} + \frac{{d\overline{w}}}{dx}} \right) $$

(19b)

From Eqs. (18) and (19) the axial stress $\overline{\sigma }_{x} (x,z)$ can be derived as follows:

$$ \overline{\sigma }_{x} (x,z) = \overline{C}_{11}^{0} e^{\gamma z} (\overline{\varepsilon }_{x0} + z\,\overline{\kappa }) $$

(20)

where

$$ \overline{\varepsilon }_{x0} = \frac{{d\overline{u}_{0} }}{dx}, $$

(21a)

$$ \overline{\kappa } = - \frac{{d^{2} \overline{w}}}{{dx^{2} }} $$

(21b)

The equivalency between the axial force $N$ and bending moment $M$, and the axial stress $\overline{\sigma }_{x}$ can be written as follows:

$$ \left\{ {N,M} \right\} = \int\limits_{0}^{h} {\overline{\sigma }_{x} \left\{ {1,z} \right\}} dz $$

(22)

By substituting Eq. (20) into Eq. (22), $\overline{\varepsilon }_{x0}$ and $\overline{\kappa }$ can be obtained as follows:

$$ \overline{\varepsilon }_{x0} = \frac{{\gamma^{2} (1 + e^{\gamma h} ( - 1 + \gamma h)M - \gamma ( - 2 + e^{\gamma h} (2 - 2\gamma h + h^{2} \gamma^{2} )N}}{{\overline{C}_{11}^{0} ( - 1 - e^{2\gamma h} + e^{\gamma h} (2 + h^{2} \gamma^{2} ))}} $$

(23a)

$$ \overline{\kappa } = \frac{{ - \gamma^{3} ( - 1 + e^{\gamma h} )M + \gamma^{2} (1 + e^{\gamma h} ( - 1 + \gamma h)N}}{{\overline{C}_{11}^{0} ( - 1 - e^{2\gamma h} + e^{\gamma h} (2 + h^{2} \gamma^{2} ))}} $$

(23b)

For the given loading $N$ and $M$ can be derived as follows:

$$ N = 0\quad M = \frac{(1 + cos(\beta L))\beta x - 2\sin (\beta x)}{{2\beta^{2} }}p_{0} $$

(24)

Thus, the expressions of the $\overline{\sigma }_{x}$ can be obtained as follows:

$$ \overline{\sigma }_{x} (x,z) = - \frac{{e^{\gamma ( - h + z)} \gamma^{2} \left( {1 + \gamma z + e^{\gamma h} ( - 1 + \gamma h - \gamma z)} \right)\left( {\beta x(1 + cos(\beta L)) - 2\sin (\beta x)} \right)}}{{2\beta^{2} \left( {2 + \gamma^{2} h^{2} - 2{\text{cosh}}(\gamma h)} \right)}}p_{0} $$

(25)

After finding the $\overline{\sigma }_{x}$, the shear stress $\overline{\tau }_{xz}$ can be obtained from Eq. (3a) as follows:

$$ \overline{\tau }_{xz} (x,z_{0} ) = - \int\limits_{0}^{{z_{0} }} {\frac{{\partial \overline{\sigma }_{x} }}{\partial x}} dz $$

(26a)

$$ \overline{\tau }_{xz} (x,z) = - \frac{{\left( {h + e^{\gamma z} ( - h + z - e^{ - \gamma h} z)} \right)\gamma^{2} \left( {1 + \cos (\beta L) - 2cos(\beta x)} \right)}}{{2\beta \left( {2 + h^{2} \gamma^{2} - 2\cosh (\gamma h)} \right)}}p_{0} $$

(26b)

Considering $w(0) = w(L) = 0$, the vertical displacement can be obtained from Eq. (21b) as follows:

$$ \begin{aligned} \overline{w}(x,z) & = (( - 1 + e^{\gamma h} )\gamma^{3} ( - L^{3} \beta^{3} x + L\beta^{3} x^{3} - L(L^{2} - x^{2} )\beta^{3} \cos (\beta L)x - 12\sin (\beta L)x \\ & \quad + 12L\sin (\beta x)x))p_{0} /(12C_{11} L\beta^{4} (1 + e^{2\gamma h} - e^{\gamma h} (2 + \gamma^{2} h^{2} ))) \\ \end{aligned} $$

(27)

Using Eq. (21a), (27) and (18b) the expression of the axial displacement $\overline{u}$ can be derived in the form:

$$ \begin{aligned} \overline{u}(x,z) & = (\gamma^{2} ( - 3\beta (1 + e^{\gamma h} ( - 1 + \gamma h))\left( {16{\text{cos}}(\frac{\beta L}{2}) + (L^{2} - 4x^{2} )\beta^{2} (1 + {\text{cos}}(\beta L)) - 16{\text{cos}}(\beta x)} \right) \\ & \quad + \frac{4}{L}( - 1 + e^{\gamma h} )\gamma z(L(L^{2} - 3x^{2} )\beta^{3} + L(L^{2} - 3x^{2} )\beta^{3} \cos (\beta L) - 12\beta L\cos (\beta x) \\ & \quad + 12\sin (\beta L))))p_{0} /(48C_{11} \beta^{4} (1 + e^{2\gamma h} - e^{\gamma h} (2 + \gamma^{2} h^{2} ))) \\ \end{aligned} $$

(28)

4 Results and Discussion

The results concern the simply supported FG monoclinic beam under the action of symmetric sinusoidally distributed transverse loading. It is aimed to shed light on the mechanical behavior of these structural members by providing several characteristics (stress and displacement components) benefiting from the abilities of the presented elasticity solution. Some of the results produced by the elasticity solution procedure are also compared with the results of classical beam formulation, when available. In order to observe the sensitivity of the beam’s response to the governing parameters, a set of values are dedicated for the parametric analysis. With this intension, three different fiber directions $\theta = 0^\circ ,45^\circ ,90^\circ$, and stiffness ratios $\Gamma = 0.2,1,5$ are selected where $\Gamma = 1$ corresponds to a homogeneous material distribution along the thickness direction. The role of beam thickness is reflected by choosing a small length-to-thickness ratio $L{/}h = 1$ and a moderate length-to-thickness ratio $L{/}h = 10$ by means of the beam theory limitations. In what follows, it is assumed that the bottom surface of the FG monoclinic beam is made of Glass/Epoxy (Gl/Ep). The material constants of the Gl/Ep composite are listed as follows: [56]: $E_{11} = 42.7\,{\text{GPa}}$, $E_{22} = E_{33} = 11.7\,{\text{GPa}}$, $\nu_{12} = \,\nu_{13} = 0.27$, $\nu_{23} = \,0.55$, $G_{12} = G_{13} = 8.238\,{\text{GPa}}$, and $G_{23} = 3.778\,{\text{GPa}}$.

Firstly, in order to verify the proposed elasticity solution a comparison study is performed. For this purpose numerical results of a special case obtained from the presented elasticity solution are compared with the elasticity solution given by Sankar [20] where isotropic FG beams are considered. Figure 3 reflects the axial displacement and the axial stress distribution of an isotropic beam of thickness $L/h = \pi$ for $\Gamma = 0.1,\,\,10$ calculated by this formulation and by the study of Sankar [20]. It is apparent from Fig. 3 that the results of the presented elasticity solution are consistent with those of Sankar [20]. It can be stated that the validity of the proposed elasticity solution is supported by literature and the proposed solution can be safely implemented for further studies to produce some benchmark results.

Fig. 3

Comparison of the axial displacement and axial stress of isotropic case with literature $(L{/}h = \pi )$

Figure 4 presents the distribution of axial stress $\sigma_{x}$ along the thickness of the beam at its midspan. From the figure, it is apparent that the axial stress is independent of material direction by means of classical beam theory. This behavior is analogous with the elasticity theory for slender beam case where all plots just coincide. Although material direction influences axial stress when the beam gets thicker, its effect is at low order. Nevertheless, this effect is more evident in the region close to the loaded surface. For both classical beam and elasticity solutions, the neutral axis deviates from the centroid of the beam’s cross-section when a nonhomogeneous material distribution is considered. Besides, even for the homogeneous material case, the elasticity solution gives the neutral axis at a point other than the centroid when the beam becomes thicker. For $\Gamma = 0.2$ the axial stress distribution approaches to an almost homogeneous state at tension zone where the material is less stiff. It is also apparent from the figure that as the parameter $\Gamma$ increases, the absolute value of extremum compressive stress of slender and thick beams reduces while the maximum of tensile stress grows.

Fig. 4

Axial stress $\sigma_{x} (L/2,y)$ distribution along the thickness of the FG monoclinic beam for various values of fiber angle θ and inhomogeneity for thick and slender beams

Figure 5 provides the distribution of out of plane stress component $\sigma_{y}$ along the thickness of the beam at its midspan. The plane strain assumption of elasticity analysis makes it possible to obtain this stress component, which cannot be extracted from the classical beam solution. In contradistinction to $\sigma_{x}$ component, $\sigma_{y}$ stress is more influenced by material orientation and this influence can be detected in both slender and thick beam cases. As it may be followed from the figure, $\sigma_{y}$ is more sensitive to a change in the material direction for smaller values of orientation angle $\theta$ especially when the beam is slender. Another important finding is that in all cases $\sigma_{y}$ reaches its extremum values at material orientation $\theta = 45^\circ$. The figure also reveals that as the parameter $\Gamma$ grows, the absolute value of extremum compressive stress decreases while maximum stress increases for both slender and thick beam cases.

Fig. 5

Out of plane normal stress $\sigma_{y} (L/2,y)$ distribution along the thickness of the FG monoclinic beam for various values of fiber angle $\theta$ and inhomogeneity for thick and slender beams

Figure 6 displays the variation of stress component $\sigma_{z}$ along the thickness at the beams’ midspan which is parallel to the loading direction and cannot be extracted from the classical beam solution. The characteristics of the stress component $\sigma_{z}$ are similar to axial stress $\sigma_{x}$. For example, the influence of material orientation is minor for thick beam configuration and becomes negligible as the beam gets slender. The gradient of the stress $\sigma_{z}$ becomes smaller at the regions close to the top and bottom surface of the beam. It must be pointed out that the stress component $\sigma_{z}$ is slightly affected by a change in the stiffness ratio $\Gamma$.

Fig. 6

Vertical normal stress $\sigma_{z} (L/2,y)$ distribution along the thickness of the FG monoclinic beam for various values of fiber angle $\theta$ and inhomogeneity for thick and slender beams

The only nonzero shear stress component in the examined problem is the transverse shear stress $\tau_{xz}$ and its distribution along the left face of the FG monolithic beam is displayed in Fig. 7. Alike the cases of the stresses $\sigma_{x}$ and $\sigma_{z}$, the material orientation does not affect the shear stress $\tau_{xz}$ when the beam is slender. Additionally, the results of the elasticity and classical beam solutions overlap for the slender beam. On the other hand, as the beam becomes thicker, material orientation influences transverse shear stress considerably and classical beam solution diverges from elasticity solution. In the case of the slender beam, a parabolic distribution of the shear stress along the beam thickness is presented where the maximum value is obtained at the centroid when $\Gamma = 1$. However, the location of maximum shear stress slides towards the stiffer zone of the section for $\Gamma \ne 1$. In the case of the thick beam, for $\Gamma = 0.2$ and $1$, the maximum shear stress is obtained when material direction $\theta = 0$ whereas, for $\Gamma = 5$, it is obtained when $\theta = 90^\circ$. Additionally, as the stiffness ratio $\Gamma$ increases, the maximum value of the shear stress over the cross-section reduces and the shear stress distribution tends to be in a more uniform pattern.

Fig. 7

Transverse shear stress $\tau_{xz} (0,z)$ distribution along the left face of the FG monoclinic beam for various values of fiber angle $\theta$ and inhomogeneity for thick and slender beams

The distribution of axial displacement $u$ along the left face of the FG monoclinic beam is depicted in Fig. 8. Elasticity solution gives a linear distribution of axial displacements for slender beam as classical beam theory does, but for thick beam case, the distribution becomes nonlinear. The axial displacement is remarkably influenced by a change in material orientation. One may observe from the figure that as the beam becomes slenderer and material direction approaches to $\theta = 0^\circ$, classical beam theory and elasticity theory produce almost identical results, whereas for $\theta = 90^\circ$ they diverge from each other utmost. Extremum values of axial displacement are obtained for material orientation $\theta = 90^\circ$ for both slender and thick beams and also for all stiffness ratios. Axial displacements have their smallest values when $\Gamma = 5$ and largest values when $\Gamma = 0.2$ which corresponds to the highest rigidity and lowest rigidity configurations, respectively.

Fig. 8

Axial displacement u(0, z) distribution along the left face of the FG monoclinic beam for various values of fiber angle $\theta$ and inhomogeneity for thick and slender beams

Figure 9 reflects the variation of vertical displacement $w(L{/}2,z)$ through the thickness at the midspan of the FG monoclinic beam. The vertical displacements obtained by elasticity solution are almost constant when the beam is slender which verifies the no-strain assumption in this direction made in classical beam theory. However, as the beam becomes thicker, a considerable change in vertical displacement along the thickness is noticed which is most apparent when $\Gamma = 5$. Material orientation has a great influence on the vertical displacement values and the level of its influence increases as the beam gets slenderer. Material orientation is also effective in the proximity of elasticity and classical beam solutions where the level of the proximity decreases with growing $\theta$. Overall, the vertical displacements grow with decreasing value of $\Gamma$ and they take their maximum values when the material direction is set to $\theta = 90^\circ$.

Fig. 9

Vertical displacement $w(L{/}2,z)$ distribution along the thickness of the FG monoclinic beam at its midspan for various values of fiber angle $\theta$ and inhomogeneity for thick and slender beams

In the following section, further results are provided to assess the variation of stress and displacement parameters throughout the beam domain. Distribution of the axial stress $\sigma_{x}$ and out of plane normal stress $\sigma_{y}$, along the loaded surface of the FG monoclinic beam are presented in Figs. 10 and 11, respectively. Overall, the influence of length to height ratio and stiffness ratio on the axial stress and out of plane normal stress characteristics is consistent with the findings from Figs. 4 and 5, where $\sigma_{x}$ and $\sigma_{y}$ distributions along the beam thickness were presented, respectively. Although the influence of material orientation on the axial stress $\sigma_{y}$ is considerable for both slender and thick beam cases, that influence becomes remarkable for $\sigma_{x}$ when the beam is thick. Transverse shear stress $\tau_{xy}$ distribution along the axis of the FG monoclinic beam is shown in Fig. 12. Considering the characteristics of all stress components, $\tau_{xz}$ is the one which is least affected by material orientation $\theta$ and stiffness ratio $\Gamma$. In other respects, the classical beam solution and elasticity solution are more compatible with the calculated results of $\tau_{xz}$ compared to the results of $\sigma_{x}$.

Fig. 10

Axial stress $\sigma_{x} (x,0)$ distribution along the loaded surface of the FG monoclinic beam for various values of fiber angle $\theta$ and inhomogeneity for thick and slender beams

Fig. 11

Out of plane normal stress $\sigma_{y} (x,0)$ distribution along the loaded surface of FG monoclinic beam for various values of fiber angle $\theta$ and inhomogeneity for thick and slender beams

Fig. 12

Transverse shear stress $\tau_{xz} (x,h/2)$ distribution along the length of FG monoclinic beam for various values of fiber angle $\theta$ and inhomogeneity for thick and slender beams

Finally, axial displacement $u$ and vertical displacement $w$ distribution along the loaded surface of the FG monoclinic beam are represented in Figs. 13 and 14, respectively (see Appendix B). It is apparent from figures that, results of classical beam theory and elasticity theory are less compatible for the vertical deflection $w$ values compared to axial displacement $u$.

Fig. 13

Axial displacement $u(x,0)$ distribution along the loaded surface of the FG monoclinic beam for various values of fiber angle $\theta$ and inhomogeneity for thick and slender beams

Fig. 14

Vertical displacement $w(x,0)$ distribution along the loaded surface of FG monoclinic beam for various values of fiber angle $\theta$ and inhomogeneity for thick and slender beams

5 Conclusions

This paper presents an analytical elasticity-based solution procedure for the static analysis of functionally graded monoclinic beams with simply supported edge conditions. The transversely loaded beam is assumed to be in a plane strain state where out of loading plane deformations are prevented. An exponential variation of the monoclinic material properties is considered throughout the beam’s thickness. Furthermore, an analytical solution for the functionally graded monoclinic beam by means of the classical Euler–Bernoulli theory is developed. In the numerical examples, the influence of governing parameters namely, stiffness ratio, material orientation, beam length to height ratio on the stress and displacement components are comprehensively evaluated. Concurrently, the results of the elasticity solution are compared with the results of the classical beam solution. Additionally, for verification purposes an isotropic case of the FG beam is considered and the results obtained from the present elasticity solution are compared with the results of an elasticity-based solution from the literature. A high consistency between the results from both procedures is reported. The results presented by this study indicate that the axial stress distribution over the cross-section of the beam is less influenced from the material direction when the beam’s length to thickness ratio increases. The findings indicate that the extremum value of the axial stress is strongly related to the inhomogeneous distribution of the material throughout the beam’s cross-section. The elasticity solution also revealed that the transverse normal stress is slightly affected by the inhomogeneity characteristics of the material. Another major finding of this study indicates that as the length to thickness ratio of the beam decreases the transverse shear stress is considerably influenced by the material orientation. It is believed that some useful outcomes are presented for a better understanding of the characteristics of FG monoclinic beams. Overall, this study has identified that for slender beams, classical beam theory captures the axial stress and transverse shear stress well enough. However, the findings clearly indicate that the elasticity theory and classical beam theory differ from each other especially in the determination of displacement components which is more apparent with the growing thickness of the beam.

Appendices

Appendix A: Details of some expressions

Expressions of $m_{j}$, $k_{j}$ and $L_{j}$ appearing in Eqs. (12) and (13) are given below

$$ m_{j} = - \frac{{\overline{C}_{55}^{0} (k_{j} + n_{j} )\beta + (\overline{C}_{13}^{0} - \overline{C}_{33}^{0} k_{j} n_{j} )(n_{j} \beta + \gamma )}}{{\overline{C}_{45}^{0} n_{j} \beta + \overline{C}_{36}^{0} (n_{j} \beta + \gamma )}} $$

(A1)

$$ \begin{aligned} k_{j} & = \left[ {\overline{C}_{16}^{0} \beta ((\overline{C}_{36}^{0} + \overline{C}_{45}^{0} )n_{j} \beta + \overline{C}_{36}^{0} \gamma ) + \overline{C}_{13}^{0} (n_{j} \beta + \gamma )( - \overline{C}_{66}^{0} \beta + \overline{C}_{44}^{0} n_{j} (n_{j} \beta + \gamma ))} \right. \\ & \quad + \left. {n_{j} ( - \overline{C}_{45}^{0} (n_{j} \beta + \gamma )((\overline{C}_{36}^{0} + \overline{C}_{45}^{0} )n_{j} \beta + \overline{C}_{36}^{0} \gamma ) + \overline{C}_{55}^{0} \xi ( - \overline{C}_{66}^{0} \beta + \overline{C}_{44}^{0} n_{j} (n_{j} \beta + \gamma )))} \right]/ \\ & \quad \left[ {((\overline{C}_{36}^{0} + \overline{C}_{45}^{0} )^{2} n_{j}^{2} + (\overline{C}_{55}^{0} - \overline{C}_{33}^{0} n_{j}^{2} )(\overline{C}_{66}^{0} - \overline{C}_{44}^{0} n_{j}^{2} ))\beta^{2} + n_{j} ((\overline{C}_{36}^{0} + \overline{C}_{45}^{0} )^{2} - \overline{C}_{44}^{0} \overline{C}_{45}^{0} - \overline{C}_{33}^{0} \overline{C}_{66}^{0} + } \right. \\ & \quad + \left. {2\overline{C}_{33}^{0} \overline{C}_{44}^{0} n_{j}^{2} )\beta \gamma + (\overline{C}_{36}^{0} \overline{C}_{45}^{0} + \overline{C}_{33}^{0} \overline{C}_{44}^{0} n_{j}^{2} )\gamma^{2} } \right] \\ \end{aligned} $$

(A2)

$$ L_{1} = 3\gamma /\beta $$

(A3)

$$ \begin{aligned} L_{2} & = (\beta^{3} \left[ { - (\overline{C}_{13}^{0} )^{2} \overline{C}_{44}^{0} + \overline{C}_{11}^{0} \overline{C}_{33}^{0} \overline{C}_{44}^{0} - 2\overline{C}_{16}^{0} \overline{C}_{33}^{0} \overline{C}_{45}^{0} - (\overline{C}_{36}^{0} )^{2} \overline{C}_{55}^{0} + 2\overline{C}_{13}^{0} (\overline{C}_{36}^{0} \overline{C}_{45}^{0} + (\overline{C}_{45}^{0} )^{2} } \right. - \\ & \quad \left. {\overline{C}_{44}^{0} \overline{C}_{55}^{0} ) + \overline{C}_{33}^{0} \overline{C}_{55}^{0} \overline{C}_{66}^{0} } \right] + \gamma^{2} \beta \left[ {3\overline{C}_{33}^{0} + (\overline{C}_{45}^{0} )^{2} - 3\overline{C}_{33}^{0} \overline{C}_{44}^{0} \overline{C}_{55}^{0} } \right])/\left( {\beta^{3} \overline{C}_{33}^{0} \left[ {(\overline{C}_{45}^{0} )^{2} - \overline{C}_{44}^{0} \overline{C}_{55}^{0} } \right]} \right) \\ & \quad \left. {\overline{C}_{44}^{0} \overline{C}_{55}^{0} ) + \overline{C}_{33}^{0} \overline{C}_{55}^{0} \overline{C}_{66}^{0} } \right] + \gamma^{2} \beta \left[ {3\overline{C}_{33}^{0} + (\overline{C}_{45}^{0} )^{2} - 3\overline{C}_{33}^{0} \overline{C}_{44}^{0} \overline{C}_{55}^{0} } \right])/\left( {\beta^{3} \overline{C}_{33}^{0} \left[ {(\overline{C}_{45}^{0} )^{2} - \overline{C}_{44}^{0} \overline{C}_{55}^{0} } \right]} \right) \\ \end{aligned} $$

(A4)

$$ \begin{aligned} L_{3} & = (2\beta^{2} \gamma \left[ { - (\overline{C}_{13}^{0} )^{2} \overline{C}_{44}^{0} + \overline{C}_{11}^{0} \overline{C}_{33}^{0} \overline{C}_{44}^{0} - 2\overline{C}_{16}^{0} \overline{C}_{33}^{0} \overline{C}_{45}^{0} - } \right.(\overline{C}_{36}^{0} )^{2} \overline{C}_{55}^{0} + 2\overline{C}_{13}^{0} (\overline{C}_{36}^{0} \overline{C}_{45}^{0} + (\overline{C}_{45}^{0} )^{2} \\ & \quad - \left. {\overline{C}_{44}^{0} \overline{C}_{55}^{0} ) + \overline{C}_{33}^{0} \overline{C}_{55}^{0} \overline{C}_{66}^{0} } \right] + \gamma^{3} \overline{C}_{33}^{0} \left[ {(\overline{C}_{45}^{0} )^{2} - \overline{C}_{44}^{0} \overline{C}_{55}^{0} } \right])/\left( {\beta^{3} \overline{C}_{33}^{0} \left[ {(\overline{C}_{45}^{0} )^{2} - \overline{C}_{44}^{0} \overline{C}_{55}^{0} } \right]} \right) \\ \end{aligned} $$

(A5)

$$ \begin{aligned} L_{4} & = (\beta^{3} \left[ {(\overline{C}_{16}^{0} )^{2} \overline{C}_{33}^{0} } \right. - 2\overline{C}_{16}^{0} (\overline{C}_{13}^{0} (\overline{C}_{36}^{0} + \overline{C}_{45}^{0} ) + \overline{C}_{36}^{0} \overline{C}_{55}^{0} ) + \overline{C}_{13}^{0} (\overline{C}_{13}^{0} + 2\overline{C}_{55}^{0} )\overline{C}_{66}^{0} + \overline{C}_{11}^{0} ((\overline{C}_{36}^{0} )^{2} + \\ & \quad \left. { + 2\overline{C}_{36}^{0} \overline{C}_{45}^{0} + (\overline{C}_{45}^{0} )^{2} - \overline{C}_{44}^{0} \overline{C}_{55}^{0} - \overline{C}_{33}^{0} \overline{C}_{66}^{0} )} \right] + \gamma^{2} \beta \left[ { - (\overline{C}_{13}^{0} )^{2} } \right.\overline{C}_{44}^{0} + \overline{C}_{11}^{0} \overline{C}_{33}^{0} \overline{C}_{44}^{0} - 2\overline{C}_{16}^{0} \overline{C}_{33}^{0} \overline{C}_{45}^{0} \\ & \quad - \left. {(\overline{C}_{36}^{0} )^{2} \overline{C}_{55}^{0} + \overline{C}_{13}^{0} (2\overline{C}_{36}^{0} \overline{C}_{45}^{0} + 3(\overline{C}_{45}^{0} )^{2} - 3\overline{C}_{44}^{0} \overline{C}_{55}^{0} ) + \overline{C}_{33}^{0} \overline{C}_{55}^{0} \overline{C}_{66}^{0} } \right])/\left( {\beta^{3} \overline{C}_{33}^{0} \left[ {(\overline{C}_{45}^{0} )^{2} - \overline{C}_{44}^{0} \overline{C}_{55}^{0} } \right]} \right) \\ \end{aligned} $$

(A6)

$$ \begin{aligned} L_{5} & = (\gamma \beta^{2} \left[ {(\overline{C}_{16}^{0} )^{2} \overline{C}_{33}^{0} } \right. - 2\overline{C}_{16}^{0} (\overline{C}_{13}^{0} (\overline{C}_{36}^{0} + \overline{C}_{45}^{0} ) + \overline{C}_{36}^{0} \overline{C}_{55}^{0} ) + \overline{C}_{13}^{0} (\overline{C}_{13}^{0} + 2\overline{C}_{55}^{0} )\overline{C}_{66}^{0} + \overline{C}_{11}^{0} ((\overline{C}_{36}^{0} \\ & \quad + \left. {\overline{C}_{45}^{0} )^{2} - \overline{C}_{44}^{0} \overline{C}_{55}^{0} - \overline{C}_{33}^{0} \overline{C}_{66}^{0} )} \right] + \gamma^{3} \overline{C}_{13}^{0} \left[ {(\overline{C}_{45}^{0} )^{2} - \overline{C}_{44}^{0} \overline{C}_{55}^{0} } \right])/\left( {\beta^{3} \overline{C}_{33}^{0} \left[ {(\overline{C}_{45}^{0} )^{2} - \overline{C}_{44}^{0} \overline{C}_{55}^{0} } \right]} \right) \\ \end{aligned} $$

(A7)

$$ L_{6} = \beta^{3} \left[ { - (\overline{C}_{16}^{0} )^{2} + \overline{C}_{11}^{0} \overline{C}_{16}^{0} } \right] + \gamma^{2} \beta \left[ { - \overline{C}_{13}^{0} \overline{C}_{16}^{0} \overline{C}_{45}^{0} + \overline{C}_{11}^{0} \overline{C}_{36}^{0} \overline{C}_{45}^{0} - \overline{C}_{16}^{0} \overline{C}_{36}^{0} \overline{C}_{55}^{0} + \overline{C}_{13}^{0} \overline{C}_{55}^{0} \overline{C}_{66}^{0} } \right] $$

(A8)

Appendix B: Figures of displacement components along the beam axis

See Figs. 13 and 14