1 Introduction

Composites are vastly applied in modern aircraft and marine structures owing to their special properties [1,2,3,4,5,6]. The most logic reasons for their use are significant strength-to-weight ratio, high corrosion resistance, fatigue resistance and flexibility to fabricate with difficult form [7,8,9]. Fiber-reinforced laminate has a high in-plane strength and stiffness. However, they frequently show low interlaminar fracture toughness [10] which makes them sensitive to delamination. An extensive damage-like delamination is owing to an impact load which can be for single or repeated application. In composites, delamination is able to present critical issues as it may achieve a decrease in the material’s stiffness and strength and a several total fractures [11].

Several methods have therefore been inspected to improve damage tolerance as a result of the increase in the resistance of delamination to progress such as 3D weaving, z-pinning, braiding, tufting and stitching [12]. Accordingly, reinforcement method through the thickness is the most current method of raising the interlaminar fracture toughness.

Three-dimensional fabric assemblies designed as braiding, weaving or transverse stitching methods showed an effective way to reduce delamination [13,14,15,16]. The invention of 3-D composites through weaving or braiding needs more or less exceptional procedures, which are expensive to be used on shipyards superstructures.

However, the conception of reinforcement stitching through thickness is much easier to fabricate and seems promising. In this case, the stitching method is classified as one of the most interesting techniques in enhancing the composite interlaminar bonding [17,18,19,20]. The reinforcement composites with stitching way are able to be created with various stitching type like tufting [11] modified-lock stitch [13] and one-side stitching (OSS) [14]. To quantify the stitching effect, one has chosen to conduct a test campaign in mode I. Indeed, the geometry of the DCB samples shows the efficient method to obtain this mode of failure under quasi-static loading conditions [15].

Experimental researches have demonstrated that with the composite joints, the transversal reinforcement using stitching is a significant technique for increasing performances of the structure [16,17,18]. Based on Greenhalgh and Hiley studies [19], the stitching method improves transversal strength of the structure, enhancing release energy on the damage boundaries. In frequent operation, stitching method that improves interfacial strength can include steps as the stitching fibers break and deformation, plowing over the laminate, and the crack tip forces delocalization. With the mode I, the stitched composites show an improvement about 15 times and for the mode II, it achieves an increase about 8% to 15% [20,21,22] in delamination toughness compared to the composites without stitching.

In another attempt, Chen et al. [23] mentioned a novel mode I test fixture to get over the unreasonable bending moment created an important density stitches on specimen arms. They checked an important density of 64 stitches per square inch for the carbon-epoxy laminates stitched using Kevlar. They indicated that the reinforced stitched samples provide a high fracture toughness around 45 times compared to the unstitched samples.

Furthermore, Aymerich and Francesconi [24] examined the efficient stitching influence using fine carbon fiber-epoxy prepreg laminates using Dyneema SK60, to make increase damage resistance with weak velocity impact. Their results discovered that composites reinforced with stitching can fight delamination phenomenon owing to the significant influence compared to the non-stitched that related directly to bridging action made by the sew.

In this paper, with stitches reinforced composite laminates, we used discrete and continuous cohesive element intended in modeling the delamination reaction [25]. Exceptional interfacial elements mentioned to as cohesive elements are applied to present the unpredicted initiation and the delamination crack propagation. A 1D micromechanical model is developed to define a stitches response. This obtained law is used to model individual stitches as discrete nonlinear springs.

This work is directed along two axes. On the one hand, a numerical work is undertaken for the modeling of initiation and delamination propagation in stitched and unstitched laminated composite. A bilinear damage-dependent cohesive traction separation law with a viscous regularization [26] was implemented to mock up the fracture of the unreinforced composite. Discrete nonlinear springs with micromechanical-based behavior were developed to present the effect of the stitching. Most work in this paper such as the use of nonlinear spring elements and cohesive element in the FEM and mode I tests is not new approaches and very commonly used [27,28,29,30,31,32]. The main strong point of this research work is to propose a new numerical tool for modeling micro-damage mechanisms in a stitched composite structure.

In the other hand, an experimental work is undertaken on the quantification of the stitch contribution on the delamination strength. For that, DCB tests are realized on two types of samples: standards without stitch and others with lightly stitched reinforcements.

In the last part of this paper, we perform matching the results of mode I simulation with the experimental results whether the model soundness is debate toward limited frequent brief.

1.1 Stitch Model

The model of the micromechanics-based has been invented to anticipate the stitching effect on mode I delamination toughness. Through this model, a descriptive elementary volume (R.E.V) is expressed as: the fiber passes through the thickness, is surrounded by resin (matrix) and is stored in two stages, the nods and the changes the fiber direction, Fig. 1. The principal assumptions for the stitches in this model are briefly reviewed.

Fig. 1
figure 1

Illustration of a stitch cross section

Full size image

1.1.1 Micromechanical Assumptions

The thread of the stitch is expected to be as circular of cross section. The present simple model considers the coupling between the slip interfacial fiber/matrix and the conditions of maintains fiber, as shown in Fig. 2.

Fig. 2
figure 2

Micromechanics of model, the effect of a the continuity and the change of direction of the fiber embedded in the composite matrix is modeled by a unidirectional spring of elastic behavior with rigidity k1 and b the nod on the fiber is represented by a unidirectional spring with elastic behavior and stiffness k2

Full size image

The physical parameters and the assumptions of the model are listed below [27,28,29,30,31]:

  • The behavior of fiber is assumed as elastic fragile, isotropic and a cylinder form (diameter df), with a Young's modulus Ef and a null Poisson’s ratio. During slipping stage, the abrasive effect of fiber is neglected.

  • Elastic adhesion among fiber and matrix is neglected. At the time of slip, only the frictional shear stress τ at the matrix/thread interface is considered. The strength of the elastic bond is completely neglected. This assumption is the strongest of the model.

  • The matrix deformation is similarly expected to be insignificant.

  • The continuity effect and the change of direction of fiber drowned in the matrix of the composite are modeled by a linear spring with an elastic rigidity k1. Thus, the effect of the nod (loop) on fiber is represented by a spring with an elastic rigidity k2.

  • The stitching thread tensile strength is supposed to be constant, σfu.

From the assumptions enumerated above, one can determine the response of fiber subjected to an axial interface displacement δ.

1.1.2 Response of the Stitch Model

In order to simplify the mechanical problem presented in Fig. 2, the stitch model is subdivided in two parts i (i = 1, 2). The coupling between each part i is ensured by the equations of continuity of the stresses and displacements. One considers that the pullout of the fiber in the matrix can be examined with two stages: an intact area and an area subject to fiber/matrix interfacial slip of length l, as in Fig. 2b. The fiber embedded end slippage distance is denoted Si(0) (displacement of spring), the relative displacement between matrix and thread is δi, and the axial fiber end stress is σf1. Hi is the embedded length of the thread in a matrix for each part i as shown in Fig. 2.

In the first example, we show the model response while varying the spring rigidity ki of each part i, with k1 = k2. The physical characteristics of the stitch model are presented in Table 1.

Table 1 Micromechanical properties of the stitch model
Full size table

It is supposed that the embedded length of the thread in two parts is equal, H1 = H2 = 2 mm. Also, the failure criterion is activated and the stitching ultimate tensile strength is σfu = 1.5 GPa. Figure 3 shows stitch bridge law (end-fiber stress, dimensionless displacement relationship) according to the properties of the material and geometrical dimensions known overhead.

Fig. 3
figure 3

Response of the micromechanical model

Full size image

It is possible to realize that end-fiber stress keeps increasing with an interface dimensionless displacement before the stitch interruptions. The apparent rigidity of the model increases with the elastic rigidity of the springs. The stages of the model response are: before spring activation (fiber elasticity), the beginning of the embedded end slippage and the break of a fiber.

1.1.3 Macro Mechanical Model

In this section, we are interested in the development of a macroscopic behavior law, which takes into account the micromechanical response of the stitch model (yarn embedded in a resin). The stitch bridge law can be assimilated as elastic, plastic with no compression. Figure 4 shows a macroscopic behavior law used to model individual stitches. The elastic–plastic law without compression relies on two couples of parameters: yield coordinates (εy, σy) that correspond to the final elastic stage, and failure coordinates (εr, σr), typifying the complete failure of the thread. Theses parameters can be estimated with a micromechanics tests, and these relations cannot be defined explicitly.

Fig. 4
figure 4

Elastic–plastic no compression law of the point decohesion element applied to the present individual stitches

Full size image

This behavior law was implemented on ABAQUS implicit [33] finite element code for a 1-D nonlinear spring elements.

1.2 Cohesive Model

The numerical part presents a significant part which is the cohesive traction–separation relations. This part was integrated to design the failure of the reinforced and the unreinforced areas of the material. With this model, the cohesive zone modeling demonstrated the interfacial failure in the form of a strip-like cohesive zone which showed the crack tip ahead instantaneously. A bilinear rate and damage based on the cohesive zone traction–separation law are employed for constituting the delamination failure of the mid-surface with the DCB samples similar to that exposed in Fig. 5.

Fig. 5
figure 5

Interfacial representation

Full size image

The bilinear formulation presented in this section is based on the works of Geubelle and Baylor [34]. This particular model describes a bilinear link of the traction and the displacement jump and is applied to the delamination problem through composite laminates and in modeling bonded joints. The continuous cohesive model is derived from damage mechanics and on the linear mechanics of cracking failure.

The greater portion of cohesive zone laws have a link among normal and tangential directions. One can define the corresponding displacement jump. This parameter is the average of the displacement jump vector, and it is employed to match diverse phases of the displacement jump state so that it is possible to define such theories as ‘loading,’ ‘unloading’ and ‘reloading.’ The corresponding displacement jump looks as nonnegative and continuous function defined as follows [35]:

$$\begin{aligned} \delta & = \sqrt {\alpha^{2} \left( {\varDelta_{1}^{2} + \varDelta_{2}^{2} } \right) + \left\langle {\varDelta_{3} } \right\rangle_{ \pm }^{2} } ;\;{\text{with}} \\ & \quad \alpha^{2} = k_{\text{s}} /k_{\text{n}} \\ \end{aligned}$$
(1)

Symbols \(\left\langle . \right\rangle_{ \pm }\) stand for the positive and negative part of the argument presented like: \(\left\langle x \right\rangle_{ \pm } = \left( {x \pm \left| x \right|} \right)/2\), the scalar factors \(k_{\text{s}}\) also \(k_{\text{n}}\) are the unloading stiffness’s in shear and traction, correspondingly, and \(\varDelta_{i}\) stands for ith component of the displacement jump vector. Within the framework of Clausius–Duhem inequality, it is possible to force limitations on damage variable d. One can assume the irreversibility of damage process for any material point such as \(\dot{d} \ge 0\), which avoids a physical phenomenon. The damage evolution is represented upon an improving scalar function fixed by Turon et al. [36]:

$$d\left( \delta \right) = \left\{ {\begin{array}{*{20}l} 0 \hfill & {\quad {\text{if}}\;\delta < \delta_{0} } \hfill \\ {\frac{{\delta_{\text{f}} \left( {\delta - \delta_{0} } \right)}}{{\delta \left( {\delta_{\text{f}} - \delta_{0} } \right)}}} \hfill & {\quad {\text{if}}\;\delta_{0} \le \delta < \delta_{\text{f}} } \hfill \\ 1 \hfill & {\quad {\text{if}}\;\delta \ge \delta_{\text{f}} } \hfill \\ \end{array} } \right.$$
(2)

\(\delta_{0}\) is the beginning of displacement jump, and it signifies the value where damage starts. The initial damage threshold is got started from the damage surface or initial damage criterion. \(\delta_{\text{f}}\) is the final displacement jump, and it represents the value for which the material is completely damaged. It is achieved from the creation of the propagation surface or propagation criterion.

1.2.1 The Delamination Criterion Onset

While the interface is exposed to pure I or II loading modes, the delamination takes place if the interlaminar-related stress influences its highest interfacial value. Clearly, with mixed-mode loading, delamination onset can arise earlier than those maximum values are gotten. The interaction among the stress components with mixed-mode loading should be occupied in consideration via a multi-axial stress criterion that is assumed as:

$$\left( {\frac{{t_{1} }}{{t_{1}^{0} }}} \right)^{2} + \left( {\frac{{\left\langle {t_{2} } \right\rangle_{ \pm } }}{{t_{2}^{0} }}} \right)^{2} = 1$$
(3)

where \(t_{2}^{0}\) and \(t_{1}^{0}\) are maximum interlaminar traction component linked with \(x_{2}\) and \(x_{1}\) directions. These boundaries are able to be linear into equation by their own displacement \(\varDelta_{2}^{0}\) and \(\varDelta_{1}^{0}\) (\(\varDelta_{i}^{0} \ge 0;\;i = 1,2\)).

1.2.2 Propagation Criterion

The propagation of the delamination takes place, while the energy achieve ratio equals its crucial value below pure mode I or mode II fracture. Mostly, the progress of the delamination takes place below mixed-mode loading. Besides, the delamination progression can take place earlier than one of the energy release rate components achieving its own crucial value. The most generally employed criterion for expecting the delamination propagation with mixed-mode loading is the power law criterion founded on the suggestion of Reeder [20]:

$$\left( {\frac{{G_{\text{I}} }}{{G_{\text{Ic}} }}} \right)^{n} + \left( {\frac{{G_{\text{II}} }}{{G_{\text{IIc}} }}} \right)^{n} = 1$$
(4)

where n is an experimental factor translating the current link among the modes and \(G_{{i\,{\text{c}}}}\) is the critical energy release rate for mode i (i = I, II).

Quadratic solid plane element with four nodes and two Gaussian points has been carefully chosen toward the numerical model. The bilinear behavior employment has been approved out as handler element subroutine (UEL) in ABAQUS Standard [33]. With several phase sizes, algorithm of Newton–Raphson has performed computations.

1.2.3 Localization Problem

The unpredictability owing to the constitutive cohesive law \(\left( {t - \varDelta } \right)\) poses a critical point for the implicit finite elements code. Indeed, the implementation of Newton–Raphson methods of resolutions for issues presenting non-stable branches of solutions can prove to be useless. This instability does not touch the exclusivity of FEM solution; however, it induces a response discontinuity that we call “solution jump.” To suppress this problem, the bilinear softening law can be influenced thru a viscous factor. With the present instance, the damage variable d expression is changed and it depends on the displacement jump rate [24]. The dependent rate cohesive model permits us to overcome this difficulty and to get Newton–Raphson scheme convergence. A detailed proposed law is done by Hamitouche et al. [25, 26].

2 Experimental Study

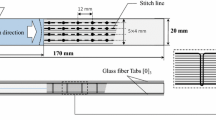
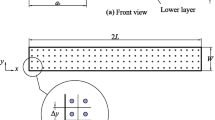
Tests of DCB are frequently conducted to get data above the resistance about the crack of the propagation in mode I. The critical energy release rate GIc can consider this resistance. The tests are followed up on both non-stitched and stitched laminate DCB specimens. Figure 6 presents a diagram of the stitch strengthened DCB sample. There is an unreinforced area of length Ld among the initial crack tip and the starting of the reinforced area. Although in the reinforced region the density of stitches is different according to the thickness, one can see the effect of the stitching.

Fig. 6
figure 6

Double-cantilever beam test for measuring mode I fracture toughness of composites

Full size image

The whole of the specimens is fabricated with glass taffetas fabric and vinylester DION 9102 matrix-reinforced laminated composites. These samples are manufactured using 10 plies, and each had 4 mm of thickness, wide with of 21.36 mm and long with of 176 mm. A tinny Teflon film is used to pre-crack the mid-plane of the laminate, and the pre-crack initial length is a0, as in Fig. 6. A uniaxial testing method is prepared on a LLYOD 1 kN max. Load testing machine worked in control mode of displacement, the cross-head speed is 1 mm/min, and the data acquisition system of a computer-based system is applied. The crack tip evolution is examined with painting the samples cross using a white correction fluid and scored at 1-mm intervals with a fine blade. In the course of the inspection, the curve of load–displacement is examined and the lengths of the crack are unceasingly determined with a numerical camera (resolution 1280 ×960 pixels, frame rate 7.5 fps) prepared with an × 8 zoom.

Three diverse approaches may be exploited to determine the toughness of the mode I fracture depending on ASTM standards [21]: The Compliance Calibration method (CC), the Modified Compliance Calibration method (MCC) and the Modified Beam Theory method (MBT) for both stitched and unstitched specimens. The initiation experimental fracture toughness values GIi are contingent on the specimens due to its strongest link to the local crack tip situations. The critical energy release ratio is methodically expected in accordance with the three previous techniques. The GIi for crack initiation and GIc for critical crack propagation of the unreinforced and reinforced through the thickness laminates are given in Figs. 7, 8 and 9. It can be observed from these figures that the lightly stitched laminate has a higher GIc than the unstitched one (\(G_{\text{Ic}} \,({\text{stitched}}) = 1.5 \times G_{\text{Ic}}\, ({\text{unstitched}})\)), whereas the values of GIi are approximately identical. One can conclude that:

Fig. 7
figure 7

Energy release rate for a the unstitched and b stitched DCB specimen

Full size image
Fig. 8
figure 8

Results of DCB test for a unstitched and b stitched samples

Full size image
Fig. 9
figure 9

R-curves of a unstitched and b stitched samples

Full size image

  • The stitch brings a resistance to delamination.

  • The stitch does not affect the crack initiation (delamination).

3 FEA: Experimental Correlation

A 2D 4-node decohesion element is employed to put on mode I fracture toughness tests on the unstitched woven vinylester glass-fiber-reinforced composite. For the stitched DCB specimen, a cohesive zone model, with a discrete nonlinear spring element, that can be seen as point decohesion elements is employed to represent the stitches influence. Indeed, spring elements behavior law is defined in the Stitch Model section as an elastic–plastic no compression law. The FE model uses 1440 decohesion elements over the entire sample length. Meshing arms were made by a systematic quadrilateral plane strain element wherever the designated element dimension is 0.1 × 0.1 mm. The boundary conditions are used by deleting the degrees of freedom on the left beam bottom end. The critical displacement is useful to the top right ends’ arms. The final material properties applied in this correlation method are ranged in Tables 1 and 2 for elastic lamina properties and cohesive zone parameters.

Table 2 DCB specimen material constants
Full size table

As discussed above, the delamination experiments were designed to study and record pure mode crack growth. For the cohesive zone model, GIc was occupied as input. The maximum interlaminar traction \(t_{2}^{0}\) was taken \(t_{2}^{0} = 50\) MPa, and it has been estimated from \(\left( {F - U} \right)\) experimental curve. This value cannot be confirmed fully with experimental where it is hard to define exactly a delamination onset traction.

The simulations are performed by varying the stitches parameters denoted as yield coordinates (εy, σy) and failure coordinates (εr, σr), characterizing the complete failure of the thread. The toughness, elastic modulus and elongation values of the PET fibers were obtained from. The fiber/matrix interfacial friction is very dependent on the material and the manufacturing process; the corresponding value was thus determined from the thesis work of Dirand [37]. The latter studied the interfacial shear coefficient for epoxy resins and vinylesters. The yield coordinates (εy, σy) have a minute effect on force–displacement behavior of DCB specimen, so the yield coordinates are kept constant and their values are determined by the microscopic fiber properties and the fiber/matrix interface. For this case, \(\left( {\varepsilon_{\text{y}} ,\sigma_{\text{y}} } \right) = (0.016,\,6.28\;{\text{MPa}})\).

Figure 10 compares the reaction versus cross-head displacement consequences with the obverse observations. We show that as the value of (εy, σy) increases, the maximum load extended matching the crack arrest at the first stitch will increase. In addition, in the reinforced region an increase in delamination resistance is observed if we compare (force–displacement) of DCB specimen modeled with a cohesive zone model (unstitched) and for DCB specimen reinforced through the thickness. In Fig. 10, in the phase of initiation (beginning of the curve softening), one notices a great difference between the numerical results and those obtained in experiments. Indeed, the phase of crack initiation can depend on several parameters, for example, thickness of the Teflon film and DCB sample geometry. However, in the phase of propagation, one notices a good correlation between simulation and the experimental one.

Fig. 10
figure 10

Comparison simulation results via an experimental curve under mode I

Full size image

4 Conclusion

In this paper, we studied the problem of the effect of the toughness of mode I fracture into composites laminates. For the first part, one presented the 3D finite element stitch model concluding that a no compression elastic–plastic brittle law is very representative of the stitching effect. In the continuation, we defined a cohesive model with a bilinear softening law about modeling of the beginning and the delamination propagation in mixed mode. This model is employed for the interlaminar fracture toughness simulation for the unstitched DCB specimen. To take account of the stitching influence into DCB samples, we used a behavior law defined previously as law of a spring element placed on the interface level.

In the experimental part, we established interlaminar fracture toughness tests in mode I for stitched and unstitched DCB specimens. From experimental results, one has shown that stitching rises the toughness of the interlaminar fracture but it does not affect the damage initiation.

The comparison made between simulations and the interlaminar resistance tests results presented a good correlation with the propagation the phase, but there is a notable difference in the phase of initiation due probably to the geometrical conditions of the DCB test. Finally, it has been established through mode I fracture toughness simulations that the micro-properties of stitch model (yield (εy, σy) and failure coordinates) can affect highly the overall response at the structural level.