Introduction

Delamination of composite laminates due to low bonding strength of the adhesive layer is an important failure mechanism, which leads to the loss of stiffness and strength of composite structures. Deep insight into the delamination failure mechanism and load-bearing ability of composites requires advanced numerical methods. From the fracture mechanics perspective, the delamination with irreversible crack propagation includes different fracture modes, e.g., mode-I, mode-II and mixed-mode I/II. Compared with the single delamination mode, mixed-mode delamination is more common for composite structures. Reeder and Crews [1] proposed a standard mixed-mode bending specimen (MMB, ASTM D6671-01) for delamination research of composites. Although the MMB has been widely accepted for testing unidirectional coupons, it requires a complex test apparatus. Subsequently, some other types of mixed-mode specimens have been proposed, in which a typical specimen is the single-leg bending (SLB) delamination coupon proposed by Yoon and Hong [2] and developed by Davidson and Sundararaman [3], Polaha et al. [4], Pieracci et al. [5] and Szekrenyes and Uj [6]. In general, the SLB was developed as a modified end-notched flexure specimen. In their work, the delamination fracture toughness was studied by analytical and experimental approaches. Compared with the MMB, the SLB is a simpler test specimen since it does not require a complex loading apparatus.

Because of very small thickness (e.g., 0.1 mm) and complicated mechanical properties of adhesive layers, modeling and simulation on the delamination crack initiation and propagation of composites are a tough task. However, analytical approaches based on the classic beam theory [3–6] cannot predict the crack propagation process of composites. Currently, the cohesive theory, which was first introduced by Dugdale [7] and Barenblatt [8] to describe discrete fracture as a material separation across the interface, has been demonstrated to be the most popular approach for the delamination analysis because it avoids the consideration of the crack-tip singularity and can predict both the delamination crack initiation and propagation. Although the MMB specimen has been widely studied using the cohesive zone model (CZM), the SLB specimen is hardly studied using CZM.

In this paper, we first perform experimental research on the SLB specimens. Second, we develop 3D finite element numerical codes for the exponential CZM proposed by Liu and Islam [9] based on the middle-plane interpolation technique by ABAQUS-UEL (User element subroutine). Finally, the purpose of this paper is to study the effects of the cohesive strength, mesh size and initial delamination crack length on the delamination behavior and load response of the SLB specimens. The developed numerical technique is also validated by comparing numerical and experimental results.

Exponential CZM

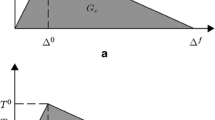
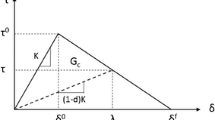
The exponential CZM proposed by Liu et al. [9] is used, where the traction–displacement jump curve is shown in Fig. 1. For single-mode delamination, the damaged cohesive laws \( T_{i} - \Delta_{i}^{\hbox{max} } \left( {\Delta_{i}^{\hbox{max} } = \hbox{max} \left( {\Delta_{i}^{\hbox{max} } ,\Delta_{i} } \right)} \right) \) are written as

$$ T_{i} = {{eT_{i}^{\text{c}} } \mathord{\left/ {\vphantom {{eT_{i}^{\text{c}} } {\Delta_{i}^{\text{c}} \Delta_{i}^{\hbox{max} } }}} \right. \kern-0pt} {\Delta_{i}^{\text{c}} \Delta_{i}^{\hbox{max} } }}\exp \left[ { - \frac{{\Delta_{i}^{\hbox{max} } }}{{\Delta_{i}^{c} }}\left( {1 - d_{i}^{\text{s}} } \right)^{ - 1} } \right],\left( {i = 1,2,3} \right), $$
(1)

where \( d_{i}^{\text{s}} \left( {i = 1,2,3} \right) \) are the damage variables in the normal and tangential directions which are written as

$$ d_{i}^{\text{s}} = \frac{{1 - \exp \left( { - \frac{{\Delta_{i}^{\hbox{max} } - \Delta_{i}^{\text{c}} }}{{\Delta_{i}^{\text{f}} - \Delta_{i}^{\text{c}} }}} \right)}}{1 - \exp ( - 1)},\left( {i = \text{1,2,3}} \right), $$
(2)

where \( \Delta_{i}^{\text{c}} \;(i = 1,2,3) \) and \( \Delta_{i}^{\text{f}} (i = 1,2,3) \) are the initial and critical failure displacement jumps, respectively. The critical displacement jump \( \Delta_{i}^{\text{f}} (i = 1,2,3) \) in Eq 2 can be numerically solved by the following equation

$$ \begin{aligned} \int_{0}^{{\Delta_{i}^{\text{f}} }} {eT_{i}^{\text{c}} /\Delta_{i}^{\text{c}} \Delta_{i}^{\hbox{max} } \exp \left( { - \Delta_{i}^{\hbox{max} } /\Delta_{i}^{\text{c}} } \right){\text{d}}\Delta_{i} } \hfill \\ = eT_{i}^{\text{c}} \Delta_{i}^{\text{c}} - eT_{i}^{\text{c}} \left( {\Delta_{i}^{\text{c}} + \Delta_{i}^{\text{f}} } \right)\exp \left( { - \Delta_{i}^{\text{f}} /\Delta_{i}^{\text{c}} } \right) = \mu G_{i}^{\text{c}} ,\left( {i = \text{1,2,3}} \right), \hfill \\ \end{aligned} $$
(3)

where \( \mu \) is a constant approximating unity and \( \Delta_{i}^{\text{f}} = 11.76\Delta_{i}^{\text{c}} (i = 1,2,3) \) is obtained at \( \mu \) = 0.9999. The traction–displacement jump relationship \( T - \Delta^{\hbox{max} } \left( {\Delta^{\hbox{max} } = \hbox{max} \left( {\Delta^{\hbox{max} } ,\Delta } \right)} \right) \) for mixed-mode delamination is assumed by

$$ T = et^{\text{c}} /\Delta^{\text{c}} \Delta^{\hbox{max} } \exp \left( { - \frac{{\Delta^{\hbox{max} } }}{{\Delta^{\text{c}} }}\frac{1}{{1 - d^{\text{s}} }}} \right), $$
(4)

where \( d^{\text{s}} \) is the scalar interfacial damage variable for mixed-mode delamination. \( \Delta^{\text{c}} = \sqrt {\left( {\Delta_{1}^{\text{c}} } \right)^{2} + \left( {\Delta_{2}^{\text{c}} } \right)^{2} + \left( {\Delta_{3}^{\text{c}} } \right)^{2} } \) and \( T^{\text{c}} = \sqrt {\left( {T_{1}^{\text{c}} } \right)^{2} + \left( {T_{2}^{\text{c}} } \right)^{2} + \left( {T_{3}^{\text{c}} } \right)^{2} } \) are the equivalent critical displacement jump and critical traction, respectively. The variable displacement jump \( \Delta = \sqrt {\left( {\Delta_{1}^{{}} } \right)^{2} + \left( {\Delta_{2}^{{}} } \right)^{2} + \left( {\Delta_{3}^{{}} } \right)^{2} } \) is assumed.

Fig. 1
figure 1

Exponential CZM

Full size image

For mixed-mode delamination, the damage variable \( d^{\text{s}} \) is given by

$$ d^{\text{s}} = \frac{{1 - \exp \left( { - \frac{{\Delta^{\hbox{max} } - \Delta^{\text{c}} }}{{\Delta^{\text{f}} - \Delta^{\text{c}} }}} \right)}}{1 - \exp ( - 1)}{\mathbf{. }} $$
(5)

The mixed-mode critical failure displacement jump \( \Delta^{\text{f}} \) can be numerically solved by

$$ \begin{aligned} \int_{0}^{{\Delta^{\text{f}} }} {eT^{\text{c}} /\Delta^{\text{c}} \Delta^{\hbox{max} } } \exp \left( { - \Delta^{\hbox{max} } /\Delta^{\text{c}} } \right){\text{d}}\Delta \hfill \\ = eT^{\text{c}} \Delta^{\text{c}} - eT^{\text{c}} \left( {\Delta^{\text{c}} + \Delta^{\text{f}} } \right)\exp \left( { - \Delta^{\text{f}} /\Delta^{\text{c}} } \right) = G^{\text{c}} , \hfill \\ \end{aligned} $$
(6)

where the mixed-mode fracture toughness \( G^{\text{c}} \) is assumed to obey the B-K law [10].

The second-order tangent stiffness tensor \( {\varvec{D}}_{{}}^{\tan } \) for mixed-mode delamination is derived from Eqs 1 and 5 by considering the interpenetration between the delaminated interface

$$ D_{{ij}}^{{\tan }} = \frac{{\partial T_{i} }}{{\partial \Delta _{j}^{{\max }} }} = \left\{ {\begin{array}{*{20}l} {\delta _{{ij}} \left[ {1 - \xi \delta _{{1j}} \left\langle { - \Delta _{j}^{{\max }} } \right\rangle /\Delta _{j}^{{\max }} } \right]\left( {1 - \Delta _{j}^{{\max }} /\Delta _{j}^{c} } \right)eT_{j}^{c} e^{{ - \Delta _{j}^{{\max }} /\Delta _{j}^{c} }} /\Delta _{j}^{c} ,} \hfill & {0 < \Delta ^{{\max }} < \Delta ^{c} ,} \hfill \\ {\delta _{{ij}} \left[ {1 - \xi {\mathbf{ }}\delta _{{1j}} \left\langle { - \Delta _{j}^{{\max }} } \right\rangle /\Delta _{j}^{{\max }} } \right]\frac{{T_{j}^{c} }}{{\Delta _{j}^{c} }}\exp \left( {1 - \frac{{\Delta _{j}^{{\max }} }}{{\Delta _{j}^{c} }}\frac{1}{{1 - d^{s} }}} \right)} \hfill & {} \hfill \\ \,\,\, { \times \left\{ {1 - \frac{{\Delta _{j}^{{\max }} }}{{\Delta _{j}^{c} }}\left[ {1 - d^{s} + \frac{{\partial d^{s} }}{{\partial \Delta _{j}^{{\max }} }}\frac{{\Delta _{j}^{{\max }} }}{{\Delta _{j}^{c} }}\frac{1}{{\left( {1 - d^{s} } \right)^{2} }}} \right]} \right\},} \hfill & {\Delta ^{c} \le \Delta ^{{\max }} < \Delta ^{f} ,} \hfill \\ 0 \hfill & {\Delta ^{{\max }} \le 0\;{\text{or }}\Delta ^{{\max }} \ge \Delta ^{f} } \hfill \\ \end{array} } \right. $$
(7)

where

$$ \frac{{\partial d^{\text{s}} }}{{\partial \Delta_{j}^{\hbox{max} } }} = \frac{{\partial d^{\text{s}} }}{{\partial \Delta_{{}}^{\hbox{max} } }}\frac{{\partial \Delta_{{}}^{\hbox{max} } }}{{\partial \Delta_{j}^{\hbox{max} } }}, $$
(8)
$$ \frac{{\partial d^{\text{s}} }}{{\partial \Delta_{{}}^{\hbox{max} } }} = \frac{1}{1 - \exp ( - 1)}\frac{1}{{\Delta^{\text{f}} - \Delta^{\text{c}} }}\exp \left( { - \frac{{\Delta_{{}}^{\hbox{max} } - \Delta_{{}}^{\text{c}} }}{{\Delta_{{}}^{\text{f}} - \Delta_{{}}^{\text{c}} }}} \right), $$
(9)
$$ \frac{{\partial \Delta_{{}}^{\hbox{max} } }}{{\partial \Delta_{i}^{\hbox{max} } }} = \frac{{\Delta_{i}^{\hbox{max} } }}{{\Delta_{{}}^{\hbox{max} } }}\left( {1 + \delta_{1i} \frac{{\left\langle { - \Delta_{i}^{\hbox{max} } } \right\rangle }}{{\Delta_{i}^{\hbox{max} } }}} \right) $$
(10)

and \( \xi \) is a penalty factor and \( \delta_{ij} \) is the Kronecker dalta.

Finite Element Formulation for Implementing CZM

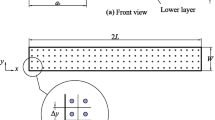
Segurado and Llorca [11] proposed a 3D finite element formulation for implementing CZM by adopting the middle-plane numerical technique, as shown in Fig. 2. Similar to the standard isoparametric element, the local coordinate system \( \left( {\xi ,\eta ,\zeta } \right) \) and the global coordinate system \( \left( {x,y,z} \right) \) are defined. The displacement jump in the local coordinate system \( [[{\varvec{u}}\text{]]} \) for the cohesive element is calculated as

$$ \Delta = \begin{array}{*{20}c} {[[{\varvec{u}}\text{]]} = {\varvec{\varphi }}^{T} [[{\varvec{u}}(\xi ,\eta )\text{]]},} & {{\varvec{\varphi }} = {\varvec{\varphi }}({\varvec{n}},\tilde{{\varvec{t}}}_{1} ,\tilde{{\varvec{t}}}_{2} )} \\ \end{array} $$
(11)

where \( {\varvec{\varphi}}({\varvec{n}},\tilde{{\varvec{t}}}_{1} ,\tilde{{\varvec{t}}}_{2} ) \) is a 3 × 3 transformation matrix of the local coordinate system to the global one and three orthotropic directions are given by

$$ \begin{array}{*{20}c} {{\varvec{n}} = \frac{{\left( {\frac{{\partial {\varvec{x}}^{R} }}{\partial \xi } \times \frac{{\partial {\varvec{x}}^{R} }}{\partial \eta }} \right)}}{{\left\| {\frac{{\partial {\varvec{x}}^{R} }}{\partial \xi } \times \frac{{\partial {\varvec{x}}^{R} }}{\partial \eta }} \right\|}},} & {\tilde{{\varvec{t}}}_{1} = \frac{{\frac{{\partial {\varvec{x}}^{R} }}{\partial \xi }}}{{\left\| {\frac{{\partial {\varvec{x}}^{R} }}{\partial \xi }} \right\|}},} & {\tilde{\varvec{t}}_{2} = \tilde{\varvec{t}}_{1} \times {\varvec{n}}} \\ \end{array} $$
(12)

where the coordinate of middle-plane point \( {\varvec{x}}^{R} \) is written as

$$ {\varvec{x}}^{R} = \frac{1}{2}\varvec{H}\left({\xi ,\eta}\right)(I_{12\times12}\quad \vert\quad I_{12\times12})(\varvec{x}+{\mathop{\varvec{u}}\limits_{\sim}})$$
(13)

where \( \varvec{x} \) and \( {\mathop{\varvec{u}}\limits_{\sim}} \) are the 24 × 1 node coordinate matrix and the 24 × 1 node displacement matrix for 3D eight-node elements, respectively. \( \varvec{H}\left( {\xi ,\eta } \right) \) is a 3 × 12 matrix for 3D eight-node elements including the shape function and \( \varvec{I}_{12 \times 12} \) is the identity matrix.

Fig. 2
figure 2

Middle-plane interpolation technique for implementing a 3D cohesive element using FEA

Full size image

The relative displacement at the point \( \left( {\xi ,\eta } \right) \) between the element sides is interpolated as a function of the relative displacement between the paired nodes

$$ [[\varvec{u}(\xi ,\eta )\text{]]} = \left\{ {\begin{array}{*{20}c} {[[u_{1} (\xi ,\eta )\text{]]}} \\ {[[u_{2} (\xi ,\eta )\text{]]}} \\ {[[u_{3} (\xi ,\eta )\text{]]}} \\ \end{array} } \right\} = \varvec{H}\left( {\xi ,\eta } \right)\text{[[}\varvec{u}_{\text{N}} ]] = \varvec{H}\left( {\xi ,\eta } \right)\varvec{\phi {\mathop{\varvec{u}}\limits_{\sim}} } = \varvec{L {\mathop{\varvec{u}}\limits_{\sim}} } $$
(14)

where \( \varvec{L} \) is a 3 × 24 matrix and \( - 1 \le \xi ,\eta \le 1 \) are local coordinates of elements. \( \varvec{\phi}= \left( {\begin{array}{*{20}c} {\left. {\begin{array}{*{20}c} {\varvec{I}_{12 \times 12} } \\ \end{array} } \right|} & {\varvec{I}_{12 \times 12} } \\ \end{array} } \right) \) is a 12 × 24 matrix. Finally, the node force vector \( \varvec{F}_{c} \left( { 2 4\times 1\;\text{matrix}} \right) \) and the stiffness matrix \( \varvec{K}_{c} \left( { 2 4\times 24\;\text{matrix}} \right) \) are written as

$$ \begin{aligned} \varvec{F}_{c} { = } & \int\limits_{{}} {\int {\varvec{L}^{T} \varvec{\varphi }^{T} } } \varvec{T}{\text{d}}A = \int\limits_{{}} {\int {\varvec{M}^{T} } } \varvec{T}{\text{d}}A = \sum\limits_{i} {\sum\limits_{j} {\omega_{i} \omega_{j} \varvec{M}^{T} \varvec{T}} } \left| J \right|, \\ \varvec{K}_{c} { = } & \frac{{\partial \varvec{F}_{c} }}{{\partial {\mathop{\varvec{u}}\limits_{\sim}}}} = \int {\int\limits_{{}} {\varvec{M}^{T} } \frac{{\partial \varvec{T}}}{{\partial {\mathop{\varvec{u}}\limits_{\sim}}}}{\text{d}}A} = \int {\int\limits_{{}} {\varvec{M}^{T} } \frac{{\partial \varvec{T}}}{{\partial [[\varvec{u}\text{]]}}}\frac{{\partial [[\varvec{u}\text{]]}}}{{\partial {\mathop{\varvec{u}}\limits_{\sim}}}}} {\text{d}}A \\ \varvec{ = } & \int {\int\limits_{{}} {\varvec{M}^{T} } \frac{{\partial \varvec{T}}}{{\partial [[\varvec{u}\text{]]}}}\frac{{\partial [[\varvec{u}\text{]]}}}{{\partial {\mathop{\varvec{u}}\limits_{\sim}}}}} {\text{d}}A = \int {\int\limits_{{}} {\varvec{M}^{T} } \frac{{\partial \varvec{T}}}{{\partial [[\varvec{u}\text{]]}}}\varvec{M}} {\text{d}}A \\ {\mathbf{ = }} & \sum\limits_{i} {\sum\limits_{j} {\omega_{i} \omega_{j} \varvec{M}^{T} \varvec{D}_{{}}^{\tan } \varvec{M}} } \left| J \right| \\ \end{aligned} $$
(15)

where \( \left| J \right| \) is the Jacobian for isoparametric transformation and \( \omega \) is the weight. \( \varvec{M} = \varvec{\varphi L} \) is a 3 × 24 shape function matrix for 3D cohesive elements.

Cohesive Zone Length

CZM introduces a length scale (generally called cohesive zone length) due to cohesive softening behavior. The cohesive zone length is defined as the distance from the crack tip to the position where the maximum cohesive traction is attained [12, 13]. If the cohesive length scale is not considered in the delamination analysis, the dissipation of delamination fracture energy cannot be accurately captured which will lead to a mesh sensitivity problem. Thus, the cohesive zone length must be properly evaluated. Turon et al. [12] suggested that three elements in the cohesive zone are sufficient to predict the delamination growth, which is adopted in this research.

SLB Experiments

Two T700/8911 SLB composite specimens with different initial delamination crack sizes were used for delamination test, as shown in Fig. 3. Geometry sizes for the two specimens are listed in Table 1. Composite specimens were prepared according to the Chinese standard-ASTM D6671/D6671M-06 [14] and a Teflon film was inserted at the middle plane of specimens to make an initial delamination crack. The loaded specimen is shown in Fig. 4. After the specimen was positioned, the displacement with a velocity of 3 mm/min was exerted on the specimen using the MTS810-25ton electro-hydraulic servo material test system. Load–displacement curves were recorded to validate the numerical results.

Fig. 3
figure 3

SLB composite specimen

Full size image
Table 1 Geometry sizes for SLB specimens
Full size table
Fig. 4
figure 4

SLB experiment

Full size image

Numerical Results Using Exponential CZM

Table 2 lists the material parameters for T700/8911 composites. The delamination analysis using CZM requires mode-I and II delamination fracture toughness \( G_{\text{I}}^{c} \) and \( G_{\text{II}}^{c} \), which are calculated using Eq 16 derived by Szekrenyes and Uj [6]

$$ \left\{ \begin{aligned} G_{\text{I}}^{c} = & \frac{{12P^{2} a^{2} }}{{16b^{2} h^{3} E_{11} }}\left[ {1 + 0.85\left( {\frac{h}{a}} \right)\left( {\frac{{E_{11} }}{{E_{33} }}} \right)^{{\frac{1}{4}}} \,+ \,0.71\left( {\frac{h}{a}} \right)^{2} \left( {\frac{{E_{11} }}{{E_{33} }}} \right)^{{\frac{1}{2}}} \,+\, 0.32\left( {\frac{h}{a}} \right)\left( {\frac{{E_{11} }}{{E_{33} }}} \right)^{{\frac{1}{2}}} \,+ \,0.1\left( {\frac{h}{a}} \right)^{2} \left( {\frac{{E_{11} }}{{G_{13} }}} \right)} \right], \\ G_{\text{II}}^{c} = & \frac{{ 9P^{2} a^{2} }}{{16b^{2} h^{3} E_{11} }}\left[ {1 + 0.22\left( {\frac{h}{a}} \right)\left( {\frac{{E_{11} }}{{G_{13} }}} \right)^{{\frac{1}{2}}} \,+\, 0.048\left( {\frac{h}{a}} \right)^{2} \left( {\frac{{E_{11} }}{{G_{13} }}} \right)} \right] \\ \end{aligned} \right. $$
(16)

where \( E_{11} \) and \( E_{33} \) are the elastic moduli and \( G_{13} \) is the shear modulus.

Table 2 Material properties for T700/8911 composites
Full size table

Liu and Islam [9] proposed an exponential cohesive model and established four-node zero-thickness cohesive elements using ABAQUS-UEL (User element subroutine) to study 2D delamination. In this research, eight-node zero-thickness interface elements are further established to study 3D delamination, where the main work in each iteration is to update the node residual force \( \Delta \varvec{F}_{c} \) and the element stiffness matrix \( \varvec{K}_{c} \left( { 2 4\times 24\;\text{matrix}} \right) \) in Eq 15.

Figure 5 shows fine and coarse mesh models for two specimens using ABAQUS. The C3D8R element is used to model the lamina and the zero-thickness cohesive element is used to model the delamination interface. The number of solid elements for two mesh models is 5520 and 22,000, respectively, and the number of cohesive element for specimen-A is 500 and 2000, and 370 and 1500 for specimen-B. Due to cohesive softening behavior, the artificial viscous force \( \varvec{F}_{\text{v}} \) is introduced to improve the convergence [15]

$$ \left\{ \begin{aligned} \varvec{F}_{\text{ext}} - \varvec{F}_{\text{c}} - \varvec{F}_{\text{v}} = \varvec{R}, \hfill \\ \varvec{F}_{\text{v}} = cM^{*} \varvec{v},\varvec{v} = \Delta {\mathop{\varvec{u}}\limits_{\sim}}/\Delta t \hfill \\ \end{aligned} \right. $$
(17)

where \( M^{*} \) is an artificial mass matrix calculated with unity density,\( \varvec{v} \) is the node velocity, \( \Delta {\mathop{\varvec{u}}\limits_{\sim}} \) is the node displacement increment, \( \varvec{R} \) is the tolerance, \( c \) is a constant damping factor and the viscous constant \( c \) = 1e−4 in Eq 17 is generally used, and \( \Delta t \) is the time increment during nonlinear iterations. It is noted the introduced viscous forces should be large enough to regularize cohesive softening behaviors but small enough not to affect the numerical accuracy. A very small time increment is required to guarantee the numerical precision (the initial, minimum and maximum time increments are \( \Delta t = \) 0.0001 s, 1e−10 s and 0.001 s, respectively). Numerical calculations were performed on the I5-2540M Lenovo computer with the main configurations: Intel Xeon CPU with 4 processors (main frequency of each processor is 2.6 GHz) and 4 GB memory.

Fig. 5
figure 5

Mesh models for two specimens

Full size image

Figure 6 shows the load–displacement curves for two specimens by comparing the numerical and experimental results at \( T_{1}^{\text{c}} = T_{2}^{\text{c}} = T_{3}^{\text{c}} = 50\,\text{MPa} \). The numerical results are basically consistent with the experimental results using the two mesh models. The delamination appears at about 1.6 mm displacement for specimen-A and at 2.6 mm displacement for specimen-B. Then, the delamination enters into an unstable stage. For the coarse mesh, more unstable delamination appears at the softening stage, which is generally called the “solution jump”. The reason for numerical oscillation using the coarse size is that the softening property of the interface element leads to the sudden release of strain energy in the lamina which leads to instantaneous failure of the element. In such a case, a non-physical limit point in the form of a snap-through or a snap-back situation arises in the numerical solution [16]. By comparison, the fine mesh contributes to alleviating this numerical problem. By comparing the two specimens, a larger stiffness is obtained before the delamination for specimen-A than that for specimen-B because of shorter initial crack length for specimen-A than for specimen-B. From the delamination initiation to stable delamination, the delamination rate is faster for specimen-A than for specimen-B. Before the collapse of the specimens, the crack propagation length is 61 mm for specimen-A and 29 mm for specimen-B. In addition, the load-bearing ability for specimen-A is higher than that for specimen-B.

Fig. 6
figure 6

Load–displacement curves for two specimens at cohesive strength 50 MPa

Full size image

Figures 7 and 8 show the load–displacement curves at different cohesive strengths for the two specimens. The cohesive strength affects the initial delamination displacement and unstable delamination behavior. With the increase of cohesive strength from 20 to 80 MPa, numerical results using CZM become gradually closer to the experimental results. However, a convergence difficulty appears at 80 MPa cohesive strength, which was also found by Alfano and Crisfield [17], Turon et al. [12] and Liu and Islam [9]. Thus, there is an integrated consideration in appropriately selecting the cohesive strength using CZM.

Fig. 7
figure 7

Load–displacement curves for specimen-A at different cohesive strengths

Full size image
Fig. 8
figure 8

Load–displacement curves for specimen-B at different cohesive strengths

Full size image

Figures 9 and 10 show the effects of the viscous constant c in [17] on the load–displacement curves. The viscous effect starts to work when the delamination initiation appears, and the predicted load and dissipated energy increase with the increase of c, which leads to slightly larger error from the delamination initiation. By comparison, c = 1e−4 is acceptable. Figures 11 and 12 show the delamination growth processes for the two specimens at different displacements. By comparison, the crack propagation rate for specimen-A is faster than that for specimen-B, and a more unstable delamination process is encountered for specimen-A than for specimen-B.

Fig. 9
figure 9

Viscous effect on the load–displacement curves for specimen-A

Full size image
Fig. 10
figure 10

Viscous effect on the load–displacement curves for specimen-B

Full size image
Fig. 11
figure 11

Delamination growth processes for specimen-A at the displacement (a) 1.6 mm, (b) 5.9 mm and (c) 9.3 mm at cohesive strength 50 MPa

Full size image
Fig. 12
figure 12

Delamination growth processes for specimen-B at the displacement (a) 1.6 mm, (b) 5.9 mm and (c) 9.3 mm at cohesive strength 50 MPa

Full size image

Conclusions

This paper develops 3D finite element codes to implement the exponential cohesive model for the delamination analysis of SLB composite specimens using ABAQUS-UEL, and aims to study the influence of the cohesive strength, mesh size and initial delamination crack length on the delamination behavior and load response of SLB specimens. From 3D finite element analysis (FEA), three main conclusions are obtained. (1) Numerical results are closer to the experimental result at large cohesive strength. However, computational efficiency becomes slow due to the increase of convergence difficulty. Thus, there is an integrated consideration in appropriately selecting the cohesive strength. (2) Different mesh sizes lead to consistent results. However, a spurious “solution jump” appears at the unstable delamination stage using the coarse mesh due to cohesive softening behavior. By comparison, the fine mesh helps to alleviate this problem. (3) The crack propagation rate for the specimen with shorter initial delamination crack length is faster, and a more unstable delamination process is also experienced. In addition, the load-bearing ability decreases when the initial delamination crack length increases.