1 Introduction

Conventional manipulators are manufactured to have maximum stiffness for the purpose of diminishing the effects of vibrations. This leads to a bulky and heavy design with intensive energy requirements and significant speed limitations. Unfortunately, vibrations in the rigid manipulators still cannot be avoided during fast movements. This results in an imprecision of the end-effector position [1]. Flexible manipulators are preferred because of theirs lightweight and insignificant energy requirements. The main problem is to control the flexible manipulator in the presence of an uncertain fluctuation.

In the literature, there are various control schemes incorporated with flexible manipulators. Mahamood and Pedro [2] have used a PID control scheme on the TLFM based on an assumed mode method (AMM) model. Performance of the controller is evaluated on the basis of tracking and vibration suppression capabilities. PID control scheme is incapable of making adjustments to the changes in the process parameters. Ahmad [3] has designed a control scheme that is a combination of linear quadratic regulator (LQR) and PID. The scheme is used efficiently in reducing the vibrations of the flexible manipulator. Miyasato [4] has developed an adaptive \(H_{\infty }\)- based control scheme for a flexible arm. The controller is robust to model uncertainties and is insensitive to parameter variations.

The development of an accurate mathematical model is a cumbersome task, particularly considering the uncertainties associated with the flexible manipulators. This encourages the use of self-tuning adaptive control strategies as well as fuzzy logic control and neural networks. Fuzzy logic controller (FLC), when applied to a nonlinear control system, gives a robust performance. This is because the FLC does not require an explicit mathematical model of the system, but is designed based on human expertise and knowledge, so it directly handles uncertainty in the system [5,6,7]. Li et al. [8] have designed an adaptive fuzzy system for the control of a single-link flexible manipulator. The designed controller is based on the Takagi Sugeno modeling and the linear matrix inequality analysis. The backstepping technique is used for tuning of the parameters. Tinkir et al. [9] have used a neuro-fuzzy control scheme for a single-link flexible manipulator. Pedro and Tshabalala [10] have developed a more complex hybrid strategy using model predictive, neural network and PID control. AMM is used for the modeling of the TLFM. PID is used for the vibration control, while model predictive-based neural network is used for the position control of the manipulator. Different payloads are considered for assessing the robustness of the control scheme, and the results have revealed the effectiveness of the proposed control scheme. Subudhi and Morris [11] have developed a neuro-fuzzy control based on the radial basis functions. AMM is used for the dynamic modeling of the TLFM. The performance of the proposed control scheme is compared with a PD adaptive control and a fuzzy control scheme.

Type-1 FLC has been used extensively in several engineering fields [12,13,14]. However, it performs poorly when it encounters a higher degree of uncertainty [15]. This led researchers to use the type-2 FLC, which is presented by Zadeh [16], to better deal with uncertainties. In the literature, the supremacy of a type-2 NFS is affirmed compared to a type-1 fuzzy system, in terms of dealing better with the uncertainties [17,18,19,20]. Type-2 NFS has higher fuzzy set dimensions; hence, it provides more degrees of freedom for the direct processing of uncertain information [21]. Önen et al. [22] have designed a neuro-fuzzy controller based on a type-2 fuzzy control system. Lagrange and AMM are used for the design of the flexible manipulator. Tracking and vibration control of the flexible manipulator is carried out efficiently. Juang and Tsao [23] have used a self-tuning fuzzy neural network system with Gaussian membership functions having fixed standard deviations and uncertain means for system identification purposes. The proposed controller has shown the capability of learning structures and parameters at the same time. Abyayev and Kaynak [24] have proposed a fuzzy neural structure based on the type-2 TSK system. The scheme proposed by the authors has the ability to adjust the ratio of upper and lower membership bounds. Juang et al. [25] have shown two types of NFS type-2 fuzzy sets: one with uncertain means but fixed standard deviations, and the other with fixed means but uncertain standard deviations. Lin et al. [26] algorithm has reduced the computation complexity of adjusting the upper-to-lower bound ratio. Gaussian membership functions are used in the antecedent part with uncertain means and fixed standard deviations, while TSK is used in the consequent part. The results are also compared with other type-1 and type-2 neural fuzzy systems. The control scheme has shown better performance with lesser rules, compared to the other schemes.

In addition to the above-mentioned uses of the type-2 NFS, the researchers have used it in many other engineering fields as well [27,28,29,30,31]. The steepest descent (SD) method is used in most of the aforementioned type-2 NFS for tuning of the parameters. It uses partial derivatives to determine the new update values of the NFS parameters. Learning speed of the SD method is slow, especially when the search space is complex, and it is widely known to have a poor convergence rate. The performance of the method depends on the appropriate selection of the parameters, such as learning rate and initial weights. Even a slight deviation in these values can deteriorate the algorithm’s performance [32,33,34]. So the motivation of this research is to look for an alternative parameter tuning method for optimizing parameters of the type-2 NFS. The conjugate gradient (CG) method used in this study has never been used before in the type-2 NFS. It adjusts the initial search direction; consequently, achieving a faster and more stable response. Compared to the SD method, the method used in this study has a global convergence property, proof of which is also given in this paper. Furthermore, the type-2 NFS in this study has T-norms in the defuzzification phase rather than the commonly used product–sum combination, so to speed up the convergence.

The paper is organized in five sections. Section 2 illustrates the modeling of a TLFM. Proposed control scheme is explained in Sect. 3. The simulation results are presented and discussed in Sect. 4. Section 5 gives the conclusion of the paper.

2 TLFM

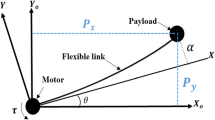
A planar flexible manipulator model by De Luca and Siciliano [35] is shown in Fig. 1.

Fig. 1
figure 1

Two-link flexible manipulator [35]

Full size image

The following coordinate frames have been utilized: \(\left\{ {{{\hat{X}}}_{0}},{{{\hat{Y}}}_{0}} \right\} \) is the inertial coordinate frame, \(\left\{ {{X}_{i}},{{Y}_{i}} \right\} \) is the ith link rigid body moving coordinate frame, and \(\left\{ {{{\hat{X}}}_{i}},{{{\hat{Y}}}_{i}} \right\} \) is the ith link flexible body moving coordinate frame. Rigid motion is defined by joint angles \({{\theta }_{i}}\) , ith link flexible transversal deflection is defined by \({{y}_{i}}\left( {{\chi }_{i}} \right) \) at a spatial point \(\chi _i \; (0\le {{\chi }_{i}}\le {{l}_{i}})\), and \({{l}_{i}}\) is the ith link length. The links are serially cascaded and actuated by the joints with individual motors. The following assumptions have been made for dynamic modeling of the flexible manipulator [36]. Each link movement is assumed in the horizontal plane only. Consequently, the effects of cross-shear and rotary inertia are insignificant. Link deflections are assumed to be small. Rotor’s kinetic energy is assumed to be because of its rotation only. The backlash in motor and friction effects are ignored. Continuous cross-sectional area and uniform material of links are assumed, i.e., constant Young’s modulus and mass density. Euler–Bernoulli beam theory is used to model link with uniform density \({{\rho }_{i}}\), flexural rigidity \({{\left( \mathrm{EI} \right) }_{i}}\) and link deflection \({{y}_{i}}({{\chi }_{i}},t)\) as follows [37].

$$\begin{aligned} {{\left( \mathrm{EI} \right) }_{i}}\frac{{{\partial }^{4}}{{y}_{i}}({{\chi }_{i}},t)}{\partial \chi _{i}^{4}}+{{\rho }_{i}}\frac{{{\partial }^{2}}{{y}_{i}}({{\chi }_{i}},t)}{\partial {{t}^{2}}}=0,\ \ i=1,\ldots ,g \end{aligned}$$
(1)

Without discretization of the flexible manipulator, the Lagrangian function has an unlimited-dimensional model with limited use for simulation and control purposes. AMM [38, 39] is used for the finite-dimensional solution of (1), which represents the link deflections \( {{y}_{i}}\in R^g \) (2) as a truncated finite modal series comprising spatial mode shape functions (3) and time-varying modal displacements (4).

$$\begin{aligned} {{y}_{i}}\left( {{\chi }_{i}},t \right) =\sum \limits _{j=1}^{{{\mathrm{d}}_{i}}}{{{\phi }_{ij}}\left( {{\chi }_{i}} \right) }{{\delta }_{ij}}(t) \end{aligned}$$
(2)

where the solution of (2) is,

$$\begin{aligned} \begin{aligned} {{\phi }_{ij}}\left( {{\chi }_{i}} \right) =&{{C}_{1,ij}}\sin ({{\beta }_{ij}}{{\chi }_{i}})+{{C}_{2,ij}}\cos ({{\beta }_{ij}}{{\chi }_{i}})\\&+{{C}_{3,ij}}\sinh ({{\beta }_{ij}}{{\chi }_{i}})+{{C}_{4,ij}}\cosh ({{\beta }_{ij}}{{\chi }_{i}}) \end{aligned} \end{aligned}$$
(3)

and,

$$\begin{aligned} {{\delta }_{ij}}(t)=\exp (j{{w}_{ij}}t) \end{aligned}$$
(4)

where \( {C}_{1,ij} \), \( {C}_{2,ij} \), \( {C}_{3,ij} \) and \( {C}_{4,ij} \) are unknown coefficients, which are to be determined by the boundary conditions, and

$$\begin{aligned} {{\beta }_{ij}}=\frac{{{\root 4 \of {\rho }}_{i}}\sqrt{{{w}_{ij}}}}{{{\root 4 \of {\mathrm{(EI)}}}_{i}}} \end{aligned}$$
(5)

where \( {w}_{ij} \) is the ith link jth natural angular frequency of the eigenvalue problem. Applying the boundary conditions, given in [35, 40], gives the homogeneous solution (6).

$$\begin{aligned} \left[ F\left( {{\beta }_{ij}} \right) \right] \left[ \begin{matrix} {{C}_{1,ij}} \\ {{C}_{2,ij}} \\ \end{matrix} \right] =0 \end{aligned}$$
(6)

where \(F\left( {{\beta }_{ij}} \right) \) is defined as,

$$\begin{aligned}&( 1+\cos ({{\beta }_{ij}}{{l}_{i}})\cosh ({{\beta }_{ij}}{{l}_{i}}) )-\frac{{{M}_{Li}}{{\beta }_{ij}}}{{{\rho }_{i}}}( \sin ( {{\beta }_{ij}}{{l}_{i}} )\cosh ( {{\beta }_{ij}}{{l}_{i}} ) \nonumber \\&\quad -\cos ( {{\beta }_{ij}}{{l}_{i}})\sinh ( {{\beta }_{ij}}{{l}_{i}} ) -\frac{{{J}_{Li}}\beta _{_{ij}}^{3}}{{{\rho }_{i}}}( \sin ( {{\beta }_{ij}}{{l}_{i}} )\cosh ( {{\beta }_{ij}}{{l}_{i}} )\nonumber \\&\quad + \cos ( {{\beta }_{ij}}{{l}_{i}} )\sinh ( {{\beta }_{ij}}{{l}_{i}} ) )+\frac{{{M}_{Li}}{{J}_{Li}}\beta _{ij}^{4}}{\rho _{_{i}}^{2}}\nonumber \\&\quad ( 1-\cos ({{\beta }_{ij}}{{l}_{i}})\cosh ({{\beta }_{ij}}{{l}_{i}}))=0 \end{aligned}$$
(7)

where \({{J}_{Li}}\) and \({{M}_{Li}}\) are the moment of inertia and mass, respectively, at the end of the ith link and are defined in [35].

The Euler–Lagrange equation gives s generalized coordinate \({{q}_{i}}\) solutions,

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}\left( \frac{\partial L}{\partial {{{\dot{q}}}_{i}}} \right) -\frac{\partial L}{\partial {{q}_{i}}}={{f}_{i}},\quad \quad i=1,\ldots ,s \end{aligned}$$
(8)

where \( s = g + \sum \limits _i {{d_i}} \), g represents the number of links and \( d_i \) represents the modes considered for each link. L is the Lagrangian, and \({{f}_{i}}\) is the force performing work on \({{q}_{i}}\). From the Euler–Lagrange equation (8), TLFM closed form of equations can be written in the form as (9). Complete modeling and detailed equations of motion of the TLFM can be found in [35, 36].

$$\begin{aligned} B\left( q \right) \ddot{q}+h\left( q,\dot{q} \right) +Kq=Qu \end{aligned}$$
(9)

where \(B \in {R^{s \times s}}\) is the inertia positive definite matrix, \(h\in {R^s}\) is the vector of centrifugal and Coriolis forces, \(K\in {R^{s \times s}}\) is the stiffness matrix, \(u \in {R^{g}}\) is the input vector and Q is the input weighting matrix defined as \({\left[ {{I_{g \times g}}\; {0_{g \times \left( {s - g} \right) }}} \right] }\).

3 Control Scheme

This section introduces the proposed adaptive neural fuzzy control (ANFC) scheme. The objective of the scheme is to control the angular positions of the TLFM links while regulating their intrinsic fluctuations. The multi-input single-output (MISO) structure of an ANFC system is shown in Fig. 2.

Fig. 2
figure 2

ANFC structure

Full size image

The structure comprises many layers. Layer 1 is the input layer, where values are in the crisp form. Layer 2 is the membership function layer, where the fuzzification process converts crisp values into fuzzy values. For fuzzification, fuzzy sets can be triangular, trapezoidal, sigmoidal, sinc and many other functions. Mitaim and Kosko [41] have used different membership functions and have achieved fast function approximations with the sinc membership function. The sinc membership function is defined as

$$\begin{aligned} \eta _{ij}(x_j)&= \dfrac{\sin \bigg (\dfrac{x_j-\nu _{ij}}{\varsigma _{ij}}\bigg )}{\bigg (\dfrac{x_j-\nu _{ij}}{\varsigma _{ij}}\bigg )} \end{aligned}$$
(10)
$$\begin{aligned}&=N({{\nu }_{ij}},{{\varsigma }_{ij}},{{x}_{i}}), \; \; {\nu }_{ij} \in \left[ {{\nu }_{ij1}},{{\nu }_{ij2}} \right] \end{aligned}$$
(11)

where \( i=1,\ldots ,r \), \( j=1,\ldots ,n \), r denotes the number of rules, n denotes the number of inputs, \(x_j \in R^n\) is the input vector, \(\nu _{ij} \in R^{r \times n}\) is the mean vector and \(\varsigma _{ij} \in R^{r \times n}\) is the variance vector of the membership function. Fuzzy type-2 membership functions are considered with uncertain means and fixed variances. The antecedent part’s upper and lower membership functions are represented as:

$$\begin{aligned} {{\bar{\eta } }_{ij}}({{x}_{j}})=&\left\{ \begin{array}{ll} N\left( {{\nu }_{ij1}},{{\varsigma }_{ij}};{{x}_{j}} \right) ,\quad &{}{{x}_{j}}<{{\nu }_{ij1}}\, \\ 1\quad &{}{{\nu }_{ij1}}\le {{x}_{j}}\le {{\nu }_{ij2}} \\ N\left( {{\nu }_{ij2}},{{\varsigma }_{ij}};{{x}_{j}} \right) ,\quad &{}{{x}_{j}}>{{\nu }_{ij2}} \\ \end{array} \right. \end{aligned}$$
(12)
$$\begin{aligned} \underline{\eta }_{ij}({{x}_{j}})=&\left\{ \begin{matrix} N\left( {\nu _{ij2}},{{\varsigma }_{ij}};{{x}_{j}} \right) ,\quad {{x}_{j}}<\frac{{\nu _{ij1}}+{\nu _{ij2}}}{2} \\ N\left( {\nu _{ij1}},{{\varsigma }_{ij}};{{x}_{j}} \right) ,\quad {{x}_{j}}>\frac{{\nu _{ij1}}+{\nu _{ij2}}}{2} \end{matrix}\right. \end{aligned}$$
(13)

The fuzzy set covers the input–output region, and the correspondent consequent part defines the mathematical functions of that region. The ith rule of NFS is defined as [42,43,44]:

$$\begin{aligned} if \; x_1 \; is \; \eta _{i1}(x_1) \cdots \mathrm{and} \; x_n \; is \; \eta _{in}(x_n) \; \mathrm{THEN}\nonumber \\ c_i = b_{i0}+b_{i1}x_1+\cdots +b_{in}x_n \end{aligned}$$
(14)

Layer 3 determines the firing strength of antecedent part’s rules. The outputs of the layer 2 are multiplied in this layer, so to represent the firing strength; hence, upper (\( \bar{\mu _i} \in R^r \)) and lower firing strengths (\( \underline{\mu _i} \in R^r \)) are determined in this layer.

$$\begin{aligned} \bar{\mu _i}=\prod \limits _{j=1}^{n}{{{\bar{\eta } }_{ij}}}, \quad \underline{\mu _i} =\prod \limits _{j=1}^{n}{{{\underline{\eta } }_{ij}}} \end{aligned}$$
(15)

T-norm and T-conorm combination introduced by Weber [45] is used rather than the widely used product–sum combination. T-norm is simple product, while T-conorm is . Using suitable T-norms enhances the performance of NFS [46].

$$\begin{aligned} \underline{p_i} =\frac{{{{\underline{\mu } }_{i}}}}{T_i\{\underline{\mu }_{i}\}}, \quad \bar{p_i}=\frac{{{{\bar{\mu } }_{i}}}}{T_i\{\bar{\mu }_{i}\}} \end{aligned}$$
(16)

where \( \bar{p_i} \in R^r \) and \( \underline{p_i} \in R^r \) are normalized degree of fulfillment. Layer 4 has consequent parameters, i.e., \(c_i \in R^r\) defined in (14), whereas \(b_{i0}\) to \(b_{in}\) are the variables. Layer 5 calculates an output by using the centroid defuzzification method.

$$\begin{aligned} u=(1-\omega )\underline{u}+ (\omega ) \bar{u} \end{aligned}$$
(17)

where \(\omega \) is the scalar variable that determines the proportion of upper and lower output, \(\underline{u}=\sum \nolimits _i\underline{p_i}c_i\) and \(\bar{u}=\sum \nolimits _i\bar{p_i} c_i\).

3.1 Self-Tuning Algorithm

The parameters in the antecedent and consequent layers are needed to be optimized. The cost function, namely mean squared error (MSE), (18) is used to optimize these parameters.

$$\begin{aligned} E = \frac{1}{2} (u - u_a)^2 \end{aligned}$$
(18)

where u and \(u_a\) in (18) are the actual and desired output, respectively. The objective of the algorithm is to minimize the cost function by optimizing the parameters. The CG method is used for tuning of the parameters, which requires the gradient of the required parameters to be evaluated. The backpropagation method is used to find out the gradient vectors of the required parameters. The gradient vectors are the derivatives of MSE with respect to the required updated parameters. A general form of the gradient of MSE with respect to the antecedent membership function mean is defined by the chain rule as:

$$\begin{aligned} \frac{\partial E}{\partial \nu _{ij}} = \frac{\partial E}{\partial u} . \frac{\partial u}{\partial \mu _i} . \frac{\partial \mu _i}{\partial \nu _{ij}} \end{aligned}$$
(19)

A general form of the gradient of MSE with respect to the antecedent membership function variance is

$$\begin{aligned} \frac{\partial E}{\partial \varsigma _{ij}} = \frac{\partial E}{\partial u} . \frac{\partial u}{\partial \mu _i} . \frac{\partial \mu _i}{\partial \varsigma _{ij}} \end{aligned}$$
(20)

Gradient of MSE with respect to the consequent parameters is

$$\begin{aligned} \frac{\partial E}{\partial b_{i0}} =&\frac{\partial E}{\partial u}.\frac{\partial u}{\partial c_i}.\frac{\partial c_i}{\partial b_{i0}} \end{aligned}$$
(21)
$$\begin{aligned} \frac{\partial E}{\partial b_{ij}} =&\frac{\partial E}{\partial u}.\frac{\partial u}{\partial c_i}.\frac{\partial c_i}{\partial b_{ij}} \end{aligned}$$
(22)

Gradient of MSE with respect to \(\omega \) is

$$\begin{aligned} \frac{\partial E}{\partial \omega }=\frac{\partial E}{\partial u}.\frac{\partial u}{\partial \omega } \end{aligned}$$
(23)

where \(\frac{\partial E}{\partial u} = e\), \(\frac{\partial u}{\partial c_i} = \frac{\mu _i}{T\{\mu _i\}} \), \(\frac{\partial u}{\partial \mu _i} = \frac{c_i - \left( 1- \prod \limits _{i = 1}^r \frac{\mu _i}{\mu _i} \right) u}{T_i\{\mu _i\}} \), \(\frac{\partial c_i}{\partial b_{i0}} = 1\), \(\frac{\partial u}{\partial \omega }=(\bar{u}-\underline{u}) \), \(\frac{\partial c_i}{\partial b_{ij}} = x_j\), and specific upper and lower membership functions mean and variance are defined as:

$$\begin{aligned}&\frac{\partial \bar{\mu }}{\partial \nu _{ij1}}=\frac{\partial \bar{\mu }}{\partial \bar{\eta }_{ij}({{x}_{j}})} \frac{\partial \bar{\eta }_{ij}({{x}_{j}})}{\partial \nu _{ij1}} \end{aligned}$$
(24)
$$\begin{aligned}&\quad =\left\{ \begin{array}{ll} \left[ \bar{\eta }_{ij}({x}_{j})-\cos \left( \frac{x_j-\nu _{ij1}}{\varsigma _{ij}}\right) \right] \frac{1}{x_j-\nu _{ij1}},&{}\quad {{x}_{j}}\le {\nu _{ij1}}\\ 0, &{}\quad \mathrm{otherwise} \end{array}\right. \end{aligned}$$
(25)
$$\begin{aligned}&\frac{\partial \bar{\mu }}{\partial \nu _{ij2}}=\frac{\partial \bar{\mu }}{\partial \bar{\eta }_{ij}({{x}_{j}})} \frac{\partial \bar{\eta }_{ij}({{x}_{j}})}{\partial \nu _{ij2}} \end{aligned}$$
(26)
$$\begin{aligned}&\quad =\left\{ \begin{array}{ll} \left[ \bar{\eta }_{ij}({x}_{j})-\cos \left( \frac{x_j-\nu _{ij2}}{\varsigma _{ij}}\right) \right] \frac{1}{x_j-\nu _{ij2}}, &{} {{x}_{j}}>{\nu _{ij2}} \\ 0, &{} \mathrm{otherwise} \end{array}\right. \end{aligned}$$
(27)
$$\begin{aligned}&\frac{\partial \underline{\mu }}{\partial \nu _{ij1}}=\frac{\partial \underline{\mu }}{\partial \underline{\eta }_{ij}({{x}_{j}})} \frac{\partial \underline{\eta }_{ij}({{x}_{j}})}{\partial \nu _{ij1}} \end{aligned}$$
(28)
$$\begin{aligned}&\quad =\left\{ \begin{array}{ll} \left[ \underline{\eta }_{ij}({x}_{j})-\cos \left( \frac{x_j-\nu _{ij1}}{\varsigma _{ij}}\right) \right] \frac{1}{x_j-\nu _{ij1}},&{} {{x}_{j}}>\dfrac{{\nu _{ij1}} + {\nu _{ij2}}}{2} \\ 0,&{} \mathrm{otherwise} \end{array}\right. \end{aligned}$$
(29)
$$\begin{aligned}&\frac{\partial \underline{\mu }}{\partial \nu _{ij2}}=\frac{\partial \underline{\mu }}{\partial \underline{\eta }_{ij}({{x}_{j}})} \frac{\partial \underline{\eta }_{ij}({{x}_{j}})}{\partial \nu _{ij2}} \end{aligned}$$
(30)
$$\begin{aligned}&\quad =\left\{ \begin{array}{ll} \left[ \underline{\eta }_{ij}({x}_{j})-\cos \left( \frac{x_j-\nu _{ij2}}{\varsigma _{ij}}\right) \right] \frac{1}{x_j-\nu _{ij2}},\,&{}{{x}_{j}}\le \dfrac{{\nu _{ij1}} + {\nu _{ij2}}}{2} \\ 0,\, &{} \mathrm{otherwise} \end{array}\right. \end{aligned}$$
(31)
$$\begin{aligned}&\frac{\partial {\bar{\mu } }}{\partial {{\varsigma }_{ij}}}=\frac{\partial {\bar{\mu } }}{\partial {{{{\bar{\eta } }}}_{ij}}({{x}_{j}})}\frac{\partial {{{{\bar{\eta } }}}_{ij}}({{x}_{j}})}{\partial {{\varsigma }_{ij}}} \end{aligned}$$
(32)
$$\begin{aligned}&\quad =\left\{ \begin{array}{ll} \frac{1}{{{\varsigma }_{ij}}}\left[ {{\bar{\eta } }_{ij}}({x}_{j})-\cos \left( \frac{{{x}_{j}}-{\nu _{ij1}}}{{{\varsigma }_{ij}}}\right) \right] ,\;\;\; &{}{{x}_{j}}\le {\nu _{ij1}} \\ \frac{1}{{{\varsigma }_{ij}}}\left[ {{\bar{\eta } }_{ij}}({x}_{j})-\cos \left( \frac{{{x}_{j}}-{\nu _{ij2}}}{{{\varsigma }_{ij}}}\right) \right] ,\;\;\; &{}{{x}_{j}}>{\nu _{ij2}} \\ 0,\;\;\; &{} \mathrm{otherwise} \end{array} \right. \end{aligned}$$
(33)
$$\begin{aligned}&\frac{\partial {\underline{\mu } }}{\partial {{\varsigma }_{ij}}}=\frac{\partial {\underline{\mu } }}{\partial {{{{\underline{\eta } }}}_{ij}}({{x}_{j}})}\frac{\partial {{{{\underline{\eta } }}}_{ij}}({{x}_{j}})}{\partial {{\varsigma }_{ij}}} \end{aligned}$$
(34)
$$\begin{aligned}&\quad =\left\{ \begin{array}{ll} \frac{1}{{{\varsigma }_{ij}}}\left[ {{\underline{\eta } }_{ij}}({x}_{j})-\cos \left( \frac{{{x}_{j}}-{\nu _{ij2}}}{{{\varsigma }_{ij}}}\right) \right] ,\;\;\; &{}{{x}_{j}}\le \frac{{\nu _{ij1}}+{\nu _{ij2}}}{2} \\ \frac{1}{{{\varsigma }_{ij}}}\left[ {{\underline{\eta } }_{ij}}({x}_{j})-\cos \left( \frac{{{x}_{j}}-{\nu _{ij1}}}{{{\varsigma }_{ij}}}\right) \right] ,\;\;\; &{}{{x}_{j}}>\frac{{\nu _{ij1}}+{\nu _{ij2}}}{2} \end{array} \right. \end{aligned}$$
(35)

Dong, Liu, Xu and Yang CG algorithm, which is named as DHS [47], is the upgraded version of Hestenes–Stiefel (HS) [48] algorithm. This CG algorithm has the form,

$$\begin{aligned} \xi _{ij}(\kappa +1)=\xi _{ij}(\kappa )+\alpha (k){{\varphi }(\kappa )} \end{aligned}$$
(36)

where \(\xi _{ij}\) is any required parameter that is needed to be updated and \( \alpha \) is the learning rate. The search direction for the algorithm is

$$\begin{aligned} {{\varphi }(\kappa )}=\Biggl \{ \begin{matrix} -{\psi (\kappa )}\, \, \, \, \, \,&{} \mathrm{condition} \, 1 \\ -{\psi (\kappa )}+\beta (\kappa ){{\varphi }(\kappa -1)} \, \, \, \, \, \,&{} \mathrm{condition} \, 2, \end{matrix} \end{aligned}$$
(37)

whereas

\(\mathrm{condition} \, 1 = \left| \psi (\kappa )^{T}\lambda (\kappa -1) \right| \left\| {{\varphi }(\kappa -1)} \right\| \ge \tau \left\| {\psi (\kappa )} \right\| \),

\(\mathrm{condition} \, 2 = \left| \psi (\kappa )^{T}\lambda (\kappa -1) \right| \left\| {{\varphi }(\kappa -1)} \right\| < \tau \left\| {\psi (\kappa )} \right\| \), and

$$\begin{aligned} \beta (\kappa )=&\max \Bigg \{ 0,\,\frac{\psi (\kappa )^{T}\lambda (\kappa -1)}{\varphi (\kappa -1)^{T}\lambda (\kappa -1)} \nonumber \\&- \iota \frac{\psi (\kappa )^{T}{{\varphi }(\kappa -1)}}{{{\left\| {\psi (\kappa )} \right\| }^{2}}}{{\left( \frac{\psi (\kappa )^{T}\lambda (\kappa -1)}{\varphi (\kappa -1)^{T}\lambda (\kappa -1)} \right) }^{2}} \Bigg \} \end{aligned}$$
(38)

where \(\psi (\kappa )=\frac{\partial E}{\partial \xi _{ij}(\kappa )}\) is the gradient vector, \(\lambda (\kappa -1)=(\psi (\kappa )-\psi (\kappa -1))\) and \(\iota \) and \( \tau \) are the constants.

3.1.1 Algorithm of the Proposed Control Scheme

As mentioned earlier, the main objective of the control scheme is to control the angular positions of the TLFM links and to regulate the deflections associated with them. The control scheme achieves this by generating the desired control action with its self-tuning algorithm. The control scheme and the TLFM are connected in a closed loop system. Direct control model is used, so the control law is based on producing the control output (17) and sending it directly to the TLFM (9). The operating procedure of the closed loop system is mentioned below.

Step 1 In the forward pass of the ANFC, all the parameters are initially defined arbitrarily and the output (17) of the ANFC is calculated.

Step 2 The error between the desired and actual output of the TLFM is measured, which is then propagated back to the earlier layers of the ANFC.

Step 3 Based on the error, the suitable control action is generated by optimizing the parameters in the antecedent and consequent layers. The update equations for each parameter (19)–(35) minimizes the cost function (18).

Step 4 The algorithm updates the search direction by calculating \( \varphi (\kappa ) \) (37) and \(\beta (\kappa ) \) (38) so that \( \left\| {{\psi (\kappa )}} \right\| \le \bar{\varepsilon } \), where \( \bar{\varepsilon } \in \left( {0,1} \right) \).

Step 5 The control scheme proceeds to the next iteration, and the process repeats from step 2 until the solution converges.

3.1.2 Assumptions

This section presents the general assumptions that are often considered for the CG method convergence analysis [49]. The set \(\varDelta = \left\{ {\left. {z \in {R^n}} \right| E(z) \le E({z_0})} \right\} \) is bounded, where \( z_0 \) is a given point. In some region \( \varDelta _o \) of \( \varDelta \), E function is continuously differentiable, and its gradient \( \psi \) is Lipschitz continuous. Moreover, a constant \( \bar{s}>0 \) exists, so that

$$\begin{aligned} \left\| {\psi (z_1) - \psi (z_2)} \right\| \le \bar{s}\left\| {z_1 - z_2} \right\| ,\;\forall \;z_1,z_2 \in {\varDelta _o} \end{aligned}$$
(39)

3.1.3 Sufficient Descent Condition

Theorem 1

Consider the CG method (36) and (37) with the parameter \( \beta _{k} \) defined by (38). Then,

$$\begin{aligned} \varphi (\kappa )^T{\psi (\kappa )} \le - \left( {1 - \frac{1}{{4\iota }}} \right) {\left\| {{\psi (\kappa )}} \right\| ^2} \end{aligned}$$
(40)

The algorithm should satisfy the necessary descent condition, which is \( \varphi (\kappa )^T{\psi (\kappa )} \le - \bar{c} {\left\| {{\psi (\kappa )}} \right\| ^2} \), where \( \bar{c}>0 \) [50, 51]. This theorem shows that the proposed algorithm satisfies this condition.

Proof

For all \( \kappa > 1 \), the following two cases are considered from (37),

Case (i):

If \( \frac{\psi (\kappa )^{T}\lambda (\kappa -1)}{\varphi (\kappa -1)^{T}\lambda (\kappa -1)} \le {\iota \frac{{\psi (\kappa )^T{\varphi (\kappa -1)}}}{{{{\left\| {{\psi (\kappa )}} \right\| }^2}}}{{\left( {\frac{{\psi (\kappa )^T{\lambda (\kappa -1)}}}{{\varphi (\kappa -1)^T{\lambda (\kappa -1)}}}} \right) }^2}} \), then \(\beta (\kappa )=0\) (38), and therefore, \( \varphi (\kappa )^T{\psi (\kappa )}=- {\left\| {{\psi (\kappa )}} \right\| ^2} \).

Case (ii):

If \( \frac{\psi (\kappa )^{T}\lambda (\kappa -1)}{\varphi (\kappa -1)^{T}\lambda (\kappa -1)} > {\iota \frac{{\psi (\kappa )^T{\varphi (\kappa -1)}}}{{{{\left\| {{\psi (\kappa )}} \right\| }^2}}}{{\left( {\frac{{\psi (\kappa )^T{\lambda (\kappa -1)}}}{{\varphi (\kappa -1)^T{\lambda (\kappa -1)}}}} \right) }^2}} \), then using this condition, multiplying (37) by \( \psi (\kappa )^T \) and using (38) gives

(41)
(42)
(43)

The inequality is used with and \( \hbar = \sqrt{\iota }\frac{{\left( {\psi (\kappa )^T{\varphi (\kappa -1)}} \right) }}{{\left\| {{\psi (\kappa )}} \right\| }}\left( {\frac{{\psi (\kappa )^T{\lambda (\kappa -1)}}}{{\varphi (\kappa -1)^T{\lambda (\kappa -1)}}}} \right) \), where \( \iota >\dfrac{1}{4} \). This completes the proof. \(\square \)

3.1.4 Global Convergence

In this section, the Zoutendijk condition [52], which is often used to prove the global convergence [53,54,55], is used to prove the global convergence of the proposed scheme.

Theorem 2

Let \( {\xi (\kappa )} \) and \( {\varphi (\kappa )} \) are generated by algorithm 3.1.1. If \( \left\| {{\psi (\kappa )}} \right\| \ge \varepsilon \), where \( \varepsilon > 0 \) is a constant, then there exists a constant \( \bar{o}>0 \) such that

$$\begin{aligned} \left\| {{\varphi (\kappa )}} \right\| \le \bar{o}\left\| {{\psi (\kappa )}} \right\| \quad \forall \;\kappa \in N \end{aligned}$$
(44)

Proof

From (37), the following two cases are considered to prove the theorem.

Case (i):

If \( \left| {\psi (\kappa )^T{\lambda (\kappa -1)}} \right| \left\| {{\varphi (\kappa -1)}} \right\| \ge \tau \left\| {{\psi (\kappa )}} \right\| \), then \( \left\| {{\varphi _{\kappa }}} \right\| = \left\| {{\psi _{\kappa }}} \right\| \) holds.

Case (ii):

If \(| {\psi (\kappa )^T{\lambda (\kappa -1)}}|\Vert {{\varphi (\kappa -1)}}\Vert < \tau \Vert {{\psi (\kappa )}}\Vert \), then using this condition, \( \beta (\kappa )\) (38) and the Cauchy–Schwarz inequality gives

$$\begin{aligned} \left| \beta (\kappa )\right|&\le \bar{\beta }(\kappa ) \end{aligned}$$
(45)
$$\begin{aligned}&\le \frac{{\left\| {{\psi (\kappa )}} \right\| }}{{\left\| {{\varphi (\kappa -1)}} \right\| }}\left[ {1 + \iota } \right] \end{aligned}$$
(46)

Using (37) and (46) gives

$$\begin{aligned} \left\| {{\varphi (\kappa )}} \right\|&\le \left\| {{\psi (\kappa )}} \right\| + \left| \beta (\kappa )\right| \left\| {{\varphi (\kappa -1)}} \right\| \end{aligned}$$
(47)
$$\begin{aligned}&\le \left\| {{\psi (\kappa )}} \right\| \left[ {2 + \iota } \right] \end{aligned}$$
(48)

Letting \( \bar{o}=2 + \iota \), the proof is completed. \(\square \)

Theorem 3

Let \( \{ \xi (\kappa )\} \) be generated by algorithm 3.1.1. Then, \( \psi (\kappa )=0 \) for some \( \kappa \) or

$$\begin{aligned} \mathop {\lim }\limits _{\kappa \rightarrow \infty } \inf \left\| {{\psi (\kappa )}} \right\| = 0 \end{aligned}$$
(49)

This theorem shows the convergence result of the proposed method.

Proof

The Zoutendijk condition defined by (50) is used to prove the theorem.

$$\begin{aligned} \sum \limits _{\kappa \ge 1} {\frac{{{{\left( {\psi (\kappa )^T{\varphi (\kappa )}} \right) }^2}}}{{{{\left\| {{\varphi (\kappa )}} \right\| }^2}}}} < \infty \end{aligned}$$
(50)

Suppose if (49) does not hold, then there exists a constant \( \varepsilon > 0\), so that

$$\begin{aligned} \left\| {{\psi (\kappa )}} \right\| \ge \varepsilon ,\forall \; \kappa \in N \end{aligned}$$
(51)

Using the inequalities from (40), (44) and (50) gives (52),

$$\begin{aligned} {\sum \limits _{\kappa \ge 1} {\left( \bar{o} \right) } ^{ - 2}}{\left\| {{\psi (\kappa )}} \right\| ^2}\le \sum \limits _{\kappa \ge 1} {\frac{{{{\left\| {{\psi (\kappa )}} \right\| }^4}}}{{{{\left\| {{\varphi (\kappa )}} \right\| }^2}}}}\nonumber \\<{\bar{h}^{ - 2}}\sum \limits _{\kappa \ge 1}{\frac{{{{\left( {\psi (\kappa )^T{\varphi (\kappa )}} \right) }^2}}}{{{{\left\| {{\varphi (\kappa )}} \right\| }^2}}}}< \infty \end{aligned}$$
(52)

where \( \bar{h}= \left( {1 - \frac{1}{{4 \iota }}} \right) \). Taken into account the assumptions in Sect. 3.1.2, (52) states that \(\mathop {\lim }\limits _{\kappa \rightarrow \infty } \left\| {{\psi (\kappa )}} \right\| = 0\), which contradicts (51), and therefore proves the theorem. \(\square \)

Fig. 3
figure 3

Block diagram of adaptive control schemes with RSFA

Full size image

4 Simulation Results

The block diagram of a TLFM incorporated with the ANFC scheme is shown in Fig. 3. The ANFC scheme has two inputs (error and derivative of error) and one output (u). Actuators are situated at the base of both links. The goal of both actuators is to perform the desired angular maneuvering of the flexible links. The intelligent scheme is not dependent on concise system modeling. It has a self-tuning mechanism, which performs suitable control actions based on the error between the desired and actual output. In this research, two AMM modes are considered for each TLFM link. Therefore, coordinates are \(q={{\left( {{\theta }_{1}}\ {{\theta }_{2}}\ {{\delta }_{11}}\ {{\delta }_{12}}\ {{\delta }_{21}}\ {{\delta }_{22}} \right) }^{\mathrm{T}}}\); these are link joint angle positions (1st and 2nd link, respectively) and modal displacements (1st link 1st mode, 1st link 2nd mode, 2nd link 1st mode and 2nd link 2nd mode, respectively). TLFM system parameters are given in [35]. For the TLFM with normal payload (\(m_p=0.1\) kg), the roots of frequency equation (7) are \(\beta _{11}=1.16\), \(\beta _{12}=2.24\), \(\beta _{21}=2.47\) and \(\beta _{22}=6.687\). Orthonormalization is performed by choosing values of \({{C}_{1,ij}}\) and \({{C}_{2,ij}}\) that normalizes the mode shape functions, so that \( \int \limits _{0}^{{{l}_{i}}}{\phi _{ij}^{2}\left( {{\chi }_{i}} \right) }d{{\chi }_{i}}={{m}_{i}}\), where \( {{m}_{i}} \) is the ith link mass. The mode shapes (3) evaluated for the TLFM with normal payload are \(\phi _{11}=0.143\), \(\phi _{11}^{'}=0.507\), \(\phi _{12}=0.092\), \(\phi _{12}^{'}=-0.233\), \(\phi _{21}=0.137\), \(\phi _{21}^{'}=0.410\), \(\phi _{22}=-0.007\) and \(\phi _{22}^{'}=-1.135\).

Fig. 4
figure 4

Case 1: Link positions and deflections for normal payload

Full size image
Fig. 5
figure 5

Case 2: Link positions and deflections for normal payload

Full size image
Fig. 6
figure 6

Case 1: Link positions and deflections for no payload

Full size image
Fig. 7
figure 7

Case 2: Links positions and deflections for no payload

Full size image

The performance of the proposed ANFC scheme (referred to as modified TSK type-2 ANFC scheme (MTSK 2) from hereafter) is compared with adaptive proportional integral derivative (APID) control scheme [56] and TSK type-1 ANFC scheme [46] (referred to as TSK 1 from hereafter). This comparison will provide a good analysis of strengths and weaknesses of the proposed scheme and other intelligent control schemes. MTSK 2 parameter \(\tau \) is defined to be \(10^{6}\).

The desired trajectory of 30 sec is described mathematically by (53). Simulations are carried out for the following two cases: In the first case, the two links are desired to follow opposite angular positions of equal magnitude, while in the second case, desired angular positions for the two links are identical. This can be achieved for the case 1 trajectory by assigning \(D=30\) for the 1st link and \(D=-30\) for the 2nd link; while for the case 2 trajectory by assigning \(D=30\) for the 1st and the 2nd link simultaneously.

$$\begin{aligned} {\theta _{\mathrm{ref}}}(\kappa )=\left\{ \begin{matrix} -D \quad \ \ \ \ \quad \quad \quad &{}\kappa \,<\,10 \\ D \,\sin \left( \frac{\pi \kappa }{2} \right) \quad \ \ \ \ &{}10\le \kappa < 20 \\ D \quad \ \ \ \ \quad \quad \quad \quad &{}20\le \kappa \le 30 \\ \end{matrix} \right. \end{aligned}$$
(53)

Figures 4 and 5 show the results of TLFM with control schemes for case 1 and case 2, respectively. For the reader’s convenience, in the following results \((\circ )_{\mathrm{APID}-1}\), \((\circ )_{\mathrm{TSK1}-1}\) and \((\circ )_{\mathrm{MTSK2}-1}\) are the plots for 1st link of TLFM with APID, TSK 1 and MTSK 2 control schemes, respectively. Furthermore, \((\circ )_{\mathrm{APID}-2}\), \((\circ )_{\mathrm{TSK1}-2}\) and \((\circ )_{\mathrm{MTSK2}-2}\) are the plots for 2nd link of TLFM with APID, TSK 1 and MTSK 2 control schemes, respectively. Figure 4a, b shows the position in degrees of 1st and 2nd link of TLFM for case 1. ANFC schemes have faster convergence compared to APID control scheme. APID control scheme is struggling to maintain the desired position, while TSK 1 and MTSK 2 control schemes have settled quickly and more efficiently. MTSK 2 has shown better transient and steady-state response than all other control schemes. Figure 4c, d shows the deflections in both links of TLFM for case 1, as expressed by (2). Despite the abrupt changes in the desired trajectory and the fast convergence of the MTSK 2, the deflections are observed to be well managed by the proposed scheme.

Figure 5a, b shows the positions in degrees of 1st and 2nd link of the TLFM for case 2. In this case, the desired trajectory is the same for both links. ANFC schemes have faster convergence compared to APID control scheme. Furthermore, Fig. 5c, d shows the deflections in both links of TLFM for case 2. Again, MTSK 2 has better convergence than all other control schemes. Angular positions of links are quickly reaching theirs targets and deflections are quite well managed by MTSK 2.

Fig. 8
figure 8

Case 1: Link positions and deflections for double payload

Full size image
Fig. 9
figure 9

Case 2: Link positions and deflections for double payload

Full size image

In order to observe the robustness of the proposed control scheme with a comparative view, the same simulation tests should be carried out in the presence of uncertainty. For this purpose, TLFM payloads are varied, but the control schemes parameters are unchanged. Ideally, since the control schemes are adaptive, they should perform better, even after the change in the TLFM parameters. In order to achieve this goal, TLFM with no payload (\(m_p=0\) kg) and double payload (\(m_p=0.2\) kg) is considered. Changing payload affects the mode frequencies (7) of the structure, so derivations and calculations are carried out again to find out the new values of the TLFM system. The roots for the TLFM with no payload are: \(\beta _{11}=1.206\), \(\beta _{12}=2.325\), \(\beta _{21}=3.6\) and \(\beta _{22}=6.72\). With these values, the mode shapes are: \(\phi _{11}=0.143\), \(\phi _{11}^{'}=0.501\), \(\phi _{12}=0.089\), \(\phi _{12}^{'}=-0.267\), \(\phi _{21}=0.136\), \(\phi _{21}^{'}=0.402\), \(\phi _{22}=-0.039\) and \(\phi _{22}^{'}=-1.441\). Likewise, for the TLFM with double payload, the roots of frequency equation of TLFM are: \(\beta _{11}=1.123\), \(\beta _{12}=2.183\), \(\beta _{21}=2.142\) and \(\beta _{22}=6.68\). Other parameters for the TLFM are: \(\phi _{11}=0.144\), \(\phi _{11}^{'}=0.512\), \(\phi _{12}=0.093\), \(\phi _{12}^{'}=-0.220\), \(\phi _{21}=0.137\), \(\phi _{21}^{'}=0.410\), \(\phi _{22}=-0.004\) and \(\phi _{22}^{'}=-1.103\).

Fig. 10
figure 10

Case 1: Position tracking IAE performance indices of TLFM

Full size image
Fig. 11
figure 11

Case 2: Position tracking IAE performance indices of TLFM

Full size image

Figure 6a, b shows the positions in degrees of 1st and 2nd link of the TLFM for case 1, whereas Fig. 6c, d shows the deflections in both links of the TLFM for case 1. MTSK 2 has faster angular position tracking for both links. 2nd link deflections of MTSK 2 are slightly higher than others, but the magnitude of deflections is quite low. Figure 7a, b shows the positions in degrees of 1st and 2nd links of the TLFM for case 2, whereas Fig. 7c, d shows the link deflections of 1st and 2nd links of the TLFM for case 2. Again, position tracking of the MTSK 2 is superior than others.

Figure 8a, b shows the positions of 1st and 2nd links of the TLFM for case 1, whereas Fig. 9a, b shows the positions of 1st and 2nd links of the TLFM for case 2. For both cases, MTSK 2 has better convergence than all other control schemes. Angular positions of links are quickly reached, and the deflections for both cases are well managed by both links of the TLFM, as shown in Figs. 8c, d, 9c, d.

For a more extensive and detailed analysis, IAE performance index [57] is used to analyze the performances of all the control schemes. Figure 10 shows the IAE performance indices for case 1 profile trajectories. For any payload conditions, the MTSK 2 has better performance compared to all other control schemes. Compared to an APID control scheme, the TSK 1 scheme has on average \(50 \%\) and \(70 \%\) better performance for 1st and 2nd link, respectively, whereas MTSK 2 scheme has on average \(80 \%\) better performance for both links. Figure 11 shows the IAE performance indices for case 2 profile trajectories. Again, the MTSK 2 scheme is better than APID and TSK 1 control schemes. Compared to an APID control scheme, the TSK 1 scheme has on average \(50 \%\) better performance for both links, respectively, whereas MTSK 2 scheme has on average \(80 \%\) better performance for both links. The results show that the MTSK 2 scheme is more consistent with its performance. Overall, all these results show that the MTSK 2 control scheme is the ideal choice for the angular positional tracking of both TLFM links while keeping the fluctuations of links in control also.

5 Conclusion

In this paper, a type-2 TSK ANFC scheme, designated as MTSK 2, has been proposed. The scheme is using a DHS-based CG algorithm instead of the traditional SD algorithm for optimizing the control parameters; moreover, it is using T-norms rather than conventional product–sum combination at the NFS defuzzification phase. The proposed control scheme is integrated with a TLFM, so to control the flexible links and to regulate the vibrations associated with them. Position control of the flexible mechanical system is a complex control problem since it is a nonlinear coupled system with infinite dimensions. The dynamics of the system is defined by a hybrid coordinate system comprising ordinary, partial and integral differential equations. AMM converts the infinite-dimensional model to finite-dimensional model, but the truncated model of the system has arbitrary dimensions and uncertainties. The proposed control scheme has a self-tuning mechanism that has handled the problem efficiently and delivered an exceptional performance. The control scheme has effectively tracked the position and regulated the vibrations of the flexible nonlinear system. For further extensive robustness analysis, varying payloads of the TLFM are considered. APID control and type-1 TSK ANFC schemes are also incorporated with the TLFM, so as to provide a comparison with the proposed control scheme. The results demonstrate that the MTSK 2 scheme has achieved better performance than the TSK 1 and APID control schemes in terms of regulation and tracking. MTSK 2 has a better convergence rate and is robust in all cases. As a result of this study, it has been affirmed that DHS CG-based type-2 TSK ANFC scheme is more efficient than other intelligent control schemes for position control of highly nonlinear flexible systems, which require simultaneous suppression of vibrations.