Abstract
A theorem of Esnault, Srinivas and Viehweg asserts that if the Chow group of 0-cycles of a smooth complete complex variety decomposes, then the top-degree coherent cohomology group decomposes similarly. In this note, we prove that (a weak version of) the converse holds for varieties of dimension at most 5 that have finite-dimensional motive and satisfy the Lefschetz standard conjecture. The proof is based on Vial’s construction of a refined Chow–Künneth decomposition for these varieties.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let X be a smooth complete variety of dimension n defined over \(\mathbb {C}\). In the 1992 paper, Esnault et al. (1993) study the multiplicative behaviour of the Chow ring \(A^*X\) versus the multiplicative behaviour of the cohomology of X. We now state the part of their result that is relevant to us. For a given partition \(n=n_1+\cdots +n_r\) (with \(n_i\in \mathbb {N}_{>0}\)), let us consider the following properties:
-
(P1)
There exists a Zariski open \(V\subset X\), such that intersection product induces a surjection
$$\begin{aligned} A^{n_1}V_{\mathbb {Q}}\otimes A^{n_2}V_{\mathbb {Q}}\otimes \cdots \otimes A^{n_r}V_{\mathbb {Q}}\ \rightarrow \ A^nV_{\mathbb {Q}}\ ; \end{aligned}$$ -
(P2)
There exists a Zariski open \(V\subset X\), such that cup product induces a surjection
$$\begin{aligned} H^{n_1}(V,\mathbb {Q})\otimes H^{n_2}(V,\mathbb {Q})\otimes \cdots \otimes H^{n_r}(V,\mathbb {Q})\ \rightarrow \ H^n(V,\mathbb {Q})/N^1\ \end{aligned}$$(here \(N^*\) denotes the coniveau filtration);
-
(P3)
Cup product induces a surjection
$$\begin{aligned} H^{n_1}(X,\mathcal O_X)\otimes H^{n_2}(X,\mathcal O_X)\otimes \cdots \otimes H^{n_r}(X,\mathcal O_X)\ \rightarrow \ H^n(X,\mathcal O_X)\ . \end{aligned}$$
In these terms, what Esnault, Srinivas and Viehweg prove is the following:
Theorem
(Esnault et al. 1993) Let X be a smooth complete variety of dimension n over \(\mathbb {C}\). Then (P1) implies (P3), and (P2) implies (P3).
The implication from (P1) to (P3) is a kind of Mumford theorem (Mumford 1969), and the proof in Esnault et al. (1993) is motivated by Bloch’s proof (Bloch 1979, 1980) of Mumford’s theorem using a “decomposition of the diagonal” argument. As noted in (Esnault et al. 1993, remark 2), the generalized Hodge conjecture would imply that (P2) and (P3) are equivalent.Footnote 1
It seems natural to conjecture the converse implication [this is discussed in (Esnault et al. 1993, remark 3)]:
Conjecture
Let X be a smooth complete variety. Then (P2) implies (P1).
This can be considered a multiplicative version of Bloch’s conjecture; indeed for surfaces of geometric genus 0 this conjecture is equivalent to Bloch’s conjecture [Esnault et al. (1993), remark 3].
The object of this note is to show this conjecture can be proven in some special cases:
Theorem
Let X be a smooth projective variety of dimension \(n\le 3\), rationally dominated by curves. Then (P2) implies (P1).
This follows from a more general statement (Theorem 3). Actually, our argument works for varieties X of dimension up to 5 that satisfy the Lefschetz standard conjecture and have finite-dimensional motive in the sense of Kimura (2005), provided we replace (P2) by a variant involving Vial’s niveau filtration \(\widetilde{N}^*\) (Vial 2013) instead of \(N^*\).
This result is hardly surprising: since the appearance of Kimura’s landmark paper (Kimura 2005), where it is shown that finite-dimensionality implies the Bloch conjecture for surfaces, there have been a great many results attesting to the usefulness of finite-dimensionality (Jannsen 2007; André 2004; Ivorra 2011; Kahn 2003; Kahn et al. 2007; Guletskiĭ and Pedrini 2002, 2003; Vial 2013; Yin 2015; Laterveer 2015). The present note is but one more instance of this general principle, illustrating how nicely finite-dimensionality allows to bridge the abyss separating homological equivalence from rational equivalence.
Convection
In this note, the word variety will refer to an irreducible reduced scheme of finite type over \(\mathbb {C}\), endowed with the Zariski topology. A subvariety is a (possibly reducible) reduced subscheme which is equidimensional. The Chow group of j-dimensional algebraic cycles on X with \(\mathbb {Q}\)-coefficients modulo rational equivalence is denoted \(A_jX\); for X smooth of dimension n the notations \(A_jX\) and \(A^{n-j}X\) will be used interchangeably. Caveat: note that what we denote \(A^jX\) is elsewhere often denoted \(CH^j(X)_{\mathbb {Q}}\). The Griffiths group \(\hbox {Griff}^j\) is the group of codimension j cycles that are homologically trivial modulo algebraic equivalence, again with \(\mathbb {Q}\)-coefficients. In an effort to lighten notation, we will often write \(H^jX\) or \(H_jX\) to indicate singular cohomology \(H^j(X,\mathbb {Q})\) resp. Borel–Moore homology \(H_j(X,\mathbb {Q})\).
2 Preliminaries
Let X be a smooth projective variety of dimension n, and \(h\in H^2(X,\mathbb {Q})\) the class of an ample line bundle. The hard Lefschetz theorem asserts that the map
obtained by cupping with \(h^{n-i}\) is an isomorphism, for any \(i< n\). One of the standard conjectures asserts that the inverse isomorphism is algebraic.
Definition 1
(Lefschetz standard conjecture) Given a variety X, we say that B(X) holds if for all ample h, and all \(i<n\) the isomorphism
is induced by a correspondence.
Remark 1
It is known that B(X) holds for the following varieties: curves, surfaces, abelian varieties (Kleiman 1968, 1994), threefolds not of general type (Tankeev 2011), n-dimensional varieties X which have \(A_i(X)_{}\) supported on a subvariety of dimension \(i+2\) for all \(i\le {n-3\over 2}\) [Vial 2013, Theorem 7.1], n-dimensional varieties X which have \(H_i(X)=N^{\llcorner {i\over 2}\lrcorner }H_i(X)\) for all \(i>n\) [Vial 2013, Theorem 4.2], products and hyperplane sections of any of these.
Definition 2
(Coniveau filtration Bloch and Ogus 1974) Let X be a quasi-projective variety. The coniveau filtration on cohomology and on homology is defined as
where Y runs over codimension \(\ge c\) subvarieties of X, and Z over dimension \(\le i-c\) subvarieties.
Vial introduced the following variant of the coniveau filtration:
Definition 3
(Niveau filtration Vial 2013) Let X be a smooth projective variety. The niveau filtration on homology is defined as
where the union runs over all smooth projective varieties Z of dimension \(i-2j\), and all correspondences \(\Gamma \in A_{i-j}(Z\times X)_{}\). The niveau filtration on cohomology is defined as
Remark 2
The niveau filtration is included in the coniveau filtration:
These two filtrations are expected to coincide; indeed, Vial shows this is true if and only if the Lefschetz standard conjecture is true for all varieties [Vial 2013, Proposition 1.1].
The main ingredient we will use in this note is Kimura’s nilpotence theorem:
Theorem 1
(Kimura 2005) Let X be a smooth projective variety of dimension n with finite-dimensional motive. Let \(\Gamma \in A^n(X\times X)_{}\) be a correspondence which is numerically trivial. Then there is \(N\in \mathbb {N}\) such that
We refer to Kimura (2005), André (2004), Ivorra (2011), Murre et al. (2013) for the definition of finite-dimensional motive. Conjecturally, any variety has finite-dimensional motive Kimura (2005). What mainly concerns us in the scope of this note, is that there are quite a few non-trivial examples, giving rise to interesting applications:
Remark 3
The following varieties have finite-dimensional motive: abelian varieties, varieties dominated by products of curves (Kimura 2005), K3 surfaces with Picard number 19 or 20 (Pedrini 2012), surfaces not of general type with vanishing geometric genus [Guletskiĭ and Pedrini 2002, Theorem 2.11], Godeaux surfaces (Guletskiĭ and Pedrini 2002), threefolds and 4folds with nef tangent bundle (Iyer 2008), [Vial 2011, Example 3.16], (Iyer 2011), certain threefolds of general type [Vial 2015, Section 8], varieties of dimension \(\le 3\) rationally dominated by products of curves [Vial 2011, Example 3.15], varieties X with \(A^i_{AJ}X_{\mathbb {Q}}=0\) for all i [Vial 2013, Theorem 4], products of varieties with finite-dimensional motive (Kimura 2005).
Remark 4
It is worth pointing out that up till now, all examples of finite-dimensional motives happen to be in the tensor subcategory generated by Chow motives of curves. On the other hand, “many” motives are known to lie outside this subcategory, e.g. the motive of a general hypersurface in \(\mathbb {P}^3\) [Ayoub 2016, Remark 2.34] (here “general” means “outside a countable union of Zariski-closed proper subsets”).
There exists another nilpotence result, which predates and prefigures Kimura’s theorem:
Theorem 2
(Voisin 1994; Voevodsky 1995) Let X be a smooth projective algebraic variety of dimension n, and \(\Gamma \in A^n(X\times X)_{}\) a correspondence which is algebraically trivial. Then there is \(N\in \mathbb {N}\) such that
3 Main result
In this section, we prove the main result of this note:
Theorem 3
Let X be a smooth projective variety over \(\mathbb {C}\) of dimension n. Suppose
-
(i)
\(n\le 5\);
-
(ii)
B(X) is true;
-
(iii)
X has finite-dimensional motive, or \(\hbox {Griff}^n(X\times X)=0\).
Given \(n_i\in \mathbb {N}\) with \(n=n_1+\cdots n_r\), suppose that
-
(P2)
Cup product induces a surjection
$$\begin{aligned} H^{n_1}(X)\otimes H^{n_2}(X)\otimes \cdots \otimes H^{n_r}(X)\ \rightarrow \ H^n(X)/\widetilde{N}^1\ . \end{aligned}$$Then
-
(P1)
There exists an open \(V\subset X\), such that intersection product induces a surjection
$$\begin{aligned} A^{n_1}V_{}\otimes A^{n_2}V_{}\otimes \cdots \otimes A^{n_r}V_{}\ \rightarrow \ A^nV_{}\ . \end{aligned}$$
In dimension \(\le 3\), the niveau filtration \(\widetilde{N}^1\) can be replaced by the coniveau filtration \(N^1\), and we obtain the result announced in the introduction:
Corollary 1
Let X be as in Theorem 3, and of dimension \(n\le 3\). Then condition (P2) can be replaced by
- (P2\(^\prime \)):
-
There is an open \(V\subset X\) such that cup product induces a surjection
$$\begin{aligned} H^{n_1}(V)\otimes \cdots \otimes H^{n_r}(V)\ \rightarrow \ H^n(V)/{N}^1. \end{aligned}$$If \(n=2\), condition (P2) can be replaced by
- (P2\(^{\prime \prime }\)):
-
There is an open \(V\subset X\) such that cup product induces a surjection
$$\begin{aligned} H^{1}(V)\otimes H^{1}(V)\ \rightarrow \ H^2(V)/{F}^1, \end{aligned}$$where \(F^*\) denotes the Hodge filtration.
Proof
(of Corollary 1) It is easily seen that (P2\(^\prime \)) implies surjectivity of
Suppose now \(n=3\). Since
[Vial 2013, page 415“Properties”], the above is equivalent to condition (P2) of Theorem 3. The case \(n=2\) is similar, using that
\(\square \)
Proof
(of Theorem 3) Since X satisfies B(X), the Künneth components \(\pi _i\) are algebraic (Kleiman 1968, 1994). Because the dimension is at most 5, the variety X satisfies conditions (*) and (**) of Vial’s (Vial 2013). This implies the existence of a refined Chow–Künneth decomposition of the diagonal
(loc. cit., Theorems 1 and 2). Here the \(\Pi _{i,j}\) are mutually orthogonal idempotents, which act on homology as projectors
(Note that \(\hbox {Gr}^j_{\widetilde{N}} H_i(X)\) is a priori not a subspace of \(H_i(X)\); however, over \(\mathbb {C}\) the existence of a polarization gives a canonical identification with a subspace of \(H_i(X)\) Vial 2013.) Assumption (P2) translates into the fact that the morphism of homological motives
is surjective, where \(\Delta ^r\) is the class in \(A^{nr}(X^{r+1})\) of the “small diagonal”
To see this, note that since B(X) holds and we are in characteristic 0, homological and numerical equivalence coincide on X and its powers (Kleiman 1968, 1994). Thus, using Jannsen’s semisimplicity result (Jannsen 1992), the motives \((X,\pi _i)\) and \((X,\Pi _{n,0})\) are contained in a full semisimple abelian subcategory \({\mathcal M}_0\) of the category \({\mathcal M}_{hom}\) of motives with respect to homological equivalence (for \({\mathcal M}_0\subset {\mathcal M}_{hom}\) one can take the subcategory generated by varieties that are known to satisfy the Lefschetz standard conjecture). Hence, we get a decomposition
But assumption (P2) gives that
so that \(M^\prime =0\in {\mathcal M}_{hom}\).
By semisimplicity of \({\mathcal M}_0\), the surjection
is a split surjection. That is, there exists a correspondence \(C\in A^{n}(X\times X^r)\) such that
For brevity, we will henceforth write
where we suppose we have made the following choice for the Künneth components \(\pi _{n_i}\) modulo rational equivalence:
Since by construction [Vial 2013, Theorems 1 and 2], all the \(\Pi _{i,j}\) for \((i,j)\not =(n,0)\) are supported on \((D\times X) \cup (X\times D)\), for some divisor \(D\subset X\), we get an equality modulo homological equivalence
with \(\Gamma _1,\Gamma _2\) supported on \(D\times X\) (resp. on \(X\times D\)).
Using one of the two nilpotence theorems (Theorem 1 in case X has finite-dimensional motive, Theorem 2 in case the Griffiths group vanishes), it follows there exists \(N\in \mathbb {N}\) such that
Developing this expression gives
where each \(Q_k\) is a composition of \(\Delta _{(n_1,\ldots ,n_r)}\) and \(\Gamma _1\) and \(\Gamma _2\):
for \(Q_k^i\in \{ \Delta _{(n_1,\ldots ,n_r)}, \Gamma _1,\Gamma _2\}\).
For reasons of dimension, \(Q_k\) does not act on \(A^nX\) as soon as \(Q_k\) contains at least one copy of \(\Gamma _1\). It follows that
It is convenient to rewrite this as follows: define
so that
Since all the \(\Pi _{i,j}\) with \((i,j)\not =(n,0)\) are supported on \((D\times X)\cup (X\times D)\) [Vial 2013, Theorems 1 and 2], we have an equality
with \(\Gamma _1, \Gamma _2\) supported on \(D\times X\) resp. on \(X\times D\). Now, Eq. (1) can be rewritten as
\(\square \)
The first term decomposes (Lemma 1 below), and the second term is supported on D; this proves the theorem with \(V=X\setminus D\).
Lemma 1
Set-up as above. Then
where \(\iota \) denotes intersection product.
Proof
Recall that by definition,
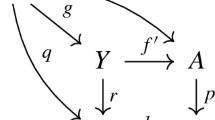
The point is that the \(\pi _{n_i}\) are supported on \(Y_{n_i}\times X\), for some \(Y_{n_i}\subset X\) of dimension \(n_i\), i.e. there exist correspondences \(\pi _{n_i}^\prime \in A_n(Y_{n_i}\times X)\) pushing forward to \(\pi _{n_i}\) [Vial 2013, Theorems1and2] (actually, this can even be achieved with \(Y_{n_i}\) a smooth hyperplane section of dimension \(n_i\) [Kahn et al. 2007, Theorem 7.7.4]). The action of the correspondence \(\Delta ^\prime _{(n_1,\ldots ,n_r)}\) on 0-cycles thus factors as

The arrow labelled \(\times _r\) is surjective (because it is a map on 0-cycles); since the diagram commutes this implies the lemma. \(\square \)
Remark 5
Here are some non-trivial cases where property (P1) is known to hold: abelian varieties (with \(V=X\) and all the \(n_j=1\), cf. Bloch 1976); the variety of lines of a cubic threefold (with \(V=X\) and \(n_1=n_2=1\), cf. [Bloch 1980, Example 1.7]); the variety of lines of a cubic fourfold (with \(V=X\) and \(n_1=n_2=2\), cf. [Shen and Vial 2016, Theorem 20.2]). Note that in the last two cases, finite-dimensionality of the motive is not known, so (P1) can not be deduced from Theorem 3; one needs some geometric arguments to establish (P1).
Remark 6
The assumption “\(\hbox {Griff}^n(X\times X)_{}=0\)” in Theorem 3 is mainly of theoretical interest, and not practically useful. Indeed, there are precise conjectures (based on the Bloch–Beilinson conjectures) saying how the coniveau filtration on cohomology should influence Griffiths groups (Jannsen 1998). For \(n=2\), it is conjectured that if \(H^1(X)=0\) then \(\hbox {Griff}^2(X\times X)_{}=0\). For \(n=3\), it is conjectured that if \(h^{0,2}(X)=h^{0,3}(X)=0\) then \(\hbox {Griff}^3(X\times X)_{}=0\). For \(n=4\), if \(h^{2,0}(X)=h^{3,0}(X)=h^{4,0}(X)=h^{2,1}(X)=0\) then \(\hbox {Griff}^4(X\times X)_{}\) should vanish. These predictions are particular instances of [Jannsen 1998, Corollary 6.8].
Unfortunately, it seems these conjectures are not known in any non-trivial cases (i.e., outside of the range of varieties with Abel–Jacobi trivial Chow groups); it would be very interesting to find (non-trivial) examples where they can be proven !
Remark 7
The Chow motive \((X,\Pi _{n,0})\) (which for varieties verifying (*) and (**) of Vial (2013) is unique up to isomorphism) can be considered the “most transcendental part” of the motive \((X,\Delta )\). When X is a surface, \((X,\Pi _{2,0})\) is the transcendental part denoted \(t_2(X)\) (and studied in detail) in Kahn et al. (2007).
Actually, following Kahn et al. (2007) one might hope that \(\Pi _{n,0}\) can be linked with the theory of birational motives of Kahn–Sujatha (Kahn and Sujatha 2009); this would perhaps give a more conceptual proof (or an extension?) of Theorem 3. I have not looked into this yet.
Remark 8
The argument of Theorem 3 also shows the following: suppose the standard conjecture of Lefschetz type holds universally. Then for any variety with finite-dimensional motive, (P2) implies (P1).
Remark 9
Suppose X satisfies the hypotheses of Theorem 3, so that
is surjective, for some open \(V\subset X\). It seems interesting to ask how many simple tensors are needed to generate \(A^nV\). For a given \(n_1,\ldots ,n_r\), let’s say \(a\in A^nV\) is k-decomposable if there is an expression
with \(a_j^i\in A^{n_i}V\). This is related to unpublished work of Nori, discussed in [Esnault et al. 1993, remark 5]. According to loc. cit., Nori proves that for any X with \(H^n(X,\mathcal O_X)\not =0\) and any k, there exist elements in \(A^nX\) that are not k-decomposable (with respect to any \((n_1,\ldots ,n_r)\) with \(r>1\)).Footnote 2 It seems likely the same is true for \(A^nV\).
The only thing I am able to prove is the following: for X satisfying the hypotheses of Theorem 3, there is an open \(V\subset X\) such that each point \(v\in V\) is 1-decomposable in \(A^nV\). (To see this, one uses (P1) to obtain a Bloch–Srinivas style decomposition of the diagonal
with \(C_i\in A^{n_i}(X\times X)\) and \(\Gamma _j\) as before; this is done in Esnault et al. (1993) using the method of Bloch and Srinivas (1983). Given a point \(v\in V\), let \(\tau _v\) denote the inclusion \(v\times X\hookrightarrow X\times X\), and let \(C_i^v\) denote the restriction \(C_i^v=(\tau _v)^*(C_i)\in A^{n_i}(v\times X)\). Now, note that
For general 0-cycles on the other hand, even when (as in the case of Theorem 3) all 0-cycles are k-decomposable for some k, it seems unlikely k can be bounded.
Notes
It is somewhat frustrating that it is not known unconditionally whether (P1) implies (P2), i.e. without assuming the generalized Hodge conjecture. Apparently Esnault, Srinivas and Viehweg had claimed to prove this in an earlier version of their paper, but the argument was found to be incomplete (Esnault et al. 1993, remark 2).
To be precise, Nori’s result is more general, as the notion of k-decomposability in Esnault et al. (1993) is broader than the notion discussed here: in loc. cit., an element \(a\in A^nV\) is defined to be k-decomposable if it can be written as \(a=\sum _{j=1}^k a_j\cdot b_j\) with \(a_j\cdot b_j\) homogeneous of degree n.
References
André, Y.: Motifs de dimension finie (d’après S.-I. Kimura, P. O’Sullivan...), Séminaire Bourbaki. vol. 2003/2004. Astérisque 299 Exp. No. 929, viii, pp. 115–145 (2004)
Ayoub, J.: Motives and algebraic cycles: a selection of conjectures and open questions (2016, preprint)
Bloch, S.: Some elementary theorems about algebraic cycles on abelian varieties. Invent. Math. 37, 215–228 (1976)
Bloch, S.: On an argument of Mumford in the theory of algebraic cycles. In: Beauville, A. (ed.) Géométrie algébrique. Sijthoff and Noordhoff, Angers (1979)
Bloch, S.: Lectures on algebraic cycles. Duke Univ. Press, Durham (1980)
Bloch, S., Ogus, A.: Gersten’s conjecture and the homology of schemes. Ann. Sci. Ecole Norm. Sup. 4, 181–202 (1974)
Bloch, S., Srinivas, V.: Remarks on correspondences and algebraic cycles. Am. J. Math. 105(5), 1235–1253 (1983)
Esnault, H., Srinivas, V., Viehweg, E.: Decomposability of Chow groups implies decomposability of cohomology. In:“Journées de Géométrie Algébrique d’Orsay, Juillet 1992”. Astérisque 218, 227–242 (1993)
Guletskiĭ, V., Pedrini, C.: The Chow motive of the Godeaux surface. In: Beltrametti, M.C., Catanese, F., Ciliberto, C., Lanteri, A., Pedrini, C. (eds.) Algebraic Geometry, a volume in memory of Paolo Francia. Walter de Gruyter, Berlin, New York (2002)
Guletskiĭ, V., Pedrini, C.: Finite-dimensional motives and the conjectures of Beilinson and Murre. K-Theory 30(3), 243–263 (2003)
Ivorra, F.: Finite dimensional motives and applications (following S.-I. Kimura, P. O’Sullivan and others). In: Autour des motifs, Asian-French summer school on algebraic geometry and number theory, Volume III, Panoramas et synthèses, Société mathématique de France (2011)
Iyer, J.: Murre’s conjectures and explicit Chow-Künneth projectors for varieties with a nef tangent bundle. Transactions of the Amer. Math. Soc. 361, 1667–1681 (2008)
Iyer, J.: Absolute Chow-Künneth decomposition for rational homogeneous bundles and for log homogeneous varieties. Mich. Math. J. 60(1), 79–91 (2011)
Jannsen, U.: Motives, numerical equivalence, and semi-simplicity. Invent. Math. 107(3), 447–452 (1992)
Jannsen, U.: Equivalence relations on algebraic cycles. In: Gordon, B., et al. (eds.) The arithmetic and geometry of algebraic cycles. Kluwer, Banff Conf. (1998)
Jannsen, U.: On finite–dimensional motives and Murre’s conjecture. In: Algebraic cycles and motives, London Math. Soc. Lecture Note Ser., vol. 344. Cambridge Univ. Press, Cambridge (2007)
Kahn, B.: Equivalences rationnelle et numérique sur certaines variétés de type abélien sur un corps fini. Ann. Sci. Ec. Norm. Sup. 36, 977–1002 (2003)
Kahn, B., Murre, J.P., Pedrini, C.: On the transcendental part of the motive of a surface. In: Algebraic cycles and motives. Vol. 2, London Math. Soc. Lecture Note Ser., vol. 344, pp. 143–202. Cambridge Univ. Press, Cambridge (2007)
Kahn, B., Sujatha, R.: Birational motives, I: pure birational motives (2009). arXiv:0902.4902v4
Kimura, S.: Chow groups are finite dimensional, in some sense. Math. Ann. 331, 173–201 (2005)
Kleiman, S.: Algebraic cycles and the Weil conjectures. In: Dix exposés sur la cohomologie des schémas, pp. 359—386. North–Holland Amsterdam, (1968)
Kleiman, S.: The standard conjectures. In: Jannsen, U., et al, (eds.) Motives. Proceedings of Symposia in Pure Mathematics, vol. 55, Part 1 (1994)
Laterveer, R.: A brief note concerning hard Lefschetz for Chow groups. Can. Math. Bull. (2015). doi:10.4153/CMB-2015-046-x
Mumford, D.: Rational equivalence of \(0\)-cycles on surfaces. J. Math. Kyoto Univ. 9(2), 195–204 (1969)
Murre, J., Nagel, J., Peters, C.: Lectures on the theory of pure motives. Amer. Math. Soc. University Lecture Series, vol. 61 (2013)
Pedrini, C.: On the finite dimensionality of a \(K3\) surface. Manuscr. Math. 138, 59–72 (2012)
Shen, M., Vial, C.: The Fourier transform for certain hyperKähler fourfolds. Mem. AMS 240(1139) (2016)
Tankeev, S.: On the standard conjecture of Lefschetz type for complex projective threefolds. II. Izvestiya Math. 75(5), 1047–1062 (2011)
Vial, C.: Algebraic cycles and fibrations. Documenta Math. 18, 1521–1553 (2013)
Vial, C.: Projectors on the intermediate algebraic Jacobians. N. Y. J. Math. 19, 793–822 (2013)
Vial, C.: Remarks on motives of abelian type (2011). arXiv:1112.1080v2
Vial, C.: Niveau and coniveau filtrations on cohomology groups and Chow groups. Proc. LMS 106(2), 410–444 (2013)
Vial, C.: Chow-Künneth decomposition for 3- and 4-folds fibred by varieties with trivial Chow group of zero-cycles. J. Algebraic Geom. 24, 51–80 (2015)
Voevodsky, V.: A nilpotence theorem for cycles algebraically equivalent to zero. Internat Math. Res. Not. 4, 187–198 (1995)
Voisin, C.: Remarks on zero-cycles on self-products of varieties, in: Moduli of vector bundles (Proceedings of the Taniguchi Congress), Maruyama Ed., Decker (1994)
Voisin, C.: Chow rings, decomposition of the diagonal, and the topology of families. Princeton University Press, Princeton and Oxford (2014)
Yin, Q.: Finite-dimensionality and cycles on powers of K3 surfaces. Comment. Math. Helv. 90, 503–511 (2015)
Acknowledgments
This note was stimulated by the Strasbourg 2014–2015 “groupe de travail” based on the monograph Voisin (2014). I want to thank all the participants of this groupe de travail for the very pleasant and stimulating atmosphere, and their interesting lectures. Thanks to Charles Vial and the referee for helpful comments. Many thanks to Yasuyo, Kai and Len for providing excellent working conditions at home in Schiltigheim.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Laterveer, R. On a multiplicative version of Bloch’s conjecture. Beitr Algebra Geom 57, 723–734 (2016). https://doi.org/10.1007/s13366-016-0296-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13366-016-0296-4
Keywords
- Algebraic cycles
- Chow groups
- Intersection product
- Finite-dimensional motives
- Bloch–Beilinson conjectures