A new signal reconstruction for damage detection on a simply supported beam subjected to a moving mass

Abstract

A new signal reconstruction is proposed for damage detection on a simply supported beam using multiple measurements of displacement induced by a moving sprung mass. The new signal is constructed from the difference between the spatially integrated deflection for the intact (baseline) and damaged beams under quasi-static loading. To that end, it is shown that the static component of displacement from the dynamic moving mass experiment may be extracted very effectively using a robust smoothing technique and that this outperforms some comparable techniques. It is shown that by measuring displacement at a modest number of points on the beam the new reconstructed signal is able to detect the location of the damage more accurately than methods that use only a single-point data. In particular, the technique is able to detect damage present simultaneously at multiple locations and can do so with a highly variable moving mass velocity. In order to construct an a posteriori baseline, the strain data from the same traverse could be used to recover the displacement-time history of the intact beam, which could enhance the method by enabling the baseline to be determined from the same experiment, further eliminating effects of experimental conditions if required. However, a Monte Carlo simulation is run to consider the effect of signal noise, showing that the proposed damage detection strategy locates damage even in the presence of noise of 50% in the measured signals (${\text {SNR}} =7\, {\text {dB}}$).

1 Introduction

Signal reconstruction and sensor arrangement are recognised recently as new challenges when conducting subtle damage detection of structures [1, 2]. This paper employs vibration techniques to derive a model-free signal-processing based method for structural health monitoring (SHM) of bridges using the static component of Vehicle–Bridge Interaction (VBI) data without an a priori baseline. For this a new signal reconstruction technique is proposed using multiple measurement points data on a bridge subjected to a moving mass.

Vibration techniques, as a category of damage detection methods, employ data recorded from a vibrating bridge structure subject to a variety of different excitation forces. In many such techniques ambient vibration data are used [3,4,5]. However, in the context of damage detection on bridge structures, sometimes a moving load or mass is applied to excite the bridge. As the main properties of the applied force such as magnitude and velocity can easily be controlled, this technique has received attention in the recent literature [6].

In most papers, a simply supported beam (bridge model) is studied as a test case. The response of the beam subjected to a moving load contains two terms. The first term, which depends directly on the velocity of the moving load, is usually referred to as the static component. The second term contains the response at the bridge’s natural frequencies and is referred to as the dynamic component. As such, structural health monitoring of bridge structures can be performed by studying either of the above parts individually or in combination [7, 8].

There are also some techniques that do not separate the response of the beam, i.e. they use raw signals. The main reason is that, as stated above, both the static and dynamic parts of the structural response contain information about damage. Recently, Zhang et al. introduced a technique which exploits multi-type vibration measurements to construct the phase trajectory of the vibration of the beam at some points on the beam [9]. In their proposed technique, it is assumed that the phase trajectory of the intact structure subjected to the equivalent moving load is available. Therefore, the Euclidean distance between these two curves after low-pass filtering is used to localise damage.

As far as exploiting the static part of the beam vibration data is concerned, it has been shown that a small velocity of the moving load can be used. As such, these techniques exploit a quasi-static moving load on the bridge to derive only the static response of the beam. Accordingly, invoking the Maxwell–Betti principle of reciprocal deflection, the response at some point A of a beam subjected to a quasi-static translating load is equal to the deflection of the beam at each load point when a static force is applied to A.

This property has been recently used by Sun et al. [10] to obtain the curvature of the beam. Yang et al. [11] had earlier shown that the curvature of the beam is sensitive to damage and, therefore, can be considered a good damage indicator. He et al. [6] also argue that the response of the bridge structure subjected to a quasi-static moving vehicle is approximately equal to displacement influence line (DIL). Therefore, they introduce a damage index based on the the area encircled by the DIL change. Ono et al. also conducted an analytical study on damage detection of a road bridge slab using displacement influence lines [12].

Wavelet transformation has been used for separation of the dynamic response of the beam for damage detection as well. He et al. argue that the moving load frequency (static) component of the response of the beam subjected to the moving load is preferred for damage localisation. The multi-scale discrete wavelet transform is used in their paper to separate the moving frequency component for damage localisation [7].

Some techniques exploit advanced signal decomposition algorithms to separate the static and dynamic parts. The most significant and widely used recent contribution to the field is empirical mode decomposition (EMD), first introduced by Huang et al. [13]. This is a technique that interpolates splines between the means of the peaks and troughs and recursively subtracts these curves (known as intrinsic mode functions, or IMFs) from the original signal.

It has been suggested that the IMFs with higher frequency content due to the structural response are more sensitive to the damage [14]. For instance, Roveri et al. exploited the EMD algorithm to separate the dynamic part and showed that the instantaneous frequency (IF) of the first (highest frequency) IMF of the vibration response of the bridge shows a peak at the time instant when the load moves over the damage [15].

For real signals, however, the highest frequency IMFs generally contain mostly noise and, therefore, these IMFs should be ignored. But because the number of IMFs can vary depending on noise level it can be difficult to automate such a detection process.

In other research, OBrien et al. apply EMD to decompose the acceleration signal of the beam subjected to a moving load into its component [16], but the first IMF is removed from the acceleration signal to exclude the data from the natural frequency vibration of the beam, leaving the low frequency or static components. The authors define a damage indicator based on the difference between the signals obtained from the intact and damage structure. It is hypothesised that this subtraction can remove the effects of excitation due to a rough road surface. This technique, however, requires baseline information measured on the undamaged structure, and assumes the effect of the road surface does not change. In other words, it deals with systematic noise, not random noise.

In baseline-free damage detection techniques, once the desired signal has been identified, there are two general trends for damage detection. A variety of techniques in both categories are proposed in the literature.

The first category of damage detection methods exploits signal processing techniques. These methods seek a peak or change in recorded vibration data representing local damage when the load is moving over the defective area. These techniques are more widely applicable as they do not rely on any finite element model of the intact structure. This category has received attention recently due to its lesser reliance on information about the intact structure [14, 15, 17]; however, generally these require the dynamic response component.

The second category comprises model-based techniques, so called because they rely on a finite element model of the intact structure. These techniques can detect the severity and the location of damage on structures more accurately, but at the expense of requiring detailed information about the structure. Model-based techniques have also received a great deal of attention by researchers during the past few decades [18, 19].

The present work seeks to exploit the advantages of both categories in that no detailed model is required, but by assuming a statically determinate structure the static response of the intact structure can be inferred from the strains in the manner described in recent work by He et al. [20].

In He et al.’s baseline-free technique for damage detection on a simply supported bridge subject to a moving load [20], the authors use the fact that the simply supported beam is statically determinate. Therefore, under quasi-static loading conditions the strain-time history of the damaged beam at an undamaged section is the same as the one from the intact beam. First, they obtain the deflection and strain time history of the beam subject to a moving load at one point on the beam. Then, the deflection time history of the intact beam is derived using information from the strain. In order to introduce a damage sensitive feature, they first show that the deflection influence line (DIL) of the beam has an analogy to the static part of the vibration data of the beam subject to a quasi-static moving load [6]. Finally, the difference between the static parts of the deflection time history of the damaged beam and the intact beam, obtained from the strain time history of the beam, is used as a damage sensitive feature (DSF). In this and related studies He et al. use the discrete wavelet transform (WT) to obtain the static part of the vibration data [6, 7, 20]. However, this technique relies on a low traverse velocity for the moving load.

Based on the above discussion, the following observations are made:

• 1. the difference between the static part of the deflection time history of the damaged and intact beam subject to a moving load is a useful feature for damage localisation [7, 16].

• 2. the strain-time history of the beam can be used to obtain the static deflection-time history of the intact beam for a baseline free damage detection if the structure is statically determinate [20]. The advantage of this is that the deflection in the baseline beam is obtained after damage from the same experiment as the deflection in the defective beam; therefore, any errors arising from imperfect experimental conditions are cancelled.

• 3. Signal decomposition techniques such as EMD, ensemble empirical mode decomposition (EEMD), variational mode decomposition (VMD) and so on can be used to decompose more complicated vibration data into its constitutive modes of oscillation, preserving all non-linearity arising from damage [13]. In this respect it is superior to linear decomposition techniques (such as WT) used by [11], and can extract the static deflection better at higher moving load velocities while preserving some critical sharp features.

Although the above elements suggest a very promising strategy, there are some concerns when using noisy measurements. It is known that applying EMD to contaminated data will reduce the accuracy of the signal decomposition; hence some information about the desired part of the signal might be lost. Also it is shown in this paper that data from more than one observation point is beneficial in deriving information about damage more rigorously when data are highly contaminated by noise. Therefore, in this paper, the authors further introduce a method based on multiple point measurement on the beam. These measured signals are then combined to construct a new signal to mitigate the effect of the noise. It is shown that the proposed method can be applied successfully for damage localisation, even in the presence of 50% noise in the vibration data (${\text {SNR}} =7$).

The novelty of the present work lies in the unique combination of the following existing individual elements discussed above: as global damage is sought, properties of statical determinacy can be exploited to simultaneously obtain deflections for both the damaged and undamaged bridge; the static component of the difference between these two signals is known to be valuable in detecting global damage, but this signal contains a sharp apex that must be preserved; the static component is easily extracted using a robust spline based smoothing technique (RST). A new integrated signal is proposed to combine multiple measurements, to improve robustness while preserving the apex in the signal. Finally, the robustness is demonstrated with a combination of road roughness, additional random signal noise, and substantial and abrupt variations in the moving load velocity.

2 The proposed damage detection procedure

In this section, a two-step damage detection strategy is proposed using data from a quasi-static moving load on a simply supported beam. Although the deflection time history of the intact beam subject to the same experiment is assumed to be available as a baseline in this paper, this information can be constructed from strain recorded from the damaged beam subject to a moving load, based on the work of He et al. [20]. This is because for a statically determinate beam the strain under static loading is unaffected by damage except locally at the point of damage itself, so data recorded at the same time as the deflection can be used. Accordingly, the only required data are deflection $\hat{s}_i(t)$ and strain $\hat{\epsilon }_i(t)$ obtained from the damaged beam at multiple points $i=1\ldots n$. However, He et al. consider only measurements at one point. It will be shown that the accuracy of the method has a direct relationship to the number of measurement points on the beam if the data are combined in an efficient way as described in this paper.

2.1 A new signal construction

In the first step, a new signal is constructed based on the obtained displacement data as follows:

Assume that $s_i(t)$ and $\hat{s}_i(t)$ are the time series obtained from the deflection time histories of, respectively, the intact and damaged beam at the ith node of the finite element model of the beam by normalising with respect to the absolute value of the displacement of the beam due to the static applied force (F) applied at the location of the measurement ($x_M$), i.e.

$$\begin{aligned} \delta =\frac{Fx_M^2(L-x_M)^2}{36EIL}. \end{aligned}$$

(1)

Note that, in the above equation F, L, and EI represent, respectively, the magnitude of the moving force applied statically, length and the flexural rigidity of the beam.

Then, signals S(t) and $\hat{S}(t)$ are constructed as the trapezoidal integration approximation to the area under the curve of the corresponding vibration data at each time step. Let us assume first that the data are measured at n equidistant points at spacing $\Delta x$ along the damaged beam. Therefore,

$$\begin{aligned} S(t)= \frac{\Delta x}{2}\left( s_1(t)+2\left( \sum _{i=2}^{n-1}s_{i}(t)\right) +s_n(t)\right) \end{aligned}$$

(2)

and,

$$\begin{aligned} \hat{S}(t)= \frac{\Delta x}{2}\left( \hat{s}_1(t)+2\left( \sum _{i=2}^{n-1}\hat{s}_{i}(t)\right) +\hat{s}_n(t)\right) . \end{aligned}$$

(3)

The use of multiple measurements in this manner improves robustness.

As the damaged beam is weakened and, therefore, more flexible, the absolute value of the static component of the signal $\hat{S}(t)$ is larger in amplitude than that of S(t); hence the static component of the normalised difference $\tilde{S}(t)=\frac{1}{\Delta x\; (2n-2)} (\hat{S}(t)-S(t))$ will always be positive. Since the static component of $\tilde{S}(t)$ will also be zero when the moving load is at either end of the beam, we hypothesise that there must be an extremum in the residual IMF of $\tilde{S}(t)$, which we propose coincides with the moving load passing the damage location.

After obtaining S(t) and $\hat{S}(t)$, the difference signal $\tilde{S}(t)=\hat{S}(t)-S(t)$ is smoothed over the timescale of the traverse using a robust discretised spline-based technique proposed in Ref. [21] and briefly outlined in Sect. 2.3. Figure 1 summarises the process of of the proposed damage detection algorithm.

Fig. 1

Diagram of the first step of the damage detection algorithm

2.2 A rationale for the proposed technique

First, by the Maxwell–Betti reciprocity theorem, and ignoring dynamic effects, the deflection at a sensor at abscissa $x_i$ due to a load P applied at abscissa $x_p$ is identical to the deflection at $x_p$ due to the same load applied at $x_i$. Therefore, by measuring $s_i(t)$ or $\hat{s}_i(t)$, and assuming that the loading can be treated as truly quasi static, we are effectively measuring the deflected shape of the beam for load P applied at the sensor location.

Next, by the principle of linear superposition the difference $\tilde{s}_i(t) = \hat{s}_i(t) - s(t)_i$ is the same as the deflection caused only by the relative rotation at the damage site, regardless of where the load is actually applied, all that needs to be known is the angle of relative rotation at the damage site caused by the load (giving rise to the term $m(c,x_i)/K_{\text {r}}$ in Eq. 4 below), which depends only on the degree of damage and the bending moment at that point.

For a statically determinate beam a relative rotation at the damage site will induce no reactions or internal forces in the structure, hence no curvature in the structural members, so $\tilde{s}_i(t)$ consists only of straight lines with an abrupt change of slope at the damage site. Therefore, an extremum in $\tilde{s}_i(t)$ must exist at the damage site. Caddemi et al. [22] derive this result, which (adapted to the present notation) is

$$\begin{aligned} \hat{s}_i(t)=\frac{1}{K_{\text {r}}}~ \tilde{M}(c,x_p(t))~m(c,x_i) , \end{aligned}$$

(4)

where c is the crack location, and the traversing load position $x_p$ has been represented as a function of time. Here $m(c,x_i)$ denotes the bending moment at the crack due to a unit virtual force applied at the sensor location and $K_{\text {r}}$ is the rotational stiffness of the ‘hinge’ representing the crack, both of which are independent of load position. $\tilde{M}(c,x_p)$ represents the bending moment at the location of the crack due to the external force P applied to the beam at abscissa $x_p(t)$, or conversely the bending moment at $x_p$ due to a load P at the crack site, and gives the $\hat{s}_i(t)$ diagram its triangular shape.

Fig. 2

Area between the deflected shape of the intact and damaged beam. Dotted area represents $W_s(x_p)$, whereas dashed area indicates the proposed value of the reconstructed signal when the mass is applied at $x_p$

This may be extended to multiple sensors (Fig. 2). By measuring $s_i(t)$ and $\hat{s}_i(t)$ at multiple locations as the load slowly traverses the beam, we are effectively measuring the static deflected profile of the beam for loads applied at each $x_i$. Each such profile will be piecewise linear with an apex always at the damage site. The integral for example

$$\begin{aligned} \tilde{S}(x_p) \equiv \tilde{S}(t) = \hat{S}(t) - S(t) = \frac{1}{K_{\text {r}}} \tilde{M}(c,x_p(t)) \int _{x_1}^{x_n} m(c,x)\,{\text {d}}x, \end{aligned}$$

(5)

(with $\hat{S}(t)$ and S(t)) defined in Eqs. 2 and 3) represents the deflection due to a load uniformly distributed between $x_1$ and $x_n$ and will again always have an apex at the damage site when plotted as a function of time (or equivalently, $x_p$), regardless of the load or sensor locations.

Two advantages are achieved by combining measurements in this way. First, as this involves an integral, sum or average, any signal noise or random measurement error present is reduced by a factor $1/\sqrt{n}$. And second, given that not all load positions will result in a large moment (hence relative rotation) at the damage site, this increases the chance that at least some of the sensor locations will respond strongly to the damage, which will be picked up by the aggregated result.

2.3 A robust discretised spline based technique RST)

The proposed signal reconstruction assumes the loading may be treated as quasi static. A good approximation to this can be achieved by decomposing or filtering the signal to remove dynamic components. Techniques such as EMD, EEMD, VMD and WT have been mentioned in the introduction and could be used. However, it was found that the robust discretised spline-based technique (RST) proposed in Ref. [21] was particularly effective. This section, therefore, briefly describes that technique, which is used to obtain the static part of the vibration data by smoothing the signal over the timescale of the traverse, thus eliminating effects of higher frequency vibrations. Other techniques are briefly outlined in Appendix 1 and have been compared with RST in Sects. 4.4 and 4.5.

RST seeks to balance the fidelity in data by minimising the goal function

$$\begin{aligned} F (\hat{y} )=||\hat{y}-y||^2 + s P (\hat{y} ), \end{aligned}$$

(6)

where y and $\hat{y}$ are, respectively, the original and smoothed signals. $P (\hat{y} )$ represents a penalty term that reflects the roughness of the smoothed data. Finally, s is a smoothing parameter, a real positive scalar that controls the degree of smoothing, in which the bigger the s, the smoother the obtained signal $\hat{y}$. Since in this paper the static part of the vibration signal is sought, a relatively large value of $10^{10}$ is chosen for s.

3 Simulation of the response of a beam subjected to a moving mass

3.1 Assumptions

In this paper, without sacrificing loss of generality of outcomes, we make a number of assumptions as follows:

• 1. It is often argued [23] that since the vehicle mass is small compared to the mass of the bridge, two-way interaction between the mass and the bridge may usually be neglected. However, in this paper, in order to account for the road surface roughness, the more general case of two-way interaction has been considered via a coupled finite element model.

• 2. Simply supported beams are very commonly used in bridge structures [24] and many researchers have focused on the damage detection of a simply supported beam [6, 7, 20]. In a similar manner, this paper also focuses on damage detection of simply supported beams using deflection. Such would need to be the case if one were to exploit the property that the baseline deflection in the intact beam can be obtained a posteriori from the strain in the damaged beam.

• 3. Generally, there are two models used to simulate damage in structures. The first category, which considers the effect of the damage more locally, studies crack damage, which itself can be open or breathing. Accordingly, the crack can be modelled as a rotational spring [15, 17, 25]. However, more often than not, damage in structures are in the form of fatigue defects which can appear over a more extended area of the beam rather than localised. This form of defect can be modelled by reducing the effective modulus of elasticity of a portion of the beam [26]. Accordingly, in a FE model, the damage can be considered as a degradation of stiffness of whole elements by introducing a damage index $\alpha$ that varies from 0 (no damage) to 1 (totally damaged). For open cracks the two methods become identical as the element length is reduced. Therefore, in this paper the latter model of damage, being simpler to implement, is used.

• 4. A completely general model of the beam would include both vertical and horizontal displacements as well as torsion. However, for a straight beam of solid or closed hollow section (i.e. warping of cross-sections due to torsion is negligible) bent about principal axes, these three components are uncoupled. Therefore, if the mass traverses the bridge centreline and/or the measurements are made on the centreline, torsion may be ignored, lateral deflections will be negligible under gravity loads, and it is sufficient to consider only vertical flexure in order to demonstrate the effectiveness of the proposed method. If these additional degrees of freedom are desired, the model proposed below may be adapted to model them using identical shape functions, and the total effects may be obtained by superposition.

3.2 Two-way finite element VBI model of a damaged beam considering road surface roughness

Fig. 3

Moving load with suspension system over a bridge with rough surface

In this section, a finite element-based VBI model is described that considers two-way interaction between the bridge and mass (see Fig. 3). Accordingly, a suspension system with stiffness $k_v$ and damping $c_v$ is considered for the moving mass $m_v$. This model can also readily incorporate beam damage, road surface roughness, and structural damping and hence will be used for subsequent simulations presented in Sect. 4 following a description of the proposed damage detection procedure.

Hermite cubic shape function for beam elements are used as follows for finite element modeling,

$$\begin{aligned} \begin{aligned} N_1&=1-3\zeta ^2+2\zeta ^3 \\ N_2&=L_e (\zeta -2\zeta ^2+\zeta ^3 ) \\ N_3&=3\zeta ^2-2\zeta ^3\\ N_4&=L_e (-\zeta ^2+\zeta ^3 ) . \end{aligned} \end{aligned}$$

(7)

As such, the cubic Hermitian interpolation vector ${[}N{]}_c$ evaluated at the contact point is constructed and used in the finite element model of the bridge–vehicle interaction as follows: [27],

$$\begin{aligned} \begin{aligned}&\left[ {\begin{array}{cc} m_v&{} 0\\ 0&{} [m_b] \end{array} } \right] \Bigg \{\begin{array}{c}\ddot{y}_v \\ \{\ddot{q}_b\} \end{array}\Bigg \}+ \left[ {\begin{array}{cc} c_v&{} -c_v\{N\}_c^\tau \\ -c_v\{N\}_c&{} [c_b]+c_v\{N\}_c\{N\}_c^\tau \end{array} } \right] \Bigg \{\begin{array}{c} \dot{y}_v \\ \{\dot{q}_b\} \end{array}\Bigg \} \\&\qquad +\left[ {\begin{array}{cc} k_v&{} -c_vV\{N^{'}\}_c^\tau -k_v\{N\}_c^\tau \\ -k_v\{N\}_c&{} [k_b]+c_vV\{N\}_c\{N^{'}\}_c^\tau +k_v\{N\}_c\{N\}_c^\tau \end{array} } \right] \Bigg \{\begin{array}{c} y_v \\ \{q_b\} \end{array}\Bigg \} \\&\quad =\Bigg \{\begin{array}{c} c_vVr^{'}_c+k_vr_c \\ -c_vVr^{'}_c\{N\}_c-k_vr_c\{N\}_c-m_vg\{N\}_c \end{array}\Bigg \},\\ \end{aligned} \end{aligned}$$

(8)

where $[m_b]$, $[c_b]$, and $[k_b]$ represent, respectively, the mass, damping and stiffness matrices of the finite element model of the beam and, as mentioned above, $m_v$, $k_v$, and $c_v$ represent, respectively, the moving mass and its suspension system. Note that in the above equation $\tau$ and $'$ represent, respectively, the transpose of a matrix and derivative with respect to the position, while $y_v$, $\{q_b\}$ and $r_c$ represent, respectively, the vertical displacement of the moving mass, the bridge beam element degrees of freedom, and the road surface roughness.

The beam damping in Eq. 8 is modelled as Rayleigh damping, i.e. of the form $[c]=\alpha [m]+\beta [k]$. This enables natural frequencies to be determined, and the constants $\alpha$ and $\beta$ were set to achieve the target beam damping ratio specified in Table 1 of $\zeta _b=5$% at the first two such frequencies.

The artificial road roughness $r_c$ was generated by the following equation from [28], which in turn is based on ISO 8608:

$$\begin{aligned} \begin{aligned} r_c(x)=\sum _{i=0}^N 2^k\times 10^{-3}\times \sqrt{\Delta n}\left( \frac{n_0}{i\Delta n}\right) \cos (2\pi i\Delta nx+\phi _i ), \end{aligned} \end{aligned}$$

(9)

where, the constant $(2^k\times 10^{-3})$ has units m$^{3/2}$; hence $r_c$ has units m if $\Delta n$ has units m$^{-1}$, and x denotes the variable abscissas on the road with respect to the reference point. Considering the length of the road profile as L, $\Delta n=\frac{1}{L}$, $n_{\text {max}}=\frac{1}{B}$ where B is the wavelength of the shortest spatial component of the roughness profile, and $N=\frac{n_{\text {max}}}{\Delta n}$. Also, in Eq. 9, the constant scalar k depends on the ISO road profile classification which takes an integers from 3 to 9, corresponding to the profiles from class A to class H (in this paper $k=3$). $n_0$ is equal to 0.1 m$^{-1}$ and $\phi _i$ is a random phase angle within the range of 0 to $2\pi$ with a uniform probabilistic distribution.

Equation 8, can be solved using the Newmark constant average acceleration method with $\beta =0.25$ and $\gamma =0.5$. In order to achieve a reasonable initial condition, it was assumed that the mass had been moving over a rough road with a length equal to the length of the bridge L before it arrived at the left-hand side of the bridge and continued moving on the bridge until it reached the right hand side. Therefore, a road profile of length of $2L_b$ was generated and used in simulations.

4 Numerical results and discussion

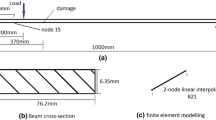
In this section, the beam with properties given in Table 1 is investigated. This beam is identical to the one used in Ref. [27]. The finite element model of the VBI problem described in Sect. 3.2 is constructed and is solved using the Newmark constant average acceleration method via Matlab. The beam is divided into 35 plane beam elements with rotational and translational degrees of freedom at each node. Figure 4 shows a randomly generated road roughness profile equal to the double length of the bridge, which is included in the model.

Table 1 VBI model constants

Fig. 4

Road roughness profile for the two times of the length of the beam ($2L_b$)

The results of the simulated VBI problem are investigated using the strategy proposed in Sect. 2 for damage detection. Several scenarios are considered.

First, a single fault at one of two possible points is detected. Road roughness is considered but no additional measurement noise is introduced. Next, the effect of significant unsteadiness in the moving mass velocity is investigated. Then, a multiple damage scenario is investigated and finally, results obtained from a single noisy measurement are compared against results from the signal $\tilde{S}(t)$ constructed from multiple sensors, as discussed in Sect. 2.1, which are also assumed to be noisy. The comparison considers the effect of the noise on the precision and reliability of damage predictions through Monte Carlo simulations.

4.1 Single fault scenario with constant moving load velocity

In this section, damage in either of elements 12 or 25 is investigated, individually, with damage severity of 40% and 30% for either case, respectively (Fig. 5).

Fig. 5

The beam is divided into 35 elements and it is assumed that either element 12 or element 25 can be defective

The first three natural frequencies of the intact and damaged beam are listed in Table 2 in Hz for each scenario. The scenarios $S_1$ and $S_2$ correspond, respectively, to loss of stiffness of element 12 (40%) or element 25 (30%), while scenario $S_3$, which will be investigated in Sect. 4.5, has damage simultaneously in both elements 12 (40%) and 25 (30%). Note that any beam with the same $fL_b/V$ (where f represents the natural frequencies) will have the same response if time is scaled appropriately. Note also for this beam that the damage has caused minimal change to the natural frequencies, so the dynamic component of the VBI data may on its own be of limited use for damage detection.

Table 2 Natural frequencies (Hz) for different damage scenarios of the beam

The location of the damage is found using the reconstructed signal based on displacement data measured at translational DOFs of nodes 6, 11, 16, 21, and 26.

Consider first the scenario with road surface roughness but no signal noise. Figure 6 shows the constructed signals S(t) and $\hat{S}(t)$ obtained, respectively, from multiple measurements on the intact and damaged beams according to Eqs. 2 and 3.

Fig. 6

Reconstructed S(t) and $\hat{S}(t)$ based on measured displacement signals at nodes 6, 11, 16, 21, and 26 for undamaged and damaged beam (a, c), and their corresponding smoothed $\tilde{S}(t)$ (b, d), when a damage occurs, respectively, at element 12 ($S_1$) (a, b) and 25 ($S_2$) (c, d) for the velocity of the moving load $V=5~$m/s

Figure 6a, b shows the vibration data obtained when only element 12 is damaged with 40% loss of stiffness, and the corresponding smoothed signal $\tilde{S}(t)$. The location of the damage is expected to occur at an exteremum point (minimum) in the graph. As can be seen in the figure, the trough of the obtained smoothed signal is very slightly to the right of the damaged element; therefore, there is a small delay in detection of the damaged element.

Now consider the case when element 25 is damaged with a lesser (30%) loss of stiffness. Figure 6c, d, shows the similar results obtained for this case. As can be seen from Fig. 6d, the location of the damage is shifted to the left in the graph.

These examples illustrate a more general result that there is always a delay in damage detection when the defective element is located in the first half-span of the beam, while on the other hand, there is always an anticipation of the damage detection when the defective element is located in the second half-span of the beam. The following hypothesis is examined to resolve this problem:

Hypothesis By reducing the speed of the moving load the defective element can be located more accurately. As such, the lower the velocity, the better the resolution of the damage localisation.

Fig. 7

Reconstructed S(t) and $\hat{S}(t)$ based on measured displacement signals at nodes 6, 11, 16, 21, and 26 for the undamaged and damaged beam (a, c), and their corresponding smoothed $\tilde{S}(t)$ (b, d), when a damage occurs, respectively, at element 12 ($S_1$) (a, b) and 25 ($S_2$) (c, d) for the velocity of the moving mass $V=2$ m/s

The above hypothesis is tested by reducing the velocity of the moving mass to 2 m/s (Fig. 7), and the results confirm that a better spatial resolution for damage localisation is obtained. This highlights the importance of a slow-moving mass to best replicate quasi-static loading conditions.

This can also be discussed with regard to the fundamental Axioms for SHM by Farrar et al. [29]; in particular Axiom VII: “The size of damage that can be detected from changes in system dynamics is inversely proportional to the frequency range of excitation”. As the present paper assumes statical determinacy in order to derive the intact structure’s deflections from strains measured on the damaged structure, it necessarily focuses on macro-level damage. In this case, as mentioned above, the natural frequencies alone contain little information about the damage, and we have argued in Sect. 2.2 that the static response will contain valuable information about the damage. Using a slower velocity of the moving mass results in lower frequency excitation of the system, enhancing the static component: it is shown in Appendix 2 that the static component is equivalent to the series of components at angular frequencies $n\pi V/L_b$, $n=1,2,\ldots$ (or $nV/(2L_b)$ if comparing to Table 2). Therefore, if these frequencies are significantly below the natural frequencies it will minimise the adverse masking effect of the natural vibrations. Axiom VII, on the other hand, implies that this is a trade-off, and the higher frequencies may still be useful in detecting local damage, which could represent the early stages of macro-level damage prior to it having a global effect. Detection of smaller localised damage would however also require a more extensive network of sensors.

4.2 Variation in the velocity of the moving load

In this part we evaluate the capability of the proposed damage detection strategy when the velocity of the moving mass is varying on the bridge. We assume that we can update the deflection time history of the intact beam using strain data measured on the damaged beam based on the technique proposed in Ref. [20].

It is hypothesised that as the quasi-static component of the loading can be isolated by the employed smoothing technique (RST), these components of deflections of the intact and damaged beam are functions of mass position only, not of its velocity. Since these are effectively measured simultaneously in the same experiment, any effect of varying moving mass velocity will not be present in $\tilde{S}(t)$.

To that end, we perform simulations in which it is assumed that the velocity of the moving mass velocity switched randomly between values of 2, 2.5, and 1 m/s during its traverse of the beam, as shown in Fig. 8. The resulting average velocity is 2.086 m/s. The damage scenario used is $S_1$, a 40% reduction of the stiffness at element 12.

Fig. 8

Plot of the velocity of the moving mass versus position along the beam span

Fig. 9

Reconstructed S(t) and $\hat{S}(t)$ based on measured displacement signals at nodes 6, 11, 16, 21, and 26 for undamaged and damaged beam (a), and their corresponding smoothed $\tilde{S}(t)$ (b), when 40% damage occurs at element 12 ($S_1$) for the variable velocity of the moving mass

As is obvious from Fig. 9, the variation of the moving mass velocity has not materially affected the damage location prediction. This is compelling evidence that the employed RST effectively isolates the static response.

4.3 Noisy measurements

In order to investigate how noise can affect the results, the reliability of detection in the presence of noise, and how the proposed integrated signal can mitigate the effect of noise, a Monte Carlo simulation was run 1000 times for each of the signal combination listed in Table 3. In all cases it was assumed that element 12 was damaged ($S_1$). Noise was added to the measured signals in addition to the random road surface roughness profile (Fig. 4), which was present in every case. A statistical measure of the precision of damage detection location was sought, and to that end the following procedure was followed.

First, 50% noise is introduced to each signal (SNR$\ =7$ dB) using the following equation [6],

$$\begin{aligned} \hat{\delta }=\delta +\frac{\kappa }{100} n_{\text {noise}} \sigma (\delta ), \end{aligned}$$

(10)

where $\hat{\delta }$ represents the vector of noisy measured translational DOF data, and $\delta$ is the corresponding noise-free vector with standard deviation $\sigma (\delta )$. $\kappa$ is the noise level in per cent ($=50$ in this case) and $n_{\text {noise}}$ is a vector with the same length as $\delta$ of random independent variables following a standard normal distribution.

Using the measured noisy translational DOFs, the new signal is constructed as before according to Sect. 2.1. Then, the obtained signal $\tilde{S}(t)$ is smoothed using the proposed RST for damaged detection. Finally, the extremum (minimum in this case) of the smoothed $\tilde{S}(t)$ is considered as the location of the damage. However, as such, the location of the damage is obtained as a real number between two integers corresponding to the right and left nodes of an element. For example, for the case of having element 12 damaged, a number between 12 and 13 is expected to be obtained. The procedure is repeated 1000 times for each combination of measured nodes and the results are presented in the box and whisker plot of Fig. 10. In this plot, the ‘box’ indicates the interquartile range and the median, while the ‘whiskers’ show extreme values, excluding outliers which are indicated (if they exist) by + and are defined as points outside approximately 2.7 standard deviations (99.3% coverage) for normally distributed data [30].

Table 3 Combinations of measurement nodes used for damage detection either with constant or variable velocity of moving mass (refer to Fig. 5 for locations)

Fig. 10

Box and whisker plots showing distributions of damage location predictions for different sensor locations and combinations (see Table 3 for combinations)

The five scenarios listed in Table 3 are considered. In the first case (S) a single measurement is used, and as can be seen from Fig. 10, the mean value obtained for the location of the damage is 18.35 with a large standard deviation of 11.10. Effectively the damage location was not able to be identified.

In the second case (C1), it is assumed that the translational DOFs corresponding to the nodes $\{6, 11, 16, 21, 26\}$ are used to construct the new signal. However, as can be seen from the Fig. 5, the nodes are chosen so that there are five elements between each successive node numbers. This is done to investigate whether a sparse or dense location of the chosen nodes can affect the accuracy of the predicted damage location. A mean damage location of 11.3 and standard deviation of 1.75 are obtained, which is substantially more accurate than using only a single measurement signal. In the third case (C2), the number of measured nodes is kept at five, except that the locations of the measurements are now adjacent, i.e. nodes $\{15, 16, 17, 18, 19 \}$ are measured. For this case, the results are still satisfactory as the mean and standard deviation are calculated, respectively, as 11.48 and 1.43, differing little from the second case.

In the fourth case (C3a), the number of measured nodes is reduced to three nodes, $\{17, 18, 19\}$. In this case a mean damage location of 11.45 is obtained, which still shows element 12 as the defective element. The standard deviation, at 1.93, is, however, negligibly worse than the two previous combinations, so the prediction is still reliable and considerably better than the single measurement point case.

Finally, in order to see how the use of a variable velocity can affect the results the same combination of signals as C3a has been considered but with varying velocity of the moving load (C3b). In this case, the mean damage location and standard deviation from the Monte Carlo simulations are, respectively, obtained as 10.8 and 1.23. Accordingly, it can be seen that the location of the damage can be still pinpointed accurately.

As a result, it can be seen that the proposed signal construction from only a few measured points can far better predict the location of the damage.

4.4 Comparison of different methods for extracting the static component

Although we have shown that RST successfully extracts the static part of the newly constructed signal for damage detection, we here justify its use further by comparing results with those obtained using two orthogonal decomposition techniques for decomposing non-stationary non-linear signals into their oscillatory components, namely empirical mode decomposition (EMD) [13] and variational mode decomposition (VMD) [31]. These are described in Appendix 1 and are examples of a classic and a more advanced decomposition technique. In this comparison damage scenario $S_1$ is considered, in which element 12 is damaged with severity 40%. The signals are simulated using a moving mass with $V=2$ m/s for both damaged and undamaged beams and are contaminated with 50% measurement noise. The location of the damage is sought using three different methods: EMD, VMD and RST.

In using each technique the following were considered:

• 1. when using EMD, the last IMF (excluding the residual IMF) was used as the static part of the signal (Appendix 1.1).

• 2. in the case of using VMD, a relatively large Lagrange multiplier $\lambda =10^7$ was used and three modes ($k=3$) are considered. The IMF with the lowest center frequency was chosen as the static part of the signal (Appendix 1.2).

• 3. when using RST, the same value for the smoothing parameter $s=10^{10}$ was used as before.

Fig. 11

Results of damage detection using the static component of the constructed signal $\tilde{S}(t)$ using a the robust spline-based technique (RST), b VMD, and c EMD

In the results presented in Fig. 11 it can be seen that all the methods show a minimum point at the location of the damaged element 12. As such, the following are the pros and cons of using each of the proposed techniques:

• 1. It can be seen in Fig. 11a, b that both RST and VMD techniques obtain almost the same curve for the static part of the signal $\tilde{S}(t)$ considering the adjusted values for the corresponding parameters. However, it is critical to consider that while RST only requires one parameter (s) to be adjusted, VMD needs several parameters to be set. The most important ones are the number of extracted modes in the decomposition, k, and the Lagrange multiplier, $\lambda$.

• 2. It can be seen, however, from the Fig. 11c that the result obtained using EMD is significantly more smoothed than for the other two techniques. Moreover, regarding using EMD one does not need to specify the number of modes or any other parameters. The accuracy of location prediction is arguably slightly better, but the precision is significantly lower. Although EMD might be then considered a better technique to obtain the static part of the vibration data, it is found to be very limiting in terms of detection of multiple damage as shown further in a following section. It has also been criticised for a phenomenon known as ‘mode mixing’ [32].

4.5 Multiple damage scenario using data only from damaged beam

In this section we assume that both elements 12 and 25 are damaged simultaneously (scenario $S_3$).

It is obvious that in practical implementation it is very difficult, if not impossible, to keep the velocity of the moving mass constant in an experiment. Therefore, a slight random oscillation in the velocity of the moving mass seems inevitable. However, this may significantly affect the results of the damage detection. To illustrate this point, the result of the damage detection using displacement data obtained from two different experiments conducted on the damaged and undamaged beam with different permutations of the random mass velocity profile of Fig. 8 are presented in Fig. 12. It is obvious that all the methods fail to detect the correct locations of damage. Although it might be concluded from Fig. 12c that EMD is relatively successful in comparison with other techniques, it is further observed in Fig. 12f that the results become distorted in the presence of 50% noise in the simulated displacement signals. On the other hand, the results obtained from both RST and VMD are persistent when noise is added (Fig. 12d, e compared, respectively, to Fig. 12a, b).

Fig. 12

Results of damage detection for the case when both elements 12 and 25 are defective with their respective loss of stiffness of 30% and 40%, using simulated data: a–c without the effect of noise; and d–f with 50% noise

It is desired, therefore, to obtain displacement data of the undamaged beam from the damaged beam using the same experiment. As mentioned in Sect. 1, this can be done following the method proposed by He et al. [20]. They use strain data measured on the damaged beam to update displacement data for an undamaged beam, eliminating the requirement of a baseline. Accordingly, a quasi-static moving mass experiment must be conducted to obtain reasonable results. The proposed method can be summarised as follows:

• 1. It is known that the strain reaches its maximum when the mass reaches the location of the measured point. Also it is known that the strain influence line (SIL) of the beam at a measured point is identical in shape to the bending moment influence line (BIL) at that point. Therefore, the strain varies linearly from zero at the left support to its maximum value at the measurement point and similarly returns linearly to zero when the mass has traversed the beam all the way to the right-hand support. As such, considering a quasi-static approximation one can obtain the location of the moving mass at each time instant from the following:

  $$\begin{aligned} x(t)=\left\{ \begin{array}{ll} \frac{\epsilon (t)}{\epsilon _M}\; x_M &{} {\text {if}} \, 0 \le t\le \frac{x_M}{V} \\ L-\frac{\epsilon (t)}{\epsilon _M}\;(L-x_M) &{} {\text {if}} \, \frac{x_M}{V} \le t\le \frac{L}{V} , \end{array} \right. \end{aligned}$$

  (11)

  where in Eq. 11, $\epsilon _M$ is the maximum value of the strain measured at $x_M$.

• 2. Then x(t) is used in the following equation to obtain the displacement of the intact beam at the location of the measurement point:

  $$\begin{aligned} y(t)=\left\{ \begin{array}{lcl} \frac{F(L-x_M)}{6 EI L} x(t) (L^2-(L-x_M)^2-x^2(t) ) &{} {\text {if }} \,\, 0 \le x(t)\le x_M \\ \frac{F(L-x_M)}{6 EI L}\left( \frac{L}{L-x_M} (x(t)-x_M)^3+(L^2-(L-x_M)^2)x(t)-x^3(t) \right) &{} {\text {if }} \,\, x_M \le x(t)\le L. \end{array} \right. \end{aligned}$$

  (12)

It is known that the strain is related to the curvature of the beam through $\epsilon =c\;\frac{{\text {d}}^2y}{{\text {d}}x^2}$ where c is the distance between the gauge (bottom of the beam) and the neutral axis (effectively the centroidal axis in the absence of a significant axial force). Given that $c=1$ m in this paper, using a five-point central difference stencil for the ith point (the point where the strain signal is to be simulated) we have,

$$\begin{aligned} \epsilon _i(t)\approx \frac{-y_{i+2}(t)+16\;y_{i+1}(t)-30\;y_i(t)+16\;y_{i-1}(t)-y_{i-2}(t)}{12\;h^2}, \end{aligned}$$

(13)

where h is the length of elements, which is 1 m in this paper. As illustration, the strain data at three different points (at locations 10, 20 and 30 m from the left support of the beam) are simulated using Eq. 13 and are shown in Fig. 13 for a mass moving at 2 m/s.

Fig. 13

Updated strain data for three different locations on the beam, i.e. 10, 20 and 30 m from the left support when the mass traverses the beam with velocity $V=2\hbox { m/s}$

As can be seen from Fig. 13, the maximum value of the strain signals occurs approximately at the location of the measurements. However, there is a slight offset due to the dynamic effect of the moving mass and the numerical calculation errors. In spite of the above shortcomings, the results obtained from Eqs. 11, 12 and 13 are used for damage detection based on simulated displacement signals at five nodes (6, 11, 16, 21, and 26) on the damaged beam. As such, the constructed signals S(t) and $\hat{S}(t)$ and the corresponding static part of the obtained $\tilde{S}(t)$ are presented in Fig. 14 where no noise is added to simulated signals, and Fig. 15 where data are contaminated by 50% noise.

Fig. 14

Reconstructed S(t) and $\hat{S}(t)$ based on simulated displacement and strain signals at nodes 6, 11, 16, 21, and 26 from the damaged beam (a), and the results of damage detection using b RST, c VMD, and d EMD considering zero noise in simulated displacement data of the damaged beam

Fig. 15

Reconstructed S(t) and $\hat{S}(t)$ based on simulated displacement and strain signals at nodes 6, 11, 16, 21, and 26 from the damaged beam (a), and the results of damage detection using b RST, c VMD, and d EMD considering 50% noise in simulated displacement data for the damaged beam

As foreshadowed in Sect. 2.2, the results for RST and VMD clearly show the sought feature of piecewise linearity with apexes near the damage sites, though some irregularity is present in the central section that masks the exact location of damage a little. Interestingly, when using RST and VMD, the results are not sensitive to noise, reinforcing the findings of Sect. 4.3. It would seem that both techniques are good candidates for extracting the static component of the signal, but, as well as being a little smoother, RST has the not insignificant advantage mentioned in Sect. 4.4 that it only requires a single parameter to be tuned.

On the other hand, while these irregularities are not present in the EMD results, it fails to give any conclusive indication of damage. However, surprisingly, it is noted that EMD seems to produce better results in the presence of noise. The fact that better results may be achieved when signals are contaminated by noise is also mentioned for example in Refs. [33, 34]. However, it is unclear if this is a genuine effect, and further investigation of the phenomenon on the proposed damage detection strategy using EMD is suggested as the subject of future work.

5 Conclusions and future work

In this paper we propose a technique that can be applied to localise damage using multiple noisy measurements of vibration data on a VBI system. Accordingly, a new signal is constructed from the measured signals. This signal is subtracted from its counterpart representing a healthy structure, which itself can be obtained using strain data measured at the same locations, recorded during the same experiment on the damaged structure. As these can be obtained simultaneously from the same experiment, it means that precise control over or knowledge of the experimental conditions (such as the moving mass velocity) is not required.

Then, a robust discretised spline-based smoothing technique (RST) is used to obtain the static part of the vibration data. It has been demonstrated through several single and multiple damage scenarios that the smoothed signal $\tilde{S}(t)$ shows a trough at the location of the damage. RST is compared with EMD and VMD as a technique for obtaining the static part of the signal. It is found to be comparable to VMD, though requires one rather than multiple parameters to be tuned, and both were found to be superior to EMD.

An example of a moving mass with suspension traversing a rough road is studied through simulations. As such, the mass and vehicle interaction with the road profile has been taken into account. The results show that by using the newly constructed signal, the damage is far more detectable. This has been demonstrated through 1000 Monte Carlo simulations of a single-point measurement experiment as well as different scenario with multiple point measurements.

The proposed technique has been applied to single and multiple damage cases. In order to distinguish between the undamaged and damaged structures, one needs to specify a threshold for the magnitude of the peak. This can be the subject of future work; however, one can easily deal with this using Monte Carlo simulations. The key remaining challenge will be to obtain a more general dimensionless threshold. The model used in this paper is a simple model of a beam subjected to a moving sprung mass, although some complexities such as interaction between the mass and beam as well as road roughness effects have been properly considered in the simulations. The model could easily be extended to include lateral and torsional degrees of freedom, but as these are uncoupled from vertical deflections, and loading can easily be arranged not to significantly excite these degrees of freedom, a more complete model is unlikely to change any of the conclusions. Further, studying the capability of the proposed technique through experimental validations can be the subject of future work.

Appendices

Appendix 1: Signal decomposition techniques

1.1 Empirical mode decomposition (EMD)

As mentioned in the main body of the paper, the static part of vibration data recorded at some point on the beam is used for damage detection. However, one can only measure the total response of the beam, which has both the static and dynamic parts in it. Therefore, a decomposition technique can be used to decompose the signal into its constructive components. The EMD algorithm has been shown to be very effective in decomposing non-stationary and nonlinear signals and, therefore, is recognised as an effective method for the purpose of this paper. EMD has been also used in other context of SHM by many researchers so far [35,36,37,38,39].

The EMD algorithm was first introduced by Huang et al. in order to decompose a signal into its oscillation modes, termed intrinsic mode functions (IMFs) [13]. IMFs are fundamentally different to the mode functions in traditional linear modal analysis in that they can be non-stationary, i.e. they can be modulated in both amplitude and frequency. However, in common with linear modal analysis, each IMF is narrow band and only involves one mode of oscillation.

Huang et al. [13] made some assumptions for a signal in order that the sifting process can be applied to it:

• 1. the signal has at least two extrema (at least one maximum and one minimum);

• 2. the characteristic time scale is defined by the time lapse between the extrema;

• 3. in the case that the signal has no extrema but contains only inflection points, it can be differentiated several times until the extrema appear. Then, the results can be obtained by integration(s).

Considering the above preliminary discussions the EMD algorithm is applied to a signal X(t) as follows:

• 1. First find all local maxima and interpolate a cubic spline curve through them; do the same for the minima.

• 2. Take the mean of the two curves (envelopes) obtained from the first step and call it $m_1$.

• 3. Compute $h_1=X(t)-m_1$ and check if $m_1$ complies with the definition of the IMF.

• 4. If not, repeat the steps 1 to 3 for $h_1$ and compute $m_{11}$ so that $h_{11}=h_1-m_{11}$. If still $h_{11}$ is not an IMF, repeat steps 1 to 3 to obtain $h_{1k}=h_{1k-1}-m_{1k}$ so that $c_1=h_{1k}$ is an IMF.

• 5. Obtain the first residual $r_1=X(t)-c_1$ and repeat steps 1 to 5 for $r_1$.

• 6. continue the sifting process until no IMF can be derived from $r_n$. In this case, $X(t)=\sum _{i=1}^{n}c_i+r_n$.

Huang et al. introduced a termination rule for the above algorithm by limiting SD, the standard deviation of two consecutive sifting results, which is calculated as

$$\begin{aligned} {\text {SD}}=\sum _{t=0}^{T} \frac{|h_{1(k-1)}(t)-h_{1k}(t)|^2}{h_{1(k-1)}^2(t)}. \end{aligned}$$

(14)

The flowchart of the basic EMD algorithm applied to an arbitrary signal X(t) is shown in Fig. 16. Refinements and improvements to the EMD algorithm have been introduced by several researchers [40, 41]. In this paper the function emd, available in Matlab (2018a and later versions) is used.

Fig. 16

Flowchart of the EMD algorithm

1.2 Variational mode decomposition (VMD)

Like EMD, VMD seeks to decompose a real-valued signal X(t) into its component modes $u_k(t)$, but based on a new definition of an IMF. In the previous section, the basic definition for an IMF in EMD is discussed. However, thereafter, the criteria for a mode to be considered as an IMF slightly changed [42, 43]. Accordingly, in VMD an IMF is an amplitude-modulated-frequency-modulated (AM-FM) sinusoid which has the following additional characteristics:

• 1. the phase is a non-decreasing function;

• 2. the envelope is non-negative;

• 3. both the envelope and the instantaneous frequency vary much more slowly than the phase;

i.e. the IMF is written as

$$\begin{aligned} u_k(t)=A_k(t)\cos (\phi _k(t)), \end{aligned}$$

(15)

where the instantaneous frequency $\omega _k(t)={\text {d}}\phi (t)/{\text {d}}t\ge 0$, and $A_k(t)$ and $\omega _k(t)$ vary much more slowly than $\phi _k(t)$.

Generally, for a given signal X(t), VMD solves the following variational optimisation problem on k IMFs $\{u_k\}=\{u_1, u_2, \ldots , u_k\}$ with center frequencies $\{\omega _k\}=\{u_1, u_2, \ldots , w_k\}$ ,

$$\begin{aligned} \underset{\{u_k\}\; \& \;\{\omega _k\}}{\min }~ \sum _k\;\bigg \Vert \partial _t\;\left( \delta (t)+\frac{j}{\pi t}\;*\;u_k(t)\right) \;{\text {e}}^{-j\omega _kt}\bigg \Vert ^2, \end{aligned}$$

(16)

where in the above equation, $*$ is the convolution operator and $X(t)=\sum _k u_k$. However, the authors of the VMD paper add two further terms to the goal function of the optimisation problem of Eq. 16. These are a quadratic penalty at finite weight, and a Lagrangian multiplier to strictly enforce the constraint, which further guarantees the achievement of convergence in the presence of noise in the signal. The reader is referred to the original paper for further study [31].

A Matlab code can be found for VMD in Ref. [44]. However, it is essential to know that there are some parameters which must be tuned when decomposing a signal using VMD. The most important ones are the number of the modes k into which the user wishes to decompose the original signal and the Lagrangian multiplier $\lambda$ that determines how much noise is allowed in the decomposition process.

Appendix 2: Static and dynamic parts of the vibration of a beam subjected to a moving mass

Fig. 17

Simply supported beam subjected to a moving load

A key component of the damage detection procedure proposed in Sect. 2 is to obtain the static part of the vibration data. We, therefore, present the analytic solution for the response of an undamped simply-supported uniform beam of length L subjected to a moving load $P=m_v g$, shown in Fig. 17. In this analytical model the static and dynamic components of response are mathematically discrete expressions.

The beam is assumed to have a continuous cross section with flexural rigidity of EI and mass per unit length $\rho A$. The response of the beam to arbitrary force f(x, t) may be obtained by modal superposition as

$$\begin{aligned} y(x,t) = \sum _{n=1}^\infty \phi _n(x)\,y^*_n(t), \end{aligned}$$

(17)

in which $\phi _n(x)$ is the nth mode shape and $y^*_n(t)$ denotes the solution to the modal differential equation,

$$\begin{aligned} \ddot{y}^*_n(t)+\omega _n^2 y^*_n(t)=\frac{1}{\rho A b}f^*_n(t), \end{aligned}$$

(18)

where in Eq. 18, $\omega _n$ is the natural frequency corresponding to mode $\phi _n(x)$ and

$$\begin{aligned} f^*_n(t)= & {} \int _0^L \phi _n(x) f(x,t) \,{\text {d}}x , \end{aligned}$$

(19)

$$\begin{aligned} b= & {} \int _0^L \phi _n^2(x) \,{\text {d}}x . \end{aligned}$$

(20)

In the case of an intact simply-supported beam the nth frequency and mode shape of the beam are, respectively, $\omega _n=\frac{n^2\pi ^2}{L^2} \sqrt{\frac{EI}{\rho A}}$ and $\phi _n (x)=\sin \left( \frac{n\pi }{L}x\right)$. Accordingly, $f^*_n(t)$ and b in Eqs. 19 and 20 are

$$\begin{aligned} f^*_n(t)= & {} -\int _0^L \sin \left( \frac{n\pi }{L}x \right) P\, \delta (x-Vt)\,{\text {d}}x =-P \sin \left( \frac{n\pi V}{L}t \right) \end{aligned}$$

(21)

$$\begin{aligned} b= & {} \int _0^L \sin ^2\left( \frac{n\pi }{L}x \right) \,{\text {d}}x =\frac{L}{2}, \end{aligned}$$

(22)

where the minus sign for the force in Eq. 21 reflects the fact that P is is pointing downwards in Fig, 17.

The modal differential equation 18 can, therefore, be solved subject to the initial conditions $y^*_n(0)=\dot{y}^*_n(0)=0$ and the response of the beam can be written in the form of Eq. 17. Following [45], the total response of the beam is then

$$\begin{aligned} y(x,t)= & {} -\frac{2PL^3}{\rho A\pi ^2} \sum _{n=1}^\infty \frac{\sin \left( \frac{n\pi }{L}x\right) }{n^2(n^2\pi ^2a^2 - V^2L^2)}\nonumber \\&\times \left\{ \sin \left( \frac{n\pi V}{L}t\right) - \frac{VL}{n\pi a}\sin (\omega _n t) \right\} \end{aligned}$$

(23)

in which

$$\begin{aligned} a=\sqrt{\frac{EI}{\rho A}}. \end{aligned}$$

The first term in the last bracketed section of Eq. 23 contains the moving load pseudo-frequencies $\frac{n\pi V}{L}$ and combines to give the static deflection component, while the second term contains the natural frequencies of the beam $\omega _n$ and is the dynamic part [10].