On the subcategories of n-torsionfree modules and related modules

Abstract

Let R be a commutative noetherian ring. Denote by ${\textsf{mod }}\,R$ the category of finitely generated R-modules. In this paper, we study n-torsionfree modules in the sense of Auslander and Bridger, by comparing them with n-syzygy modules, and modules satisfying Serre’s condition $(\mathrm {S}_n)$. We mainly investigate closedness properties of the full subcategories of ${\textsf{mod }}\,R$ consisting of those modules.

1 Introduction

The notion of n-torsionfree modules for $n\geqslant 0$ has been introduced by Auslander and Bridger [1], and actually plays an essential role in their wide and deep theory on the stable category of finitely generated modules over a noetherian ring. The modules located at the center of the n-torsionfree modules are the totally reflexive modules, which are also called Gorenstein projective modules or modules of Gorenstein dimension zero. So far a lot of studies have been done on n-torsionfree modules and totally reflexive modules; see [2, 8, 12, 14, 16] for instance.

Let R be a commutative noetherian ring. Let us denote by ${\textsf{mod }}\,R$ the category of finitely generated R-modules, by ${\textsf {TF}}_n(R)$ the full subcategory of n-torsionfree modules, by ${\textsf {Syz}}_n(R)$ the full subcategory of n-syzygy modules, and by ${\textsf {S}}_n(R)$ the full subcategory of modules satisfying Serre’s condition $(\mathrm {S}_n)$. Let us set a couple of conditions.

• (i) The ring R is locally Gorenstein in codimension $n-1$, and $R\in {\textsf {S}}_n(R)$.

• (ii) There is an equality ${\textsf {TF}}_{n+1}(R)={\textsf {Syz}}_{n+1}(R)$.

• (iii) There are equalities ${\textsf {TF}}_n(R)={\textsf {Syz}}_n(R)={\textsf {S}}_n(R)$.

Auslander and Bridger [1] prove that (i) is equivalent to (ii). Evans and Griffith [9] prove that (i) implies (iii). Goto and Takahashi [11] show that (iii) implies (i) under the additional assumption that R is local. Matsui, Takahashi and Tsuchiya [17] show that all the three conditions are equivalent.

The main purpose of this paper is to investigate the structure of the subcategory ${\textsf {TF}}_n(R)$, and toward this we shall mainly compare ${\textsf {TF}}_n(R)$ with ${\textsf {Syz}}_n(R)$ and ${\textsf {S}}_n(R)$ like the previous works mentioned above. In what follows, we explain our main results. For simplicity, we assume that R is a local ring with residue field k, and has dimension d and depth t.

We begin with considering how to describe ${\textsf {S}}_n(R)$ as the extension and resolving closures of ${\textsf {TF}}_n(R)$ and ${\textsf {Syz}}_n(R)$. We obtain a couple of sufficient conditions for ${\textsf {S}}_n(R)$ to coincide with the resolving closure of ${\textsf {TF}}_n(R)$ as in the following theorem, which are included in Proposition 3.2(4) and Theorem 3.3(1).

Theorem 1.1

It holds that ${\textsf {S}}_n(R)$ is the smallest resolving subcategory of ${\textsf{mod }}\,R$ containing ${\textsf {TF}}_n(R)$ , if the ring R satisfies $(\mathrm {S}_n)$ and either of the following holds.

• (1) The ring R is locally Gorenstein in codimension $n-2$.

• (2) One has $n\leqslant d+1$, and R is locally a Cohen–Macaulay ring with minimal multiplicity on the punctured spectrum such that for each ${\mathfrak {p}}\in \text {Sing}\,R$ there exists $M\in {\textsf {TF}}_n(R)$ satisfying $\text {pd}_{R_{\mathfrak {p}}}\,M_{\mathfrak {p}}=\infty$.

The nature of proof of the above theorem naturally tempts us to consider the n-torsionfree property of syzygies of k, as a consequence of which we can also study when ${\textsf {Syz}}_n(R)$ is closed under direct summands. We obtain various equivalent conditions for R to be Gorenstein in terms of ${\textsf {TF}}_n(R)$ and ${\textsf {Syz}}_n(R)$, which are stated in the theorem below. This is included in Theorems 4.1(3), 4.5(3), 5.4 and Proposition 5.1(5b).

Theorem 1.2

The following are equivalent.

• (1) The ring R is Gorenstein.

• (2) The nth syzygy $\Omega ^{n} k$ of the R-module k belongs to ${\textsf {TF}}_{t+2}(R)$ for some $n\geqslant t+1$.

• (3) The subcategory ${\textsf {TF}}_{t+1}(R)$ is closed under extensions.

• (4) The subcategory ${\textsf {Syz}}_{n}(R)$ is closed under extensions for some $n \geqslant t+1$.

• (5) The ring R is Cohen–Macaulay, and the syzygy $\Omega ^tk$ belongs to ${\textsf {Syz}}_{t+2}(R)$.

• (6) The ring R is Cohen–Macaulay, and the subcategory ${\textsf {Syz}}_{t+2}(R)$ is closed under direct summands.

We also obtain the following theorem, which yields sufficient conditions for ${\textsf {TF}}_n(R)$ to coincide with the subcategory ${\textsf {GP}}(R)$ of totally reflexive modules. This is included in Proposition 5.1(5) and Corollary 5.9.

Theorem 1.3

The equality ${\textsf {TF}}_n(R)={\textsf {GP}}(R)$ holds if either of the following holds.

• (1) One has $n\geqslant t+2$ , and the subcategory ${\textsf {TF}}_n(R)$ is closed under syzygies.

• (2) One has $n\geqslant t+1$ , and the subcategory ${\textsf {TF}}_n(R)$ is closed under extensions.

• (3) One has $n\geqslant 1$ , and there is an equality ${\textsf {TF}}_n(R)={\textsf {TF}}_{n+1}(R)$ of subcategories.

The organization of the paper is as follows. Section 2 is devoted to preliminaries for the later sections. In Sect. 3, we try to describe ${\textsf {S}}_n(R)$ as the resolving closure of ${\textsf {TF}}_n(R)$. We prove Theorem 1.1 and give various other related desciptions. We also derive some partial converses to Theorem 1.1(1). In Sects. 4 and 5, we prove a much more general version of Theorems 1.2 and 1.3. We also consider extending the implication (6) $\Rightarrow$ (1) in Theorem 1.2 for ${\textsf {Syz}}_n(R)$ with $n>t+2$, and provide both positive and negative answers. Finally, we investigate some other subcategories related to ${\textsf {TF}}_n(R)$ and ${\textsf {S}}_n(R)$.

2 Preliminaries

In this section, we introduce some basic notions, notations and terminologies that will be used tacitly in the later sections of the paper.

Convention 2.1

Throughout the paper, let R be a commutative noetherian ring. All modules are assumed to be finitely generated and all subcategories be strictly full. Subscripts and superscripts may be omitted unless there is a danger of confusion. We may identify each object M of a category $\mathcal {C}$ with the subcategory of $\mathcal {C}$ consisting just of M.

Notation 2.2

• (1) The singular locus of R is denoted by ${\text{Sing}}\,R$, which is defined as the set of prime ideals ${\mathfrak {p}}$ of R such that $R_{{\mathfrak {p}}}$ is singular (i.e., nonregular).

• (2) We denote by ${\textsf{mod }}\,R$ the category of (finitely generated) R-modules, by ${\textsf {proj}}\,R$ the subcategory of ${\textsf{mod }}\,R$ consisting of projective R-modules, and by ${\textsf {CM}}(R)$ the subcategory of ${\textsf{mod }}\,R$ consisting of maximal Cohen–Macaulay R-modules (recall that an R-module M is called maximal Cohen–Macaulay if ${\text{depth}}\, M_{\mathfrak {p}}=\dim R_{\mathfrak {p}}$ for all ${\mathfrak {p}}\in \text {Supp}\,M$).

• (3) We denote by $(-)^*$ the R-dual functor ${\text {Hom}}_R(-,R)$ from ${\textsf{mod }}\,R$ to itself.

• (4) Let M and N be R-modules. We write $M \lessdot N$ to mean that M is isomorphic to a direct summand of N. By $M\approx N$ we mean that $M\oplus P\cong N\oplus Q$ for some projective R-modules P and Q.

Definition 2.3

Let M be an R-module.

• (1) We denote by $\Omega M$ the kernel of a surjective homomorphism $P\rightarrow M$ with $P\in {\textsf {proj}}\,R$ and call it the first syzygy of M. Note that $\Omega M$ is uniquely determined up to projective summands. For $n\geqslant 1$ we inductively define the nth syzygy $\Omega ^nM$ of M by $\Omega ^n M:=\Omega (\Omega ^{n-1}M)$, where we put $\Omega ^0M=M$.

• (2) Let $P_1\xrightarrow {d}P_0\rightarrow M\rightarrow 0$ be a projective presentation of M. We set ${\textsf {Tr}}\,M={\text {Coker}}(d^*)$ and call it the (Auslander) transpose of M. It is uniquely determined up to projective summands; see [1] for details.

• (3) Suppose that R is local. Then one can take a minimal free resolution $\cdots \xrightarrow {d_2}F_1\xrightarrow {d_1}F_0\xrightarrow {d_0}M\rightarrow 0$ of M. We can define $\Omega ^nM$ and ${\textsf {Tr}}\,M$ as $\text {Im}\,d_n$ and ${\text {Coker}}(d_1^*)$, respectively. Recall that a minimal free resolution is uniquely determined up to isomorphism. Whenever R is local, we define syzygies and transposes by using minimal free resolutions, so that they are uniquely determined up to isomorphism.

Definition 2.4

Let $\mathcal {X}$ be a subcategory of ${\textsf{mod }}\,R$. We say that $\mathcal {X}$ is closed under extensions (closed under kernels of epimorphisms) if for an exact sequence $0\rightarrow L\rightarrow M\rightarrow N\rightarrow 0$ in ${\textsf{mod }}\,R$ with $L,N\in \mathcal {X}$ (resp. $M,N\in \mathcal {X}$) it holds that $M\in \mathcal {X}$ (resp. $L\in \mathcal {X}$). We say that $\mathcal {X}$ is resolving if it contains ${\textsf {proj}}\,R$ and is closed under direct summands, extensions and kernels of epimorphisms. Note that $\mathcal {X}$ is resolving if and only if it contains R and is closed under direct summands, extensions and syzygies (since an exact sequence $0\rightarrow L\rightarrow M\rightarrow N\rightarrow 0$ induces an exact sequence $0\rightarrow \Omega N\rightarrow L\oplus P\rightarrow M\rightarrow 0$ with $P\in {\textsf {proj}}\,R$).

Definition 2.5

Let $\mathcal {X}$ be a subcategory of ${\textsf{mod }}\,R$.

• (1) Denote by $\textsf {add}\,\mathcal {X}$ (resp. $\textsf {ext}\,\mathcal {X}$) the additive closure (resp. extension closure) of $\mathcal {X}$, that is, the smallest subcategory of ${\textsf{mod }}\,R$ containing $\mathcal {X}$ and closed under finite direct sums and direct summands (resp. closed under direct summands and extensions). Note that ${\textsf{add}}\,R={\textsf {proj}}\,R$ and $\textsf {add}\,\mathcal {X}\subseteq \textsf {ext}\,\mathcal {X}\subseteq \textsf {res}\,\mathcal {X}$.

• (2) Denote by $\Omega \mathcal {X}$ the subcategory of ${\textsf{mod }}\,R$ consisting of R-modules M that fits into an exact sequence $0\rightarrow M \rightarrow P \rightarrow X\rightarrow 0$ in ${\textsf{mod }}\,R$ with $P\in {\textsf {proj}}\,R$ and $X\in \mathcal {X}$. Denote by $\textsf {Tr}\,\mathcal {X}$ the subcategory of ${\textsf{mod }}\,R$ consisting of R-modules of the form ${\text {Coker}}(d^*)$, where $d:P_1\rightarrow P_0$ is a homomorphism of projective R-modules such that ${\text {Coker}}\, d$ belong to $\mathcal {X}$. For each $n\geqslant 0$, we inductively define $\Omega ^n\mathcal {X}$ by $\Omega ^0\mathcal {X}:=\mathcal {X}$ and $\Omega ^n\mathcal {X}:=\Omega (\Omega ^{n-1}\mathcal {X})$. Note that ${\textsf {proj}}\,R\subseteq \Omega ^n\mathcal {X}\cap \textsf {Tr}\,\mathcal {X}$. We set ${\textsf {Syz}}_n(R)=\Omega ^n({\textsf{mod }}\,R)$. Then ${\textsf {Syz}}_n(R)$ consists of those modules M that fits into an exact sequence $0\rightarrow M\rightarrow P_{n-1}\rightarrow \cdots \rightarrow P_0$ with $P_i\in {\textsf {proj}}\,R$ for each i. We say that an R-module is n-syzygy if it belongs to ${\textsf {Syz}}_n(R)$.

Definition 2.6

Let $n\geqslant 0$ be an integer. We say that R satisfies $(\mathrm {G}_n)$ if $R_{{\mathfrak {p}}}$ is Gorenstein for all prime ideals ${\mathfrak {p}}$ of R with $\dim R_{{\mathfrak {p}}}\leqslant n$. We denote by ${\widetilde{\textsf {S}}}_n(R)$ (resp. ${\textsf {S}}_n(R)$) the subcategory of ${\textsf{mod }}\,R$ consisting of R-modules M satisfying Serre’s condition $({\widetilde{\mathrm {S}}}_n)$ (resp. $(\mathrm {S}_n)$), that is to say, ${\text{depth}}\, M_{\mathfrak{p}}\geqslant \min \{n,{\text {depth}}\, R_{{\mathfrak {p}}}\}$ (resp. ${\text{depth}}\, M_{\mathfrak{p}}\geqslant \min \{n,\dim R_{{\mathfrak {p}}}\}$) for all prime ideals ${\mathfrak {p}}$ of R. By the depth lemma ${\widetilde{\textsf {S}}}_n(R)$ is a resolving subcategory of ${\textsf{mod }}\,R$ containing ${\textsf {Syz}}_n(R)$, and ${\textsf {S}}_n(R)={\widetilde{\textsf {S}}}_n(R)$ holds if (and only if) R satisfies $(\mathrm {S}_n)$.

Definition 2.7

Let M be an R-module, $\mathcal {X}$ a subcategory of ${\textsf{mod }}\,R$ and $\Phi$ a subset of $\text {Spec}\,R$.

• (1) We denote by $\text {IPD}(M)$ the infinite projective dimension locus of M, that is, the set of prime ideals ${\mathfrak {p}}$ of R with $\text {pd}_{R_{\mathfrak {p}}}\,M_{\mathfrak {p}}=\infty$. We set $\text {IPD}(\mathcal {X})=\bigcup _{X\in \mathcal {X}}\text {IPD}(X)$. We denote by $\text {IPD}^{-1}(\Phi )$ the subcategory of ${\textsf{mod }}\,R$ consisting of modules M with $\text {IPD}(M)\subseteq \Phi$. Note that $\text {IPD}^{-1}(\Phi )$ is a resolving subcategory of ${\textsf{mod }}\,R$ and $\text {IPD}({\textsf {res}}\,\mathcal {X})=\text {IPD}(\mathcal {X})\subseteq \text {Sing}\,R$. Also, $\text {IPD}({\textsf {Syz}}_n(R))=\text {Sing}\,R$ for any $n\geqslant 0$, as ${\mathfrak {p}}\in \text {IPD}(\Omega ^n_R(R/{\mathfrak {p}}))$ for ${\mathfrak {p}}\in \text {Sing}\,R$. If R satisfies $(\mathrm {S}_n)$, then $\text {IPD}({\textsf {S}}_n(R))=\text {Sing}\,R$, since ${\textsf {Syz}}_n(R)\subseteq {\textsf {S}}_n(R)$.

• (2) The nonfree locus $\text {NF}(M)$ of M is defined as the collection of all prime ideals ${\mathfrak {p}}$ of R such that $M_{{\mathfrak {p}}}$ is not $R_{{\mathfrak {p}}}$-free. We put $\text {NF}(\mathcal {X})=\bigcup _{M\in \mathcal {X}}\text {NF}(M)$. It holds that $\text {IPD}(\mathcal {X})\subseteq \text {NF}(\mathcal {X})=\text {NF}(\textsf {res}\,\mathcal {X})$. If R is Cohen–Macaulay, then ${\textsf {S}}_n(R)={\textsf {CM}}(R)$ for every $n\geqslant \dim R$ and $\text {IPD}(\mathcal {X})=\text {NF}(\mathcal {X})$ if $\mathcal {X}\subseteq {\textsf {CM}}(R)$, whence there are equalities $\text {IPD}({\textsf {CM}}(R))=\text {NF}({\textsf {CM}}(R))=\text {Sing}\,R$.

Definition 2.8

Let $a,b\in \mathbb {Z}_{\geqslant 0}\cup \{\infty \}$. By $\mathcal {G}_{a,b}$ we denote the subcategory of ${\textsf{mod }}\,R$ consisting of R-modules M such that ${\text {Ext}}^i_R(M,R)=0={\text {Ext}}^j_R({\textsf {Tr}}\,M,R)$ for all $1\leqslant i\leqslant a$ and $1\leqslant j\leqslant b$. By definition, the R-modules in $\mathcal {G}_{\infty ,\infty }$ (resp. $\mathcal {G}_{0,n}$ for $n\geqslant 0$) are the totally reflexive (resp. n-torsionfree) R-modules. We put ${\textsf {GP}}(R)=\mathcal {G}_{\infty ,\infty }$ and ${\textsf {TF}}_n(R)=\mathcal {G}_{0,n}$. Note that there are equalities ${\textsf {TF}}_1(R)={\textsf {Syz}}_1(R)$ and ${\textsf {TF}}_2(R)={\textsf {ref}}\,R$, where ${\textsf {ref}}\,R$ stands for the subcategory of ${\textsf{mod }}\,R$ consisting of reflexive R-modules.

3 Representing ${\textsf {S}}_n(R)$ as the resolving closure of ${\textsf {TF}}_n(R)$

In this section we investigate when one can represent the subcategories ${\textsf {S}}_n(R)$ and ${\widetilde{\textsf {S}}}_n(R)$ as the extension and resolving closures of ${\textsf {TF}}_n(R)$ and ${\textsf {Syz}}_n(R)$. We begin with establishing a lemma.

Lemma 3.1

Let $\mathcal {X}$ be a subcategory of ${\textsf{mod }}\,R$.

• (1) If $\mathcal {X}$ contains R and is closed under syzygies, then there is an equality $\textsf {ext}\,\mathcal {X}=\textsf {res}\,\mathcal {X}$.

• (2) If $\mathcal {X}$ is resolving, then $\Omega \mathcal {X}$ is closed under syzygies and direct summands.

Proof

• (1) It suffices to show that $\textsf {ext}\,\mathcal {X}$ is closed under syzygies. Consider the subcategory $\mathcal {Y}$ of ${\textsf{mod }}\,R$ consisting of modules M such that $\Omega M\in {\textsf {ext}}\,\Omega \mathcal {X}$. It is easy to observe that $\mathcal {Y}$ contains $\mathcal {X}$ and is closed under direct summands and extensions. Hence $\mathcal {Y}$ contains $\textsf {ext}\,\mathcal {X}$, which means that $\Omega ({\textsf {ext}}\,\mathcal {X})\subseteq {\textsf {ext}}\,\Omega \mathcal {X}$. Since $\Omega \mathcal {X}\subseteq \mathcal {X}$, we get ${\textsf {ext}}\,\Omega \mathcal {X}\subseteq {\textsf {ext}}\,\mathcal {X}$ and $\Omega (\textsf {ext}\,\mathcal {X})\subseteq \textsf {ext}\,\mathcal {X}$.

• (2) Since $\Omega \mathcal {X}\subseteq \mathcal {X}$, we have $\Omega (\Omega \mathcal {X})\subseteq \Omega \mathcal {X}$. Let $0\rightarrow M\oplus N\rightarrow F\rightarrow X\rightarrow 0$ be an exact sequence with $F\in {\textsf{add}}\,R$ and $X\in \mathcal {X}$. Then by [22, Lemma 3.1] we get exact sequences $0\rightarrow M\rightarrow F\rightarrow A\rightarrow 0$ and $0\rightarrow F\rightarrow A\oplus B\rightarrow X\rightarrow 0$. As $\mathcal {X}$ is resolving, the latter exact sequence shows $A\in \mathcal {X}$, and then from the former we obtain $M\in \Omega \mathcal {X}$. Therefore, $\Omega \mathcal {X}$ is closed under direct summands.

$\square$

Let R be a Cohen–Macaulay local ring. We say that R has minimal multiplicity if the equality ${\text {e}}(R)={\text {edim}}\, R-\dim R+1$ holds. A maximal Cohen–Macaulay R-module M is called Ulrich if ${\text {e}}(M)=\mu (M)$. We denote by ${\textsf {Ul}}(R)$ the subcategory of ${\textsf {CM}}(R)$ consisting of Ulrich R-modules. In the proposition below we provide several descriptions as extension and resolving closures.

Proposition 3.2

• (1) There are equalities ${\widetilde{\textsf {S}}}_n(R)={\textsf {ext}}\,{\textsf {Syz}}_n(R)={\textsf {res}}\,{\textsf {Syz}}_n(R)$.

• (2) If R satisfies $(\mathrm {S}_n)$ , then one has ${\textsf {S}}_n(R)={\textsf {ext}}\,{\textsf {Syz}}_n(R)={\textsf {res}}\,{\textsf {Syz}}_n(R)$ . The converse holds as well.

• (3) If R is Cohen–Macaulay, then ${\textsf {CM}}(R)={\textsf {ext}}\,{\textsf {Syz}}_n(R)={\textsf {res}}\,{\textsf {Syz}}_n(R)$ for all $n\geqslant \dim R$.

• (4) If R satisfies $(\mathrm {S}_n)$ and $(\mathrm {G}_{n-2})$ , then the equalities ${\textsf {S}}_n(R)={\textsf {ext}}\,{\textsf {TF}}_{n}(R)={\textsf {res}}\,{\textsf {TF}}_{n}(R)$ hold.

• (5) If R is a local Cohen–Macaulay ring of minimal multiplicity, then ${\textsf {CM}}(R)={\textsf {ext}}\,{\textsf {Ul}}(R)={\textsf {res}}\,{\textsf {Ul}}(R)$.

Proof

• (1) By Lemma 3.1(1), we have $\mathcal {X}:={\textsf {ext}}\,{\textsf {Syz}}_n(R)={\textsf {res}}\,{\textsf {Syz}}_n(R)\subseteq {\widetilde{\textsf {S}}}_n(R)$. For each ${\mathfrak {p}}\in \text {Spec}\,R$ the module $\Omega ^n(R/{\mathfrak {p}})$ belongs to $\mathcal {X}$. Hence $\mathcal {X}$ is dominant in the sense of [5]. Fix $M\in {\widetilde{\textsf {S}}}_n(R)$ and ${\mathfrak {p}}\in \text {Spec}\,R$, so that ${\text{depth}}\, M_{\mathfrak{p}}\geqslant \min \{n,{\text {depth}}\, R_{\mathfrak {p}}\}$. In view of [24, Theorem 1.1], it suffices to show that there exists $X\in \mathcal {X}$ with ${\text{depth}}\, M_{\mathfrak{p}}\geqslant {\text {depth}}\, X_{\mathfrak {p}}$. If ${\text {depth}}\, R_{{\mathfrak {p}}} \leqslant n$, then ${\text{depth}}\, M_{\mathfrak{p}}\geqslant {\text {depth}}\, R_{{\mathfrak {p}}}$, and we are done since $R\in \mathcal {X}$. Now suppose ${\text {depth}}\, R_{{\mathfrak {p}}} >n$. Then ${\text{depth}}\, M_{\mathfrak{p}}\geqslant n < {\text {depth}}\, R_{\mathfrak {p}}$. Setting $X=\Omega ^n(R/{\mathfrak {p}})$, we have $X\in {\textsf {Syz}}_n(R)\subseteq \mathcal {X}$ and $X_{\mathfrak {p}}\cong \Omega ^n\kappa ({\mathfrak {p}})\oplus R_{\mathfrak {p}}^{\oplus a}$ for some $a\geqslant 0$. As ${\text {depth}}\, R_{\mathfrak {p}} > n$ and ${\text {depth}}\, \kappa ({\mathfrak {p}})=0$, we have ${\text {depth}}\, \Omega ^n \kappa ({\mathfrak {p}})=n$, and so we get

  $$\begin{aligned} {\text {depth}}\, X_{\mathfrak {p}}= {\left\{ \begin{array}{ll} {\text {depth}}\,\Omega ^n\kappa ({\mathfrak {p}})=n &{}\quad \text {if }a=0,\\ \inf \{{\text {depth}}\, R_{\mathfrak {p}},\,{\text {depth}}\,\Omega ^n\kappa ({\mathfrak {p}})\} =\inf \{{\text {depth}}\, R_{\mathfrak {p}},\,n\}=n &{}\quad \text {if }a>0. \end{array}\right. } \end{aligned}$$

  Thus ${\text{depth}}\, M_{\mathfrak{p}}\geqslant n={\text {depth}}\, X_{\mathfrak {p}}$, and the proof is completed.

• (2) The first assertion follows from (1). The second assertion holds since we have $R\in {\textsf {Syz}}_n(R)\subseteq {\textsf {ext}}\,{\textsf {Syz}}_n(R)={\textsf {S}}_n(R)$.

• (3) We have $R\in {\textsf {S}}_n(R)$ for $n\geqslant 0$ and ${\textsf {CM}}(R)={\textsf {S}}_n(R)$ for $n\geqslant \dim R$. The assertion follows by (2).

• (4) We may assume $n\geqslant 1$. By [17], Theorem 2.3(2)$\Rightarrow$(6)] we have ${\textsf {TF}}_n(R)={\textsf {Syz}}_n(R)$. Apply (2).

• (5) Put $d=\dim R$. We have ${\textsf {ext}}\,{\textsf {Ul}}(R)\subseteq {\textsf {res}}\,{\textsf {Ul}}(R)\subseteq {\textsf {CM}}(R)={\textsf {ext}}\,{\textsf {Syz}}_{d+1}(R)\subseteq {\textsf {ext}}\,\Omega {\textsf {CM}}(R)$, where the equality follows from (3). It thus suffices to show $\Omega {\textsf {CM}}(R)\subseteq {\textsf {ext}}\,{\textsf {Ul}}(R)$, and for this we may assume that R is singular. Let k be the residue field of R. Take an exact sequence $0\rightarrow \Omega ^{d+2} k \rightarrow F \rightarrow \Omega ^{d+1} k \rightarrow 0$ with F nonzero and free. The modules $\Omega ^{d+1}k,\Omega ^{d+2}k\in \Omega {\textsf {CM}}(R)$ have no nonzero free summands by [7, Corollary 1.3]. It follows from [15, Proposition 3.6] that $\Omega ^{d+1}k,\Omega ^{d+2}k$ are in ${\textsf {ext}}\,{\textsf {Ul}}(R)$, so is F, and so is $R\lessdot F$. We obtain $\Omega {\textsf {CM}}(R)\subseteq {\textsf {ext}}\,{\textsf {Ul}}(R)$ by [15, Proposition 3.6] again.

$\square$

In Proposition 3.2(4) we got a description of ${\textsf {S}}_n(R)$ as the resolving closure of ${\textsf {TF}}_n(R)$ under a certain assumption on the Gorenstein locus of R. We have the same description regardless of the Gorenstein locus in the theorem below.

Theorem 3.3

Let $(R,\mathfrak {m},k)$ be a local ring of dimension d.

• (1) Suppose that R is locally a Cohen–Macaulay ring with minimal multiplicity on the punctured spectrum of R. Let $0\leqslant n\leqslant d+1$ be such that R satisfies $(\mathrm {S}_n)$. Then $\text {Sing}\,R=\text {IPD}({\textsf {TF}}_n(R))$ if and only if ${\textsf {S}}_n(R)={\textsf {res}}\,{\textsf {TF}}_n(R)$.

• (2) Assume that R is Cohen–Macaulay ring and locally has minimal multiplicity on the punctured spectrum of R. Then $\text {Sing}\,R=\text {NF}({\textsf {TF}}_n(R))$ if and only if ${\textsf {CM}}(R)={\textsf {res}}\,{\textsf {TF}}_n(R)$ for $n=d,d+1$.

Proof

(2) The assertion is immediate from (1).

(1) The “if” part is obvious. In what follows, we show the “only if” part. We may assume $n\geqslant 1$. Set $\mathcal {X}={\textsf {res}}\,{\textsf {TF}}_n(R)$. We have ${\textsf {TF}}_n(R)\subseteq {\textsf {Syz}}_n(R)\subseteq {\textsf {S}}_n(R)$ and ${\textsf {S}}_n(R)$ is resolving. Thus it is enough to show that $\mathcal {X}$ contains ${\textsf {S}}_n(R)$.

Put $t={\text {depth}}\, R$. As R satisfies $(\mathrm {S}_n)$, we have $t\geqslant \inf \{n,d\}$. As $n\leqslant d+1$ by assumption, we get

$$\begin{aligned} 1\leqslant n\leqslant t+1. \end{aligned}$$

(1)

The module ${\text {Ext}}_R^i(k,R)$ has grade at least $i-1$ for each $1\leqslant i\leqslant t+1$. By [1, Proposition (2.26)], the module $\Omega ^ik$ is i-torsionfree for each $1\leqslant i\leqslant t+1$. By (1) we get

$$\begin{aligned} \Omega ^nk\text { is } n\text{-torsionfree}. \end{aligned}$$

(2)

Fix a nonmaximal prime ideal ${\mathfrak {p}}$ of R. By assumption, the local ring $R_{\mathfrak {p}}$ is Cohen–Macaulay and has minimal multiplicity. If $R_{\mathfrak {p}}$ is regular, then $\Omega ^{{\text {ht}}\,{\mathfrak {p}}}\kappa ({\mathfrak {p}})$ is $R_{\mathfrak {p}}$-free, and belongs to $\mathcal {X}_{\mathfrak {p}}$. Suppose that $R_{\mathfrak {p}}$ is singular. By assumption we get ${\mathfrak {p}}\in \text {IPD}({\textsf {TF}}_n(R))$, which implies ${\mathfrak {p}}\in \text {IPD}(G)$ for some $G\in {\textsf {TF}}_n(R)$. Then $\Omega ^{{\text {ht}}\,{\mathfrak {p}}}G_{\mathfrak {p}}$ is a nonfree maximal Cohen–Macaulay $R_{\mathfrak {p}}$-module. It is observed by using [23, Proposition 5.2 and Lemma 5.4] and [5, Lemma 3.2(1)] that $\Omega ^{{\text {ht}}\,{\mathfrak {p}}}\kappa ({\mathfrak {p}})\in {\textsf {res}}_{R_{\mathfrak {p}}}(\Omega ^{{\text {ht}}\,{\mathfrak {p}}}G_{\mathfrak {p}})\subseteq {\textsf {add}}_{R_{\mathfrak {p}}}\,\mathcal {X}_{\mathfrak {p}}$. Thus we have

$$\begin{aligned} \Omega ^{{\text {ht}}\,{\mathfrak {p}}}\kappa ({\mathfrak {p}})\in {\textsf {add}}_{R_{\mathfrak {p}}}\,\mathcal {X}_{\mathfrak {p}}\hbox { for all nonmaximal prime ideals } {\mathfrak {p}} \,\hbox {of} \,R. \end{aligned}$$

(3)

It follows from (2) and (3) that the resolving subcategory $\mathcal {X}$ of ${\textsf{mod }}\,R$ is dominant.

Fix an R-module $M\in {\textsf {S}}_n(R)$. The proof of the theorem will be completed once we prove that M belongs to $\mathcal {X}$. Fix a prime ideal ${\mathfrak {p}}$ of R. In view of [24, Theorem 1.1], it suffices to show that ${\text{depth}}\, M_{\mathfrak{p}}$ is not less than $r:=\inf _{X\in \mathcal {X}}\{{\text {depth}}\, X_{\mathfrak {p}}\}$. As M satisfies $(\mathrm {S}_n)$, we have ${\text{depth}}\, M_{\mathfrak{p}}\geqslant \inf \{n,{\text {ht}}\,{\mathfrak {p}}\}$. If ${\text {ht}}\,{\mathfrak {p}}\leqslant n$, then ${\text{depth}}\, M_{\mathfrak{p}}\geqslant {\text {ht}}\,{\mathfrak {p}}\geqslant r$, and we are done. We may assume ${\text {ht}}\,{\mathfrak {p}}>n$, and hence ${\text{depth}}\, M_{\mathfrak{p}}\geqslant n$ and ${\text {depth}}\, R_{\mathfrak {p}}\geqslant \inf \{n,{\text {ht}}\,{\mathfrak {p}}\}=n$. It is enough to deduce that $n\geqslant r$.

Consider the case where ${\mathfrak {p}}=\mathfrak {m}$. In this case, we have ${\text {depth}}\, R\geqslant n$. Applying the depth lemma yields ${\text {depth}}\,(\Omega ^nk)_{\mathfrak {p}}={\text {depth}}\,\Omega ^nk=n$, while $\Omega ^nk\in \mathcal {X}$ by (2). Hence $n\geqslant r$. Thus we may assume ${\mathfrak {p}}\ne \mathfrak {m}$.

The inequality ${\text {ht}}\,{\mathfrak {p}}>n$ particularly says that $R_{\mathfrak {p}}$ is not artinian, which implies that ${\mathfrak {p}}\in \text {NF}(R/{\mathfrak {p}})$. By [4, Lemma 4.6], we find an R-module C with $\text {NF}(C)=\text {V}({\mathfrak {p}})$ and ${\text {depth}}\, C_\mathfrak {q}=\inf \{{\text {depth}}\, R_\mathfrak {q},{\text {depth}}\,(R/{\mathfrak {p}})_\mathfrak {q}\}$ for all $\mathfrak {q}\in \text {V}({\mathfrak {p}})$. Set $Z=\Omega ^nC$. As ${\text {depth}}\, C_{\mathfrak {p}}=0$ and ${\text {depth}}\, R_{\mathfrak {p}}\geqslant n$, the depth lemma says ${\text {depth}}\, Z_{\mathfrak {p}}=n$. For each integer $1\leqslant i\leqslant n$ there are equalities and inequalities

$$\begin{aligned} {\text {grade}}\,{\text {Ext}}_R^i(C,R)&=\inf \{{\text {depth}}\, R_\mathfrak {q}\mid \mathfrak {q}\in \text {Supp}\,{\text {Ext}}_R^i(C,R)\} \end{aligned}$$

(4)

$$\begin{aligned}&\geqslant \inf \{{\text {depth}}\, R,{\text {depth}}\, R_\mathfrak {q}\mid \mathfrak {m}\ne \mathfrak {q}\in \text {Supp}\,{\text {Ext}}_R^i(C,R)\} \end{aligned}$$

(5)

$$\begin{aligned}&=\inf \{t,{\text {ht}}\,\mathfrak {q}\mid \mathfrak {m}\ne \mathfrak {q}\in \text {Supp}\,{\text {Ext}}_R^i(C,R)\} \end{aligned}$$

(6)

$$\begin{aligned}&\geqslant \inf \{t,{\text {ht}}\,\mathfrak {q}\mid \mathfrak {m}\ne \mathfrak {q}\in \text {V}({\mathfrak {p}})\} =\inf \{t,{\text {ht}}\,{\mathfrak {p}}\}\geqslant n-1\geqslant i-1. \end{aligned}$$

(7)

here (4) follows from [3, Proposition 1.2.10(a)], the inequality (5) is an equality unless ${\text {Ext}}_R^i(C,R)=0$, and the equality (6) holds since R is locally Cohen–Macaulay on the punctured spectrum. In (7), the first inequality holds since $\text {Supp}\,{\text {Ext}}_R^i(C,R)\subseteq \text {NF}(C)=\text {V}({\mathfrak {p}})$, the equality holds since ${\mathfrak {p}}\ne \mathfrak {m}$, and the second inequality follows from (1) and the fact that ${\text {ht}}\,{\mathfrak {p}}>n$. By [1, Proposition (2.26)] the module Z is n-torsionfree, and in particular, $Z\in \mathcal {X}$. It is now seen that $n\geqslant r$. $\square$

To show our next proposition, we establish the lemma below, which is of independent interest.

Lemma 3.4

Let $(R,\mathfrak {m},k)$ be a d-dimensional Cohen–Macaulay non-Gorenstein local ring with minimal multiplicity. Then $\mathcal {G}_{i,j}={\textsf{add}}\,R$ for all $i,j\geqslant 0$ with $i+j\geqslant 2d+2$.

Proof

We freely use [14, Proposition 1.1.1]. We may assume $i+j=2d+2$ since $\mathcal {G}_{a,b}$ contains $\mathcal {G}_{a+1,b}$ and $\mathcal {G}_{a,b+1}$ for all $a,b\geqslant 0$. As the stable category of $\mathcal {G}_{i,j}$ is equivalent to that of $\mathcal {G}_{2d+2,0}$, it suffices to show that every $M\in \mathcal {G}_{2d+2,0}$ is free. Taking the faithfully flat map $R\rightarrow R[X]_{\mathfrak {m}R[X]}$, we may assume that k is infinite. Choose an R-sequence ${\varvec{x}}=x_1,...,x_d$ with $\mathfrak {m}^2={\varvec{x}}\mathfrak {m}$ by [3, Exercise 4.6.14]. We have $N:=\Omega ^dM\in \mathcal {G}_{d+2,d}\subseteq {\textsf {CM}}(R)$. Using the exact sequences $\{0\rightarrow N/{\varvec{x}}_{i-1}N\xrightarrow {x_i}N/{\varvec{x}}_{i-1}N\rightarrow N/{\varvec{x}}_iN\rightarrow 0\}_{i=1}^d$ where ${\varvec{x}}_i=x_1,\dots ,x_i$, we see that ${\text {Ext}}_R^j({\overline{N}},R)=0$ for $j=d+1,d+2$ where $\overline{(-)}=(-)\otimes _RR/({\varvec{x}})$. Hence ${\text {Ext}}_{{\overline{R}}}^j({\overline{N}},{\overline{R}})=0$ for $j=1,2$ by [3, Lemma 3.1.16]. In particular, ${\text {Ext}}_{\overline{R}}^1(L,{\overline{R}})=0$ where $L=\Omega _{{\overline{R}}}{\overline{N}}$. As $(\mathfrak {m}{\overline{R}})^2=0$, the module L is a k-vecor space. As R is non-Gorenstein, we must have $L=0$, which means ${\overline{N}}$ is ${\overline{R}}$-free, which means N is R-free (by [3, Lemma 1.3.5]), which means M is R-free (as $M\approx \Omega ^{-d}N$). $\square$

Using the above lemma, we can prove the following proposition.

Proposition 3.5

Suppose that for all minimal prime ideals ${\mathfrak {p}}$ of R the artinian local ring $R_{{\mathfrak {p}}}$ has minimal multiplicity. If $\text {NonGor}(R) \subseteq \text {NF}({\textsf {ref}}\,R)$ (e.g., if $\text {Sing}\,R\subseteq \text {NF}({\textsf {ref}}\,R)$ ), then R is generically Gorenstein.

Proof

Take any ${\mathfrak {p}}\in \text {Min}\,R$. By assumption, we have $({\mathfrak {p}} R_{\mathfrak {p}})^2=0$. If ${\mathfrak {p}} \in \text {NonGor}(R)$, then Lemma 3.4 implies $({\textsf {ref}}\,R)_{\mathfrak {p}}\subseteq {\textsf {ref}}(R_{\mathfrak {p}})={\textsf {add}}(R_{\mathfrak {p}})$. But then ${\mathfrak {p}} \notin \text {NF}({\textsf {ref}}\,R)$, contradicting our assumption. Thus if ${\mathfrak {p}} \in {\text {Min}}\,R$, then ${\mathfrak {p}} \notin \text {NonGor}(R)$, that is, $R_{\mathfrak {p}}$ is Gorenstein. $\square$

The corollary below, which is a consequence of the above proposition, gives kind of a converse to Proposition 3.2(4), and shows that in some cases the minimal multiplicity condition in Theorem 3.3(1) actually forces some stringent condition on the Gorenstein locus of R, so that in those cases Theorem 3.3(1) gives nothing newer than Proposition 3.2(4).

Corollary 3.6

Assume that R satisfies $(\mathrm {S}_2)$. Consider the following four statements.

• (1) R is generically a hypersurface.

• (2) R is generically Gorenstein.

• (3) ${\textsf {S}}_2(R)={\textsf {res}}({\textsf {ref}}\,R)$.

• (4) $\text {Sing}\,R=\text {IPD}({\textsf {ref}}\,R)$.

Then $(1)\Rightarrow (2)\Rightarrow (3)\Rightarrow (4)$ hold. If R is generically of minimal multiplicity, then the four statements are equivalent. If R is Cohen–Macaulay and $\dim R\leqslant 2$, then (4) is equivalent to $\text {Sing}\,R=\text {NF}({\textsf {ref}}\,R)$.

Proof

The last assertion is clear. It is obvious that (1) implies (2). Proposition 3.2(4) shows that (2) implies (3). Since $\text {IPD}({\textsf {S}}_2(R))=\text {Sing}\,R$, so (3) implies (4).

Suppose that R is generically of minimal multiplicity, and assume (4). Then $\text {Sing}\,R=\text {IPD}({\textsf {ref}}\,R)\subseteq \text {NF}({\textsf {ref}}\,R)$, and hence (2) holds by Proposition 3.5. Finally, (2) implies (1) by the well-known (and easy to see) fact that an artinian Gorenstein local ring with minimal multiplicity is a hypersurface. $\square$

The first example below shows the non-vacuousness of Corollary 3.6. The second says that one cannot drop the hypothesis of R being generically of minimal multiplicity in the second part of Corollary 3.6.

Example 3.7

Let k be a field.

• (1) Let $R=k[\![x,y,z]\!]/(x^2,xy,y^2z)$. Then R is a 1-dimensional Cohen–Macaulay local ring with $y-z$ a parameter. Put ${\mathfrak {p}}=(x,y)$, $\mathfrak {q}=(x,z)$ and $\mathfrak {m}=(x,y,z)$. It holds that $R_{\mathfrak {p}}\cong k[\![x,y,z]\!]_{(x,y)}/(x^2,xy,y^2)$ with z a unit, while $R_\mathfrak {q}\cong k[\![y]\!]_{(0)}$ with y a unit. We have $\ell \ell (R_{\mathfrak {p}})=2$, $\ell \ell (R_\mathfrak {q})=1$, $\text {Spec}\,R=\{{\mathfrak {p}},\mathfrak {q},\mathfrak {m}\}$, $\text {Min}\,R=\{{\mathfrak {p}},\mathfrak {q}\}$ and $\text {Sing}\,R=\text {NonGor}R=\{{\mathfrak {p}},\mathfrak {m}\}$. Hence R is generically of minimal multiplicity, R is not generically Gorenstein and ${\mathfrak {p}}$ does not belong to $\text {NF}({\textsf {ref}}\,R)$.

• (2) Let $R=k[\![x,y,z,w]\!]/(x^2,y^2,yz,z^2w)$. Then R is a 1-dimensional Cohen–Macaulay local ring with $w-z$ a parameter. Set ${\mathfrak {p}}=(x,y,z)$ and $\mathfrak {q}=(x,y,w)$. We have $R_{\mathfrak {p}}\cong k[\![x,y,z,w]\!]_{(x,y,z)}/(x^2,y^2,yz,z^2)$ with w a unit, while $R_\mathfrak {q}\cong k[\![x,z]\!]_{(x)}/(x^2)$ with z a unit. It follows that $\text {Spec}\,R=\text {Sing}\,R=\{{\mathfrak {p}},\mathfrak {q},\mathfrak {m}\}$, $\text {Min}\,R=\{{\mathfrak {p}},\mathfrak {q}\}$ and $\{{\mathfrak {p}},\mathfrak {m}\}=\text {NonGor}\,R$. So R is not generically Gorenstein. As (x, x) is an exact pair of zerodivisors (i.e., $0:x=(x)$), R/(x) is a totally reflexive R-module, and in particular, it is reflexive. We see that $\text {NonGor}\,R\subseteq \text {Sing}\,R\subseteq \text {NF}(R/(x))\subseteq \text {NF}({\textsf {GP}}(R))\subseteq \text {NF}({\textsf {ref}}\,R)\subseteq \text {NF}({\textsf {CM}}(R))=\text {Sing}\,R$. Note that $\ell \ell (R_{\mathfrak {p}})=3$, so that $R_{\mathfrak {p}}$ does not have minimal multiplicity.

In view of Corollary 3.6, we raise natural questions.

Question 3.8

• (1) For a local Cohen–Macaulay ring R (generically of minimal multiplicity) of dimension $d>1$, does the equality ${\textsf {res}}({\textsf {TF}}_{d+1}(R))={\textsf {CM}}(R)$ force any condition on the Gorenstein locus of R ?

• (2) Let R be an artinian local ring. When does the equality ${\textsf {ext}}({\textsf {ref}}\,R)={\textsf{mod}}\,R$ imply the Gorensteinness of R ? (Lemma 3.4 gives one sufficient condition that R has minimal multiplicity).

4 Syzygies of the residue field and direct summands of syzygies

The proof of Theorem 3.3(1) crucially uses the torsionfree nature of syzygies of the residue field of a local ring. So, in this section, we record some results explaining when certain syzygies of the residue field of a local ring is or is not n-torsionfree for certain n depending on the depth of the ring. We begin with the following result. For a local ring R, we denote by ${\textsf{mod}}_0\,R$ the subcategory of ${\textsf{mod}}\,R$ consisting of modules which are locally free on the punctured spectrum of R.

Theorem 4.1

Let $(R,\mathfrak {m},k)$ be a local ring of depth t. Then the following statements hold.

• (1) Let $n\geqslant 0$ be an integer, and put $m=\min \{n,t+1\}$ . Then the inclusion ${\textsf {Syz}}_n(R)\cap {\textsf {mod}}_0\,R\subseteq {\textsf {TF}}_m(R)$ holds true. In particular, the module $\Omega ^nk$ is m-torsionfree.

• (2) The module $\Omega ^t k$ is $(t+1)$ -torsionfree.

• (3) If $\Omega ^n k$ is $(t+2)$ -torsionfree for some $n\geqslant t+1$ , then R is Gorenstein. The converse is also true.

Proof

• (1) Let M be an R-module in ${\textsf {Syz}}_n(R)\cap {\textsf {mod}}_0\,R$. Since $m\leqslant n$, we have $M\in {\textsf {Syz}}_n(R)\subseteq {\textsf {Syz}}_m(R)$. Let ${\mathfrak {p}}$ be a prime ideal of R such that ${\text {depth}}\, R_{\mathfrak {p}}\leqslant m-2$. Then ${\text {depth}}\, R_{\mathfrak {p}}\leqslant m-2\leqslant t-1$, which forces ${\mathfrak {p}}\ne \mathfrak {m}$. Hence the $R_{\mathfrak {p}}$-module $M_{\mathfrak {p}}$ is free. Applying [16, Theorem 43], we obtain $M\in {\textsf {TF}}_m(R)$.

• (2) There is an R-sequence ${\varvec{x}}=x_1,\dots ,x_t$. Since $R/({\varvec{x}})$ has depth 0, there is an exact sequence $0 \rightarrow k \rightarrow R/({\varvec{x}}) \rightarrow C \rightarrow 0$. Applying $\Omega ^t=\Omega _R^t$ and remembering $\text {pd}_R\,R/({\varvec{x}})=t$, we get an exact sequence $0 \rightarrow \Omega ^tk \rightarrow F \rightarrow \Omega ^tC \rightarrow 0$ of R-modules with F free. This shows $\Omega ^tk\approx \Omega ^{t+1}C$. It follows from (1) that $\Omega ^{t+1}C\in {\textsf {Syz}}_{t+1}(R)\cap {\textsf {mod}}_0\,R\subseteq {\textsf {TF}}_{t+1}(R)$, and therefore $\Omega ^tk\in {\textsf {TF}}_{t+1}(R)$.

• (3) First we prove the $n=t+1$ case. With the notation of the proof of (1), we have $\Omega ^tk\approx \Omega ^{t+1}C$. This implies $\Omega ^{t+1}k \approx \Omega ^{t+2}C$ and $\Omega ^{t+2}C\in {\textsf {TF}}_{t+2}(R)$. It follows from [1, Corollary (4.18) and Proposition (2.26)] that ${\text {Ext}}^{t+2}_R(C,R)$ has grade at least $t+1$. Note that any nonzero R-module has grade at most $t={\text {depth}}\, R$. We thus have $0={\text {Ext}}^{t+2}_R(C,R)={\text {Ext}}^1_R(\Omega ^{t+1}C,R)={\text {Ext}}^1_R(\Omega ^t k, R)={\text {Ext}}^{t+1}_R(k,R)$. By [20, II. Theorem 2] we get $\text {id}_R\,R<t+1$. We conclude that R is Gorenstein.

  Next assume $n\geqslant t+2$. We have $\Omega ^n k=\Omega ^{t+2} (\Omega ^{n-t-2}k)\in {\textsf {TF}}_{t+2}(R)$. Again by [1, Corollary (4.18) and Proposition (2.26)], ${\text {Ext}}^{t+2}_R(\Omega ^{n-t-2}k,R)$ has grade at least $t+1$. We have $0={\text {Ext}}^{t+2}_R(\Omega ^{n-t-2}k,R)={\text {Ext}}^n_R(k,R)$, and again by [20, II. Theorem 2] we get $\text {id}_R\,R<n$ and R is Gorenstein.

$\square$

Remark 4.2

Theorem 4.1(2) vastly generalizes [10, Proposition 4.1] in that we neither use any Cohen–Macaulay assumption on the ring, nor do we have any restriction on the depth of the ring.

As an immediate consequence of Theorem 4.1, we can describe, for certain values of n, the resolving closure of n-torsionfree modules which are also locally free on the punctured spectrum.

Corollary 4.3

Let $(R,\mathfrak {m},k)$ be a local ring of depth t. Then there are equalities

$$\begin{aligned} {\textsf {res}}({\textsf {TF}}_n(R)\cap {\textsf {mod}}_0\, R)&=\{M\in {\textsf {mod}}_0\, R\mid {\text {depth}}\, M\geqslant n\}\text { for }0\leqslant n\leqslant t,\text { and}\\ {\textsf {res}}({\textsf {TF}}_{t+1}(R)\cap {\textsf {mod}}_0\, R)&=\{M\in {\textsf {mod}}_0\, R\mid {\text {depth}}\, M\geqslant t\}. \end{aligned}$$

Proof

Fix $0\leqslant n\leqslant t$ and put $\mathcal {X}_n=\{M\in {\textsf {mod}}_0\, R\mid {\text {depth}}\, M\geqslant n\}$. That $\mathcal {X}_n$ is resolving is seen by the depth lemma etc. Also, ${\textsf {TF}}_n(R)\subseteq {\textsf {Syz}}_n(R)\subseteq \mathcal {X}_n$ by the depth lemma again. Therefore, ${\textsf {res}}({\textsf {TF}}_n(R)\cap {\textsf {mod}}_0\, R)\subseteq \mathcal {X}_n$. The reverse inclusion follows from [24, Proposition 3.4] and Theorem 4.1(1): we have $M\in {\textsf {res}}\,\Omega ^n k\subseteq {\textsf {res}}({\textsf {TF}}_n(R)\cap {\textsf {mod}}_0\, R)$ whenever $M\in \mathcal {X}_n$. We obtain $\mathcal {X}_n={\textsf {res}}({\textsf {TF}}_n(R)\cap {\textsf {mod}}_0\, R)$ for every $0\leqslant n\leqslant t$. For the other equality, we have ${\textsf {res}}({\textsf {TF}}_{t+1}(R)\cap {\textsf {mod}}_0\,R)\subseteq {\textsf {res}}({\textsf {TF}}_t(R)\cap {\textsf {mod}}_0\,R)=\mathcal {X}_t$, and the opposite inclusion follows similarly as above by using [24, Proposition 3.4] and Theorem 4.1(2). $\square$

In view of Theorem 4.1(2) it would also be natural to ask if for any special classes of non-Gorenstein local Cohen–Macaulay rings $(R,\mathfrak {m}, k)$ of dimension d, one can prove $\Omega ^d k\in {\textsf {TF}}_n(R)$ or even $\Omega ^d k\in {\textsf {Syz}}_n(R)$ for some $n>d+1$. We shall show that the answer is no. For this, we record the following lemma, whose second assertion would be of independent interest. Recall that for a local ring $(R,\mathfrak {m},k)$ of depth t the number $\text {r}(R)=\dim _k{\text {Ext}}_R^t(k,R)$ is called the type of R.

Lemma 4.4

Let $(R,\mathfrak {m},k)$ be a local ring of depth t and type r.

• (1) Assume $t=0$. Suppose that there is an exact sequence $0\rightarrow M\rightarrow F_1\xrightarrow {\partial }F_0$ of R-modules with $F_0,F_1$ free, $\text {Im}\,\partial \subseteq \mathfrak {m}F_0$, $M=\bigoplus _{i=0}^n(\Omega ^ik)^{\oplus m_i}$ and $m_0=1$. It then holds that $r=1$.

• (2) The R-module $(\Omega ^t k)^{\oplus r}$ is $(t+2)$ -syzygy.

Proof

• (1) We may assume that R is not a field. Applying ${\text {Hom}}_R(k,-)$ to the exact sequence and noting ${\text {Hom}}_R(k,\partial )=0$, we get an isomorphism ${\text {Hom}}_R(k,M)\cong {\text {Hom}}_R(k,F_1)$. Setting $s=\text {rank}_R\,F_1$, we get

  $$\begin{aligned} k^{\oplus rs} \cong {\text {Hom}}_R(k,F_1) \cong {\text {Hom}}_R(k,M) \cong {\text {Hom}}_R(k,\bigoplus _{i=0}^n(\Omega ^ik)^{\oplus m_i}) \cong \bigoplus _{i=0}^n{\text {Hom}}_R(k,\Omega ^ik)^{\oplus m_i}. \end{aligned}$$

  Hence $rs=\sum _{i=0}^nu_im_i$, where $u_i:=\dim _k{\text {Hom}}_R(k,\Omega ^ik)$. Note that for each $2\leqslant i\leqslant n$ there is an exact sequence $0\rightarrow \Omega ^ik\rightarrow R^{\oplus b_{i-1}}\xrightarrow {\delta _{i-1}}R^{\oplus b_{i-2}}$ with $\text {Im}\,\delta _{i-1}\subseteq \mathfrak {m}R^{\oplus b_{i-2}}$ and $b_j=\beta _j(k)$ for each j. Similarly as above, we obtain isomorphisms $k^{\oplus u_i} \cong {\text {Hom}}_R(k,\Omega ^ik) \cong {\text {Hom}}_R(k,R^{\oplus b_{i-1}}) \cong k^{\oplus rb_{i-1}}$, which imply $u_i=rb_{i-1}$ for all $2\leqslant i\leqslant n$. As R is not a field, the map ${\text {Hom}}_R(k,\mathfrak {m})\rightarrow {\text {Hom}}_R(k,R)$ induced from the inclusion map $\mathfrak {m}\rightarrow R$ is an isomorphism. Hence $u_i=rb_{i-1}$ for all $1\leqslant i\leqslant n$. We have $u_0=\dim _k{\text {Hom}}_R(k,k)=1$, while $m_0=1$ by assumption. We obtain $rs=\sum _{i=0}^nu_im_i=u_0m_0+\sum _{i=1}^nrb_{i-1}m_i=1+\sum _{i=1}^nrb_{i-1}m_i$, and get $r(s-\sum _{i=1}^nb_{i-1}m_i)=1$. This forces us to have $r=1$.

• (2) Take an R-sequence ${\varvec{x}}=x_1,\dots ,x_t$. Then the socle of $R/({\varvec{x}})$ is isomorphic to $k^{\oplus r}$. Let $y_1,\dots ,y_n$ be elements of $\mathfrak {m}$ whose residue classes form a system of generators of $\mathfrak {m}/({\varvec{x}})$. Then we have an exact sequence $0\rightarrow k^{\oplus r}\rightarrow R/({\varvec{x}})\xrightarrow {m}(R/({\varvec{x}}))^{\oplus n}\rightarrow L\rightarrow 0$, where m is given by the transpose of the matrix $(y_1,\dots ,y_n)$. Applying the functor $\Omega ^t=\Omega _R^t$, we get an exact sequence $0\rightarrow (\Omega ^tk)^{\oplus r}\rightarrow P\rightarrow Q\rightarrow \Omega ^tL\rightarrow 0$ of R-modules with P, Q free. Consequently, we obtain the containment $(\Omega ^tk)^{\oplus r}\in {\textsf {Syz}}_{t+2}(R)$.

$\square$

Now we can prove the following theorem.

Theorem 4.5

Let $(R,\mathfrak {m},k)$ be a local ring of dimension d and depth t.

• (1) The module $\Omega ^tk$ is $(t+2)$ -syzygy if and only if the local ring R has type one.

• (2) Suppose that the subcategory ${\textsf {Syz}}_{t+2}(R)$ is closed under direct summands. Then R has type one.

• (1) Suppose that R is Cohen–Macaulay. Then the ring R is Gorenstein if and only if $\Omega ^dk$ is $(d+2)$ -syzygy, if and only if ${\textsf {Syz}}_{d+2}(R)$ is closed under direct summands.

Proof

Assertion (2) immediately follows from (1) and Lemma 4.4(2). Assertion (3) is a direct consequence of (1) and (2). The “if” part of (1) follows from Lemma 4.4(2). To show the “only if” part, put $r=\text {r}(R)$. By assumption, there is an exact sequence $0\rightarrow \Omega ^tk\rightarrow F_{t+1}\xrightarrow {\partial _{t+1}}F_t\xrightarrow {\partial _t}\cdots \xrightarrow {\partial _1}F_0\rightarrow M\rightarrow 0$ with $F_i$ free for all $0\leqslant i\leqslant t+1$. If $\Omega ^tk$ has a nonzero free summand, then R is regular by [7, Corollary 1.3] and $r=1$. We may assume that $\Omega ^tk$ has no nonzero free summand, and hence we may assume $\text {Im}\,\partial _i\subseteq \mathfrak {m}F_{i-1}$ for all $1\leqslant i\leqslant t+1$. Set $N=\text {Im}\,\partial _t$. The depth lemma shows ${\text {depth}}\, N\geqslant t$. Choose a regular sequence ${\varvec{x}}=x_1,\dots ,x_t$ on R and N with $x_i\in \mathfrak {m}\setminus \mathfrak {m}^2$ for all $1\leqslant i\leqslant t$. Putting $\overline{(-)}=(-)\otimes _RR/({\varvec{x}})$ and applying [22, Corollary 5.3], we have an isomorphism $\overline{\Omega _R^tk}\cong \bigoplus \nolimits_{i=0}^t(\Omega _{\overline{R}}^ik)^{\oplus \, \left( {\begin{array}{c}t\\ i\end{array}}\right) }$, and an exact sequence $0\rightarrow \overline{\Omega ^tk}\rightarrow \overline{F_{t+1}}\xrightarrow {\overline{\partial _{t+1}}}\overline{F_t}\rightarrow \overline{N}\rightarrow 0$ is induced. We apply Lemma 4.4(1) to obtain $r=1$. $\square$

Theorem 4.5(1) may lead us to wonder whether the condition that $\Omega ^tk$ is $(t+2)$-syzygy already implies that R is Gorenstein. The next example answers in the negative.

Example 4.6

Let R be a local ring with $R/({\varvec{z}})\cong k[\![x,y]\!]/(x^2,xy)$ for some R-sequence ${\varvec{z}}=z_1,\dots ,z_t$. Then R has depth t and type 1, so $\Omega ^tk$ is $(t+2)$-syzygy by Theorem 4.5(1), but R is not Gorenstein.

In view of Theorem 4.5, it is natural to ask the following question.

Question 4.7

Let R be a local ring with residue field k, and let $n\geqslant {\text {depth}}\, R$ be an integer. Assume that $\Omega ^n k$ is $(n+2)$-syzygy (note that this assumption is satisfied if ${\textsf {Syz}}_{n+2}(R)$ is closed under direct summands by Lemma 4.4(2)). Does then R have type one? What if we also assume R is Cohen–Macaulay?

Note that Theorem 4.5(1) exactly says that Question 4.7 has an affirmative answer when $n=t$, which is why we were able to derive Theorem 4.5(3). We record some special cases, apart from that already contained in Theorem 4.5(3), where Question 4.7 has a positive answer.

Proposition 4.8

Let $(R,\mathfrak {m},k)$ be a local ring of depth t. Suppose that ${\textsf {Syz}}_{n+2}(R)$ is closed under direct summands for some $n\geqslant t$. Then R has type one in either of the following two cases.

• (1) One has $t>0$ and there is an R-sequence ${\varvec{x}}=x_1,\dots , x_{t-1}$ such that $\mathfrak {m}/({\varvec{x}})$ is decomposable.

• (2) The module $\Omega ^t k$ is a direct summand of $\Omega ^{t+l} k$ for some $l>0$ (this holds if R is singular and Burch).

Proof

• (1) Write ${\overline{R}}=R/({\varvec{x}})$ and $\overline{\mathfrak {m}}=\mathfrak {m}/({\varvec{x}})$. Since $\overline{\mathfrak {m}}$ is decomposable, ${\overline{R}}$ is singular. Fix $s\geqslant 0$. By [19, Theorem A] we have $\Omega _{{\overline{R}}}k=\overline{\mathfrak {m}}\lessdot \Omega _{{\overline{R}}}^3L\oplus \Omega _{{\overline{R}}}^4L\oplus \Omega _{{\overline{R}}}^5L=\Omega ^{s+3}_{{\overline{R}}}N$, where $L=\Omega _{{\overline{R}}}^sk$ and $N=k\oplus \Omega _{{\overline{R}}}k\oplus \Omega ^2_{{\overline{R}}}k$. Taking the functor $\Omega _R^{t-1}$ and applying [19, Lemma 4.2], we obtain $\Omega _R^tk\oplus F\lessdot \Omega _R^{s+t+2}N\oplus G\in {\textsf {Syz}}_{s+t+2}(R)$ for some free R-modules F, G. By assumption, we can choose $s\geqslant 0$ so that ${\textsf {Syz}}_{s+t+2}(R)$ is closed under direct summands. Then we have $\Omega _R^t k\in {\textsf {Syz}}_{s+t+2}(R)\subseteq {\textsf {Syz}}_{t+2}(R)$, and Theorem 4.5(2) implies $\text {r}(R)=1$.

• (2) Applying the functor $\Omega ^l$ to the relation $\Omega ^tk\lessdot \Omega ^{t+l}k$ repeatedly, we have $\Omega ^t k\lessdot \Omega ^{t+bl}k$ for every $b\geqslant 1$. Choose b so that $t+bl\geqslant n+2$. As ${\textsf {Syz}}_{n+2}(R)$ is closed under direct summands, we get $\Omega ^t k\in {\textsf {Syz}}_{n+2}(R)$. Theorem 4.5 implies $\text {r}(R)=1$. If R is a singular Burch ring, then $\Omega ^t k\lessdot \Omega ^{t+2} k$ by [6, Proposition 5.10].

$\square$

Next we show that the converse to Theorem 4.5(2) is not true, that is, it is possible that R is a local ring of depth t and type 1 but ${\textsf {Syz}}_{t+2}(R)$ is not closed under direct summands. Moreover, we shall show that for large classes of local rings R with decomposable maximal ideal and of integers n the subcategory ${\textsf {Syz}}_n(R)$ is not closed under direct summands. For this, we begin with establishing a lemma.

Lemma 4.9

Let $(R,\mathfrak {m},k)$ be local and with ${\text {depth}}\, R=t$. Then ${\text {depth}}\, M=t$ for each $0\ne M\in {\textsf {Syz}}_{t+2}(R)$.

Proof

By the depth lemma it suffices to show ${\text {depth}}\, M\leqslant t$, which holds if $R\lessdot M$. We may let $M\cong \Omega ^{t+2}C$ for some R-module C, and get an exact sequence $0\rightarrow M\rightarrow F\xrightarrow {f} G\rightarrow N\rightarrow 0$ with F, G free, N t-syzygy and $\text {Im}\,f\subseteq \mathfrak {m}G$. Again by the depth lemma ${\text {depth}}\, N\geqslant t$. Break the exact sequence down as $0\rightarrow M\rightarrow F\rightarrow \Omega N\rightarrow 0$ and $0\rightarrow \Omega N\rightarrow G\rightarrow N\rightarrow 0$. We get exact sequences ${\text {Ext}}_R^t(k,M)\xrightarrow {a}{\text {Ext}}_R^t(k,F)\xrightarrow {b}{\text {Ext}}_R^t(k,\Omega N)$ and $0={\text {Ext}}_R^{t-1}(k,N)\rightarrow {\text {Ext}}_R^t(k,\Omega N)\xrightarrow {c}{\text {Ext}}_R^t(k,G)$. Note that $cb={\text {Ext}}_R^t(k,f)=0$. As c is injective, we have $b=0$ and a is surjective. Since ${\text {Ext}}_R^t(k,F)\ne 0$, we obtain ${\text {Ext}}_R^t(k,M)\ne 0$. $\square$

Remark 4.10

The $(t+2)$nd threshold in Lemma 4.9 is sharp. Indeed, let $(R,\mathfrak {m})$ be a local ring with $\dim R>0={\text {depth}}\, R$. Then there exists $\mathfrak {m}\ne {\mathfrak {p}}\in {\text {Ass}}\, R$. We have ${\text {depth}}\, R/{\mathfrak {p}}>0$ and $0\ne R/{\mathfrak {p}}\in {\textsf {Syz}}_1(R)$.

Now we produce the promised classes of local rings R and integers n.

Proposition 4.11

Let $(R,\mathfrak {m},k)$ be a local ring such that $\mathfrak {m}=I\oplus J$ for some nonzero ideals I, J of R.

• (1) Suppose that ${\text {depth}}\, R/I=0$ and ${\text {depth}}\, R/J\geqslant 1$. Then one has ${\text {depth}}\, R=0$, and the subcategory ${\textsf {Syz}}_n(R)$ is not closed under direct summands for every $n\geqslant 2$.

• (2) Suppose that I is indecomposable and ${\text {depth}}\, R/I \geqslant 2$. Then one has ${\text {depth}}\, R\leqslant 1$, and the subcategory ${\textsf {Syz}}_n(R)$ is not closed under direct summands for every $n\geqslant 4$.

Proof

By [19, Fact 3.1] we have ${\text {depth}}\, R=\min \{{\text {depth}}\, R/I,{\text {depth}}\, R/J,1\}\leqslant 1$.

• (1) Since $I\cong \mathfrak {m}/J\subseteq R/J$ and ${\text {depth}}\, R/J>0$, we see that ${\text {depth}}\, I\geqslant 1$. Lemma 4.9 yields $I\notin {\textsf {Syz}}_2(R)$. By [19, Theorem A] we get $I\lessdot \mathfrak {m}\lessdot \Omega ^3(\Omega ^ik)\oplus \Omega ^4(\Omega ^ik)\oplus \Omega ^5(\Omega ^ik)\in {\textsf {Syz}}_{i+3}(R)\subseteq {\textsf {Syz}}_{i+2}(R)$ for every $i\geqslant 0$. If ${\textsf {Syz}}_n(R)$ is closed under direct summands for some $n\geqslant 2$, then choosing $i=n-2$, we obtain $I\in {\textsf {Syz}}_n(R)\subseteq {\textsf {Syz}}_2(R)$, which is a contradiction.

• (2) Note that $IJ=0$. We also have $J^2\ne 0$, as otherwise $\mathfrak {m}^2=(I+J)(I+J)=I^2\subseteq I$, contradicting ${\text {depth}}\, R/I\geqslant 2$. Similarly as in the proof of (1), for each $i\geqslant 0$ there exists $X\in {\textsf {Syz}}_{i+3}(R)$ with $I\lessdot X$.

  Assuming that ${\textsf {Syz}}_n(R)$ is closed under direct summands for some $n\geqslant 4$, we shall derive a contradiction. Choosing $i=n-3$, we get $I\in {\textsf {Syz}}_n(R)\subseteq {\textsf {Syz}}_4(R)$. The equality $IJ=0$ implies that I does not have a nonzero free summand. Hence $I\cong \Omega ^4H$ for some R-module H. Putting $M=\Omega ^3H$, we get an exact sequence $0\rightarrow I\rightarrow R^{\oplus a}\rightarrow M\rightarrow 0$. Note that $M\ne 0$. By [18, Proposition 4.2] there are an R/I-module A and an R/J-module B such that $M\cong A \oplus B$. Now $I=\Omega _R M\cong \Omega _RA \oplus \Omega _R B$. Then indecopmosability of I implies $\Omega _R A=0$ or $\Omega _RB=0$, hence A or B is R-free. As $IA=0=JB$, either $A=0$ or $B=0$. If $A=0$, then we get an exact sequence $0\rightarrow I\rightarrow R^{\oplus a}\rightarrow B\rightarrow 0$ and I, B are annihilated by J, whence $J^2R^{\oplus a}=0$, contradicting $J^2\ne 0$. We get $B=0$ and an exact sequence $0\rightarrow I\rightarrow R^{\oplus a}\rightarrow A\rightarrow 0$. As $IA=0$, the surjection $R^{\oplus a}\rightarrow A$ factors through the canonical surjection $R^{\oplus a}\rightarrow (R/I)^{\oplus a}$, which induces a surjection $I\rightarrow \Omega _{R/I}A$. Since $IJ=0$, the module $\Omega _{R/I}A$ is annihilated by I, J and by $I+J=\mathfrak {m}$. Thus $\Omega _{R/I}A\cong k^{\oplus s}$ for some $s\geqslant 0$. But $\Omega _{R/I} A$ embeds inside a free R/I-module which has positive depth, hence k cannot be a summand of $\Omega _{R/I} A$, thus $\Omega _{R/I}A=0$. Therefore A is R/I-free and has depth at least 2. But $A\cong M$ has depth at most 1 by Lemma 4.9. We now have a desired contradiction.

$\square$

The ring R in the first example below shows that the converse to Theorem 4.5(2) does not hold. The second example presents a local ring R of depth 1 and type 1 such that ${\textsf {Syz}}_n(R)$ is not closed under direct summands for every $n\geqslant 4$, which concretely illustrates Proposition 4.11(2). The third example shows that the assumption ${\text {depth}}\, R/I\geqslant 2$ in Proposition 4.11(2) cannot be dropped.

Example 4.12

Let k be a field. In each of the following statements, $\mathfrak {m}$ denotes the maximal ideal of R.

• (1) Consider the local ring $R=k[\![x,y]\!]/(x^2,xy)$. Then $\mathfrak {m}=(y) \oplus (x)$, ${\text {depth}}\, R/(y)=0$ and ${\text {depth}}\, R/(x)=1$. Proposition 4.11(1) shows that ${\textsf {Syz}}_n(R)$ is not closed under direct summands for all $n\geqslant 2$.

• (2) Let $R=k[\![x,y,z]\!]/(xy,xz)$. Then $\mathfrak {m}=(x)\oplus (y,z)$ and (x) is indecomposable with ${\text {depth}}\, R/(x)=2$. Proposition 4.11(2) implies that ${\textsf {Syz}}_{n+3}(R)$ is not closed under direct summands for every $n\geqslant 4$.

• (3) Let $R=k[\![x,y]\!]/(xy)$. Then $\mathfrak {m}=(x)\oplus (y)$ and (x) is indecomposable with ${\text {depth}}\, R/(x)=1$. As R is a 1-dimensional Gorenstein ring, ${\textsf {Syz}}_n(R)={\textsf {CM}}(R)$ is closed under direct summands for any $n\geqslant 1$.

5 Closedness under extensions and syzygies, and totally reflexive modules

In this section, we derive some consequences of ${\textsf {TF}}_n (R)$ being closed under extensions or syzygies for certain values of n depending on the depth of the local ring R. We will see that in the most reasonable cases, if ${\textsf {TF}}_n(R)$ is resolving, then it coincides with the category of totally reflexive modules.

We begin with investigating when the subcategory ${\textsf {TF}}_n(R)$ is closed under extensions or syzygies. For two subcategories $\mathcal {X},\mathcal {Y}$ of ${\textsf{mod }}\,R$ we denote by $\mathcal {X}*\mathcal {Y}$ the subcategory consisting of modules X that fits into an exact sequence $0\rightarrow M\rightarrow X\rightarrow N\rightarrow 0$ with $M\in \mathcal {X}$ and $N\in \mathcal {Y}$.

Proposition 5.1

Let n be either a nonnegative integer or $\infty$ . The following statements hold.

• (1) If M is an R-module such that $({\textsf{add}}\,R)*M\subseteq {\textsf {TF}}_n(R)$, then there is a containment $\Omega M\in {\textsf {TF}}_{n+1}(R)$.

• (2) If the subcategory ${\textsf {TF}}_n(R)$ is closed under extensions, then the inclusion $\Omega {\textsf {TF}}_n(R)\subseteq {\textsf {TF}}_{n+1}(R)$ holds.

• (3) The subcategory ${\textsf {TF}}_n(R)$ is resolving if (and only if) ${\textsf {TF}}_n(R)$ is closed under extensions.

• (4) Suppose that ${\textsf {TF}}_{n+1}(R)$ is closed under extensions. If R satisfies $(\mathrm {S}_n)$, then $R_{\mathfrak {p}}$ is Gorenstein for all ${\mathfrak {p}}\in \text {Spec}\,R$ with ${\text {ht}}\,{\mathfrak {p}}=n$. If R satisfies $(\mathrm {S}_{n+1})$ and is local with $\dim R\geqslant n$, then R satisfies $(\mathrm {G}_n)$.

• (5) Suppose that R is a local ring of depth t.

  • (a) Let $n\geqslant t+2$ . Then ${\textsf {TF}}_{n}(R)={\textsf {GP}}(R)$ if (and only if) ${\textsf {TF}}_{n} (R)$ is closed under syzygies.

  • (b) Let $n\geqslant t+1$. Then ${\textsf {TF}}_n(R)={\textsf {GP}}(R)$ if (and only if) ${\textsf {TF}}_{n}(R)$ is closed under extensions. When $n=t+1$, it is also equivalent to the Gorenstein property of the local ring R.

Proof

• (1) By [1, Proposition (2.21)] and its proof, there is an exact sequence $0\rightarrow P\rightarrow N\rightarrow M\rightarrow 0$ with $P\in {\textsf{add}}\,R$, where $N={\textsf {Tr}}\,\Omega {\textsf {Tr}}\,\Omega M$. We have $N\in ({\textsf{add}}\,R)*M\subseteq {\textsf {TF}}_{n}(R)$, and hence $N\in {\textsf {TF}}_n(R)\cap \mathcal {G}_{1,0}=\mathcal {G}_{1,n}$. By [14, Proposition 1.1.1] and [1, Theorem 2.17] we get $\Omega M\approx \Omega N\in \Omega \mathcal {G}_{1,n}(R) \subseteq {\textsf {TF}}_{n+1}(R)$.

• (2) The assertion immediately follows from (1) as we have $({\textsf{add}}\,R)*{\textsf {TF}}_n(R)\subseteq {\textsf {TF}}_n(R)$ by assumption.

• (3) The assertion is a direct consequence of (2) together with the general fact ${\textsf {TF}}_{n+1}(R)\subseteq {\textsf {TF}}_n(R)$.

• (4) The second assertion follows by the first and [11, Theorem 4.1]. To show the first assertion, let ${\mathfrak {p}}\in \text {Spec}\,R$ with ${\text {ht}}\,{\mathfrak {p}}=n$, $i\geqslant 0$ and $M={\text {Ext}}_R^i(R/{\mathfrak {p}},R)$. Each $\mathfrak {q}\in \text {Supp}\,M$ contains ${\mathfrak {p}}$, so ${\text {ht}}\,\mathfrak {q}\geqslant {\text {ht}}\,{\mathfrak {p}}=n$. As R satisfies $(\mathrm {S}_n)$, we get ${\text {depth}}\, R_\mathfrak {q}\geqslant n$. By [3, Proposition 1.2.10(a)] we have ${\text {grade}}\, M\geqslant n$. It follows from [1, Proposition (2.26)] that $\Omega ^{n+1}(R/{\mathfrak {p}})\in {\textsf {TF}}_{n+1}(R)$. We see from (2) that $\Omega {\textsf {TF}}_{n+1}(R)\subseteq {\textsf {TF}}_{n+2}(R)$, and hence $\Omega ^{n+2}(R/{\mathfrak {p}})\in {\textsf {TF}}_{n+2}(R)$, which induces $\Omega ^{n+2}\kappa ({\mathfrak {p}})\in {\textsf {TF}}_{n+2}(R_{\mathfrak {p}})$. Using again the assumption that R satisfies $(\mathrm {S}_n)$, we have ${\text {depth}}\, R_{\mathfrak {p}}=n$. It follows from Theorem 4.1(3) that $R_{\mathfrak {p}}$ is Gorenstein.

• (5a) Fix $M\in {\textsf {TF}}_{n}(R)$. By assumption $\Omega M\in {\textsf {TF}}_{n}(R)$ i.e. ${\text {Ext}}_R^i({\textsf {Tr}}\,\Omega M,R)=0$ for all $1\leqslant i\leqslant n$ By [1, Theorem (2.8)] there is an exact sequence $0=\text {Tor}_1^R(M,R)\rightarrow ({\text {Ext}}_R^1(M,R))^*\rightarrow {\text {Ext}}_R^2({\textsf {Tr}}\,\Omega M,R)=0$. Hence $({\text {Ext}}_R^1(M,R))^*=0$. By [1, Proposition (2.6)], there exists an exact sequence $0\rightarrow {\text {Ext}}_R^1(M,R)\rightarrow {\textsf {Tr}}\,M\rightarrow \Omega {\textsf {Tr}}\,\Omega M\rightarrow 0$, which induces an exact sequence ${\text {Ext}}_R^i({\textsf {Tr}}\,M,R)\rightarrow {\text {Ext}}_R^i({\text {Ext}}_R^1(M,R),R)\rightarrow {\text {Ext}}^{i+1}_R(\Omega {\textsf {Tr}}\,\Omega M,R)={\text {Ext}}_R^{i+2}({\textsf {Tr}}\,\Omega M,R)$ for every $i\geqslant 0$. This implies ${\text {Ext}}_R^i({\text {Ext}}_R^1(M,R),R)=0$ for all $1\leqslant i\leqslant n-2$. Thus ${\text {Ext}}_R^i({\text {Ext}}_R^1(M,R),R)=0$ for all $0\leqslant i\leqslant n-2$, that is, ${\text {grade}}\,{\text {Ext}}_R^1(M,R)\geqslant n-1>t$. As ${\text {depth}}\, R=t$, we must have ${\text {Ext}}^1_R(M,R)=0$. Replacing M by $\Omega ^iM$ for $i\geqslant 0$, we get ${\text {Ext}}_R^{>0}(M,R)=0$ i.e. $M\in \mathcal {G}_{\infty ,0}$. So, ${\textsf {Tr}}\,M\in \mathcal {G}_{0,\infty }\subseteq {\textsf {TF}}_{n}(R)$. By what we have seen, ${\textsf {Tr}}\,M\in \mathcal {G}_{\infty ,0}$. Thus $M\in {\textsf {GP}}(R)$.

• (5b) Using (2), we observe that $\Omega {\textsf {TF}}_n(R)\subseteq {\textsf {TF}}_{n+1}(R)\subseteq {\textsf {TF}}_n(R)$. The case $n \geqslant t+2$ follows from (5a). Now we consider the case $n=t+1$. Theorem 4.1(1) yields that $\Omega ^nk\in {\textsf {TF}}_n(R)$, which implies that $\Omega ^{n+1}k\in \Omega {\textsf {TF}}_n(R)\subseteq {\textsf {TF}}_{n+1}(R)$. Theorem 4.1(3) implies that R is Gorenstein and thus ${\textsf {TF}}_n(R)={\textsf {GP}}(R)$. Therefore, R is a Gorenstein ring if (and only if) the subcategory ${\textsf {TF}}_{t+1}(R)$ is closed under extensions.

$\square$

Remark 5.2

• (1) Proposition 5.1(1) for $n=1$ recovers [13, Corollary 2.2]. Indeed, it says if ${\textsf {TF}}_{1}(R)={\textsf {Syz}}_1(R)$ is closed under extensions, then $\Omega M \in {\textsf {TF}}_{2}(R)={\textsf {ref}}\,R$ for $M\in {\textsf {TF}}_{1}(R)$. As $\Omega ^2 {\textsf {Tr}}\,M\approx M^*$, we have that if ${\textsf {Syz}}_1(R)$ is closed under extensions, then $M^*\in {\textsf {ref}}\,R$ for every $M\in {\textsf{mod }}\,R$.

• (2) The inequality $\dim R\geqslant n$ in Proposition 5.1(4) is sharp. Indeed, if $(R,\mathfrak {m})$ is a non-Gorenstein local ring with $\mathfrak {m}^2=0$, then ${\textsf {TF}}_2(R)={\textsf {proj}}\,R$ (see Lemma 3.4) is closed under extensions.

• (3) Proposition 5.1(4) refines [17], Theorem 2.3(3)$\Rightarrow$(2)] in some cases.

Next we show the proposition below, which can also be of some independent interest.

Proposition 5.3

Let $(R,\mathfrak {m},k)$ be a local ring of depth t. Let $a\in \{t,t+1 \}$ and $n\geqslant a$.

• (1) Let $K\in {\textsf {mod}}_0\,R$. If ${\text {Ext}}_R^{a+1}({\textsf {Tr}}\,M,R)=0$ for all $M\in R*\Omega ^nK$, then ${\text {Ext}}_R^{n+1}(K,R)=0$.

• (2) If ${\text {Ext}}_R^{a+1}({\textsf {Tr}}\,M,R)=0$ for every $M\in R*\Omega ^n k$, then the local ring R is Gorenstein.

Proof

• (1) As $n\geqslant t$, the conclusion is clear if R is Gorenstein. Let R be non-Gorenstein. Put $L=\Omega ^nK$. Assuming ${\text {Ext}}^{n+1}_R(K,R)={\text {Ext}}^1_R(L,R)\ne 0$, we work towards a contradiction. The choice of K implies that ${\text {Ext}}^1_R(L,R)$ has finite length. Choose a socle element $0\ne \sigma \in {\text {Ext}}^1_R(L,R)$. Let $0\rightarrow R\rightarrow N\rightarrow L\rightarrow 0$ be the exact sequence corresponding to $\sigma$. Then N is in $R*L$, and ${\text {Ext}}_R^{a+1}({\textsf {Tr}}\,N,R)=0$ by assumption. Using the snake lemma, we get the following commutative diagrams with exact rows and columns.

  

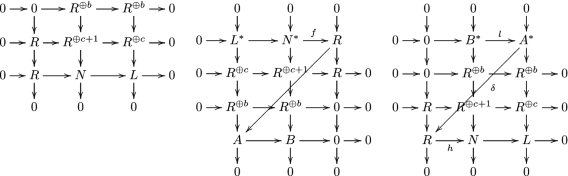
  Note that $A\approx {\textsf {Tr}}\,\Omega ^nK$ and $B\approx {\textsf {Tr}}\,N$. There is also an exact sequence $N^*\xrightarrow {f}R\xrightarrow {g}{\text {Ext}}_R^1(\Omega ^nK,R)$ with $g(1)=\sigma$. It is seen that ${\text {Coker}}\, f\cong k$. We get exact sequences $0\rightarrow k\rightarrow A\rightarrow B\rightarrow 0$, and

  $$\begin{aligned} {\text {Ext}}_R^a(B,R)\rightarrow {\text {Ext}}_R^a(A,R)\rightarrow {\text {Ext}}_R^a(k,R)\rightarrow {\text {Ext}}_R^{a+1}(B,R)={\text {Ext}}_R^{a+1}({\textsf {Tr}}\,N,R)=0. \end{aligned}$$

  (8)

  Using Theorem 4.1(1) and the general fact that ${\textsf {TF}}_{i+1}(R)\subseteq {\textsf {TF}}_i(R)$ for $i\geqslant 0$, we obtain $\Omega ^n K\in {\textsf {TF}}_a(R)$. Suppose $a\geqslant 1$. Then ${\text {Ext}}_R^a(A,R)={\text {Ext}}^a_R({\textsf {Tr}}\,\Omega ^n K,R)=0$, and it follows from (8) that ${\text {Ext}}^a_R(k,R)=0$. As $a\in \{t,t+1\}$, we must have $a=t+1$. By [20, II. Theorem 2] the ring R is Gorenstein, and we get a desired contradiction. Thus we may assume $a=0$, and then $t=0$. The slanted arrow $\delta :A^*\rightarrow R$ in the third diagram above is a zero map by the injectivity of the map h. Hence the map l is surjective (and hence an isomorphism). From (8) we get $k^*=0$, which is a contradiction to the fact that $t=0$.

• (2) By (1) we have ${\text {Ext}}_R^{n+1}(k,R)=0$. Since $n\geqslant t$, the ring R is Gorenstein by [20, II. Theorem 2].

$\square$

Applying the above proposition, we can prove the following theorem.

Theorem 5.4

Let $(R,\mathfrak {m},k)$ be local with depth t. Then R is Gorenstein if and only if ${\textsf {Syz}}_m(R)$ is closed under extensions for some integer $m>t$, if and only if $R*\Omega ^n k\subseteq {\textsf {Syz}}_{t+1}(R)$ for some integer $n\geqslant t$.

Proof

First, suppose that ${\textsf {Syz}}_m(R)$ is closed under extensions for some integer $m>t$. Then $m-1\geqslant t$ and $\Omega ^{m-1}k\in {\textsf {Syz}}_m(R)$ by Theorem 4.1(2). We obtain $R*\Omega ^{m-1}k\in {\textsf {Syz}}_m(R)\subseteq {\textsf {Syz}}_{t+1}(R)$. Next, suppose that $R*\Omega ^nk\subseteq {\textsf {Syz}}_{t+1}(R)$ for some $n\geqslant t$. Then $R*\Omega ^nk\subseteq {\textsf {Syz}}_{t+1}(R)\cap {\textsf {mod}}_0\,R\subseteq {\textsf {TF}}_{t+1}(R)$ by Theorem 4.1(1). Hence ${\text {Ext}}_R^{t+1}({\textsf {Tr}}\,M,R)=0$ for all $M\in R*\Omega ^nk$. Proposition 5.3(2) implies R is Gorenstein. $\square$

To show our next result, we prepare a lemma to get a certain property of ${\widetilde{\textsf {S}}}_n(R)$.

Lemma 5.5

If $\Omega {\widetilde{\textsf {S}}}_n(R)$ is closed under extensions, then one has the equality $\Omega {\widetilde{\textsf {S}}}_n(R)={\widetilde{\textsf {S}}}_{n+1}(R)$.

Proof

We easy see that $\Omega {\widetilde{\textsf {S}}}_n(R)\subseteq {\widetilde{\textsf {S}}}_{n+1}(R)$. The subcategory ${\widetilde{\textsf {S}}}_n(R)$ is resolving and contains ${\textsf {Syz}}_n(R)$. By assumption and by Lemma 3.1(2) the subcategory $\Omega {\widetilde{\textsf {S}}}_n(R)$ is resolving, and it contains $\Omega {\textsf {Syz}}_n(R)={\textsf {Syz}}_{n+1}(R)$. Hence $\Omega {\widetilde{\textsf {S}}}_n(R)$ contains ${\textsf {res}}\,{\textsf {Syz}}_{n+1}(R)={\widetilde{\textsf {S}}}_{n+1}(R)$ by Proposition 3.2(1). $\square$

The corollary below states several consequences of Theorem 5.4. The first two assertions of the corollary give necessary and sufficient conditions for R to be Gorenstein. In [17, Theorem 2.3(8)] it is required that R satisfies $(\mathrm {S}_n)$ along with ${\textsf {Syz}}_n(R)$ being closed under extensions. In the third assertion of the corollary, we show some special cases where the condition of $(\mathrm {S}_n)$ can be dropped.

Corollary 5.6

Let $(R,\mathfrak {m},k)$ be a local ring of dimension d and depth t.

• (1) One has that R is a Gorenstein local ring if and only if $\Omega {\widetilde{\textsf {S}}}_n(R)$ is closed under extensions for some consecutive $(t+1)$-many values of n.

• (2) The ring R is Gorenstein if and only if R is Cohen–Macaulay and $\Omega {\textsf {CM}}(R)$ is closed under extensions.

• (3) If ${\textsf {Syz}}_n(R)$ is closed under extensions for some $n\geqslant \min \{d,t+1\}$, then R is Cohen–Macaulay and ${\textsf {TF}}_i(R)={\textsf {Syz}}_i(R)$ for all $1\leqslant i\leqslant n+1$.

Proof

• (1) If R is Gorenstein, then for all $n\geqslant d$ one has ${\widetilde{\textsf {S}}}_n(R)={\textsf {CM}}(R)$ and $\Omega {\widetilde{\textsf {S}}}_n(R)={\textsf {CM}}(R)$, and ${\textsf {CM}}(R)$ is closed under extensions. This shows the “only if” part. From now on we prove the “if” part. There is an integer $l\geqslant 0$ such that $\Omega {\widetilde{\textsf {S}}}_n(R)$ is closed under extensions for $l\leqslant n\leqslant l+t$. We have $\Omega ^lk\in {\widetilde{\textsf {S}}}_l(R)$, so that $\Omega ^{t+1+l}k\in \Omega ^{t+1}{\widetilde{\textsf {S}}}_l(R)={\widetilde{\textsf {S}}}_{t+1+l}(R)$ by Lemma 5.5. Since ${\widetilde{\textsf {S}}}_{t+1+l}(R)$ is resolving, this implies $R*\Omega ^{t+1+l}k\subseteq {\widetilde{\textsf {S}}}_{t+1+l}(R)=\Omega ^{t+1}{\widetilde{\textsf {S}}}_l(R)\subseteq {\textsf {Syz}}_{t+1}(R)$. Theorem 5.4 implies that R is Gorenstein.

• (2) If R is Cohen–Macaulay, then ${\widetilde{\textsf {S}}}_n(R)={\textsf {CM}}(R)$ for all $n\geqslant d$. If R is Gorenstein, then $\Omega {\textsf {CM}}(R)={\textsf {CM}}(R)$. The assertion now follows from (1).

• (3) If $n\geqslant t+1$, then R is Gorenstein by Theorem 5.4 and ${\textsf {TF}}_i(R)={\textsf {Syz}}_i(R)$ for all $i\geqslant 0$ by [1, Corollary (4.22)]. Assume $n\geqslant d$ and R is not Cohen–Macaulay. Then $n\geqslant d\geqslant t+1$ and Theorem 5.4 implies R is Gorenstein, which contradicts the assumption that R is not Cohen–Macaulay. Thus R must be Cohen–Macaulay, hence satisfies $(\mathrm {S}_n)$. By [17], Theorem 2.3(8)$\Rightarrow$(6)] we get ${\textsf {TF}}_{n+1}(R)={\textsf {Syz}}_{n+1}(R)$, and finally by [1, Corollary 4.18] we obtain ${\textsf {TF}}_i(R)={\textsf {Syz}}_i(R)$ for all $1\leqslant i\leqslant n+1$.

$\square$

Question 5.7

Let R be a local ring of depth t such that ${\textsf {Syz}}_t(R)$ is closed under extensions. Then, is ${\textsf {TF}}_t(R)$ also closed under extensions, or at least closed under syzygies? (Note that Proposition 5.1(3) implies that if ${\textsf {TF}}_t(R)$ is closed under extensions, then it is closed under syzygies).

Here we record the following observation on $\mathcal {G}_{a,b}$. We should compare it with Proposition 5.1(5a).

Proposition 5.8

• (1) Let $0<a<\infty$ and $0\leqslant b\leqslant \infty$. Then the subcategory $\mathcal {G}_{a,b}$ is closed under syzygies if and only if there is an equality $\mathcal {G}_{a,b}={\textsf {GP}}(R)$.

• (2) Suppose that $(R,\mathfrak {m},k)$ is a local ring of depth t. Let $n\in \mathbb {Z}_{>0}\cup \{\infty \}$ be such that $\mathcal {G}_{n,0}$ is closed under syzygies. Then one has $n\geqslant t$ . If one also has $n\leqslant t+1$ , then R is a Gorenstein local ring.

Proof

• (1) For the first assertion, it suffices to show the “only if” part. Let $M\in \mathcal {G}_{a,b}$, and $i\geqslant 0$ an integer. By assumption, $\Omega ^iM$ is in $\mathcal {G}_{a,b}$. As $a>0$, we have $\Omega ^iM\in \mathcal {G}_{1,0}$, that is, ${\text {Ext}}_R^{i+1}(M,R)={\text {Ext}}_R^1(\Omega ^iM,R)=0$. Hence $M\in \mathcal {G}_{\infty ,0}$, and thus $M\in \mathcal {G}_{a,b}\cap \mathcal {G}_{\infty ,0}=\mathcal {G}_{\infty ,b}$. It follows that $\mathcal {G}_{a,b}=\mathcal {G}_{\infty ,b}$. We are done for $b=\infty$, so assume $b<\infty$. We get $\mathcal {G}_{b,a}={\textsf {Tr}}\,\mathcal {G}_{a,b}={\textsf {Tr}}\,\mathcal {G}_{\infty ,b}=\mathcal {G}_{b,\infty }$ by [14, Proposition 1.1.1]. Note that $b-a$ is an integer. Hence $\Omega ^{b-a}$ is defined, and we obtain $\mathcal {G}_{a,b}=\Omega ^{b-a}\mathcal {G}_{b,a}=\Omega ^{b-a}\mathcal {G}_{b,\infty }=\mathcal {G}_{a,\infty +b-a}=\mathcal {G}_{a,\infty }$ by [14, Proposition 1.1.1] again. It follows that $\mathcal {G}_{a,b}=\mathcal {G}_{a,\infty }$, and $\mathcal {G}_{a,b}=\mathcal {G}_{a,\infty }\cap \mathcal {G}_{\infty ,b}=\mathcal {G}_{\infty ,\infty }={\textsf {GP}}(R)$.

• (2) If $n<t$, then k is in $\mathcal {G}_{n,0}$ and so does $\Omega ^{t-n}k$ by assumption, which implies ${\text {Ext}}_R^t(k,R)=0$, a contradiction. Hence $n\geqslant t$. Suppose $n\leqslant t+1$. As $\Omega ^{t+1}k\in {\textsf {TF}}_{t+1}(R)$ by Theorem 4.1(1), applying (1) shows ${\textsf {Tr}}\,\Omega ^{t+1}k\in \mathcal {G}_{t+1,0}\subseteq \mathcal {G}_{n,0}={\textsf {GP}}(R)$. Thus $\Omega ^{t+1}k\in {\textsf {GP}}(R)$, which implies that R is Gorenstein.

$\square$

Corollary 5.9

Let $n\geqslant 0$ be an integer such that ${\textsf {TF}}_{n}(R)={\textsf {TF}}_{n+1}(R)$. Then ${\textsf {TF}}_n(R)={\textsf {GP}}(R)$.

Proof

Using [14, Proposition 1.1.1] shows $\Omega \mathcal {G}_{n+1,0}=\mathcal {G}_{n,1}\subseteq \mathcal {G}_{n,0}={\textsf {Tr}}\,{\textsf {TF}}_n(R)={\textsf {Tr}}\,{\textsf {TF}}_{n+1}(R)=\mathcal {G}_{n+1,0}$. Proposition 5.8(1) yields $\mathcal {G}_{n+1,0}={\textsf {GP}}(R)$. We conclude ${\textsf {TF}}_n(R)={\textsf {TF}}_{n+1}(R)={\textsf {Tr}}\,\mathcal {G}_{n+1,0}={\textsf {GP}}(R)$. $\square$

Remark 5.10

The dual version of Proposition 5.8(1) holds true as well: Let $0\leqslant a \leqslant \infty$ and $0<b<\infty$. Then $\mathcal {G}_{a,b}$ is closed under cosyzygies if and only if $\mathcal {G}_{a,b}={\textsf {GP}}(R)$. This is a consequence of the combination of Proposition 5.8(1), [21, Lemma 4.1] and [14, Proposition 1.1.1].