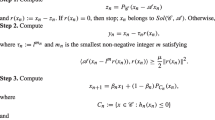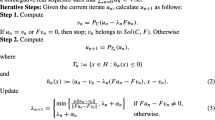1 Introduction

In this paper, we study the classical Variational Inequality (VI) of Fichera [14, 15] in real Hilbert spaces. The VI is formulated as follows: Find a point \(x^*\in C\) such that

$$\begin{aligned} \langle Ax^*,x-x^*\rangle \ge 0 \ \ \forall x\in C, \end{aligned}$$
(1)

where \(C\subseteq H\) is a nonempty, closed and convex set of a real Hilbert space H and \(A: H\rightarrow H\) is a given mapping. We denote by VI(C, A) the solution set of the VI (1).

Variational inequalities are fundamental problems which stand the core of diverse applied fields such as in economics, engineering mechanics, transportation, and many more, see for example, [2, 3, 20], just to name a few. In the last decades, many iterative methods have been constructed for solving variational inequalities and their related optimization problems, see for example the excellent book of Facchinei and Pang [13], Konnov [20] and the many references therein.

The first simplest method for solving VIs, derived from optimization theory, is known as the gradient method (GM). The iterative step of this method requires the calculation of the orthogonal projection onto the feasible set of the VI, that is C, per each iteration. Given the current iterate \(x_n\), the algorithm’s iterative step has the following form.

$$\begin{aligned} x_{n+1}=P_C(x_n-\tau Ax_n), \end{aligned}$$
(2)

where \(\tau \in (0,\dfrac{1}{L})\), L is the Lipschitz constant of A and \(P_C\) denotes the metric projection onto C. It is shown that gradient method (2) convergence under Lipschitz continuity and some restrictive monotonicity assumption, such as strong monotonicity or inverse strongly monotone, see for example [18]. Korpelevich [21] (also Antipin [1] independently) proposed a double-projection method, known as the extragradient method (EM) which enable to obtain convergence in Euclidean spaces under Lipschitz continuity and just monotonicity. Given the current iterate \(x_n\), the algorithm’s iterative step has the following form.

$$\begin{aligned} {\left\{ \begin{array}{ll} y_n=P_C(x_n-\tau Ax_n),\\ x_{n+1}=P_C(x_n-\tau Ay_n), \end{array}\right. } \end{aligned}$$
(3)

where \(\tau \) and \(P_C\) are as above. This method is studied intensively and extended and improved in various ways, for example see, e.g. [6,7,8,9,10, 25, 26, 31, 34, 35] and the references therein.

Although the extragradient method converges under weaker monotonicity assumption than the gradient method, it requires to calculate two projections onto C per each iteration. So, in case that the set C is not “easy” to project onto it, a minimum distance subproblem has to be solved twice per each iteration in order to evaluate \(P_C\), a fact which might affect the applicability and computational complexity of the method.

In a direction to overcome this obstacle, Censor et al. [7,8,9] introduced the so-called subgradient extragradient method (SEM). In this algorithm, the second projection onto C is replaced by an easy and constructible projection onto some super set which contains C. Given the current iterate \(x_n\), the algorithm’s iterative step has the following form.

$$\begin{aligned} {\left\{ \begin{array}{ll} y_n=P_C(x_n-\tau Ax_n),\\ T_n=\{x\in H \mid \langle x_n -\tau Ax_n-y_n,x-y_n\rangle \le 0\},\\ x_{n+1}=P_{T_n}(x_n-\tau Ay_n),\\ \end{array}\right. } \end{aligned}$$
(4)

where \(\tau \in (0,1/L)\).

Another method which uses only one projection onto C is projection and contraction method (PC) of He [17] (see also Sun [32]). In this method, the point \(y_n\) in calculated in the same spirit of (3), but the next iterate \(x_{n+1}\) is calculated via some adaptive step size rules. Given the current iterate \(x_n\), the algorithm’s iterative step has the following form.

$$\begin{aligned} y_n=P_C(x_n-\tau _n Ax_n), \end{aligned}$$

and then the next iterate \(x_{n+1}\) is generated via the following PC-algorithms:

$$\begin{aligned} x_{n+1}=x_n-\gamma \eta _n d(x_n,y_n), \end{aligned}$$
(5)

where \(\gamma \in (0,2), \tau _n\in (0,1/L)\) (or \(\tau _n\) is updated by some self-adaptive rule),

$$\begin{aligned} d(x_n,y_n):= x_n-y_n-\tau _n (Ax_n-Ay_n), \end{aligned}$$

and

$$\begin{aligned} \eta _n:= \dfrac{\langle x_n-y_n, d(x_n,y_n)\rangle }{\Vert d(x_n,y_n)\Vert ^2}. \end{aligned}$$

Recently, projection and contraction type methods for solving VIs have received great attention by many authors, see, e.g., [4, 11, 12], just to name a few.

Since the SEM and PC algorithms originally introduced in Euclidean spaces, a natural question which was studied is how to extend the method to infinite dimensional spaces and obtain strong convergence. In 2012, Censor et al. [8] proposed two subgradient extragradient variants, which converge strongly in real Hilbert spaces. One of the SEM variant has the following form. Given the current iterate \(x_n\), the next iterate \(x_{n+1}\) is calculated via the following.

$$\begin{aligned} {\left\{ \begin{array}{ll} y_n=P_C(x_n-\tau Ax_n),\\ T_n=\{x\in H \mid \langle x_n-\tau Ax_n-y_n,x-y_n\rangle \le 0\},\\ z_n=\alpha _n x_n+(1-\alpha _n)P_{T_n}(x_n-\tau Ay_n),\\ C_n=\{w\in H \mid \Vert z_n-w\Vert \le \Vert x_n-w\Vert \},\\ Q_n=\{w\in H \mid \langle x_n-w,x_0-x_n\rangle \ge 0\},\\ x_{n+1}=P_{C_n\cap Q_n}x_0,\ \ \forall n\ge 0. \end{array}\right. } \end{aligned}$$
(6)

Inspired by the results in [8], Kraikaew and Saejung [22] combined the subgradient extragradient method and the Halpern-type method and propose the so-called Halpern subgradient extragradient method.Given the current iterate \(x_n\), the next iterate \(x_{n+1}\) is calculated via the following.

$$\begin{aligned} {\left\{ \begin{array}{ll} y_n=P_C(x_n-\tau Ax_n),\\ T_n=\{x\in H \mid \langle x_n-\tau Ax_n-y_n,x-y_n\rangle \le 0\},\\ z_n=P_{T_n}(x_n-\tau Ay_n),\\ x_{n+1}=\alpha _nx_0+(1-\alpha _n)z_n,\ \ \forall n\ge 0, \end{array}\right. } \end{aligned}$$
(7)

where \(\tau \in (0,\dfrac{1}{L})\), \(\{\alpha _n\}\subset (0,1)\), \(\lim _{n\rightarrow \infty } \alpha _n=0\), \(\sum _{n=1}^\infty \alpha _n =+\infty \) and \(x_0\in H\). Similar to (6) of Censor et al. [8], (7) converges strongly to a specific point \(p=P_{VIP(C,A)}x_0.\)

Another two very recent and related (viscosity type methods) which are also used as comparison with our methods in Sect. 4 are Shehu and Iyiola [30, Algorithm 3.1] and Thong and Hieu [33, Algorithm 3].

The setting of Shehu and Iyiola [30, Algorithm 3.1] is as follows. Given \(\rho ,\mu \in (0,1)\) and let \(\{\alpha _n\}_{n=0}^\infty \subset (0,1)\), f a contraction and choose an arbitrary starting point \(x_1\in H\). Given the current iterate \(x_n\), calculate.

$$\begin{aligned} y_n=P_C(x_n-\lambda _n Ax_n), \end{aligned}$$

where \(\lambda _n=\rho l_n\) and \(l_n\) is the smallest nonnegative integer l such that

$$\begin{aligned} \lambda _n\Vert x_n-y_n\Vert \le \mu \Vert r_{\rho l_n}(x_n)\Vert \end{aligned}$$

where \(r_{\rho l_n}(x_n):=x_n-P_C(x_n-\rho l_n Ax_n)\). Construct the set \(T_n\) as in (4) and compute

$$\begin{aligned} z_n=P_{T_n}(x_n-\lambda _n Ay_n), \end{aligned}$$

and calculate the next iterate as follows.

$$\begin{aligned} x_{n+1}=\alpha _n f(x_n)+(1-\alpha _n)z_n. \end{aligned}$$
(8)

The setting of Thong and Hieu [33, Algorithm 3] is as follows. Given \(\rho \in [0,1)\), \(\mu ,l\in (0,1)\) and \(\gamma >0\). Let \(\{\alpha _n\}_{n=0}^\infty \subset (0,1)\), f a contraction and choose an arbitrary starting point \(x_1\in H\). Given the current iterate \(x_n\), calculate.

$$\begin{aligned} y_n=P_C(x_n-\lambda _n Ax_n), \end{aligned}$$

where \(\lambda _n\) is chosen to be the largest \(\lambda \in \{\gamma ,\gamma l, \gamma l^2,\cdots \}\) satisfying

$$\begin{aligned} \lambda \Vert Ax_n-Ay_n\Vert \le \mu \Vert x_n-y_n\Vert . \end{aligned}$$

Calculate the next iterate as follows.

$$\begin{aligned} x_{n+1}=\alpha _n f(x_n)+(1-\alpha _n)z_n \end{aligned}$$
(9)

where \(z_n=y_n-\lambda _n (Ay_n-Ax_n)\).

Motivated and inspired by the above results and the ongoing research in these directions, we suggest two modified projection-type methods, Man-type [27] and viscosity type [28], for solving monotone and Lipschitz continuous variational inequalities which converge strongly in real Hilbert spaces and does not require the knowledge of the Lipschitz constant of A a-priori.

The paper is organized as follows. We first recall some basic definitions and results in Sect. 2. Our algorithms are presented and analysed in Sect. 3. In Sect. 4 we present some numerical experiments which demonstrate the algorithms performances as well as provide a preliminary computational overview by comparing it with some related algorithms. Final remarks and conclusions are given in Sect. 5.

2 Preliminaries

Let H be a real Hilbert space and C be a nonempty, closed and convex subset of H. The weak convergence of \(\{x_n\}_{n=1}^{\infty }\) to x is denoted by \(x_{n}\rightharpoonup x\) as \(n\rightarrow \infty \), while the strong convergence of \(\{x_n\}_{n=1}^{\infty }\) to x is written as \(x_n\rightarrow x\) as \(n\rightarrow \infty .\) For each \(x,y\in H\) and \(\alpha \in \mathbb {R}\), we have

$$\begin{aligned}&\displaystyle \Vert x+y\Vert ^2\le \Vert x\Vert ^2+2\langle y,x+y\rangle . \end{aligned}$$
(10)
$$\begin{aligned}&\displaystyle \Vert \alpha x+(1-\alpha )y\Vert ^2=\alpha \Vert x\Vert ^2+(1-\alpha )\Vert y\Vert ^2-\alpha (1-\alpha )\Vert x-y\Vert ^2. \end{aligned}$$
(11)
$$\begin{aligned} \Vert \alpha x+\beta y+\gamma z\Vert ^2= & {} \alpha \Vert x\Vert ^2 + \beta \Vert y\Vert ^2 + \gamma \Vert z\Vert ^2- \alpha \beta \Vert x-y\Vert ^2 \nonumber \\&- \alpha \gamma \Vert x-z\Vert ^2 - \beta \gamma \Vert y-z\Vert ^2 \end{aligned}$$
(12)

for all \(x, y, z \in H\) and for all \(\alpha , \beta , \gamma \in [0; 1]\) with \(\alpha + \beta + \gamma = 1.\)

Definition 2.1

Let \(T:H\rightarrow H\) be an operator. Then

  1. 1.

    the operator T is called L-Lipschitz continuous with \(L>0\) if

    $$\begin{aligned} \Vert Tx-Ty\Vert \le L \Vert x-y\Vert \ \ \ \forall x,y \in H. \end{aligned}$$
    (13)

    if \(L=1\) then the operator T is called nonexpansive and if \(L\in (0,1)\), T is called contraction.

  2. 2.

    T is called monotone if

    $$\begin{aligned} \langle Tx-Ty,x-y \rangle \ge 0 \ \ \ \forall x,y \in H. \end{aligned}$$
    (14)
  3. 3.

    the fixed point set of T, denoted by Fix(T) is defined as follows.

    $$\begin{aligned} Fix(T):=\{x\in H \mid Tx=x\}. \end{aligned}$$
    (15)

For every point \(x\in H\), there exists a unique nearest point in C, denoted by \(P_Cx\) such that \(\Vert x-P_Cx\Vert \le \Vert x-y\Vert \ \forall y\in C\). \(P_C\) is called the metric projection of H onto C. It is known that \(P_C\) is nonexpansive.

Lemma 2.1

[16] Let C be a nonempty closed convex subset of a real Hilbert space H. Given \(x\in H\) and \(z\in C\). Then \(z=P_Cx\Longleftrightarrow \langle x-z,z-y\rangle \ge 0 \ \ \forall y\in C.\)

Lemma 2.2

[16] Let C be a closed and convex subset in a real Hilbert space H,  \(x\in H\). Then

  1. i)

    \(\Vert P_Cx-P_Cy\Vert ^2\le \langle P_C x-P_C y,x-y\rangle \ \forall y\in C\);

  2. ii)

    \(\Vert P_C x-y\Vert ^2\le \Vert x-y\Vert ^2-\Vert x-P_Cx\Vert ^2 \ \forall y\in C;\)

  3. iii)

    \(\langle (I-P_C)x-(I-P_C)y,x-y\rangle \ge \Vert (I-P_C)x-(I-P_C)y\Vert ^2 \ \forall y\in C.\)

For properties of the metric projection, the interested reader could be referred to Section 3 in [16].

The following Lemmas are useful for the convergence of our proposed methods.

Lemma 2.3

[22] Let \(A:H\rightarrow H\) be a monotone and L-Lipschitz continuous mapping on C. Let \(S=P_C(I-\tau A)\), where \(\tau >0\). If \(\{x_n\}\) is a sequence in H satisfying \(x_n\rightharpoonup q\) and \(x_n -Sx_n\rightarrow 0\) then \(q\in VI(C,A)=Fix(S)\).

Lemma 2.4

[24] Let \(\{a_n\}\) be a sequence of nonnegative real numbers such that there exists a subsequence \(\{a_{n_j}\}\) of \(\{a_n\}\) such that \(a_{n_{j}}<a_{n_{j}+1}\) for all \(j\in \mathbb {N}\). Then there exists a nondecreasing sequence \(\{m_k\}\) of \(\mathbb {N}\) such that \(\lim _{k\rightarrow \infty }m_k=\infty \) and the following properties are satisfied by all (sufficiently large) number \(k\in \mathbb {N}\):

$$\begin{aligned} a_{m_k}\le a_{m_{k}+1} \text { and } a_k\le a_{m_k+1}. \end{aligned}$$

In fact, \(m_k\) is the largest number n in the set \(\{1,2,\cdots ,k\}\) such that \(a_n<a_{n+1}\).

The next technical lemma is very useful and used by many authors, for example Liu [23] and Xu [36]. Furthermore, a variant of Lemma 2.5 has already been used by Reich in [29].

Lemma 2.5

Let \(\{a_n\}\) be sequence of nonnegative real numbers such that:

$$\begin{aligned} a_{n+1}\le (1-\alpha _n)a_n+\alpha _n b_n, \end{aligned}$$

where \(\{\alpha _n\}\subset (0,1)\) and \(\{b_n\}\) is a sequence such that

a) \(\sum _{n=0}^\infty \alpha _n=\infty \);

b) \(\limsup _{n\rightarrow \infty }b_n\le 0.\)

Then \(\lim _{n\rightarrow \infty }a_n=0.\)

3 Main results

In this section we introduce our two modified projection-type methods for solving VIs. For the convergence analysis of the methods, we assume the following conditions.

Condition 3.1

The VI (1) associated operator \(A:H\rightarrow H\) is monotone and L-Lipschitz continuous on H.

Condition 3.2

The solution set of the VI (1) is nonempty, that is \(VI(C,A)\ne \emptyset \).

Condition 3.3

Let \(\{\alpha _n\}\) and \(\{\beta _n\}\) be two real sequences in (0, 1) such that \(\{\beta _n\}\subset (a,b)\subset (0,1-\alpha _n)\) for some \(a>0, b>0\) and

$$\begin{aligned} \lim _{n\rightarrow \infty }\alpha _n=0, \sum _{n=1}^\infty \alpha _n=\infty . \end{aligned}$$

3.1 Mann-type projection algorithm

figure a

We start the analysis of the algorithm’s convergence by proving the validity of the stopping criterion.

Lemma 3.1

Assume that Conditions 3.1–3.2 hold. The Armijo-like search rule (16) is well defined and

$$\begin{aligned} \min \left\{ \lambda ,\dfrac{\mu l}{L}\right\} \le \tau _n\le \lambda . \end{aligned}$$

Proof

See e.g., Lemma 3.1 in [33]. \(\square \)

Lemma 3.2

Let \(\{d_n\}\) be a sequence generated by Algorithm 3.1. Then \(d_n=0\) if and only if \(x_n=y_n\).

Proof

Indeed, we will prove that

$$\begin{aligned} (1-\mu )\Vert x_n-y_n\Vert \le \Vert d_n\Vert \le (1+\mu )\Vert x_n-y_n\Vert . \end{aligned}$$
(17)

We have

$$\begin{aligned} \Vert d_n\Vert&=\Vert x_n-y_n-\tau _n(Ax_n-Ay_n)\Vert \nonumber \\&\ge \Vert x_n-y_n\Vert -\tau _n\Vert Ax_n-Ay_n\Vert \nonumber \\&\ge \Vert x_n-y_n\Vert -\mu \Vert x_n-y_n\Vert \nonumber \\&= (1-\mu )\Vert x_n-y_n\Vert . \end{aligned}$$
(18)

and it is also easy to see that

$$\begin{aligned} \Vert d_n\Vert \le (1+\mu )\Vert x_n-y_n\Vert . \end{aligned}$$
(19)

Combining (18) and (19) we obtain

$$\begin{aligned} (1-\mu )\Vert x_n-y_n\Vert \le \Vert d_n\Vert \le (1+\mu )\Vert x_n-y_n\Vert . \end{aligned}$$

It implies from (17) that \(d_n=0\) if and only if \(x_n=y_n.\) \(\square \)

Remark 3.1

From Lemma 3.2 we show that if \(d_n=0\) then stop and \(y_n\) is a solution of VI(C, A).

Lemma 3.3

Assume that Conditions 3.1 and 3.2 hold. Let \(\{z_n\}\) be a sequence generated by Algorithm 3.1. Then

$$\begin{aligned} \Vert z_n-p\Vert ^2\le \Vert x_n-p\Vert ^2-\dfrac{2-\gamma }{\gamma }\Vert x_n-z_n\Vert ^2 \ \ \forall p\in VI(C,A). \end{aligned}$$
(20)

Proof

Using (16) we have

$$\begin{aligned} \langle x_n-p,d_n\rangle&=\langle x_n-y_n,d_n\rangle +\langle y_n-p,d_n\rangle \nonumber \\&=\langle x_n-y_n,x_n-y_n-\tau _n(Ax_n-Ay_n)\rangle +\langle y_n-p,x_n-y_n\nonumber \\&\quad -\tau _n(Ax_n-Ay_n)\rangle \nonumber \\&=\Vert x_n-y_n\Vert ^2-\tau _n\langle x_n-y_n, Ax_n-Ay_n\rangle \nonumber \\&\quad +\langle y_n-p,x_n-y_n-\tau _n(Ax_n-Ay_n)\rangle \nonumber \\&\ge \Vert x_n-y_n\Vert ^2-\tau _n\Vert x_n-y_n\Vert \Vert Ax_n-Ay_n\Vert \nonumber \\&\quad +\langle y_n-p,x_n-y_n-\tau _n(Ax_n-Ay_n)\rangle \nonumber \\&\ge \Vert x_n-y_n\Vert ^2-\mu \Vert x_n-y_n\Vert ^2\nonumber \\&\quad +\langle y_n-p,x_n-y_n-\tau _n(Ax_n-Ay_n)\rangle . \end{aligned}$$
(21)

On the other hand, since \(y_n=P_C(x_n-\tau _n Ax_n)\) we get

$$\begin{aligned} \langle x_n-y_n-\tau _n Ax_n,y_n-p\rangle \ge 0, \end{aligned}$$
(22)

By the monotonicity of A and \(p\in VI(C,A)\) we have

$$\begin{aligned} \langle Ay_n,y_n-p\rangle \ge \langle Ap,y_n-p\rangle \ge 0. \end{aligned}$$
(23)

Adding (22) and (23) we get

$$\begin{aligned} \langle y_n-p,x_n-y_n-\tau _n(Ax_n-Ay_n)\rangle \ge 0 \end{aligned}$$
(24)

Combining (21) and (24) we get

$$\begin{aligned} \langle x_n-p,d_n\rangle \ge (1-\mu )\Vert x_n-y_n\Vert ^2. \end{aligned}$$
(25)

On the other hand, we have

$$\begin{aligned} \Vert z_n-p\Vert ^2= & {} \Vert x_n-\gamma \eta _n d_n-p\Vert ^2\nonumber \\= & {} \Vert x_n-p\Vert ^2-2\gamma \eta _n\langle x_n-p,d_n\rangle +\gamma ^2\eta ^2_n\Vert d_n\Vert ^2. \end{aligned}$$
(26)

It implies from (25) and (26) that

$$\begin{aligned} \Vert z_n-p\Vert ^2\le \Vert x_n-p\Vert ^2-2\gamma \eta _n(1-\mu )\Vert x_n-y_n\Vert ^2+\gamma ^2\eta ^2_n\Vert d_n\Vert ^2. \end{aligned}$$

Since \(\eta _n=(1-\mu )\dfrac{\Vert x_n-y_n\Vert ^2}{\Vert d_n\Vert ^2}\), it implies that \(\Vert x_n-y_n\Vert ^2=\dfrac{\eta _n \Vert d_n\Vert ^2}{1-\mu }\). Thus,

$$\begin{aligned} \Vert z_n-p\Vert ^2&\le \Vert x_n-p\Vert ^2-2\gamma \eta ^2_n\Vert d_n\Vert ^2+\gamma ^2\eta ^2_n\Vert d_n\Vert ^2\\&= \Vert x_n-p\Vert ^2-\gamma (2-\gamma )\Vert \eta _nd_n\Vert ^2\\&= \Vert x_n-p\Vert ^2-\dfrac{2-\gamma }{\gamma }\Vert \gamma \eta _nd_n\Vert ^2\\&= \Vert x_n-p\Vert ^2-\dfrac{2-\gamma }{\gamma }\Vert x_n-z_n\Vert ^2. \end{aligned}$$

\(\square \)

Lemma 3.4

Assume that Conditions 3.1–3.2 hold and let the sequence \(\{x_n\}\) be generated by Algorithm 3.1. Then

$$\begin{aligned} \Vert x_n-y_n\Vert ^2\le \dfrac{ (1+\mu )^2}{[(1-\mu )\gamma ]^2}\Vert x_n-z_n\Vert ^2. \end{aligned}$$
(27)

Proof

We have

$$\begin{aligned} \Vert x_n-y_n\Vert ^2= & {} \dfrac{1}{1-\mu }.\eta _n \Vert d_n\Vert ^2=\dfrac{1}{\eta _n(1-\mu )}\Vert \eta _n d_n\Vert ^2\nonumber \\= & {} \dfrac{1}{\eta _n(1-\mu )\gamma ^2}\Vert x_n-z_n\Vert ^2. \end{aligned}$$
(28)

On the other hand, from (17) we get

$$\begin{aligned} \eta _n=(1-\mu ) \dfrac{\Vert x_n-y_n\Vert ^2}{\Vert d_n\Vert ^2}\ge \dfrac{1-\mu }{(1+\mu )^2}, \end{aligned}$$

thus,

$$\begin{aligned} \dfrac{1}{\eta _n}\le \dfrac{(1+\mu )^2}{1-\mu } \end{aligned}$$
(29)

It implies from (28) and (29) that

$$\begin{aligned} \Vert x_n-y_n\Vert ^2\le \dfrac{(1+\mu )^2}{[(1-\mu )\gamma ]^2}\Vert x_n-z_n\Vert ^2. \end{aligned}$$

\(\square \)

Theorem 3.1

Assume that Conditions 3.1–3.3 hold. Then any sequence \(\{x_n\}\) generated by Algorithm 3.1 converges strongly to \(p\in VI(C,A)\), where \(\Vert p\Vert =\min \{\Vert z\Vert : z\in VI(C,A)\}\).

Proof

Thanks to Lemma 3.3 we get

$$\begin{aligned} \Vert z_n-p\Vert \le \Vert x_n-p\Vert \ \ \forall n. \end{aligned}$$
(30)

Claim 1. We prove that the sequence \(\{x_n\}\) is bounded. We have

$$\begin{aligned} \Vert x_{n+1}-p\Vert&=\Vert (1-\alpha _n-\beta _n)x_n+\beta _n z_n- p\Vert \nonumber \\&=\Vert (1-\alpha _n-\beta _n)(x_n-p)+\beta _n(z_n-p)-\alpha _n p\Vert \nonumber \\&\le \Vert (1-\alpha _n-\beta _n)(x_n-p)+\beta _n(z_n-p)\Vert +\alpha _n \Vert p\Vert . \end{aligned}$$
(31)

On the other hand, using (30) we get

$$\begin{aligned} \Vert (1-&\alpha _n-\beta _n)(x_n-p)+\beta _n(z_n-p)\Vert ^2\\&\quad =(1-\alpha _n-\beta _n)^2\Vert x_n-p\Vert ^2+2(1-\alpha _n-\beta _n)\beta _n \langle x_n-p,z_n-p \rangle \nonumber \\&\qquad +\beta ^2_n\Vert z_n-p\Vert ^2\\&\quad \le (1-\alpha _n-\beta _n)^2 \Vert x_n-p\Vert ^2+2(1-\alpha _n-\beta _n)\beta _n \Vert z_n-p\Vert \Vert x_n-p\Vert \nonumber \\&\qquad +\beta ^2_n \Vert z_n-p\Vert ^2\\&\quad \le (1-\alpha _n-\beta _n)^2 \Vert x_n-p\Vert ^2+2(1-\alpha _n-\beta _n)\beta _n \Vert x_n-p\Vert ^2 +\beta ^2_n \Vert x_n-p\Vert ^2\\&\quad = (1-\alpha _n)^2 \Vert x_n-p\Vert ^2. \end{aligned}$$

This implies that

$$\begin{aligned} \Vert (1-\alpha _n-\beta _n)(x_n-p)+\beta _n(z_n-p)\Vert \le (1-\alpha _n) \Vert x_n-p\Vert \ \ \forall n. \end{aligned}$$
(32)

From (31) and (32) we get

$$\begin{aligned} \Vert x_{n+1}-p\Vert&\le (1-\alpha _n) \Vert x_n-p\Vert +\alpha _n\Vert p\Vert \\&\le \max \{\Vert x_n-p\Vert ,\Vert p\Vert \}\\&\le \cdots \le \max \{\Vert x_{0}-p\Vert ,\Vert p\Vert \}. \end{aligned}$$

That is, the sequence \(\{x_n\}\) is bounded and \(\{z_n\}\) is also.

Claim 2. We show that

$$\begin{aligned} \beta _n \dfrac{2-\gamma }{\gamma }\Vert x_{n}-z_n\Vert ^2\le \Vert x_n-p\Vert ^2-\Vert x_{n+1}-p\Vert ^2 +\alpha _n \Vert p\Vert ^2. \end{aligned}$$
(33)

Indeed, using (12) we have

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^2&=\Vert (1-\alpha _n-\beta _n)x_n+\beta _n z_n- p\Vert ^2\nonumber \\&=\Vert (1-\alpha _n-\beta _n)(x_n-p)+\beta _n (z_n- p)+\alpha _n (-p)\Vert ^2\nonumber \\&=(1-\alpha _n-\beta _n)\Vert x_n-p\Vert ^2+\beta _n \Vert z_n- p\Vert ^2+\alpha _n \Vert p\Vert ^2-\beta _n (1\nonumber \\&\quad -\alpha _n-\beta _n)\Vert x_n-z_n\Vert ^2\nonumber \\&\quad -\alpha _n(1-\alpha _n-\beta _n) \Vert x_n\Vert ^2-\alpha _n \beta _n \Vert z_n\Vert ^2\nonumber \\&\le (1-\alpha _n-\beta _n)\Vert x_n-p\Vert ^2+\beta _n \Vert z_n- p\Vert ^2+\alpha _n \Vert p\Vert ^2, \end{aligned}$$
(34)

which, together Lemma 3.3 we obtain

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^2&\le (1-\alpha _n-\beta _n)\Vert x_n-p\Vert ^2+\beta _n \Vert x_n- p\Vert ^2\nonumber \\&\quad -\beta _n \dfrac{2-\gamma }{\gamma }\Vert x_n-z_n\Vert ^2+\alpha _n \Vert p\Vert ^2\nonumber \\&=(1-\alpha _n)\Vert x_n-p\Vert ^2-\beta _n \dfrac{2-\gamma }{\gamma }\Vert x_n-z_n\Vert ^2+\alpha _n \Vert p\Vert ^2\nonumber \\&\le \Vert x_n-p\Vert ^2-\beta _n \dfrac{2-\gamma }{\gamma }\Vert x_n-z_n\Vert ^2+\alpha _n \Vert p\Vert ^2. \end{aligned}$$
(35)

Therefore, we get

$$\begin{aligned} \beta _n \dfrac{2-\gamma }{\gamma }\Vert x_{n}-z_n\Vert ^2\le \Vert x_n-p\Vert ^2-\Vert x_{n+1}-p\Vert ^2 +\alpha _n \Vert p\Vert ^2. \end{aligned}$$

Claim 3. We show that

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^2\le & {} (1-\alpha _n)\Vert x_n-p\Vert ^2+\alpha _n[2\beta _n\Vert x_n-z_n\Vert \Vert x_{n+1}-p\Vert \nonumber \\&\quad +\,2\langle p,p-x_{n+1}\rangle ]. \end{aligned}$$
(36)

Indeed, setting \(t_n=(1-\beta _n)x_n+\beta _n z_n\). We have

$$\begin{aligned} \Vert t_n-p\Vert&=\Vert (1-\beta _n)(x_n-p)+\beta _n(z_n-p)\Vert \nonumber \\&= (1-\beta _n)\Vert x_n-p\Vert +\beta _n\Vert z_n-p\Vert \nonumber \\&\le (1-\beta _n)\Vert x_n-p\Vert +\beta _n\Vert x_n-p\Vert \nonumber \\&=\Vert x_n-p\Vert , \end{aligned}$$
(37)

and

$$\begin{aligned} \Vert t_n-x_n\Vert =\beta _n \Vert x_n-z_n\Vert . \end{aligned}$$
(38)

Using (37) and (38) we get

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^2&=\Vert (1-\alpha _n-\beta _n)x_n+\beta _n z_n-p\Vert ^2\\&=\Vert (1-\beta _n)x_n+\beta _n z_n-\alpha _n x_n-p\Vert ^2\\&=\Vert (1-\alpha _n)(t_n-p)-\alpha _n(x_n-t_n)-\alpha _n p\Vert ^2\\&\le (1-\alpha _n)^2\Vert t_n-p\Vert ^2 -2\langle \alpha _n(x_n-t_n)+\alpha _n p,x_{n+1}-p\rangle \\&= (1-\alpha _n)^2\Vert t_n-p\Vert ^2 +2 \alpha _n\langle x_n-t_n,p-x_{n+1}\rangle +2\alpha _n \langle p,p-x_{n+1}\rangle \\&\le (1-\alpha _n)\Vert t_n-p\Vert ^2 + 2\alpha _n \Vert x_n-t_n\Vert \Vert x_{n+1}-p\Vert +2\alpha _n \langle p,p-x_{n+1}\rangle \\&\le (1-\alpha _n)\Vert x_n-p\Vert ^2 + \alpha _n [2\beta _n\Vert x_n-z_n\Vert \Vert x_{n+1}-p\Vert \nonumber \\&\quad +2 \langle p,p-x_{n+1}\rangle ]. \end{aligned}$$

Claim 4. Now, we will show that the sequence \(\{\Vert x_n-p\Vert ^2\}\) converges to zero by considering two possible cases on the sequence \(\{\Vert x_n-p\Vert ^2\}\).

Case 1: There exists an \(N\in {{\mathbb {N}}}\) such that \(\Vert x_{n+1}-p\Vert ^2\le \Vert x_n-p\Vert ^2\) for all \(n\ge N.\) This implies that \(\lim _{n\rightarrow \infty }\Vert x_n-p\Vert ^2\) exists. It implies from Claim 2 that

$$\begin{aligned} \lim _{n\rightarrow \infty } \Vert x_n-z_n\Vert =0, \end{aligned}$$

which, together with Lemma 3.4, we get

$$\begin{aligned} \lim _{n\rightarrow \infty } \Vert x_n-y_n\Vert =0. \end{aligned}$$

We also have

$$\begin{aligned} \Vert x_{n+1}-x_n\Vert \le \alpha _n \Vert x_n\Vert +\beta _n\Vert x_n-z_n\Vert \rightarrow 0 \text{ as } n\rightarrow \infty . \end{aligned}$$

Since \(\{x_n\}\) is bounded we assume that there exists a subsequence \(\{x_{n_j}\}\) of \(\{x_n\}\) such that \(x_{n_j}\rightharpoonup q\) and

$$\begin{aligned} \limsup _{n\rightarrow \infty }\langle p,p-x_{n}\rangle =\lim _{j\rightarrow \infty }\langle p,p-x_{n_j}\rangle =\langle p,p-q\rangle . \end{aligned}$$

We have \(x_{n_j}\rightharpoonup q\), \(\min \{\lambda ,\dfrac{\mu l}{L}\}\le \tau _n\le \lambda \) and \(\Vert x_n-y_n\Vert =\Vert x_n-P_C(x_n-\tau _n Ax_n)\Vert \rightarrow 0\), by Lemma 2.3 we get \(q\in VI(C,A).\)

Since \(q\in VI(C,A) \) and \(\Vert p\Vert =\min \{ \Vert z\Vert : z\in VI(C,A)\}\), that is \(p=P_{VI(C,A)}0\) we obtain

$$\begin{aligned} \limsup _{n\rightarrow \infty }\langle p,p-x_{n}\rangle =\langle p,p-q\rangle \le 0. \end{aligned}$$

By \(\Vert x_{n+1}-x_n\Vert \rightarrow 0\) we get

$$\begin{aligned} \limsup _{n\rightarrow \infty }\langle p,p-x_{n+1}\rangle \le 0. \end{aligned}$$

Therefore by Claim 3 and Lemma 2.5 we get \(\lim _{n\rightarrow \infty }\Vert x_{n}-p\Vert ^2=0\), that is \(x_n\rightarrow p.\)

Case 2: There exists a subsequence \(\{\Vert x_{n_j}-p\Vert ^2\}\) of \(\{\Vert x_{n}-p\Vert ^2\}\) such that \(\Vert x_{n_j}-p\Vert ^2 < \Vert x_{n_j+1}-p\Vert ^2\) for all \(j\in \mathbb {N}\). In this case, it follows from Lemma 2.4 that there exists a nondecreasing sequence \(\{m_k\}\) of \(\mathbb {N}\) such that \(\lim _{k\rightarrow \infty }m_k=\infty \) and the following inequalities hold for all \(k\in \mathbb {N}\):

$$\begin{aligned} \Vert x_{m_k}-p\Vert ^2\le \Vert x_{m_k+1}-p\Vert ^2 \text { and } \Vert x_{k}-p\Vert ^2\le \Vert x_{m_k+1}-p\Vert ^2. \end{aligned}$$
(39)

Since \(\{\beta _n\}\subset (a,b)\) and Claim 2, we have

$$\begin{aligned} a \dfrac{2-\gamma }{\gamma }\Vert x_{m_k}-z_{m_k}\Vert ^2&\le \beta _{m_k} \dfrac{2-\gamma }{\gamma }\Vert x_{m_k}-z_{m_k}\Vert ^2\\&\le \Vert x_{m_k}-p\Vert ^2-\Vert x_{{m_k}+1}-p\Vert ^2 +\alpha _{m_k} \Vert p\Vert ^2\\&\le \alpha _{m_k} \Vert p\Vert ^2. \end{aligned}$$

Therefore, we get

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert x_{m_k}-z_{m_k}\Vert =0 . \end{aligned}$$
(40)

As proved in the first case, we obtain

$$\begin{aligned} \Vert x_{m_k+1}-x_{m_k}\Vert \rightarrow 0 \end{aligned}$$

and

$$\begin{aligned} \limsup _{k\rightarrow \infty }\langle p,p-x_{m_k+1}\rangle \le 0. \end{aligned}$$

Since Claim 3 we have

$$\begin{aligned} \Vert x_{m_k+1}-p\Vert ^2&\le (1-\alpha _{m_k})\Vert x_{m_k}-p\Vert ^2\\&\quad +\,\alpha _{m_k}[2\beta _{m_k}\Vert x_{m_k}-z_{m_k}\Vert \Vert x_{m_k+1}-p\Vert +2\langle p,p-x_{m_k+1}\rangle ]\\&\le (1-\alpha _{m_k})\Vert x_{m_k+1}-p\Vert ^2\\&\quad +\,\alpha _{m_k}[2\beta _{m_k}\Vert x_{m_k}-z_{m_k}\Vert \Vert x_{m_k+1}-p\Vert +2\langle p,p-x_{m_k+1}\rangle ]. \end{aligned}$$

This implies that

$$\begin{aligned} \Vert x_k-p\Vert ^2\le \Vert x_{m_k+1}-p\Vert ^2\le 2\beta _{m_k}\Vert x_{m_k}-z_{m_k}\Vert \Vert x_{m_k+1}-p\Vert +2\langle p,p-x_{m_k+1}\rangle . \end{aligned}$$

Therefore, we obtain \(\limsup _{k\rightarrow \infty }\Vert x_k-p\Vert \le 0\), that is \(x_k\rightarrow p\). The proof is completed. \(\square \)

3.2 Viscosity projection type algorithm

In this section, we propose our viscosity projection type algorithm for solving variational inequalities, with the usage of a \(\rho \)-contraction \(f:H\rightarrow H\).

figure b

Theorem 3.2

Assume that Conditions 3.1–3.2 hold and given a \(\rho \)-contraction \(f:H\rightarrow H\). Assume that \(\{\alpha _n\}\) is a real sequence in (0, 1) such that

$$\begin{aligned} \lim _{n\rightarrow \infty }\alpha _n=0, \sum _{n=1}^\infty \alpha _n=\infty . \end{aligned}$$

Then any sequence \(\{x_n\}\) generated by Algorithm 3.2 converges strongly to an element \(p\in VI(C,A)\), where \(p=P_{ VI(C,A)}\circ f(p)\).

Proof

Claim 1. We prove that the \(\{x_n\}\) is bounded. Indeed, According to Lemma 3.3 we have

$$\begin{aligned} \Vert z_n-p\Vert \le \Vert x_n-p\Vert . \end{aligned}$$
(42)

Using (42) we obtain

$$\begin{aligned} \Vert x_{n+1}-p\Vert&=\Vert \alpha _n f(x_n)+(1-\alpha _n)z_n-p\Vert \\&=\Vert \alpha _n(f(x_n)-p)+(1-\alpha _n)(z_n-p)\Vert \\&\le \alpha _n\Vert f(x_n)-p\Vert +(1-\alpha _n)\Vert z_n-p\Vert \\&\le \alpha _n\Vert f(x_n)-f(p)\Vert +\alpha _n \Vert f(p)-p\Vert +(1-\alpha _n)\Vert z_n-p\Vert \\&\le \alpha _n \rho \Vert x_n-p\Vert +\alpha _n\Vert f(p)-p\Vert +(1-\alpha _n)\Vert x_n-p\Vert \\&\le [1-\alpha _n(1-\rho )]\Vert x_n-p\Vert +\alpha _n(1-\rho )\dfrac{\Vert f(p)-p\Vert }{1-\rho }\\&\le \max \{\Vert x_n-q\Vert ,\dfrac{\Vert f(p)-p\Vert }{1-\rho }\}\\&\le \cdots \le \max \left\{ \Vert x_{0}-p\Vert ,\dfrac{\Vert f(p)-p\Vert }{1-\rho }\right\} . \end{aligned}$$

This implies that the sequence \(\{x_n\}\) is bounded. Consequently, \(\{f(x_n)\}, \{y_n\}\) and \(\{z_n\}\) are bounded.

Claim 2. We show that

$$\begin{aligned} (1-\alpha _n)\dfrac{2-\gamma }{\gamma }\Vert x_n-z_n\Vert ^2\le \Vert x_n-p\Vert ^2-\Vert x_{n+1}-p\Vert ^2+\alpha _n\Vert f(x_n)-p\Vert ^2. \end{aligned}$$

Indeed, using (11) and Lemma 3.3 we have

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^2&=\Vert \alpha _n(f(x_n)-p)+(1-\alpha _n)(z_n-p)\Vert ^2\\&=\alpha _n\Vert f(x_n)-p\Vert ^2+(1-\alpha _n)\Vert z_n-p\Vert ^2-\alpha _n(1-\alpha _n)\Vert f(x_n)-z_n\Vert ^2\\&\le \alpha _n\Vert f(x_n)-p\Vert ^2+(1-\alpha _n)\Vert z_n-p\Vert ^2\\&\le \alpha _n\Vert f(x_n)-p\Vert ^2+(1-\alpha _n)\Vert x_n-p\Vert ^2\nonumber \\&\quad -(1-\alpha _n)\beta _n\dfrac{2-\gamma }{\gamma }\Vert x_n-z_n\Vert ^2\\&\le \alpha _n\Vert f(x_n)-p\Vert ^2+\Vert x_n-p\Vert ^2-(1-\alpha _n)\dfrac{2-\gamma }{\gamma }\Vert x_n-z_n\Vert ^2. \end{aligned}$$

This implies that

$$\begin{aligned} (1-\alpha _n)\dfrac{2-\gamma }{\gamma }\Vert x_n-z_n\Vert ^2\le \Vert x_n-p\Vert ^2-\Vert x_{n+1}-p\Vert ^2+\alpha _n\Vert f(x_n)-p\Vert ^2. \end{aligned}$$

Claim 3. We show that

$$\begin{aligned}&\Vert x_{n+1}-p\Vert ^2\le (1-(1-\rho )\alpha _n)\Vert x_n-p\Vert ^2+(1-\rho )\alpha _n.\dfrac{2}{1-\rho }\langle f(p)\\&-p,x_{n+1}-p\rangle . \end{aligned}$$

Indeed, using (10) and (42) we have

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^2&=\Vert \alpha _nf(x_n)+(1-\alpha _n)z_n-p\Vert ^2 \nonumber \\&=\Vert \alpha _n(f(x_n)-f(p))+(1-\alpha _n)(z_n-p)+\alpha _n(f(p)-p)\Vert ^2 \nonumber \\&\le \Vert \alpha _n(f(x_n)-f(p))+(1-\alpha _n)(z_n-p)\Vert ^2\nonumber \\&\quad +2\alpha _n\langle f(p) -p,x_{n+1}-p\rangle \nonumber \\&\le \alpha _n\Vert f(x_n)-f(p)\Vert ^2+(1-\alpha _n)\Vert z_n-p\Vert ^2\nonumber \\&\quad +2\alpha _n\langle f(p) -p,x_{n+1}-p\rangle \nonumber \\&\le \alpha _n\rho \Vert x_n-p\Vert ^2+(1-\alpha _n)\Vert x_n-p\Vert ^2+2\alpha _n\langle f(p)-p,x_{n+1}-p\rangle \nonumber \\&=(1-(1-\rho )\alpha _n)\Vert x_n-p\Vert ^2+(1-\rho )\alpha _n\nonumber \\&\quad .\dfrac{2}{1-\rho }\langle f(p) -p,x_{n+1}-p\rangle . \end{aligned}$$
(43)

Claim 4. Now, we will show that the sequence \(\{\Vert x_n-p\Vert ^2\}\) converges to zero by considering two possible cases on the sequence \(\{\Vert x_n-p\Vert ^2\}\).

Case 1: There exists an \(N\in {{\mathbb {N}}}\) such that \(\Vert x_{n+1}-p\Vert ^2\le \Vert x_n-p\Vert ^2\) for all \(n\ge N.\) This implies that \(\lim _{n\rightarrow \infty }\Vert x_n-p\Vert ^2\) exists.

Since the Claim 2 and \(\lim _{n\rightarrow \infty }\alpha _n=0\) we get

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert x_n-z_n\Vert =0, \end{aligned}$$
(44)

and by Lemma 3.4

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert x_n-y_n\Vert =0. \end{aligned}$$
(45)

We also have

$$\begin{aligned} \Vert x_{n+1}-x_n\Vert&=\Vert \alpha _n f(x_n)+(1-\alpha _n)z_n-x_n\Vert \nonumber \\&\le \alpha _n \Vert f(x_n)-x_n\Vert +(1-\alpha _n)\Vert z_n-x_n\Vert \rightarrow 0. \end{aligned}$$
(46)

Since the sequence \(\{x_n\}\) is bounded, it implies that there exists a subsequence \(\{x_{n_k}\}\) of \(\{x_n\}\) that weak convergence to some \(z\in H\) such that

$$\begin{aligned} \limsup _{n\rightarrow \infty }\langle f(p)-p,x_{n}-p\rangle= & {} \lim _{k\rightarrow \infty }\langle f(p)-p,x_{n_k}-p\rangle \nonumber \\= & {} \langle f(p)-p,z-p\rangle . \end{aligned}$$
(47)

From (45) and Lemma 2.3 we have \(z\in VI(C,A)\).

By the definition of p and \(z\in VI(C,A)\) we have

$$\begin{aligned} \limsup _{n\rightarrow \infty }\langle f(p)-p,x_{n}-p\rangle =\langle f(p)-p,z-p\rangle \le 0. \end{aligned}$$
(48)

which, together with (46) and (47) we get

$$\begin{aligned} \limsup _{n\rightarrow \infty }\langle f(p)-p,x_{n+1}-p\rangle&\le \limsup _{n\rightarrow \infty }\langle f(p)-p,x_{n+1}-x_n\rangle \nonumber \\&\quad +\limsup _{n\rightarrow \infty }\langle f(p)-p,x_{n}-p\rangle \nonumber \\&=\langle f(p)-p,z-p\rangle \le 0. \end{aligned}$$
(49)

Using Lemma 2.5, (49) and Claim 3 we obtain \(x_n\rightarrow p.\)

Case 2. There exists a subsequence \(\{\Vert x_{n_j}-p\Vert ^2\}\) of \(\{\Vert x_{n}-p\Vert ^2\}\) such that \(\Vert x_{n_j}-p\Vert ^2 < \Vert x_{n_j+1}-p\Vert ^2\) for all \(j\in \mathbb {N}\). In this case, it follows from Lemma 2.4 that there exists a nondecreasing sequence \(\{m_k\}\) of \(\mathbb {N}\) such that \(\lim _{k\rightarrow \infty }m_k=\infty \) and the following inequalities hold for all \(k\in \mathbb {N}\):

$$\begin{aligned} \Vert x_{m_k}-p\Vert ^2\le \Vert x_{m_k+1}-p\Vert ^2 , \end{aligned}$$
(50)

and

$$\begin{aligned} \Vert x_{k}-p\Vert ^2\le \Vert x_{m_k}-p\Vert ^2. \end{aligned}$$
(51)

According to Claim 2 we get

$$\begin{aligned} (1-\alpha _{m_k})\dfrac{2-\gamma }{\gamma }\Vert x_{m_k}-z_{m_k}\Vert ^2&\le \Vert x_{m_k}-p\Vert ^2-\Vert x_{{m_k}+1}-p\Vert ^2\\&\quad +\alpha _{m_k}\Vert f(x_{m_k})-p\Vert ^2\\&\le \alpha _{m_k}\Vert f(x_{m_k})-p\Vert ^2. \end{aligned}$$

We obtain

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert x_{m_k}-z_{m_k}\Vert =0, \end{aligned}$$
(52)

and by Lemma 3.4 we get

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert x_{m_k}-y_{m_k}\Vert =0. \end{aligned}$$
(53)

Using the same arguments as in the proof of Case 1, we obtain

$$\begin{aligned} \limsup _{k\rightarrow \infty }\langle f(p)-p,x_{m_k+1}-p\rangle \le 0. \end{aligned}$$
(54)

Thanks to Claim 3, we have

$$\begin{aligned} \Vert x_{{m_k}+1}-p\Vert ^2&\le (1-(1-\rho )\alpha _{m_k})\Vert x_{m_k}-p\Vert ^2\nonumber \\&\quad +(1-\rho )\alpha _{m_k}.\dfrac{2}{1-\rho }\langle f(p) -p,x_{{m_k}+1}-p\rangle , \end{aligned}$$
(55)

together with (50), we deduce that

$$\begin{aligned} \Vert x_{{m_k}+1}-p\Vert ^2&\le (1-(1-\rho )\alpha _{m_k})\Vert x_{m_k+1}-p\Vert ^2\\&\quad +(1-\rho )\alpha _{m_k}.\dfrac{2}{1-\rho }\langle f(p)-,x_{{m_k}+1}-p\rangle . \end{aligned}$$

This follows that

$$\begin{aligned} \Vert x_{m_k+1}-p\Vert ^2 \le \dfrac{2}{1-\rho }\langle f(p)-p,x_{{m_k}+1}-p\rangle . \end{aligned}$$
(56)

Combining (51), (54) and (56) we get

$$\begin{aligned} \limsup _{k\rightarrow \infty }\Vert x_k-p\Vert \le 0, \end{aligned}$$
(57)

that is \(x_k \rightarrow p\). The proof is completed. \(\square \)

4 Numerical illustrations

In this section we present two numerical experiments which demonstrate the performances of our Mann-type and viscosity-type projection algorithm (Algorithms 3.1 and 3.2) in finite and infinite dimensional spaces. In both experiments the parameters are chosen as \(\lambda =7.55,\, l=0.5,\, \mu =0.85\) and \(\gamma =1.99\), \(\alpha _k=1/k, \beta _k=(k-1)/2k\).

Example 1

Suppose that \(H = L^2([0,1])\) with norm \(\Vert x\Vert :=\Big (\int _0^1 |x(t)|^2dt\Big )^{\frac{1}{2}}\) and inner product \(\langle x,y\rangle := \int _0^1 x(t)y(t)dt,~~ \forall x,y \in H\). Let \(C:=\{x \in H \mid \Vert x\Vert \le 1\}\) be the unit ball. Define operator \(A:C\rightarrow H\) by \((Ax)(t)=\max (0,x(t))\). Then it can be easily verified that A is 2-Lipschitz continuous and monotone on C (see [19]). With these given C and A, the set of solution to the variational inequality is \(\{0\} \ne \emptyset \). It is known that, see for example [5]

$$\begin{aligned} P_C(x)= \left\{ \begin{array}{ll} \frac{x}{\Vert x\Vert _{L^2}}, &{}\quad \text{ if } \ \Vert x\Vert _{L^2}> 1,\\ x, &{}\quad \text{ if } \ \Vert x\Vert _{L^2} \le 1, \end{array} \right. \end{aligned}$$

We implement our algorithm with different starting point \(x_1(t)\). We choose the stopping criterion \(||x_{n+1}-x_n||<\varepsilon \) with \(\varepsilon =10^{-30}\). The results are presented in Table 1 and Figs. 1 and 2.

Table 1 Algorithm 3.1 with different Cases
Full size table
Fig. 1
figure 1

\(x_1(t)= \frac{1}{600}\left[ sin(-3t)+cos(-10t)\right] \)

Full size image
Fig. 2
figure 2

\(x_1(t)=\frac{1}{525}\left[ t^2-e^{-t}\right] \)

Full size image

Example 2

In this example we consider a nonlinear variational inequality with \(A:\mathbb {R}^m\rightarrow \mathbb {R}^m\) which is defined as \(Ax=Mx+Fx+q\), with M an \(m\times m\) symmetric semi-definite matrix, q is a vector in \(\mathbb {R}^{m}\) and Fx is the proximal mapping of the function \(g(x)=\frac{1}{4}||x||^4\), i.e.,

$$\begin{aligned} Fx=\arg \min \left\{ \frac{||y||^4}{4}+\frac{1}{2}||y-x||^2 \mid y\in \mathbb {R}^m\right\} . \end{aligned}$$

The feasible set is a polyhedral convex set, given by \( C=\left\{ x\in \mathbb {R}^m \mid Qx\le b\right\} \), where \(Q\in \mathbb {R}^{r\times m}\) and \(b\in \mathbb {R}^l\). In this case, A is monotone and Lipschitz continuous with \(L=||M||+1\). All the entries of Q, M, q are generated randomly in \((-2,2)\) and b in (0, 1), \(m=100,r=10\) and we choose the stopping criterion \(||x_n-y_n||<\varepsilon \) with \(\varepsilon =10^{-5}\). The starting point is \(x_0=(1,1,\ldots ,1)\in \mathbb {R}^m\). The projections onto C and the evaluation of F are computed by using the MATLAB solvers fmincon. For comparison we choose two very recent viscosity type methods, Shehu and Iyiola [30, Algorithm 3.1] and Thong and Hieu [33, Algorithm 3]. In all algorithms we take the contractions \(f(x)=x/2\). The numerical results are showed in Fig. 3 with respect to the logarithmic scale. In Fig. 4 we illustrate the performances of Algorithm 3.2 for different choices of the contraction \(f(x)=0.9x,0.75x,0.5x,0.25x\).

Fig. 3
figure 3

Comparison between Algorithm 3.2 and [30, Algorithm 3.1] and [33, Algorithm 3]

Full size image
Fig. 4
figure 4

The performances of Algorithm 3.2 for different choices of the contraction \(f(x)=0.9x,0.75x,0.5x,0.25x\)

Full size image

5 Conclusions

In this paper we proposed two projection-type methods, Mann and viscosity schemes methods [27, 28] for solving variational inequalities in real Hilbert spaces. Both algorithms converge strongly under monotonicity and Lipschitz continuity of the VI associated mapping A. The algorithms require the calculation of only one projection onto the VI’s feasible set C per each iteration and by using the projection and contraction technique there is no need to know the Lipschitz constant of A in advance. These two properties emphasize the applicability and advantages over several existing results in the literature. Numerical experiments in finite and infinite dimensional spaces compare and illustrate the performance of the our new schemes.