1 Introduction

Thin-walled steel members are being the most structural element employed in modern high-rise buildings. In which, the thin-walled steel members are able to receive both vertical and horizontal loads. Among others, the rectangular hollow section (RHS) beams are attracting the interest of the engineer, due to their structural efficiency in terms of minimum weight to a given strength. Despite this advantage, thin-walled members are vulnerable against the lateral-torsional buckling phenomenon. Therefore, it is important to provide an efficient and practical method for reasonable prediction of the lateral-torsional buckling resistance without resorting to substantial computational efforts.

Numerous research works have focused on the analysis of thin-walled beams. Indeed, the pioneer contribution is of Vlasov (1962), for static analysis of thin-walled beams with open section, which was extended by Dabrowski (1968) for the curved girders. Vlasov’s theory was adapted by Fu and Hsu (1990) and Chandra et al. (1990) for the anti-symmetric box beam under a combination of lateral forces and torques.

When the thin-walled beam bent initially in its plan, about its strong axis, suddenly at a certain level of the applied force, the thin-walled member undergoes an instability induced by the changing in the equilibrium path letting appear flexural–torsional behaviour. This instability is known as lateral torsional buckling (LTB). An amount of research works attempted to understand the LTB behaviour of thin-walled structures. The early works on this subject (Timoshinko, 1961; Vlasov, 1962; Wang et al., 2004) proposed comprehensive models formulated by using a linearized approach based on Vlasov’s theory (1962). However, these linear models can lead to unrealistic LTB results, as reported in Eurocode 3 (1992). Therefore, it is unable to be used in buckling resistance verification. Alternatively, geometric non-linearity was introduced in the context of moderate torsion rotation (Hamaidia et al., 2019; Mohri et al., 2002, 2003; Osmani & Meftah, 2018; Rezaiee-Pajand et al., 2018, 2021; Saoula & Meftah, 2019; Saoula et al., 2016; Ziane et al., 2021), to assess the LTB resistance. It was recognised that these first-order nonlinear models lead to reasonable predictions of the critical buckling loads especially for thin-walled members with less geometrical ratio of inertia (Iz/Iy), such as those with "I" shape section. Unfortunately, these models drop severely, when opting for beams shape section in "H" and "RHS, having large ratio (Iz/Iy). In order to overcome the limitations induced by the first-order nonlinear approach, a substantial reformulation of kinematic models that consider large torsion was proposed (Benyamina et al., 2013; Lin & Hsiao, 2001; Mohri et al., 2008).

More illustrated approaches aimed to describe the pre- and post-buckling behaviour of thin-walled beams, based on the finite element modelling, were successively proposed in the context of large torsion deformation, without restrictions on twist angle amplitude (Mohri et al., 2015; Mohri et al., 2008; Soomin & KimYY, 2021). Unlike the linear and first-order nonlinear approaches, the current buckling solution is not evident, due to the high order nonlinear terms, appearing in the equilibrium equations and tangent stiffness matrix.

Furthermore, it should be emphasized that, in the Eurocode 3 standard, the LTB verification rules are adapted for beams with open shape sections. However, the RHS beams are not concerned with LTB resistance verification. This is due to the great torsional rigidity, characterizing RHS beams. In addition, this restriction suggested by the Eurocode 3 can be explained also by the fact that the code rules are limited to thin-walled members made with standard steel grades possessing yield strength \(f_{y} \le \, 700{\text{ MPa}}\).

Thereby, in accordance with recent developments related to the use of the manufactured high-strength steel materials with \(f_{y} > 1000{\text{ MPa}}\), in civil infrastructures, it becomes evident that the Eurocode 3 rules will be inappropriate for RHS beam verification. The accuracy loss of the linearized and first order nonlinear theories in LTB prediction is mainly attributed to the omission of geometric non-linearity effects, in addition to the contribution of shear and distortion deformations in the formulation of the LTB solution. To overcome the aforementioned limitation of the earliest models, it became important to develop efficient alternative solutions for a correct assessment of the LTB resistance of RHS beams. For this aim, the shell finite element modelling of the box beams appears to be the more reliable procedure to do LTB verification. This procedure is viable, but it is impracticable in the typical design environments.

Within this context related to the section distortion and shear deformation exhibited by RHS beams, many papers are focused on the study of this effect with the high-order Vlasov torsion theory (Choi & Kim 2020; Shen et al., 2017), which includes hierarchical sets of bending-related sectional deformation modes. In the same way, the Global beam theory (GBT) was proposed for accurate prediction of LTB resistance that covers local and distortional buckling modes (Bebiano et al., 2015; Bebianoa et al., 2018; Goncalves & Camotim 2016). Although this method is looked to be viable, but it become difficult to extend it in buckling analysis in the presence of large torsion.

Nevertheless, the GBT leads to accurate buckling results when the local buckling modes are predominant.

Alternatively, Shen et al. (2018a, 2018b, 2019) proposed an analytical solution for mixed buckling of RHS beams and Yang et al. (2019; 2017) experimentally investigated the LTB of the box section beams. However, it is well recognized that section distortion, when coupled with torsion, tends to reduce LTB resistance (Saoula & Meftah, 2019; Saoula et al., 2016; Ziane et al., 2021). In the field of the static and modal analysis of the box members, Kim and Kim (1999, 2000) pointed the importance of the section distortion, widely neglected in the classical box beam theories. Their investigations have shown that the cross-sectional distortion significantly influences the natural frequencies.

2 Main Considerations of the Present Work

The main objectives of the present paper is to overcome the mentioned difficulties in the precedent section, addressed by the linearized and first order LTB theories and also by the omission of the distortion and shear flexibility effects. The expected benefits of the present work can be summarized as:

  1. I.

    To perform pre-and post buckling analysis of the RHS members by employing a simple FEM procedure with low computational cost compared to shell and brick finite element modelling. Evidently,The proposed finite element can be used for LTB modelling of RHS beams having arbitrary boundary conditions.

  2. II.

    To purpose a reliable finite element solution able to provide accurate prediction of the LTB in pre and post-buckling ranges, applicable for various kinds of RHS beams, especially those having large geometrical ratio Iz/Iy, when the other theories, based on the eigenvalue solutions fails to furnish reasonable LTB estimation.

  3. III.

    To discuss the limitations of the available classical solutions in LTB estimation, that ignore the effect of the shear and distortion deformations, through illustrative comparative studies of RHS beams under combined lateral and compressive loads.

  4. IV.

    To effectively control the impact of the distortion deformations in the LTB resistance, by adding lateral stiffeners as a bracing system around the beam sectional contour.

For these aims, in the present investigation, an original 3D thin-walled finite element beam is formulated for elastic pre- and post-buckling analysis of RHS beams, without any restriction on the twist angle magnitude. The present model is based on the theory proposed by Benscoter (1954) in conjunction with the original kinematic models investigated in Saoula et al. (2016); Saoula & Meftah, 2019; Rezaiee-Pajand et al., 2021; Kim & Kim, 1999; Machado & Cortinez, 2005).

Under this condition, involving geometrical non-linearity effects, the displacement variables adopted within the thin-walled member are in a trigonometric form of the twist angle. Consequently, the derived equilibrium equations and tangent stiffness matrix are in turn established according to the incorporated trigonometric variables in the displacement field. The proposed finite element intrinsically includes, in addition to the ordinary classical terms, other new terms associated with distortion deformation. In the framework of the finite element analysis of RHS beams in lateral-torsional buckling, one proposes a 3D beam element with two nodes and eleven degrees of freedom per node, incorporating warping and distortion.The nonlinear problem involved was resolved by adopting the Newton–Raphson iterative method.

The proposed element is introduced in a finite element code. Many numerical examples are carried out to demonstrate the performances of the proposed finite element. The accuracy LTB prediction of the proposed model is outlined and compared with the existing analytical solutions. The effect of axial compressive load on the LTB resistance is investigated. Finally, for upgrading the LTB performances of the RHS beam, a conceptual study based on the introduction of the lateral stiffeners, attached to the contour of the beam section, is conducted.

3 Formulation of the Post Buckling Equations Problem

3.1 Kinematics

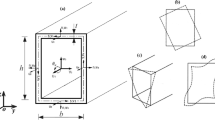
Figure 1 shows a straight thin-walled box beam with slenderness \(L\). The width and height of the rectangular cross-section with respect to the middle line are denoted by \(b\) and \(h\), respectively, and the thickness of the walls is \(t\).

Fig. 1
figure 1

The local coordinate system, the origin is located at the centre of each wall segment segment

Full size image

The displacements of the edges(or walls) of the RHS beam are derived from those of the shear centre, according to the local rectangular coordinate system \((x^{i} ,s^{i} ,n^{i} )\) attached to each wall and the global Cartesian coordinate system \((x,y,z)\), as shown in Fig. 2.

Fig. 2
figure 2

Deformation shapes of a cross section box beam, a: bending about y axis, b: bending about z axis, c: twisting, d: warping, e: distortion

Full size image

Since we will be mainly concerned with the RHS beams under bending and torsion effects, the primary displacement field at the shear centre are the displacements \(u_{0} ,w_{0}\) and \(v_{0}\) that represent the axial, vertical deflection, and lateral displacements, respectively; and \(\theta\) denotes the rotation about the x-axis. The resulting shear stress is described by the additional degrees of freedom according to Timoshenko kinematical model (Timoshenko, 1922), represented by the rotations \(\beta_{y}\) and \(\beta_{z}\) around the y- and z-axes, respectively. Additionally, the warping effect is given by \(\Omega\)(Fig. 3a–d).

Fig. 3
figure 3

Box beam element under axial and lateral loads

Full size image

Unlike thin-walled beams with an open section, the RHS members are shown to exhibit significant distortional or lozenging deformation (Saoula et al., 2016, Saoula and Meftah, 2019, Ziane et al., 2021, Kim and Kim, 1999; 2000). This one is addressed by \(\chi\) as shown in Fig. 3e.

It is worth noting that the shear centreCcoincides with the centroid G in the case of bi-symmetric shape sections such as RHS. The axial \(u{\kern 1pt}^{i} (s,x,n)\), tangential \(v{\kern 1pt}^{i} (s,x,n)\) and normal \(w{\kern 1pt}^{i} (s,x,n)\)(i = 1.0.4) displacements of the generic points of a box beamare expressed in the following form:

$$ u{\kern 1pt}^{i} (s,x,n) = \,u_{0} - Z^{i} \,(\beta_{y} cos(\theta )\, - \beta_{z} \sin (\theta )) - Y^{i} \,\,(\beta_{z} cos(\theta ) + \beta_{y} {\kern 1pt} \sin (\theta )\,) + \omega^{i} \Omega $$
(1)
$$ v{\kern 1pt}^{i} (s,x,n) = - \xi^{i}_{1} v_{0} - \xi^{i}_{2} w_{0} + h^{i} {\kern 1pt} \sin (\theta ) - s{\kern 1pt} (1 - \cos (\theta )) + \psi_{v}^{i} (s)\,\,\chi $$
(2)
$$ w{\kern 1pt}^{i} (s,x,n) = \xi_{1}^{i} w_{0} - \xi_{2}^{i} v_{0} - s\,sin(\theta ) - h^{i} (1 - \cos (\theta )) + \psi_{w}^{i} \,\,\chi $$
(3)

The functions \(Z^{i} \left( s \right)\), \(Y^{i} \left( s \right)\), \(\omega^{i} (s)\),\(h^{i} \left( s \right)\),\(\psi_{{^{v} }}^{i} (s)\) and \(\psi_{w}^{i} (s)\) describe the contour coordinates of the beam cross section. They are straightforward to write using box beam theory as follows:

$$ \xi_{1} = \frac{{\left[ {1 + ( - 1)^{i + 1} } \right]}}{2}(2 - i), $$
(4a)
$$ \xi_{2} = \frac{{\left[ {1 + ( - 1)^{i} } \right]}}{2}(3 - i),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} $$
(4b)
$$ Z^{i} (s) = \left(\xi_{{_{1} }}^{i} \,\frac{h}{2} - \xi_{{{\kern 1pt}_{2} }}^{i} s\right) $$
(4c)
$$ Y^{i} (s) = - \left(\xi_{{_{2} }}^{i} \,\frac{b}{2} + \xi {\kern 1pt}_{{_{1} }}^{i} s \right) $$
(4d)
$$\omega^{i} (s) = \left( - \left(\xi_{1}^{i} \right)^{2} \frac{h}{2} + \left(\xi_{2}^{i} \right)^{2} \frac{b}{2}\right)s $$
(4e)
$$ h^{i} (s) = \left(\xi_{1}^{i} \right)^{2} {\kern 1pt} \frac{h}{2} + \left(\xi_{2}^{i} \right)^{2} {\kern 1pt} \frac{b}{2} $$
(4f)
$$ \psi_{v}^{i} (s) = \left(\left(\xi_{2}^{i} \right)^{2} \, - \,\left(\xi_{1}^{i} \right)^{2} \right)\,\frac{b\,h}{{b + h}} $$
(4g)
$$ \psi_{w}^{i} (s) = (\xi_{1}^{i} )^{2} \psi_{H} (s) + (\xi_{2}^{i} )^{2} \psi_{V} (s) $$
(4h)
$$ \psi_{V} = \frac{ - 2h}{{b + h}}\left(\frac{{2s^{3} }}{{h^{2} }} - \frac{3s}{2}\right) $$
(4i)
$$ \psi_{H} = \frac{2b}{{b + h}}\left(\frac{{2s^{3} }}{{b^{2} }} - \frac{3s}{2}\right) $$
(4j)

In the above formulation, the functions \(\psi_{H} (s)\) and \(\psi_{V} (s)\) are selected to satisfy the in-plane moment equilibrium condition as suggested by Kim and Kim (1999, 2000).

In the case of thin-walled box section beam, the Green–Lagrange strains tensor that includes the large displacements is considered:

$$ \varepsilon {\kern 1pt}^{i}_{xx} = \frac{{\partial u{\kern 1pt}^{i} (s,x,n)}}{\partial x} + \frac{1}{2}\left( {\left( {\frac{{\partial v{\kern 1pt}^{i} (s,x,n)}}{\partial x}} \right)^{2} + \left( {\frac{{\partial w{\kern 1pt}^{i} (s,x,n)}}{\partial x}} \right)^{2} } \right) $$
(5a)
$$ \varepsilon {\kern 1pt}^{i}_{ss} \; = \; - \,n_{i} \frac{{\partial^{2} \,w\,^{i} (s,x,n)}}{{\partial \,s^{2} }}\, $$
(5b)
$$ \gamma^{i}_{xs} \; = {\kern 1pt} \frac{{\partial u^{i} (s,x,n)}}{\partial s} + \frac{{\partial v^{i} (s,x,n)}}{\partial x} + \frac{{\partial v^{i} (s,x,n)}}{\partial x}\frac{{\partial v^{i} (s,x,n)}}{\partial s} + \frac{{\partial w^{i} (s,x,n)}}{\partial x}\frac{{\partial w^{i} (s,x,n)}}{\partial s} $$
(5c)

Substituting Eqs. (1–3) into the above axial strains given in Eq. (5a), yields to the actual axial strain relations of the walls, described as function of the shear centre displacement. The resulting axial strains are decomposed into linear and nonlinear parts.

Thus, the axial linear strain is defined as:

$$ \begin{gathered} \,\varepsilon_{l}^{i} \, = \frac{{\partial u{\kern 1pt}^{i} (s,x,n)}}{\partial x} = \,u^{\prime}_{0} \, - Z^{i} \,\left[ {\beta ^{\prime}_{y} {\kern 1pt} \cos (\theta ) - \beta ^{\prime}_{z} {\kern 1pt} \sin (\theta ) - \theta ^{\prime}{\kern 1pt} (\beta ^{\prime}_{z} {\kern 1pt} \cos (\theta ) + \beta ^{\prime}_{y} {\kern 1pt} \sin (\theta ))} \right] \hfill \\ - Y^{i} \,\left[ {\beta ^{\prime}_{z} {\kern 1pt} \cos (\theta ) + \beta ^{\prime}_{y} {\kern 1pt} \sin (\theta ) - \theta ^{\prime}{\kern 1pt} (\beta ^{\prime}_{y} {\kern 1pt} \cos (\theta ) - \beta ^{\prime}_{z} {\kern 1pt} \sin (\theta ))} \right] + \omega^{i} \,\Omega ^{\prime} \hfill \\ \end{gathered} $$
(6)

(') denotes the derivative with respect to the \(x\) variables.

The Eq. (6) can be rewritten in compact vector form as follows:

$$ \varepsilon_{l}^{i} = \left\{ {\alpha_{{_{l} }}^{i} } \right\}^{T} \left\{ {q_{1} } \right\} $$
(7)

where

$$ \left\{ {\alpha_{l}^{i} } \right\}^{T} = \left\{ {\begin{array}{*{20}c} 1 & { - (Y^{i} cs_{2} - Z^{i} cs_{1} )} & { - (Z^{i} cs_{3} + Y^{i} cs_{4} )} & {\omega^{i} } \\ \end{array} } \right\} $$
(8)

with

$$ cs_{1} = \sin (\theta ) + \theta ^{\prime}{\kern 1pt} \cos (\theta ) $$
(9a)
$$ cs_{2} = \cos (\theta ) + \theta ^{\prime}{\kern 1pt} {\kern 1pt} \sin (\theta ) $$
(9b)
$$ cs_{3} = \cos (\theta ) - \theta ^{\prime}{\kern 1pt} {\kern 1pt} \sin (\theta ) $$
(9c)
$$ cs_{4} = \sin (\theta ) - \theta ^{\prime}{\kern 1pt} \cos (\theta ) $$
(9d)

and

$$ \left\{ {q_{1} } \right\}\; = \;\left\{ {\begin{array}{*{20}c} {u_{0}^{^{\prime}} } \\ {\beta_{z}^{^{\prime}} } \\ {\beta_{y}^{^{\prime}} } \\ {\Omega^{^{\prime}} } \\ \end{array} } \right\} $$
(10)

The nonlinear axial strain part is given by:

$$ \begin{gathered} \varepsilon_{nl\,}^{i} = \,\frac{1}{2}\left( {\left( {\frac{{\partial v{\kern 1pt}^{i} (s,x,n)}}{\partial x}} \right)^{2} + \left( {\frac{{\partial w{\kern 1pt}^{i} (s,x,n)}}{\partial x}} \right)^{2} } \right) = \frac{{\xi_{1}^{{i^{2} }} {\kern 1pt} + \xi_{2}^{{i^{2} }} {\kern 1pt} }}{2}\,(v_{0}^{^{\prime}2} + w_{0}^{^{\prime}2} ) \hfill \\ + \,\left[ {h^{{i^{2} }} + s^{2} (\cos^{2} (\theta ) - \sin^{2} (\theta )} \right]{\kern 1pt} \frac{{\theta ^{{\prime}{2}} }}{2} + \left[ {\psi_{v}^{{i^{2} }} + \psi_{w}^{{i^{2} }} } \right]\frac{{\chi^{^{\prime}2} }}{2} \hfill \\ + \left[ {h^{i} \left( {\xi_{2}^{i} \sin (\theta ) - \xi_{1}^{i} \cos (\theta )} \right) + s\left( {\xi_{1}^{i} \sin (\theta ) + \xi_{2}^{i} \cos (\theta )} \right)} \right]\,v_{0} ^{\prime}\theta ^{\prime} \hfill \\ + \left[ {s\left( {\xi_{2}^{i} \sin (\theta ) - \xi_{1}^{i} \cos (\theta )} \right) - h^{i} \left( {\xi_{2}^{i} \cos (\theta ) + \xi_{1}^{i} \sin (\theta )} \right)} \right]\,w_{0} ^{\prime}\theta ^{\prime} \hfill \\ - (\xi_{1}^{i} \psi_{v}^{i} + \xi_{2}^{i} \psi_{w}^{i} )v_{0} ^{\prime}\chi ^{\prime} + (\xi_{1}^{i} \psi_{w}^{i} - \xi_{2}^{i} \psi_{v}^{i} )w_{0} ^{\prime}\chi ^{\prime} \hfill \\ + \left[ {h\left( {\psi_{v}^{i} \cos (\theta ) - \psi_{w}^{i} \sin (\theta )} \right) - s\left( {\psi_{v}^{i} \sin (\theta )\psi_{w}^{i} \cos (\theta )} \right)} \right]\theta ^{\prime}\chi ^{\prime} \hfill \\ \end{gathered} $$
(11)

The above relation is rewritten in vector form as

$$ \varepsilon_{nl}^{i} = \left\{ {\alpha_{nl}^{i} } \right\}^{T} \left\{ {q_{2} } \right\} $$
(12)

where

$$ \left\{ {q_{2} } \right\}\; = \left\{ {\begin{array}{*{20}c} {v_{0}^{^{\prime}} } \\ {w_{0}^{^{\prime}} } \\ {\theta^{^{\prime}} } \\ {\chi^{^{\prime}} } \\ \end{array} } \right\} $$
(13a)

and

$$ \left\{ {\alpha_{nl}^{i} } \right\}^{T} = \left\{ {\begin{array}{*{20}c} {\left( {\frac{{\xi_{1}^{{i^{2} }} {\kern 1pt} + \xi_{2}^{{i^{2} }} {\kern 1pt} }}{2}v_{0}^{^{\prime}} + sh_{1}^{i} \theta ^{\prime} + \psi_{1}^{i} \chi } \right)^{^{\prime}} } & {\left( {\frac{{\xi_{1}^{{i^{2} }} {\kern 1pt} + \xi_{2}^{{i^{2} }} {\kern 1pt} }}{2}w_{0}^{^{\prime}} + sh_{2}^{i} \frac{\theta ^{\prime}}{2} + \psi_{2}^{i} \chi^{^{\prime}} } \right)} & {\left( {sh_{3}^{i} \theta^{^{\prime}} + sh_{4}^{i} \chi^{^{\prime}} } \right)} & {\psi_{3}^{i} \frac{{\chi^{^{\prime}} }}{2}} \\ \end{array} } \right\} $$
(13b)

with

$$ sh_{1}^{i} = h^{i} \left( {\xi_{2}^{i} \sin (\theta ) - \xi_{1}^{i} \cos (\theta )} \right) + s\left( {\xi_{1}^{i} \sin (\theta ) + \xi_{2}^{i} \cos (\theta )} \right) $$
(14a)
$$ sh_{2}^{i} = s\left( {\xi_{2}^{i} \sin (\theta ) - \xi_{1}^{i} \cos (\theta )} \right) - h^{i} \left( {\xi_{2}^{i} \cos (\theta ) + \xi_{1}^{i} \sin (\theta )} \right) $$
(14b)
$$ sh_{3}^{i} = h^{{i^{2} }} + s^{2} (\cos^{2} (\theta ) - \sin^{2} (\theta ) $$
(14c)
$$ sh_{4}^{i} = h\left( {\psi_{v}^{i} \cos (\theta ) - \psi_{w}^{i} \sin (\theta )} \right) - s\left( {\psi_{v}^{i} \sin (\theta )\psi_{w}^{i} \cos (\theta )} \right) $$
(14d)
$$ \psi_{1}^{i} = - (\xi_{1}^{i} \psi_{v}^{i} + \xi_{2}^{i} \psi_{w}^{i} ) $$
(14e)
$$ \psi_{2}^{i} = \xi_{1}^{i} \psi_{w}^{i} - \xi_{2}^{i} \psi_{v}^{i} $$
(14f)
$$ \psi_{3}^{i} = \psi_{v}^{{i^{2} }} + \psi_{w}^{{i^{2} }} $$
(14g)

Similar to the axial strain, by substituting the displacement given by Eqs. (1–3) into Eq. (5c), the derivation of the tangential strain expression is achieved, and it is decomposed into linear and nonlinear parts.

The linear part of the shear strain is given by:

$$ \begin{gathered} \gamma_{{xs_{l} }}^{i} = \frac{{\partial u^{i} (s,x,n)}}{\partial s} + \frac{{\partial v^{i} (s,x,n)}}{\partial x} = - \tilde{Z}^{i} \left( {\beta_{y} \cos (\theta ) - \beta_{z} \sin (\theta )} \right) \hfill \\ - \tilde{Y}^{i} \left( {\beta_{z} \cos (\theta ) + \beta_{y} \sin (\theta )} \right) - \xi_{1}^{i} v_{0}^{^{\prime}} - \xi_{2}^{i} w^{\prime}_{0} + \left( {h^{i} \cos (\theta ) - s\sin (\theta )} \right)\theta ^{\prime} + \tilde{\omega }^{i} \Omega + \psi_{v}^{i} \chi ^{\prime} \hfill \\ \end{gathered} $$
(15)

This relation can be rewritten in vector form as follows

$$ \gamma_{{xs_{l} }}^{i} \; = \;\left\{ {\eta_{l} } \right\}^{T} \left\{ {q_{3} } \right\} $$
(16)

where

$$ \left\{ {q_{3} } \right\}\; = \;\left\{ {\begin{array}{*{20}c} {\beta_{z} } \\ {\beta_{y} } \\ {v_{0}^{^{\prime}} } \\ {w_{0}^{^{\prime}} } \\ \begin{gathered} \theta^{^{\prime}} \hfill \\ \Omega \hfill \\ \end{gathered} \\ {\chi^{^{\prime}} } \\ \end{array} } \right\} $$
(17a)

and

$$ \left\{ {\eta_{l} } \right\}^{T} = \quad \left\{ {\begin{array}{*{20}c} {\left( {\tilde{Z}^{i} \sin (\theta ) - \tilde{Y}^{i} \cos (\theta )} \right)} & { - \left( {\tilde{Z}^{i} \cos (\theta ) + \tilde{Y}^{i} \sin (\theta )} \right)} & { - \xi_{1}^{i} } & { - \xi_{2}^{i} } & {\left( {h^{i} \cos (\theta ) - s\sin (\theta )} \right)} & {\tilde{\omega }^{i} } \\ \end{array} \begin{array}{*{20}c} {\psi_{v}^{i} } \\ \end{array} } \right\} $$
(17b)

The nonlinear part of the tangential strain is given by

$$ \begin{gathered} \gamma_{{xs_{{n_{l} }} }}^{i} = \frac{{\partial v^{i} (s,x,n)}}{\partial x}\frac{{\partial v^{i} (s,x,n)}}{\partial s} + \frac{{\partial w^{i} (s,x,n)}}{\partial x}\frac{{\partial w^{i} (s,x,n)}}{\partial s} \hfill \\ \quad \quad\, = \left( {\left( {1 - \cos (\theta )} \right)\xi_{1}^{i} + \xi_{2}^{i} \sin (\theta )} \right)v^{\prime}_{0} + \left( {\left( {1 - \cos (\theta )} \right)\xi_{2}^{i} - \xi_{1}^{i} \sin (\theta )} \right)w^{\prime}_{0} + h^{i} \theta ^{\prime}\left( {1 - \cos (\theta )} \right) \hfill \\ \quad \qquad + s\theta ^{\prime}\sin (\theta ) + \left( {\psi_{v}^{i} \left( {\cos (\theta ) - 1} \right) - \psi_{w}^{i} \sin (\theta )} \right)\chi ^{\prime} + \xi_{1}^{i} \tilde{\psi }_{w}^{i} w^{\prime}_{0} \chi ^{\prime} \hfill \\ \quad \qquad - \xi_{2}^{i} \tilde{\psi }_{w}^{i} v^{\prime}_{0} \chi ^{\prime} - \psi_{w}^{i} \left( {s\cos (\theta ) + h^{i} \sin (\theta )} \right)\theta ^{\prime}\chi ^{\prime} + \psi_{w}^{i} \tilde{\psi }_{w}^{i} \chi ^{{\prime}{2}} \hfill \\ \end{gathered} $$
(18)

by adopting the vector form expression, it results

$$ \gamma_{nl}^{i} = \left\{ {\eta_{nl} } \right\}^{T} \left\{ {q_{2} } \right\} $$
(19)

in which

$$ \left\{ {\eta_{nl} } \right\}^{T} \, = \,\left\{ {\begin{array}{*{20}c} {ss_{{^{1} }}^{i} - \xi_{2}^{i} \tilde{\psi }_{w}^{i} \chi ^{\prime}} & {ss_{2}^{i} + \xi_{1}^{i} \tilde{\psi }_{w}^{i} \chi ^{\prime}} & {sh_{5}^{i} - \psi_{4}^{i} \chi ^{\prime}} & {\psi_{5}^{i} + \psi_{6}^{i} \chi^{^{\prime}} } \\ \end{array} } \right\} $$
(20)
$$ ss_{{^{1} }}^{i} = \left( {\left( {1 - \cos (\theta )} \right)\xi_{1}^{i} + \xi_{2}^{i} \sin (\theta )} \right) $$
(21a)
$$ ss_{2}^{i} = \left( {\left( {1 - \cos (\theta )} \right)\xi_{2}^{i} - \xi_{1}^{i} \sin (\theta )} \right) $$
(21b)
$$ sh_{5}^{i} = h^{i} \left( {1 - \cos (\theta )} \right) + s\sin (\theta ) $$
(21c)
$$ \psi_{4}^{i} = \psi_{w}^{i} \left( {s\cos (\theta ) + h^{i} \sin (\theta )} \right) $$
(21d)
$$ \psi_{5}^{i} = \left( {\psi_{v}^{i} \left( {\cos (\theta ) - 1} \right) - \psi_{w}^{i} \sin (\theta )} \right) $$
(21e)
$$ \psi_{6}^{i} = \psi_{w}^{i} \tilde{\psi }_{w}^{i} $$
(21f)

Concerning the axial strain generated by the distortional deformation, only the linear part is considered in this study, one writes:

$$ \varepsilon_{ss}^{i} {\kern 1pt} = {\kern 1pt} - n_{i} \,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\psi } \,\chi = \varepsilon_{ss}^{i} {\kern 1pt} = {\kern 1pt} \left\{ \kappa \right\}^{T} \,\left\{ {q_{{}} } \right\} $$
(22)

with

$$ \left\{ q \right\} = \left\{ {\begin{array}{*{20}c} {u_{0} } \\ {v_{0} } \\ {w_{0} } \\ {\beta_{z} } \\ {\beta_{y} } \\ \theta \\ \begin{gathered} \Omega \hfill \\ \chi \hfill \\ \end{gathered} \\ \end{array} } \right\} $$
(23a)
$$ \left\{ \kappa \right\}^{T} = \left\{ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 & 0 & 0 & { - n_{i} \,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\psi } } \\ \end{array} } \right\} $$
(23b)

The geometric parameters defined above are expressed by the following derivatives:

$$ \tilde{Z}^{i} {\kern 1pt} = {\kern 1pt} \frac{{\partial Z^{i} }}{\partial s} $$
(24a)
$$ \tilde{Y}^{i} {\kern 1pt} = {\kern 1pt} \frac{{\partial Y^{i} }}{\partial s} $$
(24b)
$$ \tilde{\psi }_{w}^{{i}{}} {\kern 1pt} = {\kern 1pt} \frac{{\partial \psi_{w}^{i} }}{\partial s} $$
(24c)
$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\psi }_{w}^{i} {\kern 1pt} = {\kern 1pt} \frac{{\partial^{2} \psi_{w}^{i} }}{{\partial {\kern 1pt} s^{2} }} $$
(24d)

Once the strain components are defined, for the box beams made with elastic material, the Piola-Kirchoff stress tensor is considered as:

$$ \left\{ {\sigma^{i} } \right\} = {\kern 1pt} \left[ C \right]\,\left\{ {\varepsilon^{i} } \right\} $$
(25a)

where

$$ \left\{ {\sigma^{i} } \right\}\; = \;\left\{ {\begin{array}{*{20}c} {\sigma^{i}_{xx} } \\ {\tau^{i}_{xy} } \\ {\sigma^{i}_{ss} } \\ \end{array} } \right\};\,\left\{ {\varepsilon^{i} } \right\}\, = \;\left\{ {\begin{array}{*{20}c} {\varepsilon^{i}_{xx} } \\ {\gamma^{i}_{xy} } \\ {\varepsilon^{i}_{ss} } \\ \end{array} } \right\};\,\left[ C \right]\; = \quad \left[ {\begin{array}{*{20}c} E & 0 & 0 \\ 0 & G & 0 \\ 0 & 0 & E \\ \end{array} } \right] $$
(25b)

3.2 Finite Element Discretization

For numerical investigation of the post-buckling behaviour of the RHS beams, by considering the geometric nonlinearity effects, resulting from the trigonometric relationships between the membrane components and the twist angle \(\theta\), a 3D finite element with two nodes having eleven degrees of freedom per node is proposed. For the axial displacement \(u_{0}\);the bending rotations \(\beta_{y}\) and \(\beta_{z}\),and the distortion \(\chi\),the linear shape functions are used, while other displacements are approximated by the cubic shape functions. The global displacement vectorat the shear centre \(\left\{ q \right\}\) is linked to the nodal variables \(\left\{ r \right\}\) by:

$$ \left\{ q \right\} = \left\{ {\begin{array}{*{20}c} {u_{0} } \\ {v_{0} } \\ {w_{0} } \\ {\beta_{z} } \\ {\beta_{y} } \\ \theta \\ \begin{gathered} \Omega \hfill \\ \chi \hfill \\ \end{gathered} \\ \end{array} } \right\} = \left[ N \right]\,\left\{ r \right\} $$
(26a)

The expressions of the membrane components are obtained as follows:

$$ \varepsilon_{xx}^{i} = \varepsilon_{l}^{i} + \varepsilon_{\ln l}^{i} = \left( {\left\{ {\alpha_{{_{l} }}^{i} } \right\}^{T} \left[ {B_{l} } \right] + \left\{ {\alpha_{{_{nl} }}^{i} } \right\}^{T} \left[ {B_{nl} } \right]} \right)\left\{ r \right\} $$
(27a)
$$ \gamma_{xs}^{i} = \gamma_{{xs_{l} }}^{i} + \gamma_{{xs_{nl} }}^{i} = \left( {\left\{ {\eta_{{_{l} }}^{i} } \right\}^{T} \left[ {S_{l} } \right] + \left\{ {\eta_{{_{nl} }}^{i} } \right\}^{T} \left[ {S_{nl} } \right]} \right)\left\{ r \right\} $$
(27b)
$$ \varepsilon_{ss}^{i} = \left( {\left\{ \kappa \right\}^{T} \left[ {D_{l} } \right]} \right)\left\{ r \right\} $$
(27c)

where the shape function matrices \(\left[ N \right], \, \left[ {B_{l} } \right]{, }\left[ {B_{nl} } \right]{, }\left[ {S_{l} } \right]{, }\left[ {S_{nl} } \right]\) and \(\left[ {D_{l} } \right]\) are given in the appendix.

3.3 Variational Formulation

The total potential energy stored in the box beam is defined as the sum of the of the strain energy and the work done by the external forces denoted by \(U\) and \(W\) respectively, expressed as:

$$ \Pi = U + W $$
(28)

The strain energy \(U\) for rectangular box beam element with the length \(l\) takes the following form

$$ U\; = \;\frac{1}{2}\sum\limits_{i = 1}^{4} {\int\limits_{l} {\int\limits_{{A_{i} }} {} } (\sigma_{xx}^{i} \,\varepsilon_{xx}^{i} } + \tau_{xy}^{i} {\kern 1pt} \gamma_{xy}^{i} + \,\sigma_{ss}^{i} \varepsilon_{ss}^{i} )\,dA_{i} {\kern 1pt} \,dx $$
(29)

Inserting the membrane components expressed in Eq. (27a, 27b, 27c) into Eq. (29), and taking into account the constitutive law in Eq. (25a, 25b), the strain energy is written in the matrix form as:

$$ U\; = \;\frac{1}{2}\left\{ r \right\}^{T} \left[ {K(r)} \right]\left\{ r \right\} $$
(30)

in which

$$ \left[ {K(r)} \right] = \sum\limits_{i = 1}^{4} {\int\limits_{l} {\int\limits_{{A_{i} }} {} } } \left[ {{\rm P}^{i} (r)} \right]^{T} \left[ C \right]\left[ {{\rm P}^{i} (r)} \right]\,dA_{i} \,dx $$
(31a)

and the matrix \(\left[ {P^{i} \left( r \right)} \right]\)(dimension 3 × 22) is ranged as:

$$ \left[ {{\rm P}^{i} (r)} \right] = \left[ {\begin{array}{*{20}c} {\left\{ {\alpha_{{_{l} }}^{i} } \right\}^{T} \left[ {B_{l} } \right] + \left\{ {\alpha_{{_{nl} }}^{i} } \right\}^{T} \left[ {B_{nl} } \right]} \\ {\left\{ {\eta_{{_{l} }}^{i} } \right\}^{T} \left[ {S_{l} } \right] + \left\{ {\eta_{{_{nl} }}^{i} } \right\}^{T} \left[ {S_{{n{\text{l}} }} } \right]} \\ {\left\{ \kappa \right\}^{T} \left[ {D_{l} } \right]} \\ \end{array} } \right] $$
(31b)

In this study, the axially loaded box beams are considered. The axial force is applied at the centre of geometry and combined to the lateral one acting in the z direction, through the line \(tt^{\prime}\) with the eccentricity \(e_{z}\) as shown in Fig. 3.

Foremother, in this study we are mainly concerned with the beams under lateral forces, proportional to the load multiplier factor \(\lambda\), combined to a constant compressive force. Therefore, the work done by lateral and compressive load,\(W\), are calculated as follows:

$$ W = - \int\limits_{l} {\left( {f_{x} u_{0} (x) + \lambda f_{z} w_{t} } \right){\kern 1pt} } dx $$
(32a)

In this equation, \(w_{t}\) is the vertical displacement along the line \(tt^{\prime}\).This displacement is derived directly from Eq. (3). The resulting expression of the external work is the following

$$ W = - \int\limits_{l} {\left( {f_{x} u_{0} + \lambda f_{z} \delta w_{0} - \lambda f_{z} e_{z} {\kern 1pt} (1 - \cos (\theta )){\kern 1pt} } \right)\;{\kern 1pt} } dx $$
(33a)

or in the vector form:

$$ W = \left\{ r \right\}^{T} \left\{ {F_{e} \left( \lambda \right)} \right\} $$
(33b)

where

$$ \left\{ {F_{e} } \right\} = \left( {\begin{array}{*{20}c} {F_{x} } \\ {\lambda F_{Z} } \\ \end{array} } \right) = \int\limits_{l} {} \left[ G \right]^{T} \left\{ {\begin{array}{*{20}c} {f_{x} } \\ {\lambda f_{z} } \\ \end{array} } \right\}dx $$
(34)

the vector \(\left\{ {F_{e} } \right\}\) denotes the nodal force vector. In this investigation, only RHS beams under concentrated mid-span lateral load are considered.

Based on Eqs. (28), (30), (33b), the formulation of the total potential energy is given in the matrix form as follows:

$$ \Pi \; = \;\frac{1}{2}\left\{ r \right\}^{T} \left[ {K(r)} \right]\left\{ r \right\} + \left\{ r \right\}^{T} \left\{ {F{}_{e}\left( \lambda \right)} \right\} $$
(35)

4 Solution Strategy in the Framework of Nonlinear Problem

In order to perform the finite element method, it is necessary to adopt a matrix formulation to express the equilibrium condition. The above mathematical development is carried out using Maple software (Abell & Braselton, 1994) designed for symbolic formulation.

The required finite element equilibrium equations and the stiffness matrix of the finite element are calculated by employing algebraic operators. Thus, the equilibrium equations \(\left\{ {g\left( {r,\lambda } \right)} \right\}\) are obtained by applying directly the gradient operator to the potential energy \(\Pi\), with respect to the nodal displacement vector \(\left\{ r \right\}\) as:

$$ \left\{ {g(r,\lambda )} \right\} = gradient\left( {\Pi ,\left\{ r \right\}} \right) $$
(36)

It is obvious that the classical procedure is often employed to provide a tangent stiffness matrix \(\left[ {K_{t} } \right]\), defined as the sum of the geometric and initial stress matrices, thus needing more complex matrix development. In the present work, the currently tangent stiffness matrix \(\left[ {K_{t} } \right]\) was directly calculated by employing a simple procedure, involving the use of the Jacobian operator, applied to the resulting equilibrium \(\left\{ g \right\}\) as:

$$ \left[ {K_{t} (r)} \right] = Jacobian\left( {\left\{ {g(r,\lambda )} \right\},\left\{ r \right\}} \right) $$
(37)

The evaluation of the finite element parameters \(\left[ {K_{t} \left( r \right)} \right]\) and \(\left\{ {g\left( {r,\lambda } \right)} \right\}\) defined above is based on the numerical integration procedure. This numerical procedure is achieved with the well-known Gaussian integration method. This step is supported by Matlab software (Matlab71, 2006).

In the context of the nonlinear finite element method, the pre- and post-buckling responses of the RHS beams are obtained from the following

$$ \sum\limits_{el} {\left[ {K_{t} (r_{0} )} \right]} \,\left\{ {\Delta r} \right\} = \sum\limits_{el} {\left\{ {g(r_{0} ,\lambda )} \right\}} $$
(38)

\(\sum\limits_{el} {}\) denotes the assembly process of the tangent stiffness matrix \(\left[ {K_{t} \left( r \right)} \right]\) and equilibrium residue \(\left\{ {g\left( r \right)} \right\}\) over the basic finite elements.

The solution of Eq. (38) is achieved by resorting to the incremental iterative Newton–Raphson numerical method, implemented in the conjunction with the arc-length procedure. For this aim, an in-house finite element program was prepared in Matlab (Matlab71, 2006) incorporating an arc-length solver with the parabolic interpolation method and adopted to provide the global equilibrium path. This numerical solver is able to accurately capture the bifurcation of the equilibrium state at singular points.

In the iterative Newton–Raphson method, the unknowns of the Eq. (34) are \(\left\{ r \right\}\) and \(\lambda\). The load parameter \(\lambda\) is sought in the form:

$$ \left\{ r \right\} = \left\{ {r_{0} } \right\} + \left\{ {\Delta \,r} \right\} $$
(39a)
$$ \lambda = \lambda_{0} + \Delta \,\lambda $$
(39b)

For the sake of brevity, more details of the numerical procedure can be found in (Crisfield, (1981); Bathe, 1996; Ritto-Correa, 2008; Zhou & Murray, 1994).

5 Numerical Investigation

Firstly, the robustness and accuracy of the proposed finite element model in buckling and post-buckling analysis under large torsion of the RHS beams is carried out. For this goal, the equilibrium paths provided by the present finite element are compared with those of the finite element modelling evaluated by Abaqus software (Hibbit & Sorensen, 2003). In this comparison study, the C3D20R quadratic brick element with 20 nodes, available in the Abaqus library, was chosen to model the box beam structures as shown in Fig. 4.

Fig. 4
figure 4

Deformation aspects of the RHS100 × 50x3 under different loading states

Full size image

Secondly, the sensitivity of the LTB resistance of the box beams on the applied compressive load and lateral stiffeners attached on the box beam section contour is done by considering various boundary conditions. In this subsection, a particular attention is addressed on the control of distortional deformation to improve as far as possible the bow beam LTB resistance.

The present study involves the critical loads obtained by the present method including shear and distortional deformations; theory that ignore sthe shear and distortional deformations and quadratic brick finite element analysis, denoted by \(F_{cr}^{S} ,F_{cr}\), and \(F_{cr}^{FEM}\) respectively.

The critical load factor is evaluated by using the corresponding expression, proposed in the assessment of the critical buckling moment as follows:

  1. (a)

    For Cantilever Beam Under Tip Concentrated Load:

    $$ M_{cr} = F_{cr} L = 1.12\frac{{P_{z} }}{\sqrt k }\left[ {\sqrt {\frac{{I_{\omega } }}{{I_{z} }}} \left( {1 + 1.22\sqrt {\frac{{GJL^{2} }}{{\pi^{2} EI_{\omega } }}} } \right)} \right] $$
    (40a)

    with \(k = 1 - \frac{{I_{z} }}{{I_{y} }}\)

  2. (b)

    For Pined-Simply Supported Beam Under Combined Compressive and Mid-Span Lateral Concentrated Loads:

    $$ M_{cr} = \frac{{F_{cr} L}}{4} = c_{1} P_{z} \left[ {c_{2} e_{z} \pm \sqrt {\left( {c_{2} e} \right)^{2} + \frac{{I_{\omega } }}{{I_{z} }}\left( {1 + \frac{{GJL^{2} }}{{\pi^{2} EI_{\omega } }}} \right)} } \right]\sqrt {T(F{}_{z})} $$
    (40b)

    in which

    $$ T(F{}_{z}) = \left( {1 - \frac{{F{}_{z}}}{{P_{z} }}} \right)\,\left( {1 - \frac{{F{}_{z}}}{{P_{y} }}} \right)\left( {1 - \frac{{F{}_{z}}}{{P_{\theta } }}} \right) $$
    (41)

These critical forces are founded according to the nonlinear stability analysis and established as a function of the ratio \((I_{z} /I_{y} )\), (Lin & Hsiao, 2001; Rezaiee-Pajand et al., 2018):

\(I_{\omega }\) and \(J\) are respectively the warping and St-Venant torsion constants.

\(c_{1}\) and \(c_{2}\) are the coefficients defined as:

$$ c_{1} = \frac{1.36}{{\left( {1 - \frac{{I_{z} }}{{I_{y} }}} \right)}} $$
(42a)
$$ c_{2} = \frac{0.55}{{\left( {1 - \frac{{I_{z} }}{{I_{y} }}} \right)}}\sqrt {G(F_{z} )} $$
(42b)

where

$$ G(F{}_{z}) = \left( {1 - \frac{{F{}_{z}}}{{P_{z} }}} \right)\,\left( {1 - \frac{{F{}_{z}}}{{P_{y} }}} \right)\left( {1 - \frac{{F{}_{z}}}{{P_{\theta } }}} \right)^{ - 1} $$
(42c)

\(P_{z}\) and \(P_{y}\) are, respectively, the well-known Euler's buckling loads, while \(P_{\theta }\) is the torsional buckling load, given by:

$$ P_{z} = \frac{{EI_{z} \pi^{2} }}{{L^{2} }} $$
(43a)
$$ P_{y} = \frac{{EI_{y} \pi^{2} }}{{L^{2} }} $$
(43b)
$$ P_{\theta } = I_{0} \left( {\frac{{E\pi^{2} }}{{L^{2} }} + GJ} \right) $$
(43c)

\(I_{0}\) is the polar moment of inertia defined as:

$$ I_{0} = \frac{{I_{z} + I_{y} }}{A} $$
(43d)

5.1 Validation of the Proposed Finite Element in Buckling and Post Buckling Analysis

5.1.1 Example1: Cantilever Beam Under Tip Load

In order to validate both the proposed finite element and the numerical procedure, in this example, a steel RHS cantilever beam with geometric and material properties of \(E = 210{\text{ GPa}}\), \(G = 80.077{\text{ GPa}}\), \(h = 100\;{\text{mm}}\),\(b = 50\;{\text{mm}}\), \(t = 3\;{\text{mm}}\) and \(L = 2.5\;{\text{m}}\) is analyzed. The tip load acts on the upper flange of the beams.

The pre- and post-buckling curves of the RHS beam are reported in Figs. 5a–c for different elements size mesh. The evolution of the tip end displacements (\(w_{0} , \, v_{0}\) and \(\theta\)) is a function of the applied load \(F_{z}\). Thus, Fig. 5a depicts the variation of the deflection \(w_{0}\) with the applied load. One remarks from this figure is that the deflexion variation is linear in the pre-buckling state. By increasing the load, the evolution is nonlinearly in the post-buckling range. It was important to state that in the pre-buckling stage, both the Abaqus finite element and the new proposed element led to similar results. Table 1 provides the variation of the buckling loads with the element number, compared to the Abaqus finite element solution. Taken the finite element results as reference, it is observed from this convergence study that by the proposed method employing forty (40) finite elements, one obtains a good agreement with Abaqus solution. The relative error is of 2%. Findings lead to important overestimation of the buckling load when only twenty (20) elements is used with a relative error of 36%. Whereas, when using only teen 10 finite elements the buckling load cannot be determined as reported in Figs. 5a and b. For this case one obtains only the pre-buckling evolution without reaching the bifurcation point.

Fig. 5
figure 5

Load displacements graph of cantilever beam of the example 1

Full size image
Table 1 LTB loads comparison for the beam of example 1
Full size table

It is interesting to show that the analytical formula of Eq. 37a leads to an unrealistic higher value of the critical load with \(F_{cr} = \, 63.37{\text{ kN}}\).

Moreover, one reports that the bending stiffness in pre-buckling \((F_{cr}^{FEM} /w_{0} )\) is of \(50.89{\text{ kN/m}}\), which is close to that given by the proposed finite element \((F_{cr}^{SD} /w_{0 = } 50.48{\text{ kN/m}})\), when forty (40) finite element are considered. Figure 5b presents the variation of the angle \(\theta\) with respect to the applied load. This figure shows that the twist angle is depicted only in the post-buckling state. For the angle \(\theta > \, 0.01\),a small load increase is observed. Inspecting Fig. 5c, one observes a little lateral displacement v0 in the pre-buckling range. When the critical load is reached, the equilibrium curve given by the present finite elements is near to that provided by Abaqus simulation.

5.1.2 Example2: clamped–clamped beam

For verification purposes, in the present example, a clamped–clamped RHS steel beam with \(b = 200{\text{ mm}}\),\(h = 600{\text{ mm}}\),\(t = 20{\text{ mm}}\) and slenderness \(L = \, 12{\text{ m}}\) is analysed. The beam is divided into 10; 20; 40 and 50 proposed elements. The beam is subjected to a concentrated mid-span load, located on the shear centre. The pre-and post-buckling behaviour of this beam is plotted in Fig. 6a–c. These demonstrate the ability of the present finite element for accurate prediction of the equilibrium path, either in the pre- and post-buckling domains, when more than forty (40) proposed finite elements are employed. Figure 6a reports the evolution of the lateral displacement w0 versus the applied load. Inspection of this figure suggests the effectiveness of the proposed finite element in reproducing the correct equilibrium curves, The performance of the element to capture accurate bifurcation state is checked from the Fig. 6b and c. One notices from these figures that the bifurcation load given by the proposed finite element modelling with fifty (50) elements is \(F^{SD}_{cr} = \, 25318.83{\text{ kN}}\), which is in good agreement with that obtained by Abaqus prediction leading to \(F^{FEM}_{cr} = 26434{\text{ kN}}\). One observes also that when less than twenty (20) elements are employed the proposed model fail to reproduce correctly the post-buckling path.

Fig. 6
figure 6

Load displacements graph of clamped–clamped beam of the example 2

Full size image

Table 2 reports the buckling loads evaluated by the proposed model and Abaqus prediction. The relevant outcomes prove that a correct critical load evaluation is reached, just by using twenty (20) finite elements, with a relative error of 6%.The important error of 35% is given by teen 10 finite elements modelling.

Table 2 LTB loads comparison for the beam of example 2
Full size table

5.2 Parametric Pre- and Post-Buckling Investigation

5.2.1 Example 3

This example is proposed in order to illustrate the effect of the critical load \(F_{cr}^{SD}\) upon the applied compressive force \(F_{x}\) of the RHS steel beam (Fig. 7) under simply-pined edges, commenting also the effects of shear and distortion deformations on the nonlinear behaviour.

Fig. 7
figure 7

Pined-simply supported beam with considered in example 3

Full size image

It should be noted that, for this beam, the critical compressive load is defined as being the Euler's buckling load \(P_{z}\) expressed by Eq. (40a). For the considered beam \(P_{z} = 48.3{\text{ kN}}\).

Figures 8a–d depict the displacement (\(w_{0,} \;v_{0,} \;\theta_{0}\) and \(\chi_{0}\)) variations versus the concentrated mid-span load. The curves are drawn in both the pre-buckling and post-buckling states. Figure 8a inspects the variation of the deflection \(\left( {w_{0} , \, F_{z} } \right)\), this one is perfectly linear in the pre-buckling state. This figure reveals also that the stiffness of the beam without axial load is significantly more important compared to those under compression. Thus, the stiffness deterioration is on order of13% for the beam under \(F_{x} = 0.5P_{z}\) and approaching 20% for \(F_{x} = 0.75P_{z}\).In the post-buckling state, the displacement w0 increases slightly in the same manner, for the beam without compressive load as well as for those under compression.

Fig. 8
figure 8

Effect of the compressive load on the load–displacement curves for pined-simply supported beam of example 3

Full size image

For beams under various magnitudes of compressive load, the resulting lateral buckling loads are listed in Table 3. These outcomes manifestly demonstrate the vulnerability of the beams in compression to lateral instability. For instance, one records a relative diminution of 37% for the beam under \(F_{x} = 0.5P_{z}\), followed by that under \(F_{x} = 0.75P_{z}\), leading to a critical load decreasing of 50%.

Table 3 LTB loads comparison for the beam of example 3
Full size table

The variation of the twist angle \(\theta\) versus the load \(F_{z}\) is depicted in Fig. 8b. This twist angle is founded only in the post-buckling stage. The nonlinear branch begins to develop neighbour the critical load and increases continuously. Similarly to this typical buckling behaviour, Fig. 8c demonstrates the variation of the lateral displacement \(\left( {v_{0,} F_{z} } \right)\). The equilibrium curves show a little initial displacement which was introduced as initial imperfection to capture the nonlinear evolution. This displacement remains unchanged with \(F_{z}\) rising pressure until the critical load is reached. Beyond this value, the behaviour is perfectly nonlinear, associated with larger lateral displacement \(v_{0}\). With the same tendency, the distortional deformation \(\chi\) is reported in Fig. 8d. This figure let appear in the onset a slight evolution, much before the critical load is reached. The slope of this evolution is more significant for the beams in compression. This figure reveals that the box beam under combined compression and bending loads is very sensitive to section distortion.

The critical loads mentioned above are compared in Table 3 to those coming by the formula of Eq. (40b), in which the shear and distortion deformation effects are neglected. This comparison clearly demonstrates that the analytical formulation Eq. (40b) is inappropriate for prediction of the LTB resistance. The average error provided by the analytical formula is in order of 20%.

5.2.2 Example 4

This example is proposed to illustrate the efficiency of the lateral stiffeners to prevent the buckling modes associated with the distortional deformation. These intermediate lateral stiffeners are attached on the beam sectional contour and positioned along the beam, respecting a regular separating distance, defined by the spacing \(a\) as pictured in Fig. 9. given by:

$$ a = \frac{L}{n} $$
(44)

where \(n\) is the number of the proposed lateral stiffeners.

Fig. 9
figure 9

Cantilever RHS beam with lateral stiffeners attached on the sectional contour

Full size image

The effectiveness of lateral stiffeners is reflected by their ability to upgrade the box beam LTB resistance. Indeed, this effectiveness is evaluated by the appropriated chosen the number \(n\) of the lateral stiffeners which should enhance the critical load \(F_{cr}^{SD}\) of the beam, in such a way to approaching the value of \(F_{cr}\) corresponding to LTB without distortional deformation.

The proposed example considers a cantilever RHS steel beam with a concentrated load applied at free edges and positioned at the shear centre \(\left( {e_{z} = 0} \right)\). The geometrical characteristics are:\(b = 100{\text{ mm}}\),\(h = 300{\text{ mm}}\),\(t = 6\;{\text{mm}}\) and \(L = 4.8\;{\text{m}}\). The critical LTB load that neglects the distortional deformation \(F_{cr}\) is derived from Eq. (40a). This critical load is equal to \(F_{cr} = 394.11{\text{ kN}}\).

Figures 10(a–c) represent the curve responses by varying the number \(n\) of lateral stiffeners. The tip-displacement w0 curves are drawn in Fig. 10a. This figure shows that the lateral stiffeners do not affect the pre-buckling deflection state, but influence significantly the post-buckling equilibrium, mainly the bifurcation point magnitude. Therefore, Figs. 10b,c suggest that when only two (02) lateral stiffeners are added to the cantilever beam, no significant critical load enhancement is recorded. In this case, the critical load obtained for \(n = 2\) is of \(F_{cr}^{SD} = \, 196.75{\text{ kN}}\), which approximates to the critical load corresponding to the RHS cantilever beam without lateral stiffeners with \(F_{cr}^{SD} = 195.43{\text{ kN}}\). However, a more pronounced LTB amelioration is obtained when four (04) stiffeners are incorporated into the box beam with \(F_{cr}^{SD} = \, 287.29{\text{ kN}}\). The important LTB improvement is achieved by adding eight (08) stiffeners. In this case, the resulting critical load \(F_{cr}^{SD} = \, 376.57\;{\text{kN}}\), approaching the value of \(F_{cr} = 394.11kN\), provided by the classical theory that ignores the distortion deformation.

Fig. 10
figure 10

Effect of the stiffener number 'n' on the pre- and post-buckling response of the cantilever beam of example 4

Full size image

6 Conclusion

In this investigation, a geometrically nonlinear theory of RHS beam structures is proposed. The variational problem is formulated according to an innovative kinematic model, including large torsion, shear flexibility and distortional deformations. A 3D beam finite element with two nodes and eleven degrees of freedom per node including warping, shear, and distortional deformations is formulated. The nonlinear problem was solved by employing the Newton–Raphson method in conjunction with the arc-length procedure. A good agreement is obtained either in pre-and post-buckling behaviours by the proposed finite element model when comparing with Abaqus solutions performed by using quadratic brick C3D20R elements with 20 nodes. By considering a variety of boundary conditions and RHS beam dimensions, the present finite element model leads to acceptable buckling curve solutions by using more forty (40) elements. Through, the validation process, the capability of this discretization to minimise as far as possible the buckling load error under the threshold of 4% was fully checked.

It is also proved in the numerical studies that the classical solutions which disregard distortional and shear deformations lead inevitably to an important overestimation of the critical buckling loads with a relative error reaching 40%.

The LTB behaviour of the RHS beams under combined bending and compressive loads is considered in the numerical investigation. It worth noting that the additional compressive load may affects only the post-buckling equilibrium. The obtained results suggest that the LTB resistance of the RHS beams decreases with increasing compressive load.

In the end of the numerical study a conceptual study is conducted, that focused on the improvement of the LTB resistance of the RHS beams by adding lateral stiffeners, attached to the sectional beam contour. This may contribute efficiently to enhance the buckling load results, to reaching that provided by the classical theory. In this way, the present study reveals that a more effective LTB amelioration is obtained by adding four (04) lateral stiffeners, and the distortional effect completely vanish with the incorporation of eight (08) stiffeners.