1 Introduction

Steel plate shear wall (SPSW) is widely used as a lateral force-resisting system in high-rise buildings and earthquake-prone areas due to its high energy dissipation capacity (Elgaaly et al., 1993; Gorji Azandariani et al., 2020, 2021b; Sabouri-Ghomi & Roberts, 1992; Thorburn et al., 1983; Tromposch & Kulak, 1987). However, the weaknesses of this system are its low initial stiffness and buckling strength (Alavi & Nateghi, 2013; Berman, 2011; Hitaka & Matsui, 2003; Nakashima, 1995). Also, the buckling of the flat plate causes an unpleasant sound that disturbs the tranquillity of users (Berman & Bruneau, 2005). To minimize this weakness of SPSW, some researchers have suggested using a stiffener to increase the buckling strength of the flat plate (Alinia & Sarraf Shirazi, 2009; Brando & De Matteis, 2014; De Matteis et al., 2008; Loughlan & Hussain, 2014; Saeid Sabouri-Ghomi & Mamazizi, 2015; Saeid Sabouri-Ghomi & Sajjadi, 2012). Since thin plates are used in these systems, the cost of welding is considerably high (Takahashi et al., 1973).

In recent years, researchers have suggested using corrugated plates instead of flat plates in a shear wall. Since the plate is corrugated, its out-of-plane stiffness increases, and, as a result, its buckling strength also increases (Ibrahim et al., 2006). However, it seems that due to the lack of design methods, engineers have not used corrugated steel plates in high-rise buildings so far. That is why, in the past few years, researchers have tried to investigate the seismic behavior of corrugated steel plate shear walls (CSPSW) and provide a suitable design method. Emami et al. (2013) have studied the cyclic behavior of CSPSWs with the groove in the vertical and horizontal directions. They concluded that the energy dissipation capacity of the CSPSW was higher than that of a flat steel plate shear wall. Kalali et al. (2015) have examined the hysteresis performance of the corrugated steel plate shear wall using finite element analysis. They showed that to achieve optimal performance, they should appropriately select the geometric parameters of the shear wall. Hosseinpour et al. (2015) and Edalati et al. (2014) evaluated the behavior of steel shear walls with sinusoidal and trapezoidal corrugated plates. They showed that the steel shear walls with trapezoidal corrugated plates have a higher energy dissipation, ductility, and ultimate strength. Bhowmick et al. (2014) have studied the behavior of CSPSWs with openings. They showed that the height of the opening greatly affects the stiffness, strength, and ductility of the shear wall.

Despite those mentioned earlier numerical and experimental studies on the behavior of CSPSWs, there is a need to comprehensively investigate the behavior of this system to understand their performance better. In the present study, several important aspects of the behavior of corrugated steel plate shear walls with the corrugation in the vertical direction are investigated. These aspects include the buckling behavior of PSW, the effect of the number of stories and shear wall width-to-height ratio on the boundary frame-plate contribution shares of story shear, and the estimation of pushover curve of corrugated steel plate shear wall. To this end, 20 samples of CSPSWs structures equipped via vertically corrugated infill-plate are designed with different geometric parameters, including plate thickness (t), width-to-height ratio (L/H), and the number of stories, and then investigated by modeling and using pushover analysis in ABAQUS (2010) software.

2 Design Characteristics of the CSPSW Structure

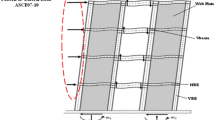
Twenty prototypes of the CSPSW structure were designed in the present study with the numbers of floors 1, 2, 4, 6, and 10 and different width-to-height ratios (L/H) of 0.85, 1.4, 2, and 2.5. The prototype plan of the CSPSWs building is exhibited in Fig. 1, which includes five bays for the perimeter gravity frames and SPSW one-bay in each direction in the outer frames of the structure. The perimeter gravity frames (PGF) bays, 4.5 m long, are considered from the center to center of the columns. Since the building had a total of two bays with CSPSWs in each direction, each of the shear walls tolerates the earthquake force induced by 50% of the seismic mass of any story. The height of all stories is 3.4 m. The dead loads of each story and roof are 4.6 and 3.2 kPa, respectively, and the live loads of each story and roof are 2.4 kPa and 1.6 kPa, respectively. CSPSW system was designed based on capacity method and according to the recommendations given in AISC Seismic Provisions (2016) and AISC Design Guide 20 (2007).

Fig. 1
figure 1

The plan proposed for the design of the steel shear wall

Full size image

According to ASCE7-10 (2010), the lateral seismic load at each story is calculated using the inverse triangular distribution. Then, the plate thickness is designed to resists 100% of story shear (AISC-20 2007). The ultimate strength of the corrugated plate on each floor was calculated by the equation represented by Emami et al. (2013). It should be noted that the corrugated plate thickness is chosen from the thicknesses available in the market. The corrugated plate geometry is similar to that in the study (Emami et al., 2013), as shown in Fig. 2. Finally, the boundary elements of the shear wall system were designed based on the yield capacity of corrugated plates, according to the Steel Design Guide-20 (2007). The sections of the boundary members of the instruments designed are presented in Table 1. This table provides the numbers for cross-sections of the boundary elements and plate thickness.

Fig.2
figure 2

Features of the used corrugated plate

Full size image
Table 1 The boundary elements and the designed plate thickness
Full size table

3 Numerical Method

3.1 Finite Element Modeling

For the numerical modeling and analysis of the SPSWs was used the FE software ABAQUS (2010). To evaluate the hysteresis behavior of SPSW and CSPSW under dynamical loading were expanded the numerical models. In the following subsections, the details of the numerical modeling, including the material properties, boundary conditions, initial imperfection, mesh details, and the applied method of analysis, are introduced. The numerical predictions are compared with the experimental results reported by Driver et al. (1998) and Emami et al. (2013).

3.1.1 Material Properties and Meshing

The nonlinear behavior of the steel infill plates and boundary members are considered through the multi-linear von Mises criterion. Material nonlinearity for steel was incorporated through the von Mises model with associated flow rule, which is available in the ABAQUS (2010) metal plasticity library. Combined isotropic and kinematic hardening rules were used for material modeling of the infill plate and boundary frame. The yield stress and ultimate tensile stress of infill plate values employed in the analysis for the model of Driver et al. (1998) 385 and 450 MPa, respectively, have been adopted. Also, the yield stress and ultimate tensile stress of boundary member values employed in the analysis for the model of Driver et al. (1998) 327 and 480 MPa, respectively, have been adopted. The yield stress and ultimate tensile stress of infill plate values employed in the analysis for the model of Emami et al. (2013) 207 and 290 MPa, respectively, have been adopted. Also, the yield stress and ultimate tensile stress of boundary member values employed in the analysis for the model of Emami et al. (2013) 300 and 456 MPa, respectively, have been adopted. The elastic Young’s modulus and Poisson’s ratios are 210 GPa and 0.3, respectively.

Three-dimension numerical models of the SPSW system were built in the ABAQUS (2010) finite element software. The boundary elements and infill plates are modeled with a reasonably fine mesh using four-node reduced integration shell elements (S4R). Mesh sensibility studies have been carried by Gorji Azandariani et al. (2021a, 2021c) to specify the better optimization and compatibility with experimental results. These studies show that the optimum mesh adopted with a grid size of 25 × 25 mm is the base element. Therefore, the meshing of the models was considered in 25 × 25 mm dimensions for all finite element models.

3.1.2 Initial Imperfection

The primary defect is an effective factor in determining the initial stiffness and structural performance of thin-walled, especially SPSWs systems and plate girders. In general, during the construction of a thin-walled structure, the effects of construction and welding cause defects in the structure. On the other hand, geometry built-in finite element software environment is without initial defects. In ABAQUS software, it is possible to create an initial defect in the geometry of the finite element model using the KEYWORD commands tool. In this method, the first buckling shape mode or a combination of several buckling shapes mode is applied to the model as a defect. For this purpose, based on reference (Gorji Azandariani et al., 2021a, 2021c), an initial imperfection pattern corresponds to the first buckling shape mode with peak amplitude equal to L/500 is applied to the models, where L is the infill plate width.

3.1.3 Boundary Conditions and Loading

According to the experiments reported details, the loading and support conditions of the SPSW and CSPSW models were considered. In other words, the experimental cyclic loading protocols were used for the respective finite element models. Also, in-plane and out-of-plane translational and rotational restraints applied to each model were in accord with the corresponding test details.

3.1.4 Analysis Methodology

An explicit analysis platform is adopted to capture complex behaviors of CSPSW and achieve numerical convergence and solution accuracy in ABAQUS (2010). This module can solve static and dynamic problems using a dynamic process with the central difference method to integrate motion equations. The time step size is calculated automatically in terms of the minimum mesh size in the model.

3.2 Verification of Models

The numerical model was established to validate the modeling approach according to the four-story SPSW specimen tested by Driver et al. (1998), as presented in Fig. 3. In the simulation, the cyclic behavior was consistent with the physical test in terms of peak strength and initial elastic stiffness; however, the simulation exhibited slightly more pinching than the test. Despite this small discrepancy, the model reasonably captures the overall behavioral trends of the SPSW systems. In addition, Fig. 3b shows the typical deformation modes and yielding distributions for the test and simulation, with good agreement evident. The plastic mechanisms observed in the SPSW test were successfully replicated in the model.

Fig. 3
figure 3

Comparison of tested by Driver et al. (1998) and finite element model: a Hysteresis curves and b Failure modes

Full size image

To further validate the modeling approach, the numerical model was established according to the one-story C-SPSW system with the corrugation in the vertical direction tested by Emami et al. (2013), as presented in Fig. 4, comparisons of the simulated results using the developed finite element model and the experimental hysteretic response of CSPSW is shown. It can be seen that the simulation results have a good correlation with the hysteretic test response, closely matching in terms of peak strength and initial elastic stiffness. Also, Fig. 4b shows the development of the tension field within the infill plates for the test and simulation, with good agreement evident. Table 2 presents the yield and maximum base forces of the finite element models and the experimental results. According to Table 2, the average error of finite element models is 1.5%, indicating that FE models well predict the maximum shear capacity of the test specimens.

Fig. 4
figure 4

Comparison of tested by Emami et al. (2013) and finite element model: a Hysteresis curves and b Failure modes

Full size image
Table 2 Results of the numerical model and experimental samples
Full size table

4 Results and Discussion

Pushover analyses were carried out to investigate the behavior of CSPSW. The lateral load was distributed at the height of the system according to ASCE7-10 (2010). The roof drift was selected as the control point and underwent a drift of 2.5%.

4.1 Behavior of CSPSW System

The behavior of the CSPSW system can be characterized by the actions of its constituent components, i.e., the web plate and the boundary frame. Figure 5 shows the base shear-roof drift diagram of the CSPSW system (model No.2 in Table 1) along with the absorbed base shears -roof drift diagram of the plate and the boundary frame.

Fig. 5
figure 5

Base shear-roof drift curve of model No.2

Full size image

At first, the diagram of the plate is explained. From the start point of loading to the drift of about 0.1% (point A in Fig. 5), the plate exhibits a fairly high stiffness. At the drift ratio of 0.1% is an interactive buckling, after which the corrugations plate started opening, causing its lateral stiffness to become negative and its base shear to drop significantly. At a drift of about 0.5% (point B in Fig. 5), a tension field is formed over some portion of the web plate between PSW beams (Fig. 6). It is worth noting that the tension field zone completely yields; for this reason, the formation of the tension field does not result in a positive stiffness in the plate.

Fig. 6
figure 6

The formation of tension field in model No.2, a numerical model, b schematic form

Full size image

Next, absorbed base shears -roof diagram of boundary frame is explained. Up to a drift ratio of about 0.9%, frame base shear increases continuously, and at a drift ratio of about 0.9% (point C in Fig. 5), the frame yields. From this point onwards, no increase is observed in the frame base shear. By the principle of superposition, the pushover diagram of the CSPSW system is obtained from the summation of the plate and boundary frame diagrams. In range A, the base cut of the system is increasing, which is achieved by increasing the base cut of the plate and the border frame. Between A and B, although the plate base shear decreases, that of the system increases due to the increase in the frame base shear, and at drifts, more than 1.03% (point C), the system base shear remains unchanged because those of the plate and frame do not change. The values of the drift ratio corresponding to key points A, B and C are applicable to all models and all models show similar performance at these points.

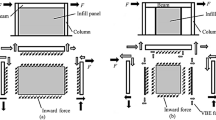
In the following, the behavior of a C-SPSW system is compared with an SPSW system. Figure 7 shows the pushover diagram of an SPSW model (Hosseinzadeh & Tehranizadeh, 2014). In contrast to the CSPSW system, no drop is observed in the strength of SPSW. Because, immediately after buckling of the plate, an elastic-state tension field is formed (Fig. 8a). Also, in Fig. 8b, it is observed that the tension field is formed on the entire surface of the SPSW, while in a C-SPSW model, the tension field is formed only between the beams. The reasons for these differences in the behavior and development of the tensile field in these two systems are due to the corrugated plate in the CSPSW system. So that, in the SPSW system under lateral loading, the whole plate is subjected to the tensile field, on the other hand, the CSPSW system during lateral loading, the length of the corrugated plate is large between the limited columns and beams, therefore, the diagonal tensile field is not formed in this region due to the long length of the plate. That is why the strength of the SPSW model is about 20% higher than that of the CSPSW model. In addition, the initial stiffness of the SPSW model is about 1480 kN/m, which is significantly decreased at the beginning of the loading due to the plate buckling, according to the study of Berman and Bruneau (2005), this reduction in the strength causes an annoying sound. But, the initial stiffness of the corrugated plate model is about 2000 kN/m, which remains unchanged up to the drift ratio of about 0.1%. This difference in the initial stiffness between the flat plate model and the corrugated plate model shows the superiority of the corrugated steel plate shear wall to the flat steel plate shear wall under earthquakes at seismic hazard levels.

Fig. 7
figure 7

Roof base shear-drift curve of Hosseinzadeh and Tehranizadeh (2014) model’s

Full size image
Fig. 8
figure 8

Tension field in a flat steel plate shear wall, Hosseinzadeh and Tehranizadeh (2014) model’s a Before yielding, b After yielding at the drift ratio of 2.5%

Full size image

4.2 Distribution of Shear Force in PSW

4.2.1 Boundary Frame-Plate Contribution Shares of Story Shear

Figure 9 shows the roof drift-base shear diagram of PSW along with its constituent components, i.e., the plate and the moment frame, for 1, 2, 4, 6, and 10-story systems. According to the principle of superposition, the pushover diagram of PSW is equal to the sum of pushover diagrams of the plate and the moment frame. As shown in Fig. 12, at low drift ratios (before the interaction buckling of the plate), a greater share of the shear force is tolerated by the plate, but after the plate buckling, a significant drop occurs in the plate stiffness, and the role of the frame in tolerating the shear force becomes more pronounced; at the drift ratios from 1 to 2.5 percent, a greater share of the shear force is tolerated by the frame.

Fig. 9
figure 9

The results of the pushover analysis: a 1-story, b 2-story, c 4-story, d 6-story, and e 10-story

Full size image

The percentage base shear resisted by the plate in different SPSWs is presented in Table 3. The results imply that although the number of stories is significantly effective on the plate share from the base shear, the value of the L/H ratio is not much effective. It is noteworthy to point out that, according to Table 3, the plate contribution share of the base shear does not reach even reach 50%.

Table 3 Contribution (in %) of the plate to the base shear for different width-to-height ratio (L/H) at 2% drift ratio
Full size table

Figure 10 shows the percentage share of the plate to the shear force versus roof displacement for 1-story CSPSWs with various L/H ratios at different levels. As shown, the percentage plate share is approximately the same at different levels for each SPSW, and the plate contribution at each level decreases after the interactive buckling. This reduction starts from a displacement of about 0.01 m and continues up to about 0.04 m when the plate yields, after which the plate share at each level remains unchanged.

Fig. 10
figure 10

Percent share of the plate to the shear force for on story CSPSWs having various L/H ratios at different levels

Full size image

Tables 4 and 5 show, respectively, the plate contribution share of the shear force at different stories of typical 4- and 6-story CSPSW having various width-to-height ratios at a 2% drift ratio. Figure 11 shows the data listed in Tables 4 and 5 for better comparison. As shown, the moment frame carries more shear force than the plate in lower stories, but in upper stories, it is vice versa: the plate has a greater role in the resisting story shear and carries as much as 130% of the story shear. Hence it can be said, the bending deformation in each frame story is the sum of those in lower stories. So at the upper stories, there is a greater flexural deformation, and consequently, the lateral stiffness of the frame decreases. On the other hand, the shear deformation at each story is proportional to the plate thickness at the same story and no other stories; therefore, at the upper stories, the frame stiffness significantly decreases as compared to the shear stiffness of the plate, and as a result, the greater share of the shear force is tolerated by the plate. The fact that the percentage plate shear exceeds 100% is similar to the behavior of the dual system of concrete shear wall and moment frame where the share of the concrete shear wall in upper floors is more than 100%.

Table 4 Percentage share of the plate to the shear force at different stories of a 4-story system
Full size table
Table 5 Percentage share of the plate to the shear force at different stories of a 6-story system
Full size table
Fig. 11
figure 11

Percentage share of the plate to the shear force at different stories of 4-story and 6-story systems for different width-to-height ratio (L/H)

Full size image

4.2.2 Contribution Shares of Left and Right Columns to the Frame Shear

According to the previous section, a significant part of the base shear is tolerated by the frame. The frame shear force is divided between the tensile (left) and compressive column (right). Figure 12 shows the percentage frame base shear resisted by the tension and compression columns of a high-rise system (10-storey) at different roof drift ratios. According to Fig. 12, the Percentage contribution of each column is about 50% at a lower drift ratio (about 1%). Also, as the drift ratio exceeds about 1%, the interaction buckling of the system plates starts. The tensile column tolerates more shear force so that at the drift ratio of about 2%, the tensile column tolerates about 80 percent of the frame base shear.

Fig. 12
figure 12

Percentage of frame base shears resisted by the tensile-compressive columns in a 10-story shear wall system at different drift ratios

Full size image

Figures 13a and b, which show frame-plate contributions to the base shear respectively before and after the formation of the tension field, have been used to explain the reason for the above issue. According to Fig. 13a, before forming the tension field, the shear force in the columns is only due to the moment frame sway, and since the system is symmetric, the shear force is evenly divided between two columns. But, after the formation of the tension field (Fig. 13b), the shear force in the columns is due to two factors: (i) The shear to the moment frame sway (VFrame); and (ii) The shear force due to the tension field in the plate (VWall). In intension columns, the shear forces due to both factors are co-directional, but in compression columns, they are anti-directional; hence, the difference between the shear force in two columns increases with increasing drift ratio.

Fig. 13
figure 13

Frame-plate contributions to the base shear in C-SPSW, a before the formation of tension field, b after the formation of tension field

Full size image

Figure 14 shows the effect of the number of stories and width-to-height ratio (L/H) in the contribution of the tensile column to the shear force. According to this Fig. 14, as the number of stories increases, the contribution of the tensile column to the frame base shear increased while it decreases as the width-to-height ratio increases. Figure 14 shows the effects of the number of stories and L/H on the contribution of the tension column to the frame base shear. As shown, an increase in the number of stories increases the contribution, but an increase in L/H decreases it.

Fig. 14
figure 14

Percentage frame base shear resisted by the tensile column for different width-to-height ratio (L/H)

Full size image

5 Tension Field Inclination Angle in a Corrugated Steel Plate Shear Wall

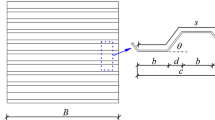
As mentioned previously, the tension field in CSPSW forms over some portion of the web plate between PSW beams (Fig. 15); this part of the plate is effective in tolerating the lateral force, but the other parts of the plate have a small role in tolerating the shear force.

Fig. 15
figure 15

Tension fields in a shear wall system, a single-story system b multi-story system

Full size image

This behavior is schematically illustrated in Fig. 16, where the stresses due to the tension field are applied to some part of the beam length (Lp). Figure 16 shows the free diagram of PSW beams, columns, and supports.

Fig. 16
figure 16

Free-body diagrams of the C-SPSW components

Full size image

In the past, this form of tension field was observed in experiments on a flat steel plate shear wall with infinitely flexible columns conducted by Thorburn et al. (1983). They proposed Eq. (1) for the angle between the tension field and the vertical axis (θ):

$$\theta = 0.5\tan^{ - 1} ({L \mathord{\left/ {\vphantom {L H}} \right. \kern-\nulldelimiterspace} H})$$
(1)

where L is the bay length and H is the story height, θ is inclination angle of the tension field measured relative to vertical axis. In the present study, to investigate the effects of plate thickness (t), the width-to-height ratio (L/H), and yield stress (Fy) parameters on the angle θ, various finite element models were investigated by changing these parameters. The results showed that in contrast to the width-to-height ratio (L/H) value, t and Fy values had no significant effect on θ. These results are consistent with those reported by Thorburn et al. (1983) in experiments on a flat steel plate shear wall with infinitely flexible columns. They proposed Eq. (1) for the angle between the tension field and the vertical axis (θ). Therefore, Eq. (2), with a general form similar to Eq. (1), has been proposed in this research to find θ in shear walls with corrugated plates.

$$\theta = \gamma .\tan^{ - 1} ({L \mathord{\left/ {\vphantom {L H}} \right. \kern-\nulldelimiterspace} H})$$
(2)

In the following, the parameter γ is determined by parametric numerical studies. For this purpose, first, the behavior of a single-story frame (similar to that in Fig. 16) was examined. In this frame, the beam-to-column connection and the column base connection were assumed to be pinned. Therefore, the plate response is isolated from the frame action, and the plate tolerates 100% of the lateral force. When the lateral load is applied to the system, the column resists only axial forces, and beams resist bending moment and axial load. The horizontal and vertical components ω (ωx and ωy, respectively), and their ratio are calculated using Eqs. (3) to (5) assuming that the tension field yields.

$$\omega_{x} = F_{y} t_{w} \cos \theta \sin \theta = 0.5F_{y} t_{w} \sin 2\theta$$
(3)
$$\omega_{y} = F_{y} t_{w} \cos \theta \cos \theta$$
(4)
$$\omega_{y} /\omega_{y} = \tan \theta$$
(5)

where θ is the tension field angle measured relative to the vertical axis. According to Fig. 16 and assuming that θ is small compare to tension field angle measured relative to the edge of the web plate (θ), the beam length affected by the tension field Lp is calculated as follows:

$$L_{P} = L - H\tan \theta = L\left(1 - \frac{\tan \theta }{{L/H}}\right)$$
(6)

Free body diagrams of the components of CSPSW are depicted in Fig. 16. Using the equilibrium equation, the maximum beam moment (Mm), the location of Mm from the right end, and axial loads in left and right columns (Pl and Pr, respectively) can be obtained respectively from Eqs. (7) to (10):

$$M_{m} = 0.125F_{y} t_{w} L^{2} (\cos \theta )^{2} \left[ {2\left(1 - \frac{\tan \theta }{{L/H}}\right) - \left(1 - \frac{\tan \theta }{{L/H}}\right)^{2} } \right]^{2}$$
(7)
$$P_{l} = 0.5F_{y} t_{w} L^{2} \left(\cos \theta \right)^{2} \left(1 - \frac{\tan \theta }{{L/H}}\right)^{2}$$
(8)
$$P_{r} = 0.5F_{y} t_{w} L\left(\cos \theta \right)^{2} \left[ {2\left(1 - \frac{\tan \theta }{{L/H}}\right) - \left(1 - \frac{\tan \theta }{{L/H}}\right)^{2} } \right]$$
(9)
$$x = 0.5L\left[ {2\left( {1 - \frac{\tan \theta }{{L/H}}} \right) - \left( {1 - \frac{\tan \theta }{{L/H}}} \right)^{2} } \right]$$
(10)

Next, numerical models with different width-to-height ratios (L/H), which should be in the range of 0.8 to 2.5 according to AISC-341 (2016), were analyzed. The results of each model were used to find the parameters of ωx, ωy, Mm, x, Pl, and Pr for both upper and lower beams at the drift ratio of 2.5%. These parameters are determined from each numerical (FE) analysis, and the model's geometric properties are substituted in Eqs. (6) to (11) to produce twelve estimates of θ for a given L/H. Figure 17 depicts the average of twelve γ values obtained for different L/H ratios. Using the cubic spline interpolation method, γ is obtained in terms of L/H as Eq. (11):

$$\gamma = 0.55\; - 0.03({\text{L}}/{\text{H}})$$
(11)
Fig. 17
figure 17

Average γ values for different L/H ratios at the drift ratio of 2%

Full size image

6 Proposed Theoretical Force–Displacement Curve for CSPSWs System

6.1 Theoretical Approach

In this section, the pushover diagram of a C-SPSW is drawn using the boundary frame-plate interaction. For this purpose, the base shear-drift diagrams of the frame and the plate are plotted separately, and then, by superimposing these two diagrams, the load–displacement diagram of the CSPSW can be obtained. Assuming the strain material hardening to be zero, Kharrazi (2005) presented the idealized load–displacement diagram of the boundary frame, as shown in Fig. 5. The yield drift θF and yield strength of the frame Vf can be calculated using equations provided by Kharrazi (2005). Then, the load–displacement behavior of the corrugated plate in a one-story CSPSW system under lateral loading is investigated. Figure 5 illustrates the idealized lateral load-drift diagram of the corrugated plate. According to Ref. (Tong & Guo, 2018), the interactive buckling force (Vp,A) and the buckling drift are estimated using Eqs. (12) and (13), respectively:

$${\text{V}}_{{{\text{p}},{\text{A}}}} = \, \tau_{{{\text{cr}}}} \cdot {\text{A}}_{{\text{w}}} = \, \tau_{{{\text{cr}}}} \cdot {\text{l}}_{{\text{p}}} \cdot {\text{t}}_{{\text{w}}}$$
(12)
$$\theta _{{{\text{P}},{\text{V}},{\text{A}}}} = \frac{{{\text{U}}_{{\text{A}}} }}{{{\text{h}}_{{\text{p}}} }}$$
(13)

where Aw, tw, and lp are the cross-section area, the thickness of the plate, and length of the corrugated plate, respectively. \(\tau_{cr,I}\) represents the interactive buckling stress of the corrugated plate which can be calculated as below:

$$\tau_{cr,I} = \frac{{\tau_{cr,L} \times \tau_{cr,G} }}{{\tau_{cr,L} + \tau_{cr,G} }}$$
(14)

The local buckling (\(\tau_{cr,L}\)) and global buckling (\(\tau_{cr,G}\)) are determined as fallow (Tong & Guo, 2018):

$$\begin{gathered} \tau_{cr,L} = k\frac{{\pi^{2} E}}{{12(1 - \nu^{2} )(\frac{a}{{t_{w} }})^{2} }} \hfill \\ k = 5.34 + 4(\frac{a}{{h_{p} }})^{2} \, \hfill \\ \end{gathered}$$
(15)
$$\tau_{cr,G} = 36\beta E\frac{1}{{\left[ {12(1 - \nu^{2} )} \right]^{0.25} }}\left[ {\frac{{(d/t)^{2} + 1}}{{6(\frac{a + b}{{a + c}})}}} \right]^{0.75} \left( {\frac{{t_{w} }}{{h_{p} }}} \right)^{2}$$
(16)

where G is the shear modulus of the corrugated plate (Tong & Guo, 2018) which can be calculated as below:

$${\text{G}} = \, \frac{{{\text{a}} + {\text{c}}}}{{{\text{a}} + {\text{b}}}}\frac{{\text{E}}}{2(1 + \nu )}$$
(17)

The parameters a, b and c are shown in Fig. 2. Based on the study of (Emami et al., 2013), using Eq. (17), the strength of point B, shown in Fig. 5, is calculated.

$$V_{p,B} = 0.5F_{y} t_{w} L^{\prime}_{p} \sin (2\theta )$$
(18)

The difference of displacement between points B and A (UA-UB) is due to the corrugations and plate buckling opening. Therefore, the drift of point B is obtained using the equation below:

$$U_{B} - U_{A} = \beta \times \frac{{L^{\prime}_{p} .h_{p} .\tan \alpha }}{{L_{p} .\cos \alpha }}$$
(19)

\(L^{\prime}_{P}\) is estimated as below:

$$L^{\prime}_{P} = m.a + n.b$$
(20)

In the following, the base shear-drift diagrams of the corrugated plates in a multi-story C-SPSW system are investigated. For this purpose, it is required to examine the drift at each floor; as shown in Fig. 18, at each floor, the drift consists of two parts: shear drift and flexural drift. The shear drift of the ith floor is independent of the drifts of other floors (Fig. 19(a)). So, the base shear force-drift curve of the ith floor is plotted in a way explained in Sec. 4.2.1. To calculate the total drift of each floor, it is required to calculate the flexural drift of that floor and add it to its shear drift. According to Fig. 19(b), it is clear that the flexural drift is due to the axial deformations in the left and right columns (increase and reduction in the lengths of the columns due to the tensile and compressive axial forces) so that the floor experiences the rigid rotation (αi). Flexural drift (\(\theta_{P,M,i}\)) is equal to αi, which can be calculated as follow:

$$\alpha_{i} = 2\frac{{\sum\nolimits_{i = 1}^{i = n} {\delta_{c,i} } }}{L} = \frac{2}{L}\left[ {\frac{{N_{c,1} \times h_{s,1} }}{{EA_{c,1} }} + \frac{{N_{c,2} \times h_{s,2} }}{{EA_{c,2} }} + ... + \frac{{N_{c,n} \times h_{s,n} }}{{EA_{c,n} }}} \right]$$
(21)
$$N_{c,i} = \frac{{M_{i} }}{L}$$
(22)

where \(\delta_{c,i}\) denotes the change in the axial length of the column in the ith floor and \(A_{c,i}\) denotes the column section area of ​​the ith floor, \(N_{c,i}\) denotes the axial force in the column of the ith floor, \(M_{i}\) denotes the flexural moment of the ith floor. By calculating the flexural drift of each floor, one can modify the pushover curve obtained in the previous section, as shown in Fig. 18. In this way, the base shear-drift diagram of the corrugated plate at each floor is plotted.

Fig. 18
figure 18

The base shear-drift diagram of the ith floor

Full size image
Fig. 19
figure 19

Flexural and shear drifts of the third floor in a 4-story shear wall, a shear drain b flexural drift,

Full size image

6.2 Comparison of Theoretical Results with Numerical and Experimental Methods

In Figs. 20 and 21, the pushover curve obtained using the proposed method was compared with the results of experiments conducted by Emami et al. (2013) and that of the finite element models (the first and third floors of the 6-story shear wall, the first and sixth floors of the 10-story shear wall). The results show that the proposed method is in good agreement with experimental results as well as the results of finite element analysis.

Fig. 20
figure 20

Comparison of the proposed method with Imami et al.'s (2013) experimental sample

Full size image
Fig. 21
figure 21

Comparison of the proposed method with numerical models, a the first floor of the 6-story model, b the third floor of the 6-story model, c the first floor of the 10-story model, d the sixth floor of the 10-story model

Full size image

7 Conclusion

In the present study, Pushover analyses were carried out to investigate the behavior of corrugated steel plate shear walls. For this purpose, 20 prototypes of CSPSWs were designed with various stories and different width-to-height ratios and then analyzed using ABAQUS Software. First, buckling, yielding, and shear distribution between the boundary frame and web-plate were studied. The following results were obtained:

  • In the CSPSW system, buckling up to a thrust ratio of approximately 0.1% does not occur in the web-plate, whereas the SPSW system is observed early in the buckling load of the web-plate.

  • The initial stiffness of the corrugated steel plate shear wall is greater than that of the flat steel plate shear wall.

  • In the CSPSW, the tension field is formed over some portion of the web-plate between beams, while in a flat SPSW, it is formed on the entire surface of ​​the plate. For this reason, the ultimate strength of a flat steel plate shear wall is greater than that of a CSPSW.

  • Before the corrugated plate buckling, a higher percentage of shear force is tolerated by the plates. On the other hand, after the plate buckling, a significant drop is observed in the plate strength, and the boundary frame tolerates a higher percentage of shear force.

  • In multi-story systems, the boundary frame at the lower stories and the plate at the upper stories play a more effective role in tolerating the shear force.

  • The tensile column has a larger contribution share of the shear force than that of the compressive column.

  • By changing the ratio of width to height of structures, no significant change in the percentage of plate and frame to shear force is observed.

  • By changing the ratio of width to height of structures, no significant change in tensile and compressive forces of boundary columns is observed.

Next, an equation was presented for determining the tension field inclination angle. According to this equation, the tension field inclination angle depends only on the width-to-height ratio (L/H) parameter. The parameters such as plate thickness and plate yield stress are ineffective on the tension field inclination angle. Finally, a method for estimation of the pushover curves of the single- and multi-story CSPSW systems is provided. This method was based on the interaction between the boundary frame and the corrugated plate, and it was validated and approved by the pushover curves of experimental and numerical samples.