1 Introduction

The growth of online social networks (OSN) like Facebook and Twitter has enabled users to interact with their friends and share information in real-time. Several research projects rely on the study and characterization of OSNs. However, due to the large size and access limitations of these networks, many large OSNs are currently studied via sampling techniques (Kurant et al. 2012; Rezvanian et al. 2019). The sampling techniques also could be applied for simulation, data mining, measuring performance of protocols, information retrieval, viral marketing experimentations, and fraud detection in social network analysis (Ahmed et al. 2010). Sampling techniques should consider every aspect of the initial network including the presence or absence of influential edges and nodes and the connection topology of these nodes and edges to present a sampled network that can preserve characteristics of the initial network. In sampling literature, most sampling techniques focus on either preserving influential nodes or influential edges, meaning they could not consider both of them. Besides, most existing sampling methods including random nodes and random edges work based on random selection, thus the topology of the original network is not considered. In this paper, we propose two novel sampling algorithms using several spanning trees with the highest number of nodes that satisfy a given degree constraint. The proposed algorithm not only takes into account important edges but also makes use of important nodes.

The proposed algorithm first finds several Spanning Trees with the Highest Number of nodes that satisfy a certain degree of Constraint (STHNC) from the input network. Based on the number of times each edge and each node in the set of computed spanning trees has appeared in the set of spanning trees, the edges and nodes with degrees greater than the given constraint are ranked. A sub-graph is constructed as the sampled network containing a fraction of nodes and edges that are highly ranked. According to the algorithm proposed, the edges with the highest number of presences in spanning trees of an arbitrary number of STHNCs with different starting points can be considered important edges that reflect several characteristics of the original network, since they reflect several characteristics of the original network. Besides STHNC, visits edges in a uniform manner which prevents the sampled network from being biased to high-degree nodes, but sometimes it is inevitable to have some nodes with degrees higher than the given constraint. These nodes preserve many connections, and in the absence of these nodes, many connections will be lost. So, considering these nodes as influential nodes helps better preserve the properties of the network.

We evaluate the efficiency of the proposed sampling algorithms via simulation. In terms of Kolmogorov-Smirnov (KS) test, Skew Divergence (SD) distance, and Normalized Distance (ND), we compare the results of the proposed algorithms with those reported in the literature recently. Our results show the superiority of our proposed algorithm over well-known algorithms in terms of several criteria.

The rest of the paper is organized as follows: In the second section, we discuss the essential information needed to understand the rest of the paper. A review of related works about sampling methods in complex networks is presented in the third section. The proposed methods are discussed in Sect. 4. In Sect. 5, simulation experiments on standard graphs of complex networks are used to assess the performance of the proposed algorithm. As a conclusion, Sect. 6 concludes the paper.

2 Preliminaries

Social networks can be represented as graph \(G=\langle V, E\rangle\) where \(V=\left\{{v}_{1}, {v}_{2},\dots , {v}_{n}\right\}\) is the vertex set that represents the users of an OSN and \(E=\left\{{e}_{1}, {e}_{2}, \dots ,{e}_{m}\right\}\) is the set of edges that represent a kind of relationship between users in an OSN.

A sampling technique on input graph \(G\) can be defined as a  function \(f:G\to {G}_{s}\) with sampling rate \(0<\varphi <1\), where \({G}_{s}=\langle {V}_{s}, {E}_{s}\rangle\) is the sampled network in which \({V}_{s}\subseteq V\) and \(\left|{V}_{s}\right|=\varphi \times \left|V\right|\) (Jalali et al. 2016).

2.1 Evaluation metrics on sampling

A sampling algorithm's quality or representativeness is evaluated using network statistics. In network statistics, edges, nodes, and sub-graphs are taken into account.

Two well-known and widely used statistical properties provide insight into sampling algorithms: clustering coefficient distribution (\(CCD\)) as a local property and degree distribution (\(DD\)) as a global property. Graph connectivity is understood by looking at degree distributions, which show the fraction of nodes with a degree \(k\) (for all \(k>0\)). A function on the number of triangles centered on a node is called the clustering coefficient. Clustering coefficient distributions show the proportion of nodes with clustering coefficients \(C\). In a network, it determines the strength of the connectivity between a node and its nearest neighbors. The distance between both distributions of the statistical property for initial graph \(G\) and sampled network \(G_s\) is computed according to some distance functions such as Kolmogorov–Smirnov Test (\(KSD\)), Skew-Divergence distance (\(SDD\)), and Normalized-Distance (\(ND\)) (Ahmed et al. 2014b). In the remainder of this section, we describe these distance measures.

When two cumulative distribution functions (CDFs) are compared, Kolmogorov's D statistic (\(KSD\)) is used to calculate the distance between them. The \(KSD\) measures the agreement between the actual distribution \({F}_{1}\) and the estimated distribution \({F}_{2}\). A value between 0 and 1 is returned by this test. Both distributions will be more similar as they get closer to zero; and as they get closer to one, they will be more different.

This measure has been defined by Eq. (1), where \({F}_{1}\) and \({F}_{2}\) denote the cumulative distribution function (CDF) of the original distribution and estimated distribution respectively. Also, \(x\) represents the random variable's range. The distance between two distributions is therefore calculated as the maximum vertical distance (James 2006).

$$KS\left({F}_{1}, {F}_{2}\right)= {max}_{x}\left|{F}_{1}\left(x\right)-{F}_{2}(x)\right|$$
(1)

A Normalized Distance (\({\varvec{N}}{\varvec{D}}\)) is a measure of how far there is a difference between two positive m-dimensional vectors that are \({F}_{1}\) and \({F}_{2}\) where \({F}_{1}\) represents the original dimensional vector and \({F}_{2}\) represents the estimated dimensional vector. \(ND\) is defined by Eq. (2) (Rezvanian et al. 2019).

$$ND\left({F}_{1}, {F}_{2}\right)=\frac{\Vert {F}_{1}-{F}_{2}\Vert }{\Vert {F}_{1}\Vert }$$
(2)

Using the Skewed Divergence Distance (\({\varvec{S}}{\varvec{D}}{\varvec{D}}\)) we can compare two probability density functions (PDF). The SDD is a Kullback–Leibler (KL) divergence between two PDFs \({F}_{1}\) and \({F}_{2}\) with no continuous support (e.g., skewed degree). KL measures the average number of bits needed to represent samples from the original distribution when using sampled distributions. Since KL divergence cannot be defined for distributions with different support areas, skew divergence smooths the two PDFs before computing the KL divergence (Rezvanian et al. 2019). Equation (3) describes \(SD\) distance, in which the constant \(\alpha\) lies between 0 and 1. The divergence of \(P\) from \(Q\) is calculated by KL.

$$SD\left({F}_{1}, {F}_{2}\right)=KL\left[\alpha {F}_{1}+\left(1-\alpha \right){F}_{2}||\alpha {F}_{2}+\left(1-\alpha \right){F}_{1}\right]$$
(3)
$$KL(P|\left|Q\right)= \sum_{i}ln\left(\frac{{P}_{i}}{{Q}_{i}}\right){P}_{i}$$
(4)

Cost measures are also defined to assess the efficiency of sampling algorithms during the construction of a sampled network (Jalali et al. 2016). It is calculated using two numbers, \({C}_{t}\) and \({C}_{p}\), and two cost units, \({c}_{1}\) and \({c}_{2}\). A sampling network is constructed by traversing edges \({C}_{t}\) times and each edge travel has a cost \({c}_{1}\). The construction of a sampling network requires \({C}_{p}\) number of pre- or post-operations. Let \({c}_{2}\) be the cost of each such process. As shown below (Eq. (5)), the cost per sample is calculated by dividing the weighted sum of these two costs by the total number of edges.

$$Cost=\frac{{c}_{1}.{C}_{t}+{c}_{2}.{C}_{p}}{|E|}$$
(5)

In Eq. (5), \(|E|\) represents the number of edges of the original graph. In any pre- or post-processing step, an edge traversal cost is constant \({c}_{1}\) and a processing operation cost is constant \({c}_{2}\).

3 Related work

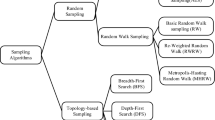
In addition to simple measures, advanced sampling techniques can be used to uncover useful information in social network graphs. However, to study OSNs directly, graph sampling is needed to reduce the size of the graphs while keeping their important features. Network sampling techniques can be classified in different ways in the literature. For instance, they can be divided into vertex sampling, edge sampling, and topology-based sampling (Ahmed et al. 2014a). Vertex sampling randomly and independently selects graph nodes. Breadth First Search (BFS) and Metropolis Hasting Random Walk (MHRW) are two examples of vertex sampling algorithms. Edge sampling randomly and independently chooses some edges of a given network. Frontier sampling (FS) is a type of edge sampling algorithm. Topology-based sampling selects nodes and edges based on the graph's structure. Snowball Sampling (SS), Forest Fire Sampling (FFS), and Random Walk Sampling (RWS) (Lovász 1993) are some topology-based sampling algorithms (Kurant et al. 2011a).

Random sampling methods are introduced as a category of sampling algorithms in (Kurant et al. 2011b), where each vertex is visited only once (Leskovec and Faloutsos 2006). Graph traversal sampling is also introduced in (Kurant et al. 2011b) as the other category of sampling algorithms. A graph traversal sampling technique, such as Random Walk Sampling (RWS), iteratively samples nodes adjacent to the last sampled node (Kurant et al. 2011b).

There are two other categories of sampling algorithms presented in (Kurant et al. 2011b): random vertex sampling and graph traversal sampling. In random vertex sampling, each vertex is visited only once and is not replaced during sampling (Leskovec and Faloutsos 2006). A graph traversal sampling technique, such as Random Walk Sampling (RWS), picks the next node iteratively according to some criteria among those adjacent to the last node sampled.

There are two types of sampling algorithms based on their processing methods: classical and modern. Classical sampling algorithms build a sampled network by choosing or visiting edges or nodes only once. Examples of these algorithms are BFS, RWS (Lovász 1993), FFS (Leskovec and Faloutsos 2006), and RDS (Gile and Handcock 2010). Modern sampling algorithms add an extra step of pre/post-processing that may involve selecting or visiting edges or nodes more than once. Some of these algorithms are DLAS (Rezvanian et al. 2014), SSP (Rezvanian and Meybodi 2015), RPN (Yoon et al. 2015), and DPL (Yoon et al. 2015). Classical sampling algorithms are fast and simple, but they have different results for each run and may not suit different network settings. Modern sampling algorithms are more accurate and adaptable but require more processing. They use extra information about the network structure, such as some measures (Peng et al. 2014), network properties (Blagus et al. 2015), or community structures (Yoon et al. 2015). This trade-off between processing and accuracy is a key challenge for modern sampling methods. It is possible to use the sampled network for a variety of applications and analyses once it is obtained. The main goal of designing a sampling algorithm is to create a sampled network that preserves the characteristics of the original network, rather than minimizing time complexity.

Leskovec et al. were among the first to study network sampling (Leskovec and Faloutsos 2006). They proposed several sampling algorithms to find a sampled graph that is similar to the original graph or a previous version of it. A comparison was also made between several algorithms for graph sampling. This comparison shows that FFS performed better than the others. As a web-based sampling algorithm, RDS was evaluated by Wejnert et al. for its effectiveness and feasibility (Wejnert and Heckathorn 2008). The analysis of Facebook users was conducted by Gjoka et. al. through the implementation and comparison of several crawling algorithms. They showed that BFS and RWS are biased, while MHRW and RWRW perform very well (Gjoka et al. 2010). Kurant et al. suggested a method to correct sampling bias (Kurant et al. 2011b). Based on their study, the BFS overestimated, and the RWS underestimated the graph degree in the absence of the graph degree. Ribeiro et. al. analyzed the steady state behavior of CTRWs on Markov dynamic networks and compared two types of rates in walking: a constant rate (CTRW-C) and a vertex degree-related rate (CTRW-D) (Ribeiro et al. 2011).

Son et al. (2012) compared BFS and RS analytically and studied their sampling biases. Siciliano et al. (2012) suggested an adaptive threshold algorithm for network research that can deal with sampling biases. Ribeiro et al. (2012) introduced a modified random walk sampling algorithm for directed graphs that can make random jumps. Papgelis et al. (2013) proposed an algorithm that can quickly collect information from the user's neighborhood in a dynamic way without visiting all the nearby nodes. They only showed the benefits of their algorithm through experiments. Pina-Garcia et. al. changed the way MHRW performed by using spirals rather than normal distributions as a probabilistic distribution (Piña-García and Gu 2013). They demonstrated that their algorithm outperformed normal MHRW in illusion spiral cases. In addition, they confirmed Gjoka et al.'s (2010) estimations. In Wang et al.'s sampling algorithm, all neighbors are considered valid samples (Wang and Lu 2013). The average degree of this algorithm improves random walk sampling.

Rezvanian et al. (2014) suggested an algorithm based on distributed learning automata (DLAS). This algorithm cooperates to sample a network. Based on KS tests, the algorithm outperformed RDS and RWS. They also achieved better results with low sampling rates. Although it relied on nodes of high degree, it still had some biases. Rezvanian and Meybodi (2015) also proposed a sampling method using the shortest path concept and demonstrated its effectiveness by simulations on well-known data sets. Peng et al. (2014) presented two sampling methods: one that improved the stratified random sampling method by selecting high-degree nodes with higher probability based on their degree distribution, and another that improved the snowball sampling method by selectively sampling the targeted nodes. Gao et al. developed a sampling method that used multiple random snowballs and Cohen's process based on snowball sampling (Gao et al. 2014). They simulated their method on model networks and verified that it preserved the network's local and global structures.

Jaouadi and Romdhane (2021) presented a parameterless model called Distributed Graph Sampling (DGS) for sampling large-scale social networks to reduce the graph’s size. A key feature of their proposal is its distributed strategy based on the MapReduce paradigm to sample a large graph in a parallel way to reduce the size of the network and conserve its key properties. In Ebadi Jokandan et al. (2021), proposed an optimization approach to efficiently sample large-scale social networks using a combination of cuckoo search (CS) and genetic algorithms (GA). In Liu et al. (2022), two concepts of node neighborhood clustering coefficient and random walk are combined to introduce a hierarchical sampling algorithm to efficiently sample nodes at different levels of the network hierarchy. Roohollahi et al. (2022), introduced an improved version of a learning automata-based approach to sampling in weighted social networks using a Levy flight-based learning automata. The authors combined Levy flights as stochastic search processes with learning automata to adapt and learn from their network environment. In Luo et al. (2024), the authors introduced a novel approach for sampling hypergraphs using joint unbiased random walks. They proposed a new random walk algorithm that efficiently explores the hypergraph structure and generates statistically unbiased samples. Their method is based on a combination of node sampling and edge sampling, which allows for more efficient and accurate sampling of hypergraphs compared to existing methods.

To name some evidence for the importance of the concept of spanning trees in network analysis, we briefly review some of these methods in the rest of this section. Spanning trees are a way of connecting vertices by a single path (White and Newman 2001) and provide the basis for any chaining algorithm (Hill 1999). Spanning trees can also reveal important information from graphs, such as the structure of romantic relationships in a social network of 800 adolescents over 18 months, as studied by Bearman et al. (2004). They showed that every romantic relationship exists in a large spanning tree. This can capture the long and extensive chains of communication between large groups of people.

A study by Ansari et al. (2004) shows that a random spanning tree can preserve the topological and modular features of a network and that the network's structure can be easily visualized from the properties of its spanning tree. Spanning trees are crucial for solving propagation problems in networks, as shown by previous studies (Bellur and Ogier 1999). Spanning trees can efficiently and reliably propagate edge states. Therefore, spanning trees can propagate complete information across a network, making them effective structures for information transmission. Tewarie et al. (2015) used a minimum-spanning tree (MST) to unbiasedly characterize a network of complex brain connections. MST is a subgraph that connects all its nodes without cycles. It can maximize a property of interest, such as brain area synchronization, that preserves both global and local properties. Jalali et al. (2016) discuss a novel method for sampling social network data using spanning trees. The authors propose an algorithm that efficiently constructs a spanning tree from a social network graph, which can be used to sample the network while maintaining important structural features. In a recent study by Blomsma et al. (2022) with the aid of the concept of a spanning tree, the authors examine the effects of network size on the analysis, as well as the sensitivity of this approach for detecting neuropsychiatric pathology. They also explore the specificity of disorder-related network alterations. The review highlights the potential of minimum spanning tree analysis as a valuable tool for understanding the organization of brain networks in health and disease.

4 Proposed sampling algorithm

As a sampling algorithm, the proposed method uses spanning trees with degree constraints to highlight some important edges. In this work, we used a set of degree constraint-spanning trees with a variety of starting points as a basis for the algorithm. It was concluded from the results that edges with a large presence in spanning trees are important edges that capture several characteristics of the original network.

Figure 1 shows the relation among proposed methods. The remainder of this section describes in detail what STHNC and SSTHNC are. We then briefly describe SPTHNC and SPSTHNC.

Fig. 1
figure 1

Relations among proposed methods

Full size image

4.1 STHNC: a spanning tree with a degree constraint

An example of the degree-constrained spanning tree problem is determining whether a given network has a particular spanning tree for a given \(c\) (Lee 2001). It is an NP-complete problem (Garey and Johnson 1979), which is shown by reducing it to the Hamiltonian path problem. This section proposes an algorithm that generates a degree-constrained spanning tree if it can find one, and if not, an approximation by minimizing the number of nodes that violate the given degree constraint. The basic idea of this algorithm is borrowed from (Sundar et al. 2012).

The proposed algorithm, STHNC, starts with a randomly initial vertex and iteratively tries to find a spanning tree with the highest number of nodes satisfying a given degree constraint. Consider the initial vertex \(v\) randomly selected in the first step of STHNC. The vertex \(v\) is added to the set of spanning tree nodes \(T\). In addition, \(v\) is marked as visited. The algorithm forms an edge set \(E^{\prime}\) containing edges of the resulting spanning tree. The algorithm runs through several iterations until \(T\) contains all the vertices of the input graph (i.e. \(V\)). Each iteration consists of two parts, described below:

Part I: A vertex \(v\) is chosen from \(T\) as the current node. The selection of the current node from set \(T\) is performed as follows:

  • If set \(T\) has only the initial vertex, then this node is considered the current node \(v\).

  • If the set \(T\) has more than one node, then the algorithm considers the degree of nodes in the spanning tree (i.e., \(deg(v, S)\)):

    1. o

      Initially, such vertices with degrees below \(c\) (\(c\) is the degree constraint) are considered in \(T\) (\(deg\left(v, S\right)<c\)). From them, node \(v\) with the least number of unvisited neighbors is chosen as the current node.

    2. o

      Else, if there is a node that violates the constraint and also has unvisited neighbors then it is selected as the current node v.

    3. o

      Otherwise, a vertex with a maximum number of unvisited neighbors is selected as the current node v.

Part II. Among unvisited neighbors of node \(v\), vertex \(u\) with the least unvisited neighbors is chosen if such a vertex exists. Whenever such a vertex does not exist, another iteration occurs. Then edge (v, u) is added to set E' and vertex v is marked as visited and added to set T. The Current node is set to vertex \(u\) (\(v\leftarrow u)\) and the algorithm goes to part II.

The pseudo-code of the algorithm is shown in Fig. 2.

Fig. 2
figure 2

The pseudo-code of the spanning tree with the highest number of nodes that satisfy the given degree constraint

Full size image

In the proposed algorithm STHNC, selecting the current node plays a significant role in obtaining a spanning tree with the highest number of nodes satisfying the degree constraint \(C\). The proposed algorithm selects a current node with the minimum number of unselected neighbors, because the greater the number of unselected neighbors, the higher the probability of the vertex being selected in the future. Using this selection strategy, the spanning tree can be satisfied with the given constraint.

However, in some cases, the algorithm encounters a situation that has to allow a vertex to break satisfying the given constraint. To reduce the number of such vertices, a vertex with a maximum number of unselected neighboring vertices is selected as the current vertex. Until this vertex has any unselected neighbors, the algorithm will not allow other nodes to violate the given constraint. As a result of this selection, the number of vertices with degrees higher than the constraint is reduced.

4.2 SSTHNC: social network sampling using a set of STHNCs

SSTHNC starts by constructing \(k\) different spanning trees with the highest number of vertices that satisfy the given degree constraint (i.e., \(k\) different STHNCs). Each STHNC starts with a random vertex. Based on the constructed STHNCs, each edge present in the set of STHNCs is ranked. Edges with more appearances in STHNCs have a higher rank.

Additionally, each vertex appearing in STHNCs is ranked based on how many times it violated the degree constraint. Afterward, the top-\(m\) vertices of the list of nodes sorted in decreasing order by rank are selected, where \(m\) represents the minimum number of degree-constraint violations in any STHNC constructed. As a result, these \(m\) vertices are referred to as hubs.

SSTHNC constructs an induced subgraphFootnote 1 as the sampled network. A new sample vertex is inserted into the sampled graph, along with all edges between it and older samples, if they do not already exist.

SSTHNC first inserts hub nodes into the sampled network. All edges between hubs are inserted into the sampled network due to the induced property of the subgraph. It is inserted sequentially the (distinct) vertices incident on the edges selected from the beginning of the list of ordered edges as long as the number of nodes in the sampled network is not greater than x fraction of the original nodes. When a vertex is added to the sampled network, its edges to previous vertices are established every time a vertex is added. Figure 3 shows the pseudocode for the proposed sampling algorithm SSTHNC.

Fig. 3
figure 3

The pseudocode of the proposed sampling graph with a set of STHNC (SSTHNC)

Full size image

4.3 SPSTHNC: social network sampling using partial STHNC

SSTHNC can be enhanced by an α-partial version of STHNC (i.e. PSTHNC) with the highest number of nodes that meet a desired degree constraint. A PSTHNC with starting vertex v is a subgraph of graph G and is a tree with starting vertex v with the number of nodes \(\alpha *|V|\) for \(0<\alpha <1\). α-PSTHNC works like STHNC, as shown in Fig. 4.

Fig. 4
figure 4

The pseudo-code of constructing an α-partial degree constraint spanning tree with the highest number of nodes that satisfy the given degree constraint

Full size image

Algorithm PSTHNC computes an α-partial spanning tree for a given α. The revised SSTHNC version, called SPSTHNC, uses PSTHNC instead of STHNC. This includes all the vertices of the input graph.

4.4 Some remarks on the proposed methods

  • By using degree constraint spanning trees, edges could be visited uniformly. This prevents the sampled graph from being biased to high-degree nodes and prevents variance from having large values. There is no doubt that when the algorithm uniformly samples the input graph, some nodes with high degrees will inevitably be sampled. Several connections would be lost if these nodes were unavailable. By considering these influential nodes, we can better preserve the network statistics.

  • By considering a spanning tree with a minimum number of hub nodes (influential nodes), the sampled network is prevented from being biased towards influential nodes in the network.

  • In a variety of fields, scale-free networks, such as online social networks, are dominated by a few nodes with many neighbors (Santos and Pacheco 2005). Also, according to the 20/80 rule, a small number of nodes typically contribute a large amount to a network's activities (Woolhouse et al. 1997). It seems that it is more convenient to consider both nodes and significant edges when looking at network samples. This is to obtain better samples.

4.5 The time complexity of the proposed algorithms

In this section, we try to analyze the time complexity of the proposed algorithms. To find the time complexity of the proposed algorithms, we need to count the number of operations that the algorithm performs in the worst case and express it as a function of the input graph size.

4.5.1 The time complexity of STHNC

The STHNC consists of two nested while loops. The outer loop iterates until all the nodes are added to the spanning tree \(T\), which is at most \(|V|\) times. The inner loop iterates until all the unvisited neighbors of the current node \(v\) are visited, which is at most \(|E|\) times in total for all the nodes. Therefore, the total number of iterations of the inner loop is \(O(|E|)\). Inside the inner loop, the algorithm performs some constant time operations, such as finding the node u with the minimum number of unvisited neighbors, marking u as visited, adding the edge \((v, u)\) to \(E^{\prime}\), adding \(u\) to \(T\), and updating \(v\). These operations take \(O(1)\) time each. Therefore, the total time complexity of the algorithm is \(O(|V|\times |E|\times 1) = {\varvec{O}}(|{\varvec{V}}|\times |{\varvec{E}}|)\).

4.5.2 The time complexity of SSTHNC

SSTHNC consists of several steps. The first step is to call STHNC, \(k\) times. The time complexity of STHNC is \(O(k\times |V|\times |E|)\). The second step is to find the edges in STHNCs and list them in descending order of appearance. This can be done by using a hash map and a sorting algorithm. The hash map can store the edges and their frequencies in \(O(|E|)\) time and space. The sorting algorithm can sort the edges in O(|E| log |E|) time. Therefore, the second step takes \(O(|E|+|E|log |E|)= O(\left|E\right|log|E|)\) time. The third step is to check the hub nodes in STHNCs and rank them based on the number of violations. This can be done by using a hash map and a sorting algorithm. Same the second step, this step takes \(O(|V|log |V|)\) time. The fourth step is to find the minimum number of hub nodes in the STHNC. This can be done by using a linear search on the sorted list of nodes. This takes \(O(|V|)\) time. The fifth step is to select the \(|E|\)-top hub nodes from the list and insert them into \({V}_{s}\). This takes \(O(|E|)\) time. The sixth step is the main loop of the algorithm, which iterates until \(L\) is empty or \({V}_{s}\) reaches the desired size. The loop body consists of some constant time operations, such as inserting and removing edges, finding the first edge that connects two nodes, and adding nodes to \({V}_{s}\). These operations take \(O(1)\) time each. Therefore, the loop body takes \(O(1)\) time. The loop condition depends on the size of \(L\) and \({V}_{s}\). In the worst case, \(L\) has m edges and \({V}_{s}\) has \(\varphi \times |V|\) nodes. Therefore, the loop condition takes \(O(|E|+\varphi \times |V|)\) time to check. Therefore, the total time complexity of the algorithm is \(O(k\times |V|\times |E|+ |E| log |E|+ |V| log |V| + |V| + |E| + (|E|+\varphi \times |V|)\times 1) = O (k\times |V|\times |E|+|E| log |E|+|V| log |V|+ \varphi \times |V|)= {\varvec{O}}\boldsymbol{ }(|{\varvec{V}}|\times |{\varvec{E}}|)\).

5 Simulation results

This section compares the proposed algorithms with other popular sampling algorithms on six graphs drawn and described in Table 1 including Squeak Foundation.org (Leskovec et al. 2005) as D1, Robots.net (Leskovec et al. 2005) as D2, Cit-HepPh (Leskovec et al. 2007), as D3, Epinions1 (Leskovec et al. 2005) as D4, Slashdot0902 (Leskovec et al. 2009) as D5, Email-EuAll (Leskovec et al. 2009) as D6. In addition, artificial graphs are also used in some experiments. Other sampling methods include Random Node Sampling (RVS) (Maiya and Berger-Wolf 2011), Random Edge Sampling (RES) (Ahmed et al. 2010), Random Walk Sampling (RWS) (Lovász 1993), Metropolis–Hastings Random Walk Sampling (MHRW) (Murai et al. 2013) and Spiral Sampling (SS) (Piña-García and Gu 2013), distributed learning automation sampling (DLAS) (Rezvanian et al. 2014) the shortest path sampling (SPS) (Rezvanian and Meybodi 2015), sampling by spanning trees (SST) (Jalali et al. 2016), Hybrid cuckoo search and genetic algorithm sampling (GACS) (Ebadi Jokandan et al. 2021), and Levy flight-Based Distributed Learning Automata sampling (LBDLA) (Roohollahi et al. 2022).

Table 1 Description of test networks
Full size table

5.1 Experiment I

This experiment is designed to study the performance of the first proposed algorithm (SSTHNC) for finding degree constraint spanning trees with the highest number of nodes that satisfy the given degree constraint on some synthetic random connected small graphs based on the Erdos–Renyi model (Erdos and Rényi 1960). The size of these networks varies from 20 to 100 nodes. The proposed algorithms are compared with brute force search, which constructs all spanning trees on a synthesis network. Among all these spanning trees, such a tree with a minimum degree would be considered the most suitable solution. In this spanning tree, the number of nodes that violate the degree constraint \(c\) is denoted as the real value (reported in Table 2). In contrast, a spanning tree can be constructed by running the proposed algorithm considering a predefined degree constraint \(c\). This will reveal the number of nodes that do not satisfy the degree constraint. Using the proposed algorithm for multiple runs, an average number can be calculated, which is also reported in Table 2.

Table 2 Comparison of results for number of vertices that do not satisfy constraints
Full size table

Besides, the SSTHNC algorithm is conducted on the chosen real networks as described in Table 1. The results of the number of vertices that do not satisfy constraints and run-time are reported in Table 3 . In this experiment degree constraint spanning tree is executed with different degree constraints varying from 2 to 5. For each experiment, the algorithm is executed 30 times, and average results are reported in Table 3. The results are shown in terms of the number of nodes with degrees higher than the given constraint and times in seconds needed to construct a degree constraint spanning tree. From the results, we may conclude that by increasing the constraint, the number of vertices that violate the constraints (also called branch vertices) will decrease and also using the algorithm in a reasonable time, it can have a degree constraint spanning trees with the highest number of nodes that satisfy the given degree constraint.

Table 3 Comparison of results for the number of vertices that do not satisfy constraints and run-time for varying degree constraints
Full size table

5.2 Experiment II

This experiment studies the minimum degree of constraint on spanning trees required to meet a given sampling rate. In the first step, the first algorithm (SSTHNC) makes some BKDSTs. SKBDST is executed with different degree constraint values from 2 to 10 to examine minimum degree constraint \(c\) for spanning trees. Results of this experiment are demonstrated for chosen networks as described in Table 1. with respect to KSD for \({\text{DD}}\), KSD for \({\text{CCD}}\), SDD for \({\text{DD}}\), SDD for \({\text{CCD}}\), ND for \({\text{DD}}\), and ND for \({\text{CCD}}\) in Fig. 5. From Fig. 5, one can conclude that for a sampling rate of 30%, depending on the type of the network at least a degree constraint \(k=5\) is required to meet a specific sampling rate. The results of this experiment will be used in other experiments to choose the right number of spanning trees.

Fig. 5
figure 5

The minimum degree of constraint on spanning trees required to meet a given sampling rate

Full size image

5.3 Experiment III

In this experiment, the minimal number of spanning trees that must be used to reach a given sampling rate is determined. In this case, we ran the first proposed algorithm, SSTHNC, for a sampling rate of 30% on different test networks as described in Table 1 and then plotted the number of spanning trees versus KSD for \({\text{DD}}\), KSD for \({\text{CCD}}\), SDD for \({\text{DD}}\), SDD for \({\text{CCD}}\), ND for \({\text{DD}}\) and ND for \({\text{CCD}}\) as given in Fig. 6. As a result of these findings, we can state that increasing the number of computed spanning trees beyond 50 will not impact any of the statistical properties discussed above. Therefore, for the following experiments, we will set the number of computed spanning trees used to construct a sample to 50 to obtain a representative sample.

Fig. 6
figure 6

A given sampling rate requires a certain number of spanning trees

Full size image

5.4 Experiment IV

This experiment examines the impact of selecting starting vertices on spanning trees based on different strategies. To achieve this, three strategies for selecting vertex have been examined: \(Rd\), \(Hd\), and \(Hb\). \(Rd\) is a random starting vertex strategy. In \(Hd\) strategy, vertices with high degrees are used as hub vertices. For \(Hb\) strategy, high betweenness vertices are used. A node's betweenness is measured as the percentage of times it is located on the shortest path among all other nodes. The transfer of information items through a network is greatly affected by nodes with high betweenness. Results of this experiment for chosen test networks as described in Table 1 with respect to KSD for \({\text{DD}}\), KSD for \({\text{CCD}}\), SDD for \({\text{DD}}\), SDD for \({\text{CCD}}\), ND for \({\text{DD}}\), and ND for \({\text{CCD}}\) are given in Table 4. We can conclude from the results that it does not matter how the starting vertices are chosen for degree constraint spanning trees.

Table 4 Results of the proposed algorithm for different starting vertex selection strategies: Rd, Hd, and Hb
Full size table

5.5 Experiment V

This experiment compares two proposed algorithms SSTHNC (the first) and SPTHNC (the second) with Random Node Sampling (RVS) (Maiya and Berger-Wolf 2011), Random Edge sampling (RES) (Ahmed et al. 2010), Random Walk sampling (RWS) (Lovász 1993), Metropolis–Hastings Random Walk sampling (MHRW) (Murai et al. 2013), Spiral Sampling (SS) (Piña-García and Gu 2013), distributed learning automation sampling (DLAS) (Rezvanian et al. 2014) the shortest path sampling (SPS) (Rezvanian and Meybodi 2015), sampling by spanning trees (SST) (Jalali et al. 2016), Hybrid cuckoo search and genetic algorithm sampling (GACS) (Ebadi Jokandan et al. 2021), and Levy flight-Based Distributed Learning Automata sampling (LBDLA) (Roohollahi et al. 2022) based on KSD for \({\text{DD}}\), KSD for \({\text{CCD}}\), SDD for \({\text{DD}}\), SDD for \({\text{CCD}}\), ND for \({\text{DD}}\), and ND for \({\text{CCD}}\). The sampling rate is 15%. The results reported are averaged over 30 runs. For statistical significance, a parametric t-test with 28 degrees of freedom was conducted at a 95% level of significance. The t-test result on SSTHNC is reported as better than (shown by “✓”), worse than (shown by “✘”), similar to (shown by “ ~ ”) that of the corresponding sampling method. This experiment's results are shown in Tables 5, 6, 7, 8, 9 and Table 10. As the results of the t-test, the boldfaced results indicate the best results in Tables 5, 6, 7, 8, 9 and 10 and also we show the percentages of the cases that the \(SSTHNC\) outperforms significantly other algorithms in the last column. Based on these results, our proposed sampling algorithm outperforms sampling algorithms based on KSD, SDD, and ND. As well as outperforming the second sampling algorithm, the first is more efficient.

Table 5 Comparison of different algorithms for sampling in D1
Full size table
Table 6 Comparison of different algorithms for sampling in D2
Full size table
Table 7 Comparison of different algorithms for sampling in D3
Full size table
Table 8 Comparison of different algorithms for sampling in D4
Full size table
Table 9 Comparison of different algorithms for sampling in D5
Full size table
Table 10 Comparison of different algorithms for sampling in D6
Full size table

5.6 Experiment VI

This experiment studies the impact of sampling rate on the performance of the first proposed sampling algorithm. This goal is achieved by running the algorithm for changes in sampling rate from 5 to 30% with an increment of 5% on different test networks. The results are given in Fig. 7. According to the results, we may say that the impact of the sampling rate on the algorithm's performance is very much dependent on the type of network. Generally, however, increasing the sampling rate leads to better results in most networks.

Fig. 7
figure 7

Comparison of KSD, SDD, and ND with respect to \(DD\) and \(CCD\) for different sampling rates

Full size image

5.7 Experiment VII

A comparison of SSTHNC and PSTHNC is presented along with a few existing two-phase sampling algorithms, including the shortest path sampling (SPS) (Rezvanian and Meybodi 2015), distributed learning automation sampling (DLAS) (Rezvanian et al. 2014), sampling by spanning trees (SST) (Jalali et al. 2016), and Levy flight-Based Distributed Learning Automata sampling (LBDLA) (Roohollahi et al. 2022). For this experiment, the sampling rate is 30%. As shortest paths or spanning trees increase, algorithms cost more. In this experiment, the accuracy of sampling algorithms is compared based on KSD for \(DD\) and KSD for \(CCD\) versus sampling cost (as defined by Eq. (5)). In Figs. 8 and 9, we present the cost results of this experiment using KSDs for \(DD\) and \(CCD\) for different two-phase sampling algorithms. As shown, increasing sampling costs result in decreasing KSDs for \(DD\) and \(CCD\). Results say that at the same cost, the PSTHNC algorithm generally outperforms other two-phase sampling algorithms at least in five of the six networks based on KDS for \(DD\) and four of the six networks based on KSD for \(CCD\). For some networks such as D3, SPS sometimes outperforms SSTHNC based on KSD for \(CCD\). For the D1 network, SSTHNC and PSTHNC produce similar results for the same KDS.

Fig. 8
figure 8

Using KSD for DD versus sampling costs to compare two-phase sampling algorithms

Full size image
Fig. 9
figure 9

Using KSD for \(CCD\) versus the sampling cost to compare two-phase sampling algorithms

Full size image

6 Conclusion

This paper proposed two sampling algorithms for social networks using degree constraint spanning trees. The idea behind these algorithms was that by building STHNCs, they could identify important nodes (those that exceed the degree limit) and edges (those that appear more often in STHNCs) that capture some features of the original network. Moreover, STHNC visited edges uniformly, which reduced the bias towards high-degree nodes in the sampled network. The proposed algorithms were evaluated by running several experiments on data sets based on social networks. Based on the results, the proposed algorithms outperformed other algorithms such as random vertex sampling, random edge sampling, random walk sampling, Metropolis–Hastings random walk sampling, spiral sampling, shortest path sampling, spanning tree sampling, and distributed learning automata sampling with respect to Kolmogorov-Simonov, skew divergence, and normalized distance tests.