1 Introduction

Complex network analysis is an emerging area of research interest, and it corresponds to analyzing the topology of complex networks (such as biological networks, citation networks, social networks and web) from a graph-theoretic perspective (Newman 2010). Random network models, like the well-known Erdos–Renyi G(N, p link) model (Erdos and Renyi 1959): where p link is the probability for a link between any two nodes, are used to theoretically model complex real-world networks as truly random networks and form the basis to assess the extent of randomness among the links of the real-world networks. Until now, the assessment has been through a collection of characteristics such as degree distribution, path length and connectedness (Barabasi 2016), but none of these can be unequivocally used to quantify the extent of randomness in any complex real-world network.

In this paper, we investigate one characteristic feature of truly random versus real-world networks (that are not truly random) that has not been explored to its fullest potential. The feature that we seek to explore is the distribution of the degree (K) versus average local clustering coefficient (LCC) of the nodes with a certain degree (hereafter, referred to as the K vs. \( \overline{\text{LCC}} (K) \) distribution). The local clustering coefficient (LCC) for a node (Newman 2010) is the probability that any two neighbors of the node are connected. The LCC (ranges from 0 to 1) for a node is measured as the ratio of the actual number of links between the neighbors of the node to that of the maximum possible number of links between the neighbors of the node. For truly random networks following the G(N, p link) model, the probability for a link between any two nodes is the same, and hence, the probability that any two neighbors of a node are connected is simply the p link value. In other words, the LCC for a node in a truly random network does not depend on the degree of the node. On the other hand, for a real-world network, a node having a smaller degree has a larger chance of having any two of its neighbor nodes to be connected (compared to a node having a larger degree). That is, for a real-world network, a node having a larger degree is more likely to have a lower LCC compared to a node having a smaller degree. Hence, for real-world networks, if we average the LCC of the nodes having a certain degree and plot the K versus \( \overline{\text{LCC}} (K) \) distribution, the distribution is more likely to exhibit a strong negative correlation [as already reported in several related works (Barabasi 2016; Foudalis et al. 2011; Pizzuti and Rombo 2014)], whereas for a truly random network generated based on the average degree and number of nodes for a real-world network graph, the K versus \( \overline{\text{LCC}} (K) \) distribution is more likely to be a flat distribution (i.e., no dependence) or sometimes exhibit a positive correlation.

The current status of the literature is to visually inspect the K versus \( \overline{\text{LCC}} (K) \) distribution and infer whether a real-world network is truly random or not. We seek to proceed one step further. We propose to quantify the extent of randomness for a complex real-world network in the form of a measure called the Randomness Index, and it is the Pearson’s correlation coefficient (ranges from −1 to 1) of the K vs. \( \overline{\text{LCC}} (K) \) values for the vertices of the network. For any complex real-world network, the closer the Randomness Index value to zero (or even positive), the larger the extent of randomness in the distribution of the links in the network, whereas the closer the Randomness Index value to −1, the lower the extent of randomness. We analyze a suite of 48 real-world networks of diverse degree distribution and observe the median of the Randomness Index values to be −0.72. Only two of the 48 real-world networks had a positive Randomness Index value, and the rest of the networks had Randomness Index values less than −0.15.

To the best of our knowledge, we have not come across a single and dimensionless quantitative measure to unequivocally quantify (that is, its range of values −1…1 remains the same, irrespective of the number of nodes and edges in the network) the extent of randomness of complex real-world networks. The Randomness Index value for a real-world network could form the basis for further exploratory studies conducted on the network. The links in a real-world network with a larger Randomness Index value are more likely to have formed due to random association, and such a network could thence be subjected to further tests that are characteristic for random networks; on the other hand, the links in a real-world network with a lower Randomness Index value are more likely to have not formed due to random association (instead, it could be due to preferential attachment), and such a network could thence be subjected to further tests that are more characteristic for non-random networks (such as scale-free networks). From a structural perspective, the Randomness Index value for a network could be considered as a quantified measure of the significance of the high-degree nodes in the network. For networks with lower Randomness Index values, the high-degree nodes are more likely to have a lower local clustering coefficient; hence, in such networks, if the high-degree nodes are removed, several structural measures such as neighborhood connectivity, network robustness, path length (for shortest path communication) and feedback capacity for diffusion (Al-Shiridah et al. 2013) are likely to be affected. On the other hand, for networks with larger Randomness Index values, the high-degree nodes are relatively less critical as the probability for any two nodes to be connected does not depend on the degree of the nodes or the degree of their neighbors.

The rest of the paper is organized as follows: In Sect. 2, we present an illustrative example to generate a truly random network for a given real-world network (that is not random), determine the K versus \( \overline{\text{LCC}} (K) \) distribution for these two networks and compute the Randomness Index values for the two network graphs. In Sect. 3, we first present an overview of the 48 real-world networks analyzed in this research and tabulate/discuss the Randomness Index values observed for these networks. We then demonstrate the uniqueness of our proposed Randomness Index metric by comparing the distribution of the values for this metric with those obtained for some of the well-known modeling parameters for complex network analysis as well as with those available to quantify the variation or correlation of node degree. In Sect. 4, we review related work and highlight the unique contributions of the paper. Section 5 concludes the paper. Throughout the paper, the terms “node” and “vertex,” “link” and “edge,” “network” and “graph” are used interchangeably. They mean the same.

2 Randomness Index: illustration

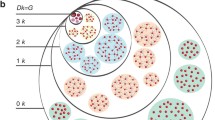
The Randomness Index of a complex network is the Pearson’s correlation coefficient (Strang 2006) of the degree (K) versus the average local clustering coefficient of the vertices with a certain degree, \( \overline{\text{LCC}} (K) \). In this section, we illustrate the computation of the Randomness Index of a real-world network and a truly random network that is generated according to the well-known Erdos–Renyi model (Erdos and Renyi 1959) on the basis of the average degree (<K>) and number of nodes (N) for the real-world network (see Fig. 1 for an illustration of the procedure).

Fig. 1
figure 1

Generation of a Truly Random Network according to the Erdos–Renyi Model based on the Average Degree and Number of Nodes for a Real-World Network

Full size image

For a given real-world network (the top graph in Fig. 1), we first compute the average degree of the nodes in the network. We then determine the probability for a link (p link = <K>/N − 1) between any two nodes if we were to generate a truly random network according to the Erdos–Renyi model based on <K> and N for the real-world network. We then consider all possible pairs of vertices (with vertex IDs ranging from 0 to N − 1). We generate a random number in the range of (0,…, 1) for each pair of vertices; if the random number generated for a pair is less than or equal to the p link value, then there is an edge between the vertices forming the pair as part of the truly random network (the bottom graph in Fig. 1); otherwise, not.

Figure 2 presents the calculation of the degree (K) versus average LCC for a particular degree (\( \overline{\text{LCC}} (K) \)) distribution for both the real-world network graph and the truly random network graph. For the real-world network graph, we observe the \( \overline{\text{LCC}} (K) \) values to decrease with increase in K; on the other hand, for the truly random network, the \( \overline{\text{LCC}} (K) \) values remain almost the same for the three K values of 3, 4 and 5.

$$ {\text{Randomness Index}} = \frac{{\sum\nolimits_{K} {\left[ {K - < K > } \right]\left[ {\overline{\text{LCC}} (K) - < \overline{\text{LCC}} (K) > } \right]} }}{{\sqrt {\sum\nolimits_{K} {\left[ {K - < K > } \right]^{2} } } \sqrt {\sum\nolimits_{K} {\left[ {\overline{\text{LCC}} (K) - < \overline{\text{LCC}} (K) > } \right]^{2} } } }} $$
(1)
Fig. 2
figure 2

Computation of the K versus \( \overline{\text{LCC}} (K) \) Values for the Real-World Network and Truly Random Network Graphs of Fig. 1

Full size image

Figures 3 and 4 present the calculation of the Randomness Index (see formulation 1) as the Pearson’s correlation coefficient of the K versus \( \overline{\text{LCC}} (K) \) values for the real-world network graph and truly random graph, respectively. Let <K> and < \( \overline{\text{LCC}} (K) \) > , respectively, denote the average of the K values (represented by <K>) and average of the \( \overline{\text{LCC}} (K) \) values (represented by <\( \overline{\text{LCC}} (K) \)>). We determine the terms [K − <K>] and [\( \overline{\text{LCC}} (K) \) − <\( \overline{\text{LCC}} (K) \)>] as well as their squares and product. We observe the Randomness Index (Fig. 3) for the real-world network graph to be −0.9665, clearly vindicating our earlier assertion that the K and \( \overline{\text{LCC}} (K) \) values typically exhibit a strong negative correlation. On the other hand, the Randomness Index (Fig. 4) for the truly random graph (generated based on the <K> and N for the real-world network graph) is 0.7038, again vindicating our assertion that the Randomness Index for the truly random graphs generated based on the parameters for the real-world network graph could be close to zero or positive.

Fig. 3
figure 3

Computation of the Randomness Index for the K versus \( \overline{\text{LCC}} (K) \) Values for the Real-World Network Graph of Fig. 1

Full size image
Fig. 4
figure 4

Computation of the Randomness Index for the K versus \( \overline{\text{LCC}} (K) \) Values for the Truly Random Graph of Fig. 1

Full size image

3 Real-world network graphs and their analysis

In this section, we first introduce the 48 real-world networks analyzed in this paper. Table 1 lists the three-character code acronym, name and the network type, the values for the number of nodes and edges as well as the average node degree (k avg) and spectral radius ratio for node degree (λ sp). All the real-world networks are modeled as undirected graphs. The spectral radius ratio for node degree (Meghanathan 2014) is a measure of the variation in node degree and is calculated as the ratio of the principal eigenvalue (Bonacich 1987) of the adjacency matrix of the graph to that of the average node degree. The spectral radius ratio for node degree is independent of the number of vertices and the actual degree values for the vertices in the graph. The spectral radius ratio for node degree is always greater than or equal to 1.0; the farther is the ratio from the value of 1.0, the larger the variation in node degree. The spectral radius ratio for node degree for the real-world network graphs analyzed in this paper ranges from 1.01 to 3.48 (indicating that the real-world network graphs analyzed range from networks with smaller variation in node degree to networks with larger variation in node degree).

Table 1 Real-World Networks used in the correlation analysis
Full size table

The networks considered cover a broad range of categories (as listed below along with the number of networks in each category): Acquaintance network (12), Friendship network (9), Co-appearance network (6), Employment network (4), Citation network (3), Literature network (3), Collaboration network (2), Political network (2), Biological network (2), Game network (2), Geographical Network, Transportation network and Trade network (1 each). A brief description about each category of networks is as follows: An acquaintance network is a kind of social network in which the participant nodes slightly (not closely) know each other, as observed typically during an observation period. A friendship network is a kind of social network in which the participant nodes closely know each other, and the relationship is not captured over an observation period. A co-appearance network is a network typically extracted from novels/books in such a way that two characters or words (modeled as nodes) are connected if they appear alongside each other. An employment network is a network in which the interaction/relationship between people is primarily due to their employment requirements and not due to any personal liking. A citation network is a network in which two papers (nodes) are connected if one paper cites the other paper as reference. A collaboration network is a network of researchers/authors who are listed as co-authors in at least one publication. A biological network is a network that models the interactions between genes, proteins, animals of a species, etc. A political network is a network of entities (typically politicians) involved in politics. A game network is a network of teams or players playing for different teams and their associations. A literature network is a network of books/papers/terminologies/authors (other than collaboration, citation or co-authorship) involved in a particular area of literature. A transportation network is a network of entities (like airports and their flight connections) involved in public transportation. A trade network is a network of countries/people involved in certain trade. The reader is referred to Meghanathan (2017) for a more detailed description of the individual real-world networks.

Table 2 lists the Randomness Index values for the 48 real-world network graphs. Only two networks (# 15—Football Network and # 32—ModMath Network) incur a positive Randomness Index value, indicating that their edges are formed due to random association. This could be justified due to the fact that the Football Network comprises of edges whose end vertices are teams that have played against each other during the round-robin league. Since the round-robin league games are arbitrarily scheduled between any two teams, it is convincing to observe a neutral or positive correlation between degree and local clustering coefficient values. Likewise, the ModMath Network comprises of school superintendents who have an edge between them if at least either of them considers the other person as someone who can effectively spread around modern Math methods among the schools in a county. In such a network, the links among the neighbor nodes of a node are more likely to be formed independent of the degree of the node.

Table 2 Randomness Index of the real-world network graphs
Full size table

Figure 5 presents the Randomness Index values of the networks in the sorted order. We observe the median of the Randomness Index values to be −0.72, and 35 of the 48 real-world networks (i.e., about 70% of the networks) exhibit Randomness Index values less than −0.60, all of which indicate a strong negative correlation, as per the ordinal scale proposed by Evans (Evans 1995). Thus, the extent of randomness in real-world networks is minimal, and links are more likely not to get arbitrarily created. However, if links are to get randomly generated, then the average local clustering coefficient of the nodes is more likely to be independent of node degree (like the truly random graph in Figs. 1, 4) and the Randomness Index of the networks is likely to be close to zero or positive.

Fig. 5
figure 5

Sorted Order of the Randomness Index of the Real-World Networks

Full size image

3.1 Comparison with the Erdos–Renyi random network graphs

In this subsection, we compare the Randomness Index values obtained for the 48 real-world network graphs with those obtained for their corresponding random network graphs generated according to the well-known Erdos–Renyi (ER) model. For each real-world network graph, we generate 1000 instances of the corresponding ER-random network graphs following the procedure described in Sect. 2 and determine the average of the Randomness Index values obtained for these 1000 random network graphs. In Fig. 6, we plot the Randomness Index values observed for a real-world network graph versus the average of the Randomness Index values observed for its corresponding random network graphs generated according to the ER model. For 43 of the 48 real-world networks (the data points lie below the diagonal line), the Randomness Index values observed for the real-world networks are lower (i.e., relatively more closer to −1) compared to the Randomness Index values observed for their corresponding ER-random graphs.

Fig. 6
figure 6

Randomness Index of the Real-World Network Graphs versus Average of the Randomness Index Values for the Corresponding Instances of the ER-Random Graphs

Full size image

The median of the average Randomness Index values of the ER-random graphs is −0.12 (see Fig. 7 for a distribution of the Randomness Index values vs. the probability for a link in the ER-random graphs corresponding to the real-world network graphs). For 13 of the 48 real-world network graphs, the average Randomness Index values of the corresponding ER-random graphs are positive (i.e., above 0.0) and for more than half of the real-world networks, the average Randomness Index values of the corresponding ER-random graphs are greater than −0.20. Such observations vindicate our earlier claim that if the links in a network came into existence due to just random association, the Randomness Index value for that network is more likely to be closer to 0 (rather than being closer to −1). Only for 3 of the 48 real-world network graphs, their corresponding ER-random graphs had average Randomness Index values that are less than −0.60, whereas, as mentioned earlier (see Fig. 5), the Randomness Index values for 35 of the 48 real-world network graphs are less than −0.60. All of the above observations demonstrate the potential of the Randomness Index measure to categorically differentiate real-world network graphs from random network graphs.

Fig. 7
figure 7

Probability for a link in the ER-Random Graphs corresponding to the Real-World Network Graphs versus Average of the Randomness Index Values for the ER-Random Graphs

Full size image

3.2 Comparison with the power-law model scale-free network graphs

Scale-free network graphs are modeled using the power-law model (Barabasi and Albert 1999) according to which the probability for observing a node with degree K is given by P(K) = CK −γ, where C is the proportionality constant and γ is the power-law exponent. Unlike the Poisson model (Erdos and Renyi 1959; Ugarte et al. 2015) of degree distribution that is characteristic for random network graphs, the power-law model of degree distribution for scale-free network graphs is characteristic of a heavy tail (i.e., there exists a few, but appreciable number of nodes, with degree centrality values that are extremely larger compared to those for the rest of the nodes). The smaller the value for γ, the larger the chances for finding one or more node(s), typically called the hub nodes, with a degree that is much larger than the rest of the nodes in the network. On the other hand, the larger the value for γ, the lower the chances for finding the hub nodes; all the nodes are more likely to be of comparable degree (such a degree distribution is characteristic of the random network graphs). The convention in the literature (Barabasi 2016) is that networks with γ values less than 3.0 are considered to be in the scale-free regime and networks with γ values greater than 3.0 are considered to fall in the random network regime.

In this section, we fit the degree distributions of the real-world networks to follow a power-law model and estimate the γ values for the corresponding scale-free networks. For each real-world network, we count the number of nodes with a certain degree K and divide that count by the total number of nodes in the network to obtain the value of P(K). Since P(K) = CK −γ, ln P(K) = ln C + (−γ)*ln (K). We model the ln (K) versus ln P(K) distribution using linear regression and determine the slope of the line (−γ). We observe the median of the estimated γ values to be 0.67, and only two of the 48 real-world networks (the # 15 FON and the # 41 TEN) have the estimated γ values greater than 3.0. However, we cannot very confidently claim that these real-world networks follow a power-law model, because the R 2 values for the power-law model fits of these networks are not appreciably high; the median of the R 2 values is only 0.43 (Table 3 displays the estimated γ values and the R 2 values of these estimates for the 48 real-world networks considered, and Fig. 8 plots the same). It is interesting to note from Fig. 8 that lower the estimated γ values, the lower the R 2 values of these estimates. Hence, even though the estimated γ values are low for the real-world networks, due to the lower R 2 values for these estimates, the γ values cannot be alone construed as a measure of the scale-freeness (or indirectly, the lack of randomness) of a real-world network.

Table 3 Estimation of the power-law exponent (γ) and the R 2 values of these estimates for the real-world network graphs
Full size table
Fig. 8
figure 8

Distribution of the Estimated Values for the Power-Law Exponent (γ) and the R 2 Values for these Estimates for the Real-World Network Graphs

Full size image

Our proposal for directly estimating the Randomness Index for a real-world network fills this gap. Rather than estimating the measure of scale-freeness of a real-world network and considering it as an indirect measure of the lack of randomness in the network, we propose to directly measure the extent of randomness of a real-world network using the Randomness Index measure. Figure 9 that plots the Randomness Index versus the estimated power-law exponent (γ) indicates the same. Real-world networks with lower γ values have the Randomness Index values spread over the entire range from [−1…0]. Hence, the power-law exponent γ would not be a sufficient measure to effectively quantify the extent of randomness of a real-world network.

Fig. 9
figure 9

Distribution of the Estimated Values for the Power-Law Exponent (γ) versus the Randomness Index Values for the Real-World Network Graphs

Full size image

3.3 Comparison with the small-worldness index

A network is considered to be a small-world network (Newman 2010) if the average path length between any two nodes is proportional to the logarithm of the number of nodes in the network as well as the average local clustering coefficient of the nodes is high. The clustering coefficient for a network (Newman 2010) is the average of the local clustering coefficient of the individual nodes in the network. Structurally, a small-world network is considered to be in between a regular network (wherein all nodes have the same degree) and random network (Newman 2010). Regular networks have a larger clustering coefficient, but a larger average path length too. On the other hand, random networks have a lower average path length, but a lower clustering coefficient too. The well-known Watts–Strogatz model (Watts and Strogatz 1998) is typically used to transform a regular network to a small-world network by arbitrarily rewiring the links of the regular network with a probability β. If β = 1, the network is truly random. Typically, β values of 0.10 or lower have been observed (Meghanathan 2015) to be appropriate to transform a regular network to a random network without significantly decreasing the clustering coefficient, but at the same time appreciably decreasing the average path length.

In Humphries and Gurney (2008), the authors proposed a metric called “Small-worldness Index” that could be used to quantify the extent of small-worldness in a real-world network. The Small-worldness Index of a real-world network is computed as follows: We generate 1000 instances of the ER-random graphs for the real-world network (using the procedure described in Sect. 2) and determine the overall average clustering coefficient of these random graphs as well as the overall average path lengths between any two nodes in these graphs. We determine the clustering coefficient ratio as the ratio of the average clustering coefficient of the real-world network and the overall average clustering coefficient for all the corresponding ER-random graphs. Likewise, we determine the path length ratio as the ratio of the average path length between any two nodes in the real-world network and the overall average path length between any two nodes in the corresponding ER-random graphs. The average path length for a real-world network is expected to be larger than the overall average path incurred for its corresponding ER-random graphs. Hence, the average path length ratio for a real-world network is expected to be larger than 1.0, but closer is the ratio to 1.0 or even lower than 1.0, the larger the extent of small-worldness. On the other hand, the average clustering coefficient for a real-world network is expected to be larger than that incurred for its corresponding ER-random graphs. Hence, the Small-worldness Index of a real-world network is computed as the clustering coefficient ratio divided by the average path length ratio. The larger the magnitude of the Small-worldness Index for a real-world network, the larger the extent of small-worldness in the network (i.e., smaller path length and larger clustering coefficient of the nodes).

Table 4 displays the Small-worldness Index values computed for the 48 real-world networks, and Fig. 10 presents a plot showing the distribution of the Randomness Index vs. Small-worldness Index values for the real-world network graphs. The median of the Small-worldness Index values is 2.85. For real-world networks with Small-worldness Index values much larger than the median (say, for example, networks with Small-worldness Index values of 6.0 or above), the Randomness Index values are less than −0.60 (except for # 30: AFB network). Though we could see such an inverse relationship between the two indexes for highly small-world networks, we are not able to generalize it for all the real-world networks studied. In particular, for 25 of the 48 real-world networks that had Small-worldness Index values less than 3.0, the Randomness Index values range from −1.0 to 0.20. Thus, the Small-worldness Index measure cannot be used as a direct measure to infer the extent of randomness of any arbitrary real-world network.

Table 4 Small-worldness Index of the real-world network graphs
Full size table
Fig. 10
figure 10

Distribution of the Randomness Index Values versus the Small-worldness Index Values for the Real-World Network Graphs

Full size image

3.4 Transitions in the pattern of the K versus \( \overline{\text{LCC}} (K) \) distribution

Figure 11 presents the K versus \( \overline{\text{LCC}} (K) \) distribution (where the degree centrality values are normalized in a scale of 0 to 1 for uniformity) for selected networks such that we capture the transitions in the pattern of the distribution as the Randomness Index values change from −1 to 1. The K versus \( \overline{\text{LCC}} (K) \) distributions for networks MUN (# 18), KCN (# 23), SJN (# 36), DON (# 8), with Randomness Index values smaller than −0.35 clearly show a negative correlation. The Author Facebook Network (# 30: AFB) shows a random pattern for the K versus \( \overline{\text{LCC}} (K) \) distribution, vindicating its Randomness Index value of −0.1667. The Football Network (# 15: FON) shows an opposite trend, wherein the \( \overline{\text{LCC}} (K) \) values increase with increase in K until certain values of K and then decrease; such a behavior is unexpected for real-world networks and can happen only when the LCC for a node is independent of the degree of the node (a characteristic of truly random networks and is also vindicated by the lowest spectral radius ratio for node degree value of 1.01 for the Football Network).

Fig. 11
figure 11

K vs.\( \overline{LCC} (K) \) Distribution for Selected Real-World Networks and Randomness Index Values

Full size image

3.5 Randomness Index versus metrics to quantify the extent of variation in node degree

Figure 12 presents a distribution of the Randomness Index values versus metrics that have been hitherto used to quantify the extent of variation in node degree (spectral radius ratio for node degree (Meghanathan 2014), ratio of the standard deviation to the average of node degree) or the heavy-tailed nature of a degree distribution (Kurtosis) or the degree–degree correlation of the end vertices of the edges (assortativity index) (Newman 2002). We do not observe any particular trend of increase or decrease in the Randomness Index values for each of these four metrics. We observe networks with lower variation in node degree (lower values for the spectral radius ratio for node degree or the ratio of the standard deviation to the average of node degree) need not have lower values for the Randomness Index, implying that the lack of variation in node degree cannot be perceived as the sole reason to expect a real-world network to exhibit randomness in the distribution of its links. For example, the Taro Exchange Network (# 41: TEN) and the Football Network (# 15: FON) have spectral radius ratio for node degree and standard deviation/average degree ratio values of (1.06, 0.265) and (1.01, 0.083), respectively; however, the Randomness Index of the TEN is −0.8712 (lack of randomness in the distribution of links among the nodes) and that of the FON is 0.8855 (significant randomness in the distribution of links among the nodes). Likewise, we also observe that two networks with vastly different Kurtosis values could have very close Randomness Index values. For example, the Anna Karenina Network (# 2: AKN) and the Fraternity College Dormitory Network (# 16: CDF) have Kurtosis values of 16.97 and 2.87, respectively, whereas their Randomness Index values (−0.8962 and −0.9336) are very close to each other. With respect to assortativity of the end vertices of the edges on the basis of node degree, we observe a majority of the real-world networks to exhibit assortativity index (calculated as the Pearson’s correlation coefficient of the degrees of the end vertices of the edges) values closer to 0, irrespective of the Randomness Index.

Fig. 12
figure 12

Randomness Index versus {Spectral Radius Ratio, Standard Deviation/Average Ratio, Kurtosis, Assortativity Index} for node degree

Full size image

4 Related work

Several works in the literature [e.g., (Foudalis et al. 2011) for social networks, (Pizzuti and Rombo 2014) for protein–protein interaction networks] have reported the negative correlation between the degree of a vertex and the local clustering coefficient of vertices with a particular degree. In (Bloznelis 2013), the authors attempted to study this phenomenon [to explore the hierarchical organization of real-world networks (Ravasz and Barabasi 2003)] using two random graph models (Godehardt and Jaworski 2001) that admit power-law degree distribution. However, there is no attempt to quantify the strength of this correlation and relate the value of the correlation coefficient with that of the extent of randomness in the network. To the best of our knowledge, ours is the first attempt to quantify the extent of randomness in the distribution of the links on the basis of the negative correlation of the K versus \( \overline{\text{LCC}} (K) \) distribution.

We use the classical Erdos–Renyi model (Erdos and Renyi 1959) as the basis for the degree-independent local clustering coefficient for the nodes (the local clustering coefficient for any node is close to the probability for a link between any two nodes) in truly random graphs. We do not advocate the use of other random network models [such as the configuration model (Britton et al. 2006)] because these models restrict the distribution of the links among the nodes in the network subject to certain constraints [such as a particular degree sequence (Meghanathan 2016) or an LCC sequence (Li and O’Riordan 2013)]. For example, in (Li and O’Riordan 2013), the authors exploited the negative K versus \( \overline{\text{LCC}} (K) \) correlation to evaluate the cooperation among the nodes as well as the robustness of the network with regard to link removals and proposed algorithms that would generate graphs with certain LCC values for the nodes for a given degree distribution. Such models cannot be used to evaluate the extent of randomness in real-world networks.

In Soffer and Vazquez (2005), the authors proposed a novel approach to determine the maximum possible number of links between the neighbors of a node as part of the formulation to compute the local clustering coefficient for a node. If the degree constraints of the neighbors of a node are taken into consideration, the maximum possible number of links among the neighbors of a node is more likely to be lower than the maximum possible number of links used in the standard LCC formulation (that is also used in this paper). For example, if a node i has four neighbors (say, A, B, C, D) and all these neighbors have degree 2, as per (Soffer and Vazquez 2005), the maximum possible number of links between these neighbors is 2 (say, A–B and C–D) and not 4(4 − 1)/2 = 6. The extent of randomness of a real-world network could not be evaluated with such a formulation for the LCC as it forces all the possible links incident on the neighbors of a node to be those connecting the neighbors of the nodes themselves (and the chances of randomness in the distribution of the links are suppressed). To corroborate our observation with regard to the computation of LCC, the K versus \( \overline{\text{LCC}} (K) \) distribution for several real-world networks based on the formulation of (Soffer and Vazquez 2005) has been observed to be a flat distribution, and with such a degree-independent distribution of LCC, the extent of randomness in a real-world network could not be evaluated.

5 Conclusions

The high-level contribution of this paper is the proposal for a quantitative metric to assess the extent of randomness in the distribution of the links in real-world networks. We make use of the fact that if a real-world network is not a truly random network, the chances for any two neighbors of a node to be connected (quantified in terms of the local clustering coefficient, LCC) decrease with increase in the degree for the node. We define the Randomness Index of a real-world network as the Pearson’s correlation coefficient of the degree and average LCC of the nodes with the particular degree. We propose that stronger the negative correlation (i.e., closer the values of the correlation coefficient to −1), the lower the extent of randomness in the distribution of the links in the network. For networks with lower values of the Randomness Index (close to −1), the chances for any two neighbors of a node to be connected decrease with increase in degree, and hence, the links are more likely to have not formed due to random association. For networks with Randomness Index closer to 0 or above 0, the chances for any two neighbors of a node to be connected do not depend on the degree of the node, and hence, the links between nodes are more likely to have formed due to random association.

We evaluate a suite of 48 real-world networks of diverse degree distribution and observe that the median of the Randomness Index values is as low as −0.72 (indicating that the extent of randomness in a majority of the real-world networks is limited). We also show that the Randomness Index values for a real-world network and its corresponding ER-random graphs are indeed different and the former is more likely to be lower. We advocate that the Randomness Index metric is a dimensionless metric (the values always range from −1 to 1 and do not depend on the actual degree values of the nodes or the number of nodes and edges in the network) that could be unequivocally used (unlike the currently used approaches of evaluating the degree distribution, standard deviation/average ratio, connectedness, assortativity index, etc.) to evaluate the extent of randomness in any real-world network. Further, we show that the Randomness Index metric is a unique metric for complex network analysis and is different from some of the well-known modeling parameters like the power-law exponent for scale-free networks and Small-worldness Index for small-world networks. We also show that it does not have similarity to any of the existing metrics to quantify the variation or correlation of node degree.