Yaw-control efficiency analysis for a diamond wing configuration with outboard split flaps

Abstract

The yaw-control device of a low-aspect ratio flying wing with diamond-shaped wing planform is investigated. Extensive low-speed wind tunnel experiments have been carried out to obtain surface pressure data and the aerodynamic forces and moments of the configuration for six different flap deflection angles at varying angles of attack and sideslip. Complementary unsteady Reynolds-averaged Navier–Stokes simulations are performed for selected configurations. The experimental data is used to examine the validity of the numerical results. The analysis is focused on the aerodynamic coefficients and derivatives. Yaw-control effectiveness, yaw-control efficiency, crosswind landing capabilities and coupling effects are discussed. The results show sufficient yaw-control effectiveness and efficiency for a wide range of considered freestream conditions. The outboard flap exhibits a non-linear characteristic with respect to the flap deflection angle and freestream conditions. The efficiency is considerably reduced at high angles of attack due to large-scale flow separation in the wing outboard section. Non-linear coupling effects with the rolling moment become obvious for moderate to large flap deflections over the whole angle of attack polar. The numerical results show good agreement with the experimental data in the surface pressure distributions and longitudinal aerodynamic coefficients. The yawing moment is overpredicted by numerical simulations for large flap deflection angles.

1 Introduction

Flying wings are a sub-category of the so-called all lifting vehicles (ALVs). ALVs are aircraft, which only exhibit horizontal oriented components. All of them are designed to contribute to the lift throughout the flight envelope [24]. The development of flying wings can be traced back to the late 1800s. Prior to 1950, the work on flying wings was mainly done by individual designers like the Horten brothers, Alexander Lippisch or John K. Northrop [24]. The intention was to design an aircraft with maximum aerodynamic efficiency [3]. With respect to military applications, the reduced visual and radar signature is an additional desired characteristic of flying wings [3, 7]. Past 1950, the work on flying wings has been more dedicated to corporations and organizations [24]. In the time frame of manned flight, more than 100 flying wings have been developed and flown [24]. However, only the Northrop Grumman B-2 obtained operational deployment [24]. Despite the long period of research on flying wings and its benefits in aerodynamic performance compared to conventional design, this is still an unconventional design with low acceptance. From a technical point of view, the main reason is the reduced stability and control of such aircraft [6,7,8, 23]. Omitting the vertical surfaces leads to a significant reduction in the directional stability. In some cases like the Northrop XP-56 Black Bullet and the YB-49, this problem had to be solved by the attachment of vertical stabilizers [3]. Considering a pure flying wing, the directional stability and controllability must be provided by control surfaces integrated in the wing. There are several concepts which have been investigated and published using all moving wing tips [12], elevons [6], split wing tips [4], blowing [10] or drag rudders [20].

The Chair of Aerodynamics and Fluid Mechanics at the Technical University of Munich (TUM-AER) investigates novel control surfaces for the directional control and stability of a low-aspect ratio flying wing configuration. The geometry of the configuration corresponds to the so-called SAGITTA flying wing demonstrator configuration [1]. The SAGITTA demonstrator was developed in the frame of an open innovation project launched by Airbus Defence & Space in 2010. The investigated flying wing represents a 1:2.5 model of the SAGITTA demonstrator configuration. The configuration is equipped with three pairs of control surfaces for the control in pitch, roll and yaw. The yaw-control devices, called outboard split flap (O/F), are placed in the wing tip area and implemented as split flaps. The up and downward deflection of the split flap about its hinge line along the leading edge creates the required yawing moment for the directional stability and control.

2 Diamond wing configuration

2.1 Wing geometry

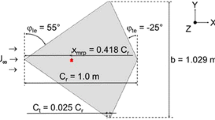
A flying wing configuration with a diamond-shaped wing planform is analyzed. The leading-edge sweep is ${\varphi _{\text {le}}=55^\circ }$, the trailing-edge sweep is ${\varphi _{\text {te}}=- \ 25^\circ }$ and the root chord is ${c_{\text {r}}=1.2\,{\text {m}}}$. It features a wing span of ${b=1.235\,{\text {m}}}$, a reference area of ${S_{\text {ref}}=0.759\,{\text {m}}^2}$, a mean aerodynamic chord of ${l_\mu =0.801\,{\text {m}}}$ and a moment reference point of ${x_{\text {mrp}}=0.501\,{\text {m}}}$, see Fig. 1 and Table 1. The diamond wing is designed with a NACA 64A012 airfoil over the whole wing span. The leading-edge contour is replaced by a sharp leading edge within the first 20% of the semi wingspan. This modification influences the flow topology in the apex area. The sharp leading edge leads to a flow separation and vortex formation at moderate to high angles of attack ($\alpha \ge 8^\circ$). Further information on the airfoil design and the influence of the modified leading edge on the aerodynamics are given by Hövelmann [13, 14].

Fig. 1

Diamond wing configuration planform and flap layout

Table 1 Parameters of the wing planform and the O/F

2.2 Outboard split flap geometry

The diamond wing is equipped with three pairs of flaps to create the aerodynamic moments about the body-fixed axes. The inboard flaps (I/F) induce the pitching moment by symmetric upward or downward deflection on both wing sides. The rolling moment is created by the midboard flaps (M/F) by asymmetric upward and downward deflection on both wing sides. The directional stability and control is provided by the outboard flaps (O/F), which are implemented in the wing tip section, see Fig. 1. The wing tip area is split with respect to the ${z=0}$ plane into an upper and lower flap surface, see Fig. 2. Both flap surfaces can be deflected about the hinge line, which is aligned almost parallel to the wing leading edge, see Fig. 2. The O/F hinge line angle is ${\varphi _{\text {HL,O/F}}=51^\circ }$ and thus $4 ^{\circ }$ smaller than the leading-edge sweep. The O/F surfaces can be deflected in the range of ${0^\circ \le \zeta \le 50^\circ }$. In this analysis, only symmetric deflections of the right O/F are considered. The flap deflection angle is consequently defined as ${\zeta =\zeta _{\text {R}}=\frac{\zeta _{\text {R,U}}+\zeta _{\text {R,L}}}{2}}$. The lateral extension of the O/F is ${0.806\le \eta \le 1}$ with ${\eta =\frac{y}{b/2}}$. The non-dimensional root chord of the flap reads ${\frac{c_{\text {r}}}{c_{\text {r,O/F}}}=0.191}$ and the non-dimensional flap area is defined as ${\frac{S_{\text {ref,O/F}}}{S_{\text {ref}}}=0.0198}$. By deflecting the O/F, the projected surface normal to the freestream direction is increased. In this way, the split flap generally acts like a spoiler device with a wake type flow behind the flap. The surface pressure at the flap front side is increased and at the flap back side is decreased. The pressure difference between front and back side creates a force normal to the flap surface generating the yawing moment. In Table 2, the projected flap surface normal to the yz-plane is introduced. The projected area is normalized to the projected area of the O/F of the zero-control configuration. It shows the non-linear increase of the projected area with a lower gradient for flap deflections of ${\zeta \le 10^\circ }$.

Fig. 2

Detail view of the outboard split flap

This O/F layout is chosen to use different effects. A conventional split flap with its hinge line parallel to the trailing edge mainly creates the yawing moment by additional drag, because the force vector is approximately normal to the hinge line. Due to the rotation of the hinge line about ${\varphi _{\text {HL,O/F}}=51^\circ }$, the surface normal vector of the deflected O/F back side is rotated as well, pointing in inboard direction. Consequently, the force vector is not aligned with the x-direction anymore but rotated about $\gamma _2$, see Fig. 3a. The force created at the O/F can be split in a x and y part. Due to the significant rotation of the hinge line of more than $45^{\circ }$, it is assumed that $F_{x,O/F}$ is of similar magnitude as $F_{y,O/F}$. Since the O/F is located behind the moment reference point $x_{\text {mrp}}$, the relative lever arm ${\frac{l_\gamma }{b/2}=1.004}$ is also larger than it would be possible with a conventional split flap. A conventional split flap would have a lever arm lower than the wing half span. The lever arm could be further elongated by adjusting the O/F hinge line to an optimal relative lever arm of ${\left( \frac{l_\gamma }{b/2}\right) _{\text {opt}}=1.087}$. Another advantage of the rotated hinge line is an additional elongation of the lever arm in y-direction by $\Delta y$ with increasing O/F deflection, see Fig. 3b. The increased lever arm contributes to a higher yawing moment. Furthermore, it is intended to use an aerodynamic effect of this O/F design. An evolving vortex at the back side of the deflected O/F should contribute to a higher yawing moment, see Fig. 3b. The flow separates at the inboard edge of the flap and the shear layer rolls up to a vortex. The high induced cross-flow velocities at the surface of the back side of the flap significantly decrease the surface pressure. This negative pressure would then additionally increase the pressure difference at the flap and thus the yawing moment. This effect, however, needs to be proven.

Table 2 Relative projected area of the O/F normal to the freestream direction at $\alpha =0^\circ$ and $\beta =0^\circ$

Fig. 3

Sketches of the intended outboard split flap effects

3 Experimental approach

3.1 Test facility and freestream conditions

The experimental investigations are performed in the wind tunnel A of TUM-AER. The Göttingen-type low-speed wind tunnel (W/T) can be run with an open or closed test section. This investigation is performed with the open test section with dimensions of $1.8\,{\text {m}} \times 2.4\,{\text {m}} \times 4.8\,{\text {m}}$ (height $\times$ width $\times$ length). In this configuration, the maximum freestream velocity is ${U_{\infty ,{\text {max}}}=65\,{\text {m/s}}}$ with a maximum turbulence intensity of $0.4\%$ and an uncertainty in the freestream direction below $0.2^\circ$. The maximum uncertainty in the temporal and spatial mean velocity distribution is $0.67\%$ and the static pressure variations along the test section is below $0.4\%$.¹ The W/T model is mounted in the test section with a rear sting on a three-axis support, see Fig. 4. The three-axis support enables the computer-controlled adjustment of the angle of attack, the angle of sideslip and the roll angle.

Fig. 4

W/T model with deflected flap in the open test section

Angles of attack of ${- \ 4^\circ \le \alpha \le 20^\circ }$ with ${{\Delta \alpha =1^\circ }}$ are measured for five different angles of sideslip ${{\beta =\left[ - \ 10^\circ , -\ 5^\circ , 0^\circ , 5^\circ , 10^\circ \right] }}$. The measurements are performed for a target Mach number of $Ma=0.13$ and a target Reynolds number of ${Re=2.3\times 10^6}$ based on the mean aerodynamic chord $l_\mu$. The freestream velocity slightly decreases with increasing angle of attack due to the increasing blockage of the test section by the W/T model. The maximum blockage at an angle of attack of ${\alpha =20^\circ }$ is approximately 7%. The effect of a reducing freestream velocity is more pronounced at ${\alpha \le 10^\circ }$. Therefore, the target freestream condition is set at ${\alpha =10^\circ }$. The deviation of the Reynolds number at ${\alpha =0^\circ }$ and ${\alpha =20^\circ }$ from ${Re(\alpha =10^\circ )}$ exhibits a maximum of $+\ 3\%$ and $- \ 1.5\%$ , respectively.

3.2 Wind tunnel model

The W/T model is an aluminum model prepared for a rear sting attachment to a three-axis support, see Fig. 4. The geometrical parameters are given in Table 1. Its partly modular composition allows the replacement of the leading-edge segments and the wing tips. The wing tip can be replaced by the O/F, which is realized from several parts which can be exchanged to obtain different flap deflection angles. In this way, seven different configurations with symmetric flap deflection angles of ${\zeta = [0^\circ ,5^\circ ,10^\circ ,20^\circ ,30^\circ ,40^\circ ,50^\circ ]}$ are realized. The W/T model also includes rapid prototyping parts, which represent the corresponding actuators for the deflection of the O/F. Including the flap deflection lever arms increases the similarity to the real actuators configuration. The W/T model is prepared for the application of force and moment measurements as well as steady surface pressure measurements. An overall number of 192 pressure taps are distributed in seven chordwise sections ${\frac{x}{c_{\text {r}}}=[0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7]}$ on the wing’s upper and lower side. Trip dots are attached near to the wing leading edge to ensure turbulent boundary-layer characteristics on the whole wing. The trip dots fix the laminar–turbulent transition at the wing leading edge and enable a comparison of the experimental data with fully turbulent numerical simulations. The trip dots feature a roughness height of $150\,\upmu {\text {m}}$, a diameter of $1.27\,{\text {mm}}$ and are placed aft the leading edge at the upper and lower wing surface. The distance from the leading edge is defined as the arc length over the mean aerodynamic chord and reads 0.00875 and the spacing between the trip dots along the leading edge relative to the trip dot diameter reads 0.5. Detailed information on the application of trip dots on low-aspect ratio configurations with round leading edges is given in the References [13, pp. 35–43] and [15, 16].

3.3 Force-measurement technique

The aerodynamic forces and moments are obtained with an internal six component strain gauge balance. The maximum sustainable loads are 900 N, 450 N, 2500 N for axial, lateral and normal forces, respectively. The maximum allowed moments are 120 Nm, 160 Nm, 120 Nm for rolling, pitching and yawing moments, respectively. The balance is calibrated for a temperature range of ${283\,{\text {K}}\le T\le 328\,{\text {K}}}$. Forces and moments are acquired over a time period of ${t_{\text {meas}}=20\,s}$ with a sampling rate of ${f_{\text {meas}}=800\,Hz}$. The presented force and moment coefficients are mean values of the obtained data. The repeatability of the aerodynamic coefficients for the applied test setup and configuration reads ${\Delta C_D=\pm 0.0007}$, ${\Delta C_Y=\pm \ 0.0003}$, ${\Delta C_{\text {L}}=\pm \ 0.0007}$, ${\Delta C_{mx}=\pm \ 0.0003}$, ${\Delta C_{my}=\pm \ 0.0002}$ and ${\Delta C_{{mz}}=\pm \ 0.0001}$. The repeatability is defined as the standard deviation of the coefficients determined from four angle of attack polar measurements. The standard deviation is determined for every angle of attack and coefficient. The mean of the standard deviations over the whole angle of attack polar corresponds to the presented repeatability.

3.4 Steady surface pressure measurement technique

Three electronic pressure scanning modules (Scanivalve ZOC 33) located in the wind tunnel model are used to acquire the surface pressure data. The pressure is measured with a sampling rate of ${f_{\text {meas}}=20\, {\text {Hz}}}$ over a time period of ${t_{\text {meas}}=10\,{\text {s}}}$. The repeatability is determined as an average of the standard deviation of all pressure taps at five different angles of attack for four repeatability measurements. The repeatability of the system for the investigated configuration reads ${\Delta c_{\text {p}}=\pm\; 0.019}$.

4 Numerical approach

4.1 Wing and flap geometry

The geometry of the diamond wing used for the numerical simulations is almost identical to the W/T model. A full model with similar dimensions is used. The rear sting is considered in the numerical model as well, see Fig. 5. It is modeled up to one root chord length downstream of the root chord trailing edge. The O/F is implemented with two minor differences to the W/T model. The screws are neglected and the actuators are simplified, see Fig. 6c. The consideration of the actuators increases the comparability of experimental and numerical data. Three different configurations are investigated numerically, namely ${\zeta = [0^\circ , 30^\circ , 50^\circ ]}$. The computational domain is bounded by a sphere with a radius of 30 times the mean aerodynamic chord length. The W/T support and test section are not considered in the numerical analyses.

Fig. 5

Wing geometry with interface boxes for the mesh generation

Fig. 6

Numerical grid

4.2 Grid generation

The geometry is meshed by unstructured hybrid grids using the grid generation software CENTAUR.² The surface of the geometry is meshed with triangles and quadrilaterals. The grid in the vicinity of the wing is created by a wall-normal extrusion of the surface mesh. This mesh should cover the boundary layer and consists of prismatic and hexahedral elements. The remaining domain is filled with tetrahedral elements. Parameters like the element size, stretching ratio and first layer thickness can be adjusted locally.

Due to the asymmetry of the geometry, it is not possible to simulate a half model with symmetry boundary condition. The full model mesh is created by a modular mesh generation approach. In a first step, the right wing side of the half model is considered. An interface box including the outboard wing section with the O/F is implemented in the half model, see Fig. 5a. An initial mesh for the half model outside and inside the interface box is created. Subsequently, the geometry inside the interface box is exchanged and only the volume inside the interface box is remeshed, see Fig. 5b. The grid nodes of the new mesh are merged on the existing grid nodes on the interface plane for proper connectivity between the grid inside and outside the interface box. In this way, the different O/F deflections are meshed very efficiently. The final configuration is obtained by mirroring the mesh of the right wing side for ${\zeta =0^\circ }$ and adding it to a mesh with deflected flap ${\zeta \ne 0^\circ }$, see Fig. 5c. Besides an efficient mesh generation for the different configurations, this approach guarantees an identical numerical grid on both wing half sides, with exception of the mesh inside the interface box. Thus, asymmetries in the numerical solution in consequence of the numerical grid can be minimized. The grids used in this analysis are created based on former numerical investigations on the zero-control configuration of this geometry. These investigations included a grid sensitivity study and $y^+$-analysis [13, pp. 123–126]. The $y^+$-analysis led to a first layer thickness of $0.003\,{\text {mm}}$, which results in a $y^+$-value of less than one for the majority of the wing surface and local areas with a maximum of ${y^+_{\text {max}}<1.3}$. The surface and prismatic grid is significantly refined in the leading and trailing-edge region, see Fig. 6a, b. The prismatic layers are extended on the wing upper side to 52 layers to include the evolving leading-edge vortex within the prismatic grid. Furthermore, the tetrahedral grid is refined in the vicinity of the wing. The mesh in the O/F region is significantly refined to capture the occurring flow patterns. Figure 6a shows a hexaherdal grid in the wake of the O/F to resolve the turbulent structures provoked by the O/F. Detailed information on the element sizes of the final grids is summarized in Table 3.

Table 3 Detailed grid information for the final grids

Due to the existing grid independence study for the zero-control configuration conducted by Hövelmann [13, pp. 123–126], only the independence of the grid in the O/F area is assessed. The influence on the lateral aerodynamic forces and moments of three different grid resolutions in the O/F area is verified. Table 4 summarizes the lateral aerodynamic coefficients for the different grid resolutions at ${\alpha =12^\circ }$ and ${\beta =0^\circ }$ for the $50^{\circ }$ deflected O/F. The values verify the use of the medium grid resolution for the analysis.

Table 4 Lateral aerodynamic coefficients and the number of grid nodes of the full model for different grid resolutions in the vicinity of the O/F at ${\alpha =12^\circ }$, ${\beta =0^\circ }$ and ${\zeta =50^\circ }$

4.3 Flow solver

The TAU code is applied for the numerical simulations. It is a CFD solver able to solve the three-dimensional compressible (unsteady) Reynolds-averaged Navier–Stokes ((U)RANS) equations and is developed by the German Aerospace Center (DLR) Institute of Aerodynamics and Flow Technology. The solver is optimized for the usage with hybrid unstructured grids and exhibits a high parallel efficiency on high-performance computers. The solver is composed of several independent modules, which are used for the partitioning, preprocessing and solving. The TAU code provides several upwind and central difference schemes for the spatial discretization. Steady-state simulations can be run using a local or global time stepping scheme. A dual-time stepping method is implemented for time-accurate simulations. Convergence acceleration is achieved by multigrid approach and residual smoothing algorithms. Turbulent flows can be modeled by one- and two-equation eddy-viscosity models as well as with Reynolds stress models (RSM) [11].

4.4 Applied numerical setup

The numerical simulations are run at freestream conditions in accordance with the experimental tests. The CFD computations are run as fully turbulent URANS simulations restarted from steady RANS simulation results. The considered angle of attack range is ${0^\circ \le \alpha \le 20^\circ }$ with an increment of ${\Delta \alpha =2^\circ }$. A second-order central scheme introduced by Jameson has been applied for the spatial discretization [19]. A matrix-dissipation scheme is applied to add the required artificial viscosity and thus leads to a more upwind biased method [22]. An implicit backward Euler scheme with a LUSGS algorithm is applied for the discretization in time. Convergence acceleration is obtained by a 3W multigrid cycle. The unsteady simulations are run with a dual-time stepping method with a time step of ${\Delta t=0.0004\,{\text {s}}}$. An overall simulation time of ${t_{\text {sim}}=0.0544\,{\text {s}}}$ is chosen, which equals a progress of the flow of two times the root chord. The turbulence is modeled by a modified version of the one-equation Spalart–Allmaras model (SA-neg) [2, 21]. This turbulence model is chosen due to former investigations on the flow separation onset at the round leading edge of the flying wing configuration. The CFD computations predicted well the flow separation scenario and subsequent vortex evolution compared to the experimental results [13]. All computations have been run in parallel mode at the GCS Supercomputer SuperMUC at the Leibnitz Supercomputing Centre (LRZ).³

5 Results and discussion

This section comprises results on the investigation of the O/F characteristics. Experimental and numerical results are utilized for the analyses. First, surface pressure distributions are used to describe the flow phenomena occurring at the configuration for the considered freestream conditions. Experimental and numerical surface pressure distributions are compared to evaluate the numerical results. Subsequently, the overall aerodynamic coefficients are discussed. The influence of the O/F on the longitudinal aerodynamic coefficients, the yaw-control effectiveness and efficiency as well as cross-coupling effects are analyzed.

5.1 Flow physics

An overview of the flow physics occurring at this configuration within the considered angle of attack and sideslip range and an evaluation of the numerical results are given. A detailed analysis of the flow physics of the zero-control configuration can be found in Ref. [13].

The small aspect ratio combined with the variable leading-edge contour results in a complex flow structure, which is discussed in the following by means of the surface pressure distribution in seven chordwise sections, see Fig. 7. Additionally, the surface pressure distribution and field streamlines from URANS results are shown in Fig. 8. At moderate angles of attack of ${\alpha < 8^\circ }$, the flow is dominated by attached flow. With increasing $\alpha$, the flow separates at the sharp leading edge in the inboard region and forms a discrete inboard leading-edge vortex (ILV), see Figs. 7b and 8a. When the leading-edge contour changes from sharp to blunt, the flow around the round leading edge is not separated anymore but attached and the leading-edge vortex moves away from the leading edge in inboard direction and is transported downstream in freestream direction. The flow does not separate from the blunt leading-edge due to a relatively large leading-edge radius of the NACA 64A012 airfoil. Simultaneously, the flow starts to separate from the round leading edge at the wing tip. The separation onset moves upstream with increasing angle of attack and forms an irregular recirculation area with flow reversal, see Figs. 7e and 8b. The flow begins to separate at the wing tip due to the short wing chord resulting in a high aerodynamic load and a significant adverse pressure gradient. The inboard leading-edge vortex increases in intensity with increasing angle of attack, which is represented by significant negative pressure peaks. At ${\alpha =20^\circ }$ and zero angle of sideslip, the flow is dominated by the inboard leading-edge vortex, attached flow in the midboard section and flow separation with flow reversal in the outboard section. Asymmetric freestream conditions show a minor influence on the flow around the wing at moderate angles of attack, see Figs. 7a–c. At high angles of attack, the flowfield significantly changes with the angle of sideslip. With a negative $\beta$, the effective leading-edge sweep increases at the leeward side and decreases at the windward side. The increased effective leading-edge sweep results in a reformation of the flow in the midboard and outboard wing section. At ${\beta =- \ 10^\circ }$, instead of a flow separation with irregular flow, the shear layer rolls up to a discrete midboard leading-edge vortex (MLV). At the windward wing side, however, the flow separation onset in the midboard wing section moves further upstream. This can be observed in the pressure distribution of the right wing side at ${\beta =10^\circ }$, see Fig. 7f. The effects occurring at the windward and leeward wing side are also illustrated in Fig. 8c.

Fig. 7

Experimental and numerical surface pressure distributions of the zero-control configuration at $\alpha =\left[ 10^\circ , 20^\circ \right]$ and $\beta =\left[ -\ 10^\circ , 0^\circ , 10^\circ \right]$

Fig. 8

Field streamlines and surface pressure coefficient distribution of the zero-control configuration at different angles of attack and sideslip

The surface pressure distributions indicate a satisfying agreement of experimental and numerical data for a wide range of considered freestream conditions. At ${\alpha =10^\circ }$, CFD predicts the leading-edge vortex in the inboard wing region as well as the attached flow in the midboard wing region, see Fig. 7b. The pressure levels show a good agreement. Only the suction peak of the ILV in the ${x/c_{\text {r}}=0.1}$ section is less pronounced in the numerical simulations. At higher angles of attack, the URANS computations predict the flow separation onset at the round leading edge very well, although it is not geometrically fixed, Fig. 7e. Only a minor difference in the pressure level is visible at the ${x/c_{\text {r}}=0.5}$ section. At ${\alpha =20^\circ }$ and ${\beta \ne 0^\circ }$, the deviations become more obvious. At the windward side, the flow separation onset is slightly too far downstream in comparison with the experiments, see section ${x/c_{\text {r}}=0.4}$ in Fig. 7f. On the leeward side, the formation of the MLV is predicted as well, but the vortex position is too far inboard, see section ${x/c_{\text {r}}=0.4}$ in Fig. 7d.

Figure 9 illustrates the surface pressure distribution for the $50^{\circ }$ deflected flap at ${\alpha =20^\circ }$ for different angles of sideslip. At ${\beta =0^\circ }$, the surface pressure distribution indicates a remarkable influence of the deflected O/F on the flow upstream of the flap. The separation onset in the midboard section is located further downstream in comparison to the zero-control configuration, see ${x/c_{\text {r}}=0.5}$ in Figs. 7e, 9b. The pressure levels near the leading edge are increased in case of the zero-control configuration due to the flow separation. The suction peak for the configuration with $50^{\circ }$ deflected O/F indicates attached flow in this section. This effect is only observed at ${\alpha \ge 17^\circ }$ and ${\beta \ge 0^\circ }$, where flow separation with flow reversal occurs, see Fig. 9b, c. The formation of the MLV is hardly affected by an O/F deflection, see Fig. 9a.

Fig. 9

Experimental and numerical surface pressure distributions of the configuration with $50^{\circ }$ deflected O/F at $\alpha =20^\circ$ and $\beta =\left[ -10^\circ , 0^\circ , 10^\circ \right]$

Figure 9b indicates the ability of the CFD computations to account for the upstream influence of the deflected O/F on the flow. The flow separation onset in the midboard region is moved downstream as it is seen in the experiments. Overall, the surface pressure distributions of the CFD computations show a satisfying agreement with the experimental data. This justifies the application of the SA-neg turbulence model with respect to the present flow structures evolving at the investigated configuration.

5.2 Longitudinal aerodynamic coefficients

Figure 10 depicts the longitudinal aerodynamic coefficients for the zero and $50^{\circ }$ deflected O/F at ${\beta =0^\circ }$, obtained from experimental and numerical data. This enables the evaluation of the longitudinal aerodynamic coefficients predicted by the numerical simulations for the zero-control configuration and for the configuration with deflected flap.

Fig. 10

Comparison of longitudinal aerodynamic coefficients obtained from experimental and numerical data versus $\alpha$ for $\zeta =0^\circ$ and $\zeta =50^\circ$ at $\beta =0^\circ$

The drag polar exhibits $C_{D0}$ at zero angle of attack for both configurations due to the symmetric profile, see Fig. 10a. In the experiments, a ${C_{D0}(\zeta =0^\circ )=0.0066}$ for the zero-control configuration and a ${C_{D0}(\zeta =50^\circ )=0.0196}$ for the configuration with deflected O/F is observed. The numerical simulations predict a higher $C_{D0}$, whereas for the zero-control configuration the difference between the numerical and experimental data in the zero drag reads ${\Delta C_{D0}(\zeta =0^\circ )=0.0025}$ and for ${\zeta =50^\circ }$ it reads ${\Delta C_{D0}(\zeta =50^\circ )=0.0063}$, see Fig. 10b. The significantly higher deviation in the $C_{D0}$ for the configuration with deflected O/F might evolve from an overprediction of the effect of the deflected O/F on the drag by the numerical simulation. With increasing angle of attack, the disagreement becomes smaller and for ${\alpha \ge 16^\circ }$ both data curves of the ${\zeta =50^\circ }$ configuration show a good agreement. The zero-control configuration exhibits a satisfying agreement between both data sources for the whole polar.

The lift coefficient for both data sources and configurations is described in Fig. 10c. For both data sources and configurations, the expected zero lift of ${C_{\text {L0}}=0}$ and zero angle of attack of ${\alpha _0 =0^\circ }$ is observed. The curves for the two configurations indicate a minor influence of the O/F deflection on the lift. The following statements are consequently valid for configurations with and without O/F deflection. The lift shows an almost linear characteristic with respect to $\alpha$ in the considered range of angles of attack. Both the experimental and numerical curve almost coincide over the whole angle of attack polar. For ${\zeta =0^\circ }$ and ${\zeta =50^\circ }$, the largest deviation reads ${\Delta C_{\text {L,max}}(\alpha =14^\circ ,\zeta =0^\circ )=0.014}$ and ${\Delta C_{\text {L,max}}(\alpha =16^\circ ,\zeta =50^\circ )=0.027}$, respectively.

The pitching moment coefficient is illustrated in Fig. 10d. Both data sources and configurations predict the same characteristics with a ${C_{my0}=0}$. With increasing angle of attack, a minor influence of the O/F deflection becomes visible resulting in slightly decreased absolute values of the pitching moment coefficient. However, the characteristic of the pitching moment does not change with the O/F deflection. Minor deviations between the data sources are observed. The numerical simulations predict slightly lower values than the W/T data with a maximum difference of ${\Delta C_{my,{\text {max}}}(\alpha =18^\circ ,\zeta =0^\circ )=- \ 0.0026}$ for the zero-control configuration and a ${\Delta C_{my,{\text {max}}}(\alpha =8^\circ ,\zeta =50^\circ )=- \ 0.0029}$ for the configuration with $50^{\circ }$ O/F deflection. Overall, the numerical and W/T results show a good agreement for the longitudinal coefficients for both configurations. Especially, the pitching moment coefficient, which is very sensitive and strongly depends on the correct flow separation onset at the round wing leading edge, is predicted well by the numerical simulations.

Figure 11 illustrates the influence of the deflected O/F on the longitudinal aerodynamic coefficients in detail by means of the experimental data at ${\beta =0^\circ }$. For this purpose, the increment of the coefficients provoked by the deflected flap is shown. The increment for an arbitrary aerodynamic coefficient $C_i$ is defined as ${\Delta C_i = C_i (\zeta )- C_i (\zeta =0^\circ )}$. Figure 11a shows the influence of the deflected O/F on the drag coefficient. The drag coefficient increment $\Delta C_D$ slightly increases with increasing $\zeta$. The maximum drag increment is observed at ${\alpha =11^\circ }$, ${\zeta =50^\circ }$ and reads ${\Delta C_D=0.0164}$. For this freestream condition, the sideforce increment in relation to the drag increment reads ${\bigl |\frac{\Delta C_Y}{\Delta C_D}\bigl |=0.96}$. Consequently, the O/F creates almost as much additional sideforce as drag, which contributes to the yawing moment. The lift coefficient $C_{\text {L}}$ indicates a slight influence of the O/F in two areas. For ${4^\circ \le \alpha \le 16^\circ }$ and ${\zeta>40^\circ }$, the lift coefficient is slightly decreased, see Fig. 11b. The outboard wing section, where the O/F is located, contributes to the overall lift for the zero-control configuration as well as for small O/F deflections. When the flap deflection is too large, less lift is created in this area, which slightly reduces the overall lift. The maximum reduction is observed at ${\alpha =10^\circ }$ and ${\zeta =50^\circ }$. The reduction of the lift by the O/F is small and reads ${\Delta C_{\text {L}}=- \ 0.0126}$. Furthermore, the lift is slightly increased for ${\alpha>14^\circ }$ and ${\zeta>20^\circ }$. This is related to the effect of the deflected O/F on the flow separation onset in the wing midboard section as described in Sect. 5.1. The O/F deflection moves the flow separation onset more downstream and thus more lift is created in this area in comparison with the zero-control configuration, which is expressed in a slightly increased overall lift coefficient. The maximum lift increment is observed at ${\alpha =20^\circ }$ and ${\zeta =40^\circ }$ and reads ${\Delta C_{\text {L}}=0.0129}$. The same effects influencing the lift coefficient also have an influence on the pitching moment, because the affected area is downstream of the moment reference point. Consequently, the reduced lift for high O/F deflections results in a nose-up pitching moment and the increased lift for high angles of attack results in a nose-down pitching moment, see Fig. 11c. The maximum positive pitching moment coefficient increment of ${\Delta C_{my}=0.0033}$ is observed at ${\alpha =18^\circ }$ and ${\zeta =50^\circ }$. The maximum negative pitching moment increment occurs at ${\alpha =20^\circ }$ and ${\zeta =30^\circ }$ and reads ${\Delta C_{my}=-\ 0.0022}$. In summary, the most significant impact of the deflected O/F is observed for the drag coefficient. The effect on the lift and pitching moment coefficient is minor. They consistently represent the effects already observed in the surface pressure distribution in Sect. 5.1.

Fig. 11

Experimental aerodynamic coefficient increments associated with the longitudinal motion versus $\alpha$ and $\zeta$ at $\beta =0^\circ$

5.3 Directional controllability and stability

The main purpose of the O/F of this flying wing configuration is to ensure the directional controllability and stability by creating a yawing moment. In the context of this investigations with only the right O/F deflected, a positive yawing moment is required. In the following, first the yaw-control effectiveness within the considered angle of attack and sideslip range is discussed.

Figure 12 illustrates the yawing moment coefficient obtained in the W/T tests versus the angle of attack and the O/F deflection angle at ${\beta =\left[ - \ 10^\circ , 0^\circ , 10^\circ \right] }$. At zero angle of sideslip, the deflection of the O/F entails a positive yawing moment at almost every considered freestream condition, see Fig. 12b. The small negative values in the yawing moment coefficient at ${\zeta =0^\circ }$ and high angles of attack should ideally be zero. They are possibly a result of small asymmetries in the wind tunnel setup. Due to the high sensitivity of the lateral coefficients, even smallest deviations from an ideal setup are visible in the coefficients. Overall, the yawing moment coefficient consistently increases with increasing O/F deflection up to an angle of attack of ${\alpha \approx 15^\circ }$. After a maximum achievable yawing moment for every O/F deflection at ${\alpha =10^\circ }$, the yaw-control effectiveness $C_{{mz}}$ decreases with increasing $\alpha$. At ${\alpha \ge 17^\circ }$, no additional yawing moment can be achieved for ${\zeta \ge 20^\circ }$. However, a small positive yawing moment coefficient can still be observed in this area. The maximum yawing moment coefficient at zero angle of sideslip ${C_{mz,{\text {max}}} (\beta =0^\circ )=0.025}$ is observed at ${\alpha =10^\circ }$ and ${\zeta =50^\circ }$. The reduction in the yaw-control effectiveness at high angles of attack is associated with the large-scale flow separation in the wing outboard section. The upper side of the deflected O/F is completely within the area of separated flow. Consequently, it contributes less to the yawing moment.

Fig. 12

Yawing moment coefficient from W/T tests versus $\alpha$ and $\zeta$ at $\beta =\left[ -10^\circ , 0^\circ , 10^\circ \right]$

For an angle of sideslip of ${\beta =10^\circ }$, a positive yawing moment is observed at every considered O/F deflection and freestream condition, see Fig. 12c. This indicates, that the O/F is able to ensure directional stability of the configuration for the considered angle of sideslip of ${\beta = 10^\circ }$. Furthermore, the cutback at high angles of attack is much less pronounced and higher yawing moment coefficients are possible at high angles of attack. The yawing moment coefficient again features a local maximum at ${\alpha =10^\circ }$ and ${\zeta =50^\circ }$, which is $16\,\%$ higher than at ${\beta =0^\circ }$ and reads ${C_{mz,{\text {max}}} (\beta =10^\circ )=0.029}$. This is also related to an effect increasing the yawing moment at positive angle of sideslip without deflected O/F. For ${\alpha \ge 10^\circ }$ the yawing moment coefficient slightly increases for ${\zeta =0^\circ }$. This is associated with the asymmetric flow conditions at the wing. On the windward wing side, the flow separation onset moves further upstream and the area of separated flow increases. In this area, the surface pressure at the leading edge is significantly increased. On the leeward wing side, the MLV evolves, inducing a high negative surface pressure at the leading edge. The components of the leading edge normal to the yz/xz-plane contribute to the yawing moment coefficient. Consequently, the increased surface pressure on the windward wing side and the reduced surface pressure at the leeward wing side result in a positive yawing moment for positive $\beta$. Therefore, the configuration features a small natural directional stability for ${\alpha \ge 10^\circ }$.

At negative angle of sideslip, the same effect is represented by negative yawing moment coefficients at ${\zeta =0^\circ }$, see Fig. 12a. Furthermore, areas of negative yawing moment coefficient can be observed at high angles of attack and ${\zeta \le 50^\circ }$. Except for the negative coefficients, the overall characteristic is comparable to the ${\beta =0^\circ }$ case. For almost every freestream condition and O/F deflection, an increase in the yawing moment coefficient is visible. Furthermore, there is also a significant cutback in the yawing moment coefficient for ${\alpha \ge 15^\circ }$, which results in negative values. At an angle of attack of $18^{\circ }$, the O/F cannot create a positive yawing moment for any deflection. Consequently, the angle of sideslip cannot be further increased, but a yawing moment turning the nose back into the freestream direction is present. The local maximum yawing coefficient reads ${C_{mz,{\text {max}}}\left( \beta =-10^\circ \right) =0.025}$. It is associated with ${\alpha =10^\circ }$, ${\zeta =50^\circ }$ and is similar to the maximum at ${\beta =0^\circ }$.

Figure 13 shows the yawing moment coefficient obtained from W/T and CFD versus the angle of attack at ${\beta =0^\circ }$ for ${\zeta =\left[ 30^\circ , 50^\circ \right] }$. The $30^{\circ }$ deflected O/F exhibits a good agreement between both data sources over a wide range of angles of attack. For ${\alpha <15^\circ }$, the largest deviation is observed at ${\alpha =0^\circ }$ and reads ${\Delta C_{{mz}}\left( \zeta =30^\circ \right) =0.0030}$. The general characteristics, however, are met well by the CFD computations. The yawing moment coefficient increases up to $\alpha \approx 10^\circ$, decreases between ${11\le \alpha \le 16^\circ }$ and increases again for ${\alpha>16^\circ }$. The decrease of the yawing moment coefficient is, however, predicted much too less in comparison with the experimental data, which results in large absolute deviations for ${\alpha>15^\circ }$. The configuration with $50^{\circ }$ deflected O/F reveals similar characteristics. However, the absolute difference between both data sources is larger. At ${\alpha =0^\circ }$, the deviation reads ${\Delta C_{{mz}}\left( \zeta =50^\circ \right) =0.0043}$. Similar to the ${\zeta =30^\circ }$ configuration, the deviation in the yawing moment coefficient at zero angle of attack indicates a deficit of the applied turbulence model in predicting the flow around the O/F correctly. The O/F is the only possible source for the present yawing moment at this freestream condition. The overprediction of the O/F effectiveness is very distinct for ${\zeta =50^\circ }$ and results in an almost constant offset between both data sources up to ${\alpha \approx 15^\circ }$. Again, the URANS computations predict a too less pronounced decrease in $C_{{mz}}$ at high angles of attack, resulting in larger deviations for ${\alpha>16^\circ }$. The comparison of the yawing moment coefficient obtained from numerical and experimental data reveals some deficits of the applied turbulence model. The overall characteristics are represented by the numerical simulations, but the effect of the O/F is predicted too strong. At high angles of attack, the deviations increase and only the overall trend of the coefficients is predicted correctly by the URANS simulations. The reason for this deviation needs to be further investigated.

Fig. 13

Yawing moment coefficient $C_{{mz}}$ obtained from W/T tests and numerical simulations versus α for $\zeta =\left[ 30^\circ , 50^\circ \right]$ at $\beta =0^\circ$

5.4 Yaw-control efficiency

To discuss the yaw-control efficiency, the O/F efficiency factor is introduced. It is defined as the derivative ${\text {d}}C_{{mz}}/{\text {d}}\zeta$. The derivatives result from a linear interpolation around the discrete data points of the experimental data. With respect to the consideration of the right O/F, positive O/F efficiency factors are desired. The higher the value the better the efficiency.

Figure 14 depicts the O/F efficiency factor for ${\beta =\left[ -\ 10^\circ ,0^\circ ,10^\circ \right] }$ obtained in the W/T tests. At zero angle of sideslip, O/F efficiency factors of ${0.025<\frac{{\text {d}}C_{\text {{mz}}}}{{\text {d}}\zeta }<0.05}$ indicate a good efficiency for a wide range of considered freestream conditions and O/F deflections, see Fig. 14b. At ${\zeta \ge 40^\circ }$, a good efficiency is provided for almost all considered angles of attack. The maximum O/F efficiency factor reads ${\frac{{\text {d}}C_{\text {{mz}}}}{{\text {d}}\zeta }=0.047}$ and is observed at ${\alpha =16^\circ }$ and ${\zeta =50^\circ }$. However, the O/F efficiency factor also reveals strong non-linear characteristics with $\zeta$ and $\alpha$. Only a small efficiency is indicated for small flap deflections ${\zeta \le 10^\circ }$ with values smaller than 0.02. The efficiency than significantly increases with increasing O/F deflection. Furthermore, the efficiency drastically decreases at high angles of attack to almost zero at ${\alpha =20^\circ }$ and ${\zeta =30^\circ }$. At negative angle of sideslip, the overall characteristic is similar to the zero angle of sideslip condition, see Fig. 14a. However, the higher O/F efficiency factor for ${\zeta \ge 30^\circ }$ indicates a slightly better yaw-control efficiency. The characteristics and values for small O/F deflections and high angles of attack are similar. In contrast to that, at positive angle of sideslip an improvement of the efficiency can be observed at high angles of attack, see Fig. 14c. For an O/F deflection larger than $30^{\circ }$, the O/F efficiency factor is considerably higher in comparison to other angles of sideslip. For all considered angles of sideslip, the flap efficiency factor shows a strong non-linear characteristic with respect to $\zeta$ and $\alpha$. A reduced efficiency for small O/F deflections of ${\zeta \le 10^\circ }$ with values of ${{\text {d}}C_{\text {{mz}}}/{\text {d}}\zeta <0.02}$ is observed for a wide range of angles of attack.

Fig. 14

Yaw-control efficiency factor ${\text {d}}C_{\text {{mz}}}/{\text {d}}\zeta$ from W/T tests versus $\alpha$ and $\zeta$ at $\beta =\left[ -10^\circ , 0^\circ , 10^\circ \right]$

The small efficiency and strong non-linear characteristic at ${\zeta <30^\circ }$ is likely to be a result of the non-linear increase of the projected O/F area, see Table 2. Due to a small increase of the projected area normal to the freestream direction, the increase in the created yawing moment is also small. The strong reduction of the O/F efficiency factor at high angles of attack can be associated with the occurring flow separation in the wing tip area. With increasing angle of attack the flow separation onset moves more upstream. At a certain $\alpha -\zeta$ combination the upper side of the O/F is completely within the area of separated flow which decreases its efficiency. The dependency of the yaw-control efficiency on the angle of sideslip is moderate. The maximum achievable O/F efficiency factors are similar and the flow conditions of good efficiency are comparable. Major difference is observed at high angles of attack and positive angle of sideslip.

5.5 Cross-coupling effects

In Sect. 5.2 it is shown, that the deflection of the O/F does not exhibit considerable coupling effects with $C_{my}$. Considering the lateral coefficients, coupling effects between the O/F deflection and the rolling moment coefficient are of interest. Coupling effects are to be expected, since the lever arm between the O/F and the moment reference point is large. The coupling effect on the rolling moment coefficient is discussed by means of the rolling moment coefficient increment ${\Delta C_{mx}=C_{mx}(\zeta )-C_{mx}(\zeta =0^\circ )}$ initiated by the O/F deflection.

Figure 15 illustrates $\Delta C_{mx}$ from the W/T tests versus the angle of attack and O/F deflection angle at ${\beta =\left[ -10^\circ , 0^\circ , 10^\circ \right] }$. At ${\beta \ge 0^\circ }$, two major areas with different effects on the rolling moment can be identified, see Fig. 15b, c. For angles of attack up to ${\alpha \approx 15^\circ }$, a positive rolling moment is provoked by an O/F deflection. The rolling moment increment increases with $\zeta$. The maximum rolling moment increment at ${\beta =0^\circ }$ is observed for ${\alpha =10^\circ }$ and ${\zeta =50^\circ }$ and reads ${\Delta C_{mx}=0.0093}$. In relation with the corresponding yawing moment coefficient increment at this flight condition, the cross-coupling effect on the rolling moment can be quantified. The cross-coupling factor is defined as ${\frac{\Delta C_{mx}}{\Delta C_{{{mz}}}}}$ and reads 0.37. For ${\beta =10^\circ }$, the maximum is observed at the same angle of attack and O/F deflection and reads ${\Delta C_{mx}=0.012}$, which corresponds to a cross-coupling factor of ${\frac{\Delta C_{mx}}{\Delta C_{{{mz}}}}=0.43}$. This significant cross-coupling effect is related to the reduced lift on the right wing side in consequence of the deflected O/F. The wing outboard section with the deflected O/F does not create as much lift as if the O/F is not deflected. The reduced lift in the wing outboard region on the wing side with deflected O/F in combination with the large lever arm to the moment reference point results in a high rolling moment increment. With the deflected O/F on the right wing side, this results in a positive induced rolling moment indicating a right wing down motion. Considering high angles of attack of ${\alpha \ge 15^\circ }$, a negative rolling moment coefficient increment is observed. The effect strengthens with $\alpha$ and $\zeta$. The maximum negative rolling moment coefficient increment of ${\Delta C_{mx}=-\ 0.0072}$ at ${\beta =0^\circ }$ is present at ${\alpha =20^\circ }$ and maximum $\zeta$. At this point, the cross-coupling factor reads ${\frac{\Delta C_{mx}}{\Delta C_{mz}}=-\ 1.3}$. Consequently, a higher absolute rolling moment than yawing moment results from an O/F deflection of ${\zeta =50^\circ }$ at this flight condition. For ${\beta =10^\circ }$, the maximum negative rolling moment coefficient increment ${\Delta C_{mx}=- \ 0.009}$ at ${\alpha =20^\circ }$ and ${\zeta =40^\circ }$ is even higher than at zero angle of sideslip. However, as the yawing moment coefficient increment is also higher, the corresponding cross-coupling factor of $- \ 0.98$ is slightly lower. This adverse effect in comparison to smaller angles of attack is a result of the upstream effect of the O/F, as it is described in Sect. 5.1. The O/F deflection leads to an increased lift on the right wing side due to the effect on the flow separation onset. The increased lift on the right wing side with deflected O/F results in a negative rolling moment indicating a right wing up motion. The absolute rolling moment increment is high, because the additional suction peaks in the area of attached flow are high and the lever arm to the moment reference point is large. Furthermore, the reduced yaw-control effectiveness in this area results in high cross-coupling factors of ${\bigl |\frac{\Delta C_{mx}}{\Delta C_{mz}}\bigl |>1}$. Figure 15a illustrates the rolling moment coefficient increment for ${\beta =- \ 10^\circ }$. Up to ${\alpha \approx 15^\circ }$, the characteristic is similar to those at other angles of sideslip. At high angles of attack, the negative $\Delta C_{mx}$ in consequence of the effect on the flow separation onset in the wing midboard section is not observed. In this area, the O/F deflection results in small positive rolling moment increments. This is an effect of the evolving MLV at the right wing side. As it is described in Sect. 5.1, the O/F deflection has almost no influence on the MLV formation. Consequently, the created lift in the wing midboard section is not affected by the O/F. At negative angles of sideslip and high angles of attack, the same effect as for the moderate angles of attack is present. Due to the deflected O/F, the created lift in the wing outboard section is decreased. Since the flow in the wing outboard section is separated at high angles of attack, the contribution of this section to the overall lift is small even for the zero-control configuration. Consequently, the reduction in lift due to the deflected flap and therefore the rolling moment increment is small.

Fig. 15

Rolling moment coefficient increment $\Delta C_{mx}$ from W/T tests versus $\alpha$ and $\zeta$ at $\beta =\left[ -10^\circ , 0^\circ , 10^\circ \right]$

Finally, the CFD results for the rolling moment coefficient are compared to the W/T data for ${\zeta =\left[ 30^\circ , 50^\circ \right] }$ at ${\beta =0^\circ }$, see Fig. 16. The URANS computations represent the general coupling effects very well. For ${\zeta =30^\circ }$, the URANS results show a good agreement with the W/T data over the complete angle of attack range. This indicates, that the applied turbulence model predicts the flow around the wing and the upstream effect of the deflected O/F well. The deviations slightly increase with $\zeta$. The cross-coupling effect is predicted less strong by the numerical simulations at ${\zeta =50^\circ }$. The positive yawing moment increment at moderate angles of attack as well as the negative yawing moment increment at high angles of attack are considerably alleviated. However, the overall characteristics are met by the URANS computations.

Fig. 16

Rolling moment coefficient $C_{mx}$ obtained from W/T tests and numerical simulations versus α for $\zeta =\left[ 30^\circ , 50^\circ \right]$ at $\beta =0^\circ$

5.6 Directional stability performance

To obtain satisfactory directional stability, a value of ${C_{mz\beta }>0.057}$ is recommended in Ref. [8] for conventional aircraft configurations and for flying wing configurations, which often feature a reduced directional stability. To ensure a sufficient directional stability for flying wing configurations with low directional stability, the O/F needs to provide a sufficient increase of $C_{mz\beta }$ by its deflection.

The directional stability of the configuration is assessed by means of the static directional stability parameter $C_{mz\beta }$ and the dynamic directional stability parameter $C_{mz\beta ,{\text {dyn}}}$ [18], which is defined as

$$\begin{aligned} C_{mz\beta ,{\text {dyn}}}=C_{mz\beta }\cdot \cos \alpha - \frac{I_z}{I_x}\cdot C_{mx\beta }\cdot \sin \alpha . \end{aligned}$$

(1)

The values for the directional stability parameter $C_{mz\beta }$ and $C_{mx\beta }$ are defined at zero angle of sideslip. The required ratio of the inertia moments is defined in accordance with the values of the SAGITTA flying wing configuration. Directional stability is obtained for positive values. Figure 17 illustrates the (dynamic) directional stability of the configuration at ${\beta =0^\circ }$. Positive values can be observed for both parameters throughout the angle of attack polar. The recommended static directional stability is, however, only observed for ${\alpha>15^\circ }$. For lower angles of attack, the static directional stability is reduced. For these angels of attack, the O/F shows a good effectiveness and can thus provide the additional required directional stability. The dynamic directional stability shows an even more stable characteristic. Due to a high $\frac{I_z}{I_x}$ ratio and negative $C_{mx\beta }$ values in the considered angle of attack regime, dynamic directional stability is obtained. For ${\alpha>20^\circ }$, however, the typical roll instability for a low-aspect ratio configuration with moderate to high leading-edge sweep is to be expected, which would then lead to significant dynamic directional instability.

Fig. 17

Static and dynamic directional stability parameter from W/T tests versus $\alpha$ at $\beta =0^\circ$ and $\zeta =0^\circ$

The NASA conducted comprehensive low-speed wind tunnel tests on the stability and control characteristics of low-aspect ratio flying wings with a leading-edge sweep of $50^{\circ }$ considering wing planforms of lambda and diamond type [9]. Among other flap configurations, they investigated outboard split flaps with its hinge line parallel to the trailing edge. The wing with an aspect ratio comparable to the configuration considered here (Wing 11, lambda wing, ${\varLambda =1.89}$) exhibits a yaw-control effectiveness $C_{mz}$ of approximately 0.015 for the $67^{\circ }$ deflected outboard split flap. The diamond wing of Ref. [9] (Wing 12, ${\varphi _{\text {TE}}=-\ 50^\circ }$, ${\varLambda =1.68}$) features a similar effectiveness as Wing 11 for the $67^{\circ }$ deflected outboard split flap. For both wings, a significant yaw-roll coupling can be observed, similar to the present investigations. However, the NASA investigations show minor non-linear characteristics of the outboard split flap with respect to $\alpha$ contrary to the present findings. In Ref. [12], the directional control of a low-aspect ratio flying wing by means of all moving wing tips has been investigated with a yaw-control effectiveness $C_{mz}$ of approximately 0.34 for the $60^{\circ }$ deflected control device. Taking the flap deflection angle into account, the O/F investigated here exhibits a comparable effectiveness $C_{mz}$ of 0.25 for ${\alpha \le 16^\circ }$.

Considering the directional controllability, an important requirement is the ability to perform crosswind landings. The requirement for crosswind landing capabilities can be derived from [5]. It defines the required yawing moment coefficient for a “crabbed” landing approach at crosswind as

$$\begin{aligned} C_{mz,{\text {req}}}=0.7\cdot \frac{U_{\text {cw}}}{U_{\text {td}}}\cdot \left( C_{mz\beta }+ C_{mx\beta }\cdot \frac{C_{mz\xi }}{C_{mx\xi }}\right) \end{aligned}$$

(2)

with $U_{\text {cw}}$ the crosswind velocity, $U_{\text {td}}$ the touchdown velocity and $C_{mz\xi },C_{mx\xi }$ the derivatives with respect to the roll control surface deflection. A 40% dynamic overswing of sideslip in response to the control device deflection is implied by the factor 0.7 [5]. The term $C_{mz\beta }$ represents the present yawing moment at sideslip due to the directional stability parameter. The term ${C_{mx\beta }\frac{C_{mz\xi }}{C_{mx\xi }}}$ represents the yawing moment in consequence of the required rolling maneuver to counteract the evolving rolling moment at sideslip. The combination of stability parameter and rolling maneuver creates a yawing moment, which must be counteracted by the O/F. The required efficiency values of the roll control device are available from former investigations on the midboard flap efficiency used for roll control [17]. For the estimation of the required yawing moment, the values of the parameters and derivatives at zero angle of sideslip and zero flap deflection are used and an angle of sidelip of $15^{\circ }$ is defined. Figure 18 depicts the required yawing moment for a crosswind landing resulting in an angle of sideslip ${\beta =\left[ 5^{\circ }; 10^{\circ }; 15^{\circ }\right] }$ and the maximum achievable yawing moment at zero angle of sideslip. At small angles of attack, the O/F creates a much higher yawing moment than required. With increasing angle of attack, however, the directional stability significantly increases and thus the required yawing moment. For ${\alpha>16^\circ }$, the O/F does not provide a yawing moment high enough for a crosswind landing case with ${\beta =15^\circ }$.

Fig. 18

Required yawing moment coefficient for crosswind landing with an angle of sidelip of $5^{\circ }$, $10^{\circ }$ and $15^{\circ }$ and achievable yawing moment coefficient from W/T tests at $\beta =0^\circ$ and $\zeta =50^\circ$

6 Conclusion

Experimental and numerical investigations on the yaw-control device of a low-aspect ratio flying wing configuration have been presented. A good yaw-control efficiency is obtained except for high angles of attack and small O/F deflections. The yawing moment coefficient confirms the ability to ensure the directional stability of the configuration by deflection of the O/F within the considered range of freestream conditions. The O/F efficiency factor indicates a strong non-linear characteristic of the flap with respect to the flap deflection and angle of attack. This can be related to the non-linear change in the projected O/F area with the flap deflection angle and the significant changes in the flow field over the angle of attack. The assessment of crosswind landing capabilities reveals satisfying capabilities for ${\alpha <16^\circ }$. At high angles of attack, the natural directional stability of the configuration increases and the O/F is not able to provide a yawing moment high enough for crosswind landings at ${\beta =15^\circ }$. The analysis of the cross-coupling effects reveals a strong coupling with the rolling moment coefficient. Positive as well as negative rolling moments are provoked depending on the freestream condition and flap deflection. Maximum cross-coupling factors of ${\bigl |\frac{\Delta C_{mx}}{\Delta C_{mz}}\bigl |>1}$ indicate a strong coupling, which is not favorable.

URANS simulation results are compared to the comprehensive experimental data set to examine the validity of the numerical data. The surface pressure coefficients show a satisfying agreement of the CFD results with the experimental data. The flow field around the wing is predicted well by the CFD simulations over the whole angle of attack polar. Occurring leading-edge vortices as well as flow separation and its onset at the round leading edge are met. Furthermore, the influence of the deflected outboard flap on the upstream flow is represented well by the URANS simulations. The O/F deflection influences the flow separation onset, which is represented by the CFD calculations. The good agreement between the experimental and numerical data is also observed in the lift, pitching and rolling moment coefficient. However, the yawing moment coefficient reveals considerable deviations between experiment and CFD, which increases with the flap deflection. The applied turbulence model seems not to be capable to predict especially the wake flow of the deflected flap with sufficient precision. The predicted characteristics of the yawing moment coefficient with respect to the angle of attack are, however, in satisfying agreement with the W/T data for a wide range of the polar. Overall, the numerical data show a satisfying agreement with the experimental data.

The discrepancy in the yawing moment coefficient between the numerical results and the experimental data needs to be analyzed in more detail. This is necessary to justify the utilization of the numerical results for a detailed investigation of the flow around the deflected outboard flap. Experimental investigations of the wake flow of the deflected O/F could give valuable data for a comparison with the numerical results.