Flap efficiency analysis for the SAGITTA diamond wing demonstrator configuration

Abstract

The efficiency of deflected midboard flaps is investigated on a diamond wing-shaped unmanned aerial vehicle, the SAGITTA demonstrator configuration. The Reynolds-Averaged Navier-Stokes equations are applied to compute numerical results for a variety of flight conditions with varying angle of attack, sideslip angle, and midboard flap deflection. Low-speed wind tunnel conditions are regarded to compare the results to existing experimental data. The focus is particularly laid on the analysis of the aerodynamic coefficients and derivatives in both the longitudinal and the lateral motion. The occurring flow phenomena are motivated and discussed by flow field illustrations that are available from the numerical computations. The results show at small to moderate angles of attack linear flap characteristics, since the overall flow field is dominated by attached flow. With increasing angle of attack and additional sideslip angle, however, the leading-edge vortex originating from the inboard sharp leading edge and the wing tip separation region affect the midboard flap efficiency. Non-linear coupling effects become obvious, which particularly affect the roll and pitch control effectiveness.

1 Introduction

Well-designed control devices are generally a key factor in aircraft design to efficiently fly and control the air vehicle. Especially for the design and development of unmanned aerial vehicles (UAVs), this aspect becomes particularly important, since they often consist of highly-swept low aspect ratio wings. Typically, delta, lambda, or diamond wing planforms are considered, for which the lever arms, that are available for the generation of control moments, are typically small. Following, the maneuverability and agility of UAVs are, amongst others, mainly determined by a sophisticated control device design. In addition, suchlike UAV configurations are commonly considered as tail-less flying wings, since radar cross-section requirements often influence the planform design [1]. This drastically reduces the directional stability, and the yaw control has to be provided by the remaining controls [2, 3]. With increasing angle of attack, the flow field of this type of wing configurations is often dominated by separated flow [1]. This can lead to non-linear aerodynamic characteristics and to a decreased efficiency of the controls. Coupling effects between different control devices may arise additionally [4, 5], which further affect the control efficiency. In general, this leads to a decreased maneuverability and agility of the flying wing configuration. Thus, the overall design of the control devices is of great interest in UAV design, since the control efficiency is essential for the performance and the application range of the aircraft.

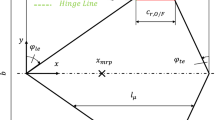
In this context, the Institute of Aerodynamics and Fluid Mechanics at the Technische Universität München (TUM-AER) investigates the aerodynamic characteristics of the SAGITTA diamond wing demonstrator configuration, Fig. 1. The analyses are associated with a joint research program of Airbus Defence and Space, which follows an “Open Innovation” approach [6]. It is aimed toward the development of a tail-less flying wing demonstrator that is designed and built by the joint partners of German universities and research institutes. The diamond wing-shaped UAV demonstrator configuration features a root chord length of $c_r = 3\,{\rm m}$ and a full wing span of $b = 3.088 \,{\rm m}$, resulting in a maximum take-off weight of $m_{MTOW} = 144\,{\rm kg}$. The intended velocity of the demonstrator vehicle ranges up to $V_{max} \approx 80\,{\rm m/s}$. Three main control devices are defined at the wing trailing edge for pitch, roll, and yaw control, Fig. 1. For the first flight test campaign of the SAGITTA demonstrator configuration being scheduled for 2015, a vertical twin-fin is added to the configuration, accounting thus for increased lateral directional stability.

Fig. 1

SAGITTA diamond wing demonstrator configuration with main control devices and the twin-fin

2 Recent research activities

The investigations on the SAGITTA diamond wing demonstrator configuration are performed both experimentally and numerically at TUM-AER. A 1:3-scaled wind tunnel (W/T) model featuring a root chord length of $c_r = 1.0\,{\rm m}$ has been built. Figure 2 and Table 1 depict the relevant planform parameters. The devices for pitch, roll, and yaw control are integrated into the W/T model and can be adjusted continuously by electrically powered model servos. Based on a NACA 64A012 airfoil with 12 % relative thickness, the configuration is equipped with varying leading-edge contours along the semi wing span. The inner part of the wing ($y/s \le 0.2$) features a sharp leading-edge contour, while the outer wing leading-edge contour is round ($r_{N}/c = 0.994\,\%$). Between $0.2 \le y/s \le 0.3$, the leading-edge contour is blended from sharp to round.

Fig. 2

Wing planform of the SAGITTA diamond wing demonstrator W/T configuration, top view xy plane

Table 1 Wing planform parameters of the SAGITTA diamond wing demonstrator W/T configuration

The aerodynamic forces and moments are measured by an external balance, as the W/T model is rear sting mounted in the test section, Fig. 3. Extensive experimental investigations have been undertaken so far, from which an aerodynamic data module (ADM) has been derived [7]. Due to the size of the W/T model and the open test section, W/T corrections have not been applied to the raw data. In addition to the analysis of the zero-control wing configuration with and without the twin-fin, numerous variations of different control device deflections and configurations with deployed landing gears or a camera gimbal have been measured. The ADM, which thus provides a broad experimental data base, has ever since been widely used within the design process of the SAGITTA demonstrator configuration [8, 9].

Fig. 3

SAGITTA diamond wing demonstrator W/T configuration within the test section of TUM-AER

In parallel, numerical analyses have been undertaken. For the zero-control wing configuration with and without the twin-fin, steady-state Reynolds-Averaged Navier–Stokes (RANS) computations have been conducted. Thereby, the occurring flow phenomena and the aerodynamic coefficients have been studied. The outcome of this analysis has already been published [7], showing the overall aerodynamic characteristics of the SAGITTA diamond wing demonstrator configuration. Moreover, selected cases with deflected inboard and midboard (I/B and M/B, respectively) flaps have been considered by computational fluid mechanics (CFD).

Here, the focus is set to a flap efficiency study of the M/B control devices. For the analysis, the first flight test configuration is regarded with the twin-fin attached (W/T size). The M/B flaps are deflected for all considered flight conditions asymmetrically on both wing half surfaces. The zero-control wing configuration serves as the baseline case. The presented results comprise numerical and experimental investigations, which are compared in detail to each other. The current CFD computations are conducted on refined grids. Thereby, the flow field phenomena are captured in more detail. In addition to the longitudinal motion, the lateral motion is regarded as well, for which flow conditions with sideslip angles are taken into consideration.

3 Numerical approach

3.1 Grid generation

The hybrid grids of the presented numerical computations are generated with the grid generation software CENTAUR¹. Based on an unstructured surface grid consisting of triangles and quadrilaterals, prismatic and hexahedral elements are used close to the wing surface in the boundary-layer region. Elsewhere in the computational domain, tetrahedral and pyramidal elements are used. The farfield boundaries are located in each direction 20 semi wing span lengths away from the diamond wing, as the computational domain is limited by a sphere. Since the present analysis requires the grid generation of several asymmetric M/B flap deflections on both wing half surfaces, the applied meshing philosophy is as follows: Within CENTAUR, the right wing half is regarded exclusively. Moreover, the M/B flap region is limited by an interface box, which is meshed in a modular way. At first, the basic grid of the right wing half including one M/B flap deflection and the tetrahedral farfield is completely built, Fig. 4a. Next, the M/B flap geometry is altered, and the new grid is only built within the interface box. The existing grid around the box serves as reference for the grid node links, Fig. 4b. Following, the basic grid including the main wing surface and the tetrahedral farfield is only built once, while the box including the M/B flap region is meshed for every M/B flap deflection and the zero-control wing configuration. The full wing grid required for the numerical computations is finally obtained by adequate tools for mirroring and adding the appropriate grid components, which are available due to the modular grid generation process, Fig. 4c. Following this approach, a symmetric grid except for the modular boxes can be ensured, which is of great importance for the numerical computations, in particular in the longitudinal motion.

Fig. 4

Modular grid approach including interface boxes for the deflected M/B flaps

In line with former numerical investigations of related low aspect ratio, vortex-dominated wing configurations [1, 5, 10], the surface grid is considerably refined close to the wing leading edge, Fig. 5a, b. To accurately compute the boundary-layer flow in the proximity of the wing surface, the prismatic grid contains in total 38 prism layers, Fig. 5b, c. The first cell height is chosen to $h_{1} \approx 0.004\,{\rm mm}$. Thereby, the viscous sublayer is resolved and the target criterion of ${y^{+}}_{max} = 1$ is respected. The first 30 prism layers feature a stretching factor in normal direction of $g = 1.235$, while the final eight prism layers exhibit a constant cell height. Then, the tetrahedral grid extends up to the farfield boundaries. Close to the diamond wing, the tetrahedral grid is additionally refined, Fig. 5a. Thereby, both the vortex structures originating from the leading edge and the tip vortices of wing tip and M/B flaps dominating the wake flow field can appropriately be captured. Table 2 summarizes the final grid sizes of the seven analyzed configurations. As it can be noticed, the absolute number of grid nodes differs only slightly between the configurations with deflected M/B flaps. Compared to the zero-control wing configuration, however, considerably more grid nodes are required.

Fig. 5

Hybrid grid of the SAGITTA diamond wing demonstrator W/T configuration with deflected M/B flaps and the twin-fin

Table 2 Grid size of the considered configurations

3.2 Flow solver

The numerical investigations performed for this analysis are computed with the TAU-Code, a CFD solver developed at the DLR (German Aerospace Center) Institute of Aerodynamics and Flow Technology [11]. It solves the three-dimensional compressible steady or unsteady (U)RANS equations on hybrid grids. Moreover, it is developed with respect to parallel efficiency on high-performance computers. The DLR TAU-Code uses a finite volume scheme and is based on a dual grid approach [12]. This implies the generation of a secondary grid during the preprocessing, which is computed according to the cell vertex grid metric from the initial (primary) grid provided by the grid generation process. The preprocessor furthermore generates the additional grids that are required for multigrid computations. Within the solver, several upwind and central schemes can be applied for finite volume discretization. The temporal discretization (local/dual/global time stepping) is dependent on steady-state or time-accurate computations. Both explicit and implicit schemes are available, which are used in combination with the multigrid technique for convergence acceleration. If turbulent flows are considered, a variety of one- and two-equation models such as Spalart-Allmaras (SA) or $k-\omega$ turbulence models as well as different kinds of Reynolds stress models (RSM) can be applied [11].

3.3 Test conditions and numerical set-up

In agreement with the conducted experimental analyses, the CFD computations have been performed at low-speed W/T conditions. A free stream Mach number of $Ma = 0.12$ and a Reynolds number of $Re = 1.7\,\times\,10^6$, based on the mean aerodynamic chord of $l_{\mu } = 0.667\, {\rm m}$, have been applied. Moreover, the CFD computations have been run fully turbulent. The W/T experiments, in contrast, did not consider any flow tripping. The moment reference point for pitching and yawing moment calculation has been set to the geometrical neutral point as introduced in Fig. 2. It results in a chordwise position of $x_{MRP}=0.418\ m$ aft of the diamond wing nose. The angle of attack varies within the CFD computations between $\alpha = 0^{\circ }$ and $\alpha = 16^{\circ }$. The maximum regarded angle of sideslip of the present analysis is $\beta = 8^{\circ }$.

Generally, numerous analyses have already shown the validity of the DLR TAU-Code. In particular, this also holds for vortex-dominated aircraft configurations with both sharp and rounded leading edges. Grid sensitivity studies and turbulence model analyses of CFD computations with the DLR TAU-Code have extensively been published [1, 4, 5, 7, 10, 13–15]. For this reason, the gained experiences of those investigations have been utilized for the numerical set-up of the present configurations. Based on a cell vertex grid metric, a second-order central scheme introduced by Jameson has been applied for spatial discretization [16]. The required artificial viscosity has been added by a matrix-valued coefficient (matrix dissipation scheme), for which the central difference scheme becomes closer to upwind biased methods [17]. For the discretization in time, an implicit Backward-Euler scheme with LUSGS algorithm has been used [18]. The steady-state RANS computations have been performed with local time stepping. Per single run, 40,000 iterations have been applied each. In order to accelerate the convergence, a 3w-multigrid cycle has further been used [19]. Turbulence has been modeled within the present computations by the one-equation model of Spalart-Allmaras [20], but in a revised version (SA-Neg). The modifications particularly allow negative values of the transport turbulence quantities and lead to a more efficient solution of the equation without changing the aerodynamic solution [21]. This turbulence model has been chosen, since former numerical results showed good correlations with experimental results for this type of wing configuration. In particular, the prediction of the pitching moment characteristics at higher angles of attack was superior to the prediction with other applied two-equation turbulence models [1, 14, 15].

The computations have been run in parallel mode at the GCS Supercomputer SuperMUC at the Leibniz Supercomputing Centre (LRZ)². For the zero-control wing configuration, 544 cores have been applied, while 624 cores have been used for the configurations with deflected M/B flaps.

4 Results and discussion

This section comprises the results of the numerical investigations carried out in the context of this analysis. Furthermore, the results are compared to existing W/T data of the SAGITTA demonstrator configuration. At the beginning, the overall computed y ⁺ contour levels are shown by example for selected flight conditions, Fig. 6. Thereby, the initial prism layer thickness chosen for the grid generation process is reviewed. At higher angles of attack, an increase of the y ⁺ values is observed in the surface regions influenced by occurring leading-edge vortices, but the values do not exceed $y^{+}=1$, Fig. 6a. For the configuration with deflected M/B flaps, the overall y ⁺ contour levels are slightly affected in the proximity of the M/B control device, Fig. 6b. However, the values remain in the same range as discussed for the zero-control wing configuration, even at higher angles of attack with present sideslip angle. Following, the y ⁺ criterion of ${y^{+}}_\mathrm{max} = 1$, which is relevant for the Spalart-Allmaras turbulence model, is mostly fulfilled by the applied grids.

Fig. 6

y⁺ contour levels of selected flight conditions

4.1 Zero-control wing configuration

4.1.1 Longitudinal motion

The aerodynamic characteristics of the SAGITTA diamond wing demonstrator configuration are considered, incipient for the zero-control wing configuration without M/B flap deflection. At first, the analysis is presented for the longitudinal motion. In order to describe the overall flow phenomena occurring at the diamond wing configuration, Figs. 7 and 8 are shown. The resulting longitudinal aerodynamic coefficients are then discussed in Fig. 9, which contains both the experimental (W/T) and the numerical (CFD) datasets.

Fig. 7

Surface streamlines of the zero-control wing configuration at $\beta = 0^{\circ }$

Fig. 8

Field streamlines and axial velocity contour slices of the zero-control wing configuration at $\beta = 0^{\circ }$

Fig. 9

Longitudinal aerodynamic coefficients of the zero-control wing configuration at $\beta = 0^{\circ }$

At low angles of attack up to $\alpha = 8^{\circ }$, the overall flow field of the SAGITTA diamond wing demonstrator configuration is mostly dominated by attached flow, Fig. 7a. In the inboard wing section, a leading-edge vortex is provoked by the sharp leading-edge contour, which is, however, relatively weak in intensity. At the diamond wing tip, the flow starts to separate and forms a recirculation area. With increasing angle of attack, the inboard leading-edge vortex grows in size and intensity, Figs. 7b and 8a. The axial fluid transport within the vortex core is not of jet type, but it is slightly retarded, Fig. 8b. The outboard separation area increases considerably at higher angles of attack and a massive region of irregular separated flow occurs, Fig. 7b. Due to the rounded leading-edge contour and the thick airfoil, this separation is not of vortex type with positive axial fluid transport. Instead, significant flow reversal is observed, Fig. 8b. Following, it corresponds to a bubble-type leading-edge separation. In the midboard section of the diamond wing configuration, the rounded leading-edge contour is still passed by attached flow. Inboard of the primary attachment line of the inboard leading-edge vortex, attached flow is present as well, Fig. 7b.

Overall, the occurring flow phenomena are relevant for the discussion of the aerodynamic coefficients. For the present diamond wing configuration, they are dominated by the regions of attached and irregular separated flow originating from the rounded leading-edge contour. The inboard leading-edge vortex emerging from the sharp leading-edge contour, in contrast, does not play the major role for the integral longitudinal aerodynamic coefficients. At first, the Lilienthal polar is regarded, Fig. 9a. Certain deviations between the two data sources W/T and CFD are noted. Compared to the numerical computations, the W/T experiments result in considerably lower drag coefficient values $C_{D}$. In particular, this is seen for the zero drag coefficient $C_{D,0}$. Since the flow in the W/T experiments has not been tripped close to the wing leading edge and the CFD computations have been run fully turbulent, it is supposed that laminar flow was also present on the diamond wing surface during the experimental analyses. Following, reduced drag coefficient values are noted in the W/T experiments, compared to the CFD simulations.

With increasing angle of attack, also the resulting lift coefficient values deviate between the experimental and the numerical results. Compared to the CFD simulations, the lift coefficient values are predicted lower in the W/T experiments. With the assumption of, at least, partly-laminar boundary-layer characteristics within the conducted W/T experiments, the differences of the lift coefficient values can be motivated. In the CFD computations employing fully-turbulent boundary-layer characteristics, the flow in the outboard wing sections is less threatened by separation than it is for laminar boundary-layer flow that presumably occurred in the W/T experiments. Following, the wing tip separation region is predicted smaller in the CFD computations, compared to the experimental analysis. This consequently leads to an increased midboard region of attached flow in the numerical analyses, which finally results to increased lift coefficient values of the CFD runs in comparison to the W/T data.

Next, the pitching moment characteristics are presented, Fig. 9b. In relation to the chosen moment reference point, the configuration is noted to be stable. The differences of the pitching moment coefficient values between the W/T experiments and the CFD computations are mainly related to the deviations of the lift coefficients as discussed above. With increasing angle of attack, the differences become slightly larger. For the present type of low aspect ratio wing configuration, however, deviations in the pitching moment characteristics are typical, as the prediction is known to be very sensitive both in CFD and in W/T investigations [1, 5].

4.1.2 Lateral motion

Next, the lateral motion of the zero-control wing configuration is regarded. For the analysis, a sideslip angle of $\beta = 8^{\circ }$ is considered. Due to a positive sideslip angle, the effective leading-edge sweep angle is generally decreased on the windward and increased on the leeward side of the diamond wing configuration. With increasing angle of attack, this leads to significant differences in the occurring flow phenomena on both wing half surfaces, which is discussed below. Thereby, the lateral aerodynamic coefficients are particularly influenced.

Figures 10, 11, and 12 depict the surface and the near-wall flow field of the zero-control wing configuration with present sideslip angle. At $\alpha = 8^{\circ }$, the streamlines are almost aligned by the sideslip angle, since the intensity of the inboard leading-edge vortex is relatively weak and the wing tip separation just begins to form, Fig. 10a. Moreover, the flow separates at the suction side of the windward fin due to the sideslip angle. In Fig. 11a, the occurring trailing-edge separation is clearly noted. Moreover, a leading-edge vortex forms at the leading edge of the windward fin. The flow incipient to the leeward fin is more aligned in chordwise direction, which results in a significantly smaller recirculation area in the trailing-edge region and a smooth flow around the fin leading edge. With increasing angle of attack, the streamline pattern at the diamond wing configuration changes significantly, Fig. 10b. Compared to the longitudinal motion as shown in Fig. 7b, asymmetric flow phenomena are clearly noted. The inboard leading-edge vortex becomes weaker in intensity on the windward and stronger on the leeward side of the diamond wing, Figs. 10b, 12a. Moreover, the separation region in the outboard wing section becomes larger on the windward side. On the leeward side, in contrast, the region of irregular flow vanishes with the present angle of sideslip, and an additional outboard leading-edge vortex emerges, Figs. 10b, 12a. This vortex, originating from a rounded leading-edge contour, is of retarded type as well, but does not show any flow reversal along the vortex core axis, Fig. 12b. Due to the mentioned flow phenomena, the incoming flow to the twin-fin is in addition more aligned in chordwise direction. Thereby, the recirculation area at the windward fin is decreased, Fig. 11b. The flow around the leeward fin, in contrast, does not change significantly in comparison to the lower angles of attack.

Fig. 10

Surface streamlines of the zero-control wing configuration at $\beta =8^{\circ }$

Fig. 11

Surface streamlines of the zero-control wing configuration at $\beta = 8^{\circ }$, detail view of the twin-fin section

Fig. 12

Field streamlines and axial velocity contour slices of the zero-control wing configuration at $\beta = 8^{\circ }$

Fig. 13

Lateral aerodynamic coefficients of the zero-control wing configuration versus angle of attack $\alpha$ at $\beta = 8^{\circ }$

Fig. 14

Aerodynamic coefficients versus angle of attack $\alpha$ and M/B flap deflection $\xi$ at $\beta = 0^{\circ }$

Fig. 15

Surface streamlines of the configuration with deflected M/B flaps ($\xi = 30^{\circ }$) at $\beta = 0^{\circ }$

The resulting lateral aerodynamic coefficients are presented in Fig. 13. For the sideslip angle of $\beta = 8^{\circ }$, the coefficients $C_{Y}$, $C_{mx},$ and $C_{mz}$ are shown versus the angle of attack. On the left-hand side, the comparison of the CFD computations and the experimental results is displayed each. Based on the numerical analyses, the graphs on the right-hand side additionally depict the portions of the single components of the diamond wing configuration. The effects observed in the lateral aerodynamic coefficients can thereby better be attributed to the occurring flow phenomena.

For the side force coefficient $C_{Y}$, small deviations are observed between both data sources, Fig. 13a. The trend of the curves, however, is matched very well. With increasing angle of attack, the negative side force is decreased. At $\alpha = 16^{\circ }$, almost no negative side force is left. This effect originates from the suction side of the diamond wing surface. Due to the asymmetric flow separation regions as introduced above, a positive side force is generated, Fig. 13d. The negative side force produced by the twin-fin, in contrast, is relatively constant with increasing angle of attack, although the trailing-edge separation region at the windward fin has been noticed to vary with angle of attack, Fig. 11.

Next, the rolling moment coefficient $C_{mx}$ is regarded. Up to the angle of attack of $\alpha = 12^{\circ }$, the $C_{mx}$ values decrease almost linearly and result in negative values, Fig. 13b. Following, this leads to a counter-clockwise rotation of the diamond wing with right wing tip up. In comparison to the W/T experiments, the values computed by CFD are less negative and show a certain deviation. On both the suction and the pressure side of the diamond wing, the rolling moment coefficients constantly decrease with increasing angle of attack, Fig. 13e. This results from the different lifts of the attached flow regions on both wing half surfaces, which occur due to the resulting effective wing sweep angles. On the windward side, the lift is increased, and on the leeward side, the lift is decreased. The twin-fin adds a negative $C_{mx}$ component as well, which is, however, almost constant over the angle of attack. Between $\alpha = 12^{\circ },$ and $\alpha = 16^{\circ }$, the gradient of the resulting $C_{mx}$ values changes sign, and the induced rolling moment is decreased again in absolute values, Fig. 13b. In relation to the W/T data, the change of the $C_{mx}$ values computed by CFD is much more distinctive. This effect originates from the changed flow topology at the suction side of the diamond wing configuration as introduced above. In Fig. 13e, the contribution of the suction side flow is clearly noticed. Due to the increased region of irregular separated flow on the windward side and the additional outboard leading-edge vortex on the leeward side, Fig. 10b, the differences in the resulting lift coefficients are attenuated. Now, the overall lift is decreased on the windward side and increased on the leeward side. Following, this diminishes the generated counter-clockwise rolling moment.

The yawing moment coefficient $C_{mz}$ varies only slightly with increasing angle of attack and results in positive values, Fig. 13c. This leads to a clockwise rotation around the yaw axis, and the nose is aligned with the freestream velocity vector. Following, a stable behavior of the diamond wing configuration is observed. Both the W/T data and the CFD computations result in very similar values of $C_{mz}$. As it can be observed from Fig. 13f, the generated yawing moment almost exclusively originates from the twin-fin that is added for the first flight campaign to provide increased directional stability. The yawing moment produced by the diamond wing configuration itself is, in contrast, very small. This shows, in turn, the problem with the directional stability of the diamond wing configuration when the twin-fin is not attached due to radar cross-section requirements. Then, the stability of the vehicle around the yaw axis must mostly be ensured by the use the control devices.

4.2 Configuration with deflected M/B flaps

4.2.1 Longitudinal motion

In the following, the SAGITTA diamond wing demonstrator configuration is considered with deflected M/B flaps. Figure 14 depicts the complete set of the aerodynamic coefficients that are shown in dependence of the angle of attack $\alpha$ and the M/B flap deflection angle $\xi$. The contour plots exclusively present the results of the CFD computations without sideslip angle, $\beta = 0^{\circ }$. A positive flap deflection angle $\xi$ results a in asymmetric configuration with right M/B flap down and left M/B flap up. The longitudinal aerodynamic coefficients $C_{D}$, $C_{L},$ and $C_{my}$, Fig. 14a–c, show the expected and desired characteristics. Due to the increased pressure drag at the M/B control devices, which is associated with the surface streamline pattern indicated in Fig. 15, the drag coefficient $C_{D}$ is found to be increased for the configurations with deflected M/B flaps. With respect to the M/B flap deflection angle, a complete symmetrical contour plot is observed. Due to the longitudinal motion, this also holds for the other two longitudinal aerodynamic coefficients, the lift coefficient $C_{L}$ and the pitching moment coefficient $C_{my}$. Moreover, they vary only slightly with varying M/B flap deflection angle, even at higher angles of attack. No relevant non-linearities are observed.

In Fig. 14d–f, the aerodynamic coefficients associated with the lateral motion are presented. Based on the longitudinal flight condition without sideslip angle, the plots indicate the available roll control effectiveness and the associated coupling effects to initiate a roll maneuver. For positive flap deflection angles $\xi$ (right M/B flap down, left M/B flap up), negative rolling moment coefficients are observed over the whole angle of attack regime and vice versa, Fig. 14e. In comparison to the $C_{mx}$ values generated by the zero-control wing configuration with present sideslip angle (Fig. 13b), the maximum achievable rolling moment coefficients are now considerably larger. The roll control effectiveness does not change significantly with increasing angle of attack, as the wing tip separation region does not influence the flow at the M/B flaps up to $\alpha = 16^{\circ }$, and vice versa. At this angle of attack, the flow affecting the M/B flaps is dominated by the inboard leading-edge vortex, which passes the wing surface in chordwise direction, Fig. 15b. The other two aerodynamic coefficients, namely $C_{Y}$ and $C_{mz}$, indicate the coupling effects associated with the deflected M/B flaps. Some roll-yaw coupling is observed, Fig. 14f. Compared to the maximum rolling moment coefficient achievable ($C_{mx, \mathrm Max} \approx \pm 0.075$), the maximum yawing moment coefficients originating from the M/B flap deflection result in $C_{mz, \mathrm Max} \approx \pm 0.01$, which roughly corresponds to a factor of 1 / 7. With increasing angle of attack, weak non-linearities are noticed. This trend also holds for the side force coefficient $C_{Y}$, Fig. 14d. The gradient with respect to $\xi$ increases at higher angles of attack, also leading to increased maximum side force coefficients.

4.2.2 Lateral motion

Next, the set of aerodynamic coefficients is presented for the lateral motion with a sideslip angle of $\beta = 8^{\circ }$, Fig. 16. In comparison to the latter case without sideslip angle, the CFD computations now result in more varying contour plots, which is caused by the different flow characteristics on both wing half surfaces. In order to discuss the relevant flow phenomena, Fig. 17 is introduced, which depicts the flow field for selected flight conditions with deflected M/B flaps and present sideslip angle. At first, the aerodynamic coefficients associated with the longitudinal motion are regarded, Fig. 16a–c. With increasing angle of attack, the drag and the lift coefficient $C_{D}$ and $C_{L}$ are slightly increased for negative M/B flap deflection angles compared to positive $\xi$ values. This is mainly caused by the different trajectories of the leeward inboard and outboard leading-edge vortices and the size of the windward separation region, Fig. 17, which occur due to positive and negative M/B flap deflections. For the pitching moment coefficient $C_{my}$, the dependency on the M/B flap deflection angle is much more distinctive. Compared to the longitudinal motion with $\beta = 0^{\circ }$, the non-linearities increase considerably at higher angles of attack, Fig. 16c. Especially for $\alpha = 16^{\circ }$ and $\xi = \pm 30^{\circ }$, the pitching moment coefficient is significantly changed.

The lateral aerodynamic coefficients $C_{Y}$, $C_{mx},$ and $C_{mz}$ are influenced more considerably by the sideslip angle of $\beta = 8^{\circ }$, Fig. 16d–f. With increasing angle of attack, the roll control effectiveness slightly decreases for negative M/B flap deflection angles, Fig. 16e, since the wing tip separation region on the windward side dominates the flow field on the right M/B flap to a greater extent. At the angle of attack of $\alpha = 16^{\circ }$, flow reversal occurs on the entire M/B flap of the right wing half, Fig. 18b. For positive $\xi$ values, in contrast, the roll control effectiveness increases, as can be noticed from Fig. 16e. The wing tip separation region on the windward side is in this case considerably smaller, and the flow field of the right M/B flap is not as much influenced by the flow reversal, Fig. 18a. The variations of the rolling moment coefficient with increasing angle of attack, however, do not result in distinct non-linearities of the $C_{mx}$ values, as the size of the wing tip separation region changes continuously with varying free stream parameters $\alpha$ and $\beta$ and the M/B flap deflection angle.

As it can be expected, the side force and the yawing moment coefficient $C_{Y}$ and $C_{mz}$ are affected as well. The absolute levels of the contour plots change considerably, which is mainly caused by the effects of the twin-fin as discussed for the zero-control wing configuration. If one compares the different levels (Figs. 14d, f, and 16d, f, respectively), the variations are in the same magnitude as the absolute values presented for the zero-control wing configuration in Fig. 13a, c. The additional coupling effects originating from the M/B flaps are discussed in the following paragraph.

Fig. 16

Aerodynamic coefficients versus angle of attack $\alpha$ and M/B flap deflection $\xi$ at $\beta = 8^{\circ }$

Fig. 17

Field streamlines of the configuration with deflected M/B flaps ($\xi = \pm 30^{\circ }$) at $\beta = 8^{\circ }$

Fig. 18

Surface streamlines of the configuration with deflected M/B flaps ($\xi = \pm 30^{\circ }$) at $\alpha = 16^{\circ }$ and $\beta = 8^{\circ }$

Fig. 19

Aerodynamic derivatives versus angle of attack $\alpha$ and M/B flap deflection $\xi$ at $\beta = 0^{\circ }$ and $\beta = 8^{\circ }$

Fig. 20

M/B flap efficiency factor $\frac{dC_{mx}}{d\xi }$ for selected flight conditions

4.2.3 M/B flap efficiency

Finally, the M/B flap efficiency is analyzed, Fig. 19. The derivatives of the lateral aerodynamic coefficients are built with respect to the M/B flap deflection angle $\xi$ by linear interpolation around the discrete data points. The resulting values of the CFD computations are shown for both sideslip angles discussed in the previous sections ($\beta = 0^{\circ }$ and $\beta = 8^{\circ }$). The most important derivative in this analysis, namely $\frac{dC_{mx}}{d\xi }$, is defined as the M/B flap efficiency factor. For the longitudinal motion, it results in a contour plane with only slightly varying values over the angle of attack and M/B flap deflection angle regime, Fig. 19b. This observation confirms the results of Sect. 4.2.1, in which the available roll control effectiveness with increasing angle of attack is discussed. At $\alpha = 16^{\circ }$, the derivative slightly decreases in its absolute value for deflected M/B flaps, which reduces the M/B flap efficiency. This effect is intensified in the lateral motion with present sideslip angle, Fig. 19e. The non-linearities in the contour plane of the M/B flap efficiency factor increase, especially at $\alpha = 12^{\circ }$ and $\alpha = 16^{\circ }$. For a more detailed discussion, Fig. 20 is additionally introduced. Both the CFD and the W/T datasets of the M/B flap efficiency factor are presented for selected flight conditions. Overall, the agreement between the results of both data sources is satisfactory, as the derivatives are predicted similar to each other. Compared to the W/T experiments, the M/B flap efficiency factor of the CFD computations is generally slightly larger. At zero angle of attack, Fig. 20a, b, the derivative is constant for all M/B flap deflections and does not change with sideslip angle either. The absolute values of the M/B flap efficiency factor are close to each other. At $\alpha = 16^{\circ }$, in contrast, the non-linearities already discussed become more obvious, Fig. 20c, d. At the angle of attack of $\alpha = 16^{\circ }$ and without sideslip angle, the M/B flap efficiency factor decreases symmetrically in its absolute value with deflected M/B flaps. For the flight condition at $\alpha = 16^{\circ }$ and $\beta = 8^{\circ }$, the maximum value of the M/B flap efficiency factor is observed at $\xi = 10^{\circ }$. Moreover, it is larger in its absolute value compared to the maximum value of the longitudinal motion.

The side force and the yawing moment derivative $\frac{dC_{Y}}{d\xi }$ and $\frac{dC_{mz}}{d\xi }$ show, even in the longitudinal motion, weak non-linearities with respect to the angle of attack, Fig. 19a, c. The overall values, however, are considerably smaller than the values of the M/B flap efficiency factor. With present sideslip angle, additional non-linearities with respect to the M/B flap deflection angle become obvious, Fig. 19d, f. The coupling effects arise due to the deflected M/B flaps and act in addition to those introduced by the swept diamond wing planform as discussed in Sect. 4.1.2.

5 Conclusion and outlook

Numerical investigations on the SAGITTA diamond wing demonstrator configuration have been presented and discussed in the present article. In order to examine the validity of the steady-state RANS computations, the numerical results have been compared to existing W/T datasets. It turns out that the overall agreement of the CFD and W/T results is satisfactory. Certain deviations are observed, which can, however, be attributed to different conditions of the boundary-layer characteristics. The CFD computations have been run fully turbulent, whereas the flow in the experimental investigations has not been tripped, leading to free transition conditions at the W/T model.

In addition to the analysis of the zero-control wing configuration, the configuration with deflected M/B flaps has been considered. Numerous CFD computations have been conducted, including variations of the angle of attack, the sideslip angle, and the M/B flap deflection angle. In particular, the flow phenomena occurring on the diamond wing configuration, the associated aerodynamic coefficients and the M/B flap efficiency have been analyzed and evaluated. For the longitudinal motion, the roll control effectiveness due to deflected M/B flaps to initiate a roll maneuver is mostly maintained with increasing angle of attack. The M/B flaps show an almost constant flap efficiency factor $\frac{dC_{mx}}{d\xi }$. At $\alpha = 16^{\circ }$, it is slightly reduced with increasing M/B flap deflection. The coupling effects with respect to the side force and the yawing moment coefficient are small. For the lateral motion with present sideslip angle, however, the non-linearities in the aerodynamic coefficients increase with increasing angle of attack, which is caused by different flow field characteristics on both wing half surfaces. On the windward side, the inboard leading-edge vortex extenuates, while the wing tip separation region with irregular flow grows in size. On the leeward side, in contrast, the inboard leading-edge vortex is strengthened and an outboard leading-edge vortex emerges due to the increased effective wing sweep. This influences the entire set of aerodynamic coefficients and their derivatives. For positive sideslip angles, the M/B flap efficiency factor $\frac{dC_{mx}}{d\xi }$ is increased in its absolute value for positive flap deflections and decreased for negative values.

Supplementary to the existing W/T datasets, which comprise only force and moment data, the numerical investigations provide a second database with additional information about the flow field characteristics of the SAGITTA diamond wing demonstrator configuration. The CFD results allow for a more detailed analysis of the occurring flow phenomena, which is essential for the assessment and discussion of the overall aerodynamic characteristics of the vehicle. Thereby, valuable add-on information is provided for the aerodynamic data module (ADM), which originates from the experimental analyses. In order to enlarge the numerical datasets even further, additional CFD computations for the other control devices are of high interest. Especially, the flow phenomena associated with the deflected split flaps at the wing tips are to be investigated, as the corresponding W/T experiments have shown non-linear effects with increasing angle of attack, sideslip angle, and flap deflection angle.