Spatiotemporal Exposure Prediction with Penalized Regression

Abstract

Exposure to ambient air pollution is a global health burden, and assessing its relationships to health effects requires predicting concentrations of ambient pollution over time and space. We propose a spatiotemporal penalized regression model that provides high predictive accuracy and greater computation speed than competing approaches. This model uses overfitting and time-smoothing penalties to provide accurate predictions when there are large amounts of temporal missingness in the data. When compared to spatial-only and spatiotemporal universal kriging models in simulations, our model performs similarly under most conditions and can outperform the others when temporal missingness in the data is high. As the number of spatial locations in a data set increases, the computation time of our penalized regression model is more scalable than either of the compared methods. We demonstrate our model using total particulate matter mass ($\hbox {PM}_{2.5}$ and $\hbox {PM}_{{10}}$) and using sulfate and silicon component concentrations. For total mass, our model has lower cross-validated RMSE than the spatial-only universal kriging method, but not the spatiotemporal version. For the component concentrations, which are less frequently observed, our model outperforms both of the other approaches, showing 15% and 13% improvements over the spatiotemporal universal kriging method for sulfate and silicon. The computational speed of our model also allows for the use of nonparametric bootstrap for measurement error correction, a valuable tool in two-stage health effects models. Supplementary materials accompanying this paper appear online.

1 Introduction

Long- and short-term exposures to total particulate matter (PM) are causally related to adverse respiratory and cardiovascular health outcomes (U.S. Environmental Protection Agency 2019), and PM contributes to 4.7% of disability-adjusted life years (DALYs) in all ages (95% uncertainty interval 3.8–5.5) (Murray et al. 2020). PM is categorized by size, typically into ranges 10 $\mu$m or 2.5 $\mu$m and smaller, denoted as $\hbox {PM}_{{10}}$ and $\hbox {PM}_{2.5}$, respectively. PM is itself a mixture of many different components, such as nitrates, sulfates, organic matter, metals, and soil dust. The health effects of each component can vary, with sulfate ($\hbox {SO}^{2-}_4$) identified as one that is associated with respiratory and cardiovascular health effects (U.S. Environmental Protection Agency 2019).

Epidemiological studies investigating relationships between air pollution and adverse health outcomes rely on the prediction of ambient PM concentrations for subjects across space and/or time. PM is subject to widespread regulatory monitoring in many countries, and these measurements can be used to develop prediction models. In the USA, regulatory monitors are often placed preferentially in urban centers or near known sources and vary in both method and frequency of measurements. PM and its components, which are measured at a subset of monitors, are subject to seasonal trends that can lead to large and highly variable measurements in some regions of the USA, making accurate predictions of ambient concentrations challenging. Other characteristics that can make predicting concentrations difficult include: differences in instrument tolerances or protocols, extreme events such as wildfires or dust storms, and the overall size of the data set. Thus, predicting a spatiotemporal exposure surface requires efficient use of both spatial and temporal information and can benefit from computationally efficient methods. The structure of monitoring data for specific components is similar to total PM, although components are often measured with more sparsity in space and time.

There are a variety of spatial or spatiotemporal models that may be used to predict ambient pollutant concentrations. These include land-use regression (Beelen et al. 2013; Hoek et al. 2008), universal kriging (Sampson et al. 2013; Xu et al. 2019), penalized regression (Paciorek et al. 2009; Bergen and Szpiro 2015; Keet et al. 2018), Gaussian processes (GP) (Datta et al. 2016; Pati et al. 2011), Gaussian Markov random fields with stochastic partial differential equations (INLA-SPDE) (Cameletti et al. 2013), quantile methods (Reich et al. 2011), spectral approaches (Reich et al. 2014), convolutional neural networks (Di et al. 2016), and models using deterministic atmospheric chemistry simulation output (Berrocal et al. 2010, 2012; Wang et al. 2016) and satellite measurements (Young et al. 2016; Berrocal et al. 2020). Different modeling approaches can also be combined into ensemble models (Di et al. 2020, 2019).

In a review of spatiotemporal exposure modeling approaches, Berrocal et al. (2020) compared the performance of common methods using daily $\hbox {PM}_{2.5}$ measurements across the USA. They found that universal kriging (UK), when fit separately to each day of data, outperformed all other tested models, including neural networks, random forests, and inverse distance weighting. The density of $\hbox {PM}_{2.5}$ monitoring is sufficient that a large number of observations are available each day, allowing the empirical best linear unbiased predictor from a kriging model to perform well (Schabenberger and Gotway 2004). However, fitting UK separately on each day of measurements ignores temporal information, which provides an opportunity for improvement. A spatiotemporal model developed by Lindström et al. (2014) extends universal kriging by combining a smooth temporal trend with spatially varying coefficients. This more flexible and complex model is implemented in the SpatioTemporal package in R.

One weakness of more complicated models is poor scaling in computation time. For both UK and the SpatioTemporal (ST) model, the computational burden lies in an iterative optimization technique to estimate covariance parameters (e.g., sill or range). High computation time can prohibit the use of bootstrap-based predictive variance estimates or measurement error corrections. These bootstrap approaches can capture uncertainty from monitoring site selection in addition to the uncertainty from parameter estimation that is found in prediction variances (Szpiro and Paciorek 2013; Bergen et al. 2016; Keller and Peng 2019). In this paper, we propose a penalized regression model that penalizes overfitting and smooths over predictions at adjacent time points. The proposed model is computationally fast and thereby feasible for bootstrapping while also providing accurate predictions over time and space.

Our motivation for fitting a spatiotemporal surface comes from ambient air pollution exposures, so we approach model description and performance with respect to this application, but the method could be applied to other contexts. In Sect. 2, we introduce our model and its methods of fitting. In Sect. 3, we evaluate the method in a set of simulations under a variety of conditions and compare against the predictive accuracy of UK and ST. In Sect. 4, we apply the method to daily measurements of total $\hbox {PM}_{2.5}$, total $\hbox {PM}_{{10}}$, sulfate, and silicon concentrations from 2017, and in Sect. 5, we provide a discussion.

2 Model

We propose a penalized regression model where, in addition to the typical overfitting penalty, there is a penalty that smooths over adjacent time points. By smoothing temporally, our method can take advantage of data from the previous and following days where spatial-only methods cannot. Furthermore, unlike the SpatioTemporal model, this penalization approach does not require the assumption of a specific smooth time trend or temporal covariance function. With our approach, we aim to match or improve on the predictive accuracy of other common methods while being computationally faster.

2.1 Penalized Regression Model

The objective function for our model is:

$$\begin{aligned}&\underset{\varvec{\beta }_{t} \in \mathbb {R}^{p} \text { for } 1 \le t \le T}{{\text {minimize}}} \; \sum _{i=1}^{n} \sum _{t=1}^{T} I_{it}\left( x_{i t}-\varvec{r}_{i t}^{\top } \varvec{\beta }_{t}\right) ^{2}+ \sum _{t=1}^{T} g_1(\lambda _1, \varvec{\beta }_t) \nonumber \\&\qquad +\lambda _{2} \sum _{i=1}^{n} \sum _{t=2}^{T} g_2 (\varvec{r}_{i t}^{\top } \varvec{\beta }_{t}, \; \varvec{r}_{i(t-1)}^{\top } \varvec{\beta }_{t-1}). \end{aligned}$$

(1)

The first term in (1) is quadratic loss and uses the indicator value $I_{it}$ to only include time points (t) and locations (i) where $x_{it}$ exists, e.g., where an ambient air pollutant concentration was measured. There are n total unique sites (locations) and T total dates (time points) where we could have observed $x_{it}$. The vector $\varvec{r}_{it}$ contains p spatiotemporal covariates (Sect. 2.2) for date t and site i, including an intercept, while $\varvec{\beta }_t$ is a p-vector of model coefficients for each date. We center and scale the covariates in $\textbf{r}_{it}$ by time point. The second term, $g_1$, discourages overfitting, and may be an $\hbox {L}_2$, $\hbox {L}_1$, or Elastic Net penalty. We use an $\hbox {L}_2$ penalty here, i.e., $g_1(\lambda _1, \varvec{\beta }_t) = \varvec{\beta }_t^\top \varvec{\Gamma }_1 \varvec{\beta }_t$, where $\mathbf {\Gamma }_1$ is a $p \times p$ diagonal matrix comprised of only the values $\lambda _1$ and 0. This matrix allows penalization of all or specific model predictors using the value $\lambda _1$ and always excludes the intercept from penalization. See Appendix in Supplementary Material for specific construction.

The third term in (1) is $g_2(\varvec{r}_{i t}^{\top } \varvec{\beta }_{t}, \; \varvec{r}_{i(t-1)}^{\top } \varvec{\beta }_{t-1}) = (\varvec{r}_{i t}^{\top } \varvec{\beta }_{t} - \varvec{r}_{i(t-1)}^{\top } \varvec{\beta }_{t-1})^2$. This term smooths over predictions that are adjacent in time by penalizing their differences and makes our model similar to trend fitting or fused lasso (Petersen and Witten 2019). Every prediction is smoothed to its immediate temporal neighbors, even if the observation at that time and place is missing. When $\lambda _2 > 0$, our model must predict using information across consecutive time points, but without the complication of spatiotemporal interaction and increased parameterization.

To make a spatiotemporal exposure surface, we must be able to predict exposure levels at any location and on any day in the spatiotemporal domain. The vector $\widehat{\varvec{\beta }} = (\varvec{\widehat{\beta }}_1^\top , \widehat{\varvec{\beta }}_2^\top , \ldots , \widehat{\varvec{\beta }}_T^\top )^\top$ that minimizes the objective function (1) includes p model coefficients for every date in the temporal domain. We can then predict an exposure level at any date and at any location for which we have the same covariate information used to fit the model, and can aggregate the resulting predictions to any desired spatial unit.

2.2 Spatial and Temporal Covariates

All spatial information for the model is provided through a set of spatial predictors included in $\textbf{r}_{it}$. For the sake of flexibility and simplicity, we use thin plate regression splines (TPRS) (Wood 2003). By fitting TPRS to site locations, we have a set of predictors that can vary in quantity through specification of degrees of freedom, i.e., the number of basis functions produced, and do not require manual tuning of knot placement. TPRS are also scaleable to a large number of site locations and provide covariate values at any location we want to predict. With this predictive flexibility comes the cost of the extra parameterization and computation time of adding a possibly large set of predictors to the model. We can also provide spatiotemporal covariates to the model. For our analysis of ambient pollutant concentrations in Sect. 4, we use just atmospheric chemical model output and meteorological data, but other variables such as land-use measures could be included if desired.

2.3 Parameter Estimation

We rewrite the objective function (1) in matrix notation for simplicity:

$$\begin{aligned} {\text {*}}{min}_{\varvec{\beta }} \; \left[ (\varvec{x}-\varvec{R}_\textrm{obs} \varvec{\beta })^{\top }(\varvec{x}-\varvec{R}_\textrm{obs} \varvec{\beta })+ \varvec{\beta }^{\top } \varvec{\Lambda }_{1} \varvec{\beta }+\lambda _{2} \varvec{\beta }^{\top } \varvec{R}^{\top } \varvec{D}^{\top } \varvec{D} \varvec{R} \varvec{\beta }\right] . \end{aligned}$$

(2)

The first sum in Eq. (2) is standard least squares loss which we write as the inner product of the difference in predicted and observed exposure vectors. To do this, we combine the covariate vectors (${\textbf {r}}_{it}$) for every observed time point at a site i in a row-wise manner to create a block-diagonal matrix. The n resulting block-diagonal matrices are stacked to form the matrix ${\textbf {R}}_\textrm{obs}$ (see Appendix in Supplementary Material). Then the vector $\varvec{R}_{obs}\varvec{\beta }$ is the set of fitted values. The second sum in (2) is an $\hbox {L}_2$ penalty on the full coefficient vector $\varvec{\beta }$. We create a set of T $\varvec{\Gamma }_1$ matrices (as in Equation (1)) and stack them to form the block-diagonal matrix $\varvec{\Lambda }_1$.

To allow the temporal smoothing of predictions at unobserved date and site combinations, a “full” $\varvec{R}$ matrix can be made by including covariate values for all site and date combinations, instead of for just those that were observed. The third sum in (2) is then written as the inner product of the vector $\textit{\textbf{D R}} \varvec{\beta }$, where $\varvec{D}$ is a diagonal block matrix and each of its n blocks is a first-order difference matrix. Every row in a block of the $\varvec{D}$ matrix contains just zeroes and the pair of values -1 or 1 where the vector $\varvec{R} \varvec{\beta }$ contains two predictions “adjacent” in time. The specific arrangements of all objects listed here are provided in Appendix in Supplementary Material.

When using an $\hbox {L}_2$ penalty for the overfitting term in the objective from Eq. (2), a closed-form solution for $\varvec{\beta }$ exists. Since the matrix $\varvec{R}_{obs}^{\top } \varvec{R}_{obs} + \varvec{\Lambda }_1 + \lambda _2 \varvec{R}^\top \varvec{D}^\top \varvec{DR}$ is positive definite for sufficiently large $\lambda _1$ and $\lambda _2$, we can find its inverse to produce:

$$\begin{aligned} \hat{\varvec{\beta }} = \left( \varvec{R}_{obs}^{\top } \varvec{R}_{obs} + \varvec{\Lambda }_{1}+\lambda _{2} \varvec{R}^{\top } \varvec{D}^{\top } \varvec{D} \varvec{R} \right) ^{-1} \varvec{R}_{obs}^{\top } \varvec{x}. \end{aligned}$$

(3)

The closed-form solution is fast to compute when taking advantage of the sparseness of the matrices $\varvec{R}$, $\varvec{R}_{obs}$, and $\varvec{D}$. If instead of the $\hbox {L}_2$ penalty, we use a non-convex overfitting penalty, or if we were to add further penalty terms, the optimization problem may no longer have a closed-form solution. A general optimization strategy, such as alternating direction method of multipliers (ADMM) (Boyd et al. 2010) is then required, which increases computational cost.

2.4 Selection of Penalty Values

We select the penalty parameters $\lambda _1$ and $\lambda _2$ using tenfold cross-validation (CV), which provides an estimate of out-of-sample root mean square error (RMSE). When cross-validating to select $\lambda _1$ and $\lambda _2$, we can use a coarse grid, e.g., every combination of 5 values for each penalty a factor of 10$^2$ apart. If a basin in the cross-validated RMSE values is identified, we can resume the search on a finer grid, e.g., combinations of values a factor of 10 apart, and repeat until we converge upon an approximately optimal fit. Using all combinations of values for the two penalties is comprehensive but slow. The alternative is to select $\lambda _1$ first, by setting $\lambda _2$ = 0 and choosing the $\lambda _1$ value that provides the lowest cross-validated RMSE. Then we repeat the process for values of $\lambda _2$ while setting $\lambda _1$ to the previously selected value. This sequential method of selecting the two penalties sacrifices some predictive accuracy if the chosen values differ from what is selected by jointly searching over every combination of values, but it requires considerably fewer model fits. In Sect. 4, we find that the two methods select the same set of penalty values when modeling ambient $\hbox {PM}_{2.5}$ concentrations.

3 Simulation

3.1 Setup

For a variety of simulated data conditions, we compare our method to universal kriging and the SpatioTemporal model. Since the motivating application for our method is PM and its components, we create data sets with some characteristics matching the concentrations modeled in Sect. 4. Specifically, the simulated data have periodic (every three or six days) measurement by some proportion of “monitoring sites” and are correlated with a spatiotemporal observed covariate.

We simulate exposure data spatially over a $[0,1] \times [0,1]$ square using a $64 \times 64$ grid of points and temporally over a set of 60 time points. The model for simulated mean exposures at any grid points $\varvec{s}$ and time point t is

$$\begin{aligned} \varvec{\mu }(\varvec{s}, t) = \varvec{\mu }_0(\varvec{s}, t) + \varvec{Z}_1(\varvec{s}, t) + \varvec{Z}_2(\varvec{s}, t), \end{aligned}$$

(4)

where $\varvec{\mu }_0(\varvec{s}, t)$ is a baseline spatiotemporal surface that is considered an observed covariate, and is unchanged for every simulated sample. All three spatiotemporal surfaces $\varvec{\mu }_0(\varvec{s}, t)$, $\varvec{Z}_1(\varvec{s}, t)$, and $\varvec{Z}_2(\varvec{s}, t)$ are Gaussian processes generated with a Gneiting-style non-separable spatiotemporal covariance function (Gneiting 2002). We use the R package RandomFields to simulate the processes using the specific covariance structure

$$\begin{aligned} C(h, u)=\frac{1}{(\psi (u)+1)} \; \; \phi \left( \frac{h}{(\psi (u)+1)^{1 / 2}}\right) , \end{aligned}$$

(5)

for spatial distance h and change in time u (Schlather et al. 2015). We use an exponential covariance function for $\phi ()$, with a range and sill both equal to 1 (i.e., $\phi (w) = e^{-w}$). For $\psi ()$, we use fractional Brownian motion, a generalized random walk that depends on a Hurst index (H). Setting $1/2< \text {H} < 1$ produces walks with positive correlation between increments, while for $0< \text {H} < 1/2$ increments are negatively correlated and the trend will alternate more often in shorter time spans. We generate $\varvec{\mu }_0(\varvec{s}, t)$ using H = 0.25, allowing for some day-to-day fluctuation, and fix H = 0.95 for $\varvec{Z}_1(\varvec{s}, t)$, resulting in a more consistent long-term trend. The Hurst index for $\varvec{Z}_2(\varvec{s}, t)$ we vary across simulations to be $H=0.5$ (standard Brownian motion with independent increments) or $H=0.05$ (high daily fluctuation).

From the 4096 grid points, we randomly select 500 training and 1000 testing locations as “monitors” and assign them simulated mean values for each of the 60 time points. To represent measurement error in the training set, we add the error term $\varvec{\epsilon }_t \sim N(0, \varvec{I} \sigma ^2)$ to each set of “monitor locations” for each time point. Thus, the training data follow the model $\varvec{Y}(\varvec{s}, t) = \varvec{\mu }(\varvec{s}, t) + \varvec{\epsilon }_t$. To evaluate predictive accuracy, we compare each model’s predictions for the testing data with the “true” simulated mean values $\varvec{\mu }(\varvec{s}, t)$ at the testing data time locations.

We simulate while adjusting three settings: the error standard deviation ($\sigma$ = 0.5 or 1.5), the temporal relation of $\varvec{Z}_2(\varvec{s}, t)$ ($H=0.5$ or 0.05), and the amount of temporal missingness in the training data. As previously mentioned, some AQS monitors record values every third or every sixth day. These monitors generally follow synchronized schedules, so that each monitor observed every third day will record a measurements on the same schedule, leaving periods when only monitors on a daily schedule are observed. We then control the daily missingness in our training data by the proportion of monitoring locations that are observed daily, every third, or every sixth day, each matching the schedule of others in its scheme. For the sake of comparison, we perform another simulation study using the same proportions of sites by observation frequency, but stagger the observation schedules so that on any given day there may be sites that record daily, every third day, and every sixth day. In this alternative set of simulations, we repeat all settings adjustments as in the original, so that the only difference is that the non-daily schedules of monitoring sites are evenly distributed across their possible starting dates. We report the results of this secondary simulation study in Figure S1 of Supplementary Material.

Under each distinct set of data conditions, we take 100 different seeded samples of training and testing data. The testing data are predicted from the training data using our model from Equation (1), UK, and ST. Each model uses the spatiotemporal covariate $\varvec{\mu }_0(\varvec{s}, t)$, unchanged from sample to sample, as a predictor. To fit our penalized regression model, the number of TPRS basis functions used as additional spatial covariates is selected via tenfold cross-validation from the possible values 5, 10, 20, 50, 100, or 175. The penalities $\lambda _1$ and $\lambda _2$ are also chosen via tenfold CV from the sets of possible values 0.1, 1, 10, 50, 100, 200, 300, 400, 500, and 0.001, 0.01, 0.1, 1, 10, 50, 100, respectively. Here we select $\lambda _1$ first before selecting $\lambda _2$, as mentioned in Sect. 2.4. We use UK per Berrocal et al. (2020), with a median set of exponential covariance parameter values from maximum likelihood fits at each time point. The SpatioTemporal model we fit with a single basis function and an exponential covariance structure with nugget for both the $\beta$-fields and the residual process $\nu$ (Lindström et al. 2014).

Fig. 1

Boxplots of RMSE values from each model on 100 replicate samples for each simulation scenario. In order, the boxplots correspond to universal kriging (UK), our penalized regression model without its temporal smoothing penalty ($\lambda _2=0$), our model with the penalty (PR), and the SpatioTemporal (ST) model. Note that H is the Hurst index for $Z_2(s, t)$, which results in a more variable temporal trend as H approaches zero, and that $\sigma$ is the standard deviation of non-spatial error added to the training data. The selected monitoring locations are observed daily, every third day, or every sixth day, according to the proportions listed on the x-axis

3.2 Results

We report the root mean square error (RMSE) values for each set of 100 simulated samples and fits as boxplots in Fig. 1. There are results for the three tested models: penalized regression, universal kriging, and SpatioTemporal, as well as for penalized regression with only the $\hbox {L}_2$ penalty ($\lambda _2=0$), which is exactly ridge regression. We provide exact median RMSE values and squared correlations between predictions and observations ($\hbox {R}^2$) in Table S1 in Supplementary Material.

Our model provides lower or matching RMSE values to universal kriging (UK) and ridge regression (denoted by $\lambda _2=0$) in every scenario, demonstrating good general predictive accuracy for a spatiotemporal model and the usefulness of the time-smoothing penalty $\lambda _2$. The SpatioTemporal (ST) model produces the lowest RMSE values of all models in each of the data scenarios except those when all locations are only observed every third or every sixth day, where instead our penalized regression model outperforms all others. When none of the monitors are observed daily, our penalized regression model will disregard the completely missing dates and fit every third day as if it were daily (see Sect. 5 for discussion on interpolation in this scenario). Here we see that despite requiring greater than forty times the computation time (see Sect. 3.3), the ST model is more affected than our penalized smoother when there are time points without any observations. If monitors on an every third day and every sixth day schedule are measured in a staggered fashion, i.e., each day had some monitors of each frequency (daily, every third, and every sixth) and every date has a similar number of observations, then we do not see our model gain a predictive advantage over ST (see Supplementary Material Figure S1 for the “staggered” simulation results). So it is when dates are completely unobserved that our model is able to outperform ST.

The results in Fig. 1 highlight additional trends across different simulation settings. As non-spatial error ($\sigma$) increases, the fit of each model worsens. Similarly, more fluctuation from day to day (H = 0.05) reduces predictive accuracy for every model, and it should be noted that the ridge regression fits ($\lambda _2=0$) lose more accuracy than our model with its time-smoothing penalty ($\lambda _2 > 0$). UK and both penalized regression models have larger error when monitors are observed in all three frequencies (daily, every third day, and every sixth day) than if every monitor is observed only every third or sixth day. Since UK is a spatial-only model and fit onto the data from each day separately, having some days with only a few measured locations can pose a serious issue for prediction.

Fig. 2

Median computation times from 10 replicate simulated data sets with increasing numbers of monitoring locations. For the “PR CV + Fit” time, we used the penalized regression model to select over penalty values and number of TPRS basis functions, and then fit the resulting best model (“PR Fit”). The universal kriging fitting time includes estimation of covariance parameters (“UK Cov + Fit”)

3.3 Computation Times

In Eq. (3), we see that a sparse pT x pT matrix must be inverted to estimate $\varvec{\beta }$. To use UK, we must first invert an nT by nT matrix (or T n x n matrices) to estimate covariance parameters. Thus, our model scales better in computation time than UK with increasing site locations n. Figure 2 shows median computation times for sets of 10 replicate samples of each specified size ($N_\textrm{train}=500$, 1000, 1500, or 2000) and compares our penalized regression model with UK. These values are also reported in Table S2 in Supplementary Material. Each of the fits was computed on the RMACC Summit Supercomputer, with a Intel Xeon E5-2680 v3 processor at 2.50 GHz, using a memory cap of 50 GB of RAM. We see in Fig. 2 that the need for cross-validating over penalty values and amounts of TPRS basis functions slows our model down to a speed similar to UK for some smaller sample sizes. However, as $N_{train}$ increases, our method is faster. We include the median computation times for the onetime fit of sample training data that occurs after selecting penalty values and the number of TPRS basis functions to include as predictors. When using nonparametric bootstrap to correct measurement error, we would reuse the same model predictors and penalty values so that only a single fit would be run on each resampling, which would require much less time than refitting the UK model.

The SpatioTemporal model uses an optimization algorithm to produce maximum likelihood estimates for its parameters in both space and time, which takes considerable time. The median computation time of the ST model to fit the sample sets with $N_{train}=500$ is 3.02 h (181.2 min) and is 91.44 h (5,486.5 min) when $N_{train}=2000$. Thus, if resources are limited and the number of training site locations is high, ST becomes infeasible when the other models would not.

Fig. 3

Average logged concentrations in 2017 of $\hbox {PM}_{2.5}$, $\hbox {PM}_{{10}}$, sulfate, and silicon at monitoring site locations in the Eastern United States

4 Analysis of Ambient Air Quality

4.1 Monitoring Data

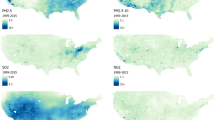
We demonstrate our method from Sect. 2 by predicting daily ambient total $\hbox {PM}_{2.5}$, total $\hbox {PM}_{{10}}$, sulfate ($\hbox {SO}^{2-}_4$), and silicon (Si) concentrations for the eastern portion of the contiguous United States in 2017 (Fig. 3). By including only the Eastern United States, we limit our analysis to monitors that are spatially dense and a region with a similar set of ambient pollution sources. Sulfate is a component of PM that is by itself associated with respiratory and cardiovascular health effects, while silicon is a component that is less studied (U.S. Environmental Protection Agency 2019). Both species are observed less frequently than total PM, and by different methods of measurement. We use Air Quality System monitoring data obtained September 18, 2019, to provide observed daily measurements of $\hbox {PM}_{2.5}$ and $\hbox {PM}_{{10}}$ with temporal and geographical metadata. Similarly, we use AQS monitoring data obtained October 16, 2019 for concentrations of sulfate and silicon at the $\hbox {PM}_{2.5}$ size. In addition, we use total $\hbox {PM}_{2.5}$ concentrations (obtained June 22, 2021) as well as sulfate and silicon $\hbox {PM}_{2.5}$ concentrations (obtained January 14, 2022) from a different monitoring network, the Interagency Monitoring of Protected Visual Environments (IMPROVE) program (Malm et al. 1994). The locations measured by IMPROVE are largely rural, while the AQS data come from mostly urban areas.

Nearly all sulfate and silicon concentrations are observed on every third or every sixth day. Total $\hbox {PM}_{2.5}$ and $\hbox {PM}_{{10}}$ are measured by some monitors more often than every three days. See Table 1 for the distribution of monitoring sites for each pollutant that record values one-sixth of the year or less or between one-sixth and one-third of the year. Figure S2 in Supplementary Material depicts the by-date monitoring frequency for each pollutant.

4.2 Spatiotemporal Predictors

We fit the data using our model from Eq. (3) with TPRS as well as exactly one or two other types of predictors. The Community Multiscale Air Quality Modeling System (CMAQ) is a mathematical model that uses atmospheric dispersion and emissions to estimate air quality levels, providing a rich though uncalibrated spatiotemporal predictor for our model (Reff, A. et al. 2020). The EPA provides daily predictions of $\hbox {PM}_{2.5}$ from CMAQ on a 12 km grid across the USA. We use data acquired June 30, 2020, and match each monitor site with the closest grid centroid. For an additional spatiotemporal predictor, we use a grid of estimated 3-hour average surface temperature values from the North American Regional Reanalysis (NARR) obtained on July 9, 2021 (Mesinger et al. 2006). We again match each monitoring site location to the closest grid point and estimate daily average temperature values for each site.

4.3 Data Filtering and Transformation

Before estimating a spatiotemporal surface, we preprocess both the $\hbox {PM}_{2.5}$ and $\hbox {PM}_{{10}}$ concentration data in the following ways. We use only the federal reference method (FRM) monitors, which use 24-hour gravimetric measurements (i.e., based on weighing mass accumulated on a filter) and are the basis of assessing compliance with the National Ambient Air Quality Standards. We remove concentrations of value zero, which are likely invalid measurements. If monitors are collocated, we remove all but one measurement per day at that site. We keep the measurement with the lowest “parameter occurrence code,” which should be the earliest registered monitor at that site. Finally, to account for the skewedness of PM concentrations, we natural-log-transform the observed concentrations and CMAQ values. See Table 1 for the summary statistics of the log-transformed $\hbox {PM}_{2.5}$ and $\hbox {PM}_{{10}}$ data and Fig. 3 for their average log-transformed concentrations by monitor location in 2017.

Similar filtering is performed on the sulfate and silicon concentrations, although the components are measured with different approaches. The sulfate concentrations are measured via ion chromatography or pulsed fluorescence, while all silicon concentrations are calculated using X-ray fluorescence. As with PM, we remove the values at zero, natural-log-transform all concentrations, and use only one measurement at a site per day, with preference to the older or non-IMPROVE monitors. We replace negative values (21 sulfate and 78 silicon measurements) with the lowest observed positive value before being log-transformed. See Table 1 and Fig. 3 for summary statistics and the average spatial distribution over 2017.

Table 1 Summary statistics for ambient pollutant concentrations in 2017 after log transformation, along with the distribution of monitoring sites by frequency of observation

4.4 Model Fits

To predict each pollutant, we fit the model from Equation (1) with daily average temperatures and TPRS basis functions as predictors. To predict $\hbox {PM}_{2.5}$, we use logged CMAQ values as an additional predictor. Since CMAQ is itself a multisource, deterministic estimate of $\hbox {PM}_{2.5}$, which we have transformed to the same scale as our observations, we exclude its coefficients from the overfitting penalization $\varvec{\Gamma }_1$. In contrast, we penalize the temperature and TPRS coefficients because we expect them to explain variation in pollution levels, but they are not direct predictions of pollution levels. As described in Sect. 2.4, we fix $\lambda _2 = 0$ and select the penalty $\lambda _1$ by lowest cross-validated RMSE, then select a $\lambda _2$ value with $\lambda _1$ fixed at the previously chosen value. Reusing this penalty selection process, we calculate cross-validated RMSE with each amount of TPRS basis functions from a chosen set of values (e.g., 100, 200, or 300 for $\hbox {PM}_{2.5}$). Our best model fit is the predictor and penalty set with lowest overall cross-validated RMSE. In the case of $\hbox {PM}_{2.5}$, we verify the accuracy of selecting penalties one at a time by also fitting models for every combination of $\lambda _1$ and $\lambda _2$ values (e.g., all combinations of the values 0.01, 0.1, 1, 10, and 100) and find that the same penalties are selected by either method. To compare with our model, we also fit UK and the ST model with tenfold cross-validation, using the same procedures as in Sect. 3.

4.5 Results

After selection through tenfold CV on the $\hbox {PM}_{2.5}$ data, the model from Equation (3) is fit with 200 TPRS basis functions and the penalty values of $\lambda _1=30$ and $\lambda _2=0.01$. Our penalized regression approach is matched by UK and outperformed by ST when estimating $\hbox {PM}_{2.5}$. Table 2 shows that the cross-validated RMSE over all dates and sites for our model (2.184 $\mu$g/$\hbox {m}^3$) lies between that of UK (2.389 $\mu$g/$\hbox {m}^3$) and ST (1.973 $\mu$g/$\hbox {m}^3$). For UK, the cross-validated RMSE over the yearly average predictions and observations for every site is lower than ST or penalized regression (0.875 $\mu$g/$\hbox {m}^3$ vs. 0.899 and 0.917, respectively). The UK method likely performs well on an annual average due to its excellent use of spatial structure but blindness to temporal structure. We can see similar behavior in Table 3, where we report summary statistics for daily cross-validated RMSE across all sites. UK has a lower daily CV RMSE on average than our model, but median daily CV RMSE for UK is higher than for penalized regression. The SpatioTemporal model has lower mean and median daily CV RMSE than the other two models.

For $\hbox {PM}_{{10}}$, we select with cross-validation 50 TPRS basis functions and the penalty values $\lambda _1=15$ and $\lambda _2=0.5$. The ST model has lower overall CV RMSE (9.275 $\mu$g/$\hbox {m}^3$) than our model (9.569 $\mu$g/$\hbox {m}^3$) and UK (13.503 $\mu$g/$\hbox {m}^3$), but our penalized regression model produces the lowest annual average cross-validated RMSE (4.375 $\mu$g/$\hbox {m}^3$ vs. 4.446 for ST and 4.746 for UK). The ST model also has the lowest daily average and median CV RMSE values of any model for $\hbox {PM}_{{10}}$. Our model has lower overall, annual average, daily mean, and daily median cross-validated RMSE values than universal kriging (Tables 2 and 3). From Fig. 3, we see that the $\hbox {PM}_{{10}}$ data have fewer observations and fewer unique locations than $\hbox {PM}_{2.5}$. There are 40 days of the year having two or fewer observed concentrations, which are not predicted by any model due to the lack of data. See Sect. 5 for a discussion of possible interpolation work-arounds for this issue. With fewer observed sites each day and greater variance (Table 1), UK may not have enough spatial information on each day to outperform our model.

On the sulfate concentrations, we choose via cross-validation 45 TPRS basis functions and the penalty values $\lambda _1=15$ and $\lambda _2=0.001$. Our penalized regression model demonstrates the best predictive accuracy in overall cross-validated RMSE (0.456 $\mu$g/$\hbox {m}^3$ vs. 0.535 for ST and 0.771 for UK), annual average CV RMSE (0.193 $\mu$g/$\hbox {m}^3$ vs. 0.223 for ST and 0.279 for UK), and both the daily average and daily median. (Tables 2 and 3). Table 1 shows that nearly all monitors that measure sulfate and silicon record concentrations every third day or less frequently. So in Table 3, we see that only 173 days of 2017 are being predicted on by our model and ST. UK predicts on 124 days of the year since it requires that a cross-validation fold contain at least two observations on a given date to create a distance matrix and estimate covariance parameters. The temporal missingness in sulfate leads to the same outcome as in Sect. 3, where our penalized smoother is able to retain the greater accuracy than its competitors. Figure S3 in Supplementary Material depicts the observations and predictions over time for sulfate concentrations at four randomly chosen monitoring sites. In East Baton Rouge, LA, where observed concentrations are more variable than at the other sites shown, our model fits more closely than the ST model. It may be that the smooth time trend applied to the ST model makes following highly variable observations difficult.

For the silicon concentrations, we cross-validate and select 55 TPRS basis functions with the penalties $\lambda _1=5$ and $\lambda _2=0.001$. Similar to sulfate, our model performs well under temporal missingness, producing the lowest overall CV RMSE (0.119 $\mu$g/$\hbox {m}^3$ vs. 0.137 for ST and 0.138 for UK) and lowest annual average CV RMSE (0.038 $\mu$g/$\hbox {m}^3$ vs. 0.047 for ST and 0.041 for UK) (Table 2). In daily CV RMSE, the average of our model lies above UK and below ST, while the median of our model is higher than both that of ST and of UK (Table 3).

Table 2 Cross-validated RMSE and $\hbox {R}^2$ values across all dates and sites (“Overall”) and from by-site annual average predictions and observations (“Annual Average”)

Table 3 Summary statistics for daily cross-validated RMSE values across all monitoring sites

5 Discussion

We have presented a penalized regression model for spatiotemporal prediction that penalizes overfitting and smooths over predictions at adjacent time points. Using spatiotemporal covariates and TPRS basis functions as predictors, we predict daily values anywhere on a spatial domain. In Sect. 3, we demonstrate in simulations that our smoothing method solving Equation (1) can outperform day-by-day universal kriging under a variety of data conditions and outperform the SpatioTemporal model when observations are less frequent than daily. When the data increase in spatial locations, we see that our model is faster than the each day application of UK while the ST model is more than forty times slower than either. In Sect. 4, we find that our model performs with cross-validated predictive accuracy close to that of day-by-day UK and worse than that of the ST model on total $\hbox {PM}_{2.5}$ and $\hbox {PM}_{{10}}$ concentrations. But on sulfate and silicon concentrations, our penalized regression model achieves the best accuracy of the models in all but two metrics, where it performs similarly.

Our model proposed in Equation (1) has spatiotemporal predictive accuracy for $\hbox {PM}_{2.5}$ concentrations that is on par with UK, a method shown to be more accurate than the several other approaches tested in Berrocal et al. (2020). Since UK is an excellent spatial model, it is difficult to outperform when, for each time point, there is a nearly spatially complete set of observations with a strong spatial signal. In Sect. 3, both increasing non-spatial error (lowering the signal-to-noise ratio) and increasing daily fluctuation in the latent Gaussian processes ($\text {H} = 0.05$) in our simulations results in a larger drop in accuracy for UK than for our model. When concentrations are observed less frequently at some sites, as in the case of $\hbox {PM}_{{10}}$, sulfate, and silicon, there are dates when only a few measurements are available and UK drops in accuracy behind our model. For sulfate and silicon, our model is more accurate than the more complex and computationally expensive SpatioTemporal model, showing that we have developed a useful prediction method for less studied ambient air pollutants.

In both the simulations (Sect. 3) and the ambient concentrations analysis (Sect. 4), our model provides predictions only on dates where at least one measurement is observed. If a time point $t^*$ is never observed in the data, there will be no p-vector of coefficients $\varvec{\beta }_{t^*}$ estimated via Equation (3). Furthermore, our model is treating any two dates with no observations between them as “adjacent in time.” In the case of the silicon concentrations in Sect. 4, all monitoring sites recorded measurements every third day, so our model penalized the differences between predictions three days apart, ignoring the two days in between them. We can define any interval of time in our data as “adjacency” by altering the matrix $\varvec{D}$ so that values at a desired amount of time apart are differenced. To obtain predictions for a date that is never observed, we may use some form of interpolation, such as simply averaging between predictions at each site before and after the missing date. Alternatively, we could average the coefficients $\varvec{\beta }_{t^*-1}$ and $\varvec{\beta }_{t^*+1}$ and use the interpolated $\widehat{\varvec{\beta }}_{t^*}$ to predict values over the unobserved date.

The selection of penalty values and predictor sets for our model is time-consuming and can require manual tuning. In our simulations and applications to observed ambient concentrations, we use a faster sequential method described in Sect. 2.4 to select penalty values and repeat for each set of TPRS basis functions. This sequential method only requires the manual input of candidate value sets for the penalties and amounts of TPRS basis functions. After the penalties and number of TPRS basis functions for our model are chosen, to predict a spatiotemporal surface we need to calculate the inverse of a sparse pT x pT matrix only once. To perform measurement error correction with nonparametric bootstrapping, we may reuse the same chosen penalty values and TPRS basis functions on each bootstrapped sample, making the computation very feasible. This is important because a nonparametric bootstrap measurement error correction can account for site selection, in addition to parameter estimation.

Extensions to the model, such as predicting multiple pollutants at once, may be possible through clever application of new penalty terms. However, if a non-convex penalty is used, the closed-form solution from Equation (3) would no longer apply. Generalized optimization techniques, such as ADMM (Boyd et al. 2010) should be able to utilize the sparse structure of the matrices and produce an accurate $\varvec{\beta }$ estimate relatively fast, but not as fast as Equation (3).

The penalized regression model proposed in this study showed spatiotemporal predictive ability that is competitive with both universal kriging applied daily and the SpatioTemporal model. When the data are missing observations for whole time points, our model achieves better predictive accuracy than either of the other models. The proposed model is also unlike more complicated counterparts in that it can be used with bootstrap-based measurement error correction for epidemiological health effects models.

6 Date Sources, Code, and Acknowledgements

The Air Quality System data used in this study is publicly available from the Environmental Protection Agency website: https://www.epa.gov/outdoor-air-quality-data/download-daily-data. Similarly, the IMPROVE observations can be accessed at the website: http://vista.cira.colostate.edu/Improve/. R code for the simulations and ambient air pollution analysis is available through the publisher.

IMPROVE is a collaborative association of state, tribal, and federal agencies, and international partners. The US Environmental Protection Agency is the primary funding source, with contracting and research support from the National Park Service. The Air Quality Group at the University of California, Davis, is the central analytical laboratory, with ion analysis provided by Research Triangle Institute, and carbon analysis provided by Desert Research Institute.