1 Introduction

Mathematical modeling using mechanistic dynamic equations (DEs)—equations relating the time derivative of a variable to a function of its current state—is a rich and diverse field with many real-world applications. Dating back to at least the inference of equations describing the motion of orbital bodies around the sun based on the positions of celestial bodies (Legendre 1806; Gauss 1809), DEs have been used to model the evolution of complex processes (e.g., the use of susceptible, infected, recovered models for epidemics) and have become ubiquitous across virtually every area of science and engineering. Generally, the DEs in a complex model are derived based on an understanding of the governing dynamics of the system of interest, sometimes termed mechanistic modeling, and like any model, represent an approximation of the real-world dynamics.

Mechanistic modeling typically adopts a deterministic perspective of the system that ignores observational uncertainty, implicitly assuming the specified dynamics adequately represent the true system. Statisticians have embedded such DEs into hierarchical Bayesian models to incorporate mechanistic information in a probabilistic framework that accounts for uncertainty across data, process, and parameters (Berliner 1996; Royle et al. 1999; Wikle et al. 2001). This approach, sometimes termed physical-statistical modeling (PSM), uses specified mechanistic relationships to motivate the parameterization of statistical process models (Berliner 2003; Kuhnert 2017). The key to this framework is that the scientific process is assumed to be latent—i.e., it is not directly observed, yet the data are described conditionally given this process. Bayesian inference then allows one to learn the latent process dynamics and associated parameters given the data. This approach has been used to study the complex dynamics in processes such as ocean surface winds (Wikle et al. 2001; Milliff et al. 2011) and the spread of avian species (Wikle 2003; Hooten and Wikle 2008), among others. Except in a few specialized cases, the DEs used to motivate these models are fairly simple representations of the true underlying dynamics since the true process dynamics are not known. Allowing parameters to be structured (spatial or temporally dependent) processes themselves can make up for the approximate nature of the DEs and allow the model to adapt to the data (e.g., see Cressie and Wikle 2011, for an overview). While these models are able to adapt to the data, they do not provide additional insight into functional form of the driving equations.

With the growing interest in “machine learning,” research has focused on methods that can discover the actual governing equation(s) that define dynamic systems. The first major breakthrough in recovering the governing system dynamics used symbolic regression (Bongard and Lipson 2007; Schmidt and Lipson 2009), but due to scalability concerns, the focus has since shifted to sparse identification and/or deep (neural network) modeling. The original sparse identification approach, termed Sparse Identification of Nonlinear Dynamics (SINDy; Brunton et al. 2016), is composed of the three distinct stages: numerical differentiation and de-noising, specification of candidate functions (termed the “feature library”), and sparse regression, which is generally performed using threshold-based regularization with a penalty term (Zheng et al. 2019; Champion et al. 2020). Since its development, the SINDy framework has been extended to partial differential equations (Rudy et al. 2017, 2019), stochastic processes (Boninsegna et al. 2018), and uncertainty quantification on the parameters (Zhang and Lin 2018; Niven et al. 2020; Fasel et al. 2022; Hirsh et al. 2021). SINDy has also been incorporated into a Python package PySINDy for broad usage (de Silva et al. 2020).

Deep learning approaches for dynamic discovery can be broadly grouped into two areas: reproducing or generating the underlying dynamical behavior of the system (Raissi et al. 2017; Raissi and Karniadakis 2018; Raissi et al. 2019, 2020; Sun et al. 2019; Wu and Xiu 2020), or recovering the dynamic equations governing the system (Both et al. 2021; Xu et al. 2021; Long et al. 2017, 2019). In the first case, neural networks can be trained to approximate the complex dynamics, producing a model that can generate realistic dynamical system behavior. Here, we define “data-driven discovery” to be the discovery of the functional form of the dynamics governing the system, not just the generation of realistic dynamics from a model trained with data. Deep models have also been successful at data-driven discovery, particularly when neural networks have been used to as function approximators for the library of possible relationships within a sparse regression approach (Both et al. 2021), in combination with a genetic algorithm to learn the library (Xu et al. 2021), and differential operators (Long et al. 2017, 2019).

Two long-standing challenges for data-driven discovery are properly accounting for observational uncertainty (i.e., missing data and measurement noise) and parameter uncertainty. It is more common to account for uncertainty in the parameters after the observed data have been first been de-noised (Zhang and Lin 2018; Fasel et al. 2022; Hirsh et al. 2021; Niven et al. 2020). In these multi-step procedures, de-noising and differentiation are preformed prior to the estimation procedure and the uncertainty associated with the de-noising is not accounted for when estimating parameters. Specifically, having observed data that is potentially corrupt with noise, the SINDy approach to approximating derivatives using numerical differentiation and constructing a feature library is used. To quantify uncertainty, either a Bayesian approach with a variable shrinkage prior placed on the coefficients associated with the features (Zhang and Lin 2018; Hirsh et al. 2021; Niven et al. 2020 or a bootstrap approach (Fasel et al. 2022) is used. While advantageous in that uncertainty quantification is provided for the discovered system, the uncertainty is highly contrived and completely dependent on the differentiation method employed. The uncertainty from the observed data, which directly produces the feature library and all derivatives, is completely ignored. Approaches have been developed to jointly account for uncertainty in the observed data and parameters (Galioto and Gorodetsky 2020; Yang et al. 2020), but these either require the functional form of the system to be known, require derivatives be computed numerically, which can lead to numerical instabilities, or do not account for missing data.

To address these limitations, we present a Bayesian hierarchical modeling approach for data-driven discovery of dynamics that explicitly accounts for observational error and parameter uncertainty. The first significant contribution of this work is that unlike other data-driven discovery methods presented in the literature, we decompose the problem in terms of a multilevel (hierarchical) model with specific model components for data, process, and parameters that are linked probabilistically. The data model accounts for the observation error (measurement and missingness) given the true, but unobserved, latent process. The dynamic system is modeled in the process level of the hierarchical model and is assumed to be latent. In the Bayesian framework, parameters are assumed to be random variables and assigned prior distributions. This ensures that the uncertainty in the model parameters propagates through the model and is accounted for in the identified dynamic process.

The second major contribution is that we explicitly account for the dependence between the dynamic process and its derivative by modeling them jointly using a basis expansion with a common set of basis coefficients. This has additional benefits in that, given the basis expansions, the derivatives can be computed analytically. This eliminates the multi-step procedure, the need to pre-filter (de-noise) the observed data, and the need for numerical approximations of the derivatives.

The third major contribution is the specification of sparsity in two different model components of the multilevel model. This favors a flexible, yet parsimonious, system of detected dynamic equations. Following the sparse identification approaches, we include a feature library and assign sparsity-inducing prior distributions on the parameters to identify important components of the system from the library.

We demonstrate the advantages of our method on data generated from the classic nonlinear chaotic Lorenz-63 (Lorenz 1963) system with varying levels of measurement noise and missing data. In the supplementary material we also apply our method on a Susceptible, Infected, Removed (SIR) epidemic model, the Lotka-Volterra (predator–prey) system, a coupled pendulum, and we compare our results with those obtained from the SINDy Python package PySINDy (de Silva et al. 2020). The simulations show that our approach is robust to measurement noise and missing data, able to learn the dynamics of complex dynamical systems, and provides formal uncertainty quantification on parameter estimates and the confidence of the discovered dynamics. Lastly, we apply our method to three real-world applications: the historic Hare-Lynx predator–prey system, a motion tracked pendulum, and Pacific sea surface temperature. In the first two applications, our estimates are consistent with the known dynamics of the system. In the third, we show that the our estimates of the dynamics can be used to predict future states of the system.

The remainder of this article is organized as follows. In Sect. 2 we give background on the general dynamical system, state how we make inference on the derivative of the system, and present the Bayesian hierarchical model. In Sect. 3 we describe parameter estimation and discuss modeling choices. In Sect. 4 we test our method on multiple simulated data sets and perform inference on three real-world data sets. Section 5 concludes the paper.

2 Bayesian Dynamic Equation Discovery

Here, we propose a general hierarchical model for making inference on nonlinear dynamic systems. Analogous to the observation and state model in state-space modeling of time series (e.g., Shumway and Stoffer 2017), we consider the dynamic process to be latent and the observed data to be a noisy realization of the “true” underlying process. As is customary in hierarchical modeling, we specify the three components of the model, namely the data model, the process model, and the parameter models in the sections below. In Sect. 2.1 we motivate the dynamic systems and describe in detail the components of the latent process. Section 2.2 describes how we use basis functions to approximate the latent process and obtain derivatives of the system. We specify the data model in Sect. 2.3 and specify the prior distributions in Sect. 2.4.

2.1 Dynamic System

Consider the ordinary differential equation (ODE) dynamic system

$$\begin{aligned} \frac{d^{(J)}}{d t^{(J)}}\mathbf {u}(t) = \mathbf {u}_{t^{(J)}}(t) = M(\mathbf {u}_{t^{(0)}}(t), \mathbf {u}_{t^{(1)}}(t), ..., \mathbf {u}_{t^{(J-1)}}(t)), \end{aligned}$$
(2.1)

where the vector \(\mathbf {u}(t) \in \mathbb {R}^N\) denotes the realization of the system at time t, the function \(M(\cdot )\) represents the (potentially nonlinear) evolution function, and \(\mathbf {u}_{t^{(j)}}(t), j = 0, ..., J\) represents the \(j^{th}\) derivative of \(\mathbf {u}(t)\). Equations of the form of Eqn. 2.1 are often used to model processes in biology, ecology, climatology, epidemiology, economics, meteorology, pharmacodynamics, and geological sciences, among others.

For illustration, we consider mechanistic systems that only have a few relevant terms that govern the dynamics (e.g., the pendulum equations, Lorenz attractor, Lotka-Volterra model; Higham et al. 2016) so the function space of \(M(\cdot )\) will be sparse. We can reparameterize Eqn. 2.1 to be intrinsically linear (in parameters) as

$$\begin{aligned} \mathbf {u}_{t^{(J)}}(t) = \mathbf {M}\mathbf {f}(\mathbf {u}_{t^{(0)}}(t), \mathbf {u}_{t^{(1)}}(t), ..., \mathbf {u}_{t^{(J-1)}}(t)), \end{aligned}$$
(2.2)

where \(\mathbf {M}\) is a \(N \times D\) sparse matrix of coefficients and \(\mathbf {f}(\cdot )\) is a vector-valued nonlinear transformation function of length D. The inputs of the function \(\mathbf {f}(\cdot )\) contain arguments that potentially relate to the dynamic system (i.e., more than just the lower-order terms of the system). That is, the functions \(f_{i}(\cdot ), i = 1, ..., D\) are any functions that potentially represent Eqn. 2.1 (e.g., polynomials, sinusoids, interactions). Crucially, these functions are chosen based on an educated understanding of the general properties of system in question (e.g., diffusion, advection, growth), with the hope that all the correct terms in the “true” system are included. Thus, D can be quite large and depending on the number of hypothesized functions chosen, Eqn. 2.2 has the potential to be drastically over-parameterized. As such, a method to induce sparseness in \(\mathbf {M}\) will be required.

As an example, consider the Lotka-Volterra system (Lotka 1920),

$$\begin{aligned} \frac{dx}{dt}&= \alpha x - \beta xy \\ \frac{dy}{dt}&= \delta xy - \gamma y, \end{aligned}$$

where \(\mathbf {u}(t) \equiv [x(t), y(t)]\), x is the number of prey, y is the number of predators, \(\alpha \) is the prey population growth rate, \(\beta \) is the rate of predation, \(\delta \) is the predator population growth, and \(\gamma \) is the death rate of the predator population. In terms of Eqn. 2.2, this can be represented as

$$\begin{aligned} \mathbf {u}_t(t)&= \begin{pmatrix} \alpha &{} 0 &{} -\beta \\ 0 &{} -\gamma &{} \delta \end{pmatrix} \begin{pmatrix} x_t \\ y_t \\ x_t y_t \end{pmatrix}. \end{aligned}$$

However, because we generally do not know \(\mathbf {f}(\mathbf {u}(t)) = [x(t), y(t), x(t) y(t)]'\), we specify \(\mathbf {f}(\mathbf {u}(t))\) in terms of possible solutions to the function (e.g., all polynomials up to the third order, sinusoids, etc.). Then, by selecting against coefficients in \(\mathbf {M}\) (i.e., identifying the terms that should be zero) we recover the solution to the dynamic equation.

In real-world problems, Eqn. 2.2 does not hold exactly. Stochastic forcing could perturb the system (e.g., weather systems, demographic stochasticity), or there could be error in the model specification. We accommodate this unknown stochasticity including an additive error term

$$\begin{aligned} \mathbf {u}_{t^{(J)}}(t) = \mathbf {M}\mathbf {f}(\mathbf {u}_{t^{(0)}}(t), \mathbf {u}_{t^{(1)}}(t), ..., \mathbf {u}_{t^{(J-1)}}(t)) + \varvec{\eta }(t), \end{aligned}$$
(2.3)

where, for example, \(\varvec{\eta }(t) \overset{\text { i.i.d. }}{\sim } N(\mathbf {0}, \varvec{\Sigma }_U)\) is a mean zero Gaussian process with variance/covariance matrix \(\varvec{\Sigma }_U\).

2.2 Basis Expansion

Define the expansion of the nth element of \(\mathbf {u}(t)\) as

$$\begin{aligned} u(t, n) = \sum _{k=1}^{\infty }A(n, k) \phi (t, k), \quad n = 1, ..., N, \end{aligned}$$

where \(\{\phi (t,k): k = 1, \ldots , \infty \}\) are basis function that are differentiable to (at least) order J and defined at any time t, and \(\{A(n, k): k = 1, \ldots , \infty \}\) are the associated basis coefficients. To reduce the dimension and transition to discretely observed time data, we keep the first \(k=1, \ldots , p_a\) terms and define \(\phi (t,k)\) at finite times \(t = 1, \ldots , T\). Let \(\mathbf {U}\approx \mathbf {A}\varvec{\Phi }\), where \(\mathbf {U}= \{\mathbf {u}(t)\}_{t = 1, \ldots , T}\) is an \(N \times T\) matrix, \(\varvec{\Phi }\) is a \(p_a \times T\) matrix of differentiable basis functions where each column is given by \(\varvec{\phi }(t) \equiv (\phi (t,1), \ldots , \phi (t,p_a))\), and \(\mathbf {A}\) is the \(N \times p_a\) matrix of basis coefficients with columns given by \(\mathbf {A}(k) \equiv (A(1,k), \ldots , A(N,k))\). We can then analytically obtain higher-order derivatives of the elements of \(\mathbf {U}\) by taking derivatives of the basis functions. Specifically, let \(\mathbf {U}_{t^{(j)}} \approx \mathbf {A}\varvec{\Phi }_{t^{(j)}}, j = 0, \ldots , J\), where \(\varvec{\Phi }_{t^{(j)}}\) is a \(p_a \times T\) matrix of the jth derivative of known basis functions \(\{\varvec{\phi }_{t^{(j)}}(t)\}\) (e.g., the tth column of \(\varvec{\Phi }_{t^{(j)}}\) is \(\varvec{\phi }_{t^{(j)}}(t) \equiv (\phi _{t^{(j)}}(t,1), \ldots , \phi _{t^{(j)}}(t,p_a))\)). For time t, \(\mathbf {u}_{t^{(j)}}(t) = \mathbf {A}\varvec{\phi }_{t^{(j)}}(t)\) with \(\varvec{\phi }_{t^{(j)}}(t) \in \mathbb {R}^{p_a}\) and Eqn. 2.3 can be rewritten,

$$\begin{aligned} \mathbf {A}\varvec{\phi }_{t^{(J)}}(t)&= \mathbf {M}\mathbf {f}(\mathbf {A}, \varvec{\phi }_{t^{(0)}}(t), \ldots , \varvec{\phi }_{t^{(J-1)}}(t)) + \varvec{\eta }_t. \end{aligned}$$

In summary, decomposing \(\mathbf {U}\) using temporal basis function expansions accomplishes two tasks. First, it enables inference on the derivative of the process, \(\{\mathbf {u}_{t^{(j)}}(t)\}\), when only the process, \(\{\mathbf {u}_{t^{(0)}}(t)\}\), is observed. Because \(\mathbf {U}_{t^{(j)}}\) is decomposed in terms of \(\mathbf {A}\) for \(j = 0, \ldots , J\), the estimate of \(\mathbf {A}\) is jointly informed by the system and the derivatives, allowing for information to be shared between the system and the derivatives. Second, by keeping \(p_a<< T\) basis functions, the resulting reconstruction of \(\mathbf {A}\varvec{\Phi }_{t^{(0)}}\) is smooth (Wang et al. 2016) (note, this implies \(\varvec{\eta }_t\) now also includes truncation error). This is important because numerically estimating the derivative (e.g., via a finite difference) when the dynamic process \(\{\mathbf {u}_{t^{(j)}}(t)\}\) is noisy can amplify the noise of the higher-order terms in the system (e.g., \(\{\mathbf {u}_{t^{(j)}}(t)\}\) for \(j = 1, \ldots , J\), Chartrand 2011). By taking derivatives analytically through basis functions, the system is more robust to noise.

2.3 Data Model

We assume \(\mathbf {v}(t)\) is an observation of the latent process \(\mathbf {u}_{t^{(0)}}(t)\) outlined in Sect. 2.2 with unknown measurement uncertainty. We model \(\mathbf {v}(t)\) using a generalization to the traditional linear data error model that links the dynamics to the observed process (e.g., see Cressie and Wikle 2011, Chapter 7). That is, we model

$$\begin{aligned} \mathbf {v}(t) = \mathbf {H}(t) \mathbf {u}_{t^{(0)}}(t) + \widetilde{\varepsilon }(t), \end{aligned}$$

where \(\mathbf {v}(t) \in \mathbb {R}^{L(t)}\) and \(\mathbf {H}(t)\) is a \(L(t) \times N\) matrix that maps the latent process to the observed process and accounts for possible missing observations at time t. Uncertainty in the observations of the process is captured by \(\widetilde{\varvec{\epsilon }}(t) \overset{\text {indep.}}{\sim } N_{L(t)}(\mathbf {0}, \widetilde{\varvec{\Sigma }_V}(t))\), where \(\widetilde{\varvec{\Sigma }_V}(t)\) is the variance/covariance matrix.

Missing data are common in applications. A benefit of the hierarchical model is that it can easily accommodate missing data. Since the latent process is fully specified and missing data are handled at the data level, missing data do not impact the process model. We handle scenarios with missing data by allowing the dimension of \(\mathbf {H}(t)\) to vary in time. If there are no missing data at time t, then \(L(t) = N\) and \(\mathbf {H}(t) = \mathbf {I}_N\). When one or more system components are missing data, then the row corresponding to the missing system component is removed. For example, if we have a three-dimensional system, say \(\mathbf {u}(t) = [a(t), b(t), c(t)]\) and the observation component for b(t) is missing at time t, then

$$\begin{aligned} \mathbf {H}(t) = \begin{bmatrix} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 \end{bmatrix}. \end{aligned}$$

This representation can also accommodate situations where an entire system component is not observed. Again, \(\mathbf {H}(t)\) is chosen such that the latent system, of dimension N, can map to the observation system of dimension \(L(t) < N\) (recall, \(\mathbf {H}(t)\) is a \(L(t) \times N\) matrix). We then allow the process model to learn the missing dynamic process based purely on the dependence that is present within the process model. However, as we will discuss in more depth through the Lorenz attractor example in Sect. 4.1, there are limitations to the extent of missing information that can be accommodated and care needs to be taken when interpreting these cases.

2.4 Parameter Model

Combining the process and observation equations results in the first two levels of our proposed Bayesian hierarchical model. As defined in Sect. 2.2 and 2.3, for discrete time points \(t = 1, \ldots , T\), the first two layers of our general model are

$$\begin{aligned} \begin{aligned} \mathbf {v}(t)&= \mathbf {H}(t) \mathbf {u}_{t^{(0)}}(t) + \widetilde{\varvec{\epsilon }}(t) = \mathbf {H}(t) \mathbf {A}\varvec{\phi }_{t^{(0)}}(t) + \varvec{\epsilon }(t) \\ \mathbf {A}\varvec{\phi }_{t^{(J)}}(t)&= \mathbf {M}\mathbf {f}(\mathbf {A}, \varvec{\phi }_{t^{(0)}}(t), \ldots , \varvec{\phi }_{t^{(J-1)}}(t)) + \varvec{\eta }(t), \end{aligned} \end{aligned}$$
(2.4)

where \(\varvec{\epsilon }(t) \overset{indep.}{\sim } N_{L(t)}(\mathbf {0}, \varvec{\Sigma }_V(t))\) and \(\varvec{\Sigma }_V(t)\) is the \(L(t) \times L(t)\) measurement error covariance matrix where L(t) is the dimension at time t (Fig. 1). For clarity, we present the details the model parameters in Table 1. Our goal is to make inference on the unknown parameters \(\mathbf {M}, \mathbf {A}, \varvec{\Sigma }_U\), and \(\varvec{\Sigma }_V\), where \(\mathbf {M}\) defines the nonlinear dynamic equation, \(\mathbf {A}\) defines the smooth latent process, \(\varvec{\Sigma }_U\) captures the error dependencies within the dynamic equation, and \(\varvec{\Sigma }_V\) captures the measurement uncertainty associated with the observed process. To complete our Bayesian hierarchical model, we define the following priors.

Fig. 1
figure 1

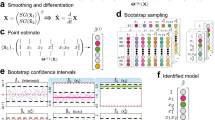
A Data model relating the observed measurements \(\mathbf {V}\) to the latent dynamic process \(\mathbf {U}_{t^{(0)}}\) and accounting for measurement error \(\widetilde{\varvec{\epsilon }}\). Note, we do not include \(\mathbf {H}\) in our pictorial representation of the equation and the error is not to scale. B Basis representation of the dynamic process where \(\mathbf {U}_{t^{(0)}} \approx \mathbf {A} \varvec{\Phi }_{t^{(0)}}\) and \(\varvec{\epsilon }\) now accounts for the approximation uncertainty. C Process model where the derivative of the dynamic process \(\mathbf {A} \varvec{\Phi }_{t^{(0)}}\) is related to the product of the parameter coefficient matrix \(\mathbf {M}\) and the library of function \(\mathbf {f}(\cdot )\) plus model uncertainty \(\varvec{\eta }\). D The recovered equation which is computed from \(\mathbf {M}\) after the model parameters have been estimated. E Resulting dynamic equation mean (a) and equation uncertainty (b) which are computed from \(\mathbf {M}\) after the model parameters have been estimated

Full size image
Table 1 List of symbols used in the Bayesian hierarchical model
Full size table

As mentioned in Sect. 2.1, \(\mathbf {M}\) has the potential to be over-parameterized. To induce sparsity into our estimate of \(\mathbf {M}\), we use the stochastic search variable selection (SSVS, George and McCulloch 1993) prior. Specifically,

$$\begin{aligned} vec(\mathbf {M})&\sim N_{ND}(\mathbf {0}, \varvec{\Sigma }_M), \\ \varvec{\Sigma }_M&= diag(\gamma ^{(c_1)}_{1}, \ldots , \gamma ^{(c_{ND})}_{ND}), \end{aligned}$$

where \(\gamma ^{(c_l)}_{l} = v_1\) if \(c_l = 1\) and \(\gamma ^{(c_l)}_{l} = v_0\) if \(c_l = 0\). The latent variable, \(c_l\), is the inclusion indicator, and the posterior of \(c_l\) specifies the probability of inclusion for any parameter in \(\mathbf {M}\). The hyperpriors \(v_0\) and \(v_1\) are chosen such that \(v_0\) is small (e.g., \(v_0 = 10^{-6}\)) and \(v_1\) is large (e.g., \(v_1 = 10^{4}\)). Whereas any method to induce sparsity in \(\mathbf {M}\) can be used, we choose SSVS because it provides the inclusion probabilities and has been shown to work well in nonlinear dynamic models (Wikle and Holan 2011).

Within the SSVS prior, \(\nu _0\) and \(\nu _1\) determine how parsimonious the selected model will be. This is due to the ratio

$$\begin{aligned} p_l = \frac{\pi [m(l)|c_{l} = 1, \cdot ]}{\pi [m(l)|c_{l} = 1, \cdot ] + (1-\pi )[m(l)|c_{l} = 0]} \end{aligned}$$

for \(\mathbf {m}\equiv vec(\mathbf {M})\) and \(l = 1, \ldots , ND\), which determines the inclusion probability for m(l), where \([m(l)|\cdot ]\) denotes the distribution of m(l) given all relevant parameters. George and McCulloch (1993), George and McCulloch (1997), and George et al. (2008) discuss the specification of \(\nu _0, \nu _1\) in detail, and we summarize some of the key points here. One should choose \(\nu _0\) and \(\nu _1\) such that if \(c_l = 0\), m(l) can safely be replaced with zero, and if \(c_l = 1\), m(l) is then a nonzero estimate that should be included with some probability \(p_l\). However, in practice we do not know which values of \(\mathbf {m}\) should or should not be included. As a general rule, we found \(\nu _0 = 10^{-6}\) and \(\nu _1 = 10^4\) work well for most of the simulations we present. However, when models have small parameter values (e.g., see the SIR example in supplementary material S1.1), we find smaller values, such as \(\nu _0 = 10^{-8}\) and \(\nu _1 = 10^2\), are needed.

Both \(\varvec{\Sigma }_V(t)\) and \(\varvec{\Sigma }_U\) have the potential to have small parameter values, and inference using traditional conjugate inverse Gamma/Wishart priors is overly sensitive to the choice of hyperpriors when estimates are small (Gelman 2006). Instead, we use the conjugate Half-t prior proposed by Huang and Wand (2013) for covariance estimation, which imposes less prior information and does not have as strong of influence on small estimates.

We restrict the measurement error to be diagonally structured (although this restriction can be removed if warranted) since it is often assumed that measurement noise is independent (Cressie and Wikle 2011). Let \(\varvec{\Sigma }_V(t) = \mathbf {H}(t) diag(\sigma ^2(1), \ldots , \sigma ^2(N)) \mathbf {H}(t)'\), where each diagonal element, \(\sigma ^2(1), \ldots , \sigma ^2(N)\), is assigned a conjugate Half-t\((2, 10^{-5})\) prior. In order to account for system dependence within the multivariate latent process error, we model \(\varvec{\Sigma }_U\) as a full rank matrix, which enables us to borrow strength across systems and improve model performance. We assign the matrix Half-t(\(\nu _k, B_k\)) prior to \(\varvec{\Sigma }_U\) with \(\nu _k = 2, B_k = 10^{-5}, k = 1, \ldots , N\).

Last, we specify the Bayesian elastic net prior (Li and Lin 2010) on \(\mathbf {A}\). Specifically, our prior is

$$\begin{aligned} \pi (\mathbf {A}) \propto \exp \{-\lambda _1\Vert \mathbf {A}\Vert _1 -\lambda _2\Vert \mathbf {A}\Vert _2^2\}, \end{aligned}$$

where \(\lambda _1, \lambda _2\) are penalty parameters. We use the elastic net prior to help regularize the basis coefficients and select against unneeded basis functions. It is possible to specify hyperpriors for the two penalty terms, but we find inference is not overly sensitive to the choice of penalty parameters and fix them to a small value (e.g., 0.1 or 0.01).

3 Algorithm and MCMC

There are five full-conditional distributions of interest, \([\mathbf {M}|\cdot ]\), \([\varvec{\Sigma }_V|\cdot ]\), \([\varvec{\Sigma }_U|\cdot ]\), \([\mathbf {A}|\cdot ]\), and \([\mathbf {c}|\cdot ]\) (see supplementary text S3 for the details of the distributions) when performing MCMC inference for this model. The four components \(\mathbf {M}, \varvec{\Sigma }_V, \varvec{\Sigma }_U\), and \(\mathbf {c}\) are updated using classical Bayesian methods, and \(\mathbf {A}\) is updated using a stochastic gradient approach. Within the general MCMC procedure, there are implementation details that warrant a more detailed discussion. Additionally, because the framework we present is general, some modeling choices are problem specific. We discuss how to address these challenges Sect. 3.1.

3.1 Basis Estimation

The basis coefficients pose an estimation challenge because they are embedded in the nonlinear function \(\mathbf {f}(\cdot )\) and since \(\mathbf {f}(\cdot )\) is problem specific, it needs to be specified generally to accommodate different problems. In principle, an Expectation-Maximization (EM) or Metropolis-Hastings (MH) algorithm could be used to estimate \(\mathbf {A}\), but they require \(\mathbf {f}(\cdot )\) to be known and convergence with either of these methods is slow in our setting. Instead, we use an adapted version of SGD with a constant learning rate (SGDCL; Mandt et al. 2016), which has been shown to scale well.

As with SGD, SGDCL relies on the gradient of a loss function and a learning rate. For SGDCL, the loss function is the negative log posterior for our parameters of interest, \(\mathbf {A}\). Here, the loss function for a single time is

$$\begin{aligned} \mathcal {L}(t)&= -\log ([\mathbf {v}(t) | \mathbf {H}(t), \mathbf {A}, \varvec{\phi }_{t^{(0)}}(t), \varvec{\Sigma }_V(t)][\mathbf {A}, \varvec{\phi }_{t^{(J)}}(t)| \mathbf {M}, \mathbf {A}, \varvec{\phi }_{t^{(0)}}(t), \ldots , \varvec{\phi }_{t^{(J-1)}}(t), \varvec{\Sigma }_U]) \\&\quad +\frac{1}{T}\left( \lambda _1 \Vert \mathbf {A}\Vert _1 + \lambda _2 \Vert \mathbf {A}\Vert _2^2 \right) . \end{aligned}$$

The gradient of the loss function is dependent on \(\frac{\partial }{\partial \mathbf {A}} \mathbf {f}(\mathbf {A}, \varvec{\phi }_{t^{(0)}}, \ldots , \varvec{\phi }_{t^{(J-1)}})\), which we generically denote as \(\overset{\text{. }}{\mathbf {F}}_t\), and the gradient of \(\mathcal {L}(t)\), \(\frac{\partial \mathcal {L}(t)}{\partial \mathbf {A}} = \nabla _{\mathbf {A}} \mathcal {L}(t)\), is

$$\begin{aligned} \nabla _{\mathbf {A}} \mathcal {L}(t)&= - \mathbf {H}(t) \varvec{\Sigma }_V^{-1}(t) \mathbf {v}(t) \varvec{\phi }_{t^{(0)}}(t)' + \mathbf {H}(t)' \varvec{\Sigma }_V^{-1}(t) \mathbf {H}(t) \mathbf {A}\varvec{\phi }_{t^{(0)}}(t) \varvec{\phi }_{t^{(0)}}(t)' \\&\quad + \varvec{\Sigma }_U^{-1} \mathbf {A}\varvec{\phi }_{t^{(J)}}(t) \varvec{\phi }_{t^{(J)}}(t)' - \varvec{\Sigma }_U^{-1} \mathbf {M}\mathbf {f}(t) \varvec{\phi }_{t^{(J)}}(t)' - \varvec{\phi }_{t^{(J)}}(t)' \mathbf {A}' \varvec{\Sigma }_U^{-1} \mathbf {M}\overset{\text{. }}{\mathbf {F}}(t) \\&\quad + \mathbf {f}(t)' \mathbf {M}' \varvec{\Sigma }_U^{-1} \mathbf {M}\overset{\text{. }}{\mathbf {F}}(t) + \frac{1}{N}\left( \lambda _1 sign(\mathbf {A}) + 2 \lambda _2 \mathbf {A}\right) . \end{aligned}$$

SGDCL methods replace the true gradient with the stochastic estimate,

$$\begin{aligned} \widehat{\nabla \mathcal {L}}_{\mathcal {Z}}(t) = \frac{1}{\mathcal {Z}}\sum _{t \in \mathcal {Z}}\nabla _{\mathbf {A}} \mathcal {L}(t), \end{aligned}$$

where \(\mathcal {Z} \subset \{1, \ldots , T\}\) is a random subset of the observations, called a mini-batch, and \(|\mathcal {Z}|\) is the cardinality of the set. Within the context of a MCMC algorithm, the \(\ell \)th update of \(\mathbf {A}\) is given by

$$\begin{aligned} \mathbf {A}^{(\ell )} = \mathbf {A}^{(\ell -1)} - \kappa \widehat{\nabla \mathcal {L}}_{\mathcal {Z}^{(\ell )}}(\mathbf {A}^{(\ell -1)}), \end{aligned}$$
(3.1)

where \(\mathcal {Z}^{(\ell )}\) denotes a random minibatch specific to the \(\ell \) update and \(\kappa \) is the learning rate. Mandt et al. (2016) show how to select the constant \(\kappa \), or a preconditioning matrix (i.e., replace \(\kappa \) with a matrix \(\mathbf {K}\)), to match the stationary distribution to the posterior. In practice, we find \(\kappa \) is problem dependent. If there is a lot of observation noise in the data, an adaptive approach may provide the best results. Specifically, an upper bound is specified for the learning rate. Then, during the burn-in process, the learning rate decreases at equal intervals from this initial value to a specified lower bound. After burn-in, the learning rate stays fixed at the specified lower bound throughout the sampling algorithm. If there is minimal to no noise, then a fixed small value for \(\kappa \) for the entirety of the sampler works best.

The final challenge to estimating \(\mathbf {A}\) is computing \(\overset{\text{. }}{\mathbf {F}}(t)\). Because \(\mathbf {f}(\cdot )\) is problem specific, \(\overset{\text{. }}{\mathbf {F}}(t)\) is also problem specific and needs to be obtained generally. To overcome this issue, we use automatic differentiation (AD). AD has become increasingly popular, especially with the increasing interest in deep models, and allows one to analytically compute the derivative of \(\mathbf {f}(\cdot )\). There are many different libraries and programs that perform AD, and for our implementation we use the ForwardDiff (Revels et al. 2016) package in Julia (Bezanson et al. 2017).

Note that we need to estimate the latent process \(\mathbf {U}_{t^{(0)}}\), and all subsequent derivatives \(\mathbf {U}_{t^{(J)}}\) for \(j = 1, \ldots , J\) in the model. Without using a basis expansion approach, estimating each of these processes requires an O(T) calculation. With the basis expansion, this reduces the computational burden to \(O(p_a)\) for each process. We further reduce the computation required using the SGDCL to \(O(|\mathcal {Z}|)\), where \(|\mathcal {Z}|<< p_a<< T\).

3.2 Choice of Functional Library

Choosing the potential solutions (the function library \(\mathbf {f}(\cdot )\)) generally requires some extra thought. Ideally, the functions are chosen based on a general mechanistic understanding of the system (e.g., diffusion, advection, growth). However, this is not always possible. In general, most ordinary differential equations are functions of polynomials and interactions (e.g., Lorenz attractor, van der Pol oscillator, Lotka-Volterra model; Higham et al. 2016). Because of this, we default to a using a library of polynomial functions and interactions when a physical understanding of the system is not applicable. While there are scenarios where more terms need to be included in the library (e.g., sinusoidal terms), using polynomials and interactions as a default library covers a wide range of potential systems.

3.3 Choice of Basis Functions

The choice of basis functions has the potential to affect the model fit. Ramsay and Silverman (2005, Chapter 3) provide a discussion on how to choose basis functions based on the “shape” of the data, and we will summarize some key points here. For our method we consider two basis function classes, the B-spline and Fourier basis, with the B-spline being a local basis function and Fourier a global basis function. While we only discuss the B-spline and Fourier basis, other basis functions could be chosen. The Fourier basis is best suited for periodic data with no strong local features and where the curvature of the function is the same order everywhere. In contrast, the B-spline basis works best with nonperiodic functions that may or may not have strong local features. With respect to differentiation, the Fourier basis is infinitely differentiable, and the m-order B-spline basis is differentiable up to order \(m-1\). However, Fourier series suffer from a ringing effect (Hewitt and Hewitt 1979), and we find the effect is worsened when derivatives greater than the first order are considered or there are local regions with little curvature. This issue makes the Fourier series less useful in practice. B-splines do not suffer from the ringing effect, making them better suited for higher-order dynamic systems. The amount of noise in the data also impacts the choice of basis. For both local and global basis functions, enough basis functions need to be included so the estimated solution curve is flexible, the dynamics are captured, and the posterior latent space is properly explored, but not so many such that unnecessary noise is captured (see examples below for relation of number of basis functions to number of observations). In general, we found the B-spline basis resulted in the best model performance and use them for all of our simulations and examples.

4 Simulations and Examples

We simulate data from the classical Lorenz-63 system (Lorenz 1963) with varying levels of measurement noise and missing data to demonstrate the ability of our methodology to recover nonlinear equations. Then, we apply our approach to three real-world data sets—the historic Hare-Lynx system, a motion tracked pendulum, and Pacific sea surface temperature. Details on parameter estimation and model fitting are included in supplementary material S1 and S2. We also apply our methodology to a Susceptible, Infected, Removed (SIR) epidemic model, the Lotka-Volterra (predator–prey) system, a coupled pendulum, and compare our results with those obtained from the SINDy Python package PySINDy (de Silva et al. 2020) in supplementary material S1.

We simulate measurement noise in the Lorenz attractor by adding mean zero Gaussian errors to the state vector; specifically \(\mathbf {v}(t) = \mathbf {u}(t) + \varvec{\epsilon }(t)\), where \(\mathbf {v}(t)\) is the simulated data, \(\varvec{\epsilon }(t) \sim N(\mathbf {0}, \zeta \mathbf {I}_{L(t)})\) is the additive noise, and \(\zeta \) is the variance. For all simulations and real-world examples, we obtain 10000 posterior samples and discard the first 5000 as burn-in. Convergence of model parameters was assessed visually via trace plots, with no issues detected.

4.1 Lorenz-63

The Lorenz-63 attractor is a classic chaotic nonlinear dynamical system originally proposed to represent a simplified atmospheric system (Lorenz 1963). This system consists of the three nonlinear ODEs

$$\begin{aligned} \frac{dx}{dt} = 10 (y - x); \quad \frac{dy}{dt} = x (28 - z) - y; \quad \frac{dz}{dt} = x y - \frac{8}{3} z, \end{aligned}$$
(4.1)

where x is proportional to the convection rate, y is proportional to the temperature difference in ascending and descending currents, and z is proportional to the vertical temperature distortion. We consider four scenarios: (A) no measurement noise \((\zeta =0)\), (B) moderate measurement noise \((\zeta =1)\) and 5% of the data missing at random, (C) large measurement noise \((\zeta =10)\), and (D) missing the \(x_t\) component of the attractor (i.e., the \(x_t\) time series is not included as data). For scenarios A-C, our library of potential solutions consists of all polynomials up to the third order with all possible interactions. We discuss the library for scenario D below.

Table 2 Posterior 95% credible intervals for the identified equations for each simulation scenario. Parameters with credible intervals that cover the true value are shown in bold
Full size table

The 95% credible intervals for the identified system for each scenario are shown in Table 2. As is expected, when there is no measurement error (scenario A), we correctly identify the true system and the credible intervals cover the true values. When there is moderate measurement error in addition to 5% missing observations, (scenario B), we do fail to identify one component of the dy system, and one parameter of the dz system does not have a credible interval that captures the true value. However, no extra terms in the library are identified as significant based on the 99% inclusion probability threshold. With large noise (scenario C), we identify the same model components as in scenario B except fewer parameters are significant based on their credible intervals containing 0. Scenarios B and C highlight the benefit of the statistical approach. As more noise and/or missing data are introduced, uncertainty estimates in the model parameters increase yet key components of the system are still identified without the inclusion of extraneous terms.

Scenario D assumes the \(x_t\) component is completely missing, which, to the best of our knowledge, precludes the use of other dynamic discovery approaches. In this case, we consider all polynomials up to the second order with all possible interactions (i.e., we removed the third-order polynomials). In practice, this is akin to having prior knowledge of the system where a missing component results in less data available to discover the dynamics of the system. In scenario D, we correctly identify six of the seven terms (Table 2) and do not include any extraneous terms. That is, we are able to infer \(x_t\) and learn the correct components driving the relationships based solely on the data from \(y_t\) and \(z_t\) and quantify the uncertainty associated with our recovered equations (see supplementary material S1.4 for more detail).

4.2 Hare and Lynx Population Dynamics

The historic Canadian lynx and snowshoe hare data were originally recorded by the Hudson’s Bay Company and documents the population dynamics between the two species from 1845 to 1939 Elton and Nicholson (1942). This classic predator–prey system has a cycle of approximately 10 years Bulmer (1974). There is some debate in the literature as to whether the Lotka-Volterra equations accurately represent the Hare-Lynx system Zhang et al. (2007) or whether another trophic level is needed accurately capture the dynamics of the system Krebs et al. (2001). Therefore, we specify our library of potential functions to include polynomials up to the third order with all possible interactions, noting that the typical predator–prey system of equations is contained within this set.

The 95% credible intervals for the identified system are shown in the top row of Table 3. We see the recovered solution has the same components as a Lotka-Volterra system, each of which is significant, suggesting predator–prey interactions provide a reasonable representation of these data.

Table 3 Posterior 95% credible intervals and identified equations for the Hare-Lynx data (top) and the motion tracked pendulum (bottom). Parameters with credible intervals that do not cover zero are shown in bold
Full size table

4.3 Motion Tracked Pendulum

Motion tracked data for a pendulum (accessed via the supplementary material of Schmidt and Lipson 2009) consists of the angle of the pendulum from vertical at time t. In this scenario, basic principles of physics suggest a solution to the system follows the theoretical equation \(d^2 \theta /dt^2 = -(g/l)\sin (\theta ) - (b/m) \omega \), where \(\theta \) is the angle from vertical and \(\omega \) is the derivative of \(\theta \). Using physics to inform our library of potential functions, we include the following components:

$$\begin{aligned}{}[\theta , \sin (\theta ), \cos (\theta ), \theta /\sin (\theta ), \theta /\cos (\theta ), \omega , \omega ^2, \omega \sin (\theta ), \omega \cos (\theta ), \sin (\omega ), \cos (\omega )]. \end{aligned}$$

The posterior mean and 95% credible intervals for the selected terms are shown in the bottom row of Table 3. While we do not know the actual parameter values for the true system, the terms identified as significant agree with the theoretical equation of the system. Thus, our framework can accommodate higher-order systems and more complex libraries consisting of the system state and its derivatives.

4.4 Sea Surface Temperature

The transitions from El Niño (anomalous warming) to La Niña (anomalous cooling) in the tropical Pacific ocean are known as the El Niño–Southern Oscillation (ENSO) cycle and occurs quasi-periodically every 3–5 years Philander (1990). ENSO influences atmospheric and ecological systems globally and governmental agencies and industries rely on accurate forecasts of the event to make management decisions. Using publicly available sea surface temperature data from the IRI/LDEO Climate Data Library and originally produced by the National Ocean and Atmospheric Administration (NOAA) (Huang et al. 2017),Footnote 1 we recover implicit dynamics of the ENSO system. The data consist of monthly sea surface temperature (SST) anomalies from January 1926 to November 2021 and include multiple ENSO cycles. We focus on two of the more recent events, the 1997–1998 and 2015–2016 ENSO cycles. We subset the data to include all time points leading up to each of these ENSO cycles—that is, January 1926 to March 1997 and January 1926 to February 2015, which we label ENSO-97 and ENSO-15, respectively. ENSO-97 and ENSO-15 are each decomposed using empirical orthogonal functions (EOFs) Cressie and Wikle (2011), where the first ten temporal principal component time series associated with the EOFs are treated as data and used to learn the dynamics.

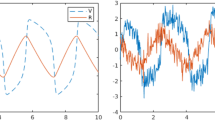
In this application, we know that we are not considering all possible mechanisms driving SST (e.g., those associated with atmospheric winds, subsurface temperatures). Motivated by the success of statistical models in long-lead forecasting of ENSO (Barnston et al. 1999; van Oldenborgh et al. 2005), our focus is on estimating the system and using it to forecast SST forward in time. As is customary in such applications, we use the average SST in the Niño 3.4 region (5S - 5N, 120W - 70W) to summarize the intensity of an El Niño event. Using the ENSO-97 and ENSO-15 data leading up to the 1997 and 2015 El Niño events, respectively, we learn the dynamics and generate a 12-month forecast of the SST for each event. For both ENSO-97 and ENSO-15, our library of potential functions are all polynomials up to the second order with all possible interactions (see supplementary material S2.3 for more detail). We then compute the mean and highest posterior density (HPD) interval of the Niño 3.4 Index for each forecast and compare to the truth (Fig. 2). For both ENSO events, we capture the parabolic increase and decrease in the Niño 3.4 Index with the point-wise HPD intervals covering the true Niño 3.4 Index for all but one forecast.

Fig. 2
figure 2

A SST as the ENSO shifts into El Niño (warming phase) shown in two-month increments. From top to bottom, the left column is the SST to March, May, and July 2015 and the right column is the SST for September, November, January 2015–2016. B Predictions of the Niño 3.4 Index for the 1997–98 ENSO event showing the true (blue), posterior predicted mean (red), and 95% highest posterior credible intervals (red bands). C Predictions of the Niño 3.4 Index for the 2015-2016 ENSO event showing the true (blue), posterior predicted mean (red), and 95% highest posterior credible intervals (red bands). Note—(B) and (C) are on different scales (Color figure online)

Full size image

5 Conclusion

We have proposed a Bayesian hierarchical method to learn complex nonlinear dynamic equations using a data-driven approach. Our proposed method is robust to measurement noise and missing data, and can accommodate situations where a component is completely unobserved. The statistical approach to dynamic equation discovery is our most significant contribution, where we provide uncertainty quantification and inclusion probabilities to the terms in the library. This is possible because of the Bayesian hierarchical model that is composed of three components: a data model accounting for the uncertainty in the observed data, a process model learning the nonlinear dynamics in a latent space, and parameter models. Additionally, we are able to bypass the need for numerical differentiation by expanding our latent process in terms of basis functions. As a whole, our proposed hierarchical model overcomes the limitations of the multi-step procedure and provides a complete statistical framework to the dynamic equation discovery problem.

Our Bayesian approach to dynamic discovery relies on full posterior inference for uncertainty quantification. A known limitation of MCMC methods for Bayesian model inference is that computation can become expensive with large data sets. Compared to the deterministic dynamic discovery approaches that can make inference on hundreds of thousands of data points, our approach targets data sets that are smaller (on the order of thousands of data points). This can be considered a strength of our approach since recovering the dynamics of systems with small data sets is problematic with many deterministic approaches. Our method can be applied to larger data sets, but to implement the approach may require additional computational efficiencies which may be the target of future research.

We see two clear extensions to our research. The most beneficial extensions relate to the specification of the feature library. Currently, the method is limited in that it is unable to identify an important function if the function is not included in the library. A library-free approach, which removes the potential bias associated with the specification of the library, would result in a truly data-driven approach. Additionally, allowing for time-varying parameters will increase the number of real-world applications for which the method can be applied. Most apparent are extensions to the SIR class of models where government intervention, variant strains, and other factors could be accounted for in the model. Another extension would be to impose restricts on different components of the system through the library. For example, when the environment may impact the population but not vice versa. Allowing this unidirectional forcing is beneficial from a physical viewpoint because it restricts the method from considering potential solutions that are not possible. Last, the work can be extended to include partial differential equations. This would allow for the discovery of nonlinear dynamic spatial processes with uncertainty quantification.